1 Introduction

The well-known Cohen-Grossberg neural networks (CGNN), which is a large class of artificial neural networks including the Hopfield neural network, the cellular neural network, the shunting neural networks, and some ecological systems, were initially proposed and studied by Cohen and Grossberg [1] in 1983. Due to their promising potential diverse applications, such as pattern recognition, signal and image processing, associative memory, combinatorial optimization, and parallel computing, CGNN have attracted increasing interest for the past few decades. In particular, a CGNN optimization solver is desired to have a globally asymptotically stable equilibrium point that corresponds to the globally optimal solution of the objective function [2]. For that purpose, the global stability of CGNNs has been extensively studied and developed [3–11].

The instantaneous perturbations and abrupt changes at certain instant are exemplary of impulsive phenomena that can affect the evolutionary process of many complex systems. Impulsive phenomena widely exist in many fields such as epidemic prevention, population dynamics, economics [12–15], and so forth. Especially in real neural networks, impulsive perturbations are likely to emerge since the states of neural networks are changed abruptly at certain moments of time [16–18]. On the other hand, switched systems are systems with dynamic switching and can be used to model real systems whose dynamics are chosen from a family of possible choices according to a switching signal [19]. In [20], Li et al. studied the exponential stability of the switching systems. Recently, switching neural networks have been also proposed [21–23]. In [23], the authors introduced the Cohen-Grossberg neural networks into the switching systems and established the so-called switching Cohen-Grossberg neural networks.

In general, the impulsive systems can be classed into two types: impulsive systems with fixed-time impulses and impulsive systems with state-dependent impulses. State-dependent impulses are usually of state dependence, and thus, different solutions have different moments of impulses. Up to now, numerous monographs and articles have focused on the fixed-time impulsive systems [24–33], and only few publications have dealt with state-dependent impulses [34–37]. However, in real world problems, the impulses of many systems do not occur at fixed times [38], for example, biological and physiological systems including artificial neural networks, saving rates control systems, and some circuit control systems. In addition, we can also utilize the state-dependent impulses in some situations. In [39], the authors studied state impulsive control strategies for a two-language competitive model with bilingualism and interlinguistic similarity. It is evident that the state-dependent impulsive systems are much more difficult in modeling and control than the fixed-time impulsive systems.

Recently, Akhmet [40] proposed and developed a powerful analytical method, B-equivalence, which can reduce the state-dependent impulsive system to the fixed-time one that is expected to be the comparison system. However, the jump operator in the comparison system might be a very complex map and can hardly be used to analyze stability. Sayli and Yilmaz tried to investigate the stability of a state-dependent impulsive system using B-equivalence method in [34, 35]. Unfortunately, they could not estimate the relationship between the original jump operator and a new jump operator of the comparison system, just simply assumed that the new jump operator is linear with respect to system state. One should emphasize that there are few results in the literature where the reduction principle based on B-equivalence is effectively applied to stability analysis of state-dependent impulsive systems.

In the light of above discussion, it is of great importance to consider both state-dependent impulses and switching in the neural network models. In recent years, hybrid impulsive and switching systems have been extensively studied [41–43]. In [41], Li et al. investigated the global stability of impulsive switching HNN. However, they only consider the fixed-time impulse, and the impulses occur at switching instants, as well as in [42] and [43]. In [44], the authors also consider the fixed-time impulse, despite the fact that the impulses do not occur at the same time as the switching signals. In [45], Song et al. discussed the state-dependent impulses in nonlinear fractional-order systems. In [46] and [47], the authors investigated the impacts of state-dependent delay on the stability of nonlinear differential systems. In the present paper, we study the global stability of switching CGNNs with state-dependent impulses, where the switches occur at the fixed time, while the impulses do not occur at fixed times. To the best of our knowledge, this is the first switching CGNNs model that takes into account the state-dependent impulses. Firstly, we give the sufficient conditions that ensure every solution of system intersects each surface of discontinuity exactly once. Nextly, we prove the existence of solution to switching CGNN with state-dependent impulse. Then, we obtain the quantitative relation between new jump operators and system state and show that the global stability of the corresponding comparison system implies the same stability of the considered state-dependent impulsive switching CGNN. Finally, we establish a stability criterion for the considered CGNN using the proposed comparison system.

The rest of this paper is organized in this fashion. In Section 2, the problem is formulated and some preliminaries are given. We state the conditions of absence of beating and introduce B-equivalent method in Section 3. The existence of solution to switching CGNN with state-dependent impulse is shown in Section 4. We establish a criterion for the global stability of switching CGNNs with state-dependent impulses in Section 5. In Section 6, two numerical examples are provided to demonstrate the effectiveness of the theoretical results. Finally, Section 7 concludes the contributions of this work and points out some problems and challenges.

2 Problem formulation and preliminaries

Throughout this paper, \(R_{+}\) and \(R^{n}\) denote, respectively, the set of nonnegative real numbers and the n-dimensional Euclidean space, \(Z_{+}\) represents the set of positive integers, and we denote by \(\Gamma_{i}=\{(t,x(t))\in R_{+}\times G: t=\theta_{i}+\tau_{i}(x(t)),t\in R_{+},i\in Z_{+},x\in G,G\subset R^{n} \}\) the ith surface of discontinuity. We denote by I the identity matrix, by \(P^{T}\) the transpose of matrix P, \(\operatorname{diag}\{\cdots\}\) the block-diagonal matrix. For \(x \in R^{n}\), \(\Vert x \Vert \) denotes the Euclidean norm of x. For matrix \(A \in R^{n\times n}\), \(\Vert A \Vert = \sqrt{\max\{|\lambda(A^{T} A)|\}}\), where \(\lambda(\cdot)\) represents the eigenvalue value.

In the present paper, we consider the following switching Cohen-Grossberg neural networks with state-dependent impulses:

$$ \textstyle\begin{cases} \dot{x}(t)= -A_{l_{i}}(x(t))[B_{l_{i}}(x(t))-C_{l_{i}}f_{l_{i}}(x(t))], \quad t\in(\theta_{i}, \theta_{i+1}],\mbox{ and } t \neq\theta_{i}+\tau _{i}(x(t)), \\ \Delta x(t) =J_{i}(x(t)), \quad t = \theta_{i}+\tau_{i}(x(t)), \end{cases} $$
(1)

with the switching Cohen-Grossberg neural networks as their continuous subsystem:

$$ \dot{x}(t)=-A_{l_{i}} \bigl(x(t) \bigr) \bigl[B_{l_{i}} \bigl(x(t) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x(t) \bigr) \bigr],\quad t \in(\theta_{i}, \theta_{i+1}], \mbox{ and } t \neq \theta_{i}+\tau_{i} \bigl(x(t) \bigr), $$
(2)

and the state jumps as their discrete subsystem:

$$ \Delta x(t)=J_{i} \bigl(x(t) \bigr), \quad t = \theta_{i}+\tau_{i} \bigl(x(t) \bigr), $$
(3)

where x is the state variable, \(x=(x_{1},\ldots,x_{n})^{T}\in G,G\subset R^{n}\), \(l_{i}\in\{1,2,\ldots,m\}\) is a discrete state parameter, where m is a positive integer. The time sequence \(\{\theta_{i}\}\) satisfies \(\theta_{0}=0<\theta_{1}<\theta_{2}<\cdots<\theta_{i}<\theta_{i+1}<\cdots\) , and \(\theta_{j}\rightarrow\infty\) as \(j\rightarrow\infty\). For \(k\in\{ 1,2,\ldots,m\}, A_{k}(x)=\operatorname {diag}(a_{1}^{(k)}(x_{1}),a_{2}^{(k)}(x_{2}),\ldots,a_{n}^{(k)}(x_{n}))\), \(B_{k}(x)=(b_{1}^{(k)}(x_{1}),b_{2}^{(k)}(x_{2}),\ldots,b_{n}^{(k)}(x_{n}))^{T}\), \(B_{k}(0)=0\), \(C_{k}=(c_{uv}^{(k)})\in R^{n\times n}\) and \(f_{k}(x)=(f_{1}^{(k)}(x_{1}),\ldots,f_{n}^{(k)}(x_{n}))^{T} \in R^{n}\) being activation functions satisfying \(f_{k}(0)=0\). \(\Delta x|_{t = \xi_{i}}=x(\xi_{i}+)-x(\xi_{i})\) with \(x(\xi_{i}+)=\lim_{t\rightarrow\xi_{i}+0}x(t)\) denotes the state jump at moment \(\xi_{i}\) satisfying \(\xi_{i}= \theta_{i}+\tau_{i}(x(\xi_{i}))\). Without loss of generality, we suppose that \(x(\xi_{i}-)=\lim_{t\rightarrow\xi_{i}-0}x(t)=x(\xi_{i})\), i.e., the solution \(x(t)\) is left continuous at the impulse point.

\(\theta_{0}\) is the initial time, especially, we have

$$ \textstyle\begin{cases} \dot{x}(t)=-A_{l_{0}}(x(t))[B_{l_{0}}(x(t))-C_{l_{0}}f_{l_{0}}(x(t))], \quad t\in[\theta_{0}, \theta_{1}], \\ x(\theta_{0})=x_{0}. \end{cases} $$

Next, we introduce the following assumptions.

Assumption A

Let \(h=l_{i}\), \(A_{h}(x(t))\), \(B_{h}(x(t))\), and activation functions \(f_{h}(x(t))\) are globally Lipschitzian, i.e., there exist positive constants \(L_{ah}\), \(L_{bh}\), \(L_{fh}\) such that

  1. (i)

    \(\Vert A_{h}(x(t))-A_{h}(y(t)) \Vert \leq L_{ah} \Vert x(t)-y(t) \Vert \) for any \(x(t),y(t)\in R^{n}\);

  2. (ii)

    \(\Vert B_{h}(x(t))-B_{h}(y(t)) \Vert \leq L_{bh} \Vert x(t)-y(t) \Vert \) for any \(x(t),y(t)\in R^{n}\);

  3. (iii)

    \(\Vert f_{h}(x(t))-f_{h}(y(t)) \Vert \leq L_{fh} \Vert x(t)-y(t) \Vert \) for any \(x(t),y(t)\in R^{n}\).

And \(A_{h}(x(t))\) are bounded, that is, \(\Vert A_{h}(x(t)) \Vert \leq \bar{a}_{h}\) for any \(x(t)\in R^{n}\).

Assumption B

For each \(i\in Z_{+}\), \(x\in G\), \(J_{i}(x):G\rightarrow G\) is continuous, satisfying that \(J_{i}(0)=0\), \(\tau_{i}(0)=0\), and there exists a positive constant \(L_{J}\) such that \(\Vert x+J_{i}(x) \Vert \leq L_{J} \Vert x \Vert \).

Remark 1

Let \(x(t)\) be a solution of system (1) at the impulsive point \(\xi_{k}\), \(x(\xi_{k}+)=x(\xi_{k})+J_{k}(x(\xi_{k}))\). We get \(\Vert x(\xi_{k}+) \Vert \leq L_{J} \Vert x(\xi_{k}) \Vert \) by Assumption B. Generally, when \(L_{J}<1\), the impulse at \(\xi _{k}\) is of stabilizing effect on system stability, it is referred to as stabilizing impulse. Otherwise, if \(\Vert x(\xi_{k}+) \Vert \geq L_{J} \Vert x(\xi_{k}) \Vert \) and \(L_{J}>1\), the impulse at \(\xi_{k}\) is of destabilizing effect on system stability, it is usually referred to as destabilizing impulse.

Remark 2

From Assumption B and the previous discussions, one can easily see that the origin of system (1) is an equilibrium point. The uniqueness of this equilibrium point can be concluded from the global asymptotic or exponential stability constructed in Section 5.

Finally, we present several definitions.

Definition 1

[41]

We say that a piecewise continuous function \(x(t)=x(t;\theta_{0},x_{0})\) is a solution of system (1) if

  1. (i)

    for \(t\in[\theta_{0}, \theta_{1}]\), \(x(t)\) satisfies the following system:

    $$ \textstyle\begin{cases} \dot{x}(t)=-A_{l_{0}}(x(t))[B_{l_{0}}(x(t))-C_{l_{0}}f_{l_{0}}(x(t))], \quad t\in[\theta_{0}, \theta_{1}], \\ x(\theta_{0})=x_{0}, \end{cases} $$
  2. (ii)

    assume that the solution has already been determined in the interval \([\theta_{0}, \theta_{i}]\), it is \(x(t)\), then for \((\theta_{i}, \theta_{i+1}]\), \(x(t)\) satisfies the following system:

    $$ \textstyle\begin{cases} \dot{x}(t)= -A_{l_{i}}(x(t))[B_{l_{i}}(x(t))-C_{l_{i}}f_{l_{i}}(x(t))], \\ \quad t\in(\theta_{i}, \theta_{i+1}],\mbox{ and } t \neq\theta_{i}+\tau _{i}(x(t)), \\ \Delta x(t) =J_{i}(x(t)), \quad t = \theta_{i}+\tau_{i}(x(t)), \end{cases} $$
  3. (iii)

    \(x(t)\) is continuous except for \(t=\xi_{i}\), and it is left continuous at \(t=\xi_{i}\), and the right limit \(x(\xi_{i}+)\) exists for \(i\in Z_{+}\).

Definition 2

[32]

Let \(V:R^{n}\rightarrow R_{+}\), then V is said to belong to class Ω if

  1. (a)

    V is continuous in \((\tau_{i-1},\tau_{i}]\times R^{n}\) and for each \(x\in R^{n},i=1,2,3,\ldots \) , \(\lim_{(t,y)\rightarrow(\tau _{i}^{+},x)}V(t,y)=V(\tau_{i}^{+},x)\) exists.

  2. (b)

    V is locally Lipschitzian in x.

From this definition, we can see that V associated with system (1) is the analog of Lyapunov function for stability analysis of ODE. Since these Lyapunov-like functions are generally discontinuous, a generalized derivative should be defined, which is known as the right and upper Dini’s derivative.

Definition 3

[32]

For \((t,x)\in(\tau_{i-1},\tau_{i}]\times R^{n}\), the right and upper Dini’s derivative of \(V\in\Omega\) with respect to time variable is defined as

$$D^{+}V(t,x)\equiv\lim_{\mu\rightarrow0^{+}}\sup(1/\mu)\bigl\{ V\bigl[t+\mu,x+\mu f(t,x)\bigr]-V(t,x)\bigr\} . $$

Definition 4

[41]

A dynamical system of the form \(\dot{x}(t)=f(t,x(t))\) is said to be a \(\pi_{1}\)-class system if there exist a positive-definite Lyapunov function \(V(t)=x^{T}Px\) and a positive constant α such that the Dini’s derivative of V along the solution of the dynamical system satisfies \(D^{+}V(t)\leq-\alpha V(t)\).

Definition 5

[20]

The origin of system (1) is said to be globally exponentially stable if there exist some constants \(\gamma>0\) and \(M>0\) such that \(\Vert x(t,t_{0},x(t_{0})) \Vert \leq M \exp(-\gamma(t-t_{0}))\) for any \(t\geq t_{0}\).

3 The conditions for absence of beating and B-equivalent method

In this section, we will seek the conditions which ensure that each solution of system (1) intersects each surface of discontinuity exactly once. Then we will formulate a fixed-time impulsive switching analog as the comparison system of (1) by using B-equivalent method. For this purpose, the following assumptions are stated.

  1. (C1)

    For each \(i\in Z_{+}, \tau_{i}(x)\) is continuous and there exists a positive constant ν such that \(0< \tau_{i}(x)\leq\nu\).

  2. (C2)

    There exist two positive numbers \(\underline{\theta}\) and θ̄ such that \(\underline{\theta}<\theta_{i+1}-\theta_{i}<\bar {\theta}\), where \(\underline{\theta}>\nu\), for all \(i\in Z_{+}\).

  3. (C3)

    Fix any \(j\in Z_{+}\), and let \(x(t): (\theta_{j}, \theta_{j}+\nu ]\rightarrow G\) be a solution of (1) in time interval \((\theta _{j}, \theta_{j}+\nu]\). One of the following two conditions is satisfied:

    $$\begin{aligned} \mathrm{(i)}&\quad \textstyle\begin{cases} \frac{d\tau_{j}(x)}{dx} \{ -A_{l_{j}}(x(t))[B_{l_{j}}(x(t))-C_{l_{j}}f_{l_{j}}(x(t))]\}>1, & x\in G, \\ \tau_{j}[x(\xi_{j})+J_{j}(x(\xi_{j}))]\geq\tau_{j}(x(\xi_{j})), & t=\xi_{j}, \end{cases}\displaystyle \\ \mathrm{(ii)}&\quad \textstyle\begin{cases} \frac{d\tau_{j}(x)}{dx} \{ -A_{l_{j}}(x(t))[B_{l_{j}}(x(t))-C_{l_{j}}f_{l_{j}}(x(t))]\}< 1, & x\in G, \\ \tau_{j}[x(\xi_{j})+J_{j}(x(\xi_{j}))]\leq\tau_{j}(x(\xi_{j})), & t=\xi_{j}, \end{cases}\displaystyle \end{aligned}$$

    where \(t=\xi_{j}\) is the discontinuity point of (1), i.e., \(\xi_{j}=\theta_{j}+\tau_{j}(x(\xi_{j}))\).

Lemma 1

Assume that conditions (C1) and (C2) are satisfied, and \(x(t):R_{+}\rightarrow G\) is a solution of (1). Then \(x(t)\) intersects every surface \(\Gamma_{i}\), \(i\in Z_{+}\).

The proof of Lemma 1 is quite similar to that of Lemma 5.3.2 in [40], so it is omitted here.

Lemma 2

Let (C3) hold. Then every solution of system (1) intersects the surface \(\Gamma_{i}\) at most once.

Proof

Assume the result is not true, then there is a solution \(x(t)\) which intersects the surface \(\Gamma_{j}\) at \((s,x(s))\) and \((s_{1},x(s_{1}))\), without loss of generality, \(s< s_{1}\), and there exists no discontinuity point of \(x(t)\) between s and \(s_{1}\). Then \(s=\theta_{j}+\tau_{j}(x(s))\) and \(s_{1}=\theta_{j}+\tau_{j}(x(s_{1}))\). For the case (i) of (C3), we get

$$\begin{aligned} s_{1}-s &=\tau_{j} \bigl(x(s_{1}) \bigr)- \tau_{j} \bigl(x(s) \bigr) \\ &\geq\tau_{j} \bigl(x(s_{1}) \bigr)- \tau_{j} \bigl[x(s)+J_{j} \bigl(x(s) \bigr) \bigr] \\ &=\tau_{j} \bigl(x(s_{1}) \bigr)- \tau_{j} \bigl(x(s+) \bigr) \\ &= \biggl\{ \frac{d\tau_{j}(x)}{dx} \bigl\{ -A_{l_{j}} \bigl(x(t) \bigr) \bigl[B_{l_{j}} \bigl(x(t) \bigr)-C_{l_{j}}f_{l_{j}} \bigl(x(t) \bigr) \bigr] \bigr\} \biggr\} _{t=\kappa\in(s,s_{1}]}(s_{1}-s) \\ &>(s_{1}-s). \end{aligned}$$

This is a contradiction. Repeating a similar process in the case (ii) of \((C3)\), we can get \(s_{1}-s< s_{1}-s\). It is also a contradiction. So the proof is completed. □

Via the above lemmas, one can get the following result.

Theorem 1

Suppose that (C1), (C2), and (C3) are fulfilled. Then every solution \(x(t):R_{+}\rightarrow G\) of system (1) intersects each surface \(\Gamma_{i}\), \(i\in\underline{Z^{+}}\), exactly once.

Now, we formulate the B-equivalent system for system (1). Let \(x^{0}(t)=x(t,\theta_{i},x^{0}(\theta_{i}))\) be a solution of (1) in \([\theta_{i},\theta_{i+1}]\). Denote by \(\xi_{i}\) the meeting moment of the solution with the surface \(\Gamma_{i}\) of discontinuity so that \(\xi_{i}= \theta_{i}+\tau_{i}(x^{0}(\xi_{i}))\). Let \(x^{1}(t)\) be a solution of (2) in \([\theta_{i},\theta_{i+1}]\) such that \(x^{1}(\xi_{i})=x^{0}(\xi_{i}^{+})=x^{0}(\xi_{i})+J_{i}(x^{0}(\xi_{i}))\).

Define the following map (as shown in Figure 1):

$$\begin{aligned} W_{i} \bigl(x^{0}(\theta_{i}) \bigr) ={}&x^{1}(\theta_{i})-x^{0}( \theta_{i}) \\ ={}&x^{1}(\xi_{i})+ \int^{\theta_{i}}_{\xi_{i}} \bigl\{ -A_{l_{i}} \bigl(x^{1}(s) \bigr) \bigl[B_{l_{i}} \bigl(x^{1}(s) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x^{1}(s) \bigr) \bigr] \bigr\} \,ds -x^{0}(\theta_{i}) \\ ={}&x^{0}(\xi_{i})+J_{i} \bigl(x^{0}( \xi_{i}) \bigr)+ \int^{\theta_{i}}_{\xi_{i}} \bigl\{ -A_{l_{i}} \bigl(x^{1}(s) \bigr) \bigl[B_{l_{i}} \bigl(x^{1}(s) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x^{1}(s) \bigr) \bigr] \bigr\} \,ds -x^{0}(\theta_{i}) \\ ={}& \int^{\xi_{i}}_{\theta_{i}} \bigl\{ -A_{l_{i}} \bigl(x^{0}(s) \bigr) \bigl[B_{l_{i}} \bigl(x^{0}(s) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x^{0}(s) \bigr) \bigr] \bigr\} \,ds \\ &{} +J_{i} \biggl(x^{0}(\theta_{i})+ \int^{\xi_{i}}_{\theta_{i}} \bigl\{ -A_{l_{i}} \bigl(x^{0}(s) \bigr) \bigl[B_{l_{i}} \bigl(x^{0}(s) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x^{0}(s) \bigr) \bigr] \bigr\} \,ds \biggr) \\ &{} + \int^{\theta_{i}}_{\xi_{i}} \bigl\{ -A_{l_{i}} \bigl(x^{1}(s) \bigr) \bigl[B_{l_{i}} \bigl(x^{1}(s) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x^{1}(s) \bigr) \bigr] \bigr\} \,ds . \end{aligned}$$
(4)
Figure 1
figure 1

Construction principle of the map \(\pmb{W_{i}(x^{0}(\theta_{i}))}\) .

Full size image

Remark 3

\((\theta_{i},x^{0}(\theta_{i}))\), which is the common point of \([\theta _{i-1},\theta_{i}]\) and \([\theta_{i},\theta_{i+1}]\), meets the solution of

$$ \textstyle\begin{cases} \dot{x}(t)=-A_{l_{k}}(x(t))[B_{l_{k}}(x(t))-C_{l_{k}}f_{l_{k}}(x(t))], & t \neq \theta_{k}+\tau_{k}(x(t)), \\ \Delta x(t)=J_{k}(x(t)), & t= \theta_{k}+\tau_{k}(x(t)), \end{cases} $$

for both \(k=i-1\) and \(k=i\).

Obviously, \(x^{0}(t)=x(t,\theta_{i},x^{0}(\theta_{i}))\) can be extended as the solution of (1) in \(R_{+}\) from Definition 1, Remark 3, and Figure 1. Furthermore, we consider the following fixed-time impulsive switching system in \(R_{+}\):

$$ \textstyle\begin{cases} \dot{x}(t)=-A_{l_{i}}(x(t))[B_{l_{i}}(x(t))-C_{l_{i}}f_{l_{i}}(x(t))], & t\in (\theta_{i}, \theta_{i+1}], \\ \Delta x=W_{i}(x^{0}(\theta_{i})), & t = \theta_{i}. \end{cases} $$
(5)

By the definition of \(W_{i}(x^{0}(\theta_{i}))\) together with Figure 1, \(x^{1}(t)=x(t,\xi_{i},x^{0}(\xi_{i}^{+}))\) can be extended as the solution of system (5) in \(R_{+}\). Clearly, \(x^{1}(t)\) is continuous on \((\theta_{i}, \theta_{i+1}]\), and \(W_{i}(x^{0}(\theta_{i}))\) is limited. On this basis, we make the following assumption.

Assumption C

For any solution \(x^{1}(t)\) to system (5), \(x^{1}(t)\) is bounded, i.e., there exists a positive constant H such that \(\Vert (x^{1}(t)) \Vert \leq H\) for any \(t\in R_{+}\).

In Section 4, we will learn that Assumption C holds if Assumptions A, B, and (C1)-(C3) are valid.

Moreover, we have the following observations without proof:

Observation 1

On time interval \((\xi_{i},\theta_{i+1}]\), \(x^{1}(t)= x^{0}(t)\), and \(x^{1}(\theta_{i}+)=x^{0}(\theta_{i})+W_{i}(x^{0}(\theta_{i}))\), \(x^{1}(\xi_{i})=x^{0}(\xi_{i}+)=x^{0}(\xi_{i})+J_{i}(x^{0}(\xi_{i}))\).

Observation 2

On time interval \((\theta_{i},\xi_{i}]\), let Assumption C hold, we have

$$\begin{aligned} &x^{1}(t)-x^{0}(t) \\ &\quad=x^{0}(\theta_{i})+W_{i} \bigl(x^{0}( \theta_{i}) \bigr)+ \int^{t}_{\theta_{i}} \bigl\{ -A_{l_{i}} \bigl(x^{1}(s) \bigr) \bigl[B_{l_{i}} \bigl(x^{1}(s) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x^{1}(s) \bigr) \bigr] \bigr\} \,ds \\ &\qquad{}-x^{0}(\theta_{i})- \int^{t}_{\theta_{i}} \bigl\{ -A_{l_{i}} \bigl(x^{0}(s) \bigr) \bigl[B_{l_{i}} \bigl(x^{0}(s) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x^{0}(s) \bigr) \bigr] \bigr\} \,ds \\ &\quad=W_{i} \bigl(x^{0}(\theta_{i}) \bigr)+ \int^{t}_{\theta_{i}} \bigl\{ -A_{l_{i}} \bigl(x^{1}(s) \bigr) \bigl[B_{l_{i}} \bigl(x^{1}(s) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x^{1}(s) \bigr) \bigr] \\ &\qquad{}+A_{l_{i}} \bigl(x^{0}(s) \bigr) \bigl[B_{l_{i}} \bigl(x^{0}(s) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x^{0}(s) \bigr) \bigr] \bigr\} \,ds \\ &\quad=W_{i} \bigl(x^{0}(\theta_{i}) \bigr)+ \int^{t}_{\theta_{i}} \bigl\{ - \bigl[A_{l_{i}} \bigl(x^{1}(s) \bigr)-A_{l_{i}} \bigl(x^{0}(s) \bigr) \bigr] \bigl[B_{l_{i}} \bigl(x^{1}(s) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x^{1}(s) \bigr) \bigr] \\ &\qquad{}+A_{l_{i}} \bigl(x^{0}(s) \bigr) \bigl[- \bigl(B_{l_{i}} \bigl(x^{1}(s) \bigr)-B_{l_{i}} \bigl(x^{0}(s) \bigr) \bigr)+C_{l_{i}} \bigl(f_{l_{i}} \bigl(x^{1}(s) \bigr)-f_{l_{i}} \bigl(x^{0}(s) \bigr) \bigr) \bigr] \bigr\} \,ds . \end{aligned}$$

From Assumption A, let \(h=l_{i}\), then \(h\in\{1,2,\ldots,m\}\), we get

$$\begin{aligned} & \bigl\Vert x^{1}(t)-x^{0}(t) \bigr\Vert \\ &\quad\leq \bigl\Vert W_{i} \bigl(x^{0}( \theta_{i}) \bigr) \bigr\Vert + \int^{t}_{\theta_{i}} \bigl\{ L_{ah} \bigl\Vert x^{1}(s)-x^{0}(s) \bigr\Vert \bigl[L_{bh} \bigl\Vert x^{1}(s) \bigr\Vert + \Vert C_{h} \Vert L_{fh} \bigl\Vert x^{1}(s) \bigr\Vert \bigr] \\ &\qquad{}+\bar{a}_{h} \bigl[L_{bh} \bigl\Vert x^{1}(s)-x^{0}(s) \bigr\Vert + \Vert C_{h} \Vert L_{fh} \bigl\Vert x^{1}(s)-x^{0}(s) \bigr\Vert \bigr] \bigr\} \,ds \\ &\quad\leq \bigl\Vert W_{i} \bigl(x^{0}( \theta_{i}) \bigr) \bigr\Vert + \bigl(L_{bh}+ \Vert C_{h} \Vert L_{fh} \bigr) (L_{ah}H+\bar{a}_{h}) \int^{t}_{\theta_{i}} \bigl\Vert x^{1}(s)-x^{0}(s) \bigr\Vert \,ds . \end{aligned}$$

Using the Gronwall-Bellman lemma [40], we find that

$$ \bigl\Vert x^{1}(t)-x^{0}(t) \bigr\Vert \leq \bigl\Vert W_{i} \bigl(x^{0}(\theta_{i}) \bigr) \bigr\Vert \exp \bigl[\nu \bigl(L_{bh}+ \Vert C_{h} \Vert L_{fh} \bigr) (L_{ah}H+\bar{a}_{h}) \bigr]. $$
(6)

Remark 4

System (5), which is a fixed-time impulsive switching system, is called the B-equivalent system of (1) from Observation 1 and [40]. We refer the reader to the book [40] for a more detailed discussion. In Section 5, we will show that its stability implies the same stability of state-dependent impulsive switching system (1).

4 The existence of solution for switching CGNN with state-dependent impulse

In this section, we will show the existence of solution of impulsive and switching systems (1) and (5).

Theorem 2

Let Assumptions  A, B, and (C1)-(C3) hold, then a solution of system (1) exists on \([\theta_{i},\theta_{i+1}]\).

Proof

To prove this theorem, we firstly show that the following claim holds:

Claim. Let \(F_{l_{i}}(t,x)=-A_{l_{i}}(x(t))[B_{l_{i}}(x(t))-C_{l_{i}}f_{l_{i}}(x(t))]\), then \(F_{l_{i}}(t,x)\) satisfies a local Lipschitz condition on \([\theta_{i},\xi_{i}]\times G\) and \((\xi_{i},\theta_{i+1}]\times G\).

Let us prove this claim. For \(P_{0}(t_{0},x_{*})\in[\theta_{i},\xi _{i}]\times G\), ∃

$$G_{0}=\bigl\{ (t,x)\mid \Vert t-t_{0} \Vert \leq a, \Vert x-x_{*} \Vert \leq b\bigr\} \subset[\theta_{i}, \xi_{i}]\times G. $$

When \((t,x_{1}),(t,x_{2})\in G_{0}\), we have

$$\begin{aligned} F_{l_{i}}(t,x_{1})-F_{l_{i}}(t,x_{2}) ={}& {-}A_{l_{i}} \bigl(x_{1}(t) \bigr) \bigl[B_{l_{i}} \bigl(x_{1}(t) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x_{1}(t) \bigr) \bigr] \\ & {}+A_{l_{i}} \bigl(x_{2}(t) \bigr) \bigl[B_{l_{i}} \bigl(x_{2}(t) \bigr)-C_{l_{i}}f_{l_{i}} \bigl(x_{2}(t) \bigr) \bigr] \\ ={}& {-} \bigl[A_{l_{i}}(x_{1})-A_{l_{i}}(x_{2}) \bigr] \bigl[B_{l_{i}}(x_{1})-C_{l_{i}}f_{l_{i}}(x_{1}) \bigr] \\ &{}+A_{l_{i}}(x_{2}) \bigl[- \bigl(B_{l_{i}}(x_{1})-B_{l_{i}}(x_{2}) \bigr)+C_{l_{i}} \bigl(f_{l_{i}}(x_{1})-f_{l_{i}}(x_{2}) \bigr) \bigr]. \end{aligned}$$

Clearly, \(\Vert x_{1} \Vert \leq \Vert x_{*} \Vert +b\), for simplicity, let \(\Vert x_{*} \Vert +b=\bar{b}\), \(h=l_{i}\). By Assumption A, we get

$$\begin{aligned} & \bigl\Vert F_{h}(t,x_{1})-F_{h}(t,x_{2}) \bigr\Vert \\ &\quad \leq L_{ah} \Vert x_{1}-x_{2} \Vert \bigl(L_{bh} \Vert x_{1} \Vert + \Vert C_{h} \Vert L_{fh} \Vert x_{1} \Vert \bigr) \\ &\qquad {}+\bar{a}_{h} \bigl(L_{bh} \Vert x_{1}-x_{2} \Vert + \Vert C_{h} \Vert L_{fh} \Vert x_{1}-x_{2} \Vert \bigr) \\ &\quad \leq \bigl(L_{bh}+ \Vert C_{h} \Vert L_{fh} \bigr) (L_{ah}\bar{b}+\bar{a}_{h}) \Vert x_{1}-x_{2} \Vert . \end{aligned}$$

Let \(L_{D}=(L_{bh}+ \Vert C_{h} \Vert L_{fh})(L_{ah}\bar{b}+\bar{a}_{h})\), then \(F_{l_{i}}(t,x)\) satisfies a local Lipschitz condition on \([\theta _{i},\xi_{i}]\times G\). Similarly, on \((\xi_{i},\theta_{i+1}]\times G\), \(F_{l_{i}}(t,x)\) also satisfies a local Lipschitz condition. Therefore, the claim holds.

It is evident that the function \(F_{l_{i}}(t,x)\) is continuous on \([\theta_{i},\xi_{i}]\times G\) and \((\xi_{i},\theta_{i+1}]\times G\), and that \(x(\xi_{i})+J_{i}(x(\xi_{i}))\in G\). So a solution of ordinary differential equation (2) exists, denoting by \(x^{0}(t)=x(t,\theta_{i},x^{0}(\theta _{i}))\) for \(t\in[\theta_{i},\xi_{i}]\). Since there is no surface of discontinuity on \([\theta_{i},\xi_{i}]\), \(x^{0}(t)=x(t,\theta_{i},x^{0}(\theta_{i}))\) is also the solution of system (1) on \([\theta_{i},\xi_{i}]\times G\). Moreover, when \(t=\xi_{i}\), we have \(x(\xi_{i}+)=x(\xi_{i})+J_{i}(x(\xi_{i}))\in G\). Taking into account that \((\xi_{i},x(\xi_{i}+))\) is an interior point of \([\theta_{i},\theta_{i+1}]\times G\), a solution of ordinary differential equation (2) with initial condition \(x(\xi_{i}+)=x(\xi _{i})+J_{i}(x(\xi_{i}))\) exists. We can proceed the solution \(x^{0}(t)=x(t,\xi_{i},x^{0}(\xi_{i}+))\) on the interval \([\xi_{i},\theta _{i+1}]\). Because of (C3), the last solution cannot meet the surface \(\Gamma_{i}\) again, then \([\theta_{i},\theta_{i+1}]\) is the maximal right interval of existence of \(x(t)\) here. Similarly, \(x^{0}(t)=x(t,\xi_{i},x^{0}(\xi_{i}+))\) is also the solution of system (1) on \((\xi_{i},\theta_{i+1}]\times G\). That is, the solution \(x^{0}(t)\) of system (1) exists on \([\theta_{i},\theta_{i+1}]\),

$$ x^{0}(t)= \textstyle\begin{cases} x(t,\theta_{i},x^{0}(\theta_{i})), & t\in[\theta_{i},\xi_{i}], \\ x(t,\xi_{i},x^{0}(\xi_{i}+)), & t\in(\xi_{i},\theta_{i+1}]. \end{cases} $$

The proof is completed. □

Based on the above discussions, the following theorem is immediate.

Theorem 3

Let Assumptions  A, B, and (C1)-(C3) be valid, then a solution of system (5) exists on \((\theta_{i},\theta_{i+1}]\).

Combining Definition 1 and Remark 3, one can get the existence of solution of impulsive and switching systems (1) and (5).

Remark 5

By the previous discussions, we can see that the solution \(x^{1}(t)\) of system (5) is piecewise continuous. Since \(\lim_{t\rightarrow\theta_{i}+}x^{1}(t)=x^{1}(\theta_{i}+)=x^{0}(\theta _{i})+W_{i}(x^{0}(\theta_{i}))\), then \(x^{1}(t)\) is bounded on \((\theta_{i},\theta _{i+1}]\). Furthermore, \(x^{1}(t)\) is bounded for any \(t\in R_{+}\). That is, Assumption C is valid if the conditions of Theorem 3 are satisfied.

5 A criterion for the stability of switching CGNN with state-dependent impulse

In this section, we will investigate the stability of impulsive and switching systems (5) and (1) and establish the stability criteria for systems (1).

Theorem 4

Let Assumptions  A, B, and (C1)-(C3) hold. For simplicity, let \(h=l_{i}\). Suppose that there exists \(V_{h}\in\Omega\) such that

$$\begin{aligned} & \mu_{h} \bigl\Vert x(t) \bigr\Vert ^{p} \leq V_{h} \bigl(x(t) \bigr)\leq\lambda_{h} \bigl\Vert x(t) \bigr\Vert ^{p}, \end{aligned}$$
(7)
$$\begin{aligned} & D^{+}V_{h} \bigl(x(t) \bigr)\leq\alpha_{h} V_{h} \bigl(x(t) \bigr),\quad t\in(\theta_{i},\xi_{i}], \end{aligned}$$
(8)

and

$$ \frac{p}{\alpha_{h}} \biggl[\exp \biggl(\frac{\alpha_{h}\nu }{p} \biggr)-1 \biggr]\bar{a}_{h} \bigl(L_{bh}+ \Vert C_{h} \Vert L_{fh} \bigr)\sqrt[p]{\mu_{h}^{-1} \lambda_{h}}< 1, $$
(9)

where \(\mu_{h}>0\), \(\lambda_{h}>0\), \(p>0\), \(\alpha_{h}\in R\), and \(x(t)\) is a solution of (2) in \((\theta_{i},\xi_{i}]\). Then

$$\begin{aligned} &\mathrm{(a)} \quad \bigl\Vert x^{0}( \theta_{i})+W_{i} \bigl(x^{0}(\theta_{i}) \bigr) \bigr\Vert \leq \beta_{h} \bigl\Vert x^{0}( \theta_{i}) \bigr\Vert , \\ &\mathrm{(b)} \quad \bigl\Vert x^{1}(t)-x^{0}(t) \bigr\Vert \leq \delta_{h} \bigl\Vert x^{0}(\theta_{i}) \bigr\Vert \quad\textit{for any } t\in(\theta_{i},\xi_{i}], \end{aligned} $$

where

$$\beta_{h}= \biggl\{ 1-\frac{p}{\alpha_{h}}\biggl[\exp\biggl( \frac{\alpha_{h}\nu}{p}\biggr)-1\biggr]\bar{a}_{h}\bigl(L_{bh}+ \Vert C_{h} \Vert L_{fh}\bigr)\sqrt[p]{ \mu_{h}^{-1}\lambda_{h}} \biggr\} ^{-1}L_{J}\sqrt[p]{\mu_{h}^{-1} \lambda_{h}}\exp\biggl(\frac{\alpha_{h}\nu}{p}\biggr), $$

\(\delta_{h}=(1+\beta_{h})\exp[\nu(L_{bh}+ \Vert C_{h} \Vert L_{fh})(L_{ah}H+\bar{a}_{h})]\), and \(x^{0}(t)=x(t,\theta_{i},x^{0}(\theta_{i}))\) is a solution of (1), which intersects the surface \(\Gamma_{i}\) of discontinuity at \(\xi_{i}\), i.e., \(\xi_{i}=\theta_{i}+\tau_{i}(x^{0}(\xi_{i}))\). And \(x^{1}(t)\) is a solution of (5) such that \(x^{1}(\theta_{i}+)=x^{0}(\theta_{i})+W_{i}(x^{0}(\theta_{i}))\) and \(x^{1}(\xi _{i})=x^{0}(\xi_{i}+)=x^{0}(\xi_{i})+J_{i}(x^{0}(\xi_{i}))\), here \(W_{i}(x^{0}(\theta_{i}))\) is defined by (4).

Proof

The following inequalities follow conditions (7) and (8), respectively:

$$\sqrt[p]{\lambda_{h}^{-1}V_{h}\bigl(x(t)\bigr)} \leq\bigl\Vert x(t) \bigr\Vert \leq\sqrt [p]{\mu_{h}^{-1}V_{h} \bigl(x(t)\bigr)} $$

and

$$V_{h}\bigl(x(t)\bigr)\leq V_{h}\bigl(x( \theta_{i}+)\bigr)\exp\bigl(\alpha_{h}(t- \theta_{i})\bigr). $$

Using the last two inequalities, we get

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert &\leq \bigl[ \mu_{h}^{-1}V_{h} \bigl(x(\theta_{i}+) \bigr)\exp \bigl(\alpha_{h}(t- \theta_{i}) \bigr) \bigr]^{1/p} \\ &\leq\sqrt[p]{\mu_{h}^{-1}\lambda_{h}}\exp \bigl( \alpha_{h}(t-\theta_{i})/p \bigr) \bigl\Vert x( \theta_{i}+) \bigr\Vert . \end{aligned} $$

Therefore

$$\bigl\Vert x^{0}(t) \bigr\Vert \leq\sqrt[p]{\mu_{h}^{-1} \lambda_{h}}\exp\bigl(\alpha _{h}(t-\theta_{i})/p \bigr) \bigl\Vert x^{0}(\theta_{i}) \bigr\Vert , $$

and

$$\bigl\Vert x^{1}(t) \bigr\Vert \leq\sqrt[p]{\mu_{h}^{-1} \lambda_{h}}\exp\bigl(\alpha _{h}(t-\theta_{i})/p \bigr) \bigl\Vert x^{0}(\theta_{i})+W_{i} \bigl(x^{0}(\theta_{i})\bigr) \bigr\Vert . $$

Next, we show that claim (a) holds. From (4), we have

$$\begin{aligned} & \bigl\Vert x^{0}(\theta_{i})+W_{i} \bigl(x^{0}(\theta_{i}) \bigr) \bigr\Vert = \bigl\Vert x^{1}(\theta_{i}+) \bigr\Vert \\ &\quad = \biggl\Vert x^{1}(\xi_{i})- \int^{\xi_{i}}_{\theta_{i}} \bigl\{ -A_{h} \bigl(x^{1}(s) \bigr) \bigl[B_{h} \bigl(x^{1}(s) \bigr)-C_{h}f_{h} \bigl(x^{1}(s) \bigr) \bigr] \bigr\} \,ds \biggr\Vert \\ &\quad \leq \bigl\Vert x^{1}(\xi_{i}) \bigr\Vert + \int^{\xi_{i}}_{\theta_{i}} \bigl\Vert A_{h} \bigl(x^{1}(s) \bigr) \bigl[B_{h} \bigl(x^{1}(s) \bigr)-C_{h}f_{h} \bigl(x^{1}(s) \bigr) \bigr] \bigr\Vert \,ds \\ &\quad \leq \bigl\Vert x^{0}(\xi_{i})+J_{i} \bigl(x^{0}(\xi_{i}) \bigr) \bigr\Vert +\bar{a}_{h} \bigl(L_{bh}+ \Vert C_{h} \Vert L_{fh} \bigr) \int^{\xi_{i}}_{\theta_{i}} \bigl\Vert x^{1}(s) \bigr\Vert \,ds \\ &\quad \leq L_{J} \bigl\Vert x^{0}(\xi_{i}) \bigr\Vert \\ &\qquad {}+\bar{a}_{h} \bigl(L_{bh}+ \Vert C_{h} \Vert L_{fh} \bigr)\sqrt[p]{\mu_{h}^{-1} \lambda_{h}} \bigl\Vert x^{0}(\theta_{i})+W_{i} \bigl(x^{0}(\theta_{i}) \bigr) \bigr\Vert \int^{\xi_{i}}_{\theta_{i}}\exp \bigl(\alpha_{h}(s- \theta_{i})/p \bigr) \,ds \\ &\quad \leq L_{J}\sqrt[p]{\mu_{h}^{-1} \lambda_{h}}\exp \biggl(\frac{\alpha_{h}\nu}{p} \biggr) \bigl\Vert x^{0}(\theta_{i}) \bigr\Vert +\frac{p}{\alpha_{h}} \biggl(\exp \biggl(\frac{\alpha_{h}\nu}{p} \biggr)-1 \biggr) \\ &\qquad {}\times\bar{a}_{h} \bigl(L_{bh}+ \Vert C_{h} \Vert L_{fh} \bigr)\sqrt[p]{\mu_{h}^{-1} \lambda_{h}} \bigl\Vert x^{0}(\theta_{i})+W_{i} \bigl(x^{0}(\theta_{i}) \bigr) \bigr\Vert , \end{aligned}$$

which implies that

$$\begin{aligned} & \bigl\Vert x^{0}(\theta_{i})+W_{i} \bigl(x^{0}(\theta_{i}) \bigr) \bigr\Vert \\ &\quad \leq \biggl\{ 1-\frac{p}{\alpha_{h}} \biggl[\exp \biggl(\frac{\alpha_{h}\nu }{p} \biggr)-1 \biggr]\bar{a}_{h} \bigl(L_{bh}+ \Vert C_{h} \Vert L_{fh} \bigr)\sqrt[p]{\mu_{h}^{-1} \lambda_{h}} \biggr\} ^{-1}\\ &\qquad{}\times L_{J}\sqrt[p]{ \mu_{h}^{-1}\lambda_{h}}\exp \biggl( \frac{\alpha_{h}\nu}{p} \biggr) \bigl\Vert x^{0}(\theta_{i}) \bigr\Vert \\ &\quad =\beta_{h} \bigl\Vert x^{0}(\theta_{i}) \bigr\Vert . \end{aligned}$$

Finally, we prove claim (b). By (6), we get

$$\begin{aligned} \bigl\Vert x^{1}(t)-x^{0}(t) \bigr\Vert &\leq \bigl\Vert W_{i} \bigl(x^{0}( \theta_{i}) \bigr) \bigr\Vert \exp \bigl[\nu \bigl(L_{bh}+ \Vert C_{h} \Vert L_{fh} \bigr) (L_{ah}H+\bar{a}_{h}) \bigr] \\ &\leq (1+\beta_{h})\exp \bigl[\nu \bigl(L_{bh}+ \Vert C_{h} \Vert L_{fh} \bigr) (L_{ah}H+\bar{a}_{h}) \bigr] \bigl\Vert x^{0}(\theta_{i}) \bigr\Vert \\ &= \delta_{h} \bigl\Vert x^{0}(\theta_{i}) \bigr\Vert . \end{aligned}$$

This completes the proof of the theorem. □

Remark 6

Let the conditions of Theorem 4 hold, and \(\delta=\max\{\delta _{1},\delta_{2},\ldots,\delta_{m}\}\), then claim (b) of Theorem 4 can be rewritten as

$$ \bigl\Vert x^{1}(t)-x^{0}(t) \bigr\Vert \leq\delta \bigl\Vert x^{0}(\theta_{i}) \bigr\Vert ,\quad t \in(\theta_{i},\xi_{i}],\mbox{ for any } i\in Z_{+}. $$
(10)

Remark 7

From Theorem 4 and Observation 1, one can see that for any solution of (1), \(x^{0}(t)\), there must exist a solution of (5), \(x^{1}(t)\), such that \(\Vert x^{1}(t)-x^{0}(t) \Vert \leq \delta \Vert x^{0}(\theta_{i}) \Vert \) for \(t\in(\theta_{i},\xi_{i}]\); and \(x^{1}(t)=x^{0}(t)\) for \(t\in[\theta _{0},\theta_{1}]\cup(\xi_{i},\theta_{i+1}]\), and vice versa.

Theorem 5

Let all assumptions of Theorem 4 hold. Then

  1. (i)

    the global asymptotic stability of the trivial solution in system (5) implies the same stability of the trivial solution in system (1).

  2. (ii)

    the origin of system (5) is globally exponentially stable implies that the origin of system (1) is also globally exponentially stable.

Proof

(i) Since the trivial solution of system (5) is globally asymptotically stable, then \(\lim_{t\rightarrow\infty }x^{1}(t)=0\), and \(\lim_{i\rightarrow\infty}x^{1}(\theta_{i})=0\).

When \(t\in[\theta_{0},\theta_{1}]\) or \(t\in(\xi_{i},\theta_{i+1}]\), we have \(\Vert x^{0}(t) \Vert = \Vert x^{1}(t) \Vert \); and when \(t\in (\theta_{i},\xi_{i}]\), by (10), we get

$$\begin{aligned} \bigl\Vert x^{0}(t) \bigr\Vert &\leq \bigl\Vert x^{1}(t)-x^{0}(t) \bigr\Vert + \bigl\Vert x^{1}(t) \bigr\Vert \\ &\leq \delta \bigl\Vert x^{0}(\theta_{i}) \bigr\Vert + \bigl\Vert x^{1}(t) \bigr\Vert \\ &= \delta \bigl\Vert x^{1}(\theta_{i}) \bigr\Vert + \bigl\Vert x^{1}(t) \bigr\Vert . \end{aligned}$$

Moreover, \(\lim_{t\rightarrow\infty} \Vert x^{0}(t) \Vert \leq\delta \lim_{i\rightarrow\infty} \Vert x^{1}(\theta_{i}) \Vert +\lim_{t\rightarrow\infty} \Vert x^{1}(t) \Vert =0\). Therefore, the trivial solution of system (1) is globally asymptotically stable.

(ii) Let \(x^{0}(t)=x(t,\theta_{i},x^{0}(\theta_{i}))\) be a solution of system (1), for the corresponding solution \(x^{1}(t)\) of system (5), we can assume that there exist positive scalars \(M_{1}>0,\gamma_{1}>0\) such that \(x^{1}(t)\) satisfies that \(\Vert x^{1}(t) \Vert \leq M_{1} \exp(-\gamma_{1}(t-\theta _{0}))\) by the global exponential stability of system (5), where \(t\geq\theta_{0}\).

When \(t\in[\theta_{0},\theta_{1}]\) or \(t\in(\xi_{i},\theta_{i+1}]\), we have \(\Vert x^{0}(t) \Vert = \Vert x^{1}(t) \Vert \leq M_{1} \exp(-\gamma _{1}(t-\theta_{0}))\); and when \(t\in(\theta_{i},\xi_{i}]\), by (10), we get

$$\begin{aligned} \bigl\Vert x^{0}(t) \bigr\Vert & \leq \bigl\Vert x^{1}(t)-x^{0}(t) \bigr\Vert + \bigl\Vert x^{1}(t) \bigr\Vert \\ &\leq \delta \bigl\Vert x^{0}(\theta_{i}) \bigr\Vert +M_{1} \exp \bigl(-\gamma_{1}(t-\theta_{0}) \bigr) \\ &\leq \delta M_{1} \exp \bigl(-\gamma_{1}( \theta_{i}-\theta_{0}) \bigr)+M_{1} \exp \bigl(- \gamma_{1}(t-\theta_{0}) \bigr) \\ &= M_{1} \bigl[1+\delta\exp \bigl(\gamma_{1}(t- \theta_{i}) \bigr) \bigr] \exp \bigl(-\gamma_{1}(t- \theta_{0}) \bigr) \\ &\leq M_{1} \bigl[1+\delta\exp(\gamma_{1}\nu) \bigr] \exp \bigl(-\gamma_{1}(t-\theta_{0}) \bigr). \end{aligned}$$

Therefore, there exist positive scalars \(M_{2}=M_{1}[1+\delta\exp(\gamma _{1}\nu)], \gamma_{2}=\gamma_{1}\) such that the solution \(x^{0}(t)\) of system (1) satisfies that \(\Vert x^{0}(t) \Vert \leq M_{2} \exp(-\gamma _{2}(t-\theta_{0}))\). That is, the origin of system (1) is globally exponentially stable. The proof is completed. □

Theorem 6

Let all assumptions in Theorem 4 be valid, but \(x(t)\) is a solution of system (5) for \(t\in(\theta_{i},\theta_{i+1}]\). And

$$ \sum_{k=1}^{i}\ln \bigl(\rho \beta_{l_{k}}^{p} \bigr)+\sum_{k=1}^{i-1} \alpha_{l_{k}}(\theta_{k+1}-\theta_{k})+ \alpha_{h}(t-\theta_{i})\leq\varphi(\theta_{0},t), $$
(11)

where \(t\in(\theta_{i},\theta_{i+1}]\), \(\rho=\max(\frac{\lambda_{u}}{\mu _{v}}),u,v\in\{1,2,\ldots,m\}\), and \(\varphi(\theta_{0},t)\) is a continuous function on \(R_{+}\).

Then \(\lim_{t\rightarrow\infty}\varphi(\theta_{0},t)=-\infty\) implies that the trivial solution of (5) is globally asymptotically stable; and \(\varphi(\theta_{0},t)\leq M-d(t-\theta_{0})\), \(t\geq\theta_{0}\), with \(M>0\) and \(d>0\) being constants, implies that the origin of system (5) is globally exponentially stable.

Proof

The following inequalities follow conditions (7) and (8), respectively:

$$ V_{h} \bigl(x(t) \bigr)\leq V_{h} \bigl(x( \theta_{i}+) \bigr)\exp \bigl(\alpha_{h}(t- \theta_{i}) \bigr), $$
(12)

and

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert &\leq \bigl[ \mu_{h}^{-1}V_{h} \bigl(x(\theta_{i}+) \bigr)\exp \bigl(\alpha_{h}(t- \theta_{i}) \bigr) \bigr]^{1/p} \\ &\leq\sqrt[p]{\mu_{h}^{-1}\lambda_{h}}\exp \bigl( \alpha_{h}(t-\theta_{i})/p \bigr) \bigl\Vert x( \theta_{i}+) \bigr\Vert . \end{aligned}$$

One can easily find that

$$ V_{h} \bigl(x(\theta_{i}+) \bigr)\leq \lambda_{h} \bigl\Vert x(\theta_{i}+) \bigr\Vert ^{p}\leq\lambda_{h}\beta_{h}^{p} \bigl\Vert x(\theta_{i}) \bigr\Vert ^{p}\leq\rho \beta_{h}^{p}V_{h} \bigl(x(\theta_{i}) \bigr). $$
(13)

Substituting (13) into (12) leads to

$$ V_{h} \bigl(x(t) \bigr)\leq\rho\beta_{h}^{p} \exp \bigl(\alpha_{h}(t-\theta_{i}) \bigr)V_{h} \bigl(x(\theta_{i}) \bigr). $$
(14)

Using (14) successively on each interval, we have the following results. For \(t\in(\theta_{i},\theta_{i+1}]\),

$$\begin{aligned} V_{h} \bigl(x(t) \bigr)&\leq \rho \beta_{h}^{p} V_{h} \bigl(x(\theta_{i}) \bigr) \exp \bigl( \alpha_{h}(t-\theta_{i}) \bigr) \\ &\leq V_{l_{0}} \bigl(x(\theta_{0}) \bigr)\prod _{k=1}^{i} \bigl(\rho\beta_{l_{k}}^{p} \bigr) \exp \Biggl(\sum_{k=1}^{i-1} \alpha_{l_{k}}(\theta_{k+1}-\theta_{k})+ \alpha_{h}(t-\theta_{i}) \Biggr) \\ &\leq V_{l_{0}} \bigl(x(\theta_{0}) \bigr)\exp \bigl(\varphi( \theta_{0},t) \bigr). \end{aligned}$$

Namely,

$$ V_{h} \bigl(x(t) \bigr)\leq V_{l_{0}} \bigl(x( \theta_{0}) \bigr)\exp \bigl(\varphi(\theta_{0},t) \bigr). $$
(15)

Substituting (7) into (15) yields

$$ \bigl\Vert x(t) \bigr\Vert \leq\sqrt[p]{\rho} \Vert x_{0} \Vert \exp \bigl(\varphi(\theta_{0},t)/p \bigr),\quad t\geq \theta_{0}, $$

which implies the desired conclusions. Thus, we complete the proof. □

Corollary 1

Let Assumptions  A, B, and (C1)-(C3) hold, \(h=l_{i}\). Suppose that there exists \(V_{h}\in\Omega\) such that

$$\begin{aligned} &\mu_{h} \bigl\Vert x(t) \bigr\Vert ^{p} \leq V_{h} \bigl(x(t) \bigr)\leq\lambda_{h} \bigl\Vert x(t) \bigr\Vert ^{p}, \\ &D^{+}V_{h} \bigl(x(t) \bigr)\leq\alpha_{h} V_{h} \bigl(x(t) \bigr), \end{aligned}$$

where \(\mu_{h}>0\), \(\lambda_{h}>0\), \(p>0\), \(\alpha_{h}\) is a constant, and \(x(t)\) is a solution of (5) in \((\theta_{i},\theta_{i+1}]\).

Then the origin of system (5) is globally exponentially stable if one of the following conditions is satisfied.

  1. (i)

    \(\alpha_{h}<-\alpha<-\varrho<0\), where α and ϱ are constants such that

    $$\ln\bigl(\rho\beta_{h}^{p}\bigr)-\varrho( \theta_{i+1}-\theta_{i})\leq0. $$
  2. (ii)

    α and η are two positive constants satisfying \(\eta >\alpha\geq|\alpha_{h}|\) such that

    $$\ln\bigl(\rho\beta_{h}^{p}\bigr)+\eta(\theta_{i+1}- \theta_{i})\leq0. $$

The proof of this corollary is quite similar to that of Corollary 1 in [41], so we omit it here.

Remark 8

It is easy to see that condition (i) of Corollary 1 suggests that all the subsystems are of \(\pi_{1}\)-class, and there is no particular requirement on the impulse of switching subsystems. In the case of condition (ii) of Corollary 1, the parameters \(\alpha_{h}\) may be positive or negative, which implies that switching subsystems might be stable or unstable; however, the impulse of each subsystem has to be stable. One can easily observe that conditions (i) and (ii) of Corollary 1 are both stricter than the counterparts in Theorem 6. However, we can derive an estimate of exponential convergence rate of the trivial solution of system (5) based on Corollary 1. In fact, if condition (i) of Corollary 1 holds, one can obtain that

$$\bigl\Vert x(t) \bigr\Vert \leq\sqrt[p]{\rho} \Vert x_{0} \Vert \exp \bigl(-(\alpha-\varrho) (t-\theta_{0})/p\bigr),\quad t\geq \theta_{0}; $$

if condition (ii) of Corollary 1 holds, we can get that

$$\bigl\Vert x(t) \bigr\Vert \leq\sqrt[p]{\rho}\exp(\eta\bar{\theta}/p) \Vert x_{0} \Vert \exp\bigl(-(\eta-\alpha) (t-\theta_{0})/p\bigr),\quad t\geq\theta_{0}. $$

Now, let us consider a special case.

Corollary 2

Let Assumptions  A, B, and (C1)-(C3) hold, \(h=l_{i}\). Suppose that there exists \(V_{h}\in\Omega\) such that

$$ \mu_{h} \bigl\Vert x(t) \bigr\Vert ^{p} \leq V_{h} \bigl(x(t) \bigr)\leq\lambda_{h} \bigl\Vert x(t) \bigr\Vert ^{p}, $$

where \(\mu_{h}>0,\lambda_{h}>0,p>0\), \(x(t)\) is a solution of (5) in \((\theta_{i},\theta_{i+1}]\), and a constant α, such that one of the following conditions holds:

  1. (i)

    \(D^{+}V_{h} (x(t) )+\alpha V_{h} (x(t) )<0\), and \(\ln (\rho\beta_{h}^{p} )-\alpha \underline{\theta}\leq0\),

  2. (ii)

    \(D^{+}V_{h} (x(t) )-\alpha V_{h} (x(t) ) < 0\), and \(\ln (\rho\beta_{h}^{p} )+\alpha\bar{\theta}\leq0\),

then the trivial solution of system (5) is globally exponentially stable.

Proof

If condition (i) holds, for \(t\in(\theta_{i},\theta_{i+1}]\), from condition (i) and Theorem 6, we can assume

$$D^{+}V_{h}\bigl(x(t)\bigr)\leq\alpha_{h} V_{h} \bigl(x(t)\bigr)\leq-\eta V_{h}\bigl(x(t)\bigr)< -\alpha V_{h}\bigl(x(t)\bigr), $$

where both \(\alpha_{h}\) and η are constants, then

$$\sum_{k=1}^{i-1}\alpha_{l_{k}}( \theta_{k+1}-\theta_{k})+\alpha_{h}(t-\theta _{i})\leq-\eta(t-\theta_{0}). $$

From \(\ln(\rho\beta_{h}^{p})-\alpha\underline{\theta}\leq0\), we get

$$\sum_{k=1}^{i}\ln\bigl(\rho \beta_{l_{k}}^{p}\bigr)\leq\alpha(\theta_{i}- \theta_{0})\leq \alpha(t-\theta_{0}). $$

So,

$$\sum_{k=1}^{i}\ln\bigl(\rho \beta_{l_{k}}^{p}\bigr)+\sum_{k=1}^{i-1} \alpha_{l_{k}}(\theta _{k+1}-\theta_{k})+ \alpha_{h}(t-\theta_{i})\leq-(\eta-\alpha) (t- \theta_{0}). $$

Letting \(\varphi(\theta_{0},t)=-(\eta-\alpha)(t-\theta_{0})\) and noting that \(\eta-\alpha>0\), we can end the proof by Theorem 6.

If condition (ii) holds, for \(t\in(\theta_{i},\theta_{i+1}]\), from condition (ii) and Theorem 6, we can assume

$$D^{+}V_{h}\bigl(x(t)\bigr)\leq\alpha_{h}V_{h} \bigl(x(t)\bigr)\leq\zeta V_{h}\bigl(x(t)\bigr)< \alpha V_{h} \bigl(x(t)\bigr), $$

where both \(\alpha_{h}\) and ζ are constants, then

$$\sum_{k=1}^{i-1}\alpha_{l_{k}}( \theta_{k+1}-\theta_{k})+\alpha_{h}(t-\theta _{i})\leq\zeta(t-\theta_{0}). $$

From \(\ln(\rho\beta_{h}^{p})+\alpha\bar{\theta}\leq0\), we have

$$\sum_{k=1}^{i}\ln\bigl(\rho \beta_{l_{k}}^{p}\bigr)\leq-\alpha(\theta_{i}- \theta_{0})\leq -\alpha(\theta_{i}-\theta_{0})+ \alpha\bar{\theta}-\alpha(t-\theta_{i})\leq \alpha\bar{\theta}-\alpha(t- \theta_{0}). $$

Therefore,

$$\sum_{k=1}^{i}\ln\bigl(\rho \beta_{l_{k}}^{p}\bigr)+\sum_{k=1}^{i-1} \alpha_{l_{k}}(\theta _{k+1}-\theta_{k})+ \alpha_{h}(t-\theta_{i})\leq\alpha\bar{\theta}-(\alpha - \zeta) (t-\theta_{0}). $$

Letting \(\varphi(\theta_{0},t)=\alpha\bar{\theta}-(\alpha-\zeta)(t-\theta _{0})\) and noting that \(\alpha-\zeta>0\), one concludes the proof. □

Remark 9

In condition (i) of Corollary 2, let \(-\eta=\max\{\alpha _{1},\alpha_{2},\ldots,\alpha_{m}\}\), we can easily find η. Similarly, in condition (ii) of Corollary 2, let \(\zeta=\max\{\alpha_{1},\alpha_{2},\ldots,\alpha _{m}\}\), one finds ζ. That is, the conditions of Corollary 2 can really hold.

It is time to present the main result for the stability criterion of system (1) by means of system (5). Based on the above discussions, the following result is immediate.

Theorem 7

Let Assumptions  A, B, and (C1)-(C3) hold \(h=l_{i}\). Suppose that there exists \(V_{h}\in\Omega\) such that

$$\begin{aligned} &(1) \quad\mu_{h} \bigl\Vert x(t) \bigr\Vert ^{p} \leq V_{h} \bigl(x(t) \bigr)\leq \lambda_{h} \bigl\Vert x(t) \bigr\Vert ^{p}, \\ &(2) \quad D^{+}V_{h} \bigl(x(t) \bigr)\leq\alpha_{h} V_{h} \bigl(x(t) \bigr), \\ &(3) \quad\frac{2}{\alpha_{h}} \biggl[\exp \biggl(\frac{\alpha_{h}\nu }{2} \biggr)-1 \biggr] \bigl( \Vert C_{h} \Vert + \Vert A_{h} \Vert L_{h} \bigr) \sqrt{\mu_{h}^{-1} \lambda_{h}}< 1, \\ &(4) \quad\sum_{k=1}^{i}\ln \bigl(\rho \beta_{l_{k}}^{p} \bigr)+\sum_{k=1}^{i-1} \alpha_{l_{k}}(\theta_{k+1}-\theta_{k})+ \alpha_{h}(t-\theta_{i})\leq\varphi(\theta_{0},t), \end{aligned}$$

where \(\mu_{h}>0\), \(\lambda_{h}>0\), \(p>0\), \(\alpha_{h}\in R\), \(x(t)\) is a solution of system (5), and \(t\in(\theta_{i},\theta_{i+1}]\).

Then \(\lim_{t\rightarrow\infty}\varphi(\theta_{0},t)=-\infty\) implies that the trivial solution of (1) is globally asymptotically stable; and \(\varphi(\theta_{0},t)\leq M-d(t-\theta_{0})\), \(t\geq\theta_{0}\), with \(M>0\) and \(d>0\) being constants, implies that the origin of system (1) is globally exponentially stable.

Similar to Corollaries 1 and 2, there is also a corresponding corollary by Theorem 7 here.

Corollary 3

Assume that all the conditions of Theorem 4 hold \(h=l_{i}\). Then the origin of system (1) is globally exponentially stable if one of the following conditions is fulfilled.

  1. (i)

    \(\alpha_{h}<-\alpha<-\varrho<0\), where α and ϱ are constants such that

    $$\ln\bigl(\rho\beta_{h}^{p}\bigr)-\varrho( \theta_{i+1}-\theta_{i})\leq0. $$
  2. (ii)

    α and η are two positive constants satisfying \(\eta >\alpha\geq|\alpha_{h}|\) such that

    $$\ln\bigl(\rho\beta_{h}^{p}\bigr)+\eta(\theta_{i+1}- \theta_{i})\leq0. $$

Corollary 4

Let Assumptions  A, B, and (C1)-(C3) hold. Assume that there exists \(V_{h}\in\Omega\) such that

$$\begin{aligned} &\mu_{h} \bigl\Vert x(t) \bigr\Vert ^{p} \leq V_{h} \bigl(x(t) \bigr)\leq \lambda_{h} \bigl\Vert x(t) \bigr\Vert ^{p}, \\ &\frac{2}{\alpha} \biggl[\exp \biggl(\frac{\alpha\nu}{2} \biggr)-1 \biggr] \bigl( \Vert C_{h} \Vert + \Vert A_{h} \Vert L_{h} \bigr) \sqrt{\mu_{h}^{-1} \lambda_{h}}< 1, \end{aligned} $$

where \(\mu_{h}>0,\lambda_{h}>0,p>0\), \(x(t)\) is a solution of (5) in \((\theta_{i},\theta_{i+1}]\), and α is a constant, such that one of the following conditions holds:

  1. (i)

    \(D^{+}V_{h} (x(t) )+\alpha V_{h} (x(t) )<0\), and \(\ln (\rho\beta_{h}^{p} )-\alpha \underline{\theta}\leq0\),

  2. (ii)

    \(D^{+}V_{h} (x(t) )-\alpha V_{h} (x(t)) < 0\), and \(\ln (\rho\beta_{h}^{p} )+\alpha\bar{\theta}\leq0\),

then the trivial solution of system (1) is globally exponentially stable.

6 Two numerical examples

In this section, two numerical examples are given to show the effectiveness of the theoretical results mentioned in the previous sections. For the sake of simplicity, in what follows, an impulsive switching CGNN model with only two neurons is analyzed, and it is supposed that each hybrid system has only two subsystems and the switching sequence is \(1 \rightarrow2 \rightarrow1 \rightarrow2 \rightarrow\cdots\) .

Example 1

Consider the following impulsive switching CGNN, noting that there is no impulse in \([\theta_{0}, \theta_{1}]\):

$$ \textstyle\begin{cases} \dot{x}(t)=-A_{1}(x(t))[B_{1}(x(t))-C_{1}f_{1}(x(t))], \\ \quad t\in(KT, KT+\sigma T], K=0,1,2,\ldots,\mbox{ and } t \neq\theta_{i}+\tau _{i}(x(t)), \\ \Delta x(t)=J_{1}(x(t)), \quad t = \theta_{i}+\tau_{i}(x(t)), i=2K, K=1,2,3,\ldots, \\ \dot{x}(t)=-A_{2}(x(t))[B_{2}(x(t))-C_{2}f_{2}(x(t))], \\ \quad t\in(KT+\sigma T, (K+1)T], K=0,1,2,\ldots,\mbox{ and } t \neq\theta_{i+1}+\tau_{i+1}(x(t)), \\ \Delta x(t)=J_{2}(x(t)), \quad t = \theta_{i+1}+\tau_{i+1}(x(t)), i=2K, K=0,1,2,\ldots, \end{cases} $$
(16)

with \(T=2\), \(\sigma=0.5\), \(\theta_{i}=i\), \(\theta_{i+1}=i+1\), \(\tau _{i}(x)=\tau_{i+1}(x)=0.2\operatorname {arccot}(x_{1}^{2})\) and \(\nu=0.1\pi\), \(J_{1}(x)=1.1x\), \(J_{2}(x)=0.6x\),

$$f_{1} \bigl(x(t) \bigr)=f_{2} \bigl(x(t) \bigr) = \begin{pmatrix} \sin x_{1}(t) \\ \sin x_{2}(t) \end{pmatrix} , $$

and

$$\begin{aligned} &A_{1}= \begin{pmatrix} 3+\sin x_{1}(t) & 0 \\ 0 & 3+\cos x_{2}(t) \end{pmatrix} , \qquad B_{1}= \begin{pmatrix} 0.5 & 0 \\ 0 & 0.5 \end{pmatrix} , \qquad C_{1}= \begin{pmatrix} 0.2 & 0 \\ -0.2 & 0.1 \end{pmatrix} . \\ &A_{2}= \begin{pmatrix} 2+\sin x_{1}(t) & 0 \\ 0 & 2+\cos x_{2}(t) \end{pmatrix} , \qquad B_{2}= \begin{pmatrix} 0.7 & 0 \\ 0 & 0.7 \end{pmatrix} , \qquad C_{2}= \begin{pmatrix} 0.3 & 0 \\ -0.3 & 0.2 \end{pmatrix} . \end{aligned}$$

Note that

$$\begin{aligned} & \frac{d\tau_{i}(x)}{dx} \bigl\{ -A_{1} \bigl(x(t) \bigr) \bigl[B_{1} \bigl(x(t) \bigr)-C_{1}f_{1} \bigl(x(t) \bigr) \bigr] \bigr\} \\ &\quad= 0.4x_{1} \biggl(-\frac{1}{1+x_{1}^{4}},0 \biggr) \begin{pmatrix} (3+\sin x_{1})(-0.5x_{1}+0.2\sin x_{1}) \\ (3+\cos x_{2})(-0.5x_{2}-0.2\sin x_{1}+0.1\sin x_{2}) \end{pmatrix} \\ &\quad=0.4x_{1}\frac{(3+\sin x_{1})(0.5x_{1}-0.2\sin x_{1})}{1+x_{1}^{4}} \\ &\quad \leq\frac{1.12x_{1}^{2}}{1+x_{1}^{4}} \\ &\quad< 1. \end{aligned}$$

Moreover,

$$\tau_{i}\bigl(x+J_{i}(x)\bigr)-\tau_{i}(x)=0.2 \bigl[\operatorname {arccot}\bigl((1+1.1)^{2}x_{1}^{2}\bigr)- \operatorname {arccot}\bigl(x_{1}^{2}\bigr)\bigr]\leq0, $$

i.e., \(\tau_{i}(x+J_{i}(x))\leq\tau_{i}(x)\).

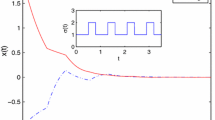
Analogously, \(\frac{d\tau_{i+1}(x)}{dx} \{ -A_{2}(x(t))[B_{2}(x(t))-C_{2}f_{2}(x(t))]\}<1\), \(\tau_{i+1}(x+J_{i}(x))\leq\tau _{i+1}(x)\). Thus, assumption (C3) holds. One can easily get that all assumptions in Theorem 7 are satisfied. Therefore, the origin of system (16) is globally stable, as shown in Figure 2.

Figure 2
figure 2

The time response curves of ( 16 ) in Example 1 with \(\pmb{x(0)=(0.6 \ -0.6)^{T}}\).

Full size image

Remark 10

One can see from Figure 2 that our conditions are very conservative, and we look forward to improving these conditions in future research.

Example 2

Consider again the hybrid impulsive and switching CGNN, noting that there is no impulse in \([\theta_{0}, \theta_{1}]\):

$$ \textstyle\begin{cases} \dot{x}(t)=-A_{1}(x(t))[B_{1}(x(t))-C_{1}f_{1}(x(t))], \\ \quad t\in(KT, KT+\sigma T], K=0,1,2,\ldots,\mbox{ and } t \neq\theta_{i}+\tau_{i}(x(t)), \\ \Delta x(t)=J_{1}(x(t)), \quad t = \theta_{i}+\tau_{i}(x(t)), i=2K, K=1,2,3,\ldots, \\ \dot{x}(t)=-A_{2}(x(t))[B_{2}(x(t))-C_{2}f_{2}(x(t))], \\ \quad t\in(KT+\sigma T, (K+1)T], K=0,1,2,\ldots,\mbox{ and } t \neq \theta_{i+1}+\tau_{i+1}(x(t)), \\ \Delta x(t)=J_{2}(x(t)), \quad t = \theta_{i+1}+\tau_{i+1}(x(t)), i=2K, K=0,1,2,\ldots, \end{cases} $$
(17)

with \(T=2\), \(\sigma=0.5\), \(\theta_{i}=i\), \(\theta_{i+1}=i+1\), \(\tau _{i}(x)=\tau_{i+1}(x)=[\arctan(x_{1})]^{2}/(2\pi)\) and \(\nu=0.125\pi\), \(J_{1}(x)=-1.4x\), \(J_{2}(x)=-1.3x\),

$$f_{1} \bigl(x(t) \bigr)=f_{2} \bigl(x(t) \bigr) = \begin{pmatrix} \sin x_{1}(t) \\ \sin x_{2}(t) \end{pmatrix} , $$

and

$$\begin{aligned} &A_{1}= \begin{pmatrix} 2+\cos x_{1}(t) & 0 \\ 0 & 2+\cos x_{2}(t) \end{pmatrix} , \qquad B_{1}= \begin{pmatrix} 0.2 & 0 \\ 0 & 0.2 \end{pmatrix} , \qquad C_{1}= \begin{pmatrix} 0.4 & 0 \\ -0.2 & 0.4 \end{pmatrix} . \\ &A_{2}= \begin{pmatrix} 3+\cos x_{1}(t) & 0 \\ 0 & 3+\cos x_{2}(t) \end{pmatrix} , \qquad B_{2}= \begin{pmatrix} 0.3 & 0 \\ 0 & 0.3 \end{pmatrix} , \qquad C_{2}= \begin{pmatrix} 0.5 & 0 \\ -0.3 & 0.5 \end{pmatrix} . \end{aligned}$$

Note that

$$\begin{aligned} & \frac{d\tau_{i}(x)}{dx} \bigl\{ -A_{1} \bigl(x(t) \bigr) \bigl[B_{1} \bigl(x(t) \bigr)-C_{1}f_{1} \bigl(x(t) \bigr) \bigr] \bigr\} \\ &\quad= \frac{1}{\pi}\arctan x_{1} \biggl(\frac{1}{1+x_{1}^{2}},0 \biggr) \begin{pmatrix} (2+\cos x_{1})(-0.2x_{1}+0.4\sin x_{1}) \\ (2+\cos x_{2})(-0.2x_{2}-0.2\sin x_{1}+0.4\sin x_{2}) \end{pmatrix} \\ &\quad =\frac{1}{\pi}\arctan x_{1}\frac{(2+\cos x_{1})(-0.2x_{1}+0.4\sin x_{1})}{1+x_{1}^{2}} \\ &\quad \leq \frac{1.5|{-}0.2x_{1}+0.4\sin x_{1}|}{1+x_{1}^{2}} \\ &\quad \leq \frac{0.9|x_{1}|}{1+x_{1}^{2}} \\ &\quad < 1. \end{aligned}$$

Furthermore,

$$\begin{aligned} &\tau_{i} \bigl(x+J_{i}(x) \bigr)-\tau_{i}(x) \\ &\quad=\frac{1}{2\pi} \bigl\{ \bigl[\arctan \bigl( \bigl(1+(-1.4) \bigr)x_{1} \bigr) \bigr]^{2}- \bigl[\arctan(x_{1}) \bigr]^{2} \bigr\} \\ &\quad=\frac{1}{2\pi} \bigl\{ \bigl[\arctan \bigl( \vert {-}0.4x_{1} \vert \bigr) \bigr]^{2}- \bigl[\arctan \bigl( \vert x_{1} \vert \bigr) \bigr]^{2} \bigr\} \\ &\quad=\frac{1}{2\pi} \bigl[\arctan \bigl( \vert 0.4x_{1} \vert \bigr)+\arctan \bigl( \vert x_{1} \vert \bigr) \bigr] \bigl[\arctan \bigl( \vert 0.4x_{1} \vert \bigr)-\arctan \bigl( \vert x_{1} \vert \bigr) \bigr] \\ &\quad\leq0, \end{aligned}$$

that is, \(\tau_{i}(x+J_{i}(x))\leq\tau_{i}(x)\).

Similarly, \(\frac{d\tau_{i+1}(x)}{dx} [-C_{2}(x(t))+A_{2}f_{2}(x(t))]<1\), \(\tau_{i+1}(x+J_{i}(x))\leq\tau_{i+1}(x)\). Hence, assumption (C3) is satisfied. One observes that the conditions of Theorem 7 can all hold for system (17). Therefore, the origin of system (17) is globally stable, as shown in Figure 3.

Figure 3
figure 3

The time response curves of ( 17 ) in Example 2 with \(\pmb{x(0)=(0.5 \ -0.4)^{T}}\) .

Full size image

Remark 11

It can be seen from Figure 3 that stabilizing impulses can stabilize the unstable continuous subsystem at its equilibrium point, which is inconsistent with the theoretical prediction.

7 Conclusions and discussions

In the present paper, we have studied the impacts of state-dependent impulses on the stability of switching Cohen-Grossberg neural networks using B-equivalence method. Moreover, we have obtained a stability criterion for the considered CGNN. However, the estimation on the norm of transformation map \(W_{i}(x)\) is very conservative, which leads to conservative stability conditions. It is expected to release these conditions for certain CGNN and to extend the presented method to delayed systems or more general impulsive switching systems.