1 Introduction

The aim of this paper is to investigate the dynamic behaviors of the following discrete competitive model:

$$\begin{aligned} \begin{aligned}& x_{1}(n+1)=x_{1}(n)\exp{\biggl[r_{1}-a_{1}x_{1}(n)- \frac {b_{1}x_{2}(n)}{1+c_{2}x_{2}(n)}\biggr]}, \\ & x_{2}(n+1)=x_{2}(n)\exp{\biggl[r_{2}-a_{2}x_{2}(n)- \frac {b_{2}x_{1}(n)}{1+c_{1}x_{1}(n)}\biggr]}, \end{aligned} \end{aligned}$$
(1.1)

where \(x_{i}(n)\) \((i=1,2)\) are the population density of the species \(x_{1}\) and \(x_{2}\) at the nth generation. \(r_{i}, a_{i}, b_{i},c_{i}\) \((i=1,2)\) are all positive constants, \(r_{i}, a_{i}, b_{i}\) \((i=1,2)\) represent the intrinsic growth rates, the rates of intraspecific competition of species \(x_{1}\) and \(x_{2}\), the rates of interspecific competition of species \(x_{1}\) and \(x_{2}\), respectively. We focus on the local and global stability properties of the system.

Chen and Teng [1] proposed and studied the dynamic behaviors of the following two-species competitive system:

$$\begin{aligned} \begin{aligned} &x(n+1)=x(n)\exp{\biggl[r_{1}\biggl(1- \frac{x(n)}{K_{1}}-\mu _{2}y(n)\biggr)\biggr]}, \\ &y(n+1)=y(n)\exp{\biggl[r_{2}\biggl(1-\mu_{1}x(n)- \frac {y(n)}{K_{2}}\biggr)\biggr]}, \end{aligned} \end{aligned}$$
(1.2)

where \(x(n)\) and \(y(n)\) represent the population densities of the species x and y at the nth generation, respectively. \(r_{i},K_{i}\), and \(\mu_{i}\) \((i=1,2)\) are positive constants and represent the intrinsic growth rates, the carrying capacities, and the competition coefficients of species x and y, respectively. The authors investigated the local and global stability properties of the positive equilibrium of the system when the intraspecific and interspecific competition coefficients are both linear in system (1.2), and the assumption of linear changes made the analysis of dynamic behaviors relatively easy. However, a more practical model need to be characterized by nonlinearities.

Qin, Liu, and Chen [2] argued that a more plausible competition model should be nonlinear and proposed the following two-species discrete competition model with nonlinear interspecific competition terms:

$$\begin{aligned} \begin{aligned} x_{1}(n+1)=x_{1}(n)\exp{\biggl[r_{1}(n)-a_{1}(n)x_{1}(n)- \frac {b_{1}(n)x_{2}(n)}{1+x_{2}(n)}\biggr]}, \\ x_{2}(n+1)=x_{2}(n)\exp{\biggl[r_{2}(n)-a_{2}(n)x_{2}(n)- \frac {b_{2}(n)x_{1}(n)}{1+x_{1}(n)}\biggr]}, \end{aligned} \end{aligned}$$
(1.3)

where \(r_{i}(n),a_{i}(n),b_{i}(n)\) \((i,j=1,2;i\neq j)\) are periodic sequences bounded above and below by positive constants. Set

$$f^{U}=\sup_{n\in N}f(n),\qquad f^{L}=\inf _{n\in N}f(n), $$

where \(\{f(n)\}\) is a bounded sequence, and N is the set of nonnegative integer numbers.

Concerned with the persistent property and stability property of the system, the authors obtained the following results (Theorems 2.4 and 3.3 in [2]).

Theorem A

Suppose that

$$\begin{aligned} r_{1}^{L}>b_{1}^{U} \quad\textit{and}\quad r_{2}^{L}>b_{2}^{U}. \end{aligned}$$
(1.4)

Then system (1.3) is permanent.

Theorem B

In addition to (1.4), assume further that

$$\begin{aligned} \begin{aligned}&\lambda_{1}\stackrel{\mathrm{def}}{=}\max\bigl\{ \bigl\vert 1-a_{1}^{l}m_{1} \bigr\vert , \bigl\vert 1-a_{1}^{U}M_{1} \bigr\vert \bigr\} +b_{1}^{U}< 1, \\ &\lambda_{2}\stackrel{\mathrm{def}}{=}\max\bigl\{ \bigl\vert 1-a_{2}^{l}M_{2} \bigr\vert , \bigl\vert 1-a_{2}^{U}M_{2} \bigr\vert \bigr\} +b_{2}^{U}< 1. \end{aligned} \end{aligned}$$
(1.5)

Then the positive periodic solution of system (1.3) is globally stable.

As a direct corollary of Theorems A and B, for the autonomous case of system (1.3) (i.e., all the coefficients of the system are positive constants), we have the following result.

Theorem C

Suppose that the following assumptions are satisfied:

$$\begin{aligned} \begin{aligned} &r_{1}>b_{1},\qquad r_{2}>b_{2}, \\ &\lambda_{1}\stackrel{\mathrm{def}}{=}\max\bigl\{ \bigl\vert 1-(r_{1}-b_{1})\exp \bigl(r_{1}- \exp(r_{1}-1)-b_{1}\bigr) \bigr\vert , \bigl\vert 1- \exp(r_{1}-1) \bigr\vert \bigr\} +b_{1}< 1, \\ &\lambda_{2}\stackrel{\mathrm{def}}{=}\max\bigl\{ \bigl\vert 1-(r_{2}-b_{2})\exp \bigl(r_{2}- \exp(r_{2}-1)-b_{2}\bigr) \bigr\vert , \bigl\vert 1- \exp(r_{2}-1) \bigr\vert \bigr\} +b_{2}< 1. \end{aligned} \end{aligned}$$
(1.6)

Then the autonomous case of system (1.3) admits a global stable positive positive equilibrium.

Note that conditions (1.6) are sufficient conditions. We propose an interesting issue: whether the conditions are good enough or the conditions still have room to improve? To give some hint on this problem, let us consider the following example.

Example 1.1

$$\begin{aligned} \begin{aligned} & x_{1}(n+1)=x_{1}(n)\exp{ \biggl[0.3-0.5x_{1}(n)- \frac {0.31x_{2}(n)}{1+x_{2}(n)}\biggr]}, \\ &x_{2}(n+1)=x_{2}(n)\exp{\biggl[0.2-0.1x_{2}(n)- \frac {0.4x_{1}(n)}{1+x_{1}(n)}\biggr]}, \end{aligned} \end{aligned}$$
(1.7)

where, correspondingly to system (1.3), we take \(r_{1}(n)=0.3, r_{2}(n)=0.2, a_{1}(n)=0.5, a_{2}(n)=0.1, b_{1}(n)=0.31, b_{2}(n)=0.4\). By simple computation it follows that

$$r_{1}< b_{1},\qquad r_{2}< b_{2},\qquad \lambda_{1}\approx1.32>1,\qquad \lambda_{2}\approx1.50>1. $$

Hence, none of the conditions in Theorem C holds. However, numeric simulation (Figure 1) shows that system (1.7) admits a unique positive equilibrium, which is globally stable. Example 1.1 shows that Theorems A and B still have room to improve, or one may find out some other different conditions to ensure the global stability of the positive equilibrium. The success of Chen and Teng [1] and Qin, Liu, and Chen [2] stimulated us to propose a slightly more complicated system (1.1) and investigated the stability property of model (1.1).

Figure 1
figure 1

Dynamic behaviors of system ( 1.7 ) with the initial conditions \(\pmb{(x(0), y(0))=(0.14, 0.19), (0.37, 0.009), (0.95, 0.024)}\) , and \(\pmb{(0.60, 0.82)}\) , respectively.

Full size image

On the other hand, Chen [3] studied the following competitive system:

$$\begin{aligned} \begin{aligned}& \frac{dy_{1}(t)}{dt}=y_{1}(t)\biggl[r_{1}-a_{1}y_{1}- \frac {b_{1}y_{2}}{1+y_{2}}\biggr], \\ &\frac{dy_{2}(t)}{dt}=y_{2}(t)\biggl[r_{2}-a_{2}y_{2}- \frac {b_{2}y_{1}}{1+y_{1}}\biggr], \end{aligned} \end{aligned}$$
(1.8)

where \(r_{i}, a_{i}, b_{i}\), \(i=1,2\), are all positive constants. Concerned with the stability property of the positive equilibrium of system (1.8), Chen obtained the following result.

Theorem D

Assume that the following inequalities hold:

$$\begin{aligned} r_{1}(a_{2}+r_{2})>b_{1}r_{2},\qquad r_{2}(a_{1}+r_{1})>b_{2}r_{1}. \end{aligned}$$
(1.9)

Assume further that one of the following conditions holds:

  1. (i)
    $$\begin{aligned} a_{2}-b_{2}+r_{2}\neq0; \end{aligned}$$
    (1.10)
  2. (ii)
    $$\begin{aligned} a_{2}-b_{2}+r_{2}=0, \qquad a_{1}r_{2}-a_{2}r_{1}>0. \end{aligned}$$
    (1.11)

    Then system (1.8) admits a unique positive equilibrium on the rectangle \((0, \frac{r_{1}}{a_{1}})\times(0, \frac {r_{2}}{a_{2}})\), which is globally stable.

Here, condition (1.9) is natural, whereas conditions (1.10) and (1.11) seem very strange. By careful check of the conditions, we can see that if \(a_{2}-b_{2}+r_{2}=0\), then, together with the second inequality in (1.9), we can easily obtain that

$$a_{1}r_{2}-a_{2}r_{1}=a_{1}r_{2}-(b_{2}-r_{2})r_{1}=r_{2}(a_{1}+r_{1})-b_{2}r_{1}>0, $$

that is, (1.11) always holds. Hence, conditions (1.10) and (1.11) in Theorem D are unnecessary and may be dropped.

It is well known that, compared to the continuous-time systems, the discrete-time ones are more difficult to deal with. Stimulated by the works of Chen and Teng [1], Qin, Liu, and Chen [2], and Chen [3], in this paper, we focus our attention on the dynamic behavior of system (1.1); more precisely, we investigate the local and global stability properties of the system. Throughout this paper, we assume that the coefficients of system (1.1) satisfy

$$(H_{1})\quad r_{i}(a_{j}+c_{j}r_{j})>b_{i}r_{j}, \quad i,j=1,2 \mbox{ and } i\neq j. $$

Lemma 1.1

Assume that \((H_{1})\) holds. Then system (1.1) admits a unique positive equilibrium \((x^{*}_{1},x^{*}_{2})\) on the rectangle \((0, \frac{r_{1}}{a_{1}})\times(0, \frac{r_{2}}{a_{2}})\).

Proof

The positive equilibrium of system (1.1) is the solution of the equation system

$$\begin{aligned} \textstyle\begin{cases} r_{1}-a_{1}x_{1}- \frac{b_{1}x_{2}}{1+c_{2}x_{2}}=0,\\ r_{2}-a_{2}x_{2}- \frac{b_{2}x_{1}}{1+c_{1}x_{1}}=0, \end{cases}\displaystyle \end{aligned}$$
(1.12)

which is equivalent to

$$\begin{aligned} \textstyle\begin{cases} A_{1}x_{1}^{2}+A_{2}x_{1}+A_{3}=0,\\ B_{1}x_{2}^{2}+B_{2}x_{2}+B_{3}=0, \end{cases}\displaystyle \end{aligned}$$
(1.13)

where

$$\begin{aligned} &A_{1}=a_{1}a_{2}c_{1}+a_{1}c_{1}c_{2}r_{2}-a_{1}b_{2}c_{2},\\ &A_{2}=a_{1}a_{2}+a_{1}c_{2}r_{2}-a_{2}c_{1}r_{1}+b_{1}c_{1}r_{2}-b_{1}b_{2}+b_{2}c_{2}r_{1}-c_{1}c_{2}r_{1}r_{2},\\ & A_{3}=-a_{2}r_{1}+b_{1}r_{2}-c_{2}r_{1}r_{2},\\ & B_{1}=a_{1}a_{2}c_{2}+a_{2}c_{1}c_{2}r_{1}-a_{2}b_{1}c_{1},\\ &B_{2}=a_{1}a_{2}+a_{2}c_{1}r_{1}-a_{1}c_{2}r_{2}+b_{1}c_{1}r_{2}-b_{1}b_{2}+b_{2}c_{2}r_{1}-c_{1}c_{2}r_{1}r_{2},\\ &B_{3}=-a_{1}r_{2}+b_{2}r_{1}-c_{1}r_{1}r_{2}. \end{aligned}$$

Since we focus on the positive equilibrium of system (1.1), we only need to consider the case \(x_{1}>0, x_{2}>0\). To ensure the first equality in (1.12), \(x_{1}\) should lie in the interval \((0, \frac {r_{1}}{a_{1}})\). Similarly, to ensure the second equality of (1.12), \(x_{2}\) should lie in the interval \((0, \frac {r_{2}}{a_{2}})\). We will further investigate the positive equilibrium of system (1.1) on the rectangle \((0, \frac{r_{1}}{a_{1}})\times (0, \frac{r_{2}}{a_{2}})\).

Now let us consider the function

$$F(x_{1})=A_{1}x_{1}^{2}+A_{2}x_{1}+A_{3}. $$

From \((H_{1})\) we have

$$F(0)=A_{3}< 0 $$

and

$$F\biggl( \frac{r_{1}}{a_{1}}\biggr)= \frac {b_{1}(a_{1}r_{2}+c_{1}r_{1}r_{2}-b_{2}r_{1})}{a_{1}}>0. $$

Therefore, from the continuity of the function \(F(x_{1})\), \(F(x_{1})=0\) has at least one positive solution on the interval \((0, \frac {r_{1}}{a_{1}})\). We now prove that the equation \(F(x_{1})=0\) has at most one positive solution on the interval \((0, \frac {r_{1}}{a_{1}})\). We discuss this in three cases.

Case 1. If \(A_{1}>0\), then \(F(+\infty)=F(-\infty)=+\infty \). Since \(F(0)<0\), it follows that \(F(x_{1})=0\) has at least one solution on the intervals \((-\infty,0)\) and \((0,+\infty)\), respectively. Therefore \(F(x_{1})=0\) has only one solution on the interval \((0, \frac{r_{1}}{a_{1}})\);

Case 2. If \(A_{1}=0\), then, since \(F(x_{1})\) is a linear function of \(x_{1}\), \(F( \frac{r_{1}}{a_{1}})>0\), and \(F(0)<0\), it follows that \(F(x_{1})=0\) has only one solution on the interval \((0, \frac{r_{1}}{a_{1}})\);

Case 3. If \(A_{1}<0\), then \(F(+\infty)=-\infty\), and since \(F( \frac{r_{1}}{a_{1}})>0\) and \(F(0)<0\), it follows that \(F(x_{1})\) has at least one solution on the intervals \((0, \frac{r_{1}}{a_{1}})\) and \(( \frac {r_{1}}{a_{1}},+\infty)\). So \(F(x_{1})=0\) has only one solution on the interval \((0, \frac{r_{1}}{a_{1}})\).

The above analysis shows that \(F(x_{1})=0\) has only one solution on the interval \((0, \frac{r_{1}}{a_{1}})\). We denote it as \(x^{*}_{1}\). Similarly, we can prove that there exists \(x^{*}_{2} \) in the interval \((0, \frac{r_{2}}{a_{2}})\) that satisfies \(B_{1}x_{2}^{2}+B_{2}x_{2}+B_{3}=0\). Then system (1.1) admits a unique positive equilibrium \((x^{*}_{1},x^{*}_{2})\) on the rectangle \((0, \frac{r_{1}}{a_{1}})\times(0, \frac {r_{2}}{a_{2}})\). This ends the proof of Lemma 1.1. □

The rest of the paper is arranged as follows. With the help of several useful lemmas, we investigate the local stability in Section 2 and prove the global stability result (Theorem 3.1) in Section 3. Four examples, together with their numeric simulations, are presented in Section 4 to show the feasibility of our results. We end this paper by a brief discussion. For more work about competitive systems, we can refer to [2, 4–23] and the references cited.

2 Local stability

We give a strict proof of the local stability in this section. From the biological background of system (1.1), we assume that initial values \(x_{1}(0)>0\) and \(x_{2}(0)>0\) in system (1.1). It is clear that any solution of system (1.1) is defined on \(N=\{0, 1, 2, \ldots\}\) and remains positive for all \(n\geq0\). Now let us state several useful lemmas.

Lemma 2.1

[1]

Consider the function \(F(\lambda )=\lambda^{2}+B\lambda+C\), where both B and C are constants. Suppose \(F(1)>0\) and let \(\lambda_{1},\lambda_{2}\) be two roots of the quadratic equation \(F(\lambda)=0\). Then we can easily prove that

  1. 1.

    \(\vert \lambda_{1} \vert <1\) and \(\vert \lambda _{2} \vert <1\) if and only if \(F(-1)>0\) and \(C<1\);

  2. 2.

    \(\vert \lambda_{1} \vert >1\) and \(\vert \lambda _{2} \vert >1\) if and only if \(F(-1)>0\) and \(C>1\);

  3. 3.

    \(\vert \lambda_{1} \vert <1\) and \(\vert \lambda _{2} \vert >1\) if and only if \(F(-1)<0\);

  4. 4.

    \(\lambda_{1}=-1\) and \(\vert \lambda_{2} \vert \neq1\) if and only if \(F(-1)=0\) and \(B\neq0,2\);

  5. 5.

    \(\lambda_{1}\) and \(\lambda_{2}\) are a pair of conjugate complex roots and \(\vert \lambda_{1} \vert = \vert \lambda_{2} \vert =1\) if and only if \(B^{2}-4C<0\) and \(C=1\).

Here, if \(\lambda_{1}\) and \(\lambda_{2}\) are two roots of the characteristic equation \(F(\lambda)=\lambda^{2}+B\lambda +C=0\) of \(J(x,y)\), then we have the following definitions.

  1. 1.

    If \(\vert \lambda_{1} \vert <1\) and \(\vert \lambda _{2} \vert <1\), then \(J(x,y)\) is called a sink and is locally asymptotic stable;

  2. 2.

    If \(\vert \lambda_{1} \vert >1\) and \(\vert \lambda _{2} \vert >1\), then \(J(x,y)\) is called a source and is unstable;

  3. 3.

    If \(\vert \lambda_{1} \vert >1\) and \(\vert \lambda _{2} \vert <1\) (or \(\vert \lambda _{1} \vert <1\) and \(\vert \lambda_{2} \vert >1\)), then \(J(x,y)\) is called a saddle and is unstable;

  4. 4.

    If \(\lambda_{1}=1\) or \(\vert \lambda_{2} \vert =1\), then \(J(x,y)\) is called nonhyperbolic.

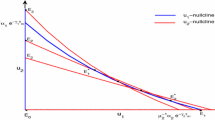
We first discuss the existence of the equilibria of model (1.1). Obviously, \(E_{1}(0,0)\), \(E_{2}( \frac{r_{1}}{a_{1}},0)\), and \(E_{3}(0, \frac {r_{2}}{a_{2}})\) are three equilibria of model (1.1). If \((H_{1})\) holds, system (1.1) admits a unique positive equilibrium \(E_{4}(x^{*}_{1},x^{*}_{2})\).

The Jacobian matrix of model (1.1) at an equilibrium \(E(x_{1},x_{2})\) is

$$\begin{aligned} J(E)=\left( \begin{matrix} (1-a_{1}x_{1})E^{*}&x_{1}(- \frac{b_{1}}{1+c_{2}x_{2}}+ \frac{b_{1}c_{2}x_{2}}{(1+c_{2}x_{2})^{2}})E^{*} \\ x_{2}(- \frac{b_{2}}{1+c_{1}x_{1}}+ \frac {b_{2}c_{1}x_{1}}{(1+c_{1}x_{1})^{2}})E_{*}&(1-a_{2}x_{2})E_{*} \end{matrix} \right), \end{aligned}$$

where \(E^{*}=\exp{(r_{1}-a_{1}x_{1}- \frac{b_{1}x_{2}}{1+c_{2}x_{2}} )}\) and \(E_{*}=\exp{(r_{2}-a_{2}x_{2}- \frac {b_{2}x_{1}}{1+c_{1}x_{1}})}\). The corresponding characteristic equation of \(J(E)\) can be written as

$$\begin{aligned} \lambda^{2}-\operatorname{tr}J(E)\lambda+\operatorname{det}J(E)=0. \end{aligned}$$
(2.1)

Now we are in the position of discussing the local stability of the equilibria of model (1.1).

Case 1. For \(E_{1}(0,0)\), we have

$$\begin{aligned} J(E_{1})=\left( \begin{matrix} \exp(r_{1})&0 \\ 0&\exp(r_{2}) \end{matrix} \right). \end{aligned}$$

Since two eigenvalues of \(J(E_{0})\) are \(\lambda_{1}=e^{r_{1}}>1\) and \(\lambda _{2}=e^{r_{2}}>1\), respectively, from Lemma 2.1 we obtain that \(E_{0}(0,0)\) is a source.

Case 2. For \(E_{2}( \frac{r_{1}}{a_{1}},0)\), we have

$$\begin{aligned} J(E_{2})=\left( \begin{matrix} 1-r_{1}&- \frac{r_{1}b_{1}}{a_{1}} \\ 0&\exp( \frac{a_{1}r_{2}-b_{2}r_{1}+c_{1}r_{1}r_{2}}{c_{1}r_{1}+a_{1}} ) \end{matrix} \right). \end{aligned}$$

In view of \(a_{1}r_{2}-b_{2}r_{1}+c_{1}r_{1}r_{2}>0\), from Lemma 2.1 we have the following conclusions:

  1. 1.

    If \(0< r_{1}<2\), then \(E_{2}( \frac{r_{1}}{a_{1}},0)\) is a saddle.

  2. 2.

    If \(r_{1}=2\), then \(E_{2}( \frac{r_{1}}{a_{1}},0)\) is nonhyperbolic.

  3. 3.

    If \(r_{1}>2\), then \(E_{2}( \frac{r_{1}}{a_{1}},0)\) is a source.

Case 3. For \(E_{3}(0, \frac{r_{2}}{a_{2}})\), we have

$$J(E_{3})=\left( \begin{matrix} \exp( \frac{a_{2}r_{1}-b_{1}r_{2}+c_{2}r_{1}r_{2}}{c_{2}r_{2}+a_{2}})&0 \\ - \frac{r_{2}b_{2}}{a_{2}}&1-r_{2} \end{matrix} \right). $$

In view of \(a_{2}r_{1}-b_{1}r_{2}+c_{2}r_{1}r_{2}>0\), from Lemma 2.1 we have the following conclusions:

  1. 1.

    If \(0< r_{2}<2\), then \(E_{3}(0, \frac{r_{2}}{a_{2}})\) is a saddle.

  2. 2.

    If \(r_{2}=2\), then \(E_{3}(0, \frac{r_{2}}{a_{2}})\) is nonhyperbolic.

  3. 3.

    If \(r_{2}>2\), then \(E_{3}(0, \frac{r_{2}}{a_{2}})\) is a source.

Case 4. For \(E_{4}(x^{*}_{1},x^{*}_{2})\), we have

$$J(E_{4})=\left( \begin{matrix} 1-a_{1}x^{*}_{1}&x^{*}_{1}(- \frac {b_{1}}{1+c_{2}x^{*}_{2}}+ \frac {b_{1}c_{2}x^{*}_{2}}{(1+c_{2}x^{*}_{2})^{2}}) \\ x^{*}_{2}(- \frac{b_{2}}{1+c_{1}x^{*}_{1}}+ \frac{b_{2}c_{1}x^{*}_{1}}{(1+c_{1}x^{*}_{1})^{2}})&1-a_{2}x^{*}_{2} \end{matrix} \right). $$

The corresponding characteristic equation of \(J(E_{4})\) can be written as

$$\begin{aligned} \lambda^{2}-\operatorname{tr}J(E_{4})\lambda+\operatorname{det}J(E_{4})=0, \end{aligned}$$
(2.2)

where

$$\begin{aligned} \operatorname{tr}J(E_{4})=2-a_{1}x^{*}_{1}-a_{2}x^{*}_{2},\qquad \operatorname{det}J(E_{4})=\bigl(1-a_{1}x^{*}_{1} \bigr) \bigl(1-a_{2}x^{*}_{2}\bigr)-x^{*}_{1}x^{*}_{2}A_{1}A_{2} \end{aligned}$$

and

$$A_{1}= \frac{b_{1}}{1+c_{2}x^{*}_{2}}- \frac {b_{1}c_{2}x^{*}_{2}}{(1+c_{2}x^{*}_{2})^{2}},\qquad A_{2}= \frac {b_{2}}{1+c_{1}x^{*}_{1}}- \frac{b_{2}c_{1}x^{*}_{1}}{(1+c_{1}x^{*}_{1})^{2}}. $$

Hence,

$$\begin{aligned} F(1)= \frac{x^{*}_{1}x^{*}_{2} [a_{1}a_{2}(1+c_{1}x^{*}_{1})^{2}(1+c_{2}x^{*}_{2})^{2}-b_{1}b_{2} ]}{(1+c_{1}x^{*}_{1})^{2}(1+c_{2}x^{*}_{2})^{2}}. \end{aligned}$$

Obviously, if \(b_{1}b_{2}< a_{1}a_{2}(1+c_{1}x^{*}_{1})^{2}(1+c_{2}x^{*}_{2})^{2}\stackrel{\mathrm {def}}{=}{K_{1}}\), then \(F(1)>0\).

Furthermore, we have

$$\begin{aligned} F(-1)= \frac {(1+c_{1}x^{*}_{1})^{2}(1+c_{2}x^{*}_{2})^{2}(a_{1}x^{*}_{1}-2)(a_{2}x^{*}_{2}-2)-b_{1}b_{2}x^{*}_{1}x^{*}_{2}}{(1+c_{1}x^{*}_{1})^{2}(1+c_{2}x^{*}_{2})^{2}}. \end{aligned}$$

Hence, if

$$b_{1}b_{2}= \frac {(1+c_{1}x^{*}_{1})^{2}(1+c_{2}x^{*}_{2})^{2}(a_{1}x^{*}_{1}-2)(a_{2}x^{*}_{2}-2)}{x^{*}_{1}x^{*}_{2}}\stackrel {\mathrm{def}}{=} {K_{2}}, $$

then \(F(-1)=0\). Assume that \(a_{1}x^{*}_{1}-2>0\) and \(a_{2}x^{*}_{2}-2>0\). If \(b_{1}b_{2}< K_{2}\), then we have \(F(-1)>0\), and if \(b_{1}b_{2}>K_{2}\), then we have \(F(-1)<0\).

On the other hand, we have

$$\operatorname{det}J(E_{4})-1= \frac {(1+c_{1}x^{*}_{1})^{2}(1+c_{2}x^{*}_{2})^{2}(a_{1}a_{2}x^{*}_{1}x^{*}_{2}-a_{1}x^{*}_{1}-a_{2}x^{*}_{2})-b_{1}b_{2}x^{*}_{1}x^{*}_{2}}{(1+c_{1}x^{*}_{1})^{2}(1+c_{2}x^{*}_{2})^{2}}. $$

Hence, if

$$b_{1}b_{2}= \frac {(1+c_{1}x^{*}_{1})^{2}(1+c_{2}x^{*}_{2})^{2}(a_{1}a_{2}x^{*}_{1}x^{*}_{2}-a_{1}x^{*}_{1}-a_{2}x^{*}_{2})}{x^{*}_{1}x^{*}_{2}}\stackrel {\mathrm{def}}{=} {K_{3}}, $$

then \(\operatorname{det}J(E_{4})=1\). Assume that \(a_{1}a_{2}x^{*}_{1}x^{*}_{2}-a_{1}x^{*}_{1}-a_{2}x^{*}_{2}>0\). If \(b_{1}b_{2}>K_{3}\), then we have \(\operatorname{det}J(E_{4})<1\), and if \(b_{1}b_{2}< K_{3}\), then we have \(\operatorname{det}J(E_{4})>1\).

Now, we are concerned with the stability property of the positive equilibrium \(E_{4}(x^{*}_{1},x^{*}_{2})\). Assume that \(a_{1}x^{*}_{1}-2>0, a_{2}x^{*}_{2}-2>0\), and \(a_{1}a_{2}x^{*}_{1}x^{*}_{2}-a_{1}x^{*}_{1}-a_{2}x^{*}_{2}>0\). By simple calculation we have \(K_{1}>K_{3}>K_{2}\). Then from Lemma 2.1 it follows that:

  1. 1.

    If \(b_{1}b_{2}< K_{2}\), then \(E_{4}(x^{*}_{1},x^{*}_{2})\) is a source.

  2. 2.

    If \(K_{2}< b_{1}b_{2}< K_{1}\), then \(E_{4}(x^{*}_{1},x^{*}_{2})\) is a saddle.

  3. 3.

    If \(K_{2}=b_{1}b_{2}< K_{1}\), then \(E_{4}(x^{*}_{1},x^{*}_{2})\) is nonhyperbolic.

3 Global stability

Previously, we have discussed the local stability of the equilibria of system (1.1). In this section, we give a set of sufficient conditions that ensure the global attractivity of the unique positive equilibrium on the rectangle \((0, \frac{r_{1}}{a_{1}})\times(0, \frac {r_{2}}{a_{2}})\).

Theorem 3.1

In addition to \((H_{1})\), further assume that

$$(H_{2})\quad r_{i}\leq1,\quad i=1,2. $$

Then system (1.1) admits a unique positive equilibrium \((x^{*}_{1},x^{*}_{2})\), which is globally stable.

Now let us state several lemmas, which will be useful in the proof of Theorem 3.1.

Lemma 3.1

[1]

Let \(f(u)=u\exp(\alpha -\beta u)\), where α and β are positive constants. Then \(f(u)\) is nondecreasing for \(u\in(0, \frac{1}{\beta}]\).

Lemma 3.2

[1]

Assume that the sequence \({u(n)}\) satisfies

$$u(n+1)=u(n)\exp\bigl(\alpha-\beta u(n)\bigr),\quad n=1,2,\ldots, $$

where α and β are positive constants, and \(u(0)>0\). Then:

  1. (i)

    If \(\alpha<2\), then \(\lim_{n\rightarrow+\infty} u(n)= \frac{\alpha}{\beta}\).

  2. (ii)

    If \(\alpha\leq1\), then \(u(n)\leq\frac{1}{\beta}, n=2,3,\ldots\) .

Lemma 3.3

[15]

Suppose that the functions \(f,g: Z_{+}\times[0,\infty)\) satisfy \(f(n,x)\leq g(n,x) (f(n,x)\geq g(n,x))\) for \(n\in Z_{+}\) and \(g(n,x)\) is nondecreasing with respect to x. If \({u(n)}\) are the nonnegative solutions of the difference equations

$$\begin{aligned} x(n+1)=f\bigl(n,x(n)\bigr), \qquad u(n+1)=g\bigl(n,u(n)\bigr), \end{aligned}$$

respectively, and \(x(0)\leq u(0)\) \((x(0)\geq u(0))\), then

$$\begin{aligned} x(n)\leq u(n), \qquad\bigl(x(n)\geq u(n)\bigr)\quad \textit{for all } n\geq0. \end{aligned}$$

Proof of Theorem 3.1

Let \({(x_{1}(n),x_{2}(n))}\) be any positive solution of system (1.1). Denoting

$$\begin{aligned} &\liminf_{n\rightarrow+\infty}x_{1}(n)=m_{1},\qquad \limsup _{n\rightarrow+\infty} x_{1}(n)=M_{1}, \\ &\liminf_{t\rightarrow+\infty}x_{2}(n)=m_{2},\qquad \limsup _{n\rightarrow+\infty} x_{2}(n)=M_{2}, \end{aligned}$$

we claim that, under the assumptions of Theorem 3.1, \(M_{1}=m_{1}=x^{*}_{1}\) and \(M_{2}=m_{2}=x^{*}_{2}\).

From the first equation of system (1.1) we obtain

$$\begin{aligned} x_{1}(n+1)&=x_{1}(n)\exp{ \biggl[r_{1}-a_{1}x_{1}(n)- \frac {b_{1}x_{2}(n)}{1+c_{2}x_{2}(n)} \biggr]} \\ &\leq x_{1}(n)\exp{\bigl[r_{1}-a_{1}x_{1}(n) \bigr]}. \end{aligned}$$
(3.1)

Consider the following auxiliary equation:

$$\begin{aligned} u(n+1)=u(n)\exp{\bigl[r_{1}-a_{1}u(n) \bigr]}. \end{aligned}$$
(3.2)

By Lemma 3.2(ii), because of \(r_{1}\leq1\), we obtain \(u(n)\leq \frac{1}{a_{1}}\) for all \(n\geq2\), where \(u(n)\) is an arbitrary positive solution of (3.2) with initial value \(u(0)>0\). By Lemma 3.1, \(f(u)=u\exp(r_{1}-a_{1}u)\) is nondecreasing for \(u\in (0, \frac{1}{a_{1}}]\). Based on Lemma 3.3, we obtain \(x_{1}(n)\leq u(n)\) for all \(n\geq2\), where \(u(n)\) is the solution of (3.2) with initial value \(u(2)=x_{1}(2)\). By Lemma 3.2(i) we obtain that

$$\begin{aligned} M_{1}=\limsup_{n\rightarrow+\infty} x_{1}(n)\leq\lim_{n\rightarrow+\infty} u(n)= \frac{r_{1}}{a_{1}}. \end{aligned}$$
(3.3)

From the second equation of system (1.1) we obtain

$$\begin{aligned} x_{2}(n+1)&=x_{2}(n)\exp{\biggl[r_{2}-a_{2}x_{2}(n)- \frac {b_{2}x_{1}(n)}{1+c_{1}x_{1}(n)}\biggr]} \\ &\leq x_{2}(n)\exp{\bigl[r_{2}-a_{2}x_{2}(n) \bigr].} \end{aligned}$$

Similarly to the analysis of (3.1)-(3.3), we have

$$\begin{aligned} M_{2}=\limsup_{n\rightarrow+\infty} x_{2}(n) \leq\frac {r_{2}}{a_{2}}. \end{aligned}$$
(3.4)

Then, for a sufficiently small constant \(\varepsilon>0\), without loss of generality, it follows from (3.3) and (3.4) that there exists an integer \(n_{1}>2\) such that, for all \(n>n_{1}\),

$$\begin{aligned} x_{1}(n)< \frac{r_{1}}{a_{1}}+\varepsilon\stackrel{ \mathrm {def}}{=} {M^{(1)}_{1}},\qquad x_{2}(n)< \frac{r_{2}}{a_{2}}+\varepsilon \stackrel{\mathrm{def}}{=} {M^{(1)}_{2}}. \end{aligned}$$
(3.5)

For \(n>n_{1}\), the second inequality of (3.5), combined with the first equation of system (1.1), leads to

$$\begin{aligned} x_{1}(n+1)&=x_{1}(n)\exp{ \biggl[r_{1}-a_{1}x_{1}(n)- \frac {b_{1}x_{2}(n)}{1+c_{2}x_{2}(n)} \biggr]} \\ &\geq x_{1}(n)\exp{\biggl[r_{1}-a_{1}x_{1}(n)- \frac {b_{1}M^{(1)}_{2}}{1+c_{2}M^{(1)}_{2}}\biggr]}. \end{aligned}$$
(3.6)

Consider the auxiliary equation

$$\begin{aligned} u(n+1)=u(n)\exp{\biggl[r_{1}-a_{1}u(n)- \frac {b_{1}M^{(1)}_{2}}{1+c_{2}M^{(1)}_{2}}\biggr]}. \end{aligned}$$
(3.7)

Since \(r_{1}\leq1\), according to Lemma 3.2(ii), we obtain \(u(n)\leq \frac{1}{a_{1}}\) for all \(n\geq n_{1}\), where \(u(n)\) is an arbitrary positive solution of (3.7) with initial value \(u(n_{1})>0\). By Lemma 3.1, \(f(u)=u\exp(r_{1}-a_{1}u- \frac {b_{1}M^{(1)}_{2}}{1+c_{2}M^{(1)}_{2}})\) is nondecreasing for \(u\in (0, \frac{1}{a_{1}}]\). According to Lemma 3.3, we obtain \(x_{1}(n)\geq u(n)\) for all \(n\geq n_{1}\), where \(u(n)\) is the solution of (3.7) with the initial value \(u(n_{1})=x_{1}(n_{1})\). According to Lemma 3.2(i), we have

$$\begin{aligned} m_{1}=\liminf_{n\rightarrow+\infty} x_{1}(n)\geq\lim_{n\rightarrow+\infty} u(n)= \frac{r_{1}- \frac {b_{1}M^{(1)}_{2}}{1+c_{2}M^{(1)}_{2}}}{a_{1}}. \end{aligned}$$
(3.8)

The first inequality of (3.5), combined with the second equation of system (1.1), leads to

$$\begin{aligned} x_{2}(n+1)&=x_{2}(n)\exp{\biggl[r_{2}-a_{2}x_{2}(n)- \frac {b_{2}x_{1}(n)}{1+c_{1}x_{1}(n)}\biggr]} \\ &\geq x_{2}(n)\exp{\biggl[r_{2}-a_{2}x_{2}(n)- \frac {b_{2}M^{(1)}_{1}}{1+c_{1}M^{(1)}_{1}}\biggr].} \end{aligned}$$

Similarly to the analysis of (3.6)-(3.8), we have

$$\begin{aligned} m_{2}=\liminf_{n\rightarrow+\infty} x_{2}(n) \geq\frac {r_{2}- \frac{b_{2}M^{(1)}_{1}}{1+c_{1}M^{(1)}_{1}}}{a_{2}}. \end{aligned}$$
(3.9)

Then, for the above \(\varepsilon>0\), there exists an integer \(n_{2}>n_{1}\) such that, for all \(n>n_{2}\),

$$\begin{aligned} \begin{aligned} & x_{1}(n)> \frac{r_{1}- \frac {b_{1}M^{(1)}_{2}}{1+c_{2}M^{(1)}_{2}}}{a_{1}}-\varepsilon\stackrel{ \mathrm {def}}{=} {m^{(1)}_{1}}, \\ & x_{2}(n)> \frac{r_{2}- \frac {b_{2}M^{(1)}_{1}}{1+c_{1}M^{(1)}_{1}}}{a_{2}}-\varepsilon\stackrel{\mathrm {def}}{=} {m^{(1)}_{2}}. \end{aligned} \end{aligned}$$
(3.10)

For \(n>n_{2}\), the second inequality of (3.10), combined with the first equation of system (1.1), leads to

$$\begin{aligned} x_{1}(n+1)&=x_{1}(n)\exp{ \biggl[r_{1}-a_{1}x_{1}(n)- \frac {b_{1}x_{2}(n)}{1+c_{2}x_{2}(n)} \biggr]} \\ &\leq x_{1}(n)\exp{\biggl[r_{1}-a_{1}x_{1}(n)- \frac {b_{1}m^{(1)}_{2}}{1+c_{2}m^{(1)}_{2}}\biggr]}. \end{aligned}$$
(3.11)

Similarly to the analysis of (3.1)-(3.3), we have

$$\begin{aligned} M_{1}=\limsup_{n\rightarrow+\infty} x_{1}(n)\leq\frac {r_{1}- \frac{b_{1}m^{(1)}_{2}}{1+c_{2}m^{(1)}_{2}}}{a_{1}}. \end{aligned}$$
(3.12)

The first inequality of (3.10), combined with the second equation of system (1.1), leads to

$$\begin{aligned} x_{2}(n+1)&=x_{2}(n)\exp{\biggl[r_{2}-a_{2}x_{2}(n)- \frac {b_{2}x_{1}(n)}{1+c_{1}x_{1}(n)}\biggr]} \\ &\leq x_{2}(n)\exp{\biggl[r_{2}-a_{2}x_{2}(n)- \frac {b_{2}m^{(1)}_{1}}{1+c_{1}m^{(1)}_{1}}\biggr]}. \end{aligned}$$
(3.13)

Similarly to the analysis of (3.1)-(3.3), we have

$$\begin{aligned} M_{2}=\limsup_{n\rightarrow+\infty} x_{2}(n) \leq\frac {r_{2}- \frac{b_{2}m^{(1)}_{1}}{1+c_{1}m^{(1)}_{1}}}{a_{2}}. \end{aligned}$$
(3.14)

Then, for the above \(\varepsilon>0\), it follows from (3.12) and (3.14) that there exists an integer \(n_{3}>n_{2}\) such that, for all \(n>n_{3}\),

$$\begin{aligned} \begin{aligned}&x_{1}(n)< \frac{r_{1}- \frac {b_{1}m^{(1)}_{2}}{1+c_{2}m^{(1)}_{2}}}{a_{1}}+ \frac{\varepsilon }{2} \stackrel{\mathrm{def}}{=} {M^{(2)}_{1}}, \\ &x_{2}(n)< \frac{r_{2}- \frac {b_{2}m^{(1)}_{1}}{1+c_{1}m^{(1)}_{1}}}{a_{2}}+ \frac{\varepsilon }{2}\stackrel{ \mathrm{def}}{=} {M^{(2)}_{2}}. \end{aligned} \end{aligned}$$
(3.15)

Obviously,

$$\begin{aligned} M^{(2)}_{1}< M^{(1)}_{1},\qquad M^{(2)}_{2}< M^{(1)}_{2}. \end{aligned}$$
(3.16)

For \(n>n_{3}\), the second inequality of (3.15), combined with the first equation of system (1.1), leads to

$$\begin{aligned} x_{1}(n+1)&=x_{1}(n)\exp{ \biggl[r_{1}-a_{1}x_{1}(n)- \frac {b_{1}x_{2}(n)}{1+c_{2}x_{2}(n)} \biggr]} \\ &\geq x_{1}(n)\exp{\biggl[r_{1}-a_{1}x_{1}(n)- \frac {b_{1}M^{(2)}_{2}}{1+c_{2}M^{(2)}_{2}}\biggr]}. \end{aligned}$$
(3.17)

Similarly to the analysis of (3.6)-(3.8), we have

$$\begin{aligned} m_{1}=\liminf_{n\rightarrow+\infty} x_{1}(n)\geq\frac {r_{1}- \frac{b_{1}M^{(2)}_{2}}{1+c_{2}M^{(2)}_{2}}}{a_{1}}. \end{aligned}$$
(3.18)

The first inequality of (3.15), combined with the second equation of system (1.1), leads to

$$\begin{aligned} x_{2}(n+1)&=x_{2}(n)\exp{\biggl[r_{2}-a_{2}x_{2}(n)- \frac {b_{2}x_{1}(n)}{1+c_{1}x_{1}(n)}\biggr]} \\ &\geq x_{2}(n)\exp{\biggl[r_{2}-a_{2}x_{2}(n)- \frac {b_{2}M^{(2)}_{1}}{1+c_{1}M^{(2)}_{1}}\biggr].} \end{aligned}$$

Similarly to the analysis of (3.6)-(3.8), we have

$$\begin{aligned} m_{2}=\liminf_{n\rightarrow+\infty} x_{2}(n) \geq\frac {r_{2}- \frac{b_{2}M^{(2)}_{1}}{1+c_{1}M^{(2)}_{1}}}{a_{2}}. \end{aligned}$$
(3.19)

Then, for the above \(\varepsilon>0\), it follows from (3.18) and (3.19) that there exists an integer \(n_{4}>n_{3}\) such that, for all \(n>n_{4}\),

$$\begin{aligned} \begin{aligned}& x_{1}(n)> \frac{r_{1}- \frac {b_{1}M^{(2)}_{2}}{1+c_{2}M^{(2)}_{2}}}{a_{1}}- \frac{\varepsilon }{2} \stackrel{\mathrm{def}}{=} {m^{(2)}_{1}}, \\ &x_{2}(n)> \frac{r_{2}- \frac {b_{2}M^{(2)}_{1}}{1+c_{1}M^{(2)}_{1}}}{a_{2}}- \frac{\varepsilon }{2}\stackrel{ \mathrm{def}}{=} {m^{(2)}_{2}}. \end{aligned} \end{aligned}$$
(3.20)

Obviously,

$$\begin{aligned} m^{(1)}_{1}< m^{(2)}_{1},\qquad m^{(1)}_{2}< m^{(2)}_{2}. \end{aligned}$$
(3.21)

Continuing the above steps, we can get four sequences \(\{M^{(n)}_{i}\}, \{m^{(n)}_{i}\}, i=1,2, n=1,2,\ldots\) , such that, for \(n\geq2\),

$$\begin{aligned} \begin{aligned}& M^{(n)}_{1}= \frac{r_{1}- \frac {b_{1}m^{(n-1)}_{2}}{1+c_{2}m^{(n-1)}_{2}}}{a_{1}}+ \frac {\varepsilon}{n}; \qquad M^{(n)}_{2}= \frac{r_{2}- \frac{b_{2}m^{(n-1)}_{1}}{1+c_{1}m^{(n-1)}_{1}}}{a_{2}}+ \frac {\varepsilon}{n}; \\ &m^{(n)}_{1}= \frac{r_{1}- \frac {b_{1}M^{(n)}_{2}}{1+c_{2}M^{(n)}_{2}}}{a_{1}}- \frac{\varepsilon }{n};\qquad m^{(n)}_{2}= \frac{r_{2}- \frac {b_{2}M^{(n)}_{1}}{1+c_{1}M^{(n)}_{1}}}{a_{2}}- \frac{\varepsilon }{n}. \end{aligned} \end{aligned}$$
(3.22)

Clearly, we have

$$\begin{aligned} m^{(n)}_{i}\leq m_{i}\leq M_{i}\leq M^{(n)}_{i},\quad i=1,2, n=1,2,\ldots. \end{aligned}$$
(3.23)

Now, by means of the inductive method we will prove that \(\{ M^{(n)}_{1}\}, \{M^{(n)}_{2}\}\) are decreasing and \(\{m^{(n)}_{1}\} , \{m^{(n)}_{2}\}\) are increasing.

First of all, from (3.16) and (3.21) it is clear that

$$M^{(2)}_{i}< M^{(1)}_{i},\qquad m^{(2)}_{i}>m^{(1)}_{i},\quad i=1,2. $$

Let us assume that our claim is true for n, that is,

$$M^{(n)}_{i}< M^{(n-1)}_{i},\qquad m^{(n)}_{i}>m^{(n-1)}_{i},\quad i=1,2. $$

Again, since the function \(g(x)= \frac{bx}{1+cx}\ (b,c>0)\) is strictly increasing, we immediately obtain

$$\begin{aligned} &M^{(n+1)}_{1}= \frac{r_{1}- \frac {b_{1}m^{(n)}_{2}}{1+c_{2}m^{(n)}_{2}}}{a_{1}}+ \frac{\varepsilon }{n+1}< \frac{r_{1}- \frac {b_{1}m^{(n-1)}_{2}}{1+c_{2}m^{(n-1)}_{2}}}{a_{1}}+ \frac {\varepsilon}{n}\stackrel{\mathrm{def}}{=} {M^{(n)}_{1}}; \\ &M^{(n+1)}_{2}= \frac{r_{2}- \frac {b_{2}m^{(n)}_{1}}{1+c_{1}m^{(n)}_{1}}}{a_{2}}+ \frac{\varepsilon }{n+1}< \frac{r_{2}- \frac {b_{2}m^{(n-1)}_{1}}{1+c_{1}m^{(n-1)}_{1}}}{a_{2}}+ \frac {\varepsilon}{n}\stackrel{\mathrm{def}}{=} {M^{(n)}_{2}}; \\ &m^{(n+1)}_{1}= \frac{r_{1}- \frac {b_{1}M^{(n+1)}_{2}}{1+c_{2}M^{(n+1)}_{2}}}{a_{1}}- \frac {\varepsilon}{n+1}> \frac{r_{1}- \frac {b_{1}M^{(n)}_{2}}{1+c_{2}M^{(n)}_{2}}}{a_{1}}- \frac{\varepsilon }{n}\stackrel{\mathrm{def}}{=} {m^{(n)}_{1}}; \\ &m^{(n+1)}_{2}= \frac{r_{2}- \frac {b_{2}M^{(n+1)}_{1}}{1+c_{1}M^{(n+1)}_{1}}}{a_{2}}- \frac {\varepsilon}{n+1}> \frac{r_{2}- \frac {b_{2}M^{(n)}_{1}}{1+c_{1}M^{(n)}_{1}}}{a_{2}}- \frac{\varepsilon }{n}\stackrel{\mathrm{def}}{=} {m^{(n)}_{2}}. \end{aligned}$$

These inequalities show that \({\{M^{(n)}_{1}\}}\) and \({\{M^{(n)}_{2}\} }\) are decreasing, \({\{m^{(n)}_{1}\}}\) and \({\{m^{(n)}_{2}\}}\) are increasing. Let

$$\begin{aligned} & \lim_{n\rightarrow+\infty} {M^{(n)}_{1}}= \bar {x}_{1},\qquad \lim_{n\rightarrow+\infty} {M^{(n)}_{2}}= \bar {x}_{2}, \end{aligned}$$
(3.24)
$$\begin{aligned} & \lim_{n\rightarrow+\infty} {m^{(n)}_{1}}= \underline {x}_{1}, \qquad \lim_{n\rightarrow+\infty} {m^{(n)}_{2}}= \underline{x}_{2}. \end{aligned}$$
(3.25)

Letting \(n\rightarrow+\infty\) in (3.22), we obtain

$$\begin{aligned} & \bar{x}_{1}= \frac{r_{1}- \frac{b_{1}\underline {x}_{2}}{1+c_{2}\underline{x}_{2}}}{a_{1}},\qquad \bar{x}_{2}= \frac {r_{2}- \frac{b_{2}\underline{x}_{1}}{1+c_{1}\underline {x}_{1}}}{a_{2}}, \end{aligned}$$
(3.26)
$$\begin{aligned} &\underline{x}_{1}= \frac{r_{1}- \frac{b_{1}\bar {x}_{2}}{1+c_{2}\bar{x}_{2}}}{a_{1}},\qquad \underline{x}_{2}= \frac{r_{2}- \frac{b_{2}\bar{x}_{1}}{1+c_{1}\bar{x}_{1}}}{a_{2}}. \end{aligned}$$
(3.27)

Equations (3.26) and (3.27) are equivalent to

$$\begin{aligned} & a_{1}\bar{x}_{1}+ \frac{b_{1}\underline{x}_{2}}{1+c_{2}\underline {x}_{2}}=r_{1},\qquad a_{2}\bar{x}_{2}+ \frac{b_{2}\underline {x}_{1}}{1+c_{1}\underline{x}_{1}}=r_{2}, \end{aligned}$$
(3.28)
$$\begin{aligned} & a_{1}\underline{x}_{1}+ \frac{b_{1}\bar{x}_{2}}{1+c_{2}\bar {x}_{2}}=r_{1},\qquad a_{2}\underline{x}_{2}+ \frac{b_{2}\bar {x}_{1}}{1+c_{1}\bar{x}_{1}}=r_{2}. \end{aligned}$$
(3.29)

Equations (3.28) and (3.29) show that \((\bar {x}_{1},\bar {x}_{2})\) and \((\underline{x}_{1},\underline{x}_{2})\) are solutions of system (1.1). However, under the assumptions of Theorem 3.1, system (1.1) admits a unique positive solution \((x^{*}_{1},x^{*}_{2}) \). Therefore

$$\begin{aligned} M_{1}=m_{1}= \lim_{n\rightarrow+\infty }x_{1}(n)=x^{*}_{1},\qquad M_{2}=m_{2}= \lim_{n\rightarrow+\infty} x_{2}(n)=x^{*}_{2}. \end{aligned}$$
(3.30)

Thus, the unique interior equilibrium \(E(x^{*}_{1},x^{*}_{2})\) is globally attractive. This completes the proof of Theorem 3.1. □

4 Numeric simulations

In this section, we give four examples to illustrate the feasibility of the main results.

Example 4.1

Consider the following competitive system:

$$\begin{aligned} \begin{aligned}&x_{1}(n+1)=x_{1}(n)\exp{ \biggl[0.5-0.5x_{1}(n)- \frac {x_{2}(n)}{1+x_{2}(n)}\biggr]}, \\ &x_{2}(n+1)=x_{2}(n)\exp{\biggl[0.7-1.5x_{2}(n)- \frac {x_{1}(n)}{1+x_{1}(n)}\biggr]}. \end{aligned} \end{aligned}$$
(4.1)

Correspondingly to system (1.1), we have \(r_{1}=0.5,r_{2}=0.7, a_{1}=0.5,a_{2}=1.5, b_{1}=b_{2}=1, c_{1}=c_{2}=1\). By calculation we see that the positive equilibrium \(E(x^{*}_{1},x^{*}_{2})\approx (0.6667, 0.2000)\), \(r_{1}(a_{2}+c_{2}r_{2})= \frac {11}{10}>b_{1}r_{2}= \frac {7}{10}\), \(r_{2}(a_{1}+c_{1}r_{1})= \frac {7}{10}>b_{2}r_{1}= \frac{1}{2}\), \(r_{1}, r_{2}<1\). All the conditions of Theorem 3.1 are satisfied, and the unique positive equilibrium \(E(x^{*}_{1},x^{*}_{2})\) is globally attractive. Figure 2 also supports our finding. Figure 3 shows the bifurcation diagrams of species \(x_{1}\) with initial condition \((x(0), y(0))=(0.14, 0.19)\) and \(r_{1}=0.5:0.001:4\). The system undergoes a series of periodic-doubling bifurcations wherein a \(2^{k}\)-cycle loses stability.

Figure 2
figure 2

Numeric simulations of system ( 4.1 ) with initial conditions \(\pmb{(x(0), y(0))=(0.14, 0.19), (0.37, 0.009), (0.95, 0.024)}\) , and \(\pmb{(0.60, 0.82)}\) .

Full size image
Figure 3
figure 3

The flip bifurcation of the first component of the solution \(\pmb{(x_{1}(n),x_{2}(n))}\) of system ( 4.1 ) with initial condition \(\pmb{(x(0), y(0))=(0.14, 0.19)}\) .

Full size image

Example 4.2

Consider the following competitive system:

$$\begin{aligned} \begin{aligned}& x_{1}(n+1)=x_{1}(n)\exp{ \biggl[0.4-0.3x_{1}(n)- \frac {0.1x_{2}(n)}{1+x_{2}(n)}\biggr]}, \\ &x_{2}(n+1)=x_{2}(n)\exp{\biggl[0.2-0.1x_{2}(n)- \frac {0.3x_{1}(n)}{1+x_{1}(n)}\biggr]}. \end{aligned} \end{aligned}$$
(4.2)

Correspondingly to system (1.1), we have \(r_{1}=0.4,r_{2}=0.2, a_{1}=0.3,a_{2}=0.1, b_{1}=0.1,b_{2}=0.3, c_{1}=c_{2}=1\). By calculation we see that the positive equilibrium \(E(x^{*}_{1},x^{*}_{2})\approx (1.25,0.33333)\), \(r_{1}(a_{2}+c_{2}r_{2})= \frac {3}{25}>b_{1}r_{2}= \frac {1}{50}\), \(r_{2}(a_{1}+c_{1}r_{1})= \frac {7}{50}>b_{2}r_{1}= \frac{3}{25}\), \(r_{1}, r_{2}<1\). All the conditions of Theorem 3.1 are satisfied, and the unique positive equilibrium \(E(x^{*}_{1},x^{*}_{2})\) is globally attractive. Figure 4 also supports our finding. Figure 5 shows the bifurcation diagrams of species \(x_{1}\) with initial condition \((x(0), y(0))=(0.14, 0.19)\) and \(r_{1}=0.4:0.001:4\). The system undergoes a series of periodic-doubling bifurcations wherein a \(2^{k}\)-cycle loses stability.

Figure 4
figure 4

Numeric simulations of system ( 4.2 ) with initial conditions \(\pmb{(x(0), y(0))=(0.14, 0.19), (0.37, 0.009), (0.95, 0.024) }\) and \(\pmb{(0.60, 0.82)}\) .

Full size image
Figure 5
figure 5

The flip bifurcation of the first component of the solution \(\pmb{(x_{1}(n),x_{2}(n))}\) of system ( 4.2 ) with initial condition \(\pmb{(x(0), y(0))=(0.14, 0.19)}\) .

Full size image

Example 4.3

Consider the following competitive system:

$$\begin{aligned} \begin{aligned}&x_{1}(n+1)=x_{1}(n)\exp{ \biggl[0.3-0.5x_{1}(n)- \frac {0.1x_{2}(n)}{1+x_{2}(n)}\biggr]}, \\ &x_{2}(n+1)=x_{2}(n)\exp{\biggl[0.2-0.1x_{2}(n)- \frac {0.4x_{1}(n)}{1+x_{1}(n)}\biggr]}. \end{aligned} \end{aligned}$$
(4.3)

Corresponding to system (1.1), we have \(r_{1}=0.3,r_{2}=0.2, a_{1}=0.5,a_{2}=0.1, b_{1}=0.1,b_{2}=0.4, c_{1}=c_{2}=1\). By calculating, we see that the positive equilibrium \(E(x^{*}_{1},x^{*}_{2})\approx (0.52297, 0.62645)\), \(r_{1}(a_{2}+c_{2}r_{2})= \frac {9}{100}>b_{1}r_{2}= \frac {1}{50}\), \(r_{2}(a_{1}+c_{1}r_{1})= \frac {4}{25}>b_{2}r_{1}= \frac{3}{25}\), \(r_{1}, r_{2}<1\). All the conditions of Theorem 3.1 are satisfied, and the unique positive equilibrium \(E(x^{*}_{1},x^{*}_{2})\) is globally attractive. Figure 6 also supports our finding. Figure 7 shows the bifurcation diagrams of species \(x_{1}\) with initial conditions \((x(0), y(0))=(0.14, 0.19)\) and \(r_{1}=0.3:0.001:4\). The system undergoes a series of periodic-doubling bifurcations wherein a \(2^{k}\)-cycle loses stability.

Figure 6
figure 6

Numeric simulations of system ( 4.3 ) with initial conditions \(\pmb{(x(0), y(0))=(0.14, 0.19), (0.37, 0.009), (0.95, 0.024)}\) , and \(\pmb{(0.60, 0.82)}\) .

Full size image
Figure 7
figure 7

The flip bifurcation of the first component of the solution \(\pmb{(x_{1}(n),x_{2}(n))}\) of system ( 4.3 ) with the initial conditions \(\pmb{(x(0), y(0))=(0.14, 0.19)}\) .

Full size image

Example 4.4

Considering the following competitive system:

$$\begin{aligned} \begin{aligned}& x_{1}(n+1)=x_{1}(n)\exp{ \biggl[1.5-0.65x_{1}(n)- \frac {2x_{2}(n)}{1+x_{2}(n)}\biggr]}, \\ &x_{2}(n+1)=x_{2}(n)\exp{\biggl[1.5-0.75x_{2}(n)- \frac {2x_{1}(n)}{1+x_{1}(n)}\biggr]}. \end{aligned} \end{aligned}$$
(4.4)

Correspondingly to system (1.1), we have \(r_{1}=r_{2}=1.5, a_{1}=0.65,a_{2}=0.75, b_{1}=b_{2}=2, c_{1}=c_{2}=1\). By calculation we see that the positive equilibrium \(E(x^{*}_{1},x^{*}_{2})\approx (1.2736, 0.50624)\), \(r_{1}(a_{2}+c_{2}r_{2})= \frac {27}{8}>b_{1}r_{2}=3\), \(r_{2}(a_{1}+c_{1}r_{1})= \frac {129}{4}>b_{2}r_{1}=3\), \(r_{1}, r_{2}>1\). Condition \((H_{2})\) in Theorem 3.1 does not hold. However, numeric simulation (Figure 8) also shows that the system admits a unique positive equilibrium, which is globally attractive. Figure 9 shows the bifurcation diagrams of species \(x_{1}\) with initial condition \((x(0), y(0))=(0.14, 0.19)\) and \(r_{1}=1.5:0.001:4\). The system also undergoes a series of periodic-doubling bifurcations wherein a \(2^{k}\)-cycle loses stability.

Figure 8
figure 8

Numeric simulations of system ( 4.4 ) with the initial conditions \(\pmb{(x(0), y(0))=(0.14, 0.19), (0.37, 0.009), (0.95, 0.024)}\) , and \(\pmb{(0.60, 0.82)}\) .

Full size image
Figure 9
figure 9

The flip bifurcation of the first component of the solution \(\pmb{(x_{1}(n),x_{2}(n))}\) of system ( 4.4 ) with initial condition \(\pmb{(x(0), y(0))=(0.14, 0.19)}\) .

Full size image

Examples 4.1-4.3 show that the coefficients satisfy the conditions of Theorem 3.1. In Example 4.1, we can verify that \(A_{1}>0\), which represents case 1 in Lemma 1.1, whereas Examples 4.2 and 4.3 represent cases 2 and 3 in Lemma 1.1, respectively (\(A_{1}=0\), \(A_{1}<0\)). As for Example 4.4, though the coefficients of system (4.4) do not satisfy \((H_{2})\) in Theorem 3.1, Figure 8 also implies that the positive equilibrium is still globally attractive.

5 Disscussion

Chen and Teng [1] studied the local and global stability of positive equilibrium of system (1.2). In this paper, we studied the dynamic behavior of system (1.1) adding the nonlinear interinhibition terms into the model. When \(c_{1}=c_{2}=0\), system (1.1) reduces to (1.2), and conditions reduce to \(r_{1}<1, r_{2}<1, a_{1}r_{2}>b_{2}r_{1}, a_{2}r_{1}>b_{1}r_{2}\), and those conditions are equivalent to the conditions \(r_{1}<1, r_{2}<1, 1-\mu_{1}K_{1}>0, 1-\mu _{2}K_{2}>0\) in [1].

From \((H_{1})\) we obtain \(r_{1}> \frac {b_{1}r_{2}}{a_{2}+r_{2}}\) and \(r_{2}> \frac{b_{2}r_{1}}{a_{1}+r_{1}}\). Our results show that the intrinsic growth rate plays an important role in the stability property of the system. We know that when the intrinsic growth rates of the two species are fixed, if the rates of interspecific competitive coefficients are small enough, then condition \((H_{1})\) always holds, and consequently, two species can coexist in a stable state. This means that smaller interspecific competitive coefficients have positive effect to the stability property of the system.

By developing the analysis technique of [3, 24] we also obtain a set of sufficient conditions that ensure the global attractivity of the positive equilibrium. We relax the conditions in [3] and [2]. Numeric simulations also support our findings. However, Example 4.4 does not satisfy all the conditions of Theorem 3.1, and the system still admits a unique globally stable positive equilibrium. We conjecture that the conditions \(r_{i}\leq1\) in Theorem 3.1 can be relaxed to \(0< r_{i}<2\ (i=1,2)\), that is, the conditions of Theorem 3.1 still have room to improve. However, at present, we have difficulty in proving this conjecture. With the change of \(r_{i}\), we found the bifurcations in the above figures, wherein a \(2^{k}\)-cycle loses stability. We leave these two problems for future study.