1 Introduction

In 1963, Lorenz et al. found the famous Lorenz chaotic system, which can be described by the following autonomous differential equations [1]:

$$\textstyle\begin{cases} \frac{dx}{dt} = \sigma ( y - x ), \\ \frac{dy}{dt} = \rho x - y - xz, \\ \frac{dz}{dt} = xy - rz. \end{cases} $$

Since then, chaotic systems have been extensively studied, such as the Rössler system [2], Chua’s circuit [3], the Chen system [4], the Lü system [5–7], the hyperchaos Lorenz system [8], the Shimizu-Morioka system [9], the Liu system [10]. Various complex dynamical behaviors of chaotic systems are studied due to its various applications in the field of population dynamics, electric circuits, cryptology, fluid dynamics, lasers, engineering, stock exchanges, chemical reactions, etc. [11–32].

In the recent years, motivated by different applications, much work has been reported in constructing the new chaotic and hyperchaotic models [2, 10, 19, 22]. On the one hand, the hyperchaos theory is still a new field of research. On the other hand, there is no general method to obtain hyperchaotic systems. Compared with chaotic systems, hyperchaotic systems have at least two positive Lyapunov exponents and, therefore, their lowest dimension is four. To generate a hyperchaotic system, it is essential to increase the system dimension [33]. Hyperchaotic systems can be obtained by adding one more state variable to a three-dimensional chaotic system [33]. In 2009, Li et al. constructed a new chaotic system based on the Lorenz chaotic system [22]:

$$ \textstyle\begin{cases} \frac{dx}{dt} = a ( y - x ), \\ \frac{dy}{dt} = xz - y, \\ \frac{dz}{dt} = b - xy - cz. \end{cases} $$
(1)

According to the chaotic system (1), by introducing a linear feedback controller w in the first equation, and adding a first-order nonlinear differential state equation with respect to w, one gets a new 4D Lorenz-type chaotic system as follows:

$$ \textstyle\begin{cases} \frac{dx}{dt} = a ( y - x ) - ew, \\ \frac{dy}{dt} = xz - hy, \\ \frac{dz}{dt} = b - xy - cz, \\ \frac{dw}{dt} = ky - dw, \end{cases} $$
(2)

where x, y, z and w are state variables and a, b, c, d, e, h are positive parameters of system (2).

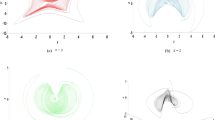
The Lyapunov exponents of the dynamical system (2) are calculated numerically for the parameter values \(a = 5\), \(b = 20\), \(c = 1\), \(d = 0.1\), \(k = 0.1\), \(e = 20.6\), \(h = 1\) with the initial state \(( x_{0},y_{0},z_{0},w_{0} ) = ( 3.2,8.5,3.5,2.0 )\). System (2) has Lyapunov exponents as \(\lambda_{\mathrm{LE}_{1}} = 0.24\), \(\lambda_{\mathrm{LE}_{2}} = 0.23\), \(\lambda_{\mathrm{LE}_{3}} = 0\), \(\lambda_{\mathrm{LE}_{4}} = - 7.56\) and the Lyapunov dimension is 3.06 for the parameters listed above (see Refs. [27] and [28] for a detailed discussion of Lyapunov exponents of strange attractors in dynamical systems). This means system (2) is really a dissipative system, and the Lyapunov dimension of system (2) is fractional. Thus, system (2) has two positive Lyapunov exponents and the strange attractor, which means the new system (2) can exhibit a variety of interesting and complex chaotic behavior. System (2) has a hyperchaotic attractor, as shown in Figure 1 and Figure 2.

Figure 1
figure 1

Chaotic attractors of system ( 2 ) in 3D spaces with \(\pmb{a = 5}\) , \(\pmb{b = 20}\) , \(\pmb{c = 1}\) , \(\pmb{d = 0.1}\) , \(\pmb{k = 0.1}\) , \(\pmb{e = 20.6}\) , \(\pmb{h = 1}\) and the initial state \(\pmb{( x_{0},y_{0},z_{0},w_{0} ) = ( 3.2,8.5,3.5,2.0 )}\) .

Full size image
Figure 2
figure 2

Chaotic attractor of system ( 2 ) in \(\pmb{yOz}\) plane with \(\pmb{a = 5}\) , \(\pmb{b = 20}\) , \(\pmb{c = 1}\) , \(\pmb{d = 0.1}\) , \(\pmb{k = 0.1}\) , \(\pmb{e = 20.6}\) , \(\pmb{h = 1}\) and the initial state \(\pmb{( x_{0},y_{0},z_{0},w_{0} ) = ( 3.2,8.5,3.5,2.0 )}\) .

Full size image

In this paper, all the simulations are carried out by using the fourth-order Runge-Kutta method with time-step \(h = 0.01\).

A coupled dynamo system can be described by the following differential equations with appropriate normalization of variables [29, 30]:

$$ \textstyle\begin{cases} \frac{dx_{1}}{dt} = - u_{1}x_{1} + x_{2}w_{1}, \\ \frac{dx_{2}}{dt} = - u_{2}x_{2} + x_{1}w_{2}, \\ \frac{dw_{1}}{dt} = q_{1} - \varepsilon_{1}w_{1} - x_{1}x_{2}, \\ \frac{dw_{2}}{dt} = q_{2} - \varepsilon_{2}w_{2} - x_{1}x_{2}, \end{cases} $$
(3)

where \(w_{1}\) and \(w_{2}\) represent the angular velocities of the rotors of two dynamos, \(x_{1}\) and \(x_{2}\) represent the currents of two dynamos, \(q_{1}\) and \(q_{2}\) are the torques applied to the rotors, \(u_{1}\), \(u_{2}\), \(\varepsilon_{1}\) and \(\varepsilon_{2}\) are positive parameters representing dissipative effects of the disk dynamo system (3).

When \(u_{1} = 0.001\), \(u_{2} = 0.0002\), \(q_{1} = 0.19\), \(q_{2} = 0.21\), \(\varepsilon_{1} = 0.15\), \(\varepsilon_{2} = 0.15\) with the initial state \(( x_{1} ( 0 ),x_{2} ( 0 ),w_{1} ( 0 ),w_{2} ( 0 ) ) = ( 3.2,8.5,3.5,2.0 )\), system (3) has a chaotic attractor, as shown in Figure 3 (also see [29]).

Figure 3
figure 3

Chaotic attractors of system ( 3 ) in 3D spaces with \(\pmb{u_{1} = 0.001}\) , \(\pmb{u_{2} = 0.0002}\) , \(\pmb{q_{1} = 0.19}\) , \(\pmb{q_{2} = 0.21}\) , \(\pmb{\varepsilon_{1} = 0.15}\) , \(\pmb{\varepsilon_{2} = 0.15}\) and the initial state \(\pmb{( x_{1} ( 0 ),x_{2} ( 0 ),w_{1} ( 0 ),w_{2} ( 0 ) ) = ( 3.2,8.5,3.5,2.0 )}\) .

Full size image

When \(u_{1} = 0.2\), \(u_{2} = 0.5\), \(q_{1} = 5.9\), \(q_{2} = 9.15\), \(\varepsilon_{1} = 0.5\), \(\varepsilon_{2} = 0.1\) with the initial state \(( x_{1} ( 0 ),x_{2} ( 0 ),w_{1} ( 0 ),w_{2} ( 0 ) ) = ( 2.2,2.0,10.5,20 )\), system (3) has a chaotic attractor, as shown in Figure 4 (also see [29])

Figure 4
figure 4

Chaotic attractors of system ( 3 ) in 3D spaces with \(\pmb{u_{1} = 0.2}\) , \(\pmb{u_{2} = 0.5}\) , \(\pmb{q_{1} = 5.9}\) , \(\pmb{q_{2} = 9.15}\) , \(\pmb{\varepsilon_{1} = 0.5}\) , \(\pmb{\varepsilon_{2} = 0.1}\) and the initial state \(\pmb{( x_{1} ( 0 ),x_{2} ( 0 ),w_{1} ( 0 ),w_{2} ( 0 ) ) = ( 2.2,2.0,10.5,20 )}\) .

Full size image

The rest of this paper is organized as follows. The invariant sets of chaotic systems (2) and (3) are analyzed in Section 2. In Section 3, ultimate bound sets for the chaotic attractors in (2) and (3) are studied using Lyapunov stability theory. To validate the ultimate bound estimation, numerical simulations are also provided. Finally, the conclusions are drawn in Section 4.

2 Invariance analysis for the chaotic attractors in (2) and (3)

The positive z-axis is invariant under the flow generated by system (2), that is to say, z-axis is positively invariant under the flow generated by system (2). However, this is not the case on the positive x-axis, y-axis and w-axis for system (2). \(x_{1}\)-axis, \(x_{2}\)-axis, \(w_{1}\)-axis and \(w_{2}\)-axis are all not positively invariant under the flow generated by system (3).

3 Ultimate bound sets for the chaotic attractors in (2) and (3)

Recently, ultimate bound estimation of chaotic systems and hyperchaotic systems has been discussed in many research studies [7, 17, 20, 31]. It is well known that there is a bounded ellipsoid in \(R^{3}\) for the Lorenz system which all orbits of the Lorenz system will eventually enter for all positive parameters [20, 31]. The ultimate bound sets can be used in chaos control and synchronization [32]. Also, the ultimate bound sets can be employed for estimation of the fractal dimension of chaotic and hyperchaotic attractors, such as the Hausdorff dimension and the Lyapunov dimension [12, 34].

Motivated by the above discussion, we will investigate the bounds of the new 4D Lorenz-type hyperchaotic system (2) and the disk dynamo system (3) in this section. The main results are described by Theorem 1 and Theorem 2.

3.1 Ultimate bound sets for the chaotic attractors in system (2)

Theorem 1

Suppose that \(\forall a > 0\), \(h > 0\), \(c > 0\), \(d > 0\). Let \(( x ( t ),y ( t ),z ( t ),w ( t ) )\) be an arbitrary solution of system (2). Then the set

$$\Omega = \biggl\{ ( x,y,z,w ) \Big\vert x^{2} \le \frac{ ( ad + ke )^{2}R^{2}}{a^{2}d^{2}},y^{2} + z^{2} \le R^{2},w^{2} \le \frac{k^{2}R^{2}}{d^{2}} \biggr\} $$

is the ultimate bound set of chaotic system (2), where

$$R^{2} = \frac{b^{2}}{\theta c},\quad \theta = \min ( h,c ) > 0. $$

Proof

Define the function

$$f ( z ) = - cz^{2} + 2bz,\quad \forall c > 0. $$

Then we can get

$$\max_{z \in R}f ( z ) = \frac{b^{2}}{c}. $$

Construct the Lyapunov function

$$ V ( X ) = V ( y,z ) = y^{2} + z^{2}. $$
(4)

Computing the derivative of \(V ( y,z )\) along the trajectory of system (2), we have

$$\begin{aligned} \frac{dV ( y,z )}{dt} \bigg|_{\text{(2)}} &= 2y\frac{dy}{dt} + 2z \frac{dz}{dt} \\ &= 2y ( xz - hy ) + 2z ( b - xy - cz ) \\ &= - 2hy^{2} - 2cz^{2} + 2bz \\ &\le - hy^{2} - cz^{2} - hy^{2} - cz^{2} + 2bz \\ &\le - hy^{2} - cz^{2} - cz^{2} + 2bz \\ &\le - \theta V ( y,z ) + f ( z ) \\ &\le - \theta V ( y,z ) + \frac{b^{2}}{c} \\ &\le - \theta \biggl( V ( y,z ) - \frac{b^{2}}{\theta c} \biggr) \\ &= - \theta \bigl( V ( y,z ) - R^{2} \bigr). \end{aligned}$$

Integrating both sides of the above inequality yields

$$V \bigl( X ( t ) \bigr) \le V \bigl( X ( t_{0} ) \bigr)e^{ - \theta ( t - t_{0} )} + \int_{t_{0}}^{t} \theta R^{2}e^{ - \theta ( t - \tau )} \,d \tau = V \bigl( X ( t_{0} ) \bigr)e^{ - \theta ( t - t_{0} )} + R^{2} \bigl( 1 - e^{ - \theta ( t - t_{0} )} \bigr). $$

Thus, we can get the following inequality:

$$\bigl[ V \bigl( X ( t ) \bigr) - R^{2} \bigr] \le \bigl[ V ( X_{0} ) - R^{2} \bigr]e^{ - \theta ( t - t_{0} )}. $$

By the definition, taking the upper limit on both sides of the above inequality as \(t \to + \infty\) results in

$$ \mathop{\overline{\lim}}_{t \to + \infty} V ( y,z ) \le R^{2}. $$
(5)

From inequality (5), we can get

$$ \vert y \vert \le R,\qquad \vert z \vert \le R. $$
(6)

Let us define another function

$$g ( w ) = - dw^{2} + 2kR \vert w \vert ,\quad \forall d > 0. $$

Then we can get

$$\max_{w \in R}g ( w ) = \frac{k^{2}R^{2}}{d}. $$

Construct another Lyapunov function

$$ V_{1} ( w ) = w^{2}, $$
(7)

Computing the derivative of Lyapunov function (7) along the trajectory of system (2), we have

$$\begin{aligned} \frac{dV_{1} ( w )}{dt} \bigg|_{\text{(2)}} &= 2w\frac{dw}{dt} \\ &= 2w ( ky - dw ) \\ &= - 2dw^{2} + 2kyw \\ &\le - dw^{2} - dw^{2} + 2k \vert y \vert \vert w \vert \\ &\le - dw^{2} - dw^{2} + 2kR \vert w \vert \\ &\le - dw^{2} + g ( w ) \\ &\le - dw^{2} + \frac{k^{2}R^{2}}{d} \\ &\le - d \biggl( V_{1} ( w ) - \frac{k^{2}R^{2}}{d^{2}} \biggr). \end{aligned} $$

Similarly, taking the upper limit on both sides of the above inequality as \(t \to + \infty\), we can get

$$ \mathop{\overline{\lim}}_{t \to + \infty} V_{1} \bigl( w ( t ) \bigr) \le \frac{k^{2}R^{2}}{d^{2}}. $$
(8)

From inequality (8), we can get

$$ \vert w \vert \le \frac{kR}{d}. $$
(9)

Define another function

$$h ( x ) = - a \vert x \vert ^{2} + 2R \biggl( a + \frac{ek}{d} \biggr) \vert x \vert ,\quad \forall a > 0. $$

Then we can get

$$\max_{x \in R}h ( x ) = \frac{ ( ad + ke )^{2}R^{2}}{ad^{2}}. $$

Construct another Lyapunov function

$$ V_{2} ( x ) = x^{2}, $$
(10)

Computing the derivative of Lyapunov function (10) along the trajectory of system (2), we have

$$\begin{aligned} \frac{dV_{2} ( x )}{dt} \bigg|_{\text{(2)}} &= 2x\frac{dx}{dt} \\ &= 2x ( ay - ax - ew ) \\ &= - 2ax^{2} + 2axy - 2exw \\ &= - ax^{2} - ax^{2} + 2 ( ay - ew )x \\ &\le - ax^{2} - a \vert x \vert ^{2} + 2 \bigl( a \vert y \vert + e \vert w \vert \bigr) \vert x \vert \\ &\le - ax^{2} - a \vert x \vert ^{2} + 2R \biggl[ a + \frac{ek}{d} \biggr] \vert x \vert \\ &\le - ax^{2} + h ( x ) \\ &\le - ax^{2} + \frac{ ( ad + ke )^{2}R^{2}}{ad^{2}} \\ &\le - a \biggl( V_{2} ( x ) - \frac{ ( ad + ke )^{2}R^{2}}{a^{2}d^{2}} \biggr). \end{aligned} $$

Similarly, taking the upper limit on both sides of the above inequality as \(t \to + \infty\), we can obtain the following inequality:

$$ \mathop{\overline{\lim}}_{t \to + \infty} V_{2} \bigl( x ( t ) \bigr) \le \frac{ ( ad + ke )^{2}R^{2}}{a^{2}d^{2}}. $$
(11)

This completes the proof. □

Remark 1

(i) According to Theorem 1 in this paper, we can get

$$\Delta = \bigl\{ ( y,z ) \vert y^{2} + z^{2} \le R^{2} \bigr\} $$

is the ultimate bound set of \(y ( t )\), \(z ( t )\) of chaotic system (2), where

$$R^{2} = \frac{b^{2}}{\theta c},\quad \theta = \min ( h,c ) > 0. $$

When \(a = 5\), \(b = 20\), \(c = 1\), \(d = 0.1\), \(k = 0.1\), \(e = 20.6\), \(h = 1\), we can see that

$$\Delta = \bigl\{ ( y,z ) \vert y^{2} + z^{2} \le 20^{2} \bigr\} $$

is the ultimate bound set of \(y ( t )\), \(z ( t )\) of chaotic system (2).

In Figure 5, we give the localization of the chaotic attractor of system (2) formed by Δ.

Figure 5
figure 5

Localization of chaotic attractor of system ( 2 ) by Δ with \(\pmb{a = 5}\) , \(\pmb{b = 20}\) , \(\pmb{c = 1}\) , \(\pmb{d = 0.1}\) , \(\pmb{k = 0.1}\) , \(\pmb{e = 20.6}\) , \(\pmb{h = 1}\) and the initial state \(\pmb{( x_{0},y_{0},z_{0},w_{0} ) = ( 3.2,8.5,3.5,2.0 )}\) .

Full size image

(ii) From Figure 5, we can see that the bounds estimate for the chaotic attractors of system (2) is conservative, we can get a smaller bound of chaotic attractors of system (2) with the help of the iteration theorem in [32] (see [32] for a detailed discussion of the bounds of chaotic systems).

3.2 Bounds for the chaotic attractors in system (3)

El-Gohary and Yassen studied the equilibrium points, chaotic attractors, limits cycles, chaos behaviors, and optimal control of system (3) in [29, 30]. We will investigate the globally attractive set of the chaotic system (3) here. We use the following generalized Lyapunov-like function:

$$ V_{\lambda,m} ( X ) = mx_{1}^{2} + \lambda x_{2}^{2} + m ( w_{1} + \lambda \eta )^{2} + \lambda ( w_{2} - m\eta )^{2}, $$
(12)

which is obviously positive definite and radially unbounded. Here, \(\lambda > 0\), \(m > 0\) and \(\eta \in R\) are arbitrary constants. Let \(X ( t ) = ( x_{1} ( t ),x_{2} ( t ),w_{1} ( t ),w_{2} ( t ) )\) be an arbitrary solution of system (3). We have the following results for system (3).

Theorem 2

Suppose that \(u_{1} > 0\), \(u_{2} > 0\), \(\varepsilon_{1} > 0\), \(\varepsilon_{2} > 0\), and let

$$L_{\lambda,m}^{2} = \frac{1}{\theta} \biggl[ \frac{m ( q_{1} + \lambda \eta \varepsilon_{1} )^{2}}{\varepsilon_{1}} + \frac{\lambda ( q_{2} - m\eta \varepsilon_{2} )^{2}}{\varepsilon_{2}} \biggr],\quad \theta = \min ( u_{1},u_{2}, \varepsilon_{1},\varepsilon_{2} ) > 0. $$

Then the estimation

$$ \bigl[ V_{\lambda,m} \bigl( X ( t ) \bigr) - L_{\lambda,m}^{2} \bigr] \le \bigl[ V_{\lambda,m} \bigl( X ( t_{0} ) \bigr) - L_{\lambda,m}^{2} \bigr]e^{ - \theta ( t - t_{0} )}. $$
(13)

holds for system (3), and thus \(\Omega_{\lambda,m} = \{ X \vert V_{\lambda,m} ( X ) \le L_{\lambda,m}^{2} \}\) is the globally exponential attractive set and positive invariant set of system (3), i.e., \(\overline{\lim}_{t \to + \infty} V_{\lambda,m} ( X ( t ) ) \le L_{\lambda,m}^{2}\).

Proof

Define the following functions:

$$ f ( w_{1} ) = - m\varepsilon_{1}w_{1}^{2} + 2mq_{1}w_{1},\qquad g ( w_{2} ) = - \lambda \varepsilon_{2}w_{2}^{2} + 2\lambda q_{2}w_{2}, $$
(14)

then we can get

$$\max_{w_{1} \in R}f ( w_{1} ) = \frac{mq_{1}^{2}}{\varepsilon_{1}},\qquad \max _{w_{2} \in R}g ( w_{2} ) = \frac{\lambda q_{2}^{2}}{\varepsilon_{2}}. $$

Differentiating the Lyapunov-like function \(V_{\lambda,m} ( X )\) in (12) with respect to time t along the trajectory of system (3) yields

$$\begin{aligned} &\frac{dV_{\lambda,m} ( X ( t ) )}{dt} \bigg|_{\text{(3)}}\\ &\quad = 2mx_{1} \frac{dx_{1}}{dt} + 2\lambda x_{2}\frac{dx_{2}}{dt} + 2m ( w_{1} + \lambda \eta )\frac{dw_{1}}{dt} + 2\lambda ( w_{2} - m\eta )\frac{dw_{2}}{dt} \\ &\quad = - 2mu_{1}x_{1}^{2} - 2\lambda u_{2}x_{2}^{2} - 2m\varepsilon_{1}w_{1}^{2} + 2m ( q_{1} - \lambda \eta \varepsilon_{1} )w_{1} - 2\lambda \varepsilon_{2}w_{2}^{2} \\ &\quad \quad {}+ 2 ( \lambda q_{2} + \lambda m\eta \varepsilon_{2} )w_{2} + 2\lambda m\eta ( q_{1} - q_{2} ) \\ &\quad \le - mu_{1}x_{1}^{2} - \lambda u_{2}x_{2}^{2} - m\varepsilon_{1} ( w_{1} + \lambda \eta )^{2} - \lambda \varepsilon_{2} ( w_{2} - m\eta )^{2} + f ( w_{1} ) \\ &\quad \quad {}+ g ( w_{2} ) + m\varepsilon_{1} \lambda^{2}\eta^{2} + \lambda \varepsilon_{2}m^{2} \eta^{2} + 2m\lambda \eta ( q_{1} - q_{2} ) \\ &\quad \le - \theta V_{\lambda,m} ( X ) + f ( w_{1} ) + g ( w_{2} ) + \bigl( m\varepsilon_{1}\lambda^{2} + \lambda \varepsilon_{2}m^{2} \bigr)\eta^{2} + 2m \lambda \eta ( q_{1} - q_{2} ) \\ &\quad \le - \theta V_{\lambda,m} ( X ) + \max_{w_{1} \in R}f ( w_{1} ) + \max_{w_{2} \in R}g ( w_{2} ) + \bigl( m \varepsilon_{1}\lambda^{2} + \lambda \varepsilon_{2}m^{2} \bigr)\eta^{2} + 2m\lambda \eta ( q_{1} - q_{2} ) \\ &\quad = - \theta V_{\lambda,m} ( X ) + \frac{mq_{1}^{2}}{\varepsilon_{1}} + \frac{\lambda q_{2}^{2}}{\varepsilon_{2}} + m\varepsilon_{1}\lambda^{2}\eta^{2} + \lambda \varepsilon_{2}m^{2}\eta^{2} + 2m\lambda \eta ( q_{1} - q_{2} ) \\ &\quad = - \theta V_{\lambda,m} ( X ) + \frac{m ( q_{1} + \lambda \eta \varepsilon_{1} )^{2}}{\varepsilon_{1}} + \frac{\lambda ( q_{2} - m\eta \varepsilon_{2} )^{2}}{\varepsilon_{2}} \\ &\quad = - \theta \bigl[ V_{\lambda,m} ( X ) - L_{\lambda,m}^{2} \bigr]. \end{aligned} $$

Thus, we have

$$\bigl[ V_{\lambda,m} \bigl( X ( t ) \bigr) - L_{\lambda,m}^{2} \bigr] \le \bigl[ V_{\lambda,m} \bigl( X ( t_{0} ) \bigr) - L_{\lambda,m}^{2} \bigr]e^{ - \theta ( t - t_{0} )} $$

and

$$\mathop{\overline{\lim}}_{t \to + \infty} V_{\lambda,m} \bigl( X ( t ) \bigr) \le L_{\lambda,m}^{2} $$

which clearly shows that \(\Omega_{\lambda,m} = \{ X \vert V_{\lambda,m} ( X ) \le L_{\lambda,m}^{2} \}\) is the globally exponential attractive set and positive invariant set of system (3).

The proof is complete. □

Remark 2

(i) In particular, let us take \({m} = 1\) in Theorem 2, we can get the results that obtained in [35]. The results presented in Theorem 2 contain the existing results in [35] as special cases.

(ii) Let us take \(u_{1} = 0.2\), \(u_{2} = 0.5\), \(q_{1} = 5.9\), \(q_{2} = 9.15\), \(\varepsilon_{1} = 0.5\), \(\varepsilon_{2} = 0.1\), \(\lambda = 1\), \(m = 1\), and \(\eta = 0\), then we can see that

$$ \Omega_{1,1} = \bigl\{ ( x_{1},x_{2},w_{1},w_{2} ) \vert x_{1}^{2} + x_{2}^{2} + ( w_{1} )^{2} + ( w_{2} )^{2} \le 95.2^{2} \bigr\} $$
(15)

is the globally exponential attractive set and positive invariant set of system (3) according to Theorem 2. Figure 6 shows chaotic attractors of system (3) in the \(( x_{1},x_{2},w_{2} )\) space defined by \(\Omega_{1,1}\). Figure 7 shows chaotic attractors of system (3) in the \(( x_{1},x_{2},w_{1} )\) space defined by \(\Omega_{1,1}\). Figure 8 shows chaotic attractors of system (3) in the \(( x_{1},w_{1},w_{2} )\) space defined by \(\Omega_{1,1}\). Figure 9 shows chaotic attractors of system (3) in the \(( x_{2},w_{1},w_{2} )\) space defined by \(\Omega_{1,1}\).

Figure 6
figure 6

Chaotic attractors of ( 3 ) in the \(\pmb{( x_{1},x_{2},w_{2} )}\) space defined by \(\pmb{\Omega_{1,1}}\) with \(\pmb{u_{1} = 0.2}\) , \(\pmb{u_{2} = 0.5}\) , \(\pmb{q_{1} = 5.9}\) , \(\pmb{q_{2} = 9.15}\) , \(\pmb{\varepsilon_{1} = 0.5}\) , \(\pmb{\varepsilon_{2} = 0.1}\) and the initial state \(\pmb{( x_{1} ( 0 ),x_{2} ( 0 ),w_{1} ( 0 ),w_{2} ( 0 ) ) = ( 2.2,2.0,10.5,20 )}\) .

Full size image
Figure 7
figure 7

Chaotic attractors of ( 3 ) in the \(\pmb{( x_{1},x_{2},w_{1} )}\) space defined by \(\pmb{\Omega_{1,1}}\) with \(\pmb{u_{1} = 0.2}\) , \(\pmb{u_{2} = 0.5}\) , \(\pmb{q_{1} = 5.9}\) , \(\pmb{q_{2} = 9.15}\) , \(\pmb{\varepsilon_{1} = 0.5}\) , \(\pmb{\varepsilon_{2} = 0.1}\) and the initial state \(\pmb{( x_{1} ( 0 ),x_{2} ( 0 ),w_{1} ( 0 ),w_{2} ( 0 ) ) = ( 2.2,2.0,10.5,20 )}\) .

Full size image
Figure 8
figure 8

Chaotic attractors of ( 3 ) in the \(\pmb{( x_{1},w_{1},w_{2} )}\) space defined by \(\pmb{\Omega_{1,1}}\) with \(\pmb{u_{1} = 0.2}\) , \(\pmb{u_{2} = 0.5}\) , \(\pmb{q_{1} = 5.9}\) , \(\pmb{q_{2} = 9.15}\) , \(\pmb{\varepsilon_{1} = 0.5}\) , \(\pmb{\varepsilon_{2} = 0.1}\) and the initial state \(\pmb{( x_{1} ( 0 ),x_{2} ( 0 ),w_{1} ( 0 ),w_{2} ( 0 ) ) = ( 2.2,2.0,10.5,20 )}\) .

Full size image
Figure 9
figure 9

Chaotic attractors of ( 3 ) in the \(\pmb{( x_{2},w_{1},w_{2} )}\) space defined by \(\pmb{\Omega_{1,1}}\) with \(\pmb{u_{1} = 0.2}\) , \(\pmb{u_{2} = 0.5}\) , \(\pmb{q_{1} = 5.9}\) , \(\pmb{q_{2} = 9.15}\) , \(\pmb{\varepsilon_{1} = 0.5}\) , \(\pmb{\varepsilon_{2} = 0.1}\) and the initial state \(\pmb{( x_{1} ( 0 ),x_{2} ( 0 ),w_{1} ( 0 ),w_{2} ( 0 ) ) = ( 2.2,2.0,10.5,20 )}\) .

Full size image

(iii) From Figures 6-9, we can see that the bounds estimate for the chaotic attractors of system (3) is conservative, we can get a smaller bound of chaotic attractors of system (3) with the help of the iteration theorem in [32] (see [32] for a detailed discussion of the bounds of chaotic systems).

4 Conclusions

This paper presents a new 4D autonomous hyperchaotic system based on Lorenz chaotic system and another coupled dynamo chaotic system. By means of Lyapunov stability theory as well as optimization theory, the bounds of the new 4D autonomous hyperchaotic system and the coupled dynamo chaotic system are estimated. To show the ultimate bound region, numerical simulations are provided.