1 Introduction

Fractional calculus is an extension of derivatives and integrals to non-integer orders and it has been widely used to model engineering and scientific problems. Many physical problems are governed by fractional differential and integral equations, and finding the solutions of these equations has been the subject of many investigators in recent years. However, it is difficult to derive the analytical solutions to most of the fractional equations. Therefore, there has been significant interest in developing numerical schemes for their solutions. Some numerical methods include the homotopy perturbation method (HPM) [1], the homotopy analysis method (HAM) [2], the variational iteration method (VIM) [3], the Adomian decomposition method (ADM) [4], and different wavelet methods, such as the Legendre wavelet [5, 6], Haar wavelet [7], Chebyshev wavelet [8–14], Bernoulli wavelet [15], and ultraspherical wavelet methods [16, 17].

The Riccati equations play a significant role in many fields of engineering and applied science such as the theory of random processes, diffusion problems, transmission-line phenomena and optimal control theory. Thus, the solving methods for the Riccati differential equations are important. There have been several methods for solving the Riccati differential equations, such as He’s variational iteration method (HVIM) [18], ADM [19], HPM [20] and piecewise VIM [21]. Moreover, Saha et al. [22] used the modified ADM method to solve the fractional Riccati differential equations, Odibat and Momani [23], Hosseinnia et al. [24] and Khan et al. [25] used the modified homotopy perturbation method (MHPM) to solve the fractional Riccati differential equations. Khan [26] used the Laplace-Adomian-Padé method, Abd-Elhameed et al. [27] used the spectral wavelets algorithms, and Mehmet et al. [28] applied an iterative reproducing kernel Hilbert space method to get the solutions of fractional Riccati differential equations.

In this paper, we consider the following Riccati differential equation:

$$ D^{\alpha}y(t)=u(t)+v(t)y(t)+w(t){\bigl[y(t) \bigr]}^{2},\quad n \leq\alpha< n+1, t>0, $$
(1)

with the initial conditions

$$ y^{(k)}(0)=g_{k},\quad k=1, 2, \ldots, n-1. $$
(2)

where α is a parameter describing of the order of fractional derivative, n is an integer, \(u(t)\), \(v(t)\) and \(w(t)\) are given functions, and \(g_{k}\) is a constant. When α is a positive integer, the fractional equation becomes the classical Riccati differential equation. Our main aim is to solve the Riccati differential equations by using sine-cosine wavelet. The sine-cosine wavelet was proposed in [29] and used to solve the variational problem. Furthermore, the sine-cosine wavelet has been used to solve the integro-differential equation [30].

We notice that the sine-cosine wavelet was constructed by sine and cosine functions, and it is more suitable to solve periodic solution problem. Moreover, since the basis functions used to construct the sine-cosine wavelet are orthogonal and have compact support, it makes the more useful and simple in actual computations. Also, the numbers of mother wavelet’s components are restricted to one, so they do not lead to the growth of complexity of calculations comparing with other wavelets. It is worthy to mention here that the CAS wavelet [31] has similar properties to the sine-cosine wavelet, but they have completely different constructs and expressions. In this paper, the sine-cosine wavelet operational matrix of fractional integration is derived firstly and used to solve the Riccati differential equations, the wavelet operational matrix method is computer oriented. The efficiency and accuracy of the presented method are shown by several examples.

The rest of the paper is organized as follows. In the next section, some necessary definitions and mathematical preliminaries of the fractional calculus are introduced. In Section 3 the error analysis of the sine-cosine wavelet bases and the sine-cosine wavelet operational matrix of fractional integral are obtained. The sine-cosine wavelet method for solving (1) with initial conditions (2) is presented in Section 4. Numerical examples are presented in Section 5. A conclusion is given in Section 6.

2 Preliminaries and notations

In this section, we present some definitions, notations and preliminaries of the fractional calculus theory which will be used in this paper.

The Riemann-Liouville fractional integral operator of order \(\alpha> 0\) of a function is defined as

$$\begin{aligned}& \bigl(I^{\alpha}u\bigr) (t)= \frac{1}{\Gamma(\alpha)} \int^{t}_{0} (t-\tau)^{\alpha-1}u(\tau)\, \mathrm{d}\tau, \quad \alpha>0, t>0, \end{aligned}$$
(3)
$$\begin{aligned}& \bigl(I^{0} u\bigr) (t)= u(t). \end{aligned}$$
(4)

The Riemann-Liouville fractional derivative of order \(\alpha>0\) is normally used,

$$ \bigl(D^{\alpha}_{l} u\bigr) (t)= \biggl( \frac{\mathrm{d}}{\mathrm{d}t} \biggr)^{n}\bigl(I^{n-\alpha} u\bigr) (t),\quad n-1< \alpha\leq n, $$
(5)

where n is an integer.

It has the following properties:

$$\begin{aligned} (\mathrm{i})&\quad I^{\alpha}I^{\beta}=I^{\alpha+\beta}, \\ (\mathrm{ii})&\quad I^{\alpha}I^{\beta}=I^{\beta}I^{\alpha}, \\ (\mathrm{iii})&\quad I^{\alpha}t^{\nu}=\frac{\Gamma(\nu+1)}{\Gamma(\alpha+\nu+1)}t^{\alpha+\nu}. \end{aligned}$$

The Caputo definition of fractal derivative operator is given by

$$ \bigl(D^{\alpha}u\bigr) (t)=\frac{1}{\Gamma(n-\alpha)} \int^{t}_{0} (t-\tau)^{n-\alpha-1}u^{(n)}( \tau)\, \mathrm{d}\tau,\quad n-1< \alpha\leq n, $$
(6)

where \(t>0\), \(n \in N\). It has the following two basic properties for \(n-1<\alpha\leq n\):

$$ \bigl(D^{\alpha}I^{\alpha}u\bigr) (t)=u(t) $$
(7)

and

$$ \bigl(I^{\alpha} D^{\alpha} u\bigr) (t)=u(t)-\sum _{k=0}^{n-1}u^{(k)}\bigl(0^{+}\bigr) \frac{t^{k}}{k!},\quad t>0. $$
(8)

More details of the mathematical properties of fractional derivatives and integrals can be found in [32, 33].

3 Sine-cosine wavelet and operational matrix of the fractional integration

3.1 Wavelet and sine-cosine wavelet

Wavelets constitute a family of functions constructed from dilation and translation of a single function \(\psi(x)\) called the mother wavelet. When the dilation parameter a and the translation parameter b vary continuously we have the following family of continuous wavelets [34–37]:

$$ \psi_{ab}(t)=|{a}|^{-\frac{1}{2}}\psi \biggl(\frac{t-b}{a} \biggr),\quad a, b\in R, a\neq0. $$

If we restrict the parameters a and b to discrete values by \(a=a_{0}^{-k}\), \(b=nb_{0}a_{0}^{-k}\), \(a_{0}>1\), \(b_{0}>0\), we have the following family of discrete wavelets:

$$ \psi_{kn}(t)=|a_{0}|^{\frac{k}{2}}\psi \bigl(a_{0}^{k}t-nb_{0}\bigr),\quad k,n\in Z, $$

where \(\psi_{kn}\) form a wavelet basis for \(L^{2}(R)\). In particular, when \(a_{0}=2\) and \(b_{0}=1\) then \(\psi _{kn}(t)\) form an orthonormal basis.

Sine-cosine wavelets \(\psi_{n,m}(t)=\psi(k,n,m,t)\) involve four arguments, \(k=0, 1, 2,\ldots\) , \(n=0,\ldots,2^{k}-1\), the values m are given in equation (10) and t is the normalized time. They are defined on the interval \([0,1)\) as [29, 30]

$$ \psi_{n,m}(t)= \textstyle\begin{cases} 2^{\frac{k+1}{2}}{f_{m}}(2^{k}t-n),& {\frac{n}{2^{k}}\leq t< \frac {n+1}{2^{k}}}, \\ 0, &\text{otherwise}, \end{cases} $$
(9)

where

$$ {f_{m}}(t)= \textstyle\begin{cases} \frac{1}{\sqrt{2}},& {m=0}, \\ \cos(2m\pi t),& {m=1, 2, \ldots, L}, \\ \sin(2(m-L)\pi t), &{m=L+1, L+2, \ldots, 2L}, \end{cases} $$
(10)

where L is any positive integer. The set of sine-cosine wavelet is an orthonormal set.

3.2 Function approximation

A function \(u(t)\) defined over \([0,1)\) may be expanded as

$$ u(t)=\sum_{m=0}^{\infty}\sum _{n=0}^{\infty}c_{n,m} \psi_{n,m}(t), $$
(11)

where

$$ c_{n,m}=\bigl(u(t),\psi_{n,m}(t)\bigr)= \int_{0}^{1}\psi_{n,m}(t)u(t)\, \mathrm{d}t, $$
(12)

in which \((\cdot, \cdot)\) denotes the inner product in \(L^{2}[0,1]\). If the infinite series in equation (11) is truncated, then it can be written as

$$ u(t)\approx \sum_{m=0}^{2L} \sum_{n=0}^{2^{k}-1}c_{n,m} \psi_{n,m}(t)=C^{\mathrm{T}}\Psi (t)=\hat{u}(t), $$
(13)

where C and \(\Psi(t)\) are \(2^{k}(2L+1)\times1\) matrices given by

$$ C=[c_{0,0},c_{0,1},\ldots,c_{0,{2L}},c_{1,0}, \ldots,c_{1,{2L}},\ldots ,c_{2^{k}-1,0},\ldots,c_{2^{k}-1,2L}]^{\mathrm{T}} $$
(14)

and

$$ \Psi(t)=[\psi_{0,0},\psi_{0,1},\ldots, \psi_{0,{2L}},\psi_{1,0},\ldots,\psi _{1,{2L}},\ldots, \psi_{2^{k}-1,0},\ldots,\psi_{2^{k}-1,2L}]^{\mathrm{T}}. $$
(15)

Notation: From now on we define \(m'=2^{k}(2L+1)\).

Taking the collocation points as follows:

$$ t_{i}=\frac{2i-1}{2m'},\quad i=1,2,\ldots, m', $$
(16)

we define sine-cosine wavelet matrix \(\Phi_{m'\times m'}\) as

$$ \Phi_{m'\times m'}=\bigl[\textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} \Psi(\frac{1}{2m'})& \Psi(\frac{3}{2m'}) &\cdots &\Psi (\frac{2m'-1}{2m'}) \end{array}\displaystyle \bigr]. $$
(17)

Correspondingly, we have

$$ \hat{u}_{m'}=\bigl[\textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} \hat{u}(\frac{1}{2m'}) &\hat{u}(\frac{3}{2m'}) &\cdots &\hat {u}(\frac{2m'-1}{2m'})\end{array}\displaystyle \bigr]=C^{\mathrm{T}} \Phi_{m'\times m'}. $$
(18)

Because the sine-cosine wavelet matrix \(\Phi_{m'\times m'}\) is an invertible matrix, the sine-cosine wavelet coefficient vector \(C^{\mathrm{T}}\) can be gotten by

$$ C^{\mathrm{T}}=\hat{u}_{m'}\Phi^{-1}_{m'\times m'}. $$
(19)

3.3 Error analysis of the sine-cosine wavelet bases

In this section, the error analysis of the sine-cosine wavelet is derived. We can conclude that the sine-cosine wavelet expansion of a function \(u(t)\), with bounded second derivative, converges uniformly to \(u(t)\).

Lemma 3.1

If the sine-cosine wavelet expansion of a continuous function \(u(t)\) converges uniformly, then the sine-cosine wavelet expansion converges to the function \(u(t)\).

Proof

Let

$$ v(t)=\sum_{m=0}^{\infty}\sum _{n=0}^{\infty}c_{n,m}\psi_{n,m}(t), $$

where \(c_{n,m}\) is shown in equation (12). Multiplying \(\psi_{p,q}(t)\), in which p, q are fixed and then integrating term-wise, justified by uniform convergence, on \([0, 1]\), we have

$$\begin{aligned} \int_{0}^{1}\psi_{p,q}(t)v(t) \, \mathrm{d}t =& \int_{0}^{1}\sum_{m=0}^{\infty}\sum_{n=0}^{\infty}c_{n,m} \psi_{p,q}(t) \, \mathrm{d}t \\ = & \sum_{m=0}^{\infty}\sum _{n=0}^{\infty}c_{n,m} \int_{0}^{1}\psi _{p,q}(t) \, \mathrm{d}t=c_{p,q}. \end{aligned}$$

Thus, \(c_{n,m}=(v(t),\psi_{n,m}(t))\) for \(n \in N\), \(m \in N\). Consequently u, v have the same Fourier expansions with the sine-cosine wavelet basis and therefore \(u(t) = v(t)\). □

Theorem 3.2

A function \(u(t) \in L^{2}[0, 1]\), with bounded second derivative, say \(|u''(t)|\leq\delta\), can be expanded as an infinite sum of the sine-cosine wavelet and the series converges uniformly to \(u(t)\), that is \(u(t)=\sum_{m=0}^{\infty}\sum_{n=0}^{\infty}c_{n,m}\psi _{n,m}(t)\). Furthermore, we have

$$ \bigl\vert \hat{u}(t)-u(t) \bigr\vert \leq\frac{\delta}{\sqrt{2}\pi^{2}}\sum _{m=2L+1}^{\infty}\sum_{n=2^{k}}^{\infty}\frac{1}{(n+1)^{5/2}M^{2}}, \quad t \in[0,1], $$

where \(M=m\textit{ or }m-L\).

Proof

From equation (12), it follows that

$$ c_{n,m} = \int_{0}^{1}\psi_{n,m}(t)u(t)\, \mathrm{d}t = \int_{\frac {n}{2^{k}}}^{\frac{n+1}{2^{k}}}2^{\frac{k+1}{2}}f_{m} \bigl(2^{k}t-n\bigr)u(t)\, \mathrm{d}x. $$

Substituting \(2^{k} t - n = x\) into above equation yields

$$ c_{n,m} = 2^{\frac{1-k}{2}} \int_{0}^{1}f_{m}(x)u\biggl( \frac{x+n}{2^{k}}\biggr)\, \mathrm {d}x = 2^{\frac{1-k}{2}} \int_{0}^{1}u\biggl(\frac{x+n}{2^{k}}\biggr) \, \mathrm{d}F_{m}(x), $$

where \(F'_{m}(x)=f_{m}(x)\), so we have

$$\begin{aligned} c_{n,m} =& 2^{\frac{1-k}{2}}u\biggl(\frac{x+n}{2^{k}} \biggr)F_{m}(x)|_{0}^{1}- 2^{\frac {1-3k}{2}} \int_{0}^{1}F_{m}(x)u' \biggl(\frac{x+n}{2^{k}}\biggr) \, \mathrm{d}x \\ =& -2^{\frac{1-3k}{2}} \int_{0}^{1}u'\biggl( \frac{x+n}{2^{k}}\biggr) \, \mathrm{d}G_{m}(x), \end{aligned}$$

where \(G''_{m}(x)=f_{m}(x)\). Thus, we have

$$\begin{aligned} c_{n,m} =& 2^{\frac{1-3k}{2}}u'\biggl(\frac{x+n}{2^{k}} \biggr)G_{m}(x)|_{0}^{1} + 2^{\frac{1-5k}{2}} \int_{0}^{1}G_{m}(x)u'' \biggl(\frac{x+n}{2^{k}}\biggr)\, \mathrm{d}x \\ =& -2^{\frac{1-5k}{2}}\frac{1}{(2M\pi)^{2}} \int_{0}^{1}u''\biggl( \frac {x+n}{2^{k}}\biggr)f_{m}(x) \, \mathrm{d}x, \end{aligned}$$

where \(M=m\) or \(M=m-L\).

So, we obtain

$$\begin{aligned} \vert c_{n,m} \vert ^{2} \leq& \biggl\vert \frac{1}{2^{\frac{5k-1}{2}}(2M\pi)^{2}} \int _{0}^{1}u''\biggl( \frac{x+n}{2^{k}}\biggr)f_{m}(x) \,\mathrm{d}x \biggr\vert \\ \leq& \biggl(\frac{1}{2^{\frac{5k-1}{2}}(2M\pi)^{2}}\biggr)^{2} \int_{0}^{1} \biggl\vert u'' \biggl(\frac {x+n}{2^{k}}\biggr) \biggr\vert ^{2} \,\mathrm{d}x \int_{0}^{1} \bigl\vert f_{m}(x) \bigr\vert ^{2} \,\mathrm{d}x \\ \leq& \biggl(\frac{\delta}{2^{\frac{5k-1}{2}}(2M\pi)^{2}} \biggr)^{2}. \end{aligned}$$

Since \(n\leq2^{k}-1\), we have \(|c_{n,m}|\leq\frac{\delta}{2^{\frac {3}{2}}\pi^{2}(n+1)^{\frac{5}{2}}M^{2}}\). Hence, the series \(\sum_{n=0}^{\infty}\sum_{m=0}^{\infty}c_{n,m}\) is absolutely convergent. On the other hand, we have

$$ \Biggl\vert \sum_{n=0}^{\infty}\sum _{m=0}^{\infty}c_{n,m}\psi_{n,m}(t) \Biggr\vert \leq\sum_{n=0}^{\infty}\sum _{m=0}^{\infty} \vert c_{n,m} \vert \vert \psi_{n,m} \vert \leq2\sum_{n=0}^{\infty}\sum_{m=0}^{\infty} \vert c_{n,m} \vert < \infty. $$

Using Lemma 3.1, the series converges to \(u(t)\). Moreover, we can conclude that

$$\begin{aligned} \bigl\vert \hat{u}(t)-u(t) \bigr\vert \leq& \Biggl\vert \sum _{m=2L+1}^{\infty}\sum_{n=2^{k}}^{\infty}c_{n,m}\psi_{n,m}(t) \Biggr\vert \\ \leq& 2\sum_{m=2L+1}^{\infty}\sum _{n=2^{k}}^{\infty} \vert c_{n,m} \vert \\ \leq& \frac{\delta}{\sqrt{2}\pi^{2}}\sum_{m=2L+1}^{\infty}\sum_{n=2^{k}}^{\infty}\frac{1}{(n+1)^{5/2}M^{2}}. \end{aligned}$$

 □

3.4 Sine-cosine wavelet operational matrix of the fractional integration

The integration of the vector \(\Psi(t)\) defined in equation (15) can be obtained:

$$ \int_{0}^{t} \Psi(\tau)\, \mathrm{d}\tau\approx P \Psi(t), $$

where P is the \(m'\times m'\) operational matrix for integration. The operational matrix of integration of the sine-cosine wavelet has been derived by [30].

Now, we derive the sine-cosine wavelet operational matrix of the fractional integration. If \(u(t)\) is expanded in the sine-cosine wavelet, as shown in equation (13), the Riemann-Liouville fractional integration becomes

$$ \bigl(I^{\alpha}u\bigr) (t)=\frac{C^{\mathrm{T}}}{\Gamma(\alpha)} \int^{t}_{0} (t-\tau)^{\alpha-1}\Psi(\tau)\, \mathrm{d}\tau=\frac{C^{\mathrm{T}}}{\Gamma (\alpha)}t^{\alpha-1}\ast \Psi(t), $$
(20)

where \(\alpha\in R\) is the order of the integration, \(\Gamma(\alpha)\) is the Gamma function and \(t^{\alpha-1}\ast\Psi(t)\) denotes the convolution product of \(t^{\alpha-1}\) and \(\Psi(t)\).

Also, we define a m-set of block pulse function (BPF) over the interval \([0,T)\) by

$$ b_{i}(t)= \textstyle\begin{cases} 1, &iT/m\leq t< (i+1)T/m, \\ 0, &\text{otherwise}, \end{cases} $$
(21)

where \(i=0, 1, 2,\ldots, m-1\).

The functions \(b_{i}(t)\) are disjoint and orthogonal. That is

$$\begin{aligned}& b_{i}(t)b_{l}(t)= \textstyle\begin{cases} 0, &i\neq l, \\ b_{i}(t),& i=l, \end{cases}\displaystyle \end{aligned}$$
(22)
$$\begin{aligned}& \int_{0}^{1} b_{i}(\tau)b_{l}( \tau)\, \mathrm{d}\tau= \textstyle\begin{cases} 0, &i\neq l,\\ 1/m,& i=l. \end{cases}\displaystyle \end{aligned}$$
(23)

From the orthogonality property of BPF, it is possible to expand functions into their block pulse series, this means that the sine-cosine wavelet may be expanded into an \(m'\)-term BPF as

$$ \Psi(t)=\Phi_{m'\times m'} B_{m'}(t), $$
(24)

where

$$ B_{m'}(t)=\bigl[b_{0}(t), b_{1}(t), \ldots, b_{m'-1}(t)\bigr]^{\mathrm{T}}, $$

Kilicman [38] has given the block pulse operational matrix of the fractional integration \(F^{\alpha}\) as follows:

$$ \bigl(I^{\alpha}B_{m}\bigr) (t)\approx F^{\alpha}B_{m}(t), $$
(25)

where

$$ F^{\alpha}=\frac{1}{m^{\alpha}}\frac{1}{\Gamma(\alpha+2)}\left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 1&\xi_{1}&\xi_{2}&\xi_{3}&\cdots&\xi_{m-1}\\ 0&1&\xi_{1}&\xi_{2}&\cdots&\xi_{m-2}\\ 0&0&1&\xi_{1}&\cdots&\xi_{m-3}\\ \vdots&\vdots&\ddots&\ddots& &\vdots\\ 0&0&\cdots&0&1&\xi_{1}\\ 0&0&0&\cdots&0&1 \end{array}\displaystyle \right ], $$
(26)

with \(\xi_{k}=(k+1)^{\alpha+1}-2k^{\alpha+1}+(k-1)^{\alpha+1}\).

Next, we derive the sine-cosine wavelet operational matrix of the fractional integration. Let

$$ \bigl(I^{\alpha}\Psi\bigr) (t)\approx P_{m'\times m'}^{\alpha} \Psi(t), $$
(27)

where the matrix \(P_{m'\times m'}^{\alpha}\) is called the sine-cosine wavelet operational matrix of the fractional integration.

Using equations (24) and (27), we have

$$ \bigl(I^{\alpha}\Psi\bigr) (t)\approx\bigl(I^{\alpha} \Phi_{m'\times m'}B_{m'}\bigr) (t)=\Phi_{m'\times m'} \bigl(I^{\alpha}B_{m'}\bigr) (t)\approx \Phi_{m'\times m'}F^{\alpha}B_{m'}(t). $$
(28)

From equations (27) and (28) we get

$$ P_{m'\times m'}^{\alpha}\Psi(t)= P_{m'\times m'}^{\alpha} \Phi_{m'\times m'}B_{m'}(t)=\Phi_{m'\times m'}F^{\alpha}B_{m'}(t). $$
(29)

Then the sine-cosine wavelet operational matrix of the fractional integration \(P_{m'\times m'}^{\alpha}\) is given by

$$ P_{m'\times m'}^{\alpha}=\Phi_{m'\times m'}F^{\alpha} \Phi^{-1}_{m'\times m'}. $$
(30)

In particular, for \(k=1\), \(L=1\), \(\alpha=0.5\), the sine-cosine wavelet operational matrix of fractional order integration \(P_{m'\times m'}^{\alpha}\) is given by

$$ P_{6\times6}^{0.5}=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 0.5319& -0.0209& -0.1715& 0.4407& 0.0182& 0.0821\\ -0.0209& 0.1651& 0.0991& 0.0180& 0.0061& 0.0148\\ 0.1715& -0.0991& 0.2243& -0.0821& -0.0148& -0.0449\\ 0& 0& 0& 0.5319& -0.0209& -0.1715\\ 0& 0& 0& -0.0209& 0.1651& 0.0991\\ 0& 0& 0& 0.1715& -0.0991& 0.2243 \end{array}\displaystyle \right ]. $$

4 Applications of the operational matrix of fractional integration

Consider the Riccati differential equation

$$ D^{\alpha}y(t)=u(t)+v(t)y(t)+w(t){\bigl[y(t) \bigr]}^{2},\quad n\leq\alpha< n+1, t>0, $$
(31)

subject to the initial conditions

$$ y^{(k)}(0)=g_{k},\quad k=1, 2, \ldots, n-1, $$
(32)

where α is a parameter describing of the order of fractional derivative, n is an integer, \(u(t)\), \(v(t)\) and \(w(t)\) are given functions, and \(g_{k}\) is constant.

The functions \(D^{\alpha}y(t)\), \(u(t)\), \(v(t)\), and \(w(t)\) may be approximated by the sine-cosine wavelet as follows:

$$ D^{\alpha}y(t)\approx Y^{\mathrm{T}}\Psi(t), \qquad u(t)\approx U^{\mathrm{T}}\Psi (t),\qquad v(t)\approx V^{\mathrm{T}} \Psi(t),\qquad w(t)\approx W^{\mathrm{T}}\Psi(t), $$
(33)

where U, V, W, Y are given in equation (14), and \(\Psi(t)\) is given in equation (15).

Using equations (8), (27) and \(D^{\alpha}y(t)\approx Y^{\mathrm{T}}\Psi (t)\), we have

$$\begin{aligned} y(t) \approx& Y^{\mathrm{T}}P_{{m'}\times {m'}}^{\alpha}\Psi(t)+\sum _{k=0}^{{m'}-1}y^{(k)}\bigl(0^{+}\bigr) \frac{t^{k}}{k!} \\ \approx& Y^{\mathrm{T}}P_{{m'}\times {m'}}^{\alpha} \Psi(t)+Y^{\mathrm{T}}_{0}\Psi(t)=A^{T} \Psi(t), \end{aligned}$$
(34)

where \(A={(Y^{T}P_{{m'}\times {m'}}^{\alpha}+Y^{\mathrm{T}}_{0})}^{T}\). Substituting equations (33) and (34) into equation (31), we have

$$ Y^{\mathrm{T}}\Psi(t)=U^{\mathrm{T}} \Psi(t)+V^{\mathrm{T}}\Psi(t)\Psi ^{T}(t)A+W^{\mathrm{T}} \Psi(t){\bigl[\Psi^{T}(t)A\bigr]}^{2}. $$
(35)

According to equation (24), we have

$$ \Psi(t)\Psi^{T}(t)A= \Phi_{{m'}\times {m'}}B_{m'}(t)B^{T}_{m'}(t) \Phi^{T}_{m'\times m'}A. $$
(36)

By equations (22) and (23), we have

$$ B_{m'}(t)B^{T}_{m'}(t)= \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} b_{1}(t)& &\mathbf{0}\\ & b_{2}(t)& \\ &\ddots&\\ \mathbf{0}&&b_{m'}(t) \end{array}\displaystyle \right ]. $$

Define

$$ \Phi^{\mathrm{T}}_{{m'}\times {m'}}A=[a_{1}, a_{1}, \ldots, a_{{m'}}]. $$
(37)

Thus, we have

$$\begin{aligned} \Phi_{{m'}\times {m'}}B_{m'}(t)B^{T}_{m'}(t) \Phi^{T}_{m'\times m'}A =& \Phi_{{m'}\times {m'}}\left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_{1}& &\mathbf{0}\\ & a_{2}& \\ &\ddots&\\ \mathbf{0}&&a_{m'} \end{array}\displaystyle \right ]B_{m'}(t) \\ =&\Phi_{{m'}\times {m'}} \operatorname{diag}\bigl(\Phi^{\mathrm{T}}_{{m'}\times {m'}}A \bigr)B_{m'}(t). \end{aligned}$$
(38)

Hence, we have

$$ V^{\mathrm{T}}\Psi(t)\Psi^{T}(t)A=V^{\mathrm{T}} \Phi_{{m'}\times {m'}}\operatorname{diag}\bigl(\Phi^{\mathrm{T}}_{{m'}\times {m'}}A \bigr)B_{m'}(t). $$
(39)

From equation (24), the nonlinear term of equation (35) can be rewritten

$$ W^{\mathrm{T}}\Psi(t){\bigl[\Psi^{T}(t)A \bigr]}^{2}=W^{\mathrm{T}}\Phi_{{m'}\times {m'}}B_{m'}(t){ \bigl[B^{T}_{m'}(t)\Phi^{\mathrm{T}}_{{m'}\times {m'}}A \bigr]}^{2}. $$
(40)

Using equation (37), we will have

$$ W^{\mathrm{T}}\Psi(t){\bigl[\Psi^{T}(t)A \bigr]}^{2}=W^{\mathrm{T}}\Phi_{{m'}\times {m'}}\operatorname{diag} \bigl(a_{1}^{2}\quad a_{2}^{2}\quad \cdots \quad a_{m'}^{2}\bigr)B_{m'}(t). $$
(41)

Substituting equations (39) and (41) into equation (35), together with equation (24), we have

$$\begin{aligned} Y^{\mathrm{T}}\Phi_{{m'}\times{m'}} =&U^{\mathrm{T}} \Phi_{{m'}\times {m'}}+V^{\mathrm{T}}\Phi_{{m'}\times{m'}}\operatorname{diag}(a_{1} \quad a_{2}\quad \cdots\quad a_{m'}) \\ &{}+W^{\mathrm{T}}\Phi_{{m'}\times{m'}}\operatorname{diag} \bigl(a_{1}^{2}\quad a_{2}^{2}\quad \cdots \quad a_{m'}^{2}\bigr), \end{aligned}$$
(42)

which is a nonlinear system of algebraic equations. By solving this system we can obtain the approximate solution of equation (31) according to equation (34).

5 Numerical examples

In this section, we demonstrate the effectiveness and simplicity of the proposed method with three examples.

Example 1

Consider the following the nonlinear fractional Riccati differential equation:

$$ D^{\alpha}y(t)+{\bigl[y(t)\bigr]}^{2}=1,\quad 0 < \alpha\leq1, t>0, $$
(43)

subject to the initial state \(y(0)=0\), which is studied by [23] by using the MHPM. Here we use the sine-cosine wavelet operational matrix of the fractional integration to solve it.

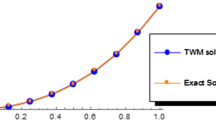
Figure 1 shows the numerical results for different values of \(m'\) and \(0 <\alpha\leq1\). For \(\alpha=1\), Figure 1 shows the behavior of the numerical solutions for various k and L, which are in agreement with the exact solution, \(y(t)=\frac{e^{2t}-1}{e^{2t}+1}\).

Figure 1
figure 1

The comparison between approximate solutions and exact solution of Example  1 for some k and L .

Full size image

To show the efficiency of the proposed method, we use the root-mean-square error (RMSE) to reveal the accuracy of the method. RMSE is defined as

$$\begin{aligned} \bigl\Vert e_{m'}(t) \bigr\Vert _{2} =& \biggl( \int_{0}^{1} e_{m'}^{2}(t)\, \mathrm{d}t \biggr)^{1/2}\approx \Biggl( \frac{1}{N}\sum _{i=0}^{N} e_{m'}^{2}(t_{i}) \Biggr)^{1/2} \\ =& \Biggl( \frac{1}{N}\sum_{i=0}^{N} \bigl(y(t_{i})-y_{m'}(t_{i})\bigr)^{2} \Biggr)^{1/2}, \end{aligned}$$

where \(y(t)\) is the exact solution and \(y_{m'}(t)\) is the approximation solution obtained by equation (34).

The errors in the case \(\alpha=1\), for different values of k and L are shown in Table 1. As one can see, approximate solutions converge to the exact solution while k is increased and the absolute error decreases.

Table 1 Approximate norm-2 of absolute error for some k and L
Full size table

We also use the sine-cosine operational matrix method for solving the equation with the solution in the interval \([0,10]\). A comparison of our result with \(m'=48\) (\(k=4\), \(L=1\)) and that obtained by the MHPM for \(a = 1\) is shown in Figure 2. Figure 3 shows a comparison between sine-cosine wavelet method and MHPM for \(\alpha=0.5, 0.75\). As Figure 2 shows, our result is in well agreement with the exact solution, while convergent regions of solution obtained by MHPM is small. From Figures 2 and 3, we can see that the sine-cosine wavelet method is accurate and is able to solve this nonlinear Riccati differential equation in a very wider region.

Figure 2
figure 2

The comparison between sine-cosine method and MHPM of Example  1 for \(\pmb{\alpha=1}\) .

Full size image
Figure 3
figure 3

The comparison between sine-cosine method and MHPM of Example  1 . (a) \(\alpha=0.5\) and (b) \(\alpha=0.75\).

Full size image

Example 2

Consider the following initial value problem [39]:

$$ D^{\alpha}y(t)=1+2y(t)-{\bigl[y(t)\bigr]}^{2}, \quad 0< \alpha\leq1, t>0, $$
(44)

with the initial condition \(y(0) = 0\).

Figure 4 shows the numerical results for different values of \(m'\) and α. The errors in the case \(\alpha=1\), for different values of k and L are shown in Table 1. As one can see that the conclusions are the same as for Example 1.

Figure 4
figure 4

The comparison between approximate solutions and exact solution of Example  2 for some k and L .

Full size image

In Table 2, we compare the numerical solutions resulting from the application of sine-cosine wavelet method (\(k=4\), \(L=1\)), with the HPM [23] and ultraspherical wavelets collocation method (UWCM) [27]. As can be seen from Table 2, the sine-cosine wavelet method and UWCM method are superior to the HPM. The numerical results of sine-cosine method are closer to those of the UWCM. However, it must be pointed out that the sine-cosine wavelet basis functions are trigonometric function and they are more suitable for solving the numerical solution of the periodic problem.

Table 2 Comparison between sine-cosine, HPM and UWCM for Example  2 for \(\pmb{\alpha= 1/2, 3/4}\)
Full size table

When \(\alpha= 1\), equation (44) is a classical Riccati equation, which have been studied by using ADM, VIM, HPM, MHPM and NHPM. Figure 5 shows the exact solution and approximate solutions obtained by ADM, VIM, HPM, MPHM, NPHM and our method in the interval \([0,10]\). As Figure 5 shows, our results are in well agreement with the exact solution, convergent regions of solution obtained by ADM, VIM, HPM, MHPM and NHPM are small. This comparison indicates that the sine-cosine wavelet method is accurate and is able to solve this nonlinear Riccati differential equation in a very wider region.

Figure 5
figure 5

The comparison between sine-cosine method and other different methods of Example  2 for \(\pmb{\alpha=1}\) .

Full size image

Example 3

Consider fractional Riccati equation [25, 40]

$$ D^{\alpha}y(t)=-y(t)+{\bigl[y(t)\bigr]}^{2}, $$
(45)

subject to the initial state \(y(0)=\frac{1}{2}\). When \(\alpha=1\) the exact solution of the above equation was found to be of the form

$$ y(t)=\frac{e^{-t}}{1+e^{-t}}. $$

Figure 6 shows the behavior of the numerical solutions for various \(m'\) and α. The error for different values of k and L, for \(\alpha=1\), is shown in Table 1. Figure 7 shows the exact solution and approximate solutions obtained by NHPM and our method in the interval \([0,10]\).

Figure 6
figure 6

The comparison between approximate solutions and exact solution of Example  3 for some k and L .

Full size image
Figure 7
figure 7

The exact solution and approximate solutions obtained by our method and NHPM for \(\pmb{\alpha=1}\) .

Full size image

6 Conclusion

In this paper, we proposed the sine-cosine wavelet operational matrix method to solve nonlinear fractional Riccati differential equations. The sine-cosine wavelet operational matrix of fractional order integration is obtained. Compared to ADM, HPM, VIM, MHPM and NHPM, the sine-cosine wavelet method is simple and easy to implement; moreover, it enables us to approximate the solution more accurate in a bigger interval. However, we have also noticed that the sine-cosine wavelet is constructed from the trigonometric polynomials and has periodicity. It is more suitable for solving the periodic problem.