1 Introduction

In this paper, we consider the following p-Laplacian prescribed mean curvature Liénard equation:

$$ \biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'+f\bigl(t,u(t)\bigr)u'(t)+g \bigl(u(t)\bigr)=e(t), $$
(1.1)

where \(\phi(s)=|s|^{p-2}s\), p is a positive constant, and \(p>1\), \(f:\mathbb{R}\times\mathbb{R}\to\mathbb{R}\) is an \(L^{2}\)-Carathéodory function and \(f(t+T,\cdot)\equiv f(t,\cdot)\), \(g:(0,+\infty)\to \mathbb{R}\) is the continuous function and has a singularity at the origin, \(e\in L^{\sigma}(\mathbb{R})\) is T-periodic function and \(1\leq\sigma<\infty\), T is a positive constant.

During the past 30 years, the problem of existence of positive periodic solutions to Liénard equations with singularity was extensively studied by many researchers [1–9]. In [9], Zhang discussed the existence of a positive periodic solution to equation (1.1), where \(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}}=u'(t)\), \(p=2\), \(f(t,u)=f(u)\) and \(e(t)\equiv0\), g satisfies a semilinear condition and has a strong singularity of repulsive type, i.e.,

$$ \lim_{u\to0^{+}} g(u)=-\infty\quad\mbox{and}\quad \lim _{u\to 0^{+}} \int^{1}_{u}g(\nu)\,d\nu=+\infty. $$
(1.2)

After that, Yu and Lu [7] improved the results of [9], showing in their Theorem 2.1 (see [7]) that g may possess weak and strong singularities. Zhang and Yu’s proof was based on coincidence degree theory.

Compared with Liénard equations, only a few works focus on prescribed mean curvature Liénard equations, especially p-Laplacian prescribed mean curvature Liénard equations. As far as we know, prescribed mean curvature \(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}}\) of \(u(t)\) appears in different geometry and physics problems [10–16]. Using coincidence degree theory, Feng [17] and Lu [18] et al. investigated respectively the existence of a positive periodic solution for equation (1.1) without singularity and with a strong singularity of repulsive type, where \(p=2\), \(f(t,u)=f(u)\), and g satisfying a semilinear condition.

Inspired by [7, 9, 17, 18], in this paper, we further consider the existence of a positive periodic solution for equation (1.1) by means of an extension of Mawhin’s continuation theorem due to Ge and Ren [19]. It is worth mentioning that conditions on f, g and the work for estimating a priori bounds of positive periodic solutions for equation (1.1) are more complex than in [7, 9, 17, 18]. Firstly, the friction term \(f(u(t))u'(t)\) in [7, 9, 17, 18] satisfies \(\int^{T}_{0}f(u(t))u'(t)\,dt=0\), which is crucial to estimating a priori bounds of positive periodic solutions for these equations. However, the friction term of this paper, \(f(t,u(t))u'(t)\), may not satisfy \(\int^{T}_{0}f(t,u(t))u'(t)\,dt=0\). Secondly, g of this paper possesses weak and strong singularities of attractive type (or weak and strong singularities of repulsive type) at the origin. Thirdly, g of this paper may satisfy sublinearity, semilinearity, or superlinearity conditions at infinity. Therefore, we extend and improve the results in [7, 9, 17, 18].

2 Positive periodic solution for equation (1.1) when \(p> 1\)

In this section, we study the existence of a positive periodic solution to equation (1.1). Since \((\phi_{p} (\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} ) )'\) is a nonlinear term, coincidence degree theory does not apply directly. The traditional study method is to translate equation (1.1) into the following two-dimensional system:

$$ \textstyle\begin{cases} u_{1}'(t)=\frac{\phi_{q}(u_{2}(t))}{\sqrt{1-\phi^{2}_{q}(u_{2}(t))}},\\ u_{2}'(t)=-f(t,u_{1}(t))u_{1}'(t)-g(u_{1}(t))+e(t), \end{cases} $$

where \(\frac{1}{p}+\frac{1}{q}=1\), for which coincidence degree theory can be applied. However, from the first equation of the above system it is obvious that \(\|u_{2}\|<1\), where \(\|u_{2}\|:=\max_{t\in\mathbb{R}}|u'(t)|\). Therefore, estimating an upper bound of \(u_{2}(t)\) is very complicated; in order to get around this difficulty, we find other methods to study equation (1.1). We first investigate the following second-order prescribed mean curvature equation:

$$ \biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'=\tilde{f}\bigl(t,u(t),u'(t) \bigr), $$
(2.1)

where \(\tilde{f}:[0,T]\times\mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}\) is a Carathéodory function. Applying the extension of Mawhin’s continuous theorem due to Ge and Ren [19, Theorem 2.1], we get the following conclusion.

Lemma 2.1

AssumeΩis an open bounded set in\(C^{1}_{T}:=\{u\in C^{1}(\mathbb{R},\mathbb{R}): u(t+T)\equiv u(t) \textit{ and } u'(t+T)\equiv u'(t), \forall t\in\mathbb{R}\}\). Suppose the following conditions hold:

  1. (i)

    For each\(\lambda\in(0,1)\), the equation

    $$ \biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'=\lambda \tilde{f}\bigl(t,u(t),u'(t) \bigr) $$

    has no solution on∂Ω.

  2. (ii)

    The equation

    $$F(a):=\frac{1}{T} \int^{T}_{0}\tilde{f}(t,a,0)\,dt=0 $$

    has no solution on\(\partial\varOmega\cap\mathbb{R}\).

  3. (iii)

    The Brouwer degree

    $$\deg\{F,\varOmega\cap\mathbb{R},0\}\neq0. $$

    Then equation (2.1) has at least oneT-periodic solution onΩ̄.

Proof

First, operators M and \(N_{\lambda}\) are defined by

$$\begin{aligned} & M:\operatorname{dom}M\cap X\to Z,\quad (Mu) (t)= \biggl(\phi_{p} \biggl( \frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)',\quad t\in \mathbb{R}, \\ & N_{\lambda}:X\to Z, (N_{\lambda}u) (t)=\lambda\tilde{f} \bigl(t,u(t),u'(t)\bigr). \end{aligned}$$

Obviously, equation (2.1) can be converted into

$$Mu=N_{\lambda}u,\quad \lambda\in(0,1). $$

By [20, Lemmas 3.1 and 3.2], we know that M is a quasilinear operator, \(N_{\lambda}\) is M-compact. From assumption (i), one finds

$$Mu\neq N_{\lambda}u, \lambda\in(0,1) \quad\mbox{and}\quad u\in\partial\varOmega, $$

and assumptions (ii) and (iii) imply that \(\deg\{JQN,\varOmega\cap \ker M,\theta\}\) is valid and

$$\deg\{JQN,\varOmega\cap \ker M,\theta\}\neq0. $$

Therefore, applying the extension of Mawhin’s continuous theorem, equation (2.1) has at least one T-periodic solution. □

In the following, applying Lemma 2.1, we prove the existence of a positive periodic solution for equation (1.1) with a singularity of repulsive type.

Theorem 2.1

Assume that equation (1.2) holds. Furthermore, suppose the following conditions hold:

\((H_{1})\):

There exists a positive constantγsuch that\(\inf_{(t,u)\in[0,T]\times\mathbb{R}}|f(t,u)|\geq\gamma>0\).

\((H_{2})\):

There exist two positive constants\(d_{1}\), \(d_{2}\)with\(d_{1}< d_{2}\)such that\(g(u)-e(t)<0\)for\((t,u)\in[0,T]\times(0,d_{1})\)and\(g(u)-e(t)>0\)for\((t,u)\in[0,T]\times(d_{2},+\infty)\).

Then equation (1.1) has at least one positive periodic solution.

Proof

We embed equation (1.1) into the following family of equations:

$$ \biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'+\lambda f\bigl(t,u(t)\bigr)u'(t)+ \lambda g\bigl(u(t)\bigr)=\lambda e(t), $$
(2.2)

where \(\lambda\in(0,1]\). Firstly, we claim that there exist two points \(\tau, \xi\in(0,T)\) such that

$$ u(\tau)\geq d_{1} \quad\mbox{and}\quad u(\xi)\leq d_{2}. $$
(2.3)

In fact, since \(\int^{T}_{0}u'(t)\,dt=0\), it is easy to verify that there exist two point \(t_{1}, t_{2}\in(0,T)\) such that

$$u'(t_{1})\leq0 \quad\mbox{and}\quad u'(t_{2}) \geq0. $$

Therefore, we get

$$\phi_{p} \biggl(\frac{u'(t_{1})}{\sqrt{1+(u'(t_{1}))^{2}}} \biggr)\leq 0 \quad\mbox{and}\quad \phi_{p} \biggl(\frac{u'(t_{2})}{\sqrt{1+(u'(t_{2}))^{2}}} \biggr)\geq0. $$

Letting \(\overline{t}, \underline{t}\in(0,T)\) be maximum and minimum points of the prescribed mean curvature term \(\phi_{p} (\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} )\), the above inequalities imply

$$ \phi_{p} \biggl(\frac{u'(\overline{t})}{\sqrt{1+(u'(\overline{t}))^{2}}} \biggr) \geq0\quad \mbox{and}\quad \biggl(\phi_{p} \biggl(\frac{u'(\overline{t})}{\sqrt{1+(u'(\overline {t}))^{2}}} \biggr) \biggr)'=0; $$
(2.4)

and

$$ \phi_{p} \biggl(\frac{u'(\underline{t})}{\sqrt{1+(u'(\underline {t}))^{2}}} \biggr) \leq0 \quad\mbox{and}\quad \biggl(\phi_{p} \biggl(\frac{u'(\underline{t})}{\sqrt{1+(u'(\underline {t}))^{2}}} \biggr) \biggr)'=0. $$
(2.5)

Applying equations (2.5) into (2.2), we deduce

$$ g\bigl(u(\underline{t})\bigr)-e(\underline{t})=-f\bigl( \underline{t},u(\underline {t})\bigr)u'(\underline{t}). $$
(2.6)

By condition \((H_{1})\), we know that f may not change sign (i.e., \(f(t,u)>0\) or \(f(t,u)<0\), for \((t,u)\in[0,T]\times\mathbb{R}\)). Without loss of generality, suppose \(f(t,u)>0\), for \((t,u)\in[0,T]\times\mathbb{R}\). Besides, since

$$\phi_{p} \biggl(\frac{u'(\underline{t})}{\sqrt{1+(u'(\underline {t}))^{2}}} \biggr)= \biggl\vert \frac{u'(\underline{t})}{\sqrt{1+(u'(\underline {t}))^{2}}} \biggr\vert ^{p-2} \frac{u'(\underline{t})}{\sqrt{1+(u'(\underline{t}))^{2}}}\leq0, $$

then it is clear that \(u'(\underline{t})\leq0\). By condition \((H_{2})\) and since \(g(u(\underline{t}))-e(\underline{t})\leq0\), we get that \(u(\underline{t})\geq d_{1}\).

Similarly, by condition \((H_{2})\) and equation (2.4), we obtain that \(u(\overline{t})\leq d_{2}\). Taking \(\tau=\underline{t}\) and \(\xi=\overline{t}\), (2.3) is proved.

Multiplying both sides of equation (2.2) by \(u'(t)\) and integrating from 0 to T, we have

$$ \begin{aligned}[b] &\int^{T}_{0} \biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'u'(t) \,dt+ \lambda \int^{T}_{0}f\bigl(t,u(t)\bigr) \bigl\vert u'(t) \bigr\vert ^{2}\,dt+\lambda \int^{T}_{0}g\bigl(u(t)\bigr)u'(t) \,dt\hspace{-24pt}\\&\quad=\lambda \int^{T}_{0}e(t)u'(t)\,dt.\end{aligned} $$
(2.7)

Substituting

$$\begin{aligned} &\int^{T}_{0} \biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'u'(t) \,dt\\&\quad=\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr)u'(t)\bigg|^{T}_{0} - \int^{T}_{0}\phi_{p} \biggl( \frac{u'}{\sqrt{1+(u')^{2}}} \biggr)\,du'=0\end{aligned} $$

and \(\int^{T}_{0}g(u(t))u'(t)\,dt=0\) into (2.7), it is clear that

$$\biggl\vert \int^{T}_{0}f(t,u) \bigl\vert u'(t) \bigr\vert ^{2}\,dt \biggr\vert = \biggl\vert \int^{T}_{0}e(t)u'(t)\, dt \biggr\vert . $$

By condition \((H_{1})\) and Hölder inequality, the above equality implies

$$ \begin{aligned} \gamma \int^{T}_{0} \bigl\vert u'(t) \bigr\vert ^{2}\,dt&\leq \biggl\vert \int^{T}_{0}f\bigl(t,u(t)\bigr) \bigl\vert u'(t) \bigr\vert ^{2}\, dt \biggr\vert \\ &\leq \int^{T}_{0} \bigl\vert e(t) \bigr\vert \bigl\vert u'(t) \bigr\vert \,dt \\ &\leq \biggl( \int^{T}_{0} \bigl\vert e(t) \bigr\vert ^{2}\,dt \biggr)^{\frac{1}{2}} \biggl( \int ^{T}_{0} \bigl\vert u'(t) \bigr\vert ^{2}\,dt \biggr)^{\frac{1}{2}}. \end{aligned} $$

Since \(\int^{T}_{0}|u'(t)|^{2}\,dt\neq0\) and \(\gamma>0\), we arrive at

$$ \biggl( \int^{T}_{0} \bigl\vert u'(t) \bigr\vert ^{2}\,dt \biggr)^{\frac{1}{2}}\leq \frac{ \Vert e \Vert _{2}}{\gamma}, $$
(2.8)

where \(\|e\|_{2}:= (\int^{T}_{0}|e(t)|^{2}\,dt )^{\frac{1}{2}}\). From equations (2.3) and (2.8), using Hölder inequality, we get

$$ \begin{aligned}[b] u(t)&\leq d_{2}+ \int^{T}_{0} \bigl\vert u'(t) \bigr\vert \,dt \\ &\leq d_{2}+T^{\frac{1}{2}} \biggl( \int^{T}_{0} \bigl\vert u'(t) \bigr\vert ^{2}\,dt \biggr)^{\frac {1}{2}} \\ &\leq d_{2}+\frac{T^{\frac{1}{2}} \Vert e \Vert _{2}}{\gamma}:=M_{1}. \end{aligned} $$
(2.9)

From equation (2.8) and using Hölder inequality, we deduce

$$ \bigl\Vert u' \bigr\Vert = \frac{1}{T} \int^{T}_{0} \bigl\Vert u' \bigr\Vert \,dt\leq T^{-\frac{1}{2}} \biggl( \int^{T}_{0} \bigl\Vert u' \bigr\Vert ^{2}\,dt \biggr)^{\frac{1}{2}}\leq T^{-\frac{1}{2}} \frac{ \Vert e \Vert _{2}}{\gamma}:=M_{2}. $$
(2.10)

On the other hand, let \(\tau\in(0,T)\) be as in equation (2.3). Multiplying both sides of equation (2.2) by \(u'(t)\) and integrating over the interval \([\tau,t]\), where \(t\in[\tau,T]\), we see that

$$ \begin{aligned} \lambda \int^{u(t)}_{u(\tau)}g(u)\,du={}&\lambda \int^{t}_{\tau}g\bigl(u(s)\bigr)u'(s)\,ds \\ ={}&{-} \int^{t}_{\tau}\biggl(\phi_{p} \biggl(\frac{u'(s)}{\sqrt{1+(u'(s))^{2}}} \biggr) \biggr)'u'(s)\,ds- \lambda \int^{t}_{\tau}f\bigl(s,u(s)\bigr) \bigl\vert u'(s) \bigr\vert ^{2}\,ds\\&+\lambda \int^{t}_{\tau}e(s)u'(s)\,ds. \end{aligned} $$

Furthermore, from equations (2.2), (2.9) and (2.10), applying Hölder inequality, the above equation implies

$$ \begin{aligned}[b] \lambda \biggl\vert \int^{u(t)}_{u(\tau)}g(u)\,du \biggr\vert \leq{}& \int^{T}_{0} \biggl\vert \biggl( \phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)' \biggr\vert \bigl\vert u'(t) \bigr\vert \,dt \\ &+\lambda \int^{T}_{0} \bigl\vert f\bigl(t,u(t)\bigr) \bigr\vert \bigl\vert u'(t) \bigr\vert ^{2}\,dt+ \lambda \int^{T}_{0} \bigl\vert e(t) \bigr\vert \bigl\vert u'(t) \bigr\vert \,dt \\ \leq{}&\lambda M_{2} \biggl( \int^{T}_{0} \bigl\vert f\bigl(t,u(t)\bigr) \bigr\vert \bigl\vert u'(t) \bigr\vert \,dt+ \int^{T}_{0} \bigl\vert g\bigl(u(t)\bigr) \bigr\vert \,dt+ \int ^{T}_{0} \bigl\vert e(t) \bigr\vert \,dt \biggr)\hspace{-12pt} \\ &+\lambda M_{2}^{2} \int^{T}_{0} \bigl\vert f\bigl(t,u(t)\bigr) \bigr\vert \,dt+\lambda M_{1}T^{\frac{1}{2}} \Vert e \Vert _{2} \\ \leq{}&2\lambda M_{2}\bigl(M_{2}T \Vert f_{M_{1}} \Vert +T^{\frac{1}{2}} \Vert e \Vert _{2} \bigr)+\lambda M_{2} \int^{T}_{0} \bigl\vert g\bigl(u(t)\bigr) \bigr\vert \,dt, \end{aligned} $$
(2.11)

where \(\|f_{M_{1}}\|:=\max_{(t,u)\in[0,T]\times(0,M_{1}]}|f(t,u)|\).

Next, we consider \(\int^{T}_{0}|g(u(t))|\,dt\). Integrating equation (2.2) over the interval \([0,T]\), we obtain

$$ \int^{T}_{0}\bigl(f\bigl(t,u(t) \bigr)u'(t)+g\bigl(u(t)\bigr)-e(t)\bigr)\,dt=0. $$
(2.12)

From equation (2.12), we see that

$$ \begin{aligned}[b] \int^{T}_{0} \bigl\vert g\bigl(u(t)\bigr) \bigr\vert \,dt={}& \int_{g(u(t))\geq0}g\bigl(u(t)\bigr)\,dt- \int_{g(u(t))\leq 0}g\bigl(u(t)\bigr)\,dt \\ ={}&2 \int_{g(u(t))\geq0}g^{+}\bigl(u(t)\bigr)\,dt+ \int^{T}_{0}f\bigl(t,u(t)\bigr)u'(t) \,dt- \int ^{T}_{0}e(t)\,dt \\ \leq{}&2 \int^{T}_{0}g^{+}\bigl(u(t)\bigr)\,dt+ \int^{T}_{0} \bigl\vert f\bigl(t,u(t)\bigr) \bigr\vert \bigl\vert u'(t) \bigr\vert \,dt+ \int ^{T}_{0} \bigl\vert e(t) \bigr\vert \,dt, \end{aligned} $$
(2.13)

where \(g^{+}(u):=\max\{g(u),0\}\). Since \(g^{+}(u(t))\geq0\), form conditions \((H_{2})\) and equation (1.2), we know that there exists a positive constant \(d_{2}^{*}\) with \(d_{2}^{*}>d_{1}\) such that \(u(t)\geq d_{2}^{*}\). Therefore, from equations (2.9) and (2.10), equation (2.13) implies

$$ \begin{aligned}[b] \int^{T}_{0} \bigl\vert g\bigl(u(t)\bigr) \bigr\vert \,dt\leq{}&2T \bigl\Vert g^{+}_{M_{1}} \bigr\Vert + \int ^{T}_{0} \bigl\vert f\bigl(t,u(t)\bigr) \bigr\vert \bigl\vert u'(t) \bigr\vert + \int^{T}_{0} \bigl\vert e(t) \bigr\vert \,dt \\ \leq{}&2T \bigl\Vert g^{+}_{M_{1}} \bigr\Vert +M_{2}T \Vert f_{M_{1}} \Vert +T^{\frac{1}{2}} \Vert e \Vert _{2} , \end{aligned} $$
(2.14)

where \(\|g^{+}_{M_{1}}\|:=\max_{d_{2}^{*}\leq u\leq M_{1}}g^{+}(u)\). Applying equations (2.14) into (2.11), we have

$$ \lambda \biggl\vert \int^{u(t)}_{u(\tau)}g(u)\,du \biggr\vert \leq3\lambda M_{2}\bigl(M_{2}T \Vert f_{M_{1}} \Vert +T^{\frac{1}{2}} \Vert e \Vert _{2}\bigr)+2\lambda M_{2}T \bigl\Vert g^{+}_{M_{1}} \bigr\Vert . $$

According to equation (1.2), we see that there exists a positive constant \(M_{3}'\) such that

$$ u(t)\geq M_{3}',\quad \mbox{for } t \in[\tau,T]. $$
(2.15)

If \(t\in[0,\tau]\), we can handle this case similarly.

From equations (2.9), (2.10), and (2.15), we obtain that a periodic solution u of equation (2.2) satisfies

$$ M_{3}< u(t)< M_{1},\quad\quad \bigl\Vert u' \bigr\Vert < M_{2}, $$

where \(M_{3}:=\min\{d_{1},M_{3}'\}\). Then condition (1) of Lemma 2.1 is satisfied. For a possible solution C to equation

$$g(C)-\frac{1}{T} \int^{T}_{0}e(t)\,dt=0, $$

we have \(C\in[M_{3},M_{1}]\). Therefore, condition (2) of Lemma 2.1 holds. Finally, by condition \((H_{2})\), we arrive at

$$g(M_{3})-\frac{1}{T} \int^{T}_{0}e(t)\,dt< 0 \quad\mbox{and}\quad g(M_{1})-\frac{1}{T} \int^{T}_{0}e(t)\,dt>0. $$

So condition (3) of Lemma 2.1 is also satisfied. By Theorem 2.1, equation (1.1) has at least one positive periodic solution. □

In equation (1.2), the nonlinear term g requires a strong singularity of repulsive type (i.e., \(\lim_{u\to 0^{+}}\int^{1}_{u}g(\nu)\,d\nu=+\infty\)). It is clear that the method of Theorem 2.1 is no longer applicable to estimate a lower bound on a periodic solution \(u(t)\) of equation (1.1) in the case of a weak singularity of repulsive type (i.e., \(\lim_{u\to 0^{+}}\int^{1}_{u}g(\nu)\,d\nu<+\infty\)). Therefore, we need to find another method to consider equation (1.1) in the case of a weak singularity of repulsive type.

Theorem 2.2

Assume that conditions\((H_{1})\)and\((H_{2})\)hold. If\(\frac{T^{\frac{1}{2}}\|e\|_{2}}{2\gamma}< d_{1}\), here\(d_{1}\)is defined in Theorem2.1, then equation (1.1) has at least one positive periodic solution.

Proof

We follow the same strategy and notation as in the proof of Theorem 2.1. Next, we consider the lower bound on a periodic solution \(u(t)\) of equation (1.1). From equations (2.3) and (2.8), applying Hölder inequality, we get

$$\begin{aligned} u(t)&=\frac{1}{2} \bigl(u(t)+u(t-T)\bigr) \\ &=\frac{1}{2} \biggl(u(\tau)+ \int^{t}_{\tau}u'(s)\,ds+u(\tau)- \int^{\tau}_{t-T}u'(s)\,ds \biggr) \\ &\geq u(\tau)-\frac{1}{2} \biggl\vert \int^{t}_{\tau}u'(s)\,ds- \int^{\tau}_{t-T}u'(s)\,ds \biggr\vert \\ &\geq u(\tau)-\frac{1}{2} \biggl( \int^{t}_{\tau}\bigl\vert u'(s) \bigr\vert \,ds+ \int^{\tau}_{t-T} \bigl\vert u'(s) \bigr\vert \,ds \biggr) \\ &=u(\tau)-\frac{1}{2} \int^{t}_{t-T} \bigl\vert u'(s) \bigr\vert \,ds \\ &\geq d_{1}-\frac{1}{2} \int^{T}_{0} \bigl\vert u'(s) \bigr\vert \,ds \\ &\geq d_{1}-\frac{1}{2}T^{\frac{1}{2}} \biggl( \int^{T}_{0} \bigl\vert u'(s) \bigr\vert \,ds \biggr)^{\frac {1}{2}} \\ &\geq d_{1}-\frac{T^{\frac{1}{2}} \Vert e \Vert _{2}}{2\gamma_{2}}:=M_{3}>0, \end{aligned}$$

since \(\frac{T^{\frac{1}{2}}\|e\|_{2}}{2\gamma}< d_{1}\). The remaining part of the proof is the same as that of Theorems 2.1. □

Comparing Theorems 2.1 to 2.2, Theorem 2.2 is applicable to weak as well as strong singularities, whereas Theorem 2.1 is only applicable to a strong singularity. Besides, equation (1.2) is relatively weaker than condition \(\frac{T^{\frac{1}{2}}\|e\|_{2}}{2\gamma}< d_{1}\). On the other hand, Theorems 2.1 and 2.2 require that g possesses a singularity of repulsive type (i.e., \(\lim_{u\to0^{+}}g(u)=-\infty\)). In the following, we consider that g possesses a singularity of attractive type (i.e., \(\lim_{u\to0^{+}}g(u)=+\infty\)). It is obvious that the attractivity condition and equation (1.2) with \((H_{2})\) contradict each other. Therefore, we have to find other conditions to consider equation (1.1) with a singularity of attractive type.

Theorem 2.3

Assume that\((H_{1})\)holds. Furthermore, suppose the following conditions hold:

\((H_{3})\):

There exist two positive constants\(d_{3}\), \(d_{4}\)with\(d_{3}< d_{4}\)such that\(g(u)-e(t)>0\)for\((t,u)\in[0,T]\times(0,d_{3})\)and\(g(u)-e(t)<0\)for\((t,u)\in[0,T]\times(d_{4},+\infty)\).

\((H_{4})\):

(Strong singularity of attractive type)

$$\lim_{u\to0^{+}}g(u)=+\infty \quad\textit{and}\quad \lim_{u\to 0^{+}} \int^{1}_{u}g(\nu)\,d\nu=-\infty. $$

Then equation (1.1) has at least one positive periodic solution.

Proof

We follow the same strategy and notation as in the proof of Theorem 2.1. Next, we consider \(\int^{T}_{0}|g(u(t))|\,dt\). From equations (2.12) and (2.13), we see that

$$ \begin{aligned}[b] \int^{T}_{0} \bigl\vert g\bigl(u(t)\bigr) \bigr\vert \,dt={}& \int_{g(u(t))\geq0}g\bigl(u(t)\bigr)\,dt- \int_{g(u(t))\leq 0}g\bigl(u(t)\bigr)\,dt \\ ={}&{-}2 \int_{g(u(t))\leq0}g^{-}\bigl(u(t)\bigr)\,dt- \int^{T}_{0}f\bigl(t,u(t)\bigr)u'(t) \,dt+ \int ^{T}_{0}e(t)\,dt \\ \leq{}&2 \int^{T}_{0} \bigl\vert g^{-}\bigl(u(t)\bigr) \bigr\vert \,dt+ \int^{T}_{0} \bigl\vert f\bigl(t,u(t)\bigr) \bigr\vert \bigl\vert u'(t) \bigr\vert \,dt+ \int ^{T}_{0} \bigl\vert e(t) \bigr\vert \,dt, \end{aligned} $$
(2.16)

where \(g^{-}(u):=\min\{g(u),0\}\). Since \(g^{-}(u(t))\leq0\), form conditions \((H_{3})\) and \((H_{4})\), we know that there exists a positive constant \(d_{4}^{*}\) with \(d_{4}^{*}>d_{3}\) such that \(u(t)\geq d_{4}^{*}\). Therefore, from equations (2.9) and (2.10), equation (2.16) implies

$$ \int^{T}_{0} \bigl\vert g\bigl(u(t)\bigr) \bigr\vert \,dt\leq 2T \bigl\Vert g^{-}_{M_{1}} \bigr\Vert +M_{2}T \Vert f_{M_{1}} \Vert +T^{\frac{1}{2}} \Vert e \Vert _{2} , $$

where \(\|g^{-}_{M_{1}}\|:=\max_{d_{4}^{*}\leq u\leq M_{1}}|g^{-}(u)|\). The remaining part of the proof is the same as that of Theorem 2.1. □

By Theorems 2.2 and 2.3, we obtain the following conclusion.

Theorem 2.4

Assume that conditions\((H_{1})\)and\((H_{3})\)hold. If\(\frac{T^{\frac{1}{2}}\|e\|_{2}}{2\gamma}< d_{3}\), then equation (1.1) has at least one positive periodic solution.

Finally, we illustrate our results with two numerical examples.

Example 2.1

Consider the following prescribed mean curvature Liénard equation with a strong singularity of repulsive type

$$ \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr)'+\bigl(( \sin t+3)u^{4}(t)+1\bigr)u'(t)+\sum _{i=1}^{n} u^{i}(t)= \frac{6}{u^{\mu}(t)}+e^{\cos t}, $$
(2.17)

where μ is a positive constant and \(\mu\geq1\), n is a positive integer.

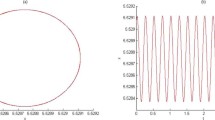
It is clear that \(T=2\pi\), \(f(t,u)=(\sin t+3)u^{4}+1\), \(g(u)=\sum_{i=1}^{n} u^{i}-\frac{6}{u^{\mu}}\), \(e(t)=e^{\cos t}\). We know that \(|f(t,u)|=(\sin t+3)u^{4}+1\geq1\). Take \(\gamma=1\), \(d_{1}=0.01\), \(d_{2}=3\). Then conditions \((H_{1})\) and \((H_{2})\) hold. Since \(\lim_{u\to 0^{+}}\int^{1}_{u}g(\nu)\,d\nu=\lim_{u\to 0^{+}}\int^{1}_{u} (\sum_{i=1}^{n} \nu^{i}-\frac{6}{\nu^{\mu}} )\,d\nu=+\infty\), equation (1.2) is satisfied. Therefore, by Theorem 2.1, equation (2.17) has at least one positive 2π-periodic solution.

Example 2.2

Consider the following prescribed mean curvature Liénard equation with a weak singularity of attractive type:

$$ \biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'-\bigl((\cos2 t+5)u^{6}(t)+100 \bigr)u'(t)-u^{5}(t)+\frac{4}{u^{\frac{1}{2}}(t)}=\sin2t, $$
(2.18)

where \(p> 1\).

It is obvious that \(T=\pi\), \(f(t,u)=-(\cos2 t+5)u^{6}-100\), \(g(u)=-u^{5}+\frac{4}{u^{\frac{1}{2}}}\), \(e(t)=\sin2t\). Taking \(\gamma=100\), \(d_{3}=0.09\), \(d_{4}=4\), conditions \((H_{1})\) and \((H_{3})\) are satisfied. Furthermore, we consider

$$\frac{T^{\frac{1}{2}} \Vert e \Vert _{2}}{2\gamma}=\frac{\pi}{200}< 0.09. $$

Hence, applying Theorem 2.4, equation (2.18) has at least one positive π-periodic solution.

3 Positive periodic solution for equation (1.1) when \(p> 1\) and \(p\neq2\)

In the following, by Lemma 2.1 and Theorem 2.1, we prove the existence of a positive periodic solution for equation (1.1) with a singularity of repulsive type.

Theorem 3.1

Assume that conditions\((H_{1})\), \((H_{2})\)and\(p\neq2\)hold. Then equation (1.1) has at least one positive periodic solution.

Proof

Let \(t^{*}, t_{*}\in(0,T)\) be the maximum and minimum points of \(u(t)\), and \(u'(t^{*})=u'(t_{*})=0\). Besides, we claim that there exists a positive constant ε such that

$$ u'(t)\geq0, \quad\mbox{for } t\in\bigl(t^{*}- \varepsilon,t^{*}+\varepsilon\bigr). $$
(3.1)

Assume, by way of contradiction, that inequality (3.1) does not hold. Then \(u'(t)<0\) for \(t\in(t^{*}-\varepsilon,t^{*}+\varepsilon)\). Therefore, \(u(t)\) is strictly decreasing for \(t\in(t^{*}-\varepsilon,t^{*}+\varepsilon)\), this contradicts the definition of \(t^{*}\). Hence, equation (3.1) is true. Since

$$ \biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)' = \biggl( \biggl\vert \frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr\vert ^{p-2} \biggl(\frac {u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'. $$
(3.2)

Applying equations (3.1) into (3.2), we get

$$ \begin{aligned}[b] \biggl(\phi_{p} \biggl( \frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)' &= \biggl( \biggl( \frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr)^{p-1} \biggr)' \\ &=(p-1) \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr)^{p-2} \biggl( \frac{2u''(t)+u''(t)(u'(t))^{2}}{\sqrt{1+(u'(t))^{2}}} \biggr), \end{aligned} $$
(3.3)

for \(t\in(t^{*}-\varepsilon,t^{*}+\varepsilon)\). From equation (3.3) and \(p\neq2\), we obtain

$$ \biggl(\phi_{p} \biggl(\frac{u'(t^{*})}{\sqrt{1+(u'(t^{*}))^{2}}} \biggr) \biggr)'=0. $$
(3.4)

From equations (2.2) and (3.4), we have

$$g\bigl(t^{*},u\bigl(t^{*}\bigr)\bigr)-e\bigl(t^{*}\bigr)=0. $$

By condition \((H_{2})\), we get

$$ d_{1}\leq u\bigl(t^{*}\bigr)\leq d_{2}. $$
(3.5)

Similarly, by condition \((H_{2})\), we obtain

$$ d_{1}\leq u(t_{*})\leq d_{2}. $$
(3.6)

Therefore, from equations (3.5) and (3.6), we see that

$$ d_{1}\leq u(t)\leq d_{2}, \quad\mbox{for } t\in\mathbb{R}. $$
(3.7)

By Theorem 2.1, we get that there exist a positive constant \(M_{2}^{*}\) such that

$$\bigl\Vert u' \bigr\Vert \leq M_{2}^{*}. $$

The remaining part of the proof is the same as that of Theorem 2.1. □

Comparing Theorems 2.1 and 3.1, Theorem 3.1 is applicable to weak and strong singularities. Theorem 2.1 is only applicable to a strong singularity. However, Theorem 3.1 does not cover the case of \(p=2\), while Theorem 2.1 covers the case of \(p=2\). Therefore, Theorem 2.1 can be more general. Besides, Theorem 3.1 requires that g possesses a singularity of repulsive type. In the following, we consider that g possesses a singularity of attractive type. It is obvious that attractivity condition and \((H_{2})\) contradict each other. By Theorems 2.3 and 3.1, we obtain the following conclusion.

Theorem 3.2

Assume that conditions\((H_{1})\), \((H_{3})\)and\(p\neq2\)hold. Then equation (1.1) has at least one positive periodic solution.

It is worth mentioning that the method of Theorem 3.1 is also applicable to the case where g is nonautonomous, i.e., \(g(u(t))= g(t,u(t))\). Then equation (1.1) is rewritten as the following form:

$$ \biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'+f\bigl(t,u(t)\bigr)u'(t)+g \bigl(t,u(t)\bigr)=e(t). $$
(3.8)

Applying Lemma 2.1 and Theorem 3.1, we obtain the following conclusion.

Theorem 3.3

Assume that conditions\((H_{1})\)and\(p\neq2\)hold. Furthermore, suppose the following condition holds:

\((H_{5})\):

There exist two positive constants\(d_{5}, d_{6}\)with\(d_{5}< d_{6}\)such that\(g(t,u)-e(t)<0\)for\((t,u)\in[0,T]\times(0,d_{5})\)and\(g(t,u)-e(t)>0\)for\((t,u)\in[0,T]\times(d_{6},+\infty)\).

Then equation (3.8) has at least one positive periodic solution.

Proof

Consider the following equation:

$$ \biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'+\lambda f\bigl(t,u(t)\bigr)u'(t)+ \lambda g\bigl(t,u(t)\bigr)=\lambda e(t), $$
(3.9)

where \(\lambda\in(0,1)\). From equation (3.7) and \((H_{5})\), we get

$$ d_{1}\leq u(t)\leq d_{2}, \quad\mbox{for } t\in\mathbb{R}. $$
(3.10)

Multiplying both sides of equation (3.9) by \(u'(t)\) and integrating from 0 to T, we have

$$ \begin{aligned}[b] &\int^{T}_{0} \biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'u'(t) \,dt+ \lambda \int^{T}_{0}f\bigl(t,u(t)\bigr)u'(t) \,dt+\lambda \int^{T}_{0}g\bigl(t,u(t)\bigr)u'(t) \,dt\hspace{-24pt}\\&\quad=\lambda \int^{T}_{0}e(t)u'(t)\,dt.\end{aligned} $$
(3.11)

Substituting \(\int^{T}_{0} (\phi_{p} (\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} ) )'u'(t)\,dt=0\) into equation (3.11), it is clear that

$$\biggl\vert \int^{T}_{0}f\bigl(t,u(t)\bigr)u'(t) \,dt \biggr\vert = \biggl\vert - \int^{T}_{0}g\bigl(t,u(t)\bigr)u'(t) \, dt+ \int^{T}_{0}e(t)u'(t)\,dt \biggr\vert . $$

By condition \((H_{1})\) and equation (3.10), the above equation imply

$$ \begin{aligned} \gamma \int^{T}_{0} \bigl\vert u'(t) \bigr\vert ^{2}\,dt&\leq \biggl\vert \int^{T}_{0}f\bigl(t,u(t)\bigr)u'(t) \,dt \biggr\vert \\ &\leq \int^{T}_{0} \bigl\vert g\bigl(t,u(t)\bigr) \bigr\vert \bigl\vert u'(t) \bigr\vert \,dt+ \int^{T}_{0} \bigl\vert e(t) \bigr\vert \bigl\vert u'(t) \bigr\vert \,dt \\ &\leq \Vert g_{1} \Vert T^{\frac{1}{2}} \biggl( \int^{T}_{0} \bigl\vert u'(t) \bigr\vert ^{2}\,dt \biggr)^{\frac{1}{2}} + \biggl( \int^{T}_{0} \bigl\vert e(t) \bigr\vert ^{2}\,dt \biggr)^{\frac{1}{2}} \biggl( \int ^{T}_{0} \bigl\vert u'(t) \bigr\vert ^{2}\,dt \biggr)^{\frac{1}{2}} \\ &\leq\bigl( \Vert g_{1} \Vert T^{\frac{1}{2}}+ \Vert e \Vert _{2}\bigr) \biggl( \int^{T}_{0} \bigl\vert u'(t) \bigr\vert ^{2}\,dt \biggr)^{\frac{1}{2}}, \end{aligned} $$

where \(\|g_{1}\|:=\max_{d_{1}\leq u(t)\leq d_{2}}|g(t,u)|\). Since \(\int^{T}_{0}|u'(t)|^{2}\,dt\neq0\) and \(\gamma>0\), we arrive at

$$ \biggl( \int^{T}_{0} \bigl\vert u'(t) \bigr\vert ^{2}\,dt \biggr)^{\frac{1}{2}}\leq \frac{ \Vert g_{1} \Vert T^{\frac{1}{2}}+ \Vert e \Vert _{2}}{\gamma}:=M_{2}'', $$
(3.12)

From equation (3.12), using Hölder inequality, we get

$$ \bigl\Vert u' \bigr\Vert = \frac{1}{T} \int^{T}_{0} \bigl\Vert u' \bigr\Vert \,dt\leq T^{-\frac{1}{2}} \biggl( \int^{T}_{0} \bigl\Vert u' \bigr\Vert ^{2}\,dt \biggr)^{\frac{1}{2}}\leq T^{-\frac{1}{2}}M_{2}'':=M_{2}^{**}. $$
(3.13)

The remaining part of the proof is the same as that of Theorem 2.1. □

Theorem 3.3 requires that g of equation (3.8) possesses a singularity of repulsive type. In the following, by Theorems 2.3 and 3.3, we discuss equation (3.8) with a singularity of attractive type.

Theorem 3.4

Assume that conditions\((H_{1})\)and\(p\neq2\)hold. Furthermore, suppose the following condition holds:

\((H_{6})\):

There exist two positive constants\(d_{7}\), \(d_{8}\)with\(d_{7}< d_{8}\)such that\(g(t,u)-e(t)>0\)for\((t,u)\in[0,T]\times(0,d_{7})\)and\(g(t,u)-e(t)<0\)for\((t,u)\in[0,T]\times(d_{8},+\infty)\).

Then equation (3.8) has at least one positive periodic solution.

Finally, we illustrate our results with one numerical example.

Example 3.1

Consider the following prescribed mean curvature Liénard equation with a weak singularity of repulsive type

$$ \begin{aligned}[b]&\biggl(\phi_{p} \biggl(\frac{u'(t)}{\sqrt{1+(u'(t))^{2}}} \biggr) \biggr)'+\bigl(\bigl(\sin^{2} t \bigr)u^{8}(t)+1\bigr)u'(t)+\bigl( \cos^{2}t+2\bigr)u^{3}(t)-\frac{\sin^{2}t+1}{u^{\frac {1}{5}}(t)}\\&\quad=e^{\cos2t},\end{aligned} $$
(3.14)

where \(p=5\).

It is clear that \(T=\pi\), \(f(t,u)=(\sin^{2} t)u^{8}(t)+1\), \(g(t,u)=(\cos^{2}t+2)u^{3}(t)-\frac{\sin^{2}t+1}{u^{\frac{1}{5}}(t)}\), \(e(t)=e^{\cos2t}\). Take \(\gamma=1\), \(d_{5}=0.01\), \(d_{6}=3\). Then conditions \((H_{1})\) and \((H_{5})\) hold. Therefore, by Theorem 3.3, equation (3.14) has at least one positive π-periodic solution.

4 Conclusions

In this paper, applying an extension of Mawhin’s continuation theorem, we first investigate the existence of a periodic solution for equation (1.1) in the case that \(p>1\), where g possesses weak and strong singularities of attractive type, or weak and strong singularities of repulsive type, and g may satisfy sublinearity, semilinearity, or superlinearity conditions at infinity. After that, we consider the existence of a periodic solution for equation (1.1) when \(p>1\) and \(p\neq2\). Note that the conditions which f, g satisfy and the work of estimating a priori bounds of positive periodic solutions for equation (1.1) are more complex than in [7, 9, 17, 18]. Firstly, the friction term \(f(u(t))u'(t)\) in [7, 9, 17, 18] satisfies \(\int^{T}_{0}f(u(t))u'(t)\,dt=0\), which is crucial to estimate a priori bounds of positive periodic solutions for these equations. However, the friction term of this paper, \(f(t,u(t))u'(t)\), may not satisfy \(\int^{T}_{0}f(t,u(t))u'(t)\,dt=0\). Secondly, g of this paper possesses weak and strong singularities of attractive type (or weak and strong singularities of repulsive type) at the origin. Thirdly, g of this paper may satisfy sublinearity, semilinearity, or superlinearity conditions at infinity. Therefore, we extend and improve the results in [7, 9, 17, 18].