The numerical solution of forward and inverse Robin problems for Laplace’s equation

Abstract

The Robin boundary value problem for Laplace’s equation in the elliptic region (which is a forward problem) and its related inverse problem can be used to reconstruct Robin coefficients from measurements on a partial boundary (inverse problem). We present a numerical solution of the forward problem that uses a boundary integral equation method, and we propose a fast solver based on one that reduces the computational complexity to $\mathcal{O}(N\log (N))$, where N is the size of the data. We compute the solution of the inverse problem using a preconditioned Krylov subspace method where the preconditioner is based on a block matrix decomposition. The structure of the matrix is then exploited to solve the direct problem. Numerical examples are presented to illustrate the effectiveness of the proposed approach.

1 Introduction

Laplace’s equation is of particular importance in applied mathematics because it is applicable to a wide range of different physical and mathematical phenomena, including electromagnetism, fluid and solid mechanics, conductivity. It has the special status of being the most straightforward elliptic partial differential equation for the description of all sorts of steady state phenomena. When attached to Robin boundary conditions it is able to handle the spherical geometry of the largest to the smallest structures in the universe [1]. If a domain Ω in $R^{2}$ is assumed to have a smooth boundary $\partial \varOmega =\varGamma$, the Robin boundary value problem for Laplace’s equation can be stated as follows:

$$ \textstyle\begin{cases} \Delta u =0, & \text{in } \varOmega , \\ \frac{\partial u}{\partial \nu }+p u=g, & \text{on } \partial \varOmega =\varGamma , \end{cases} $$

(1.1)

where ν is an outward-facing unit normal vector on Γ; $p=p(x)$ is the Robin coefficient, which is non-negative and not identical for $\varGamma _{1}\subset \varGamma$; and $g=g(x)$ is a given input function.

However, Laplace’s equation is known to present a number of boundary value problems that can be complex to solve and, when it comes to computation, this can demand significant quantities of computational work. There is therefore an ongoing need to come up with more efficient algorithms to solve these kinds of boundary value problems. This paper addresses such a need.

If p in Eq. (1.1) is given, a unique solution, u, can be determined. This is known as the forward problem. The forward map from p to u has already been discussed in the literature, and a number of its properties has been identified, including uniqueness, continuity with respect to proper norms, differentiability and various forms of stability (see [2,3,4,5,6,7]).

However, a more challenging problem is the inverse problem, which aims to recover the Robin coefficient p from a partial boundary measurement of function u. In other words, how to obtain p by using $u=u_{0}$ on a part, $\varGamma _{0}$, of the boundary, where $\varGamma _{0} \cap \varGamma _{1}=\emptyset$. It is well-known that the inverse problem is currently ill-conditioned, which can cause significant computational difficulties. This issue is of concern because a number of applications seek a solution of the problem, notably various kinds of nondestructive evaluation (NDE) [8].

A lot of research over recent years has been devoted to developing a numerical solution to the inverse problem [9,10,11,12,13]. Lin and Fang transformed the Robin inverse problem into a linear integral equation by introducing a new variable v, then located a way of regularizing v [14]. From this, it was possible to derive a linear least-square-based methods for estimation of the Robin coefficient. Jin solved the Robin inverse problem by using conjugate gradient (CG) methods [15], then analyzing the convergence of different regular terms. Jin and Zou looked at ways of estimating piecewise constant Robin coefficients by using a concave-convex procedure to minimize the Modica–Mortola functional [16]. Chaabane et al. also considered the possibility of estimation of piecewise constant Robin coefficients, in their case by using the Kohn–Vogelius method [17]. Jiang et al. [18] discussed the convergence properties for elliptic and parabolic inverse robin problems.

The solution of an inverse problem usually depends upon a forward solver that is capable of expanding upon the current state to assess whether it can be proved given the current conditions. This makes the speed of forward solver a critical consideration. It is possible to discretize Eq. (1.1) directly by using a finite difference method or a finite element method (see, for instance, [19]) or wavelet method (see, for instance, [20, 21]). Equation (1.1) can also be reformulated as a boundary integral equation. The resulting integral equation can then be discretized by using a boundary element method or numerical quadratures [14, 15, 22, 23]. Out of these, using a boundary integral equation (BIE) appears to the best option because the resulting discrete system is much smaller than it is if one uses the original partial differential equation. This has led to a BIE approach being used by many researchers who take an interest in inverse problems, and we, too, will be adopting this method.

After Eq. (1.1) has been transformed into a BIE and the discretization scheme set up, it can be found that the structure of the coefficient matrix of the resulting discrete system is the sum of the circulant. This makes it possible for a fast algorithm for matrix-vector products to be developed by using a fast Fourier transform (FFT) approach where only $\mathcal{O}(N\log (N))$ operations are required instead of the standard $\mathcal{O}(N^{2})$. In this way, numerical methods for solving the inverse problem can be effectively sped up by using this faster forward solver. Aside from this, we shall be looking at a preconditioner that can exploit the structure of the forward problem matrix. A variant of the symmetric quasi-minimal residual (SQMR) method is employed to accomplish this. SQMR is known to offer significant economy in solving large-scale problems. As the preconditioner is not formed explicitly, we also present an algorithm that can obtain the product of the preconditoner with a given vector.

The paper is organized as follows. In Sect. 2, the Robin inverse problem is transformed into an equivalent BIE. We then derive a fast algorithm for discretization of its linear system by exploiting the special properties of certain relevant kernel functions. In Sect. 3, we look at how the preconditioner used in the Krylov subspace method for the Karush–Kuhn–Tucker (KKT) system might be used to further enhance our approach. In Sect. 4, we conclude with numerical examples to demonstrate the effectiveness of our proposed fast solver for the Robin inverse problem.

2 Fast solution of the forward problem

Let $\varPhi =\varPhi (x,y)$ be the fundamental solution for Laplace’s equation in $\mathbb{R}^{2}$. Thus:

$$ \varPhi (x,y)=\frac{1}{2\pi }\ln \frac{1}{ \vert x-y \vert }\quad \text{for } x\neq y. $$

We will first introduce a formulation of the BIE for the boundary value problem presented in Eq. (1.1). Using Green’s formula, the solution, u, to Eq. (1.1) in domain Ω can be represented in terms of its boundary value by the following:

$$ u(x) = - \int _{\varGamma } \biggl(\frac{\partial \varPhi (x,y)}{\partial \nu _{y}}+p(y)\varPhi (x,y) \biggr)u(y)\,ds_{y}+ \int _{\varGamma }\varPhi (x,y)g(y)\,ds _{y},\quad x\in \varGamma , $$

where $ds_{y}$ denotes the arc length differential. After moving x in Ω to the boundary Γ, one can arrive at the following BIE on the boundary Γ:

$$ \frac{1}{2}u(x)+ \int _{\varGamma } \biggl(\frac{\partial \varPhi (x,y)}{ \partial \nu _{y}}+p(y)\varPhi (x,y) \biggr)u(y)\,ds_{y}= \int _{\varGamma } \varPhi (x,y)g(y)\,ds_{y},\quad x\in \varGamma . $$

(2.1)

Hence, solving Eq. (1.1) in Ω can be reduced to solving the above BIE, (2.1), on Γ.

The double-layer and single-layer operators can be defined, respectively, by

$$ \begin{aligned} &(\mathcal{D}u) (x)= \int _{\varGamma }\frac{\partial \varPhi (x,y)}{\partial \nu _{y}} u (y)\,ds_{y}, \\ &(\mathcal{S}u) (x)= \int _{\varGamma }\varPhi (x,y)u(y)\,ds_{y}, \end{aligned} \quad \text{for } x\in \varGamma , $$

and, by denoting $\mathcal{A}(p)(u)= (\frac{1}{2}\mathcal{I}+ \mathcal{D} )u+\mathcal{S}(pu)$, we can re-write Eq. (2.1) in terms of its operators as follows:

$$ \mathcal{A}(p) (u)=f, $$

(2.2)

where $f=\mathcal{S}g$.

Let us now suppose that Ω is an ellipse in $\mathbb{R}^{2}$. So,

$$ \varOmega = \biggl\{ (x_{1},x_{2}): \biggl(\frac{x_{1}}{a} \biggr)^{2}+\biggl(\frac{x_{2}}{b}\biggr)^{2} < 1 \biggr\} , $$

where $a, b >0$. The usual parametrization for Γ is

$$ (x_{1},x_{2})=\bigl(\phi (t),\psi (t)\bigr)=\bigl(a \cos (2 \pi t),b \sin (2\pi t)\bigr), \quad \text{for } 0\leq t \leq 1. $$

The kernels in the integral operators $\mathcal{D}$ and $\mathcal{S}$ can be explicitly expressed as follows:

$$\begin{aligned}& K_{d}(t,s) = -\frac{ab}{2(a^{2}\sin ^{2}(\pi (t+s))+b^{2}\cos ^{2}( \pi (t+s)))}, \\& K_{s}(t,s) = \ln \bigl(2 \bigl\vert \sin \bigl(\pi (t-s) \bigr) \bigr\vert \bigr)\sqrt{a^{2}\sin ^{2}\bigl(\pi (t+s) \bigr)+b ^{2}\cos ^{2}\bigl(\pi (t+s)\bigr)} \\& \hphantom{K_{s}(t,s) =}{} \times \sqrt{a^{2}\sin ^{2}(2\pi s)+b^{2}\cos ^{2}(2\pi s)} \end{aligned}$$

for $0\leq t$, $s \leq 1$.

For discretization of the integral equation (2.1) with the given parametrization of Γ, a Nyström method can be applied by using the mid-point quadrature rule. If we partition the interval $[0,1]$ into N uniform subintervals $[(i-1)h,ih]$ ($i = 1,2,\dots ,N$) with $h = 1/N$, then the quadrature points will be $t_{i} = (i-1/2)h$. With the mid-point quadrature rule, we can denote the matrix representation of the kernels $K_{d}$ and $K_{s}$ by D and S, respectively. As $K_{d}(t,s)$ is smooth, the rectangular rule can be applied to obtain the following discrete representation:

$$ D=h\biggl[-\frac{ab}{2(a^{2}\sin ^{2}(\pi (t_{i}+t_{j}))+b^{2}\cos ^{2}( \pi (t_{i}+t_{j})))}\biggr]_{i,j=1}^{n}. $$

However, because the kernel function $\mathcal{S}$ is weakly singular at $s=t$ and $(t,s)=(0,1)$ and $(1,0)$, discretizing $\int _{0}^{1}K _{s}(t,s)u(s)\,ds$ requires special measures to avoid large errors. By denoting

$$\begin{aligned}& K_{s1}(t,s) = \ln \bigl(2 \bigl\vert \sin \bigl(\pi (t-s)\bigr) \bigr\vert \bigr), \\& K_{s2}(t,s) = \ln \sqrt{a^{2}\sin ^{2}\bigl(\pi (t+s)\bigr)+b^{2}\cos ^{2}\bigl( \pi (t+s)\bigr)}, \\& K_{s3}(s) = -\sqrt{a^{2}\sin ^{2}\bigl(2\pi (s) \bigr)+b^{2}\cos ^{2}\bigl(2 \pi (s)\bigr)}, \end{aligned}$$

it is possible to decompose $K_{s}(t,s)$ as follows:

$$ K_{s}(t,s)=\bigl(K_{s1}(t,s)+K_{s2}(t,s) \bigr)K_{s3}(t,s). $$

If we now use a singularity subtraction technique, we get

$$ S=h \Biggl[K_{s}(t_{i},t_{j})-\delta _{i,j}\sum_{k=1}^{n} K_{s1}(t_{i},t _{k})K_{s3}(t_{i}) \Biggr]_{i,j=1}^{n}, $$

where $\delta _{ij}$ is the Kronecker delta.

Let us now denote $K_{s}=hK_{s}(t_{i},t_{j})$, $K_{s1}=hK_{s1}(t_{i},t _{j})$, $K_{s2}=hK_{s2}(t_{i},t_{j})$, $K_{s3}=K_{s3}(t_{i})$. For a given vector v, the product Sv can then be obtained as follows:

$$\begin{aligned} Sv =& \Biggl[h K_{s}(t_{i},t_{j})- \delta _{i,j}h\sum_{k=1}^{n} K_{s1}(t _{i},t_{k})K_{s3}(t_{i}) \Biggr]_{i,j=1}^{n} v \\ :=&K_{s} v -(K_{s1}1).*(K_{s3}.*v) \\ =&(K_{s1}+K_{s2}) (K_{s3}.*v)-(K_{s1}1).*(K_{s3}.*v) \\ =&K_{s1}(K_{s3}.*v)+K_{s2}(K_{s3}.*v)-(K_{s1}1).*(K_{s3}.*v), \end{aligned}$$

where 1 denotes the vector whose elements are all one and $a.*b$ denotes element-by-element multiplication of the vectors a and b. For more techniques to deal with the singular integral operators we refer to [24, 25].

In general, it is necessary to choose specific quadrature rules for the Nyström method to be able to discretize the BIEs. Nyström techniques can then be used to build faster algorithms [14]. In our case, we want to exploit the special structure of the matrices D and S to devise a fast algorithm that can solve Eq. (2.1) or (2.2).

From the above operator expression, it can be observed that the discretized matrix D is a Hankel matrix, where $D_{i,j}$ is an element of D and satisfies $D_{i,j}=D_{i-1,j+1}$. For a given vector v, we can use a fast algorithm to compute the product of D times vector v with the help of an FFT. Obviously, $K_{s1}$ is a Toeplitz matrix, which has constant values along its negative-sloping diagonals, whilst $K_{s2}$ is a Hankel matrix. This enables us to get the product of S with a given vector v by using the FFT.

Generally, the discretized form of the direct problem (2.2) is as follows:

$$ A(\mathbf{p}) \mathbf{u}:=\biggl(\frac{1}{2}I+D+S\mathbf{p}\biggr) \mathbf{u}= \mathbf{f}, $$

where $\mathbf{p}=\operatorname{diag}(\mathrm{p})$, which can be solved by using a Gaussian elimination method (GE). However, in this paper we will be using an iterative method to solve the problem. For each iteration, we compute the product of the matrix $\frac{1}{2}I+D+S \mathbf{p}$ with a given vector x by using the FFT algorithm. For the given vector x:

$$\begin{aligned} A(\mathbf{p}) \mathbf{u} =&\biggl(\frac{1}{2}I+D+S\mathbf{p} \biggr)x \\ =&\frac{1}{2}x+Dx+S(\mathbf{p}x) \\ =&\frac{1}{2}x+Dx+K_{s1}(K_{s3}.* \mathbf{p}x)+K_{s2}(K_{s3}.* \mathbf{p}x)-(K_{s1}1).*(K_{s3}.* \mathbf{p}x), \end{aligned}$$

(2.3)

where $\mathbf{p}x=\mathbf{p}.*x$.

Note that all of the matrix-vector products involved can be rapidly obtained using FFT method, whereby the computational complexity can be reduced to $\mathcal{O}(N\log (N))$. This allows for a straightforward solution of the direct problem. As will be seen, the numerical results show that our fast algorithm is superior to the Gaussian elimination (GE) method.

3 The Robin inverse problem and preconditioner

The Robin inverse problem we specifically focus on was that, given $u = u_{0}$ on $\varGamma _{0}$, one recover the Robin coefficient p on $\varGamma _{1}$ with $\varGamma _{0} \cap \varGamma _{1} = \emptyset$. That is,

$$ \text{Find } p \text{ such that}: u, \text{the solution of Eq. (2.1)}, \text{also verifies } u|_{\varGamma _{0}} = u_{0}. $$

A solution to the inverse problem does not depend continuously on the data even if this does exist, because of the ill-conditioned nature of the Robin inverse problem for Laplace’s equation. For this reason, the precess of regularization is required to obtain a relatively smooth solution to a nearby problem [10]. In view of this, the inverse problem can be transformed into the following constrained minimization problem:

$$ \textstyle\begin{cases} \min_{p,u}\frac{1}{2} \Vert \mathcal{R}_{0}u-u_{0} \Vert ^{2}_{L^{2}(\varGamma _{0})} +\frac{\alpha }{2} J(p), \\ \text{s.t.}\quad A(p)(u)= f, \end{cases} $$

(3.1)

where $\mathcal{R}_{0}$ is restriction operator from Γ to $\varGamma _{0}$. As for regularization function, we choose the $H^{1}$ semi-norm of $p(x)$:

$$ J(p) = \int _{\varGamma _{1}} \bigl\vert p'(x) \bigr\vert ^{2}\,ds_{x}, $$

and the regularization parameter $\alpha >0$ to balance the data fidelity $\|\mathcal{R}_{0}u-u_{0}\|^{2}_{L^{2}(\varGamma _{0})}$ and regularization terms $J(p)$.

Various nonlinear programming methods have been developed for constrained optimization. These methods seek a critical point for the Lagrangian function:

$$ \mathcal{L}(u, p, \lambda ) = \frac{1}{2} \Vert \mathcal{R}_{0}u-u_{0} \Vert ^{2} _{L^{2}(\varGamma _{0})} +\frac{\alpha }{2} J(p) +\lambda ^{T}\bigl[A(p) (u)- f \bigr], $$

(3.2)

where λ is a Lagrangian multiplier. The goal here is to get a solution to the large system of nonlinear equations:

$$\begin{aligned} &\mathcal{L}_{\mathbf{u}} =\mathcal{R}_{0}^{T}( \mathcal{R}_{0}u-u_{0})+A ^{T}\lambda =0, \end{aligned}$$

(3.3a)

$$\begin{aligned} &\mathcal{L}_{\mathbf{p}} =\alpha J_{p}+G^{T}\lambda =0, \end{aligned}$$

(3.3b)

$$\begin{aligned} &\mathcal{L}_{\lambda } =Au-f=0, \end{aligned}$$

(3.3c)

where

$$ J_{p}=J_{p}(p)=\frac{\partial J}{\partial p}, \qquad G=G(u,p)= \frac{\partial (Au)}{\partial p}. $$

To solve these nonlinear equations, we can use a Newtonian method to obtain the following KKT system:

$$H_{kkt}\left(\begin{array}{c}\delta u\\ \delta p\\ \delta \lambda \end{array}\right)=-\left(\begin{array}{c}{\mathcal{L}}_u\\ {\mathcal{L}}_p\\ {\mathcal{L}}_{\lambda }\end{array}\right),$$

(3.4)

where

$$H_{kkt}=\left(\begin{array}{ccc}{R}_0^T{R}_0& K& A^T\\ K^T& \alpha J_{pp}+T& G^T\\ A& G& 0\end{array}\right)$$

with

$$ K = K(p, \lambda ) = \frac{\partial {(A(p)^{T}\lambda )}}{\partial p},\qquad J_{pp} = J_{pp}(p) = \frac{\partial {J_{p}}}{\partial p},\qquad T = T(u, p, \lambda ) = \frac{\partial {(G^{T}\lambda )}}{\partial p}. $$

Therefore, the main computational step in the solution process is the repeated solution of large linear systems in the KKT system. To solve the discretized KKT system expressed in Eq. (3.4), there are two basic approaches—a reduced sequential quadratic programming method (SQP) [26] and a full space method [27]. SQP seems preferable because it significantly reduces the dimensions of the problem. However, the major disadvantage here is that it is necessary to solve the variables for u and the Lagrange multipliers λ at each iteration.

The full space method, by contrast, is able to solves KKT systems in such a way that u, λ and p can be obtained simultaneously. The KKT system expressed in (3.4) is relatively straightforward to solve by using Krylov subspace methods. In this paper, we apply a preconditioned Krylov subspace method directly to the KKT system (3.4), and compute a solution to the inverse problem and to the direct problem simultaneously. The sky step here is choosing an appropriate preconditioner for the fast solver of the above KKT system. Recently, the idea of using indefinite preconditioners for KKT systems has come to the fore [28, 29]. However, although it is no longer necessary for the product of the preconditioner within the KKT system (3.4) to be symmetrical, a symmetrical algorithm still be applied to solve the system. In this paper, we assume the preconditioners are symmetrical but far from being positive definite. This is possible because the matrix $H_{kkt}$ of the KKT system has similar properties. To this end, we shall be looking at how to use a fast symmetrical quasi-minimal residual algorithm (SQMR) to solve the system. We can find that it is possible to apply a symmetric QMR variant to the solution of the system, although the product of the preconditioner with the KKT system (3.3a)–(3.3c) is no longer symmetric.

3.1 A preconditioned reduced method for the KKT system

In view of the similarity between a preconditioned Krylov subspace approach and a preconditioned reduced approach, we will first of all introduce a reduced Hessian system. In this way, we can eliminate $\delta _{u}$, then $\delta _{\lambda }$, and finally solve for $\delta _{p}$ in (3.4):

$$ \delta _{p} = -H_{\mathrm{red}}^{-1}p, $$

(3.5)

where

$$\begin{aligned} & H_{\mathrm{red}} = H_{\mathrm{red}}(u, p, \lambda )=M^{T}M+\alpha J_{pp}+T-S-S^{T}, \end{aligned}$$

(3.6a)

$$\begin{aligned} & M = M(u, p)=-R_{0}A(p)^{-1}G, \end{aligned}$$

(3.6b)

$$\begin{aligned} & S = S(u, p, \lambda )=K^{T}A(p)^{-1}G, \end{aligned}$$

(3.6c)

and

$$ p = p(u,p,\lambda ) = \alpha J_{p} +M^{T}\bigl( \mathcal{R}_{0}A^{-1}f-u _{0}\bigr)-K \bigl(u-A^{-1}f\bigr). $$

In the Gauss–Newton approximation, second-order information can be dropped by setting $K = 0$ and $T = 0$. This produces a symmetric positive-definite matrix:

$$ H_{\mathrm{red}} = M^{T}M+\alpha J_{pp}. $$

(3.7)

Thus, we are able to draw upon the classical Gauss–Newton method. In this paper, we will use a preconditioned conjugate gradient (PCG) method to solve Eq. (3.5).

3.2 A preconditioned Krylov subspace method for the KKT system

As the invertible block in $H_{kkt}$ is only on the cross-diagonal axis, the matrix $H_{kkt}$ is singular. To find an appropriate preconditioner, we can first of all permute the block rows and columns in matrix $H_{kkt}$ so that there is an invertible block on the diagonal, and obtain an invertible matrix:

$$H=\left(\begin{array}{ccc}A& 0& G\\ R_0^T{R}_0& A^T& K\\ K^T& G^T& \alpha J_{pp}+T\end{array}\right).$$

For the permuted matrix H we can obtain a block LU decomposition as follows:

$$ H=LU, $$

(3.8)

where

$$L=\left(\begin{array}{ccc}I& 0& 0\\ {\mathcal{R}}_0^T{\mathcal{R}}_0{A}^{-1}& I& 0\\ K^T{A}^{-1}& G^T{A}^{-T}& I\end{array}\right),U=\left(\begin{array}{ccc}A& 0& G\\ 0& A^T& K+{\mathcal{R}}_0^{T}M\\ 0& 0& H_{\mathrm{red}}\end{array}\right).$$

(3.9)

Note that H is invertible, such that

$$ H^{-1}=U^{-1}L^{-1}, $$

with

$$\begin{array}{c}{L}^{-1}=\left(\begin{array}{ccc}I& 0& 0\\ -{\mathcal{R}}_0^T{\mathcal{R}}_0{A}^{-1}& I& 0\\ -(K^T+M^T{\mathcal{R}}_0)A^{-1}& -G^T{A}^{-T}& I\end{array}\right),\hfill \\ U^{-1}=\left(\begin{array}{ccc}{A}^{-1}& 0& -A^{-1}G{H}_{\mathrm{red}}^{-1}\\ 0& A^{-T}& -A^{-T}(K+{\mathcal{R}}_0^{T}M)H_{\mathrm{red}}^{-1}\\ 0& 0& H_{\mathrm{red}}^{-1}\end{array}\right).\hfill \end{array}$$

If we let B be an approximation of $A^{-1}$ and $M_{\mathrm{red}}$ be an approximation of $H^{-1}_{\mathrm{red}}$, we can get the following definitions:

$$\begin{array}{c}\hat{L}=\left(\begin{array}{ccc}I& 0& 0\\ -{\mathcal{R}}_0^T{\mathcal{R}}_{0}B& I& 0\\ -(K^T+M^T{\mathcal{R}}_0)B& -G^T{B}^T& I\end{array}\right),\hfill \\ \hat{U}=\left(\begin{array}{ccc}B& 0& -BG{M}_{\mathrm{red}}\\ 0& B^T& -B^T(K+{\mathcal{R}}_0^T\overline{M})M_{\mathrm{red}}\\ 0& 0& M_{\mathrm{red}}\end{array}\right),\hfill \end{array}$$

where $\bar{M} = -\mathcal{R}_{0}BG$. These two matrices, L̂ and Û, are approximations of the matrices $L^{-1}$ and $U^{-1}$, respectively. So, if we let

$$ M = \hat{U}\hat{L}, $$

(3.10)

we can obtain an approximate inverse, M, of the permuted KKT matrix H. Furthermore, if B and $M_{\mathrm{red}}$ are chosen to satisfy a product with a vector that can be rapidly calculated, we can also obtain the product with a vector of the approximate inverse, M, rapidly.

However, we do need not to specify the preconditioner, M, explicitly to able to calculate the product of the matrix with a given vector. In fact, given a vector $v=[v_{\lambda }^{T}, v_{u}^{T}, v_{p}^{T}]^{T}$, the product $x = [x^{T}_{u}, x^{T}_{\lambda }, x^{T}_{p}]^{T} = Mv$ can be obtained in six stages:

• (1) $w_{1}=Bv_{\lambda }$;

• (2) $w_{2}=B^{T}(v_{u}-\mathcal{R}_{0}^{T}\mathcal{R}_{0}w_{1})$;

• (3) $w_{3}=v_{p}-G^{T}w_{2}-K^{T}w_{1}$;

• (4) $x_{p}=M_{\mathrm{red}}w_{3}$;

• (5) $x_{u}=w_{1}-BGx_{p}$;

• (6) $x_{\lambda }=B^{T}(v_{u}-\mathcal{R}_{0}^{T}\mathcal{R}_{0}x_{u}-Kx _{p})$.

In this paper, we have chosen $B = A^{-1}$ because it enables a fast solution of the direct problem. On the basis of this, we can rapidly calculate the first, second and fifth stages. In our algorithm, we need to reorder the components in v and x to get the corresponding preconditioner for (3.4). This reorder ensures that the corresponding preconditioning matrix of (3.4) is symmetrical. Then we can use a preconditioned symmetric QMR algorithm to solve the KKT system.

4 Numerical examples

We will first of all consider a numerical solution of the direct problem.

Example 1

(Fast algorithm of the direct problem)

For this numerical experiment, we assumed that there was an ellipse with the following standard parametrization:

$$ x=x(t)=\bigl(a\cos (2\pi t),b\sin (2\pi t)\bigr), \quad 0\leq t\leq 1, $$

where $a=1$ and $b = 0.1$. The two segments $\varGamma _{0}$ and $\varGamma _{1}$ were

$$ \begin{aligned} & \varGamma _{0}=\bigl\{ \bigl(a\cos (2\pi t),b\sin (2\pi t)\bigr):t\in [0.55,0.85]\bigr\} , \\ &\varGamma _{1}=\bigl\{ \bigl(a\cos (2\pi t),b\sin (2\pi t)\bigr):t\in [0.15,0.45]\bigr\} . \end{aligned} $$

The function for $g(t)$ was

$$ \begin{aligned} &g\bigl(a\cos (2\pi t)\bigr),b\sin (2\pi t))= \textstyle\begin{cases} 1 & \text{if } t\in [0.4,0.6], \\ 0 & \text{elsewhere on }\varGamma . \end{cases}\displaystyle \end{aligned} $$

The Robin coefficient $p(t)$ was

$$ \begin{aligned} &p(t)= \textstyle\begin{cases} -(\frac{20}{3})^{6}(t-0.15)^{3}(t-0.45)^{3} & \text{if } t\in [0.15, 0.45], \\ 0 & \text{else other}. \end{cases}\displaystyle \end{aligned} $$

For the interval $[0,1]$, we set n equal-length intervals with $\{t_{i}\}_{i=0}^{n}$ nodes. The tests were carried out by using Matlab. In all of the tests, we first selected ${p}(t)$, then obtained approximate values of the solution, $u(t)$, at the various grid points by solving the linear system as a the direct problem. For comparison, the tests were also conducted using conventional GE.

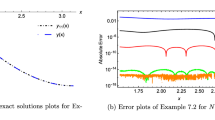
Table 1 shows the results of the fast algorithm for the forward equation when using the discretized matrices. Uniform partitions were set on the parameter domain $[0,1]$ at $n = 800$. As can be seen from the table, when n exceeded 400, the proposed algorithm was faster than GE, it becoming proportionally faster as n increased.

Table 1 Temporal performance for the proposed (fast) algorithm and Gaussian elimination (GE) when solving the direct problem

For the other examples, we will look at the numerical test results for our preconditioned symmetrical quasi-minimal residual method (PSQMR) for the recovery of the Robin coefficients from measurements on $\varGamma _{0}$. The boundary conditions were the same as those given for the direct problem.

For the approximate inverse $M_{\mathrm{red}}$, an incomplete LU decomposition was recalled with a threshold $(\operatorname{ILU}(t))$ of $M^{T}M$.

Example 2

(Comparing of the PCG and PSQMR)

In this example, we compare the PCG for the reduced Hessian system with the PSQMR for the KKT system. The related iterative processes were stopped when the residual was below 10⁻⁵.

Table 2 presents iteration counts (‘itns’) for the various values of α because the regular parameters play an important role and need to be quite small. More computations are typically involved in a PCG iteration than in a PSQMR iteration, even though the same types of matrix-vector product are used in both algorithms. We also display flop counts (‘work’) to indicate the total computational work required by each algorithm. The results shown in this table indicate that the number of PSQMR iterations was larger than the number of PCG iteration. However, the overall work when using PSQMR was substantially lower than it was with PCG. This was especially the case when the ILU preconditioner was utilized, because more matrix-vector products were required to arrive at a solution to the forward problem.

Table 2 Iterations and flop counts for the reduced Hessian and KKT solvers

Example 3

(Recovery of the Robin coefficient)

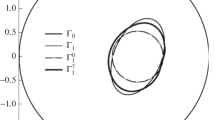
The performance of the two methods was also compared in the elliptic domain. In Fig. 1, the exact p profile generated when using the PSQMR and PCG is plotted together with two reconstructed profiles. For both methods, the regularization parameter α was obtained by employing a discrepancy principle based on our knowledge of noise levels and statistics. The stop criterion was when the norm of the gradient gets below 10⁻⁵. It can be seen that under low noise conditions, both method performed well. However, as the noise increased, PCG performed less well, while the PSQMR method remained robust.

Figure 1

Comparison of effectiveness at recovery of the Robin coefficient for PCG and PSQMR