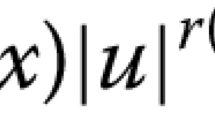Abstract
In this paper, we prove that the following \((p_{1},p_{2},\ldots,p_{n})\)-Laplacian elliptic system with a nonsmooth potential has at least three weak solutions:
The proof is based on a three critical points theorem for nondifferentiable functionals. Some recent results in the literature are generalized and improved.
Similar content being viewed by others
1 Introduction
As we know many free boundary problems and obstacle problems may be reduced to partial differential equations with nonsmooth potentials. The area of nonsmooth analysis is closely related to the development of critical point theory for nondifferentiable functionals, in particular, for locally Lipschitz continuous functionals based on Clarke’s generalized gradient [1]. The existence of multiple solutions for Dirichlet boundary value problems with discontinuous nonlinearities has been widely investigated in recent years. In 1981, Chang [2] extended the variational methods to a class of nondifferentiable functionals and directly applied the variational method to prove some existence theorems for PDE with discontinuous nonlinearities. It provides an appropriate mathematical framework to extend the classic critical point theory for \(C^{1}\)-functionals in a natural way and to meet specific needs in applications, such as in nonsmooth mechanics and engineering. For a comprehensive understanding, we refer to the monographs [3,4,5] and references [6,7,8,9,10,11].
The study of quasilinear elliptic systems, which have been used in a great variety of applications, has received considerable attention in recent years. For example, in [12] the authors studied a class of quasilinear elliptic systems involving the p-Laplacian operator and the right-hand sides of systems being closely related to the critical Sobolev exponent. Then they proved the existence of at least one nontrivial solution under some additional assumptions on the nonlinearities. In [13], Li and Tang considered a class of quasilinear elliptic systems involving the \((p,q)\)-Laplacian of the type
where Ω is a bounded, nonempty, and open subset of \(\mathbb{R}^{N}\) with a \(C^{1}\)-boundary ∂Ω, \(F:\varOmega \times \mathbb{R}\rightarrow \mathbb{R}\) is a Carathéodory function, \(F_{u}\) denotes the partial derivative of F with respect to u. By utilizing a three critical points theory, they proved that problem (1.1) has at least three weak solutions. In [14], Kristály guaranteed the existence of an interval \(\varLambda \subset [0,+\infty ]\) such that for each \(\lambda \in \varLambda \) elliptic system (1.2) has at least two distinct nontrivial solutions by using an abstract critical point result of Ricceri. In [15], Zhang et al. discussed the Nehari manifold for a class of quasilinear elliptic systems involving a pair of \((p,q)\)-Laplacian operators and a parameter, and proved the existence of a nonnegative nonsemitrivial solution for a system by discussing properties of the Nehari manifold, and so global bifurcation results were obtained. More results can be found in [16,17,18,19,20,21,22] and the references therein.
Motivated by the above facts, a natural question arises. Is there a similar result to consider (1.1) from a more extensive viewpoint? With this aim in mind the present paper is to improve and generalize the main results of [13] into nonsmooth case. Let \(\varOmega \subset \mathbb{R}^{N}\ (N\geq 1)\) be a non-empty bounded open set with \(C^{2}\)-boundary ∂Ω, \(p_{i}>N\) for \(1\leq i\leq n\) and \(\lambda >0\). We study the following elliptic system with a nonsmooth potential (hemivariational inequality):
where \(\Delta _{p_{i}}u_{i}=\operatorname{div}(|\nabla u_{i}|^{p_{i}-2}\nabla u_{i})\) is a \(p_{i}\)-Laplacian operator, \(b_{i}(x)\in L^{\infty }(\varOmega )_{+}, 1 \leq i\leq n\). We denote by \(\partial u_{i} F(x,u_{1},\ldots,u_{n})\ (1 \leq i\leq n)\) the partial generalized gradient of \(F(x,u_{1},\ldots ,u_{n})\) at the point \(u_{i}\ (1\leq i\leq n)\). Employing a nonsmooth version of Ricceri’s three critical points theorem, we obtain that problem (1.1) has at least three weak solutions in \(W^{1,p_{1}}_{0}( \varOmega )\times \cdots \times W^{1,p_{n}}_{0}(\varOmega )\). By a weak solution of problem (1.1), we mean that, for all \(u=(u_{1},\ldots,u _{n})\in W^{1,p_{1}}_{0}(\varOmega )\times \cdots \times W^{1,p_{n}}_{0}( \varOmega )\),
where \((y_{1},\ldots,y_{n})\in W^{1,p_{1}}_{0}(\varOmega )\times \cdots \times W^{1,p_{n}}_{0}(\varOmega )\) and \(\gamma _{i}\in \partial _{u_{i}}F(x,u _{1},\ldots,u_{n})\ (1\leq i\leq n)\).
We extend the main results of [13] in two directions. Our contribution can be briefly described as follows:
1. We extend the constant exponent case of \((p, q)\)-Laplacian to the general case of \((p_{1},p_{2}, \ldots,p_{n})\)-Laplacian. Some estimates will become more difficult by the increase of restrictions. So a careful analysis is necessary in lots of estimates. We not only obtain the multiplicity of solutions for problem (1.2), but also extend the results to other cases(see Corollaries 2.1–2.4). This is a very comprehensive job for a class of elliptic systems.
2. Our study includes the case where the nonlinear term \(F_{u_{i}}\ (i=1, \ldots,n)\) has discontinuous terms with respect to \(u_{i}\ (i=1,\ldots ,n)\). Due to this fact, we reformulate problem (1.1) into a differential inclusion system. By using Clarke’s gradient for locally Lipschitz functionals, we are able to guarantee the existence and multiplicity of solutions for differential inclusion systems.
We notice that our hypothesis does not require continuity on the functions \(F_{u_{i}}\ (i=1,\ldots,n)\) with respect to \(u_{i}\ (i=1, \ldots,n)\). So (1.1) may not have a solution. To avoid this situation, we consider functions \(F_{u_{i}}\ (i=1,\ldots,n)\) as a multivalued mapping, which is locally essentially bounded, and fill the discontinuity gaps of \(F_{u_{i}}\ (i=1,\ldots,n)\) by an interval \([f_{11},f_{12}], \ldots , [f_{n1},f_{n2}]\), where
Then, it is well known that \(F(x,u_{1},\ldots,u_{n})=\int ^{u_{1}} _{0}F_{t}(x,t,u_{2},\ldots,u_{n})\,dt=\cdots =\int ^{u_{n}}_{0}F_{t}(x,u _{1}, \ldots, u_{n-1},t)\,dt\) is locally Lipschitz with respect to \(u_{1},\ldots,u_{n}\) and \(\partial _{u_{1}}F(x,u_{1},\ldots,u_{n})=[f _{11}(x,u_{1}, u_{2}, \ldots,u_{n}),f_{12}(x,u_{1},u_{2},\ldots,u _{n})], \ldots , \partial _{u_{n}}F(x,u_{1},\ldots,u_{n})=[f_{n1}(x,u _{1},u_{2},\ldots,u_{n}),f_{n2}(x,u_{1},u_{2}, \ldots,u_{n})]\).
The purpose of this paper is to establish the existence of at least three solutions for problem (1.2) with a nonsmooth potential by using a three critical points theorem (see Theorem 1.1) established by Marano and Motreanu in [23], which is a nonsmooth version of Ricceri’s three critical points theorem (see [24]). We extend the main results of [13] into general cases, which satisfy more general conditions than those employed in [13] and so on. The paper is organized as two sections. The main results will be introduced in Sect. 2.
In the following, for convenience, we briefly present some mathematical tools which are used in the analysis of problem (1.2).
Definition 1.1
A function \(\varphi : X\rightarrow \mathbb{R}\) is locally Lipschitz if, for every \(u\in X\), there exist a neighborhood U of u and \(L>0\) such that, for every ν, \(\omega\in U\),
If φ is locally Lipschitz on bounded sets, then clearly it is locally Lipschitz.
Definition 1.2
Let \(\varphi : X\rightarrow \mathbb{R}\) be a locally Lipschitz functional, u, \(\nu \in X\). Define the generalized derivative of φ in u along the direction ν:
It is easy to see that the function \(\nu \rightarrow \varphi ^{0}(u; \nu )\) is sublinear, continuous and so is the support function of a nonempty, convex, and \(\omega ^{*}\)-compact set \(\partial \varphi (u) \subset X^{*}\) defined by
If \(\varphi \in C^{1}(X)\), then
Clearly, these definitions extend those of the Gâteaux directional derivative and gradient.
A point \(u\in X\) is a critical point of φ if \(0\in \partial \varphi (u)\). It is easy to see that, if \(u\in X\) is a local minimum of φ, then \(0\in \partial \varphi (u)\). For more details on locally Lipschitz functionals and their subdifferential calculus, we refer the reader to Clarke [1].
Definition 1.3
Let \(m^{\varphi }(u)= \inf_{u^{*}\in \partial \varphi (u)}\|u^{*}\|_{X^{*}}\). If \(\varphi:X \rightarrow \mathbb{R}\) is a locally Lipschitz functional, then we say that φ satisfies the PS-condition if the following holds:
Every sequence \(\{u_{n}\}\subset X\), such that
has a strongly convergent subsequence.
The following theorem is the main tool in proving our main results in this paper.
Theorem 1.1
(see [23] Theorem 2.1)
Let X be a separable and reflexive real Banach space, and let Φ, \(\varPsi: X\rightarrow \mathbb{R}\) be two locally Lipschitz functionals. Assume that there exists \(u_{0}\in X\) such that \(\varPhi (u_{0})=\varPsi (u _{0})=0\) and \(\varPhi (u)\geq 0\) for every \(u\in X\), and there exist \(u_{1}\in X\) and \(r>0\) such that
-
(i)
\(r<\varPhi (u_{1})\);
-
(ii)
\(\sup_{\varPhi (u)< r}\varPsi (u)< r\frac{\varPsi (u_{1})}{ \varPhi (u_{1})}\), and further we assume that the functional \(\varPhi - \lambda \varPsi \) is sequentially weakly lower semicontinuous and satisfies the PS-condition;
-
(iii)
\(\lim_{\|u\|\rightarrow +\infty }(\varPhi (u)-\lambda \varPsi (u))=+\infty \) for any \(\lambda \in [0,\bar{a}]\), where \(\bar{a}=\frac{hr}{r\frac{\varPsi (u_{1})}{\varPhi (u_{1})}-\sup_{\varPhi (u)< r} \varPsi (u)}\), with \(h>1\). Then there exist an open interval \(\varLambda _{1}\subset [0,\bar{a}]\) and a positive real number σ such that, for every \(\lambda \in \varLambda _{1}\), the function \(\varPhi (u)-\lambda \varPsi (u)\) admits at least three critical points whose norms are less than σ.
2 Main results
In this section, we present our main results. We firstly fix some notations. Let X be the Cartesian product of n Sobolev spaces \(W^{1,p_{1}}_{0}(\varOmega )\), ⋯ and \(W^{1,p_{n}}_{0}(\varOmega )\), i.e., \(X=W^{1,p_{1}}_{0}(\varOmega )\times \cdots \times W^{1,p_{n}}_{0}(\varOmega )\) equipped with the norm
\((X,\|\cdot \|)\) denotes a (real) Banach space and \((X^{*},\|\cdot \| _{*})\) denotes its topological dual, while \(x_{n}\rightarrow x\) (respectively, \(x_{n}\rightharpoonup x\)) in X means that the sequence \(\{x_{n}\}\) converges strongly to x (respectively, weakly) in X. Set
Since \(p_{i}>N\) for \(1\leq i\leq n\), one has \(c<+\infty\). Furthermore, it is known from [25] (Formula (6b)) that
for \(1\leq i\leq n\), where Γ denotes the gamma function and \(m(\varOmega )\) is the Lebesgue measure of the set Ω, and equality occurs when Ω is a ball.
Fix \(x^{0}\in \varOmega \) and choose \(\rho >0\) such that \(B(x^{0},\frac{ \rho }{2})\subset B(x^{0},\rho )\subset \varOmega \).
The hypotheses on the nonsmooth potential function \(F(x,u_{1},\ldots ,u_{n})\) are the following: \(H(F)_{1}\): \(F:\varOmega \times \mathbb{R} ^{n}\rightarrow \mathbb{R}\) is a function such that \(F(x,\zeta _{1}, \ldots,\zeta _{n} )\) satisfies \(F(x,0,\ldots,0)=0\) and also
-
(i)
for all \((\zeta _{1},\ldots,\zeta _{n})\in \mathbb{R} ^{n}\), \(\varOmega \ni x\mapsto F(x,\zeta _{1},\ldots, \zeta _{n})\) is measurable;
-
(ii)
for almost all \(x\in \varOmega \), \(\mathbb{R}^{n} \ni (\zeta _{1},\ldots,\zeta _{n})\mapsto F(x,\zeta _{1},\ldots,\zeta _{n} )\in \mathbb{R}\) is locally Lipschitz;
-
(iii)
\(F(x,\zeta _{1},\ldots,\zeta _{n})\leq a(x)(1+\sum_{i=1}^{n} |\zeta _{i}|^{t_{i}})\) for almost all \(x\in \bar{\varOmega }\) and all \(\zeta _{i}\in \mathbb{R}\), \(t_{i}< p_{i}\) (\(1\leq i\leq n\)), where \(a(x)\in L^{\infty }(\varOmega )_{+}\);
-
(iv)
\(F(x,\zeta _{1},\ldots,\zeta _{n})\geq 0\) for each \((x,\zeta _{1},\ldots,\zeta _{n})\in (\bar{\varOmega }\setminus B(x^{0},\frac{ \rho }{2}))\times [0,d]\times \cdots \times [0,d]\) with \(d>0\);
-
(v)
\(m(\varOmega )\sum_{i=1}^{n}\frac{1}{p_{i}} (d^{p_{i}}R _{i}^{p_{i}}+B_{i}^{p_{i}}) \max_{(x,\zeta _{1},\ldots,\zeta _{n}) \in \bar{\varOmega }\times V}F(x, \zeta _{1},\ldots,\zeta _{n})<\frac{\beta }{\prod^{n}_{i=1}p_{i} } \int _{B(x^{0},\frac{\rho }{2})} F(x,d,\ldots,d)\,dx\), where \(B_{i}=(c \bar{b}_{i} d^{p_{i}}\omega _{N}\rho ^{N})^{\frac{1}{p_{i}}}\), \(R_{i}=\frac{2}{\rho } (\frac{c\rho ^{N} (1-\frac{1}{2^{N}}) \pi ^{\frac{N}{2}}}{\varGamma (1+\frac{N}{2})} )^{\frac{1}{p_{i}}}\) and \(V=\{(\zeta _{1},\ldots,\zeta _{n})|\sum^{n}_{i=1}\frac{|\zeta _{i}|^{p _{i}}}{p_{i}}\leq \frac{\beta }{\prod^{n}_{i=1}p_{i} }\}\) for some \(\beta >0\) and \(1\leq i\leq n\).
We now state our main results.
Theorem 2.1
If there exist positive constants β, d with \(\sum_{i=1}^{n}\frac{(dR_{i})^{p_{i}}}{p_{i}}>\frac{\beta }{ \prod^{n}_{i=1}p_{i}}\) and hypotheses \(H(F)_{1}\) hold, then there exist an open interval \(\varLambda \subset [0,+\infty )\) and a constant σ such that, for each \(\lambda \in \varLambda \), problem (1.1) has at least three solutions in X whose norms are less than σ.
Proof
Let
and
for each \(u= (u_{1},\ldots,u_{n})\in X\). Our method is to apply Theorem 1.1 to Φ and Ψ. From standard results, we can obtain that Φ is locally Lipschitz and weakly sequentially lower semicontinuous. Since \(W^{1,p_{i}}_{0} (\varOmega )\ (p_{i}>N, i=1, \ldots,n)\) is compactly embedded into \(C(\bar{\varOmega })\) and F satisfies hypotheses \(H(F)_{1}\) (ii) and (iii), the above assertion remains true for Ψ. Furthermore, from hypothesis \(H(F)_{1}\) (iii), for each \(\lambda >0\), one has
Now, given \(\lambda >0\), we claim that \(\varPhi (u)-\lambda \varPsi (u)\) satisfies nonsmooth PS-condition. Let \(\{( u_{1,k},\ldots,u_{n,k})\} _{k\geq 1}\subset X\) be a sequence such that
Set \((u_{1,k}^{*}\cdots,u_{n,k}^{*})\in \partial \varphi (u_{1,k}, \ldots,u_{n,k})\) satisfying \(m^{\varphi }(u_{1,k},\ldots,u_{n,k})= \|(u_{1,k}^{*}\cdots,u_{n,k}^{*})\|_{X^{*}}, k\geq 1\). The interpretation of \((u_{1,k}^{*}\cdots,u_{n,k}^{*})\in \partial \varphi (u_{1,k},\ldots,u_{n,k})\) is that \(u_{1,k}^{*}\in \partial _{u_{1}}\varphi (u_{1,k},\ldots,u_{n,k}), \ldots, u_{n,k}^{*}\in \partial _{u_{n}} \varphi (u_{1,k},\ldots,u_{n,k})\). We know that
where \(\gamma _{i,k}\in \partial _{u_{i}}F(x,u_{1,k},\ldots,u_{n,k})\) for \(1\leq i\leq n\).
for all \(y_{i}\in W^{1,p_{i}}_{0}(\varOmega )\), \(1\leq i\leq n\). By virtue of (2.1), the sequences \(\{(u_{1,k},\ldots,u_{n,k})\}\) are bounded. Hence, by passing to a subsequences if necessary, we may assume that \(u_{i,k}\rightharpoonup u_{i,0}\) in \(W^{1,p_{i}}_{0}(\varOmega )\), \(u_{i,k}\rightarrow u_{i,0}\) in \(L^{p_{i}}(\varOmega )\), \(u_{i,k}\rightarrow u_{i,0}\) as \(k\rightarrow +\infty \) for a.a. \(x\in \varOmega \), \(u_{i,k}\in L^{p_{i}}(\varOmega )\) and \(1\leq i\leq n\). From (2.2), we obtain
where \(\gamma _{i,k}\in \partial _{u_{i}}F(x,u_{1,k},\ldots,u_{n,k})\) for \(1\leq i\leq n\), \(\varepsilon _{k}\rightarrow 0\) as \(k\rightarrow + \infty \). Since
and
we have
Noting that \(A_{1},\ldots,A_{n}\) are mappings of type \((S_{+})\), we obtain \(u_{1,k}\rightarrow u_{1,0}\) in \(W^{1,p_{1}}_{0}(\varOmega ), \ldots , u_{n,k}\rightarrow u_{n,0}\) in \(W^{1,p_{n}}_{0}(\varOmega )\). This means that \((u_{1,k},\ldots,u_{n,k})\rightarrow (u_{1,0},\ldots ,u_{n,0})\) in X. So we have proved that the function φ satisfies the nonsmooth PS-condition.
Next, we need to show that Φ and Ψ satisfy (i) and (ii) of Theorem 1.1. Let \(v(x)=(v_{1}(x),\ldots, v_{n}(x))\) satisfying
and \(r=\frac{\beta }{c\prod_{i=1}^{n}p_{i}}\). It is obvious that \(v=(v_{1},\ldots,v_{n})\in X\). In particular, from computation, we have that
for \(1\leq i\leq n\). It follows from the above equality that
and
where \(\bar{b_{i}}=\sup_{x\in \varOmega }b_{i}(x)\), \(\omega _{N}=\frac{ \pi ^{\frac{N}{2}}}{\frac{\pi }{2}\varGamma (\frac{N}{2})}\) is the measure of the N-dimensional unit ball. Since \(\sum^{n}_{i=1}\frac{(dR_{i})^{p _{i}}}{p_{i}}>\frac{\beta }{\prod^{n}_{i=1}p_{i}}\), we have \(\varPhi (v)>r\). We claim that \(\sup_{\varPhi (u)< r}\varPsi (u)< r\frac{\varPsi (v)}{\varPhi (v)}\). By virtue of condition \(H(F)_{1}(iv)\), we have
From hypothesis \(H(F)_{1}(v)\), (2.4), and (2.5)
Therefore, we have tested all the conditions of Theorem 1.1 and the proof is completed. □
In the following, from Theorem 2.1, we will deduce some results. Consider the following elliptic system:
The hypotheses on the nonsmooth potential F are the following:
\(H(F)_{2}:F:\varOmega \times \mathbb{R}^{n}\rightarrow \mathbb{R}\) is a function such that \(F(x,\zeta _{1},\ldots,\zeta _{n})\) satisfies \(F(x,0,\ldots,0)=0\), (i), (ii), (iii), (iv) are the same as those in hypotheses \(H(F)_{1}\).
-
(v)
\(m(\varOmega )\sum_{i=1}^{n}\frac{(dR_{i})^{p_{i}}}{p _{i}} \max_{(x,\zeta _{1},\ldots,\zeta _{n}) \in \bar{\varOmega }\times V}F(x, \zeta _{1},\ldots,\zeta _{n})<\frac{\beta }{\prod^{n}_{i=1}p_{i} } \int _{B(x^{0},\frac{\rho }{2})} F(x,d,\ldots,d)\,dx\), where \(R_{i}=\frac{2}{ \rho } (\frac{c\rho ^{N} (1-\frac{1}{2^{N}})\pi ^{\frac{N}{2}}}{ \varGamma (1+\frac{N}{2})} )^{\frac{1}{p_{i}}}\) and \(V= \{( \zeta _{1},\ldots,\zeta _{n})|\sum^{n}_{i=1}\frac{|\zeta _{i}|^{p_{i}}}{p _{i}}\leq \frac{\beta }{\prod^{n}_{i=1}p_{i} } \}\) for \(1\leq i \leq n\).
Then we have the following corollary.
Corollary 2.1
Assume that there exist positive constants d and β with \(\sum^{n}_{i=1}\frac{(dR_{i})^{p_{i}}}{p_{i}}>\frac{ \beta }{\prod^{n}_{i=1}p_{i}}\) and hypotheses \(H(F)_{2}\) hold, then there exists a constant \(\sigma >0\) such that problem (2.6) has at least three radically symmetric weak solutions in X whose norms are less than σ.
Next, we consider the following elliptic system:
Firstly, we give our assumptions on the nonsmooth potential F.
\(H(F)_{3}\): \(F:\mathbb{R}^{n}\rightarrow \mathbb{R}\) is a function such that \(F(0,\ldots,0)=0\) and also
-
(i)
for almost all \(\mathbb{R}^{n}\ni (\zeta _{1},\ldots ,\zeta _{n})\mapsto F(\zeta _{1},\ldots,\zeta _{n} )\in \mathbb{R}\) is locally Lipschitz;
-
(ii)
\(F(\zeta _{1},\ldots,\zeta _{n})\leq \alpha (1+ \sum_{i=1}^{n}|\zeta _{i}|^{t_{i}})\) for almost all \(\zeta _{i}\in \mathbb{R}\), \(t_{i}< p_{i}\), \(1\leq i\leq n\), α is a positive constant;
-
(iii)
\(F(\zeta _{1},\ldots,\zeta _{n})\geq 0\) for each \((\zeta _{1},\ldots,\zeta _{n}) \in [0,d]\times \cdots \times [0,d]\) with \(d>0\);
-
(iv)
\(m(\varOmega )\sum_{i=1}^{n}\frac{1}{p_{i}} (d^{p_{i}}R _{i}^{p_{i}}+B_{i}^{p_{i}})\max_{(\zeta _{1},\ldots,\zeta _{n}) \in V}F( \zeta _{1},\ldots,\zeta _{n})<\frac{\beta \rho ^{N} \pi ^{\frac{N}{2}}}{2^{N} \varGamma (1+\frac{N}{2})\prod^{n}_{i=1}p_{i} } F(d,\ldots,d)\), where \(B_{i}=(c\bar{b}_{i} \,d^{p_{i}}\omega _{N}\rho ^{N})^{\frac{1}{p_{i}}}\), \(R_{i}=\frac{2}{\rho } (\frac{c\rho ^{N} (1-\frac{1}{2^{N}}) \pi ^{\frac{N}{2}}}{\varGamma (1+\frac{N}{2})} )^{\frac{1}{p_{i}}}\) and \(V= \{(\zeta _{1},\ldots,\zeta _{n})|\sum^{n}_{i=1}\frac{| \zeta _{i}|^{p_{i}}}{p_{i}}\leq \frac{\beta }{\prod^{n}_{i=1}p_{i} } \}\), for some \(\rho >0\), \(\beta >0\), \(1\leq i\leq n\).
The corollary is the following.
Corollary 2.2
If there exist positive constants \(d, \rho \), and β with \(\sum^{n}_{i=1}\frac{(dR_{i})^{p_{i}}}{p_{i}}>\frac{ \beta }{\prod^{n}_{i=1}p_{i}}\) and hypotheses \(H(F)_{3}\) hold, then there exist an open interval \(\varLambda \subset [0,+\infty )\) and a constant σ such that, for each \(\lambda \in \varLambda \), problem (2.7) has at least three solutions in X whose norms are less than σ.
Now, we consider another particular elliptic problem with a nonsmooth potential.
Our assumptions on the nonsmooth potential are the following:
\(H(F)_{4}\): \(F:\varOmega \times \mathbb{R}\mapsto \mathbb{R}\) is a function such that \(F(x,0)=0\) and
-
(i)
for all \(\zeta \in \mathbb{R}\), \(\varOmega \ni x\mapsto F(x,\zeta )\) is measurable;
-
(ii)
for almost all \(x\in \varOmega \), \(\mathbb{R}\ni \zeta \mapsto F(x,\zeta )\in \mathbb{R}\) is locally Lipschitz;
-
(iii)
\(F(x,\zeta )\leq a(x)(1+|\zeta |^{t})\) for almost all \(x\in \bar{\varOmega }\) and all \(\zeta \in \mathbb{R}\), \(t< p\);
-
(iv)
\(F(x,\zeta )\geq 0\) for each \((x,\zeta )\in (\bar{ \varOmega }\setminus B(x^{0},\frac{\rho }{2}))\times [0,d]\) for some \(d>0\);
-
(v)
\(m(\varOmega ) (\frac{2^{p-N}d^{p}c\rho ^{N}(2^{N}-1) \pi ^{\frac{N}{2}}}{\rho ^{p}\varGamma (1+\frac{N}{2})} +c\bar{b} d^{p} \omega _{N}\rho ^{N} )\max_{(x,\zeta )\in \bar{\varOmega }\times V}F(x, \zeta )\leq \beta \int _{B(x_{0},\frac{\rho }{2})}F(x,d)\,dx\), where \(V= \{\zeta |-\beta ^{\frac{1}{p}}<\zeta < \beta ^{\frac{1}{p}} \}\).
Corollary 2.3
If there exist positive constants d and β with \((dR)^{p}>\beta \) and hypotheses \(H(F)_{4}\) hold, where \(R=\frac{2}{\rho } (\frac{c\rho ^{N}(2^{N}-1)\pi ^{\frac{N}{2}}}{2^{N} \varGamma (1+\frac{N}{2})} )^{\frac{1}{p}}\), then there exist an open interval \(\varLambda \subset [0,+\infty )\) and a constant σ such that, for each \(\lambda \in \varLambda \), problem (2.8) has at least three solutions in X whose norms are less than σ.
If we drop the x-dependence in \(F(x,u)\), then problem (2.8) turns into
The hypotheses on the nonsmooth potential functional F are the following:
\(H(F)_{5}\): \(F:\mathbb{R}\rightarrow \mathbb{R}\) is a function such that \(F(0)=0\) and
-
(i)
for almost all \(\mathbb{R}\ni \zeta \mapsto F(\zeta )\in \mathbb{R}\) is locally Lipschitz;
-
(ii)
\(F(\zeta )\leq \alpha (1+|\zeta |^{t})\) for almost all \(|\zeta |\in \mathbb{R}\), where \(t< p\) and α is a positive constant;
-
(iii)
\(F(\zeta )\geq 0\) for each \(\zeta \in [0,d]\) and \(d>0\);
-
(iv)
\(m(\varOmega )(R^{p}+B^{p}) \max_{|\zeta |\leq \beta ^{\frac{1}{p}}}F(\zeta )<\frac{\beta \rho ^{N} \pi ^{\frac{N}{2}}}{2^{N} \varGamma (1+\frac{N}{2})}F(d)\), where \(R= (\frac{2p^{-N}d^{p}c\rho ^{N} (2^{N} -1)\pi ^{\frac{N}{2}}}{ \rho ^{p} \varGamma (1+\frac{N}{2})} )^{\frac{1}{p}}\), \(B=(c \bar{b} d^{p} \omega _{N} \rho ^{N})^{\frac{1}{p}}\).
Corollary 2.4
If there exist positive constants \(d, \rho \), and β with \((dR)^{p}>\beta \) and hypotheses \(H(F)_{5}\) hold, then there exist an open interval \(\varLambda \subset [0,+\infty )\) and a number σ such that, for each \(\lambda \in \varLambda \), problem (2.9) has at least three solutions in X whose norms are less than σ.
In the following, we give an example. For the purpose of simplicity, we drop the x-dependence in F.
Example
Set
where \(\varOmega =\{(x,y)\in \mathbb{R}^{2}:x^{2}+y^{2}<36\}\). Choose \(x^{0}=(0,0)\), \(p=4, \rho =2, N=2\), \(\beta =1\), \(d=4\). Then from a simple computation, we have \(c=\frac{12}{\pi ^{\frac{3}{2}}}\), \(R=\frac{4\sqrt{6}}{\pi ^{\frac{1}{8}}}\), \(B= \frac{2^{\frac{7}{2}} \times 3^{\frac{1}{4}}}{\pi ^{\frac{3}{8}}}\). It is easy to see that \(F(u)\) satisfies hypotheses \(H(F)_{5}\).
References
Clarke, F.: Optimization and Nonsmooth Analysis. Wiley, New York (1983)
Chang, K.: Variational methods for nondifferentiable functionals and their applications to partial differential inequalities. J. Math. Anal. Appl. 80, 102–129 (1981)
Motreanu, D., Rädulescu, V.: Variational and Non-Variational Methods in Nonlinear Analysis and Boundary Value Problems. Kluwer Academic, Boston (2003)
Motreanu, D., Pangitoplous, P.: Minimax Theorems and Qualitative Properties of the Solutions of Hemivariational Inequalities. Kluwer Academic, Dordrecht (1998)
Gasiński, L., Papageorgiou, N.: Nonsmooth Critical Point Theory and Nonlinear Boundary Value Problems. Chapman and Hall/CRC Press, Boca Raton (2005)
Filippaks, M., Gasiński, L., Papageorgiou, N.: On the existence of positive solutions for hemivariational inequalities driven by the p-Laplacian. J. Glob. Optim. 31, 173–189 (2005)
Denkowski, Z., Gasiński, L., Papageorgiou, N.: Existence and multiplicity of solutions for semilinear hemivariational inequalities at resonance. Nonlinear Anal. 66, 1329–1340 (2007)
Iannizzotto, A., Papageorgiou, N.: Existence of three nontrivial solutions for nonlinear Neumann hemivariational inequalities. Nonlinear Anal. 70, 3285–3297 (2009)
Kyritsi, S., Papageorgiou, N.: Multiple solutions of constant sign for nonlinear nonsmooth eigenvalue problems near resonance. Calc. Var. Partial Differ. Equ. 20, 1–24 (2004)
Zhang, J., Zhou, Y.: Existence of a nontrivial solutions for a class of hemivariational inequality problems at double resonance. Nonlinear Anal. 74, 4319–4329 (2011)
Goeleven, D., Motreanu, D., Panagiotopoulos, P.: Multiple solutions for a class of eigenvalue problems in hemivariational inequalities. Nonlinear Anal. 29, 9–26 (1997)
Djellit, A., Tas, S.: Quasilinear elliptic systems with critical Sobolev exponents in \(\mathbb{R}^{N}\). Nonlinear Anal. 66, 1485–1497 (2007)
Li, C., Tang, C.: Three solutions for a class of quasilinear elliptic systems involving the \((p,q)\)-Laplacian. Nonlinear Anal. 69, 3322–3329 (2008)
Kristály, A.: Existence of two non-trivial solutions for a class of quasilinear elliptic variational systems on strip-like domains. Proc. Edinb. Math. Soc. 48(2), 465–477 (2005)
Zhang, G., Liu, X., Liu, S.: Remarks on a class of quasilinear elliptic systems involving the \((p,q)\)-Laplacian. Electron. J. Differ. Equ. 2005, 20 (2005)
Bozhkova, Y., Mitidieri, E.: Existence of multiple solutions for quasilinear systems via fibering method. J. Differ. Equ. 190, 239–267 (2003)
Djellit, A., Tas, S.: On some nonlinear elliptic systems. Nonlinear Anal. 59, 695–706 (2004)
Teramoto, T.: On positive radial entire solutions of second-order quasilinear elliptic systems. J. Math. Anal. Appl. 282, 531–552 (2003)
Goyal, S., Sreenadh, K.: Existence and multiplicity of solutions for p-Laplace equation with sign-changing nonlinearities. Adv. Nonlinear Anal. 4(1), 37–58 (2015)
Mukherjee, T., Screenadh, K.: On doubly nonlocal p-fractional coupled elliptic system. Topol. Methods Nonlinear Anal. 51(2), 609–636 (2018)
Giacomoni, J., Mukherjee, T., Screenadh, K.: Multiplicity results for critical growth Choquard systems. J. Math. Anal. Appl. 467, 638–672 (2018)
Jiao, F., Yu, J.: On the existence of bubble-type solutions of nonlinear singular problems. J. Appl. Anal. Comput. 1(2), 229–252 (2011)
Marano, S., Motreanu, D.: On a three critical points theorem for nondifferentiable functions and applications to nonlinear boundary value problems. Nonlinear Anal. 48, 37–52 (2002)
Ricceri, B.: On a three critical points theorem. Arch. Math. 75, 220–226 (2000)
Talenti, G.: Best constant in Sobolev inequality. Ann. Mat. Pura Appl. 110, 353–372 (1976)
Acknowledgements
The authors would like to thank the editors and the reviewers for their helpful suggestions.
Availability of data and materials
Not applicable.
Funding
Research is supported by Doctoral Start-up Foundation of Tongren University (trxyDH1804).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yuan, Z., Wang, Y. & Liu, S. Multiplicity of solutions for a class of \((p_{1},p_{2},\ldots,p_{n})\)-Laplacian elliptic systems with a nonsmooth potential. Bound Value Probl 2019, 50 (2019). https://doi.org/10.1186/s13661-019-1164-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-019-1164-6