Abstract
In this paper, we put up and study a competition and cooperation model of two enterprises with multiple delays and feedback controls. A set of sufficient conditions which ensure the existence of periodic solution of the two-enterprise competition and cooperation model with multiple delays and feedback controls are established by applying the fixed point theorem of strict-set-contraction. An example is given to check the obtained theoretical findings. The derived results are completely new and complement earlier publications.
Similar content being viewed by others
1 Introduction
It is well known that the interaction between two enterprises plays an extremely important role in enterprise operation. In order to grasp the internal mechanism, operating law, administrative procedure, risk and efficiency, etc. [1], to improve the management level of enterprises, it is necessary for us to establish the interaction model of two enterprises and analyze their dynamical behavior. In recent decades, some scholars have considered this topic. For example, Tian and Nie [2] proposed the following two-enterprise interaction model:
where \(u_{1}(t)\), \(u_{2}(t)\) denote the output of enterprises A and B, \(\gamma_{1}\), \(\gamma_{2}\) stand for the intrinsic growth rate, \(\kappa_{i}\) (\(i=1,2\)) represents the carrying capacity of mark under natural unlimited conditions, a, b denote the competitive coefficients of two enterprises, \(\sigma_{1}\), \(\sigma_{2}\) represent the initial production of two enterprises. Let \(\alpha_{1}=\frac{\gamma_{1}}{\kappa_{1}}\), \(\alpha_{2}=\frac{\gamma_{2}}{\kappa_{2}}\), \(\beta_{1}=\frac{\gamma _{1}a}{\kappa_{2}}\), \(\beta_{2}=\frac{\gamma_{2}b}{\kappa_{1}}\), then system (1.1) becomes
Considering that the parameters of (1.2) vary with time, Li and Zhang [1] established the following modified two-enterprise interaction model with variable coefficients:
In 2012, Xu [3] established some sufficient criteria to guarantee the existence of periodic solutions of (1.3) by using the coincidence degree method and differential inequality technique. In many cases, the environment often varies and the output of two enterprises is subjected to rapid change at certain instants in time. Xu and Shao [4] established the following two-enterprise interaction model with impulses:
where \(\Delta_{i}(t_{k})=u_{i}(t_{k}^{+})-u_{i}(t_{k}^{-})\) are the impulses at moments \(t_{k}\) and \(t_{1} < t_{2} < \cdots\) is a strictly increasing sequence such that \(\lim_{k\rightarrow+\infty}t_{k} =+\infty\) and q is a positive integer. Using continuation theorem and constructing an appropriate Lyapunov functional, Xu and Shao [4] discussed the periodic solution and global attractivity of (1.4). Considering the different effect of time delay on the two-enterprise interaction, Liao et al. [5] investigated the stability and Hopf bifurcation of the following two-enterprise interaction model with delays:
where υ is the time delay in the interior of enterprises and among different enterprises. In 2014, Liao et al. [6] studied the bifurcation behavior of the following two-enterprise interaction model with two different delays:
where \(\upsilon_{i}\) (\(i=1,2\)) is the time delay in the interior of enterprises and among different enterprises. Li et al. [7] considered the stability and bifurcation behavior of the following two-enterprise interaction model with four different delays:
where \(\upsilon_{i}\) (\(i=1,2,3,4\)) is the time delay in the interior of enterprises and among different enterprises. For more related works, we refer the readers to [8,9,10,11]. Here we would like to point out that the output of enterprises A and B is often affected by unpredictable forces which can be expressed as disturbance functions [12,13,14,15,16]. In addition, there usually exists a time delay in unpredictable forces. Stimulated by this viewpoint, we can establish the following competition and cooperation model of two enterprises with multiple delays and feedback controls:
where \(v_{1}\), \(v_{2}\) are the control variables. The existence of periodic solution of the competition and cooperation model of two enterprises plays an important role in running mechanism, administering process, economic performance of enterprises. Thus the study on the existence of periodic solution of the competition and cooperation model of two enterprises has theoretical significance and practical application [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. The main objective of this paper is to focus on the periodic solutions of model (1.8).
The remainder of the paper is organized as follows: in Sect. 2, basic notations, assumptions, definitions, and lemmas are prepared. In Sect. 3, a set of sufficient conditions which ensure the existence of periodic solution of the system are established. In Sect. 4, an example with its simulations is given to illustrate the correctness of the obtained results in Sect. 3. A simple conclusion is given in Sect. 5.
2 Preliminaries
In this section, we shall first state some notations, assumptions, definitions, and lemmas.
Let R and \(R^{+}\) denote the sets of all real numbers and nonnegative real numbers, respectively. Let \(\bar{l}=\max\{l(t):t\in [0,\varpi]\}\) and \(\underline{l}=\min\{l(t):t\in[0,\varpi]\}\), where l is a continuous bounded ϖ-periodic function on R.
Throughout this paper, we give the following assumptions:
-
(H1)
For \(i=1,2\), \(\gamma_{i}\), \(\alpha_{i}\), \(\beta_{i}\), \(\sigma _{i}\), \(a_{i}\), \(\eta_{i}\), \(\delta_{i}\), \(\varrho_{1}\), \(\zeta_{i}\) are all continuous ϖ-periodic functions and
$$\begin{aligned}& \delta_{i}^{*}=e^{\int_{0}^{\varpi}\delta_{i}(s)\,ds}>1, \quad\quad \gamma_{i*}=e^{-\int_{0}^{\varpi}\gamma_{i}(s)\,ds}< 1, \\& A_{i}(t,s)=\frac{e^{\int_{t}^{s}\delta_{i}(s)\,ds} }{ e^{\int_{0}^{\varpi}\delta_{i}(s)\,ds}-1 },\quad\quad B_{i}(t,s)= \frac{e^{-\int_{t}^{s}\gamma_{i}(s)\,ds} }{ 1-e^{\int_{0}^{\varpi}\gamma_{i}(s)\,ds} }, \\& G_{i}(t)= \int_{t}^{t+\varpi}A_{i}(t,s) \varrho_{i}(s) \,ds, \\& K_{i}= \int_{0}^{\varpi}\bigl[\gamma_{i*} \alpha_{i}(s) +\gamma_{i*}\beta_{i}(s) \Vert u \Vert +\gamma _{i*}a_{i}(s)G_{i}\bigl(s- \eta_{i}(s)\bigr)\bigr]\,ds, \\& P_{i}= \int_{0}^{\varpi}\bigl[\alpha_{i}(s) + \beta_{i}(s) \Vert u \Vert +a_{i}(s)G_{i} \bigl(s-\eta_{1}(s)\bigr)\bigr]\,ds. \end{aligned}$$ -
(H2)
The following inequalities hold:
$$\begin{aligned} &\alpha_{1}(t)\gamma_{1*} \Vert u \Vert + \beta_{1}(t)\gamma_{2*} \Vert u \Vert ^{2}+2 \beta_{1}(t)\sigma_{2}(t)\gamma_{2*} \Vert u \Vert \\ &\quad{} + \beta_{1}(t)\sigma_{2}^{2}(t)+ \gamma_{1*}a_{1}(t)G_{1}\bigl(t-\eta _{1}(t)\bigr) \Vert u \Vert \geq0 \end{aligned} $$and
$$\alpha_{2}(t)\gamma_{2*} \Vert u \Vert +\gamma _{2*}a_{2}(t)G_{2}\bigl(t-\eta_{2}(t) \bigr) \Vert u \Vert \geq0. $$ -
(H3)
For \(i=1,2\), the following inequality holds:
$$\frac{(1+\underline{\gamma}_{i*})(\gamma_{i*})^{2}}{1-\gamma _{i*}}K_{i}\geq\max\bigl\{ \alpha_{i}(s) + \beta_{i}(s) \Vert u \Vert +a_{i}(s)G_{i} \bigl(s-\eta_{1}(s)\bigr), t\in [0,\varpi]\bigr\} . $$ -
(H4)
For \(i=1,2\), the following inequality holds:
$$\frac{1-\bar{\gamma}_{i*}}{\gamma_{i*}(1-\gamma_{i*})}P_{i}\leq \min\bigl\{ \gamma_{i*} \alpha_{i}(t) +\gamma_{i*}\beta_{i}(t) \Vert u \Vert +\gamma _{i*}a_{i}(t)G_{i}\bigl(t- \eta_{i}(t)\bigr), t\in [0,\varpi]\bigr\} . $$
Definition 2.1
Let B be a Banach space and C be a closed, nonempty subset of B. We say that C is a cone if (1) \(a\alpha+b\beta\in\mathbf{C}\) for all \(\alpha,\beta\in\mathbf{C}\) and all \(a,b>0\), (2) \(\alpha,-\alpha\in \mathbf{C}\) imply \(\alpha=0\).
Let B be a Banach space and C be a cone in B. The semi-order induced by the cone C is denoted by “≤”, i.e., \(\alpha\leq\beta\) if and only if \(\beta-\alpha\in\mathbf{C}\). For a bounded subset \(\mathbf{E}\subset\mathbf{B}\), let \(a_{\mathbf{B}}(\mathbf{E})\) denote the measure (Kuratowski) of non-compactness defined by
where \(\operatorname{diam} (\mathbf{B}_{i})\) represents the diameter of the set \(\mathbf{B}_{i}\).
Definition 2.2
Let C, D be two Banach spaces and \(\mathbf{F} \subset\mathbf{C}\), a continuous and bounded map \(\varGamma: \mathbf{F}\rightarrow\mathbf{D}\) is called κ-set-contractive if for any bounded set \(\mathbf{S}\subset \mathbf{F}\) we get \(a_{\mathbf{D}}(\varGamma({\mathbf{S}}))\leq {\kappa} a_{\mathbf{C}}(\mathbf{S})\). Γ is called strict-set-contractive if it is κ-set-contractive for some \(0\leq\kappa\leq1\).
Lemma 2.1
Let Q be a cone of the real Banach space B and \(\varOmega_{R_{1}}=\{x\in{\mathbf{B}}:\Vert x\Vert< R_{1} \}\), \(\varOmega_{R_{2}}=\{x\in{\mathbf{B}}:\Vert x\Vert< R_{2} \}\), where \(R_{1}>R_{2}>0\). Assume that \(\varGamma:{\mathbf{Q}}\cap\bar{\varOmega}_{R_{1}} \setminus\varOmega_{R_{2}}\rightarrow\mathbf{Q}\) is strict-set-contractive such that one of the following two conditions are satisfied: (1) Not \(\varGamma x\geq x\) for all \(x\in {\mathbf{Q}}\cap \partial\varOmega_{R_{2}}\). (2) Not \(\varGamma x\leq x\) for all \(x\in {\mathbf{Q}}\cap \partial\varOmega_{R_{1}}\). Then Γ has at least one fixed point in \({\mathbf{Q}}\cap\bar{\varOmega}_{R_{1}} \setminus\varOmega_{R_{2}}\).
3 Existence of periodic solution
In this section, we will consider the existence of at least one positive periodic solution of system (1.8) by applying the fixed point theorem for the strict-set-contraction.
It is easy to see that each ϖ-periodic solution of the equation
is equivalent to that of the equation
and each ϖ-periodic solution of the equation
is equivalent to that of the equation
Then the existence of ϖ-periodic solution of (1.8) can be equivalent to the existence of ϖ-periodic solution of the following equations:
Let
with the norm \(\Vert u\Vert=\max\{\vert u_{i}(t)\vert:t\in[0,\varpi ], i=1,2\}\). Then \(C_{\varpi}\) is a Banach space. Let
Let
where \(R_{1}>R_{2}>0\). Define the map Γ as follows:
where
Lemma 3.1
In addition to (H1)–(H3), assume that \(\bar{\gamma}_{i}<1\) (\(i=1,2\)) holds, then \(\varGamma:{\mathbf{Q}}\rightarrow{\mathbf{Q}}\) is well defined.
Proof
\(\forall u\in{\mathbf{Q}}\) we have \(\varGamma u\in C_{\varpi}\). In view of (H2), for \(t\in[0,\varpi]\), we have
In addition, for \(t\in[0,\varpi]\),
Then, for \(t\in[0,\varpi]\), we have
By (3.10) and (3.11), we get \(\varGamma u\in{\mathbf{Q}}\). The proof of Lemma 3.1 is complete. □
Lemma 3.2
In addition to (H1)–(H3), if \(\kappa=\max_{i=1,2} \{\frac{R_{1}^{2}}{1-\gamma_{i*}}[2\alpha _{1}(s)+3\beta_{1}(s)R_{1}] \}<1\), then \(\varGamma:{\mathbf{Q}}\cap\bar{\varOmega}_{R_{1}} \setminus\varOmega_{R_{2}}\rightarrow\mathbf{Q}\) is strict-set-contractive.
Proof
Obviously, Γ is continuous and bounded. Now we prove that \(a_{C_{\varpi}}(\varGamma({\mathbf{S}}))\leq{\kappa} a_{\mathbf{C}}(\mathbf{S})\) for any bounded set \({\mathbf{S}}\subset{\mathbf{Q}}\cap\bar{\varOmega}_{R_{1}}\). For any \(\epsilon>0\), there is a finite family of subsets \({\mathbf{S}}\subset\bigcup_{i}{\mathbf{S}}_{i}\) with \(\operatorname{diam} ({\mathbf{S}}_{i})\leq\epsilon\). Then \(\Vert u-v\Vert\leq\epsilon\) for any \(u,v\in{\mathbf{S}}_{i}\). For \(t\in[0,\varpi]\), we have
In view of (3.12) and (3.13), we have
Then \(\varGamma:{\mathbf{Q}}\cap\bar{\varOmega}_{R_{1}} \setminus\varOmega_{R_{2}}\rightarrow\mathbf{Q}\) is strict-set-contractive. This completes the proof. □
Theorem 3.1
In addition to (H1)–(H3), if \(\kappa=\max_{i=1,2} \{\frac{R_{1}^{2}}{1-\gamma_{i*}}[2\alpha _{1}(s)+3\beta_{1}(s)R_{1}] \}<1\), then system (1.8) has at least one positive ϖ-periodic solution.
Proof
Let
and
Clearly \(R_{1}>R_{2}>0\). In view of Lemmas 3.1 and 3.2, we get \(\varGamma:{\mathbf{Q}}\cap\bar{\varOmega}_{R_{1}} \setminus\varOmega_{R_{2}}\rightarrow\mathbf{Q}\) is strict-set-contractive. If \(u^{*}\in{\mathbf{Q}}\cap\partial\varOmega_{R_{2}}\) or \(u^{*}\in{\mathbf{Q}}\cap\partial\varOmega_{R_{1}}\) such that \(\varGamma u^{*}=u^{*}\), then system (1.8) has at least one positive ϖ-periodic solution. Now we check that (ii) of Lemma 2.1 is true.
If \(\varGamma u\geq u\), then \(\varGamma u-u\in{\mathbf{Q}}\). Thus \(\varGamma u_{1}-u_{1}\geq\gamma_{1*}\Vert\varGamma u_{1}-u_{1}\Vert\geq0\) for \(t\in[0,\varpi]\). In addition,
Then
which is a contradiction. Next we only need to check that for \(u\in{\mathbf{Q}}\cap\partial\varOmega_{R_{1}}\), Not \(\varGamma u\leq u\). If there exists \(u\in{\mathbf{Q}}\cap\partial\varOmega_{R_{1}}\) such that \(\varGamma u>u\), then \(\varGamma u-u\in{\mathbf{Q}}\setminus\{0\}\). For \(t\in[0,\varpi]\), one has
Thus
Then \(\Vert u\Vert>\Vert\varGamma u\Vert>R_{1}\), which is a contradiction. By Lemma 3.1, we can conclude that Γ has at least one nonzero fixed point in \({\mathbf{Q}}\cap\bar{\varOmega}_{R_{1}} \setminus\varOmega_{R_{2}}\). Therefore system (1.8) has at least one positive ϖ-periodic solution. This completes the proof. □
4 Examples
In this section, we give two examples with their numerical simulations to illustrate the feasibility of our results.
Example 4.1
Consider the following system:
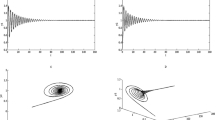
where \(\gamma_{1}(t)=1\), \(\gamma_{2}(t)=2\), \(\delta_{1}(t)=0.5\), \(\delta_{2}(t)=0.8\), \(\alpha_{1}(t)=0.8\vert\sin\pi t\vert\), \(\alpha_{2}(t)=0.3\vert\cos\pi t\vert\), \(\beta_{1}(t)=0.7\vert\sin \pi t\vert\), \(\beta_{2}(t)=0.9\vert\sin\pi t\vert\), \(\sigma _{1}(t)=0.2\vert\cos\pi t\vert\), \(\sigma_{2}(t)=0.5\vert\cos\pi t\vert\), \(\eta_{1}(t)=0.4\vert\cos \pi t\vert\), \(\eta_{2}(t)=0.4\vert\cos\pi t\vert\), \(\varrho_{1}(t)=0.7\vert \sin\pi t\vert\). Thus one can check that all the conditions in Theorem 3.1 are fulfilled. Then we can conclude that system (1.8) has at least one positive 1-periodic solution which is shown in Figs. 1–4.
Times series of \(u_{1}\) of system (4.1)
Times series of \(u_{2}\) of system (4.1)
Times series of \(v_{1}\) of system (4.1)
Times series of \(v_{2}\) of system (4.1)
5 Conclusions
In the present paper, we propose a competition and cooperation model of two enterprises with multiple delays and feedback controls. Applying fixed point theorem of strict-set-contraction, we obtain a sufficient criterion to guarantee the existence of periodic solution of the two-enterprise competition and cooperation model with multiple delays and feedback controls. It is shown that the feedback control terms and time delays have important effect on the periodic behavior. The research reveals that under fairish conditions, the competition of two species can remain a periodic vibration. The derived results are new and complement the earlier publications (for example, [1,2,3,4,5,6,7,8,9]). In recent years, there have been rare reports on the competition and cooperation model of two enterprises with stochastic perturbation, which might be our future investigation topic.
References
Li, Y.K., Zhang, T.W.: Global asymptotical stability of a unique almost periodic solution for enterprise clusters based on ecology theory with time-varying delays and feedback controls. Commun. Nonlinear Sci. Numer. Simul. 17(2), 904–913 (2012)
Tian, X.H., Nie, Q.K.: On model construction of enterprises’ interactive relationship from the perspective of business ecosystem. South. Econ. J. 4, 50–57 (2006)
Xu, C.J.: Periodic behavior of competition and corporation dynamical model of two enterprises on time scales. J. Quant. Econ. 29(2), 1–4 (2012)
Xu, C.J., Shao, Y.F.: Existence and global attractivity of periodic solution for enterprise clusters based on ecology theory with impulse. J. Appl. Math. Comput. 39(1–2), 367–384 (2012)
Liao, M.X., Xu, C.J., Tang, X.H.: Stability and Hopf bifurcation for a competition and cooperation model of two enterprises with delay. Commun. Nonlinear Sci. Numer. Simul. 19(10), 3845–3856 (2014)
Liao, M.X., Xu, C.J., Tang, X.H.: Dynamical behavior for a competition and cooperation model of enterprises with two delays. Nonlinear Dyn. 75(1–2), 257–266 (2014)
Li, L., Zhang, C.H., Yan, X.P.: Stability and Hopf bifurcation analysis for a two-enterprise interaction model with delays. Commun. Nonlinear Sci. Numer. Simul. 30(1–3), 70–83 (2016)
Liu, P., Li, Y.K.: Permanence for a competition and cooperation model of enterprise cluster with delays and feedback controls. Electron. J. Differ. Equ. 2013, 22 (2013)
Li, Y.K., Zhang, T.W.: Global asymptotical stability of a unique almost periodic solution for enterprise cluster based on ecology theory with time-varying delays and feedback controls. Commun. Nonlinear Sci. Numer. Simul. 17, 904–913 (2012)
Zhi, Y.H., Ding, Z.L., Li, Y.K.: Permanence and almost periodic solution for an enterprise cluster model based on ecology theory with feedback controls on time scales. Discrete Dyn. Nat. Soc. 2013, Article ID 639138 (2013)
Xu, C.J., Liao, M.X.: Global asymptotic stability for a stochastic competition and cooperation model of two enterprises. Ital. J. Pure Appl. Math. 34, 705–716 (2015)
Chen, F.D.: Permanence of a discrete n-species food-chain system with time delays. Appl. Math. Comput. 185(1), 719–726 (2007)
Dhar, J., Jatav, K.S.: Mathematical analysis of a delayed stage-structured predator-prey model with impulsive diffusion between two predators territories. Ecol. Complex. 16, 59–67 (2013)
Liu, S.Q., Chen, L.S.: Necessary-sufficient conditions for permanence and extinction in Lotka–Volterra system with distributed delay. Appl. Math. Lett. 16(6), 911–917 (2003)
Liao, X.Y., Zhou, S.F., Chen, Y.M.: Permanence and global stability in a discrete n-species competition system with feedback controls. Nonlinear Anal., Real World Appl. 9(4), 1661–1671 (2008)
Hu, H.X., Teng, Z.D., Jiang, H.J.: On the permanence in non-autonomous Lotka–Volterra competitive system with pure-delays and feedback controls. Nonlinear Anal., Real World Appl. 10(3), 1803–1815 (2009)
Bianca, C., Pennisi, M., Motta, S., Ragusa, M.A.: Immune system network and cancer vaccine. AIP Conf. Proc. 1389, 945–948 (2011)
Bianca, C., Pappalardo, F., Motta, S., Ragusa, M.A.: Persistence analysis in a Kolmogorov-type model for cancer-immune system competition. AIP Conf. Proc. 1558, 1797–1800 (2013)
Costa, R.M.S., Van Andel, T., Pavone, P., Pulvirenti, S.: The pre-Linnaean herbarium of Paolo Boccone (1633–1704) kept in Leiden (the Netherlands) and its connections with the imprinted one in Paris. Plant Biosyst. 152(3), 489–500 (2018)
Costa, R.M.S., Pavone, P., Caruso, R., Pulvirenti, S.: Diachronic analysis of biodiversity: study of a herbarium “reviewed” by Francesco Cupani (1657–1710) at the end of the 17th century. Plant Biosyst. 150(4), 834–845 (2016)
Costa, R.M.S., Pavone, P., Carbonaro, R.A., Pulvirenti, S.: Francesco Cupani’s Panphyton Siculum. The rediscovery of a copy with handwritten corrections by his pupil Antonio Bonanno. Bot. Lett. 163(2), 203–216 (2016)
Pavone, P., Spampinato, G., Tomaselli, V., Minissale, P., Costa, R., Sciandrello, S., Ronsisvalle, F.: Map of the habitats of the EEC Directive 92/43 in the biotopes of the Syracuse province (eastern Sicily). Fitosociologia 44(2), suppl. 1, 183–193 (2007)
Pulvirenti, S., Pavone, P., Carbonaro, R.A., Costa, R.M.S.: Taxonomic study of the plants to be found in the only herbarium of Paolo Boccone (1633–1704) at present existing in Italy. Plant Biosyst. 151(4), 745–759 (2017)
Pulvirenti, S., Pavone, P., Carbonaro, R.A., Costa, R.M.S.: The controversial biography of Paolo Boccone (1633–1704) and his “Grand Tour” from the Mediterranean to northern Europe. Plant Biosyst. 151(3), 377–380 (2017)
Zuo, M.Y., Hao, X.A., Liu, L.S., Cui, Y.J.: Existence results for impulsive fractional integro-differential equation of mixed type with constant coefficient and antiperiodic boundary conditions. Bound. Value Probl. 2017, 161 (2017)
Wang, Y., Jiang, J.Q.: Existence and nonexistence of positive solutions for the fractional coupled system involving generalized p-Laplacian. Adv. Differ. Equ. 2017, 337 (2017)
Wang, Y.Q., Liu, L.S.: Positive solutions for a class of fractional 3-point boundary value problems at resonance. Adv. Differ. Equ. 2017, 7 (2017)
Li, M.M., Wang, J.R.: Exploring delayed Mittag-Leffler type matrix functions to study finite time stability of fractional delay differential equations. Appl. Math. Comput. 324, 254–265 (2018)
Wang, Y., Jiang, J.Q.: Existence and nonexistence of positive solutions for the fractional coupled system involving generalized p-Laplacian. Adv. Differ. Equ. 2017, 337 (2017)
Zhu, B., Liu, L.S., Wu, Y.H.: Existence and uniqueness of global mild solutions for a class of nonlinear fractional reaction-diffusion equations with delay. Comput. Math. Appl. (2016). https://doi.org/10.1016/j.camwa.2016.01.028
Feng, Q.H., Meng, F.W.: Traveling wave solutions for fractional partial differential equations arising in mathematical physics by an improved fractional Jacobi elliptic equation method. Math. Methods Appl. Sci. 40(10), 3676–3686 (2017)
Zhang, X.G., Liu, L.S., Wu, Y.H., Wiwatanapataphee, B.: Nontrivial solutions for a fractional advection dispersion equation in anomalous diffusion. Appl. Math. Lett. 66, 1–8 (2017)
Chen, S.T., Tang, X.H.: Improved results for Klein–Gordon–Maxwell systems with general nonlinearity. Discrete Contin. Dyn. Syst., Ser. A 38(5), 2333–2348 (2018)
Chen, S.T., Tang, X.H.: Geometrically distinct solutions for Klein–Gordon–Maxwell systems with super-linear nonlinearities. Appl. Math. Lett. 90, 188–193 (2019)
Tang, X.H., Chen, S.T.: Ground state solutions of Nehari–Pohoz̆aev type for Kirchhoff-type problems with general potentials. Calc. Var. Partial Differ. Equ. 56(4), 1–25 (2017)
Tang, X.H., Lin, X.Y.: Existence of ground state solutions of Nehari–Pankov type to Schrödinger systems. Sci. China Math. 62 (2019). https://doi.org/10.1007/s11425-017-9332-3
Acknowledgements
The work is supported by the National Natural Science Foundation of China (No. 61673008), Project of High-level Innovative Talents of Guizhou Province ([2016]5651), Major Research Project of the Innovation Group of the Education Department of Guizhou Province ([2017]039), Project of Key Laboratory of Guizhou Province with Financial and Physical Features ([2017]004), and Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering (Changsha University of Science & Technology) (2018MMAEZD21). The authors would like to thank the referees and the editor for helpful suggestions incorporated into this paper.
Availability of data and materials
Not applicable.
Authors’ information
Changjin Xu’s research interests are the bifurcation theory of delayed differential equations. Peiluan Li’s research topics are nonlinear systems, functional differential equations, boundary value problems. Qimei Xiao’s research topics are rough set and formal concept analysis. Shuai Yuan’s research topics are theory and application of functional differential equations.
Funding
The work is supported by the National Natural Science Foundation of China (No. 61673008), Project of High-level Innovative Talents of Guizhou Province ([2016]5651), Major Research Project of the Innovation Group of the Education Department of Guizhou Province ([2017]039), Project of Key Laboratory of Guizhou Province with Financial and Physical Features ([2017]004), and Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering (Changsha University of Science & Technology) (2018MMAEZD21).
Author information
Authors and Affiliations
Contributions
All authors have read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Xu, C., Li, P., Xiao, Q. et al. New results on competition and cooperation model of two enterprises with multiple delays and feedback controls. Bound Value Probl 2019, 36 (2019). https://doi.org/10.1186/s13661-019-1145-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-019-1145-9