Three-dimensional free convective flow of a second-grade fluid through a porous medium with periodic permeability and heat transfer

Abstract

In this study, we model and theoretically analyze a free convective three-dimensional flow of an incompressible second-grade fluid through a highly porous medium bounded by an infinite vertical porous plate subjected to a constant suction. We assume the permeability of the medium to be periodic and the free stream velocity to be uniform. The assumption of either constant or time-dependent permeability of a porous medium leads to two-dimensional flows; however, the flow becomes three-dimensional due to variable permeability of the porous medium. We obtain analytic solutions for velocity field, pressure, skin friction components, temperature distribution, and discuss and graphically visualize effects of physical parameters emerging in the mathematical model of the physical phenomenon on these physical quantities. We note that the main flow velocity component decreases due to enhancement in non-Newtonian parameter; however, the pressure rises due to thickening of the fluid.

1 Introduction

In the recent years, natural convection flows through a porous medium, which are quite prevalent in nature, have attracted the attention of many workers due to their many scientific and engineering applications. For example, in the field of chemical engineering for purification and filtration processes, in agriculture engineering to study seepage of water in river beds, the underground water resources, etc. In view of such important applications, Stuart [1] investigated a two-dimensional flow past a porous infinite plate subjected to constant suction in the presence of periodic free stream velocity, Soundalgekar [2] analyzed a free convective flow past a vertical oscillatory plate, Varshney [3] presented a fluctuating flow of a viscous fluid through a porous medium bounded by a porous plate, Raptis [4] described an unsteady free convective flow of a viscous fluid through a porous medium, and Raptis and Perdikis [5] examined a free convective oscillatory flow of a viscous fluid through a porous medium.

The permeability of the porous medium of all the studies stated has been assumed to be constant. A porous medium, however, containing fluid is an inhomogeneous medium, and therefore there can be various inhomogeneities existing in a porous medium. Therefore the permeability of the porous medium may not unavoidably be constant. Singh and Kumar [6] studied an unsteady two-dimensional free convective flow through a porous medium bounded by vertical porous infinite plate considering the permeability of the medium fluctuating in time about a constant mean.

Most of the workers have limited their studies to the two-dimensional flows only by considering the permeability of the porous medium either constant or time-dependent. Nevertheless, there may occur situations where the flow fields may be essentially three-dimensional, for instance, when the permeability distribution varies transversely to the potential flow. Many workers [7, 8] have studied the effects of such a transverse permeability distribution on the flow of an incompressible viscous fluid through a porous medium. Further, Singh and Sharma [9] analyzed a three-dimensional free convective flow through a porous medium with periodic permeability and heat transfer effect, Jain et al. [10] presented the influence of periodic permeability and temperature of a free convective three-dimensional flow of a viscous fluid through porous medium in the presence of slip. Recently, Reddy et al. [11] have explored the free convective magnetohydrodynamic three-dimensional flow through a highly porous medium with periodic permeability. They noted that the velocity of the fluid reduces due to heat sink and magnetic field. On the contrary, the heat transfer coefficient increases in the presence of heat absorption parameter.

All studies mentioned have been scrutinized for Newtonian fluids. Although the Navier–Stokes equations can manage the flows of Newtonian fluids, such equations are inadequate to describe the properties of non-Newtonian fluids. Various workers [12,13,14,15,16] analyzed viscoelastic fluids through porous medium/in a vertical channel/over a stretching sheet under different physical conditions.

The aim of the present study is to explore a three-dimensional free convective flow of a second-grade fluid through highly porous medium subjected to periodic permeability and its impact on the heat transfer rate. A second-grade fluid is the simplest non-Newtonian differential type fluid model possessing the normal stress difference phenomenon (non-Newtonian phenomenon). To the best of our knowledge, no attempt is made to explore the free convective three-dimensional flow of a second grade through highly porous medium when permeability of the medium varies periodically. In view of these facts, the main aim of our study is to explore such a problem. To achieve this goal, the layout of this work is as follows. Section 2 presents the problem description, whereas Sect. 3 describes the modeling of the problem. Section 4 investigates the model in two and three dimensions for the solutions of a secondary flow, energy equation, and main flow by perturbation technique. At the end of this section, friction coefficients along the x- and z-directions have been computed, and the coefficient of the rate of heat transfer has also been given. Section 5 incorporates results and discussion for the characteristics of the problem, whereas Sect. 6 briefs conclusions.

2 Problem description

In this paper, we investigate a three-dimensional incompressible second-grade fluid through a highly porous medium with constant suction bounded by an infinite porous plate. The plate lying vertically on the xz-plane with x-axis is taken along the plate in upward direction, and the normal to the plane of the plate is taken along the y-axis. A three-dimensional fluid has a laminar flow with uniform free stream velocity U. The porous medium has a variable permeability of the form

$$ K(z)=\frac{K_{0}}{( 1+\varepsilon \cos \pi z/l)}, $$

(2.1)

where $K_{0}$ is the mean permeability of the medium, l is the wave length of the permeability of the distribution, and ε (≪1) is the amplitude of the permeability variation. Such a permeability variation shows that the problem is three-dimensional. All the fluid properties are supposed to be constant; however, the effect of the density variation with temperature is considered in the body-force term. The velocity field is

$$ \vec{V}=\bigl[u(y,z),v(y,z), w(y,z)\bigr], $$

(2.2)

where u, v, w are the velocity components in the x-, y-, z-directions, respectively. All the physical quantities will be independent of x because of the infinite length of the plate in the x-direction; of course, the flow remains three-dimensional due to variation of periodic permeability (Fig. 1).

Figure 1

Geometry

3 Modeling the problem

We have the following continuity, momentum, and energy equations, respectively, governing the fluid flow described in Sect. 2 [17, 18]:

$$\begin{aligned}& \nabla \cdot \vec{V}=0, \end{aligned}$$

(3.1)

$$\begin{aligned}& \rho \frac{d\vec{V}}{dt}=\nabla \cdot \tilde{\tau }, \\ \end{aligned}$$

(3.2)

$$\begin{aligned}& \rho \frac{d\varrho }{dt}=-\nabla \cdot \vec{q}, \end{aligned}$$

(3.3)

where ρ is the density of the fluid, $\varrho =c_{p}T$, $\vec{q}=-k _{t}\nabla T$, T is the temperature, $c_{p}$ is the specific heat at constant pressure, ∇ is the vector operator, $k_{t}$ is the thermal conductivity, and τ̃ is the Cauchy stress tensor for second-grade fluid defined in [19] as

$$ \tilde{\tau }=-p\tilde{I}+\mu \tilde{A}_{1}+\alpha _{1}\tilde{A}_{2}+ \alpha _{2} \tilde{A}_{1}^{2}, $$

(3.4)

where $\alpha _{1}$ and $\alpha _{2}$ are material constants, Ĩ is the identity tensor, μ is the dynamic viscosity, p is the pressure, $\tilde{A}_{1}$ and $\tilde{A}_{2}$ are the Rivlin–Ericksen tensors defined as

$$\begin{aligned}& \tilde{A}_{1}=({\operatorname{grad}\vec{V}})^{T}+{ \operatorname{grad}\vec{V}}, \end{aligned}$$

(3.5)

$$\begin{aligned}& \tilde{A}_{2}=\frac{d\tilde{A}_{1}}{dt}+({\operatorname{grad}\vec{V}})^{T} \tilde{A}_{1}+\tilde{A}_{1}({\operatorname{grad}\vec{V}}). \end{aligned}$$

(3.6)

For the model to be compatible with (3.4) and the thermodynamics in the sense that all motions meet the Clausius–Duhem inequality and assumption that the specific Helmholtz free energy is a minimum in equilibrium [19], we assume that

$$ \mu \geq 0, \qquad \alpha _{1}\geq 0,\qquad \alpha _{1}+\alpha _{2}=0. $$

(3.7)

Equations (2.1)–(3.7) yield

$$\begin{aligned}& \frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0, \end{aligned}$$

(3.8)

$$\begin{aligned}& \rho \biggl( v\frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z}\biggr)=g \rho \beta (T-T_{\infty })+\mu \biggl[ \frac{\partial ^{2}u}{\partial y ^{2}}+\frac{\partial ^{2}u}{\partial z^{2}} \biggr] \\& \hphantom{\rho \biggl( v\frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z}\biggr)=} {}+\alpha _{1} \biggl[ v\frac{\partial ^{3}u}{\partial y^{3}}+w \frac{ \partial ^{3}u}{\partial y ^{2}\partial z}+v\frac{\partial ^{3}u}{ \partial y\partial z ^{2}}+w\frac{\partial ^{3}u}{\partial z ^{3}} \biggr]- \frac{ \mu }{K}(u-U), \end{aligned}$$

(3.9)

$$\begin{array}{c}\rho (v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z})=-\frac{\partial p}{\partial y}+\mu [\frac{{\partial }^{2}v}{\partial y^2}+\frac{{\partial }^{2}v}{\partial z^2}]\hfill \\ \phantom{\rho (v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z})=}+{\alpha }_1\left[\begin{array}{c}v\frac{{\partial }^{3}v}{\partial y^3}+w\frac{{\partial }^{3}v}{\partial y^2\partial z}+v\frac{{\partial }^{3}v}{\partial y\partial z^2}+w\frac{{\partial }^{3}v}{\partial z^3}+\frac{\partial v}{\partial z}\frac{{\partial }^{2}v}{\partial y\partial z}\\ +\frac{\partial u}{\partial z}\frac{{\partial }^{2}u}{\partial y\partial z}+5\frac{\partial v}{\partial y}\frac{{\partial }^{2}v}{\partial y^2}+\frac{\partial v}{\partial z}\frac{{\partial }^{2}w}{\partial y^2}+2\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial y^2}\\ +2\frac{\partial w}{\partial y}\frac{{\partial }^{2}w}{\partial y2}+\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial z^2}+\frac{\partial v}{\partial y}\frac{{\partial }^{2}v}{\partial z^2}\end{array}\right]-\frac{\mu }{K}v,\hfill \end{array}$$

(3.10)

$$\begin{array}{c}\rho (v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z})=-\frac{\partial p}{\partial z}+\mu [\frac{{\partial }^{2}w}{\partial y^2}+\frac{{\partial }^{2}w}{\partial z^2}]\hfill \\ \phantom{\rho (v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z})=}+{\alpha }_1\left[\begin{array}{c}w\frac{{\partial }^{3}w}{\partial y^2\partial z}+v\frac{{\partial }^{3}w}{\partial y^3}+v\frac{{\partial }^{3}w}{\partial y\partial z^2}+w\frac{{\partial }^{3}w}{\partial z^3}+\frac{\partial w}{\partial y}\frac{{\partial }^{2}w}{\partial y\partial z}\\ +\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial y\partial z}+5\frac{\partial w}{\partial z}\frac{{\partial }^{2}w}{\partial z^2}+\frac{\partial w}{\partial y}\frac{{\partial }^{2}v}{\partial z^2}+2\frac{\partial u}{\partial z}\frac{{\partial }^{2}u}{\partial z^2}\\ +2\frac{\partial v}{\partial z}\frac{{\partial }^{2}v}{\partial z^2}+\frac{\partial u}{\partial z}\frac{{\partial }^{2}u}{\partial y^2}+\frac{\partial w}{\partial z}\frac{{\partial }^{2}w}{\partial y^2}\end{array}\right]-\frac{\mu }{K}w,\hfill \end{array}$$

(3.11)

and

$$\begin{aligned} \rho \biggl(v\frac{\partial T}{\partial y}+w \frac{\partial T}{\partial z} \biggr)= \frac{k_{t}}{c_{p}} \biggl[ \frac{\partial ^{2}T}{ \partial y^{2}}+\frac{\partial ^{2}T}{\partial z^{2}} \biggr]. \end{aligned}$$

(3.12)

The appropriate boundary conditions [9, 11, 20] are

$$\begin{aligned}& \left . \begin{aligned} & u =0, \qquad v=-V_{0},\qquad w=0,\qquad T=T_{w} \quad \text{at } y=0, \\ &u=U, \qquad w=0,\qquad p=p_{\infty },\qquad T=T_{\infty } \quad \text{as } y \rightarrow \infty , \end{aligned} \right \} \end{aligned}$$

(3.13)

where $V_{0}>0$ is the suction velocity, which is constant, and the negative sign occurs due to suction toward plate, $p_{\infty }$ is a constant pressure in a free stream, and the temperature of the plate and the fluid temperature far away from the plate are $T_{w}$ and $T_{\infty }$, respectively. We define the following dimensionless variables:

$$\begin{aligned} \left . \begin{aligned} &ly^{\triangleright }=y,\qquad lz^{\triangleright }=z,\qquad Uu^{\triangleright }=u,\qquad V _{0}v^{\triangleright }=v, \qquad V_{0}w^{\triangleright }=w, \\ & \rho V_{0}^{2}p^{\triangleright }=p,\qquad l^{2}K^{\triangleright }_{0}=K_{0}, \qquad \theta^{\triangleright } = \frac{T-T_{\infty }}{T_{w}-T_{\infty }}, \end{aligned} \right \} \end{aligned}$$

(3.14)

where $y^{\triangleright }$, $z^{\triangleright }$, $u^{\triangleright }$, $v ^{\triangleright }$, $w^{\triangleright }$, $p^{\triangleright }$, $K^{\triangleright }_{0}$, and $\theta^{\triangleright }$ are nondimensional variables. Then Eqs. (3.8)–(3.12) and the boundary conditions (3.13) have the following form after the omission of the symbol “▷” for convenience:

$$\begin{aligned}& \frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0, \end{aligned}$$

(3.15)

$$\begin{aligned}& v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z} =GR_{e} \theta -\frac{1}{R_{e}K_{0}}(1+\varepsilon \cos \pi z) (u-1)+\frac{1}{ R_{e}} \biggl[ \frac{\partial ^{2}u}{\partial y^{2}}+\frac{\partial ^{2}u}{ \partial z^{2}} \biggr] \\& \hphantom{v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z} =}{}+L \biggl[ v\frac{\partial ^{3}u}{\partial y^{3}}+w\frac{\partial ^{3}u}{ \partial y^{2}\partial z}+v \frac{\partial ^{3}u}{\partial y\partial z ^{2}}+w \frac{\partial ^{3}u}{\partial z^{3}} \biggr], \end{aligned}$$

(3.16)

$$\begin{array}{c}v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}=-\frac{\partial p}{\partial y}-\frac{1}{R_e{K}_0}(1+\epsilon cos\pi z)v+\frac{1}{R_e}[\frac{{\partial }^{2}v}{\partial y^2}+\frac{{\partial }^{2}v}{\partial z^2}]\hfill \\ \phantom{v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}=}+L\left[\begin{array}{c}v\frac{{\partial }^{3}v}{\partial y^3}+w\frac{{\partial }^{3}v}{\partial y^2\partial z}+v\frac{{\partial }^{3}v}{\partial y\partial z^2}+w\frac{{\partial }^{3}v}{\partial z^3}+\frac{\partial v}{\partial z}\frac{{\partial }^{2}v}{\partial y\partial z}\\ +{\alpha }^2\frac{\partial u}{\partial z}\frac{{\partial }^{2}u}{\partial y\partial z}+5\frac{\partial v}{\partial y}\frac{{\partial }^{2}v}{\partial y^2}+\frac{\partial v}{\partial z}\frac{{\partial }^{2}w}{\partial y^2}+2{\alpha }^2\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial y^2}\\ +2\frac{\partial w}{\partial y}\frac{{\partial }^{2}w}{\partial y^2}+{\alpha }^2\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial z^2}+\frac{\partial v}{\partial y}\frac{{\partial }^{2}v}{\partial z^2}\end{array}\right],\hfill \end{array}$$

(3.17)

$$\begin{array}{c}v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}=-\frac{\partial p}{\partial z}-\frac{1}{R_e{K}_0}(1+\epsilon cos\pi z)w+\frac{1}{R_e}[\frac{{\partial }^{2}w}{\partial y^2}+\frac{{\partial }^{2}w}{\partial z^2}]\hfill \\ \phantom{v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}=}+L\left[\begin{array}{c}w\frac{{\partial }^{3}w}{\partial y^2\partial z}+v\frac{{\partial }^{3}w}{\partial y^3}+v\frac{{\partial }^{3}w}{\partial y\partial z^2}+w\frac{{\partial }^{3}w}{\partial z^3}+\frac{\partial w}{\partial y}\frac{{\partial }^{2}w}{\partial y\partial z}\\ +{\alpha }^2\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial y\partial z}+5\frac{\partial w}{\partial z}\frac{{\partial }^{2}w}{\partial z^2}+\frac{\partial w}{\partial y}\frac{{\partial }^{2}v}{\partial z^2}+2{\alpha }^2\frac{\partial u}{\partial z}\frac{{\partial }^{2}u}{\partial z^2}\\ +2\frac{\partial v}{\partial z}\frac{{\partial }^{2}v}{\partial z^2}+{\alpha }^2\frac{\partial u}{\partial z}\frac{{\partial }^{2}u}{\partial y^2}+\frac{\partial w}{\partial z}\frac{{\partial }^{2}w}{\partial y^2}\end{array}\right],\hfill \end{array}$$

(3.18)

$$\begin{aligned}& v\frac{\partial \theta }{\partial y}+w\frac{\partial \theta }{\partial z} =\frac{1}{R_{e}\mathit{Pr}} \biggl[ \frac{\partial ^{2}\theta }{\partial y ^{2}}+\frac{\partial ^{2}\theta }{\partial z^{2}} \biggr], \end{aligned}$$

(3.19)

subject to the boundary conditions

$$\begin{aligned} \left . \begin{aligned} &\text{at } y=0:\quad u =0, \qquad v=-1,\qquad w=0,\qquad \theta =1, \\ &\text{as } y\rightarrow \infty :\quad u =1,\qquad w=0,\qquad p=p_{\infty },\qquad \theta =0, \end{aligned} \right \} \end{aligned}$$

(3.20)

where the nondimensional parameters (Grashof number, Reynolds number, elastic parameter, suction parameter, and Prandtl number) are:

$$\begin{aligned} G=\frac{\nu g\beta (T_{w}-T_{\infty })}{UV_{0}^{2}},\qquad R_{e}=\frac{V_{0}l}{\nu }, \qquad L=\frac{\alpha _{1}}{\rho l^{2}},\qquad \alpha =\frac{U}{V_{0}},\qquad \mathit{Pr}= \frac{\mu c_{p}}{k_{t}}. \end{aligned}$$

(3.21)

4 Investigation of the mathematical model

For the solution of Eqs. (3.15)–(3.19), we assume that in a neighborhood of the medium,

$$ g=g_{0}+\epsilon g_{1}+\epsilon ^{2}g_{2}+\cdots , $$

(4.1)

where ε is a very small parameter, and g stands for any of variables u, v, w, p, and θ.

4.1 Model in two dimensions

For $\epsilon =0$, the problem transfers into two dimensions, so we have

$$\begin{aligned}& \frac{dv_{0}}{dy}=0, \end{aligned}$$

(4.2)

$$\begin{aligned}& L\frac{d^{3}u_{0}}{dy^{3}}-\frac{1}{R_{e}}\frac{d^{2}u_{0}}{ dy^{2}}- \frac{du _{0}}{dy} +\frac{1}{R_{e}K_{0}}u_{0}=\frac{1}{R_{e}K_{0}}+GR_{e} \theta _{0}, \end{aligned}$$

(4.3)

$$\begin{aligned}& 2L\alpha ^{2}\frac{du_{0}}{dy}\frac{d^{2}u_{0}}{dy^{2}}+2L \frac{dw_{0}}{dy}\frac{d^{2}w_{0}}{ dy^{2}}+\frac{1}{R_{e}K_{0}}=\frac{dp _{0}}{dy}, \end{aligned}$$

(4.4)

$$\begin{aligned}& LR_{e}\frac{d^{3}w_{0}}{dy^{3}}+\frac{d^{2}w_{0}}{ dy^{2}}+R_{e} \frac{dw _{0}}{dy}-\frac{1}{K_{0}}w_{0}=0, \end{aligned}$$

(4.5)

$$\begin{aligned}& \frac{d^{2}\theta _{0}}{dy^{2}}+R_{e}\mathit{Pr}\frac{d\theta _{0}}{ dy}=0, \end{aligned}$$

(4.6)

subject to boundary conditions

$$\begin{aligned} \left . \begin{aligned} &u_{0}=0,\qquad v_{0} =-1,\qquad w_{0} =0,\qquad \theta _{0} =1, \quad \text{at } y=0, \\ &u_{0}=1,\qquad w_{0} =0,\qquad \theta _{0} =0, \qquad p_{0} =p_{\infty }\quad \text{as } y \rightarrow \infty . \end{aligned} \right \} \end{aligned}$$

(4.7)

The order of differential equation is increased from 2 to 3 due to the presence of an elasticity parameter. We are required three boundary conditions for a unique solution of Eqs. (4.3) and (4.5). To remove this difficulty, we assume the solution to be of the form

$$ u_{0}=u_{00}+Lu_{01}+O \bigl(L^{2}\bigr), $$

(4.8)

where L is a very small parameter. Solving Eqs. (4.2) and (4.4)–(4.6), we get the following solutions:

$$\begin{aligned} v_{0}=-1, \qquad w_{0} =0,\qquad p_{0} =p_{\infty },\qquad \theta _{0} = e^{-R_{e}\mathit{Pr}y}. \end{aligned}$$

(4.9)

Using Eq. (4.8) in Eq. (4.3) and comparing the coefficients of $O(L^{0})$ and $O(L)$, we get the following boundary value problems:

$$\begin{aligned}& \left . \begin{aligned} &\frac{d^{2}u_{00}}{dy^{2}}+R_{e} \frac{du_{00}}{dy}-\frac{1}{K_{0}}u _{00}=-\frac{1}{K_{0}}-GR^{2}_{e}e^{-R_{e}\mathit{Pr}y}, \\ &u_{00}(0) =0,\qquad u_{00}(\infty ) =1, \end{aligned} \right \} \end{aligned}$$

(4.10)

$$\begin{aligned}& \left . \begin{aligned} &R_{e} \frac{d^{3}u_{00}}{dy^{3}}-\frac{d^{2}u_{01}}{dy^{2}}- R_{e}\frac{du _{01}}{dy}+ \frac{1}{K_{0}}u_{01}=0, \\ &u_{01}(0) =0,\qquad u_{01} ( \infty ) =0. \end{aligned} \right \} \end{aligned}$$

(4.11)

Solving the boundary value problems (4.10)–(4.11), in view of Eq. (4.8), we get

$$ u_{0}(y)=(G\lambda _{0}-1)e^{-\lambda y}+1-G \lambda _{0}e^{- R_{e}\mathit{Pr}y}+LG \lambda ^{2}_{0}R^{2}_{e}{ \mathit{Pr}} ^{3}\bigl(e^{-R_{e}\mathit{Pr}y}-e^{-\lambda y}\bigr). $$

(4.12)

The results of [9] are retrieved for $L=0$.

4.2 Model in three dimensions

When $\epsilon \neq 0$, the flow becomes three-dimensional, and the solution of the resulting problem can be obtained by taking a solution of the form given in Eq. (4.1). Then following partial differential equations are obtained from Eqs. (3.15)–(3.19) by comparing the first-order terms of ε:

$$\begin{aligned}& \frac{\partial v_{1}}{\partial y}+\frac{\partial w_{1}}{\partial z}=0, \end{aligned}$$

(4.13)

$$\begin{aligned}& -\frac{\partial u_{1}}{\partial y}+v_{1}\frac{\partial u_{0}}{ \partial y}=GR_{e} \theta _{1}-\frac{1}{R_{e}K_{0}}u_{1}+\frac{1}{R_{e}} \biggl( \frac{ \partial ^{2}u_{1}}{\partial y^{2}}+ \frac{\partial ^{2}u_{1}}{\partial z^{2}} \biggr) \\& \hphantom{-\frac{\partial u_{1}}{\partial y}+v_{1}\frac{\partial u_{0}}{ \partial y}=}{}+L \biggl( -\frac{ \partial ^{3}u_{1}}{\partial y^{3}}- \frac{\partial ^{3}u_{1}}{ \partial y\partial z^{2}}+v_{1} \frac{\partial ^{3}u_{0}}{ \partial y^{3}} \biggr)-\frac{1}{R_{e}K_{0}}(u_{0}-1)\cos \pi z, \end{aligned}$$

(4.14)

$$\begin{aligned}& - \frac{\partial v_{1}}{\partial y}=- \frac{\partial p_{1}}{\partial y}+ \frac{1}{R_{e}} \biggl( \frac{ \partial ^{2}v_{1}}{\partial y^{2}}+\frac{ \partial ^{2}v_{1}}{\partial z^{2}} \biggr) -L \biggl( \frac{\partial ^{3}v_{1}}{\partial y^{3}}+\frac{ \partial ^{3}v_{1}}{\partial y\partial z^{2} } \biggr) \\& \hphantom{- \frac{\partial v_{1}}{\partial y}=}{}-\frac{1}{R_{e}K_{0}}(v_{1}-\cos \pi z), \end{aligned}$$

(4.15)

$$\begin{aligned}& -\frac{\partial w_{1}}{\partial y}=-\frac{\partial p_{1}}{\partial z}+ \frac{1}{R_{e}} \biggl( \frac{\partial ^{2}w_{1}}{\partial y^{2}}+\frac{ \partial ^{2}w_{1}}{\partial z^{2}} \biggr) -L \biggl( \frac{\partial ^{3}w _{1}}{\partial y^{3}}+\frac{\partial ^{3}w_{1}}{\partial y\partial z ^{2} } \biggr)-\frac{1}{R_{e}K_{0}}w_{1} , \end{aligned}$$

(4.16)

$$\begin{aligned}& -\frac{\partial \theta _{1}}{\partial y}+v_{1}\frac{\partial \theta _{0}}{ \partial y}= \frac{1}{R_{e}\mathit{Pr}} \biggl( \frac{\partial ^{2}\theta _{1}}{\partial y^{2}}+ \frac{\partial ^{2}\theta _{1}}{\partial z^{2}} \biggr). \end{aligned}$$

(4.17)

Similarly, the boundary conditions (3.20) yield

$$\begin{aligned} \left . \begin{aligned} &u_{1} =0,\qquad v_{1}=0,\qquad w_{1}=0,\qquad \theta _{1}=0 \quad \text{at } y=0, \\ &u_{1} =0,\qquad w_{1}=0, \qquad p_{1} =p_{\infty },\qquad \theta _{1}=0 \quad \text{as } y\rightarrow \infty . \end{aligned} \right \} \end{aligned}$$

(4.18)

The set of linear partial differential equations (PDEs) (4.13)–(4.18) describe the free convective three-dimensional flow.

4.3 Secondary flow solution

For the solution of PDEs (4.13)–(4.17), we first consider Eqs. (4.13), (4.15), and (4.16) being independent of the main flow and temperature field.

Assume that the solutions $v_{1}$, $w_{1}$, and $p_{1}$ are of the forms

$$ \begin{aligned} &v_{1}(y,z)=-v_{11}(y)\cos \pi z,\qquad w_{1}(y,z)=\frac{1}{\pi }v_{11}^{{\prime }}(y) \sin \pi z, \\ & p_{1}(y,z)=p_{11}(y)\cos \pi z, \end{aligned} $$

(4.19)

where $v_{11}(y)$ has the derivative $v_{11}'(y)$ with respect to y. The expressions in (4.19) satisfy the equation of continuity (4.13). Substituting Eqs. (4.19) into Eqs. (4.15) and (4.16), we have

$$\begin{aligned}& LR_{e}v_{11}^{{\prime \prime \prime }}-v_{11}^{{\prime \prime }}- \bigl(L \pi ^{2}+1\bigr)R_{e}v_{11}^{{\prime }}+ \biggl(\pi ^{2}+\frac{1}{K_{0}}\biggr)v_{11}=R _{e}p_{11}^{{\prime }}-\frac{1}{K_{0}}, \end{aligned}$$

(4.20)

$$\begin{aligned}& L R_{e}v_{11}^{iv}-v_{11}^{{\prime \prime \prime }}- \bigl(L\pi ^{2}+1\bigr)R _{e}v_{11}^{{\prime \prime }}+ \biggl(\pi ^{2}+\frac{1}{K_{0}}\biggr)v_{11}^{{ \prime }}= \pi ^{2}R_{e}p_{11}, \end{aligned}$$

(4.21)

subject to the boundary conditions

$$ v_{11}(0)=0,\qquad v_{11}^{{\prime }}(0)=0, \qquad v_{11}^{{\prime }}(\infty )=0. $$

(4.22)

On solving both Eqs. (4.20) and (4.21) simultaneously to eliminate the pressure $p_{11}$, we get the following differential equation:

$$\begin{aligned}& LR_{e} v_{11}^{v}-v_{11}^{iv}- \bigl(2L\pi ^{2}+1\bigr)R_{e}v_{11}^{{\prime \prime \prime }} +\biggl(2\pi ^{2}+\frac{1}{K_{0}}\biggr)v_{11}^{{\prime \prime }}+ \pi ^{2}\bigl(L\pi ^{2}+1\bigr) R_{e}v_{11}^{{\prime }} \\& \quad {}-\pi ^{2}\biggl(\pi ^{2}+\frac{1}{K_{0}} \biggr)v_{11}=\frac{\pi ^{2}}{K_{0}}. \end{aligned}$$

(4.23)

Equation (4.23) can be solved by the method of perturbation. Assume that

$$ v_{11}=v_{00}+Lv_{01}+O \bigl(L^{2}\bigr), $$

(4.24)

where L is a very small parameter. Substituting Eq. (4.24) into Eq. (4.23) and boundary conditions (4.22) and then solving the resulting equations, we get

$$ v_{11}=\frac{1}{(\pi -\lambda _{1} )(\pi ^{2}K_{0}+1)}\bigl(\pi e^{-\lambda _{1} y}- \lambda _{1} e^{-\pi y}-\pi +\lambda _{1}\bigr). $$

(4.25)

In view of (4.1), (4.9), and (4.19), we finally get

$$\begin{aligned}& v(y,z)=-1-\frac{\varepsilon }{(\pi -\lambda _{1} )(\pi ^{2}K_{0}+1)}\bigl( \pi e^{-\lambda _{1} y}-\lambda _{1} e^{-\pi y}-\pi +\lambda _{1}\bigr)\cos \pi z, \end{aligned}$$

(4.26)

$$\begin{aligned}& w(y,z)=\frac{\varepsilon \lambda _{1}}{(\pi -\lambda _{1} )(\pi ^{2}K _{0}+1)}\bigl( e^{-\pi y}- e^{-\lambda _{1} y}\bigr)\sin \pi z. \end{aligned}$$

(4.27)

4.4 Pressure and temperature field

Using Eqs. (4.1), (4.9), (4.19), (4.21), and (4.26), we can obtain the value of pressure given by

$$p(y,z)=p_{\mathrm{\infty }}+\frac{\epsilon {\lambda }_{1}cos\pi z}{\pi R_e(\pi -{\lambda }_1)({\pi }^2{K}_0+1)}\left(\begin{array}{c}L{R}_e{\lambda }_1({\lambda }_1^2-{\pi }^2)e^{-{\lambda }_{1}y}\\ +(R_e\pi +\frac{1}{K_0})e^{-\pi y}\end{array}\right).$$

(4.28)

To find an expression for the temperature distribution, we take

$$ \theta _{1}(y,z)=\theta _{11}(y)\cos \pi z. $$

(4.29)

Then the PDE (4.17) subject to the boundary conditions

$$ \theta _{11}(0)=0,\qquad \theta _{11}(\infty )=0 $$

(4.30)

yields

$$\begin{aligned} \theta (y,z) =&e^{-R_{e}\mathit{Pr}y}+\frac{\varepsilon R^{2}_{e}\mathit{Pr}^{2}\cos \pi z}{(\pi -\lambda _{1} )(\pi ^{2}K_{0}+1)}\biggl[ \biggl(A-B-\frac{\pi -\lambda _{1}}{\pi ^{2}}\biggr)e^{-\beta y} \\ &{}+Be^{-(\lambda _{1}+R_{e}\mathit{Pr}) y}-Ae^{-(\pi +R_{e}\mathit{Pr}) y}+\frac{\pi - \lambda _{1}}{\pi ^{2}} e^{-R_{e}\mathit{Pr}y} \biggr], \end{aligned}$$

(4.31)

where $A=\frac{\lambda _{1}}{\pi R_{e}\mathit{Pr}}$, $B=\frac{\pi }{\lambda ^{2}_{1}+R_{e}\mathit{Pr}\lambda _{1}-\pi ^{2}}$, $\lambda _{1}=\frac{R_{e}}{2}+\sqrt{(\frac{R _{e}}{2})^{2}+\pi ^{2}+\frac{1}{K_{0}}}$, $\lambda =\frac{R_{e}}{2}+\sqrt{(\frac{R_{e}}{2})^{2}+\frac{1}{K _{0}}}$, $\lambda _{0}=\frac{R^{2}_{e}}{R^{2}_{e}\mathit{Pr}(\mathit{Pr}-1)-\frac{1}{K _{0}}}$, $\beta =\frac{R_{e}\mathit{Pr}}{2}+\sqrt{(\frac{R_{e}\mathit{Pr}}{2})^{2}+ \pi ^{2}}$.

4.5 Main flow solution

The main flow velocity can be obtained from the PDE (4.14). Similarly to the previous sections, we assume that

$$\begin{aligned} u_{1}(y,z)=u_{11}(y)\cos \pi z \end{aligned}$$

(4.32)

as solution of (4.14) and

$$ u_{11}=u_{100}+Lu_{110}+O \bigl(L^{2}\bigr). $$

(4.33)

After huge calculations, we get

$$\begin{array}{c}{u}_{100}(y)=(D+E)e^{-{\lambda }_{1}y}-D{e}^{-\lambda y}-E{e}^{-R_e\mathit{Pr}y}\hfill \\ \phantom{u_{100}(y)=}-\frac{R_e}{(\pi -{\lambda }_1)({\pi }^2{K}_0+1)}\left[\begin{array}{c}F{e}^{-\beta y}+H{e}^{-({\lambda }_1+R_e\mathit{Pr})y}-I{e}^{-(\pi +R_e\mathit{Pr})y}\\ +J{e}^{-R_e\mathit{Pr}y}-M{e}^{-({\lambda }_1+\lambda )y}+N{e}^{-(\pi +\lambda )y}\\ -O{e}^{-\lambda y}-P{e}^{-{\lambda }_{1}y}\end{array}\right],\hfill \end{array}$$

(4.34)

$$\begin{array}{c}{u}_{110}(y)=(C_2-C_1)e^{-{\lambda }_{1}y}+C_1{e}^{-R_e\mathit{Pr}y}-C_2{e}^{-\lambda y}\hfill \\ \phantom{u_{110}(y)=}+\frac{R_e}{(\pi -{\lambda }_1)({\pi }^2{K}_0+1)}\left[\begin{array}{c}{C}_3{e}^{-\beta y}+C_4{e}^{-({\lambda }_1+R_e\mathit{Pr})y}+C_5{e}^{-(\pi +R_e\mathit{Pr})y}\\ +C_6{e}^{-R_e\mathit{Pr}y}+C_7{e}^{-({\lambda }_1+\lambda )y}+C_8{e}^{-(\pi +\lambda )y}\\ -C_9{e}^{-\lambda y}-C_{10}{e}^{-{\lambda }_{1}y}\end{array}\right].\hfill \end{array}$$

(4.35)

Equations (4.34) and (4.35) in view of Eqs. (4.33), (4.32), and (4.1) give the final main flow solution. It is worth mentioning that the results of [9] are recovered for $L=0$. The constants involved in solutions (4.34) and (4.35) are as follows:

$$\begin{aligned}& D=\frac{G\lambda _{0}-1}{\pi ^{2}K_{0}} ,\qquad E=\frac{G\lambda _{0}}{K _{0}[R^{2}_{e}\mathit{Pr}(\mathit{Pr}-1)-(\pi ^{2}+\frac{1}{K_{0}})]} , \\& F=\frac{GR^{3} _{e}\mathit{Pr}^{2}(A-B-\frac{\pi -\lambda _{1}}{\pi ^{2}})}{\beta ^{2}-R_{e} \beta -(\pi ^{2}+\frac{1}{K_{0}})} , \\& H=\frac{G(R^{2}_{e}\mathit{Pr}B+\pi \lambda _{0})}{R_{e}(\mathit{Pr}-1)+2\lambda _{1}} ,\qquad I=\frac{GR_{e}pr(R^{2}_{e}\mathit{Pr}A+\lambda _{1}\lambda _{0})}{R^{2}_{e}\mathit{Pr}(\mathit{Pr}-1)+ \pi R_{e}(2\mathit{Pr}-1)-\frac{1}{K_{0}}} , \\& J=\frac{GR_{e}\mathit{Pr}(\pi -\lambda _{1})(\frac{R^{2}_{e}\mathit{Pr}}{\pi ^{2}}- \lambda _{0})}{R^{2}_{e}\mathit{Pr}(\mathit{Pr}-1)-(\pi ^{2} +\frac{1}{K_{0}})},\qquad M=\frac{\pi \lambda (G\lambda _{0}-1)}{2\lambda _{1}\lambda +\frac{1}{K _{0}}}, \\& N=\frac{\lambda _{1}\lambda (G\lambda _{0}-1)}{\pi (2\lambda -R_{e})}, \qquad O=\frac{\lambda (\pi -\lambda _{1})(G\lambda _{0}-1)}{\pi ^{2}}, \\& P=F+H-I+J-M+N-O, \\& A_{1}=R^{2}pr\biggl[E\bigl(R^{2}_{e} \mathit{Pr}^{2}-\pi ^{2}\bigr)+\frac{1}{K_{0}G\lambda ^{2} _{0}}\mathit{Pr}^{2} \biggr], \\& A_{2}=R_{e}\lambda \biggl(\lambda ^{2}-\pi ^{2}D-\frac{1}{K _{0}}G\lambda ^{2}_{0}r^{2}_{e}\mathit{Pr}^{3} \biggr), \\& A_{3}=GR^{3}_{e}\mathit{Pr}^{3}\lambda _{0}(1+\mathit{Pr}\lambda _{0}),\qquad A_{4}=G\lambda ^{2}_{0}R^{2} _{e}\mathit{Pr}^{3}+ \lambda ^{2}(G\lambda _{0}-1), \\& C_{1}=\frac{A_{1}}{R^{2}_{e}\mathit{Pr}(\mathit{Pr}-1)-(\pi ^{2}+\frac{1}{K_{0}})}, \qquad C_{2}= \frac{A_{2}}{\pi ^{2}}, \qquad C_{3}=\frac{R_{e}F\beta (\beta ^{2}- \pi ^{2})}{\beta ^{2}-R_{e}\beta -(\pi ^{2}+\frac{1}{K_{0}})}, \\& C_{4}=\frac{R_{e}H(\lambda _{1}+R_{e}\mathit{Pr})[(\lambda _{1}+R_{e}\mathit{Pr})^{2}-\pi ^{2}]+\pi A_{3}}{R^{2}_{e}\mathit{Pr}(\mathit{Pr}-1)+2\lambda _{1}R_{e}\mathit{Pr}}, \\& C_{5}=\frac{R_{e}I(\pi +R_{e}\mathit{Pr})[\pi ^{2}-(\pi +R_{e}\mathit{Pr})^{2}]-\lambda _{1}A_{3}}{R^{2}_{e}\mathit{Pr}(\mathit{Pr}-1)+\pi R_{e}(2\mathit{Pr}-1)-\frac{1}{K_{0}}}, \\& C_{6}=\frac{JR^{2}_{e}\mathit{Pr}(R^{2}_{e}\mathit{Pr}^{2}-\pi ^{2})-(\pi -\lambda )A _{3}}{R^{2}_{e}\mathit{Pr}(\mathit{Pr}-1)-(\pi ^{2}+\frac{1}{K_{0}})}, \\& C_{7}= \frac{R_{e}M(\lambda _{1}+\lambda )[\pi ^{2}-(\lambda _{1}+\lambda )^{2}]-\pi \lambda A_{4}}{2\lambda _{1}\lambda +\frac{1}{K_{0}}}, \\& C_{8}=\frac{R_{e}N(\pi +\lambda )[(\pi +\lambda )^{2}-\pi ^{2}]+ \lambda _{1}\lambda A_{4}}{\pi (2\lambda -R_{e})}, \\& C_{9}= \frac{R_{e}O(\pi ^{2}-\lambda ^{2})+(\pi -\lambda _{1})\lambda A _{4}}{\pi ^{2}},\\& C_{10}=C_{3}+C_{4}+C_{5}+C_{6}+C_{7}+C_{8}-C_{9}. \end{aligned}$$

4.6 Skin friction coefficients

After getting the velocity field, the important physical quantities such as the skin friction component can be computed. The nondimensional skin friction component along the x-direction is as follows:

$$\begin{aligned} \tau ^{\triangleright }_{x}=\frac{\tau _{yx}}{\rho UV_{0}}= \frac{\nu }{V _{0}l}\biggl(\frac{\partial u}{\partial y}\biggr)_{y=0}. \end{aligned}$$

(4.36)

Omitting the sign of “▷” for convenience, we get the following result:

$$\begin{aligned} \tau _{x}=S_{0}+\varepsilon S_{1}(R_{e}, \mathit{Pr}, G, K_{0}, L)\cos \pi z, \end{aligned}$$

(4.37)

where

$$\begin{aligned} S_{0}=\frac{1}{R_{e}} \biggl\vert \frac{du_{0}}{dy} \biggr\vert _{y=0}-L \biggl\vert \frac{du ^{2}_{0}}{dy^{2}} \biggr\vert _{y=0} \end{aligned}$$

(4.38)

and

$$\begin{aligned} S_{1}(R_{e}, \mathit{Pr}, G, K_{0}, L)= \frac{1}{R_{e}} \biggl\vert \frac{du_{11}}{dy} \biggr\vert _{y=0}-L \biggl\vert \frac{du^{2}_{11}}{dy^{2}} \biggr\vert _{y=0}. \end{aligned}$$

(4.39)

Similarly, the skin friction component in the nondimensional form along the z-direction is

$$\begin{aligned} \tau _{z}=\frac{\tau _{yz}}{\mu V_{0}/l}= \biggl\vert \frac{\partial w}{ \partial y} \biggr\vert _{y=0}+LR_{e} \biggl\vert v\frac{\partial ^{2} w}{\partial y^{2}} \biggr\vert _{y=0}=-\varepsilon S_{2}(R_{e}, L, K_{0})\sin \pi z, \end{aligned}$$

(4.40)

where

$$\begin{aligned} S_{2}(R_{e}, L, K_{0})= \frac{\lambda _{1}}{\pi ^{2}K_{0}+1}\bigl(1+LR_{e}( \pi +\lambda _{1})\bigr). \end{aligned}$$

(4.41)

4.7 Heat flux

The Nusselt number Nu can be obtained from the rate of heat transfer coefficient of temperature field given by

$$\begin{aligned} Nu=\frac{-q}{\rho V_{0}c_{p}(T_{w}-T_{\infty })}. \end{aligned}$$

(4.42)

Nondimensioning and simplifying the resulting equation, we get

$$\begin{aligned} Nu =&\frac{k_{t}}{\rho V_{0}c_{p}l}\biggl(\frac{\partial \theta }{\partial y} \biggr)_{y=0} \\ =&\frac{1}{R _{e}\mathit{Pr}}\biggl(\frac{d\theta _{0}}{dy}+\varepsilon \frac{\partial \theta _{1}}{ \partial y}\biggr)_{y=0} \\ =&Nu_{0}+\varepsilon S_{3}(R_{e}, \mathit{Pr}, K_{0}) \cos \pi z, \end{aligned}$$

(4.43)

where

$$\begin{aligned} Nu_{0}=-1, \end{aligned}$$

(4.44)

and

$$\begin{aligned} S_{3}(R_{e}, \mathit{Pr}, K_{0}) =& \frac{R_{e}pr}{(\pi - \lambda _{1})(\pi ^{2}K _{0}+1)} \biggl[-\beta \biggl(A-B-\frac{\pi -\lambda _{1}}{\pi ^{2}} \biggr) \\ &{}-B(\lambda _{1} +R_{e}pr) +A(\pi +R_{e}\mathit{Pr})-\biggl(\frac{\pi -\lambda _{1}}{\pi ^{2}}\biggr)R_{e}\mathit{Pr}\biggr]. \end{aligned}$$

(4.45)

5 Results and discussion

In this work, a three-dimensional steady flow of a second-grade fluid through a porous medium with periodic permeability and heat transfer is modeled and analyzed theoretically. Analytical solutions for the velocity field, skin friction, pressure, and heat flux are obtained using the regular perturbation method. The effects of nondimensional parameters, such as the Reynolds number $R_{e}$, Prandtl number Pr, elastic parameter L, permeability parameter $K_{0}$, and Grashof number G, on these physical quantities are visualized graphically.

Figure 2 displays the effect of the Reynolds number on the velocity field, pressure, and temperature distribution when all other nondimensional parameters are fixed ($\mathit{Pr}=7$, $K_{0}=1$, $G=1$, $z=0$, $L=0.01$, $\varepsilon =0.01$) and the Reynolds number is varied: $R_{e}=1,3,5$. It is observed that with the increase of the Reynolds number, the main flow velocity component u (Fig. 2(a)) also increases and reaches its maximum value at the boundary for each value of the Reynolds number taken in this regard. Moreover, the boundary layer thickness decreases with an increase in Reynolds number. Similarly, the magnitude of the velocity component v (Fig. 2(b)) increases with an increase in Reynolds number. On the other hand, it is noted that the magnitude of this velocity component decreases as we move away from the plate, which seems physically correct, because it is well established that the suction effect on the flow is maximum near the plate. It is observed from Fig. 2(c) that for a fixed value of $R_{e}$, the velocity component w increases exponentially near the plate, attains its maximum value, then decreases rapidly, and finally converges to zero as $y\rightarrow \infty$. A parabolic profile near the plate is obtained. It is also noted that this velocity component increases with an increase in Reynolds number $R_{e}$. Physically, this means that the effect of inertial forces is dominant over viscous forces near the plate. The pressure also increases with an increase in Reynolds number $R_{e}$ near the plate (Fig. 2(d)). Its value is maximum at the free surface. Figure 2(e) demonstrates the effect of Reynolds number $R_{e}$ on the temperature distribution. It shows that the thermal boundary layer decreases with an increase in Reynolds number $R_{e}$.

Figure 2

Effect of Reynolds number on velocity field, pressure, and temperature field

Figure 3 illustrates the effect of permeability parameter $K_{0}$ on the velocity components, pressure, and temperature distribution when all other nondimensional parameters are fixed ($\mathit{Pr}=7$, $R_{e}=1$, $G=1$, $z=0$, $L=0.01$, $\varepsilon =0.01$) and permeability parameter varies: $K_{0}=0.1,0.5,1$. It is detected that the main flow velocity component u (Fig. 3(a)) decreases with an increase in permeability parameter $K_{0}$. The minimum and maximum values of the velocity component occur at the boundaries. A similar effect of permeability parameter $K_{0}$ on the velocity component v is perceived from Fig. 3(b). It is witnessed from Fig. 3(c) that, for a fix value of $K_{0}$, the velocity component w increases exponentially near the plate, attains its maximum value, then decreases rapidly, and finally converges to zero as $y\rightarrow \infty$. A parabolic profile near the plate is obtained. It is also noted that this velocity component decreases with an increase in $K_{0}$. On the contrary, the pressure increases with an increase in permeability parameter $K_{0}$ near the plate (Fig. 3(d)). Its value is maximum at the free surface. Figure 3(e) demonstrates the effect of permeability parameter $K_{0}$ on the temperature distribution. A weak dependence of the temperature distribution upon permeability parameter $K_{0}$ is noted.

Figure 3

Effect of Permeability parameter on velocity field, pressure, and temperature field

Figure 4 shows the effect of the Prandtl number on the main flow velocity component u and temperature field. This figure reveals that an increase in Prandtl number causes a decrease in the velocity component. It is evident from this figure that the temperature of the fluid decreases with an increase in Prandtl number Pr causing reduction in thermal boundary layer thickness. In fact, at high Prandtl number, the fluid has a low thermal conductivity resulting in reduction in thermal layer thickness. Therefore, this observation quite agrees with the physical situation that the boundary layer thickness decreases with an increase in Prandtl number.

Figure 4

Effect of Prandtl numbers on velocity component and temperature field

Figure 5 exhibits the effect of the non-Newtonian parameter L on the main flow velocity component u and pressure P. It is perceived that an increase in the non-Newtonian parameter leads to a decrease in the velocity component, which seems physically correct because an increase in the non-Newtonian parameter causes fluid thickening resulting in reduction in the velocity. The increase in non-Newtonian parameter also leads to a decrease in pressure due to thickening of the fluid.

Figure 5

Effect of non-Newtonian parameter on velocity component and pressure

Figure 6 displays the effect of the Grashof number (free convection parameter) on the main flow velocity component u for cooling of the plate. It is obvious from this Figure that the velocity component increases due to greater cooling of the channel, that is, as the Grashof number G increases.

Figure 6

Effect of Grashof number on main flow

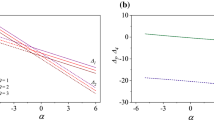
In Fig. 7, the nondimensional skin friction component along the main flow direction is plotted against the Reynolds number for different values of elastic parameter L, permeability parameter $K_{0}$, Grashof number G, and Prandtl number Pr. The skin friction exerted by the plate on the fluid increases with an increase in Reynolds number in all cases. For small values of elastic parameter L (<0.1), the skin friction component tends to zero, which physically means that the effect of inertial and viscous forces balance each other, resulting in zero effect of the skin friction component along the x-axis. It, however, increases by increasing the elastic parameter L (Fig. 7(a)). Figure 7(b) shows that the skin friction component decreases with an increase in permeability parameter $K_{0}$. Depending upon the value of permeability parameter $K_{0}$, for small values of the Reynolds number $R_{e}$, the skin friction is exerted by the fluid on the plate, and, of course, the behavior is reversed for large values of $R_{e}$. A similar effect of the Grashof number G on the skin friction is noted (Fig. 7(c)). On the contrary, an increase in the Prandtl number boosts the skin friction (Fig. 7(d)). The numerical values of the skin friction component with the variation of nondimensional parameters are also presented in Table 1.

Figure 7

Effect of non-dimensional parameters on skin friction component along main flow (x-direction)

Table 1 Effect of parameters on skin friction along x-axis

Figure 8 is plotted for the nondimensional skin friction component along the z-direction versus the Reynolds number for different values of the elastic parameter L and permeability parameter $K_{0}$. It is observed that an increase in $R_{e}$ leads to an increase in the skin friction component in both cases. It is also noted that the skin friction exerted by the fluid on the plate enhances by increasing the elastic parameter. However, an opposite trend is noted for the permeability parameter. The numerical values in Table 2 are clearly the evidence of Figs. 8(a) and 8(b).

Figure 8

Effect of non-dimensional parameters on skin friction component along cross flow (z-direction)

Table 2 Effect of parameters on skin friction along z-axis

In Fig. 9 the variation of the nondimensional heat transfer coefficient is plotted against the Reynolds number for different values of the Prandtl number and permeability number. It is witnessed that an increase in Reynolds number enhances the heat transfer coefficient. In contrast, an increase in either the Prandtl number or the permeability number leads to a decrease of the heat transfer coefficient.

Figure 9

Effects of Prandtl and permeability parameter on Nusselt number

6 Final remarks

The present analysis aims to present approximate solutions for the three-dimensional free convective flow of a second-grade fluid through a porous medium with periodic permeability in the presence of heat transfer. Analytic solutions for the velocity field, skin friction components, and temperature distribution using regular perturbation are obtained and analyzed theoretically. The main findings of this study are as follows.

• The Reynolds number provides a mechanism to control the skin friction along the x-axis and along the z-axis.

• The permeability is an economical parameter to reduce the pressure causing reduction in energy consumption.

• The permeability is a tool to minimize the skin friction components (Tables 1 and 2).

• The non-Newtonian parameter causes a reduction of the main flow velocity component. However, it enhances the pressure due to thickening of the fluid.

• The main flow velocity component increases due to high cool of the channel.

• A weak dependence of the temperature field on the permeability parameter is noted.

• The results of [9] are recovered in the absence of the non-Newtonian parameter L.