Abstract
The Cauchy problem of the modified Helmholtz-type equation is severely ill-posed, i.e., the solution does not depend continuously on the given Cauchy data. Thus the regularization methods are required to recover the numerical stability. In this paper, we propose a quasi-reversibility regularization method to deal with this ill-posed problem. Convergence estimates are obtained under a-priori bound assumptions for the exact solution and the selection of regularization parameter. Some numerical results are given to show that this method is stable and feasible.
Similar content being viewed by others
1 Introduction
In this study, a Cauchy problem of the Helmholtz-type equation is considered as follows:
By solving equations (1.2) and (1.3) as follows, respectively, the solution to equation (1.1) can be obtained.
and
where \(u(x,y): [0,\pi]\times[0,T]\rightarrow R, v(x,y): [0,\pi ]\times [0,T]\rightarrow R\) and \(w(x,y): [0,\pi]\times[0,T]\rightarrow R\) are all second-order continuous differentiable functions.
This problem appears in many applications [1] such as in Debye–Huckel theory, implicit marching strategies of the heat equation, the linearization of the Poisson–Boltzmann equation [2,3,4], and so on. The direct problems of the Helmholtz-type equation have been studied widely in the past century [5, 6]. In recent years, some new methods have been proposed for the Helmholtz problems, such as fast solution of three-dimensional modified Helmholtz equations by the method of fundamental solutions [7], a new radial basis function for Helmholtz problems [8], a new investigation into regularization techniques for the method of fundamental solutions [9], the blow-up of radial solutions to a cubic non-linear system equation in dimension 2 [10], and a modified and simple algorithm for fractional modelling arising in unidirectional propagation of long wave in dispersive media by using the fractional homotopy analysis transform method [11]. However, the noisy data can be obtained only on a part of the boundary or at some interior points in some practical problems giving rise to an inverse problem [12]. Problem (1.1) is well known to be a highly ill-posed problem, which means the solution does not depend continuously on the given Cauchy data, i.e., any small change in the given data may cause large error to the solution [13, 14]. In recent years, the Cauchy problems associated with the Helmholtz-type equation have been studied by using different numerical methods such as the conjugate gradient method [15], the Landweber method with boundary element method [16], Tikhonov-type regularization method [17], the method of fundamental solutions [18,19,20], quasi-reversibility and truncation methods [21], and so on. In paper [22], a non-local boundary value problem method is used to solve a Cauchy problem for elliptic equations in a cylindrical domain. Recently this method has been used to solve the backward heat conduction problem [23,24,25,26] and the Cauchy problem for hyper-parabolic partial differential equations [27].
In this study, a quasi-reversibility regularization method will be considered to construct stable approximate solutions to problems (1.2) and (1.3). Our method has a little difference with the one in [21]. There are two ways to propose quasi-reversibility methods: by modifying the disturbance equation or by modifying the initial-boundary value condition. In [21], the main strategy is to modify the disturbance equation. In our paper, the initial-boundary value condition is modified. Here the initial conditions \(u(x,0)=\varphi(x)\) in (1.2) and \(v_{y}(x,0)=\psi(x)\) in (1.3) are replaced with
respectively, where \(p\geq1\) is an integer and \(\alpha>0\) is the regularization parameter. In order to overcome the ill-posedness of problems (1.2) and (1.3), the perturbation conditions (1.4) and (1.5) will be adopted. For compatibility of physical dimension, here we make the regularization parameter α include some coefficients of thermodynamics.
The remainder of this paper is organized as follows. In Sect. 2, a quasi-reversibility regularization method and error estimates are given. In Sect. 3, numerical results are shown. Some conclusions are given in Sect. 4.
2 Regularization method and error estimates
Firstly, as for equation (1.2), the solution to the following perturbation equation will be adopted to approach the solution to equation (1.2):

where \(p\geq1\) is an integer, \(\alpha>0\) is a regularization parameter, and the measured data \(\varphi^{\delta}\in L^{2}(0,\pi)\) satisfies
in which \(\|\cdot\|\) denotes the \(L^{2}\)-norm and the constant \(\delta>0\) is called an error level.
By the technique of separation of variables, we can obtain a solution to equation (1.2) as follows:
where
Similarly, the solution to problem (2.1a)–(2.1d) is
where
Next, the deduction of (2.5) will be given. By the technique of separation of variables, let \(u^{\delta}_{\alpha}(x,y)=X(x)T(y)\), and plug that into equation (2.1a). We can obtain
By separation of variables, we have
Since the left-hand side is independent of t and the right-hand side is independent of x in equation (2.5a), we can let equation (2.5a) equal −λ(constant).
Hence, we can obtain two second-order linear ordinary differential equations as follows:
Now, plug \(u^{\delta}_{\alpha}(x,y)=X(x)T(y)\) into equation (2.1d), and we have
Apparently, \(T(y)\not\equiv0\), we have
So, the Sturm–Liouville eigenvalue problems of equations (2.5b) and (2.5c) can be obtained, and we can obtain all eigenvalues \(\lambda _{n}=n^{2},n=1,2,3,\ldots\) , and eigenfunctions
For any \(\lambda_{n}=n^{2},n=1,2,3,\ldots\) , from equation (2.5b) we have
From equations (2.5e) and (2.5f), we can obtain
We plug equation (2.5g) into equation (2.1c), and we have
Hence, we can obtain \(C_{n}=D_{n}\), \(T_{n}(y)=2C_{n}\cosh({\sqrt {k^{2}+n^{2}}}y)\), and
From equations (2.5f) and (2.1b), we can obtain
From equation (2.5i), we have
Therefore, from equations (2.5g) and (2.5j), we can obtain equation (2.5).
In the following Theorem 2.1, we will prove that solution (2.5) depends continuously on the Cauchy data \(\varphi^{\delta}\).
Theorem 2.1
Suppose that \(u^{\delta}_{\alpha1}\) is the solutions to equation (2.1a)–(2.1d) corresponding to the data \(\varphi^{\delta}_{1}\), and \(u^{\delta}_{\alpha2}\) is the solutions to equation (2.1a)–(2.1d) corresponding to the data \(\varphi^{\delta}_{2}\), then, for \(\alpha< T\), we obtain
Proof
The case that p is even will be considered first. From (2.5), we can obtain
where \(\varphi^{\delta}_{i,n}=\frac{2}{\pi}\int_{0}^{\pi}\varphi_{i}^{\delta}(x)\sin(nx)\,dx\) for \(i=1,2\).
For \(x>0\), we define the function
It is easy to prove that \(h(x)\) has a unique maximizer \(x_{0}\) as \(\alpha< T\) such that
Then, from Parseval equality, equation (2.11), and Bessel inequality, we have
Next, the case that p is odd will be discussed. From (2.5), using the inequality \(\frac{\cosh (\sqrt{k^{2}+n^{2}}T )}{\sinh (\sqrt {k^{2}+n^{2}}T )}\leq\frac{2}{1-e^{-2(\sqrt{k^{2}+n^{2}}T)}}\leq\frac{2}{ 1-e^{-2T}}\), we can obtain
By (2.12), (2.13), we have (2.7). □
In Theorem 2.2 below, we will verify that a stable approximation to the exact solution u given by (2.3) is the regularized solution \(u^{\delta}_{\alpha}\) given by (2.5).
Theorem 2.2
Let u be the solution to equation (1.2) and \(u^{\delta}_{\alpha}\) be the solution to equation (2.1a)–(2.1d). Suppose that the measured data \(\varphi^{\delta}\) satisfies \(\|\varphi^{\delta}-\varphi\|\leq\delta\) and the exact solution u satisfies \(\|\frac{\partial^{p} u}{\partial y^{p}}(\cdot,T)\| \le E\) with \(p\ge1\). We choose the regularization parameter
Then, for fixed \(0< y\leq T\) and \(\delta< T\), we can obtain the following error estimate:
where \(C=\frac{2}{1-e^{-2T}}T (1+E )\).
Proof
Denote by \(u_{\alpha}\) the solution of equation (2.1a)–(2.1d) corresponding to the exact data φ. We have
When p is even, from Theorem 2.1, we get
From (2.2), (2.3), (2.5), (2.11), we can obtain
From (2.16) and the above two estimates, we have
In the following equation, the case that p is odd is considered. From Theorem 2.1 and the inequality \(\frac{\cosh(\sqrt{k^{2}+n^{2}}T)}{\sinh(\sqrt{k^{2}+n^{2}}T)}\leq\frac {2}{1-e^{-2(\sqrt{k^{2}+n^{2}}T)}}\leq\frac{2}{1-e^{-2T}}\), we have
From (2.14), (2.18), (2.19), we get
By (2.17), (2.20), the estimate form of (2.15) can be obtained. □
Secondly, as for equation (1.3), the following perturbation equation is considered:
where \(p\ge1\) is an integer, α is a regularization parameter, and the measured data \(\psi^{\delta}\in L^{2}(0,\pi)\) satisfies
the \(\|\cdot\|\) denotes \(L^{2}\)-norm and the constant \(\delta>0\) is an error level.
By the technique of separation of variables, we get a solution to equation (1.3) as follows:
where
In a similar way, we get that the solution to equation (2.21) is
where
Lemma 2.3
Suppose \(0< y< T\), then for \(\alpha<1\) we get
Lemma 2.3 is required in the following proof, and its proof can be found in [28].
Theorem 2.4
Let v be the solution to equation (1.3) and \(v^{\delta}_{\alpha}\) be the solution to equation (2.21). Suppose that the measured data \(\psi^{\delta}\) satisfies \(\|\psi^{\delta}-\psi\|\leq\delta\) and the exact solution v satisfies \(\|\frac{\partial^{p}v}{\partial y^{p}}(\cdot,T)\| \le E\) with \(p\ge1\). We choose the regularization parameter
Then, for fixed \(0< y\leq T\) and \(\delta<2\), we get the following error estimate:
Proof
Firstly, the case that p is odd will be proved. From the condition \(\|\psi^{\delta}-\psi\|\leq\delta\) we derive
Then, from (2.23), (2.25), (2.30), note that \(n\geq1\), we get
From (2.27) in Lemma 2.3, for \(\delta<2\), we have
And
thus
To even p, note that \(n\geq1\), \(\sinh(\sqrt{k^{2}+n^{2}}T)\ge1/2 e^{\sqrt {k^{2}+n^{2}}T} (1-e^{-2T})\), we have
From (2.27) in Lemma 2.3, for \(\delta<2(1-e^{-2T})^{-1}\), we can obtain
And
Then, from (2.27) in Lemma 2.3, we have
Using (2.34), (2.35), we can obtain the error estimate (2.29). □
3 Numerical experiments
In order to verify the accuracy and efficiency of the proposed regularization method, two numerical examples are performed.
Example 1
The following direct problem for the modified Helmholtz equation is considered:
where we take \(T=1\).
By the technique of separation of variables, we can obtain the solution to the direct problem (3.1) as follows:
where \(\varphi_{n}=\frac{2}{\pi\cosh({k^{2}+n^{2}})}\,d_{n}\), \(d_{n}=\int _{0}^{\pi}x(\pi-x)(1+x)\sin(nx)\,dx \), which can be computed by employing the Simpson formulation.
Next, the initial data \(\varphi(x)\) is chosen as follows:
We give the measured data \(\varphi^{\delta}(x_{i})=\varphi(x_{i})+\varepsilon\operatorname{rand}(i)\), where ε is an error level and
The function \(\operatorname{rand}(\cdot)\) denotes a random number uniformly distributed in the interval \([0,1]\). The relative root mean square error between the exact and regularization solution is given by
where
In the numerical computations, we only consider the cases when \(p=1,2,3\), and always take \(N_{1}=N_{2}=31\). We choose the regularization parameter α by (2.14).
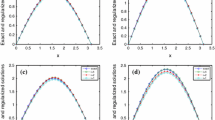
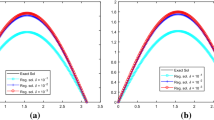
We have shown the numerical results in Figs. 1–4 and Tables 1–2. The numerical results for \(u(\cdot,y)\) and \(u^{\delta}_{\alpha}(\cdot,y)\) with \(k=0.5\) and \(\varepsilon=0.001,0.01\) are respectively shown in Fig. 1 and Fig. 2. The numerical results for \(u(\cdot,y)\) and \(u^{\delta}_{\alpha}(\cdot,y)\) with \(k=1.2\) and \(\varepsilon=0.001,0.01\) are respectively shown in Fig. 3 and Fig. 4. The relative root mean square errors for the computed solution versus the error levels ε are respectively shown in Table 1 (\(k=0.5\)) and Table 2 (\(k=1.2\)).
Example 2
The following direct problem for the modified Helmholtz equation is considered:
where \(T=1\).
By the technique of separation of variables, we get the solution to the direct problem (3.7) as follows:
Then
where \(\psi_{n}=\frac{2n}{\pi\sinh({k^{2}+n^{2}})}e_{n}\), \(e_{n}=\int_{0}^{\pi}x(\pi-x)\sin(nx)\,dx \).
We give the initial data
and the measured data \(\psi^{\delta}(x_{i})=\psi(x_{i})+\varepsilon\operatorname{rand}(i)\), where ε is an error level.
We have shown the numerical results in Figs. 5–8 and Tables 3–4. The numerical results for \(v(\cdot,y)\) and \(v^{\delta}_{\alpha}(\cdot,y)\) with \(k=0.5\) and \(\varepsilon=0.001,0.01\) are respectively shown in Fig. 5 and Fig. 6. The numerical results for \(v(\cdot,y)\) and \(v^{\delta}_{\alpha}(\cdot,y)\) with \(k=1.2\) and \(\varepsilon=0.001,0.01\) are respectively shown in Fig. 7 and Fig. 8. The relative root mean square errors for the computed solution versus the error levels ε are respectively shown in Table 3 (\(k=0.5\)) and Table 4 (\(k=1.2\)).
By Figs. 1–8 and Tables 1–4, we observe that our proposed method is effective and stable. From Tables 1–2 and 3–4, we note that the smaller ε is, the better the calculation effect is, which means that our proposed regularization method is convergent with respect to decreasing the noise level ε. In addition, from Tables 1 to 4, we can see the relative root mean square errors \(\epsilon(u)=0.0014\) and \(\epsilon(v)=0.0313\) for various noise levels when \(k=0.5,\varepsilon=0.0001,p=1\), and the relative root mean square errors \(\epsilon(u)=0.0018\) and \(\epsilon(v)=0.0204\) for various noise levels when \(k=1.2,\varepsilon=0.0001,p=1\). Since \(\epsilon(u)=0.0014\) is less than \(\epsilon(v)=0.0313\) and \(\epsilon(u)=0.0018\) is less than \(\epsilon(v)=0.0204\), our proposed method is more effective to problem (1.2) than to (1.3) when \(p=1\). These results show that our proposed method is applicable in dealing with Cauchy problem (1.2) and (1.3).
4 Conclusions
In this study, we propose a quasi-reversibility regularization method to solve a Cauchy problem for the modified Helmholtz-type equation. The error and stability estimates for \(0< y\leq T\) have been obtained under a-priori bound assumptions for the exact solution. Some numerical results show that our proposed regularization method is effective and stable. In addition, our proposed method is easy to be extended to the three-dimensional case and the proofs are similar. It should be mentioned that the method of separation of variables is used to give the expression of solution, so the proposed method in this paper can be extended to solve the Cauchy problems of Helmholtz-type equation in a cylindrical domain. But it cannot be applied in more general geometries, which is a limit of the non-local boundary value problem method.
References
Cheng, H.W., Huang, J.F., Leiterman, T.J.: An adaptive fast solver for the modified Helmholtz equation in two dimensions. J. Comput. Phys. 211(2), 616–637 (2006)
Juffer, A.H., Botta, E.F.F., Van Keulen, B.A.M., Ploeg, A.V.D., Berendsen, H.J.C.: The electric potential of a macromolecule in a solvent: a fundamental approach. J. Comput. Phys. 97(4), 144–171 (1991)
Liang, J., Subramaniam, S.: Computation of molecular electrostatics with boundary element methods. Biophys. J. 73(4), 1830–1841 (1997)
Russel, W.B., Saville, D.A., Schowalter, W.R.: Colloidal Dispersions. Cambridge University Press, Cambridge (1991)
Li, X.: On solving boundary value problems of modified Helmholtz equations by plane wave functions. J. Comput. Appl. Math. 195(1), 62–82 (2006)
Yoneta, A., Tsuchimoto, M., Honma, T.: Analysis of axisymmetric modified Helmholtz equation by using boundary element method. IEEE Trans. Magn. 26(2), 1015–1018 (1990)
Lin, J., Chen, C.S., Liu, C.S.: Fast solution of three-dimensional modified Helmholtz equations by the method of fundamental solutions. Commun. Comput. Phys. 20(2), 512–533 (2016)
Lin, J., Chen, W., Sze, K.Y.: A new radial basis functions for Helmholtz problems. Eng. Anal. Bound. Elem. 36(12), 1923–1930 (2012)
Lin, J., Chen, W., Wang, F.: A new investigation into regularization techniques for the method of fundamental solutions. Math. Comput. Simul. 81(6), 1144–1152 (2011)
Goubet, O., Hamraoui, E.: Blow-up of solutions to cubic nonlinear Schrödinger equations with defect: the radial case. Adv. Nonlinear Anal. 6(2), 183–197 (2017)
Kumar, S., Kumar, D., Singh, J.: Fractional modelling arising in unidirectional propagation of long waves in dispersive media. Adv. Nonlinear Anal. 5(4), 383–394 (2016)
Hadamard, J.: Lectures on Cauchy’s Problem in Linear Partial Differential Equations. Dover Publications, New York (1953)
Tikhonov, A.N., Arsenin, V.Y.: Solutions of ill-posed problems New York (1977)
Isakov, V.: Inverse Problems for Partial Differential Equations, vol. 127. Springer, New York (1998)
Marin, L., Elliott, L., Heggs, P.J., Ingham, D.B., Lesnic, D., Wen, X.: Conjugate gradient boundary element solution to the Cauchy problem for Helmholtz-type equations. Comput. Mech. 31, 367–377 (2003)
Marin, L., Elliott, L.: BEM solution for the Cauchy problem associated with Helmholtz-type equations by the Landweber method. Eng. Anal. Bound. Elem. 28, 1025–1034 (2004)
Wen, D.W., Qin, H.H.: Tikhonov type regularization method for the Cauchy problem of the modified Helmholtz equation. Appl. Math. Comput. 203(2), 617–628 (2008)
Marin, L., Lesnic, D.: The method of fundamental solutions for the Cauchy problem associated with two-dimensional Helmholtz-type equations. Comput. Struct. 83, 267–278 (2005)
Wei, T., Hon, Y.C.: Solving Cauchy problems of elliptic by the method of fundamental solutions in boundary elements xxvii. WIT Trans. Model. Simul. 39, 57–65 (2005)
Wei, T., Hon, Y.C., Ling, L.: Method of fundamental solutions with regularization techniques for Cauchy problems of elliptic operators. Eng. Anal. Bound. Elem. 31(4), 373–385 (2007)
Qin, H.H., Wei, T.: Quasi-reversibility and truncation methods to solve a Cauchy problem for the modified Helmholtz equation. Math. Comput. Simul. 80(2), 352–366 (2009)
Hao, D.N.N., Duc, V., Sahli, D.: A non-local boundary value problem method for the Cauchy problem for elliptic equations. Inverse Probl. 25, 055002 (2009)
Denche, M., Bessila, K.: A modified quasi-boundary value method for ill-posed problems. J. Math. Anal. Appl. 301(2), 419–426 (2005)
Hao, D.N.N., Duc, V., Sahli, H.: A non-local boundary value problem method for parabolic equations backward in time. J. Math. Anal. Appl. 345(2), 805–815 (2008)
Melnikova, I.V.: Regularization of ill-posed differential problems. Sib. Mat. Zh. 33(2), 125–134 (1992)
Trong, D.D., Tuan, N.H.: A nonhomogeneous backward heat problem: regularization and error estimates. Electron. J. Differ. Equ. 2008, 33 (2008)
Showalter, R.E.: Cauchy problem for hyper-parabolic partial differential equations. In: Trends in the Theory and Practice of Non-Linear Analysis (1983)
Xiong, X.T.: A regularization method for a Cauchy problem of the Helmholtz equation. J. Comput. Appl. Math. 233(8), 1723–1732 (2010)
Acknowledgements
This work was supported by the Natural Science Foundation of China (No. 61763044) and the Natural Science Foundation of Gansu Province (No. 18JR3RA096). The authors are very grateful to the anonymous referees for their valuable suggestions.
Availability of data and materials
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
HY and QYY completed the main study together. HY wrote the manuscript, QYY checked the proofs process and verified the calculation. Moreover, all the authors read and approved the last version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
All of the authors of this article claim that together they have no competing interests.
Additional information
Abbreviations
Not applicable.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yang, H., Yang, Y. A quasi-reversibility regularization method for a Cauchy problem of the modified Helmholtz-type equation. Bound Value Probl 2019, 29 (2019). https://doi.org/10.1186/s13661-019-1142-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-019-1142-z