Suction/injection effects on an unsteady MHD Casson thin film flow with slip and uniform thickness over a stretching sheet along variable flow properties

Abstract

In this investigation the attention is given to a mathematical model of the non-Newtonian Casson liquid over an unsteady stretching sheet under the combined effects of different natural parameters with heat transfer in the presence of suction/injection phenomena. The movement of a laminar thin liquid film and associated heat transfer from a horizontal stretching surface is studied. Magnetic field is proposed perpendicular to the direction of flow, while surface tension is varied quadratically with temperature of the conducting fluid. Further, variable viscosity and thermal conductivity (linear function of temperature) of the flow are examined. The transformation allows to convert the boundary layer model to a system of nonlinear ODEs (ordinary differential equations). Analytical and numerical solutions of the resulting nonlinear ODEs are obtained by using HAM and BVP4C package. Thickness of the boundary layer is investigated by both methods for a classical selection of the unsteadiness parameter. A selection of the parameter ranges is studied for better solution of the problem. Present observation displays the joined effects of magnetic field, surface tension, suction/injection, and slippage at the boundary is to improve the thermal boundary layer thickness. Results for the heat flux (Nusselt number), skin friction coefficient, and free surface temperature are granted graphically and in a table form. Similarly, the effects of natural parameters on the velocity and temperature profiles are investigated.

1 Introduction

A large number of industrial processes, the effect of boundary layer flow with heat transfer over an unsteady stretching sheet with free surface flow have wide use in wire coating, drawing of plastic sheets, metal and polymer extrusion, foodstuff processing, daily life uses equipments, etc. Rate of heat transfer in the stretching sheet describes the good and bad quality of coating during manufacturing of the wire. Therefore, a number of experiments have been discussed under the primary effects of the boundary layer phenomena in a different frame of reference. Crane [1] started his work from the steady stretching sheet by considering Newtonian liquids under the assumption that velocity will vary in the direction of flow and that it must be linear to the distance from the specific point. Soon a researcher Winter [2] added a viscous dissipated term to the temperature equation that contributed a very important role to the energy distribution and determined the effects of energy during the heat transfer in the sheet. Meanwhile, Wang [3] took Newtonian fluid and discussed the time-dependent stretching sheet under the lead of Newtonian flow on the sheet. Navier–Stokes equations were converted to the sample equations of one independent variable called ordinary differential equations by the use of well form transformation, and solution was achieved by two methods, numerical and analytical. Similarly, Thompson and Troian [4] investigated the effects of slip velocity by assuming that slip velocity is directly dependent on the wall shear rate, i.e., slip length and shear rate (due to the diverging slip length). Dandapat et al. [5] presented the analysis of the heat transfer by considering the work of Wang [3]. Then they [6] extended his work by considering surface tension and constructed thermocapillary number in the work of Dandapat et al. [5]. They presented different physical effects on the heat transfer. The power-law model of the non-Newtonian liquid was discussed by assuming the unsteady liquid flow over a stretching sheet and a brief result on the heat transfer was presented; this was done by Chen [7]. Wang and Pop [8] took a step towards the solution of the problem presented by Chen [7] and solved it by HAM. Again Chen [9] discussed viscous dissipation effects to his work [7]. Abbas et al. [10] studied the effects of second grade liquid by introducing an unsteady stretching sheet of second grade liquid. Mahmoud and Megahed [11] developed a variation of thermal conductivity and viscosity in the thin liquid fluid over an unsteady stretching sheet in the presence of Hartmann number to the power-law liquid. Abel et al. [12] continued the concept of previous work and introduced viscous dissipation with magnetic effects to a plane stretching sheet over laminar fluid film.

Mukhopadhay et al. [13] presented a two-dimensional problem of unsteady non-Newtonian liquid over a stretching surface with defined surface temperature. They used the Casson liquid model for the observation of non-Newtonian liquid with its physical behavior, and the result was obtained by the well-known method called shooting method. Moreover, an approximate solution was obtained for the steady momentum equation. Meanwhile, Nadeem et al. [14] discussed the effects of MHD Casson liquid flow with boundary layer momentum equation attached with the exponentially admitted shrinking sheet. They used Adomian decomposition method (ADM) for the analytical solution to the ODEs, and different graphs were constructed for arbitrary parameters to the velocity profiles and their possible conclusions. Mahdy [15] presented a numerical solution for the unsteady MHD Casson liquid over the stretching sheet with the presence of slip effect at the boundary, suction/blowing, and the defined surface temperature. Different physical behaviors were discussed for the local similar result of Casson model with the admission of robust computer algebra software MATLAB. Recently, Prasad et al. [16] discussed heat transfer of a Casson liquid flow having laminar boundary layer phenomena in a horizontal cylinder with heat and hydrodynamic slip boundary, where constant temperature was considered at the surface of the cylinder. The naturally parabolic boundary layer equation was normalized with the use of non-similar form, and then they used a scheme, which is efficient, well-tested, stable, and implicit, called Keller– box finite-difference scheme. A conducted viscoplastic fluid passing from a conducted channel was discussed for the MHD flow and heat transfer to their theoretical results by Akbar et al. [17]. They proposed a robust Casson model in the presence of magnetic field applied to the flow side along viscous dissipation term. Makinde and Rundora [18] studied heat decomposition in a time-dependent mixed convection reactive Casson liquid flow in a filled perpendicular channel existing saturated suction/injection medium. Walls of the channel were also porous with injection from the right wall and suction out from the left wall. Solution was discussed by using a finite difference method, a semi-discretized method, and along with the scheme of Runge–Kutta–Fehlberg integration of fourth order. Recently, a numerical solution for the flow of unsteady Casson thin film liquid over an unsteady sheet with the presence of variation in heat flux and viscous dissipation along the slip parameter at boundary condition were discussed by Megahed [19]. Results were obtained for the heat transfer with respect to different parameters by the help of shooting method, while the results of previous papers were compared. Furthermore, the influence of MHD on fluid flow in various geometries was studied in [20,21,22]. These are very resent works in the fluid mechanics having MHD flow over thin film with heat and mass transfers.

Motivated by the given investigation, the formulation of the constructed problem is to investigate the unsteady non-Newtonian Casson liquid over a stretching sheet under the combined effects of different natural parameters with Casson boundary layer flow and heat transfer. The movement of a laminar thin liquid film and associated heat transfer from a horizontal stretching surface will be studied. Magnetic field will be normal to the flow direction and surface tension will vary quadratically with temperature of the conducting fluid for viscous incompressible free surface flow. Further, the observation of variation of thermal conductivity and viscosity of the fluid flow will be observed for their linear functions of temperatures. The transformation will allow us to convert the boundary layer model to a system of nonlinear ODEs. Solutions of the resulting nonlinear ODEs will be obtained by using HAM and shooting method. Thickness of the boundary layer is investigated by both methods for a classical selection of the unsteadiness parameter. Present observation displays the joined effects of Casson liquid, suction/injection, and slip effect at the boundary, and magnetic field is to improve the thermal boundary layer thickness. Different parameters will be discussed for their physical importance such as Nusselt number, skin friction coefficient, free surface temperature, suction/injection, Casson parameter, slip parameter, Hartmann number, thermocapillary number, and Prandtl number.

2 Problem formulation

2.1 Governing equations

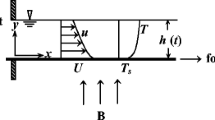
Assume that an infinite elastic flat sheet is set at $y=0$ in a Cartesian coordinate system of fixed reference frame, while the sheet is emerging from a narrow slit placed at the origin of a system. Unsteady flow of the Casson fluid is considered in two dimensions with uniform thickness denoted by h(t) over a sheet. Magnetic field expressed by $B=B_{0}/(1-\alpha t)^{1/2}$ is proposed to be normal to the direction of the stretched sheet with admission of transverse velocity. Furthermore, the sheet is stretched in the direction of horizontal axis, while thermal conductivity and viscosity are considered to be varied in the linear format of temperature. Meanwhile, the flow is considered under the suction/injection and slip effects at the boundary for the physical phenomena on heat transfer to the boundary layer model. Assume that there is no gravity, no entrance and exit effects, and thickness is uniform for the viscous incompressible free surface flow. The governing equations for MHD unsteady Casson flow of momentum with heat equation are

$$\begin{aligned}& \frac{\partial u}{\partial x}+\frac{\partial \nu }{\partial y}=0, \end{aligned}$$

(1)

$$\begin{aligned}& \begin{aligned}[b] &\rho \biggl(\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+ \nu \frac{\partial u}{\partial y} \biggr) \\ &\quad = \biggl(1+\frac{1}{\beta } \biggr) \biggl[2\frac{\partial \mu }{\partial x} \frac{\partial u}{\partial x}+2\mu \frac{\partial ^{2} u}{\partial x^{2}}+\frac{\partial \mu }{\partial y}\frac{\partial u}{\partial y}+\mu \frac{\partial ^{2} u}{\partial y^{2}}+ \frac{\partial \mu }{\partial y}\frac{\partial \nu }{\partial x}+\mu \frac{\partial ^{2} \nu }{\partial y\,\partial x} \biggr]-\hat{\sigma }B^{2}u, \end{aligned} \end{aligned}$$

(2)

$$\begin{aligned}& \begin{aligned}[b] &\rho \biggl(\frac{\partial \nu }{\partial t}+u \frac{\partial \nu }{\partial x}+\nu \frac{\partial \nu }{\partial y} \biggr) \\ &\quad = \biggl(1+\frac{1}{\beta } \biggr) \biggl[\frac{ \partial \mu }{\partial x} \frac{\partial u}{\partial y}+\mu \frac{ \partial ^{2} u}{\partial x\,\partial y}+\mu \frac{\partial ^{2} \nu }{ \partial x^{2}}+\frac{\partial \mu }{\partial x} \frac{\partial \nu }{ \partial x}+2\mu \frac{\partial ^{2} \nu }{\partial y^{2}}+2\frac{ \partial \mu }{\partial y}\frac{\partial \nu }{\partial y} \biggr], \end{aligned} \end{aligned}$$

(3)

$$\begin{aligned}& \rho C_{p} \biggl(\frac{\partial T}{\partial t}+u \frac{\partial T}{\partial x}+\nu \frac{\partial T}{\partial y} \biggr)= \biggl[\kappa \frac{\partial ^{2} T}{ \partial x^{2}}+\frac{\partial \kappa }{\partial x} \frac{\partial T}{ \partial x}+\kappa \frac{\partial ^{2} T}{\partial y^{2}}+\frac{\partial \kappa }{\partial y}\frac{\partial T}{\partial y} \biggr]. \end{aligned}$$

(4)

Deformation equation describing flow matter of the Casson fluid is defined by Mustafa et al. [23] as follows:

$$\begin{aligned} \tau _{p,q}\equiv \textstyle\begin{cases} 2(\frac{\mu _{\beta }\sqrt{\varphi }+P_{y}}{\sqrt{\varphi }}) e _{p,q}, & \varphi _{c} < \varphi, \\ 2(\frac{\mu _{\beta }\sqrt{\varphi }+P_{y}}{\sqrt{\varphi }}) e _{p,q}, & \varphi _{c} > \varphi \end{cases}\displaystyle \end{aligned}$$

the notation $\tau _{p,q}$ represents stress tensor, where $(p,q)$ refers to the component. Similarly, $e_{p,q}$ represents the deformation rate of the $(p,q)$th component, where $\varphi =e_{p,q}e_{p,q}$ denotes the square of a deformation rate, the expression $\mu _{\beta }$ is a non-Newtonian plastic dynamic viscosity of the fluid, the expression $\varphi _{c}$ is used for square of the deformation rate depending on the model of the non-Newtonian liquid, and $P_{y}$ expresses a fluid yield stress. The reason for solid structure is when shear stress is less than $P_{y}$ and the flow motion stopped; similarly, if $P_{y}$ is less than shear stress, then fluid flows and deformation starts. Equations (1)–(4) can be converted to their dimensionless form by using the following non-dimensional scalings:

$$ \begin{gathered} x=Lx^{\ast }, \qquad y=y^{\ast }\hat{ \delta }, \qquad u=Uu^{\ast }, \qquad \nu = \nu ^{\ast } \frac{U \hat{\delta }}{L}, \\ T=(T_{s}-T_{0})T^{\ast }+T _{0}, \qquad t=t^{\ast }\frac{L}{U}, \end{gathered} $$

(5)

the notations δ̂ and L are the respective non-dimensional vertical and horizontal length parameters, where the possible fraction is $\frac{\hat{\delta _{1}}}{L_{1}}\ll1$, the temperature $T_{0}$ is the temperature at the surface of the sheet, and the temperature $T_{s}$ is a temperature at the surface of the fluid. After the instalment of the above scaling in Eqs. (1)–(4), the following equations can obtained:

$$\begin{aligned}& \begin{aligned}[b] &\rho \biggl(\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+ \nu \frac{\partial u}{\partial y} \biggr) \\ &\quad = \biggl(1+\frac{1}{\beta } \biggr) \biggl[2\frac{\partial }{\partial x} \biggl( \frac{1}{R_{e}}\frac{\partial u}{\partial x} \biggr)+\frac{ \partial }{\partial y} \biggl( \biggl( \frac{L}{\hat{\delta }} \biggr)^{2}\frac{1}{R_{e}} \mu \frac{\partial u}{\partial y}+ \frac{1}{R_{e}}\frac{\partial \nu }{\partial x} \biggr)) \biggr]-\frac{L}{U}\hat{ \sigma }B^{2}u, \end{aligned} \end{aligned}$$

(6)

$$\begin{aligned}& \begin{aligned}[b] & \biggl(\frac{\hat{\delta }}{L} \biggr)^{2} \biggl( \frac{\partial \nu }{\partial t}+u \frac{ \partial \nu }{\partial x}+\nu \frac{\partial \nu }{\partial y} \biggr) \\ &\quad = \biggl(1+\frac{1}{ \beta } \biggr) \biggl[\frac{\partial }{\partial x} \biggl( \frac{1}{R_{e}}\frac{\partial u}{ \partial y}+ \biggl( \frac{\hat{\delta }}{L} \biggr)^{2}\frac{1}{R_{e}}\frac{\partial \nu }{\partial x} \biggr)+2 \frac{\partial }{\partial y} \biggl(\frac{1}{R_{e}}\frac{ \partial \nu }{\partial y} \biggr) \biggr], \end{aligned} \end{aligned}$$

(7)

$$\begin{aligned}& \rho C_{p} \biggl(\frac{\partial T}{\partial t}+u \frac{\partial T}{\partial x}+\nu \frac{\partial T}{\partial y} \biggr)=\frac{\partial }{\partial x} \biggl(\frac{1}{R _{e}} \frac{\partial T}{\partial x} \biggr)+\frac{\partial }{\partial y} \biggl( \biggl(\frac{L}{ \hat{\delta }} \biggr)^{2}\frac{1}{R_{e}}\kappa \frac{\partial T}{\partial y} \biggr). \end{aligned}$$

(8)

As L is very large and δ̂ is very small, so $\frac{L}{ \hat{\delta }}\gg1$ and $\frac{\hat{\delta }}{L}\ll1$. Similarly, $R_{e}\gg1$ and $\frac{1}{R_{e}}\ll1$. Also, $(\frac{\hat{\delta }}{L})^{2}\ll1$, so Eq. (7) vanishes, therefore this implies that

$$\begin{aligned}& \frac{\partial u}{\partial x}+\frac{\partial \nu }{\partial y}=0, \end{aligned}$$

(9)

$$\begin{aligned}& \biggl(\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+\nu \frac{ \partial u}{\partial y} \biggr)= \frac{1}{\rho } \biggl(1+\frac{1}{\beta } \biggr) \biggl[\frac{ \partial \mu }{\partial y} \frac{\partial u}{\partial y}+\mu \frac{ \partial ^{2} u}{\partial y^{2}} \biggr]-\frac{1}{\rho } \frac{L \hat{\sigma } B^{2}}{U}u, \end{aligned}$$

(10)

$$\begin{aligned}& \biggl(\frac{\partial T}{\partial t}+u \frac{\partial T}{\partial x}+\nu \frac{ \partial T}{\partial y} \biggr)= \frac{1}{\rho C_{p}} \biggl(\frac{\partial \kappa }{ \partial y}\frac{\partial T}{\partial y}+\kappa \frac{\partial ^{2} T}{ \partial y^{2}} \biggr), \end{aligned}$$

(11)

and the mentioned boundary conditions [6] imply that

$$\begin{aligned}& u=\zeta _{1} \biggl(1+\frac{1}{\beta } \biggr)\frac{\partial u}{\partial y}+U_{s}, \qquad \nu =V_{w}, \qquad T=T_{s} \quad \text{at } y=0, \end{aligned}$$

(12)

$$\begin{aligned}& \biggl(1+\frac{1}{\beta } \biggr) \mu \frac{\partial u}{\partial y}=\frac{\partial \sigma }{\partial x}, \qquad \nu =\frac{dh}{dt}, \qquad \frac{\partial T}{ \partial y}=0, \quad \text{at } y=h, \end{aligned}$$

(13)

where x, y are in the directions of u and ν, respectively, $\zeta _{1}=\zeta (1+\alpha t)^{\frac{1}{2}}\beta$ depends on time and is called velocity slip factor, where ζ denotes the initial value of the factor, Casson parameter is $\beta =\mu \sqrt{2\varphi _{c}}/P _{y}$, the velocity $V_{w}$ represents mass transfer, the notation κ represents thermal diffusivity, and μ represents viscosity. Similarly, temperature is denoted by T, $h(t)$ is the fluid thickness (uniform thickness), electrical conductivity is denoted by σ̂, t expresses time, the kinematic viscosity is υ, ρ is density, the expression $B=B_{0}/(1-\alpha t)^{1/2}$ represents magnetic field, and the surface tension is denoted by σ which quadratically depends on temperature. This implies that

$$ \sigma =\frac{\sigma _{0}}{2\upsilon _{0}} \biggl[1-\frac{h_{1}(T-T_{0})}{2} \biggr] \frac{ \delta (T_{0}-T)}{\sqrt{(1-\alpha t)}}, $$

(14)

the notations δ and $h_{1}$ are non-negative fluid constants. The surface stretching velocity is defined in [24] and mass transfer velocity as follows:

$$ U_{s}=\frac{\alpha }{2}\frac{x}{(1-\alpha t)}, \qquad V_{w}=-\frac{\alpha \beta I_{0}}{2}\sqrt{\frac{(\upsilon _{0}/b)}{(1-\alpha t)}}, $$

(15)

both α and b are constants and always positive. Further, b is a rate of initial stretch, while $b/(1-\alpha t)$ is called an effective stretching rate. For simplicity, we suppose that the surface is smooth and has no waves. In 2008, Liu and Anderson [25] considered the stretching surface velocity free of location for developing uniform film thickness as shown in (15), and this was first proposed by Dandapat [26], denoted by $h(t)$, and named unsteady film thickness. Surface temperature at the stretching sheet implies that

$$ T_{s}=T_{0}-T_{\mathrm{ref}} \frac{\alpha ^{2}}{2} \frac{x^{2}}{(1-\alpha t)}, $$

(16)

here subscript ref means reference, so the constant $T_{\mathrm{ref}}$ is a reference temperature provided that $t<1/\alpha$, where the temperature of the stretching sheet is $T_{0}$.

2.2 Similarity transformation

The following transformations will be used to transform the modeled equations from PDEs to ODEs:

$$\begin{aligned}& u=\frac{\alpha }{2}\frac{x}{(1-\alpha t)} f'(\eta ), \end{aligned}$$

(17)

$$\begin{aligned}& \nu =-\frac{\alpha }{2}\frac{\sqrt{(\upsilon _{0}/b)}}{\sqrt{(1- \alpha t)}}\beta f(\eta ), \end{aligned}$$

(18)

$$\begin{aligned}& T=T_{0}-T_{\mathrm{ref}}\frac{\alpha ^{2}}{2}\frac{x^{2}}{(1-\alpha t)}\theta ( \eta ), \end{aligned}$$

(19)

where the notion η is called similarity variable and is selected from [8] as

$$ \eta =\sqrt{\frac{b}{\upsilon _{0}}}\frac{1}{\beta \sqrt{(1-\alpha t)}} y, $$

(20)

the film thickness in a dimensionless form is β selected from [8] as

$$ \beta =\sqrt{\frac{b}{\upsilon _{0}}}\frac{h(t)}{ \sqrt{(1-\alpha t)}}. $$

(21)

The variation of viscosity μ and thermal conductivity κ are defined as follows:

$$\begin{aligned}& \mu =\mu _{0} \bigl[h_{1}(T_{0}-T)+1 \bigr] \quad \Rightarrow \quad \mu =\mu _{0}[A\theta +1], \end{aligned}$$

(22)

$$\begin{aligned}& \kappa =\kappa _{0} \biggl[N\frac{T-T_{0}}{T_{s}-T_{0}}+1 \biggr] \quad \Rightarrow \quad \kappa =\kappa _{0}[N\theta +1], \end{aligned}$$

(23)

the notations $\mu _{0}$ and $\kappa _{0}$ refer to the viscosity and thermal conductivity of the fluid at temperature $T_{0}$, respectively, where $A=(T_{0}-T_{s})h_{1}$, and the notation $N=(T_{0}-T_{s})h_{2}$ refers to the viscosity and thermal conductivity parameters, while $h_{1}$ and $h_{2}$ are liquid(fluid) constants. By the use of Eqs. (14)–(23) into Eqs. (9)–(13), we get the following nonlinear ODEs:

$$\begin{aligned}& \biggl(1+\frac{1}{\beta } \biggr) \bigl((A\theta +1)f'''+Af'' \theta ' \bigr)- \frac{\varUpsilon }{2} \bigl[S \bigl(f^{\prime 2}+ \eta f''+2f'-f f'' \bigr)+2Maf' \bigr]=0, \end{aligned}$$

(24)

$$\begin{aligned}& (N\theta +1)\theta ''+N\theta ^{\prime 2}- \frac{\varUpsilon }{2} S \mathit{Pr} \bigl[2\theta +2\theta f'+\eta \theta '-f\theta ' \bigr]=0, \end{aligned}$$

(25)

with the boundary conditions

$$\begin{aligned}& f''(1)=M\theta (1), \qquad f(1)=1, \qquad \theta '(1)=0, \end{aligned}$$

(26)

$$\begin{aligned}& f'(0)=1+\lambda \biggl(1+\frac{1}{\beta } \biggr)f''(0), \qquad f(0)=I_{0},\qquad \theta (0)=1. \end{aligned}$$

(27)

The prime notation represents derivatives with respect to the non-dimensional variable η, $I_{0}>0$ is the suction parameter, where $I_{0}<0$ is the injection parameter, unsteady parameter is $S=\frac{\alpha }{b}$, velocity slip parameter is denoted by $\lambda =\zeta (\frac{b}{\nu _{0}})^{\frac{1}{2}}$, $\mathit{Ma}=L \hat{\sigma } B_{0}^{2} /U\rho b$ is the Hartmann number, film thickness is $\varUpsilon =\beta ^{2}$, and Prandtl number is $\mathit{Pr} =\mu _{0}c_{p}/ \kappa _{0}$, but M is the thermocapillary number and it is defined as follows: $M=\frac{\delta \sigma _{0} \alpha T_{\mathrm{ref}} \beta }{\mu _{0} \sqrt{b\nu _{0}}}$.

In view of the formulation structure, some limitations of the model problem are the following: The modeled problem is invalid for the flow of gases due to η mentioned in (20), because by the use of viscosity it becomes undefined. Similarly, for $S=0$, the problem reduces from unsteady to steady state. Further, if $\mathit{Ma}=0$, then there is no magnetic force, and we get a model having no magnetic force.

The obtained Eqs. (24) and (25) are analytically calculated by applying the method of HAM (Liao [27]) with the physical boundary conditions(constrains) mentioned in Eqs. (26) and (27) and the initial guesses for the functions $\theta (\eta )$ and $f(\eta )$ are

$$\begin{aligned}& \theta _{0}(\eta )=1, \end{aligned}$$

(28)

$$\begin{aligned}& \begin{aligned}[b] f_{0}(\eta )&=\bigl(2I_{0}\beta \bigl(2+ \eta \bigl(-2I_{0}+(-3+\eta )\eta \bigr)\bigr)-12I _{0}(1+ \beta ) \bigl(-1+(1+I_{0})\eta \bigr)\lambda \\ &\quad {} +M(-1+\eta )\eta \bigl(\beta \eta +2(1+\beta ) (1+\eta )\lambda \bigr) \theta _{0}(\eta )\bigr) \\ &\quad {}/\bigl(4(\beta +3 \lambda +3\beta \lambda )\bigr), \end{aligned} \end{aligned}$$

(29)

and for Eqs. (28) and (29) the linear operators are $\pounds _{\theta }=\partial ^{2}/\partial \eta ^{2}$ and $\pounds _{f}= \partial ^{4}/\partial \eta ^{4}$, respectively, with the following equations:

the constants , , , and are used to represent constants of integral.

3 Solution approach

For solution purpose, we have the following subsections.

3.1 Skin friction coefficient and Nusselt number

The interesting physical parameters are the skin friction coefficient $C_{fx}$ and the Nusselt number $\mathrm{Nu}_{x}$ mentioned in [19]. The statements of these quantities are $C_{fx}=\frac{\tau _{w}}{\rho U^{2}/2}$, $\mathrm{Nu}_{x}=\frac{x q_{w}}{ \kappa (T_{\mathrm{ref}})}$, respectively. The notation $\tau _{w}$ represents wall surface shearing stress, and $q_{w}$ expresses the rate of heat transfer from an elastic sheet. The detailed expressions are as follows: $\tau _{w}=(1+\frac{1}{\beta })\mu (\frac{\partial u}{\partial y})_{y=0}$, $q_{w}=-\kappa (\frac{\partial T}{\partial y})_{y=0}$.

By the admission of the transformation to the above quantities, we get the following:

$$\begin{aligned}& C_{fx}\equiv \biggl(1+\frac{1}{\beta } \biggr) \frac{2^{\frac{3}{2}}(A\theta +1)}{ \beta S} f''(0) \mathit{Re}_{x}^{-1}, \end{aligned}$$

(32)

$$\begin{aligned}& \mathrm{Nu}_{x}\equiv \frac{2U_{s}\sqrt{b\nu _{0}}}{\beta }\theta '(0) \mathit{Re}_{x}, \end{aligned}$$

(33)

where $\mathit{Re}_{x} =U_{s} x/\upsilon$ is called local Reynolds number.

Figure 1

Geometry of the problem

3.2 Optimal convergence control parameters

To reduce the total average square residual error, we use a package BVPh2.0 with the help of Mathematica introduced by Zhao and Liao [28]. Before discussing physical investigation of the problem, first it is important to discuss error for the validity of the method. For this purpose, different parameters are varied and Figs. 2–6 are drawn. Similarly, Tables 1–3 are constructed to know the error and convergence for the corresponding order of approximation and auxiliary number. It is to be noted that during calculation minimum error 10⁻³⁵ is adjusted in package BVPh2.0. The basic influence of HAM package is the self-decision of the solution area with the attached rate of homotopy expansion series in the form of auxiliary parameters $\hbar _{\theta } \neq 0$ and $\hbar _{f}\neq 0$. For the optimal values of $\hbar _{ \theta }$ and $\hbar _{f}$, Liao [27] introduced the average residual error as follows:

$$\begin{aligned}& \varepsilon ^{\theta }_{\ell }=\frac{1}{n+1}\sum _{j=0}^{n} \Biggl[\aleph _{ \theta } \Biggl(\sum _{i=0}^{\ell }F(\eta ) \sum _{i=0}^{\ell }\varTheta (\eta ) \Biggr)_{ \eta =j\delta \eta } \Biggr]^{2}\,d\eta , \end{aligned}$$

(34)

$$\begin{aligned}& \varepsilon ^{f}_{\ell }=\frac{1}{n+1}\sum _{j=0}^{n} \Biggl[\aleph _{f} \Biggl(\sum _{i=0}^{\ell }F(\eta )\sum _{i=0}^{\ell }\varTheta (\eta ) \Biggr)_{\eta =j \delta \eta } \Biggr]^{2}\,d\eta , \end{aligned}$$

(35)

by Liao [27] the sum of all these are the total average residual error with $\delta \eta =0.5$, $n=20$ written as

$$ {\varepsilon ^{t}_{\ell }=\varepsilon ^{\theta }_{\ell }+\varepsilon ^{f}_{\ell }.} $$

(36)

Different values for parameter β have been selected with $\beta ^{2}=0.127013$, $I_{0}=0.0$, $A=0.3$, $S=0.4$, $\mathit{Ma}=1.0$, $N=0.2$, $M=1.0$, $\lambda =0.2$, and $\mathit{Pr} =1.0$ to discuss the error as shown in Fig. 2. Here Fig. 2 illustrates that while increasing the orders of approximation, we observe their corresponding maximum average squared residual error. When $\beta =0.2$ is selected, then Fig. 2(a) is plotted, and we observe that with the increase in the order of approximation, the corresponding averaged squared residual errors and the corresponding total averaged squared residual errors become smaller and smaller, but when we select $\beta =1.0$, then the errors are reduced as compared to the case for $\beta =0.2$, shown in Fig. 2(a) and Fig. 2(b). Further, we also discuss error for f (azimuthal velocity) and θ (temperature) for arbitrary values of β as displayed in Figs. 3–6.

Figure 2

Maximum average squared residual error at different orders of approximation, where $\lambda =0.2$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\varUpsilon =0.127013$, $\mathit{Pr} =1$, $I_{0}=0$, and $\beta =0.2$

Figure 3

Error of azimuthal velocity f at 20th-order HAM via Mathematica package BVPh2.0 approximation, where $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\varUpsilon =0.127013$, $\mathit{Pr} =1$

Figure 4

Error of $\theta (\eta )$ at 20th-order HAM via Mathematica package BVPh2.0 approximation, where $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\varUpsilon =0.127013$, $\mathit{Pr} =1$

Figure 5

Error of azimuthal velocity f at 20th-order HAM via Mathematica package BVPh2.0 approximation, where $\beta =1$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\varUpsilon =0.127013$, $\mathit{Pr} =1$

Figure 6

Error of $\theta (\eta )$ at 20th-order HAM via Mathematica package BVPh2.0 approximation, where $\beta =1$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\varUpsilon =0.127013$, $\mathit{Pr} =1$

Table 1 Optimal value of convergence control parameters versus different orders of approximation

Further, Table 1 explores different orders of approximation to the optimal values of convergence control parameters and to the total averaged squared residual error for $\lambda =0.2$, $\beta =0.20$, $I_{0}=0.0$, $N=0.20$, $A=0.30$, $\mathit{Ma}=1.0$, $S=0.40$, $\beta ^{2}=0.1270130$, $M=1.0$, and $\mathit{Pr} =1.0$. In addition, selecting the parameter values of $\lambda =0.20$, $I_{0}=0.0$, $\beta =0.20$, $N=0.20$, $A=0.30$, $\mathit{Ma}=1.0$, $S=0.40$, $\beta ^{2}=0.1270130$, $M=1.0$, $\mathit{Pr} =1.0$ and keeping different quantities of an auxiliary parameter, the corresponding separate average squared residual errors using self-determination of optimal values by using Mathematica, package BVPh2.0, are shown in Table 2. Furthermore, Table 3 represents the twenty decimal place accuracy when $\lambda =0.20$, $\beta =0.20$, $I_{0}=0.0$, $N=0.20$, $A=0.30$, $\mathit{Ma}=1.0$, $S=0.40$, $\beta ^{2}=0.1270130$, $M=1.0$, and $\mathit{Pr} =1.0$ for $f''(0)$ (local skin fraction) and $-\theta (0)$ (local Nusselt number) after fifteen orders of approximation. Hence, to obtain convergence results, the optimal HAM is an excellent choice for selecting the set of local convergence control parameters.

Table 2 Individual averaged squared residual errors using optimal values of auxiliary parameters

Table 3 Convergence of HAM on the basis of skin friction $f''(0)$ and heat flux $-\theta '(0)$ for selected values of $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\varUpsilon =0.127013$, $\mathit{Pr} =1$

3.3 Results and discussion

The modeled problem consists of a couple of ODEs shown in Eqs. (24) and (25) with the defined physically admitted boundary conditions mentioned in (26) and (27). They are solved by the well-known methods called HAM and shooting method for arbitrary values of the interesting non-dimensional parameters listed as Grashof number, unsteady parameter, skin friction, thermal conductivity parameter, heat flux, Hartmann parameter, variable viscosity parameter, film thickness, free surface temperature, suction/injection parameter, Prandtl number, Casson parameter, slip velocity parameter, and thermocapillary number.

Interesting effects of convergence control parameters $\hbar _{f}$ and $\hbar _{\theta }$ on the physical parameters $-\theta '(0)$, $\varUpsilon =\beta ^{2}$, $\theta (1)$, and $f''(0)$ are shown in Table 4 for selected values of $A=0.3$, $\mathit{Pr} =1.0$, $I_{0}=0.0$, $N=0.2$, $S=0.4$, $M=1.0$, $\mathit{Ma}=1.0$, $\beta =0.2, 1.0$ at $\lambda =0.2$ by using HAM 20th order approximation. Similarly the same case is discussed in Table 4 for the fixed quantities of all the parameters except $\lambda =0.5, 1.0$ at $\beta =0.2$. The importance of β, λ, Pr, M, Ma, and S on $-\theta '(0)$, $f''(0)$, $\beta ^{2}$, and $\theta (1)$ is illustrated in Tables 5–10. Further, for the purpose of solution, two methods, HAM and shooting method, are used to compare the results.

Table 4 Variation of $\beta =\varUpsilon ^{\frac{1}{2}}$, $f''(0)$, $\theta (1)$, and $-\theta '(0)$ using 20th-order HAM via Mathematica package BVPh2.0 approximation when $A=0.3$, $I_{0}=0$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$

Table 5 Comparison of the values of $\beta =\varUpsilon ^{\frac{1}{2}}$, $f''(0)$, $\theta (1)$, and $-\theta '(0)$ using 20th-order HAM via Mathematica package BVPh2.0 approximation and shooting method for the case $\lambda =0.2$, $I_{0}=0$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$ and several values of β

In addition to Table 5, as the Casson parameter β is increased and the film thickness $\beta ^{2}$ is reduced, i.e., by stretching the sheet, heat flux and skin friction are reduced, while free surface temperature is raised for fixed values of the remaining parameters. Similarly, by increasing the Casson parameter β and reducing the film thickness $\beta ^{2}$, 4th decimal place accuracy was noticed between both the methods, HAM and shooting method, in Table 5. In view of Table 6, by increasing the velocity slip parameter λ and reducing the thickness of the sheet $\beta ^{2}$, free surface temperature and skin friction are increased, while heat flux is decreased for fixed values of the remaining parameters and by the use of HAM. In the display of Table 7, by increasing the value of Prandtl number Pr and reducing the film thickness $\beta ^{2}$, heat flux and local skin friction are first increased and then decreased, while free surface temperature is decreased up to some extent and then increased for fixed values of the remaining parameters. In the arrangement of Table 8, by increasing the Hartmann number Ma and reducing the film thickness $\beta ^{2}$, heat flux and local skin friction are decreased, while free surface temperature is increased for fixed values of the remaining parameters. In the construction of Table 9, by increasing the thermocapillary number M and reducing the film thickness $\beta ^{2}$, heat flux and skin friction are reduced, while free surface temperature becomes increased for fixed values of the remaining parameters. In Table 10, by increasing the unsteady parameter S and reducing the film thickness $\beta ^{2}$, i.e., by stretching the sheet, heat flux and skin friction are increased up to some limit and then decreased, while free surface temperature is decreased and then increased for fixed values of the remaining parameters. In this very last Table 11, observations are done for the arbitrary choice of suction/injection parameter on the heat flux $-\theta '(0)$, free surface temperature $\theta (1)$, and skin friction $f''(0)$ while keeping fixed values for the remaining parameters. For understanding, this investigation is divided into two parts, one is named suction case and the other is named injection case. Usually, we have two types of operations on the porous medium: one is called suction and the other is called injection. For the operation at the suction side, a low pressure is exerted at the suction face called inlet, therefore fluid can easily enter the medium through inlet. Similarly, for the operation at the injection side, a high pressure is exerted at the injection face called outlet, therefore by force fluid can out to the medium through outlet. Pressure sensing device is used at the medium on the suction side for the operation of the fluid flow through media.

Table 6 Comparison of the values of $\beta =\varUpsilon ^{\frac{1}{2}}$, $f''(0)$, $\theta (1)$, and $-\theta '(0)$ using 20th-order HAM via Mathematica package BVPh2.0 approximation and shooting method for the case $\beta =0.2$, $I_{0}=0$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$ and several values of λ

Table 7 Comparison of the values of $\beta =\varUpsilon ^{\frac{1}{2}}$, $f''(0)$, $\theta (1)$, and $-\theta '(0)$ using 20th-order HAM via Mathematica package BVPh2.0 approximation and BVP4C for the case $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$ and several values of Pr

Table 8 Comparison of the values of $\beta =\varUpsilon ^{\frac{1}{2}}$, $f''(0)$, $\theta (1)$, and $-\theta '(0)$ using 20th-order HAM via Mathematica package BVPh2.0 approximation and shooting method for the case $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Pr} =1$, $M=1$ and several values of Ma

Table 9 Comparison of the values of $\beta =\varUpsilon ^{\frac{1}{2}}$, $f''(0)$, $\theta (1)$, and $-\theta '(0)$ using 20th-order HAM via Mathematica package BVPh2.0 approximation and shooting method for the case $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Pr} =1$, $\mathit{Ma}=1$ and several values of M

Table 10 Comparison of the values of $\beta =\varUpsilon ^{\frac{1}{2}}$, $f''(0)$, $\theta (1)$, and $-\theta '(0)$ using 20th-order HAM via Mathematica package BVPh2.0 approximation and shooting method for the case $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $M=1$, $\mathit{Pr} =1$, $\mathit{Ma}=1$ and several values of S

Table 11 Different values of $\beta =\varUpsilon ^{\frac{1}{2}}$, $f''(0)$, $\theta (1)$, and $-\theta '(0)$ using 20th-order HAM via Mathematica package BVPh2.0 approximation for the case $S=0.4$, $\beta =0.2$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $M=1$, $\mathit{Pr} =1$, $\mathit{Ma}=1$ and several values of $I_{0}$

Suction case $I_{0} > 0$:

Based on Table 11, by increasing the value of suction parameter $I_{0}$ and reducing the film thickness $\beta ^{2}$, heat flux and local skin friction coefficient of suction side are decreased, while free surface temperature is increased for fixed values of the remaining parameters. Physically, due to the low pressure at the inlet face, the fluid enters through medium, and due to the higher pressure at the outlet face, the fluid outs at the discharge side.

Injection case $I_{0} < 0$:

Similarly, based on Table 11, by decreasing the value of injection parameter $I_{0}$ and reducing the thickness of the sheet $\beta ^{2}$, free temperature and skin friction coefficient of suction side are increased, while heat flux is decreased for fixed values of the remaining parameters. Usually, it happens that due to the higher pressure at the injection face, the fluid is forced out through medium, and due to the lower pressure at the suction face, the fluid enters at the discharge side. Excellent agreements are observed between both the techniques, shooting method and HAM, for a variety of physical parameter values as displayed in Table 5.

The velocity and temperature profiles for hydrodynamics of the non-Newtonian MHD unsteady viscous incompressible free surface flow over a sheet with variable thermal conductivity and viscosity for the physical phenomena on heat transfer to the boundary layer model appear in Figs. 7–24 when λ, β, N, A, S, Ma, Pr, $\beta ^{2}$, M are kept varied individually. One can see the effects of β (Casson parameter) in Figs. 7 and 8 for the corresponding velocity and temperature profiles. By increasing the value of β, velocity is increased up to $\eta =0.47$ and then decreased as shown in Fig. 7. Similarly, with the increase of β, the flow temperature remains unchanged; as a result, no change in heat flux takes place for a fixed value of $N=0.2$, $A=0.3$, $I_{0}=0.0$, $\beta ^{2}=1.927011$, $\mathit{Ma}=1.0$, $S=0.4$, $\mathit{Pr} =1.0$, $M=1.0$, and $\lambda =0.2$ (see Fig. 8). In Fig. 9, the increase in λ (velocity slip parameter) leads to the decrease in velocity for a fixed value of $N=0.2$, $A=0.3$, $I_{0}=0.0$, $\beta ^{2}=1.927011$, $\mathit{Ma}=1.0$, $S=0.4$, $\mathit{Pr} =1.0$, $M=1.0$, and $\beta =0.2$. Further, in Fig. 10, the increase in λ has no effect on temperature profile for a fixed value of $N=0.2$, $A=0.3$, $I_{0}=0.0$, $\beta ^{2}=1.927011$, $\mathit{Ma}=1.0$, $S=0.4$, $\mathit{Pr} =1.0$, $M=1.0$, and $\beta =0.2$. In view of Fig. 11, as the value of A (viscosity) is increased, the corresponding flow velocity slightly rises and then decelerates; therefore, the corresponding temperature of the flow rises slightly as shown in Fig. 12 for a fixed value of $N=0.2$, $\lambda =0.2$, $I_{0}=0.0$, $\beta ^{2}=1.927011$, $\mathit{Ma}=1.0$, $S=0.4$, $\mathit{Pr} =1.0$, $M=1.0$, and $\beta =0.2$. It can be noted that during fluid flow the velocity and friction both are in opposite effects. Therefore, this leads to physical phenomena as by increasing viscosity of the fluid, the corresponding friction between the molecules is increased and it is a fact that internally the force of attraction increases, which causes resistance to the speed of the fluid molecules and as a result velocity reduces finally. A reaction heat transfer rate decreases and free temperature increases slightly, and this phenomenon is agreeable with the physical phenomena. In addition, in Figs. 13 and 14, as the value of N (thermal conductivity) is increased, the corresponding flow velocity is decreased while the corresponding temperature rises for fixed values of the remaining parameters. This leads to the fact that, with the increase of thermal conductivity, the flow speed reduces and the fluid flow temperature increases, and hence skin friction and heat flux are increased while free surface temperature is decreased. Furthermore, Figs. 15 and 16 are constructed for the variation of S (unsteady number) to the different flow properties. When S is increased, velocity profile increases while temperature decreases as displayed in Figs. 15, 16 for fixed values of the remaining parameters. The compatible physical phenomenon is as follows: increase in S leads to speeding up and cooling down of the fluid flow. As an output, the decrease of heat flux is seen in the boundary layer domain. Similarly, in Figs. 17 and 18, the increasing of $\beta ^{2}$ (film thickness) decreases velocity and increases temperature, respectively, for fixed values of the remaining parameters, and this is agreeable with the physical phenomena. Further, to check the effectiveness of M (surface tension), when we increased M, the flow velocity is decreased while temperature is slightly decreased as shown in Figs. 19 and 20, respectively, for fixed values of the remaining parameters. According to the physical phenomena, when M is increased, higher heat diffusivity is seen on the sheet, and thus the non-dimensional number $\mathrm{Nu}_{x}$ (Nusselt number) increases and flow cools down; therefore, the decrease in temperature leads to the vibrating force between the fluid molecules. According to the law of mass conservations, when force is reduced in the direction of fluid flow, then $C_{f}$ (skin friction) also reduces. For further investigation, in Figs. 21 and 22, we increase the value of Ma (Hartmann number), the corresponding velocity increases while temperature is unchanged as shown in Figs. 21 and 22, respectively, for fixed values of the remaining parameters. This physical phenomenon is due to the reason that the presence of Ma (magnetic field) leads to the Lorentz force or resistance force, and the reduction in the Lorentz force leads to low resistance to the flow molecules, which provides speed up to the fluid flow. In extension of Figs. 23 and 24, by increasing the value of Pr (Prandtl number), the flow velocity increases while temperature decreases for fixed values of the remaining parameters. It is very clear from Fig. 24 that by increasing Pr, heat flux reduces and this reduction is seen in the whole fluid region, which causes the temperature to rise and therefore flow speed increases (see Fig. 23).

Figure 7

The effect of β on velocity profile with $\lambda =0.2$, $I_{0}=0$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $\varUpsilon =1.927011$

Figure 8

The effect of β on temperature profile with $\lambda =0.2$, $I_{0}=0$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $\varUpsilon =1.927011$

Figure 9

The effect of λ on velocity profile with $\beta =0.2$, $I_{0}=0$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $\varUpsilon =1.927011$

Figure 10

The effect of λ on temperature profile with $\beta =0.2$, $I_{0}=0$, $A=0.3$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $\varUpsilon =1.927011$

Figure 11

The effect of A on velocity profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $\varUpsilon =1.927011$

Figure 12

The effect of A on temperature profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $N=0.2$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $\varUpsilon =1.927011$

Figure 13

The effect of N on velocity profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $\varUpsilon =1.927011$

Figure 14

The effect of N on temperature profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $S=0.4$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $\varUpsilon =1.927011$

Figure 15

The effect of S on velocity profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $\varUpsilon =1.927011$

Figure 16

The effect of S on temperature profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $\varUpsilon =1.927011$

Figure 17

The effect of ϒ on velocity profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $S=0.4$

Figure 18

The effect of ϒ on temperature profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $\mathit{Ma}=1$, $M=1$, $\mathit{Pr} =1$, $S=0.4$

Figure 19

The effect of M on velocity profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $\mathit{Ma}=1$, $\mathit{Pr} =1$, $S=0.4$, $\varUpsilon =1.927011$

Figure 20

The effect of M on temperature profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $\mathit{Ma}=1$, $\mathit{Pr} =1$, $S=0.4$, $\varUpsilon =1.927011$

Figure 21

The effect of Ma on velocity profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $M=1$, $\mathit{Pr} =1$, $S=0.4$, $\varUpsilon =1.927011$

Figure 22

The effect of Ma on temperature profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $M=1$, $\mathit{Pr} =1$, $S=0.4$, $\varUpsilon =1.927011$

Figure 23

The effect of Pr on velocity profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $M=1$, $\mathit{Ma}=1$, $S=0.4$, $\varUpsilon =1.927011$

Figure 24

The effect of Pr on temperature profile with $\beta =0.2$, $I_{0}=0$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $M=1$, $\mathit{Ma}=1$, $S=0.4$, $\varUpsilon =1.927011$

In addition, Figs. 25 and 26 are plotted for the observation of azimuthal velocity, velocity, and temperature profiles by varying some parameters. In Fig. 25 we vary the Casson parameter and check the effect of suction/injection($I _{0}>0$ and $I_{0}<0$) parameter on different physical properties. The increasing of β (Casson parameter) increases azimuthal velocity in the suction case. For the injection case, however, the same azimuthal velocity is decreased as shown in Fig. 25(a). It is also observed that in the injection case the azimuthal velocity is lower than that of the suction case for a fixed value of $I_{0}=0.5, -0.5$, $\lambda =0.2$, $\mathit{Ma}=1.0$, $A=0.3$, $N=0.2$, $S=0.4$, $M=1.0$, $\mathit{Pr} =1.0$, and $\beta ^{2}=0.127013$. Similarly, the increasing of β increases velocity up to $\eta =0.45$ and then decreases in the suction case, but for the injection case, the same velocity decreases up to $\eta =0.45$ and then increases as shown in Fig. 25(b). It is also observed that in the injection case the azimuthal velocity is lower than that of the suction case for a fixed value of $I_{0}=0.5, -0.5$, $\lambda =0.2$, $\mathit{Ma}=1.0$, $A=0.3$, $N=0.2$, $S=0.4$, $M=1.0$, $\mathit{Pr} =1.0$, and $\beta ^{2}=0.127013$. Furthermore, the increasing of β increases temperature in the suction case. For the injection case, however, the same temperature is decreased as shown in Fig. 25(c). It is also seen that in the injection case the temperature of liquid flow is lower than that of the suction case for a fixed value of $I_{0}=0.5, -0.5$, $\lambda =0.2$, $\mathit{Ma}=1.0$, $A=0.3$, $N=0.2$, $S=0.4$, $M=1.0$, $\mathit{Pr} =1.0$, and $\beta ^{2}=0.127013$. Now, in Fig. 26, we check the effect of $I_{0}$ for the suction and injection case. By the increase of $I_{0}$ (in both cases, suction and injection) the corresponding azimuthal velocity increases (see Fig. 26(a)). Further, by the increase of $I_{0}$ (in both cases, suction and injection) the corresponding velocity decreases (see Fig. 26(b)). Meanwhile, for both cases the increase of the porosity parameter $I_{0}$ causes the rise in temperature and the flow becomes heated, while comparatively the temperature of injection is lower than that of the suction case (see Fig. 26(c)).

Figure 25

The effect of β on azimuthal velocity, velocity, and temperature profiles with $\mathit{Pr} =1$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $M=1$, $\mathit{Ma}=1$, $S=0.4$, $\varUpsilon =0.127013$, $\mathit{Pr} =1$

Figure 26

The effect of $I_{0}$ on azimuthal velocity, velocity, and temperature profiles with $\beta =0.2$, $\mathit{Pr} =1$, $\lambda =0.2$, $A=0.3$, $N=0.2$, $M=1$, $\mathit{Ma}=1$, $S=0.4$, $\varUpsilon =0.127013$, $\mathit{Pr} =1$

Further, parameter’ ranges are picked to achieve enough error by the use of HAM method. We have chosen the lower limit and the upper limit of a parameter in such a way that the minimum error 10⁻⁶ and the maximum error 10⁻²⁵ are obtained. For this purpose, we plotted error versus various non-dimensional parameters as shown in Figs. 27(a)–27(f). Here, the domain for each sub-figure is captured from the available previous information used in this analysis. If the existing judgment leads to the engineering aim, the exact physical parameters with the required accuracy must be selected from these ranges. At the end we have given the auxiliary parameter profiles for both velocity field and temperature field to determine the region for the solution of the problem. Profile of h-curve for the case of velocity field $f''(0)$ is given by Fig. 28(a) and profile of h-curve for the case of temperature field $\theta '(0)$ is given by Fig. 28(b).

Figure 27

Error versus parameters range for velocities and temperature profiles

Figure 28

(a) h-curve for velocity field $f''(0)$ and (b) h-curve for temperature field $\theta '(0)$

4 Concluding remarks

In this manuscript, the Casson liquid is considered for the thin film flow that admitted the constitutive equations of non-Newtonian liquid with possible heat transfer over a time-dependent stretching sheet in lead of the variation of thermal conductivity and viscosity with the attachment of magnetic number. The governing nonlinear PDEs obtained from momentum and temperature equations are transformed to the system of ODEs by the use of well-defined transformations attached to the physical geometry of the model. Presentation of the non-dimensional parameters is adopted for the possible effects of different physical phenomena in the style of tables and graphs. These results are possible with the establishment of a numerical method (shooting method) and an analytical method (HAM) for their comparison. Satisfactory results are seen from both methods in the form of a table. The following conclusions have been drawn during this investigation:

• 1. As β is increased, the corresponding velocity increases and the corresponding temperature remains unchanged.

• 2. As λ is increased, the corresponding flow speed reduces but the corresponding temperature is unchanged.

• 3. The increase of A causes the flow velocity slightly rise and then decelerate; therefore, the corresponding temperature of the flow rises slightly.

• 4. When N is increased, the corresponding flow velocity decreases while the corresponding temperature rises.

• 5. Increasing of S increases the velocity profile while temperature decreases.

• 6. The increasing of $\beta ^{2}$ decreases velocity and increases temperature.

• 7. Increased M leads to decrease in flow velocity while temperature is slightly decreased.

• 8. Increased value of Ma results in the increased corresponding velocity while temperature is unchanged.

• 9. Increasing the value of Pr increases the flow velocity while decreasing the temperature.

• 10. The increase in $I_{0}$ (in both cases, suction and injection) the corresponding azimuthal velocity increases while velocity decreases and the rise of temperature is seen.