Abstract
In this study, we discuss some theorems related to the oscillatory behavior of nonlinear fractional difference equations equipped with well-known fractional Riemann–Liouville difference operator. Then we give an example for the illustration of the results obtained.
Similar content being viewed by others
1 Introduction and preliminaries
Fractional calculus has proved to be valuable tools in describing and solving a large number of problems in various fields of sciences and engineering [1, 2]. Their treatment from the viewpoint of difference equations can additionally open up new perspectives. Thus we decided to study fractional difference equations.
Up to now, many authors have investigated the oscillatory behaviors of solutions of various equations, including differential equations, fractional differential equations, difference equations, fractional difference equations, partial differential equations, fractional partial differential equations and dynamic equations on time scales [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Motivated by this work, we are concerned with the following equations:
where \(t\in \mathbf{N} _{t_{0}+1-\alpha}\), \(G ( t ) =\sum_{s=t_{0}}^{t-1+\alpha} ( t-s-1 ) ^{ ( -\alpha ) }x ( s ) \), \(q ( t ) \) and \(r ( t ) \) is positive sequences, \(f:\mathbf{R} \rightarrow \mathbf{R} \) is continuous function satisfies \(xf ( x ) >0\) for \(x\neq0\) and \(\Delta^{\alpha}\) denotes the Riemann–Liouville fractional difference operator of order \(0<\alpha\leq1\). Throughout the study, we consider
and \(\lim_{t\rightarrow\infty}R ( t ) =\infty\).
By a solution of Eq. (1), we mean a real-valued sequence \(x ( t ) \) satisfying Eq. (1) for \(t\in \mathbf{N} _{t_{0}}\). A solution \(x ( t ) \) of Eq. (1) is called oscillatory if for every positive integers \(T_{0}>t_{0}\) there exists \(t\geq T_{0}\) such that \(x ( t ) x ( t+1 ) \leq0\), otherwise it is called non-oscillatory. Equation (1) is called oscillatory if all its solutions are oscillatory.
Definition 1
([28])
Let \(v>0\). The vth fractional sum f is defined by
where f is defined for \(s\equiv a\mod ( 1 ) \), \(\Delta^{-v}f\) is defined for \(t\equiv ( a+v ) \mod ( 1 ) \) and \(t^{ ( v ) }=\frac{\varGamma ( t+1 ) }{\varGamma ( t-v+1 ) }\). The fractional sum \(\Delta ^{-v}f\) maps functions defined on \(\mathbf{N} _{a}\) to functions defined on \(\mathbf{N} _{a+v}\), where \(\mathbf{N} _{t}= \{ t,t+1,t+2,\ldots \} \).
Definition 2
([28])
Let \(v>0\) and \(m-1<\mu<m\), where m denotes a positive integer, \(m= \lceil \mu \rceil \). Set \(v=m-\mu\). The μth fractional difference is defined as
where \(\lceil \mu \rceil \) is the ceiling function of μ.
2 Main result
Lemma 1
([25])
Let \(x ( t ) \) be a solution of Eq. (1) and let
then
Theorem 1
Suppose that
and
Then every solution of (1) is oscillatory.
Proof
Suppose to the contrary that \(x(t)\) is a non-oscillatory solution of Eq. (1). Then, without loss of generality, we assume that \(x ( t ) \) is eventually positive solution of (1) on \([ t_{0},\infty ) \), then \(G ( t ) >0\) on \([ t_{0},\infty ) \). From (1), we have
That is, \(r ( t ) \Delta^{\alpha}x ( t ) \) is an eventually nonincreasing sequence on \([ t_{0},\infty ) \). We claim that \(r ( t ) \Delta^{\alpha}x ( t ) >0\) on \([ t_{1},\infty ) \), where \(t_{1}\) is sufficiently large. Otherwise, assume that there exists a \(t_{2}>t_{1}\) such that \(r ( t ) \Delta ^{\alpha}x ( t ) <0\) on \([ t_{2},\infty ) \). Then we have
or
Then we get
Summing both sides of (9) from \(t_{2}\) to \(t-1\), we have
Letting \(t\rightarrow\infty\), we get \(\lim_{t\rightarrow\infty}G ( t ) =-\infty\), which contradicts the fact that \(G ( t ) >0\) on \([ t_{0},\infty ) \). Hence we obtain \(r ( t ) \Delta^{\alpha}x ( t ) >0\) on \([ t_{1},\infty ) \). Hence we obtain \(\Delta^{\alpha}x ( t ) >0\) and \(\Delta ( r ( t ) \Delta^{\alpha}x ( t ) ) <0\) on \([ t_{1},\infty ) \). Now we consider that
Then \(k>0\) is finite or infinite.
Case 1 \(k>0\) is finite.
Since f is a continuous function, we get
This implies we have for sufficiently large \(t_{3}>t_{2}\) and \(t\geq t_{3}\)
Substituting (10) in (8), we get
or
Then summing both sides of the last inequality from \(t_{3}\) to \(t-1\), we have
Hence we obtain for \(t\geq t_{3}\)
which contradicts with (6).
Case 2 \(k=\infty\).
From the condition (7), we have
Then we can choose a positive constant c and sufficiently large \(t_{4}>t_{3}\) such that for \(t\geq t_{4}\)
This implies
Summing the last inequality from \(t_{4}\) to \(t-1\), we get
Thus
which contradicts (6). Then the proof is complete. □
Theorem 2
Assume that
Then every bounded solution of (1) is oscillatory.
Proof
Proceeding as in the proof of Theorem 1 with the assumption that \(x ( t ) \) is a bounded non-oscillatory solution of (1), from (11), we have for \(t\geq t_{0}\) where \(t_{0}\) is sufficiently large
Additionally we have
and summing both sides of the last inequality from \(t_{0}\) to \(t-1\), we get
That is,
Since \(x ( t ) \) is bounded, we can choose a positive constant c such that
which is a contradiction to the assumption of the theorem. □
Theorem 3
Assume that (6), f is non-decreasing and there is a non-negative constant M such that
and there exists a \(r_{1} ( t ) \) positive subsequence of \(r ( t ) \) such that \(r_{1} ( t ) \leq1\). Then the fractional difference \(\Delta^{\alpha}x ( t ) \) of every solution \(x ( t ) \) of (1) oscillates.
Proof
Suppose to the contrary that Eq. (1) has a solution \(x(t)\) such that its fractional difference \(\Delta^{\alpha}x ( t ) \) is non-oscillatory. Firstly we assume that \(\Delta^{\alpha}x ( t ) \) is eventually negative. Then there exists a positive integer \(t_{0}\) such that \(\Delta^{\alpha}x ( t ) <0\) and \(G ( t ) \) is decreasing on \([ t_{0},\infty ) \). This implies that \(x ( t ) \) is also non-oscillatory. Then we consider the following function for \(t\geq t_{1}\geq t_{0}\):
Thus
That is,
Summing both sides of last inequality from \(t_{1}\) to \(t-1\), we have
That is,
thus \(f ( G ( t ) ) >0\) and hence
From (17), for sufficiently large \(t_{2}>t_{1}\) and \(t\geq t_{2}\)
Then we obtain
or
Set \(\lim_{t\rightarrow\infty}G ( t ) =L\). Then \(L\geq0\). We claim that \(L=0\). If \(L>0\), then \(\lim_{t\rightarrow\infty}f ( G ( t ) ) =f ( L ) >0\) by the continuity of f. For sufficiently large \(t_{3}>t_{2}\) and \(t\geq t_{3}\) we get
Substituting the last inequality in (19), we have
in other words
Summing both sides of the last inequality from \(t_{3}\) to \(t-1\), we obtain
This implies \(\lim_{t\rightarrow\infty}G ( t ) =-\infty\), which contradicts (18). Thus \(\lim_{t\rightarrow\infty}G ( t ) =0\). By the assumption (16), we get
Then for sufficiently large \(t_{4}>t_{3}\) and \(t\geq t_{4}\) we obtain
That is,
From (19), we obtain
Then we consider subsequence \(r_{1} ( t ) \),
and we have
or
which contradicts (18). The case that \(\Delta^{\alpha}x ( t ) \) is eventually positive can be proved in a similar manner and so the proof is complete. □
3 Applications
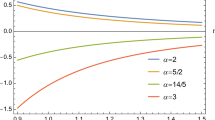
Example
Consider the following fractional difference equation:
This corresponds to Eq. (1) with \(\alpha\in ( 0,1 ] \), \(r ( t ) =t\), \(q ( t ) =t^{7}\) and \(f ( x ) =xe^{x}\). Then we have \(\lim_{t\rightarrow\infty}R ( t ) =\infty\), \(xf ( x ) >0\),
and
References
Diethelm, K.: The Analysis of Fractional Differential Equations. Springer, Berlin (2010)
Kilbas, A., Srivastava, H., Trujillo, J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Grace, S.R., Agarwal, R.P., Graef, J.R.: Oscillation criteria for certain third order nonlinear difference equations. Appl. Anal. Discrete Math. 3, 27–38 (2009)
Li, T., Baculíková, B., Džurina, J., Zhang, C.: Oscillation of fourth-order neutral differential equations with p-Laplacian like operators. Bound. Value Probl. 2014, 56 (2014)
Fišnarová, S., Mařík, R.: Oscillation criteria for neutral second-order half-linear differential equations with applications to Euler type equations. Bound. Value Probl. 2014, 83 (2014)
Szafrański, Z., Szmanda, B.: Oscillation of solutions of some nonlinear difference equations. Publ. Mat. 40, 127–133 (1996)
Selvaraj, B., Kaleeswari, S.: Oscillation of solutions of second order nonlinear difference equations. Bull. Pure Appl. Math. 32e, 83–92 (2013)
Hasil, P., Veselı, M.: Oscillation and non-oscillation criteria for linear and half-linear difference equations. J. Math. Anal. Appl. 452(1), 401–428 (2017)
Öğrekçi, S.: Interval oscillation criteria for second-order functional differential equations. SIGMA 36(2), 351–359 (2018)
Zhang, C., Agarwal, R.P., Bohner, M., Li, T.: Oscillation of fourth-order delay dynamic equations. Sci. China Math. 58(1), 143–160 (2015)
Grace, S.R., Agarwal, R.P., Sae-Jie, W.: Monotone and oscillatory behavior of certain fourth order nonlinear dynamic equations. Dyn. Syst. Appl. 19(1), 25–32 (2010)
Grace, S.R., Bohner, M., Sun, S.: Oscillation of fourth-order dynamic equations. Hacet. J. Math. Stat. 39, 545–553 (2010)
Grace, S.R., Argawal, R.P., Pinelas, S.: On the oscillation of fourth order superlinear dynamic equations on time scales. Dyn. Syst. Appl. 20, 45–54 (2011)
Öğrekçi, S.: New interval oscillation criteria for second-order functional differential equations with nonlinear damping. Open Math. 13(1), 239–246 (2015)
Sadhasivam, V., Kavitha, J., Nagajothi, N.: Oscillation of neutral fractional order partial differential equations with damping term. Int. J. Pure Appl. Math. 115(9), 47–64 (2017)
Qin, H., Zheng, B.: Oscillation of a class of fractional differential equations with damping term. Sci. World J. 2013, 685621 (2013)
Ogrekci, S.: Interval oscillation criteria for functional differential equations of fractional order. Adv. Differ. Equ. 2015, 3 (2015)
Muthulakshmi, V., Pavithra, S.: Interval oscillation criteria for forced fractional differential equations with mixed nonlinearities. Glob. J. Pure Appl. Math. 13(9), 6343–6353 (2017)
Chen, D.-X.: Oscillation criteria of fractional differential equations. Adv. Differ. Equ. 2012, 33 (2012)
Zheng, B.: Oscillation for a class of nonlinear fractional differential equations with damping term. J. Adv. Math. Stud. 6(1), 107–115 (2013)
Liu, T., Zheng, B., Meng, F.: Oscillation on a class of differential equations of fractional order. Math. Probl. Eng. 2013, Article ID 830836 (2013)
Secer, A., Adiguzel, H.: Oscillation of solutions for a class of nonlinear fractional difference equations. J. Nonlinear Sci. Appl. 9(11), 5862–5869 (2016)
Bai, Z., Xu, R.: The asymptotic behavior of solutions for a class of nonlinear fractional difference equations with damping term. Discrete Dyn. Nat. Soc. 2018, Article ID 5232147 (2018)
Chatzarakis, G.E., Gokulraj, P., Kalaimani, T., Sadhasivam, V.: Oscillatory solutions of nonlinear fractional difference equations. Int. J. Differ. Equ. 13(1), 19–31 (2018)
Sagayaraj, M.R., Selvam, A.G.M., Loganathan, M.P.: On the oscillation of nonlinear fractional difference equations. Math. Æterna 4, 220–224 (2014)
Selvam, A.G.M., Sagayaraj, M.R., Loganathan, M.P.: Oscillatory behavior of a class of fractional difference equations with damping. Int. J. Appl. Math. Res. 3(3), 220–224 (2014)
Sagayaraj, M.R., Selvam, A.G.M., Loganathan, M.P.: Oscillation criteria for a class of discrete nonlinear fractional equations. Bull. Soc. Math. Serv. Stand. 3(1), 27–35 (2014)
Atici, F.M., Eloe, P.W.: Initial value problems in discrete fractional calculus. Proc. Am. Math. Soc. 137(3), 981–989 (2008)
Acknowledgements
The author is grateful to the scholars who provided the literature sources.
Availability of data and materials
Not applicable.
Author information
Authors and Affiliations
Contributions
HA contributed to the work totally, and he read and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Adiguzel, H. Oscillation theorems for nonlinear fractional difference equations. Bound Value Probl 2018, 178 (2018). https://doi.org/10.1186/s13661-018-1098-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-018-1098-4