Abstract
In this paper, we examine thermal radiation effect of the nonlinear form on the dissipative nanofluids containing carbon nanotubes past a moving horizontal thin needle. We also perform a second law analysis with viscous dissipation. Single-wall carbon nanotube and multiple-wall carbon nanotube drop in \(H_{2}O\) base fluid. Introducing suitable dimensionless variables, we reduce the governing equations to self-similar nonlinear differential equations. Matlab in-built boundary value solver bvp4c and shooting method are applied for the solution of the reduced set of self-similar differential equations. The numerical results thus obtained are compared, which agree well with respect to desired accuracy. Various graphs are depicted and illustrate qualitatively the influence of flow controlling parameters such as Eckert number, heating parameter, radiation parameters, nanoparticles solid volume fraction, and size of thin needle on entropy generation, temperature distribution, and Bejan number.
Similar content being viewed by others
1 Introduction
The innovative idea of reducing the entropy generation in convective heat transfer phenomenon is introduced by Bejan [1]. Basically, entropy generation is a measure of molecular disorder or randomness generated in a thermodynamic system. In the light of the second law of thermodynamics, the quality of energy reduces with increasing molecular disorderness. Bejan [2] reported that heat transfer due to temperature difference and energy dissipation are the key sources of entropy generation. Later on, numerous researchers performed a second law analysis in the presence of different geometries and physical conditions. For example, Afridi et al. [3] reported entropy generation in a viscous fluid flow past over an inclined stretching sheet under the influence of Lorentz force. The analysis reveals that more entropy is generated in the presence of magnetic field due to nonconservative nature of the applied magnetic field. The impacts of variable viscosity and Newtonian heating on entropy generation are investigated by Makinde [4]. Gul et al. [5] reported the influence of mixed convection on entropy generation in the Poiselle flow of Jeffry nanofluid. Recently, Butt et al. [6] examined the entropy generation in a second-grade nanofluid with effects of porous medium. Besides all these mentioned studies, some of the recent investigations on entropy generation are reported in [7–11].
In heat transfer and entropy generation analysis, energy dissipation is very significant, especially in boundary layer flows where the velocity gradients are significantly high. Historically, for the first time, Gebhart [12] studied the viscous dissipation effects on natural convection flow of Newtonian fluid. Gebhart [12] reported a significant rise in temperature due to dissipation effect. The rise in temperature is because of the work done against the viscous forces, which irreversibly convert the kinetic energy of the fluid into internal energy. Mohamed et al. [13] examined the impact of viscous dissipation on heat transfer in mixed convection flow past over a circular cylinder. Recently, Afridi and Qasim [14] performed the irreversibility analysis in a three- dimensional flow with viscous dissipation. Saritha et al. [15] performed the heat transfer analysis of boundary layer flow of power law fluid with viscous dissipation. Mohamed et al. [16] numerically studied the effects of viscous dissipation on a flow of nanofluid over a moving flat plate. Some recent studies on the heat transfer analysis with and without viscous dissipation effects are reported in [17–27].
Boundary layer flow with heat transfer over different body shapes, such as a horizontal cylinder, stretching sheet, stretching disk, flat plate, a sphere, an elastic sheet with variable thickness, Riga plat, and stretching cylinder, is investigated by numerous researchers. Historically, Lee [28] introduced the boundary layer flow over a thin needle moving horizontally in a parallel free stream. Ishak et al. [29] extended the work of Lee [28] and performed the heat transfer analysis under constant wall temperature. They found that temperature rises with increasing size of the thin needle. Soid et al. [30] studied the flow of nanofluid over a thin needle with heat transfer effects by taking the Tiwari and Dass model. Liu and Chan [31] investigated a mixed convection flow over a thin axisymmetric body. The impacts of mass transfer and mixed convection on heat transfer and fluid flow over a thin needle are reported by Kafoussias [32]. Some very interesting studies on boundary layer flow over a thin needle with different effects and imposed boundary conditions are reported in [33–36].
Working fluids such as water, engine oil, kerosene oil, and so on have low thermal conductivity. To enhance the thermal conductivity of working fluids, different types of nanoparticles such as copper, silver, Graphene, gold, and CNTs are added in the working fluids. Historically, the term nanofluid was introduced by Choi [37], who reported that the addition of nanoparticles in base fluids enhances the thermal conductivity to great extent. For the very first time, Khan and Pop [38] reported a boundary layer flow of nanofluid. In 1991, Lijima [39] introduced carbon nanotubes. Xue [40] proposed a model for the effective thermal conductivity of CNTs suspended nanofluids. CNTs have tube-shape nanostructure and are composed of carbon allotropes. Two types of CNTs are reported in the literature [41, 42]; one is a single-walled carbon nanotube (SWCNT), and the second one is a multiple-walled carbon nanotube (MWCNT). The impacts of CNTs on boundary layer flow and heat transfer are studied in [43–45].
After a careful review of the literature, we have come to conclusion that heat transfer and entropy generation of CNTs suspended nanofluids over a thin needle in the presence of viscous dissipation and nonlinear thermal radiation is important but has never been reported. Therefore, to fill this gap, in this study, we perform heat transfer and irreversibility (second law) analysis by taking the effects of nonlinear Rosseland thermal radiation and viscous dissipation. A thin needle is supposed to be moving in a parallel free stream. We utilize Matlab bvp4c solver to obtain the numerical solutions of a reduced set of self-similar equations. Variations of temperature distribution \(\theta ( \xi ) \), entropy generation number Ns, and irreversibility ratio (Bejan number Be) with physical flow parameters are depicted graphically and discussed physically in detail.
2 Mathematical formulation
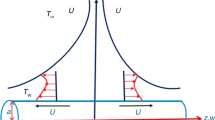
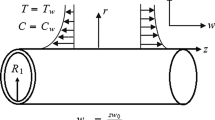
Consider the two-dimensional \(( 2D ) \) flow of water-based CNTs over a moving horizontal thin needle of thickness a. The surface of the thin needle is maintained at constant temperature \(T_{w}\). The velocities of moving thin needle and fluid outside the boundary layer are denoted by \(u_{w}\) and \(u_{\infty } \), respectively, and supposed to be constant. We also assume that the thermophysical properties of nanofluids are constant. In addition, the terms corresponding to nonlinear thermal radiation and viscous dissipation are incorporated into the energy equation. The axial coordinate x̄ of cylindrical coordinates is parallel to the moving thin needle, whereas the radial coordinate r̄ is normal to the flow direction as shown in Fig. 1.
By taking the assumptions mentioned alongside the usual boundary layer approximations, the governing flow equations can be written as
The subjected boundary conditions are
where ū and v̄ are the velocity components in increasing directions of x̄ and r̄, respectively, \(R(x)\) shows the shape of the surface of the thin needle, T̄ is the dimensional temperature of the nanofluids, \(\mu_{nf}\), \(\rho_{nf}\), \(( \rho c _{p} ) _{nf}\), and \(k_{nf}\) represent effective dynamic viscosity, the density of nanofluids, effective heat capacitance, and effective thermal conductivity of nanofluids and are defined as follows:
Introduce the variables
where ψ stands for the stream function defined so that \(\bar{u} = \frac{1}{\bar{r}}\frac{\partial \psi }{\partial \bar{r}}\) and \(\bar{v} = - \frac{1}{\bar{r}}\frac{\partial \psi }{\partial \bar{x}}\), \(g ( \xi ) \) denotes the dimensionless stream function, ξ is the similarity variable, θ represents the dimensionless temperature distribution, the subscripts nf and bf respectively denote nanofluid and base fluid, \(\bar{U} = \bar{u} _{w} + \bar{u}_{\infty } \ne 0\) indicates the composite velocity. By setting \(\xi = a\) in Eq. (8) we get \(R(\bar{x}) = ( \frac{a\nu _{bf}\bar{x}}{\bar{U}} ) \).
Equation (1) is identically satisfied by Eq. (8), whereas Eqs. (2)–(5) yield
Here ε stands for the velocity ratio parameter, Ec is the Eckert number, \(\theta_{r}\) is the heating parameter, Pr is the Prandtl number, ϕ is the solid volume fraction of nanoparticles, and \(N_{r}\) is the radiation parameter. These physical parameters are defined as
The expressions for the local skin friction coefficients \(( C _{fx} ) \) and the local Nusselt number \(( Nu_{x} ) \) are given by
where \(\operatorname{Re}_{x} = \frac{\bar{U}x}{\nu_{bf}}\) is the local Reynold number.
3 Second law analysis
The rate of entropy generation inside the 2D boundary layer flow of nanofluid in the presence of viscous dissipation and nonlinear thermal radiation is given by
Entropy generation has two sources: (i) thermal irreversibility (TI) represented by the first term of Eq. (13) and (ii) viscous irreversibility (VI) represented by the second term of Eq. (13). The characteristic entropy generation \(( \dot{S}'''_{\mathrm{Gen}} ) _{o}\) is defined as
With the help of similarity transformations and Eq. (14), the entropy generation number \(N_{s}\) takes the form
Here
The irreversibility parameter known as the Bejan number \(( Be ) \) is defined as
By Eq. (8) the Bejan number takes the following form:
4 Results and discussions
In the present work, we investigate theoretically the heat transfer and entropy generation in carbon nanotubes suspended nanofluids flow over a horizontally moving thin needle. Interesting aspects of viscous dissipation and nonlinear Rosseland thermal radiations are also incorporated in the expression for entropy generation and energy equation. The modeled equations are reduced to a system of self-similar nonlinear ordinary differential equations by utilization of conventional similarity transformations. Shooting method and bvp4c (Matlab built-in boundary value solver) are used to solve the reduced system for selected values of physical flow parameters. The numerical values of thermophysical properties of nanoparticles and base fluid used in the numerical simulation are tabulated in Table 1. Numerical values of \(g'' ( 0 ) \) and \(- \theta ' ( 0 ) \) are tabulated in Table 2. It is observed that the obtained numerical values are close to each other and hence validate our solution procedure. Table 3 shows a comparison of present results with the results in the literature and found to be in good agreement. This is a second validation test of the numerical procedure. The numerical values of skin friction coefficient against the different values of a, ϕ, and ε are tabulated in Table 4. It can be seen that the skin friction coefficient enhances with decreasing size of thin needle for both types of SWCNT and MWCNT suspended nanofluids. By increasing the solid volume fraction of nanoparticles the numerical values of the skin friction coefficient increase for both types of nanofluids. The decreasing behavior of the skin friction coefficient is observed with increasing values of the velocity ratio parameter ε. The local Nusselt number increases with decreasing size of a thin needle, increasing the velocity ratio parameter, the solid volume fraction of nanoparticles, and the heating parameter for both types of nanofluids as shown in Table 5. Further, it is observed that the Nusselt number decreases with increasing values of the Eckert number and thermal radiation parameter.
The present section is devoted to examining the variations in temperature distribution \(\theta ( \xi ) \), the entropy generation number Ns, and the Bejan number Be with embedding flow parameters. Figures 2–6 are plotted for the said purpose. Figure 2(a) is depicted to explore the influences of the Eckert number on the temperature distribution of nanofluid containing carbon nanotubes. We noticed that the temperature of both SWCNT-water nanofluid and MWCNT-water nanofluid increases with enhancing values of the Eckert number. This is because the thermal energy is stored in the fluid due to the frictional heating and consequently enhances the fluid temperature in the flow region. The analysis further reveals that the temperature profile of SWCNT-water nanofluid is high as compared to MWCNT-water nanofluid. This is in fact because of the high thermal conductivity of SWCNT. Figure 2(b) is plotted to see the impacts of the number Ec on the entropy generation number Ns. As the kinetic energy is converted into the heat energy due to viscous dissipation, which in turn increases the molecular disorder of the system, Ns increases with increasing values of the number Ec. In addition, more entropy is generated in the flow region of nanofluid containing SWCNT as compared to nanofluid containing MWCNT. The influence of the Eckert number on the Bejan number Be is displayed in Fig. 2(c). Increasing the Eckert number reduces the Bejan number, which means that the influence of fluid friction on entropy generation increases. For large values of the Eckert number, the fluid friction irreversibility is dominant over the heat transfer effects on the surface of thin needle and the region near the edge of the boundary layer. Further, it is clearly seen that frictional irreversibility is high in MWCNT suspended nanofluid as compared to SWCNT. In addition, due to highly thermal conductivity of SWCNT, the contribution of thermal effects in entropy generation is high as compared to MWCNT suspended nanofluid. Figure 3(a) shows the influence of the size of a thin needle \(( a ) \) on the temperature distribution \(\theta ( \xi ) \) of SWCNT and MWCNT suspended nanofluids. The decreasing value of a depreciates the magnitude of temperature \(\theta ( \xi ) \) and results in a thinner thermal boundary layer for both CNTs. Physically speaking, a nanofluid containing MWCNT has lower temperature as compared to a nanofluid containing SWCNT, and this is due to the low thermal conductivity of MWCNT. With the decreasing size of a thin needle, the entropy generation number Ns reduces as shown in Fig. 3(b). It is also clear from Fig. 3(b) that Ns attains its maximum value at the surface of a thin needle and goes to zero asymptotically toward the edge of the boundary layer. Further, it is noticed that, for fixed size of a thin needle, entropy generation in MWCNTs suspended nanofluid is less as compared to SWCNT suspended nanofluid. Figure 3(c) is plotted to observe the influence of the size of a thin needle on the Bejan number Be. It seems that Be reduces with decrement in the size of a thin needle. The core reason is that the thermal gradient reduces with decreasing size of a thin needle and hence reduces the Bejan number.
The variation of temperature profile \(\theta ( \xi ) \) with increment in radiation parameter \(N_{r}\) is exhibited in Fig. 4(a). We noticed that \(\theta ( \xi ) \) attains its maximum value (i.e., one) at the surface of the needle and approaches to zero asymptotically at a certain distance away from the solid boundary. The temperature of both types of nanofluid drops and thermal boundary layer gets thinner when \(N_{r}\) is increased. Figure 4(b) indicates a decrement in Ns with increasing values of \(N_{r}\). This analysis implies that to reduce Ns inside the boundary layer flow over a horizontally moving needle, the value of \(N_{r}\) should be high. Figure 4(c) shows the behavior of the Bejan number with different values of \(N_{r}\). The results indicate that the Bejan number reduces with increment in the radiation parameter \(N_{r}\) for both types of nanofluids. Thus it can be deduced that the impact of the fluid friction irreversibility increases with increasing values of \(N_{r}\). Figure 5(a) indicates the variations of the temperature distribution for different values of nanoparticles solid volume fraction ϕ. It is observed that the thermal boundary layer and temperature distribution both decrease for increasing values of ϕ. From physical point of view, by adding more nanoparticles the effective thermal conductivity of nanofluid enhances and hence rises the fluid temperature. In addition, the thermal boundary layer of the nanofluid containing SWCNT is thicker than that of the nanofluid containing MWCNT. In Figs. 5(a), (b) the entropy generation number Ns and the Bejan number Be are intended for different values of ϕ. Both Ns and Be are found to be increasing functions of ϕ. Figure 6(a) relates the temperature distribution \(\theta ( \xi ) \) to the heating parameter \(\theta_{r}\). Increase in the fluid temperature is observed with increasing heating parameter. Physically, as \(\theta_{r}\) increases, there is an increase in the operating temperature \(\bar{T}_{w} - \bar{T}_{\infty } \), and consequently the temperature increases. According to the Fig. 6(b), entropy generation increases with increasing values of \(\theta_{r}\), and this is because of increasing temperature difference between the boundary and fluid outside the boundary layer. From Fig. 6(c) it is observed that as heating parameter increases \(\theta_{r}\), the Bejan number I increases. Further, it is noticed that fluid friction irreversibility is dominant over the thermal irreversibility at the surface and away from the surface of a needle. In addition, thermal effects are prominent near the boundary due to high thermal gradients.
5 Concluding remarks
Entropy generation in CNTs (single- and multi-wall carbon nanotubes) suspended nanofluids is performed with energy dissipation and nonlinear thermal radiation effects. The main outcomes of the study are summarized as follows:
-
*
The temperature distribution enhances with increasing values of the Eckert number, heating parameter, and nanoparticle solid volume fraction for both SWCNT suspended nanofluid and MWCNT suspended nanofluid.
-
*
High temperature profile is observed for SWCNT suspended nanofluid.
-
*
Increasing values of the thermal radiation parameter and decreasing the size of a thin needle result in reducing the temperature for both SWCNT and MWCNT suspended nanofluids.
-
*
Increasing values of the heating parameter, the Eckert number and nanoparticle solid volume fraction enhances entropy generation number, but it is higher for SWCNT suspended nanofluid as compared to MWCNT suspended nanofluids.
-
*
The quality of energy increases by reducing the size of a thin needle and increasing the thermal radiation parameter.
-
*
The contribution of fluid friction in the entropy generation enhances with increasing values of the thermal radiation parameter and the Eckert number and decreasing the size of a needle.
-
*
The Bejan number increases with heating parameter and nanoparticle solid volume fraction for both SWCNT and MWCNT suspended nanofluids.
Abbreviations
- CNTs:
-
Carbon nano tubes
- SWCNTs:
-
Single-wall carbon nanotubes
- MWCNTs:
-
Multiple-wall carbon nanotubes
References
Bejan, A.: A study of entropy generation in fundamental convective heat transfer. ASME. J. Heat Transfer. 101, 718–725 (1979)
Bejan, A.: Second law analysis in heat transfer. Energy 5, 721–732 (1980)
Afridi, M.I., Qasim, M., Khan, I., Shafie, S., Alshomrani, A.S.: Entropy generation in magnetohydrodynamic mixed convection flow over an inclined stretching sheet. Entropy 19, 1–11 (2017)
Makinde, O.D.: Second law analysis for variable viscosity hydromagnetic boundary layer flow with thermal radiation and Newtonian heating. Entropy 13, 1446–1464 (2011)
Gul, A., Khan, I., Makhanov, S.S.: Entropy generation in a mixed convection Poiseuille flow of molybdenum disulphide jeffry nanofluid. Results Phys. 9, 947–954 (2018)
Butt, A.S., Ali, A., Masood, R., Hussain, Z.: Parametric study of entropy generation effects in magnetohydrodynamic radiative flow of second grade nanofluid past a linearly convective stretching surface embedded in a porous medium. J. Nanofluids 7, 1004–1023 (2018)
Afridi, M.I., Qasim, M.: Comparative study and entropy generation analysis of CU-H2O and AG-H2O nanofluids flow over a slendering stretching surface. J. Nanofluids 7, 783–790 (2018)
Das, S., Jana, R.N., Makinde, O.D.: Entropy generation in hydromagnetic and thermal boundary layer flow due to radial stretching sheet with Newtonian heating. J. Heat Mass Transf. Res. 2, 51–61 (2015)
Rashidi, M.M., Mahmud, S., Freidoonimehr, N., Rostami, B.: Analysis of entropy generation in an MHD flow over a rotating porous disk with variable physical properties. Int. J. Exergy 16, 481–503 (2015)
Rashidi, M.M., Freidoonimehr, N.: Analysis of entropy generation in MHD stagnation- point flow in porous media with heat transfer. Int. J. Comput. Methods Eng. Sci. Mech. 15, 345–355 (2014)
Afridi, M.I., Qasim, M., Makinde, O.D.: Second law analysis of boundary layer flow with variable fluid properties. ASME. J. Heat Transf. 139, 104505 (2017)
Gebhart, B.: Effect of viscous dissipation in natural convection. J. Fluid Mech. 14, 225–235 (1962)
Mohamed, M.K.A., Salleh, M.Z., Noar, N.A.Z., Ishak, A.: The viscous dissipation effects on the mixed convection boundary layer flow on a horizontal circular cylinder. J. Teknol. 78, 73–79 (2016)
Afridi, M.I., Qasim, M.: Entropy generation in three-dimensional flow of dissipative fluid. Int. J. Appl. Comput. Math. 16, 1–11 (2018)
Saritha, K., Rajasekhar, M.N., Reddy, B.S.: Radiation effects on MHD non-Newtonian power-law fluid past over a non-linearly stretching surface with viscous dissipation. Int. J. Appl. Eng. Res. 11, 2729–2736 (2016)
Mohamed, M.K.A., Noar, N.A.Z., Salleh, M.Z., Ishak, A.: Mathematical model of boundary layer flow over a moving plate in a nanofluid with viscous dissipation. J. Appl. Fluid Mech. 9, 2369–2377 (2016)
Hsiao, K.L.: Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 112, 983–990 (2017)
Marin, M., Baleanu, D.: On vibrations in thermoelasticity without energy dissipation for micropolar bodies. Bound. Value Probl. 2016, 1 (2016)
Pal, D., Mandal, G., Vajravelu, K.: Mixed convective–radiative magnetohydrodynamics heat and mass transfer of nanofluids over a stretching/shrinking sheet with viscous-ohmic dissipation and heat source/sink. J. Nanofluids 5, 340–350 (2016)
Hsiao, K.L.: Heat and mass mixed convection for MHD visco-elastic fluid past a stretching sheet with ohmic dissipation. Commun. Nonlinear Sci. Numer. Simul. 15, 1803–1812 (2010)
Ezzat, M.A., Othman, M.I.A., Helmy, K.A.: A problem of a micropolar magneto-hydrodynamic boundary layer flow. Can. J. Phys. 77, 813–882 (1999)
Lin, Y., Zheng, L., Chen, G.: Unsteady flow and heat transfer of pseudo-plastic nanoliquid in a finite thin film on a stretching surface with variable thermal conductivity and viscous dissipation. Powder Technol. 274, 324–332 (2015)
Sharma, R.P., Avinash, K., Sandeep, N., Makinde, O.D.: Thermal radiation effect on non-Newtonian fluid flow over a stretched sheet of non-uniform thickness. Defect Diffus. Forum 377, 242–259 (2017)
Krishna, P.M., Sandeep, N., Sharma, R.P., Makinde, O.D.: Thermal radiation effect on 3D slip motion of \(AlCu\)-water and Cu-water nanofluids over a variable thickness stretched surface. Defect Diffus. Forum 377, 141–154 (2017)
Makinde, O.D., Khan, W.A., Khan, Z.H.: Stagnation point flow of MHD chemically reacting nanofluid over a stretching convective surface with slip and radiative heat. J. Process Mech. Eng. 231, 695–703 (2017)
Othman, M.I.A.: Electrohydrodynamic stability in a horizontal visco-elastic fluid layer in the presence of a vertical temperature gradient. Int. J. Eng. Sci. 39, 1217–1232 (2001)
Makinde, O.D., Animasaun, I.L.: Bioconvection in MHD nanofluid flow with nonlinear thermal radiation and quartic autocatalysis chemical reaction past an upper surface of a paraboloid of revolution. Int. J. Therm. Sci. 109, 159–171 (2016)
Lee, L.L.: Boundary layer over a thin needle. Phys. Fluids 10, 820–822 (1967)
Ishak, A., Nazar, R., Pop, I.: Boundary layer flow over a continuous moving thin needle in a parallel free stream. Chin. Phys. Lett. 24, 2895–2897 (2007)
Soid, S.K., Ishak, A., Pop, I.: Boundary layer flow past a continuous moving thin needle in a nanofluid. Appl. Therm. Eng. 114, 58–64 (2017)
Liu, C.Y., Chan, W.K.: Note on mixed convection flow about slender bodies of revolution. Int. Commun. Heat Mass Transf. 15, 375–378 (1988)
Kafoussias, N.G.: Mixed free convection and mass transfer flow along a vertical needle. Int. J. Energy Res. 16, 43–49 (1992)
Narain, J.P., Uberoi, M.S.: Combined forced convection and free convection over thin needles. Int. J. Heat Mass Transf. 16, 1505–1512 (1973)
Cebeci, T., Na, T.Y.: Laminar free-convection heat transfer from a needle. Phys. Fluids 12, 463–465 (1969)
Chen, J.L.S., Smith, T.N.: Forced convection heat transfer from nonisothermal thin needles. J. Heat Transf. 100, 358–362 (1978)
Trimbitas, R., Grosan, T.: Mixed convection boundary layer flow along vertical thin needles in nanofluids. Int. J. Numer. Methods Heat Fluid Flow 24, 579–594 (2012)
Choi, S.U.S.: Enhancing thermal conductivity of fluids with nanoparticles. In: The Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, vol. 66, pp. 99–105. ASME, San Francisco (1995)
Khan, W.A., Pop, I.: Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 53, 2477–2483 (2010)
Lijima, S.: Helical microtubules of graphitic carbon. Nature 354, 56–58 (1991)
Xue, Q.: Model for thermal conductivity of carbon nanotube based composites. Physica B, Condens. Matter 368, 302–307 (2005)
Khan, W.A., Khan, Z.H., Rahi, M.: Fluid flow and heat transfer of carbon nanotubes along a flat plate with Navier slip boundary. Appl. Nanosci. 4, 633–641 (2014)
Aman, S., Khan, I., Ismail, Z., Salleh, M.Z., Al-Mdallal, Q.M.: Heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids. Sci. Rep. 7, 1–13 (2017)
Zhang, P., Hong, W., Wu, J.F., Liu, G.Z., Xiao, J., Chen, Z.B., Cheng, H.B.: Effects of surface modification on the suspension stability and thermal conductivity of carbon nanotubes nanofluids. Energy Proc. 69, 699–705 (2015)
Kandasamy, R., Muhaimin, I., Mohammad, R.: Single walled carbon nanotubes on MHD unsteady flow over a porous wedge with thermal radiation with variable stream conditions. Alex. Eng. J. 55, 275–285 (2016)
Ebaid, A., Sharif, A., Sharif, M.A.A.: Application of Laplace transform for the exact effect of a magnetic field on heat transfer of carbon nanotubes-suspended nanofluids. Z. Naturforsch. A 70, 471–475 (2015)
Acknowledgements
Not applicable.
Availability of data and materials
All data are fully available without restriction.
Authors’ information
Muhammad Idrees Afridi is a PhD scholar at COMSATS University, Islamabad, Pakistan, in the department of mathematics. Dr. Iskander Tlili is working as a researcher at University of Monastir, Monastir, Tunisia in the Energy department. Dr. Muhammad Qasim is assistant professor at COMSATS University, Islamabad, Pakistan, in the department of mathematics. Dr. Ilyas Khan is working as an assistant professor at Majmaah University, Saudi Arabia.
Funding
No funding was received.
Author information
Authors and Affiliations
Contributions
MIA and MQ formulated the problem. MIA, MQ, and IK solved the problem. MIA and IT computed the results. All the authors equally contributed in writing and proof reading of the paper. All the authors reviewed the manuscript. All authors approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Afridi, M.I., Tlili, I., Qasim, M. et al. Nonlinear Rosseland thermal radiation and energy dissipation effects on entropy generation in CNTs suspended nanofluids flow over a thin needle. Bound Value Probl 2018, 148 (2018). https://doi.org/10.1186/s13661-018-1062-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-018-1062-3