On the linear fuzzy model associated with Caputo–Fabrizio operator

Abstract

In this paper, we introduce the fuzzy Caputo–Fabrizio operator under generalized Hukuhara differentiability concept. In this setting, we study the linear fuzzy fractional initial value problems and present the general form of their solutions. Some examples are given to illustrate our results.

1 Introduction

During the last decades, the subject of fractional calculus has gained an increase of importance, mainly because it has become a powerful tool with accurate and successful results in modeling several complex phenomena in numerous seemingly diverse and widespread fields of science and engineering [14, 17, 18]. Fractional calculus is not only a productive and emerging field, it also represents a new philosophy to constructing and applying a certain type of nonlocal operators to real world problems. The ones possessing both nonlocal effects as well as uncertainty behaviors represent interesting phenomena. Researchers started to combine, in an intelligent way, the notions “fractional” and “fuzzy”, therefore a hybrid operator, called fuzzy fractional operator, emerged [1].

In one of the earliest works, Agarwal et al. [2] took the initiative and introduced fuzzy fractional calculus to handle fractional-order systems with uncertain initial values or uncertain relationships between parameters. Arshad and Lupulescu [4, 5] have deduced some existence and uniqueness results for fuzzy fractional differential equations under Riemann–Liouville derivative. In [13], the authors used Schauder fixed point theorem to study the existence of solution for fuzzy fractional differential equations.

It has been demonstrated that the fractional-order modeling is particularly useful to represent systems where the memory plays a significant role, this quality is the most significant advantage. The Riemann–Liouville definition entails physically unacceptable initial conditions; conversely, for the Caputo representation, the initial conditions are expressed in terms of integer-order derivatives having direct physical significance [1]. These definitions have the disadvantage that their kernels have singularity, therefore both definitions cannot accurately describe the full effect of the memory. Due to this inconvenience, Caputo and Fabrizio in [10] presented a new definition of fractional derivative without singular kernel, the Caputo–Fabrizio (CF) fractional derivative. This fractional operator possesses very interesting properties; for instance, this definition allows for the description of mechanical properties related with damage, fatigue, material heterogeneities, and structures at different scales [1]. Later Losada and Nieto [16] introduced the fractional integral corresponding to this new concept. They also modified the definition of Caputo and Fabrizio and proposed a new definition for fractional operator that we use in this paper. Properties and applications of this new fractional operator are reviewed in detail in [1, 6]. A model of resistance, inductance, capacitance circuit using the Caputo–Fabrizio operator with fractional order is proposed in [6]. In [11], the authors applied the Caputo–Fabrizio operator to the diffusion and the diffusion–advection equation. In [7], Baleanu et al. studied the existence of solutions for some infinite coefficient-symmetric Caputo–Fabrizio fractional integro-differential equations. A new scheme to find the fuzzy approximate solution of fractional differential equations under uncertainty with Caputo-type derivative based on the generalized Hukuhara differentiability is presented in [3]. Recently, in [20], Salahshour et al. generalized the concept of fractional derivative in the sense of Caputo–Fabrizio derivative for interval-valued function under uncertainty. They studied three real-world systems, such as the falling body problem, Basset and Decay problem, using fractional interval differential equations under Caputo–Fabrizio derivative.

In [12], the authors studied first-order linear fuzzy differential equations and presented the general form of solutions. In this paper, we introduce fuzzy Caputo–Fabrizio fractional operator under the generalized Hukuhara differentiability concept. We investigate a linear fuzzy fractional initial value problem with new Caputo–Fabrizio operator and present the form of the solution in the general case.

The paper is organized as follows. In Sect. 2, we recall some basic knowledge of fuzzy calculus and fractional calculus. In Sect. 3, we recall some results for linear fractional differential equations with Caputo–Fabrizio operator. In Sect. 4, we study a linear fuzzy model, and in Sect. 5 some examples are given.

2 Preliminaries

In this section, we give some definitions and useful results and introduce the necessary notation which will be used throughout the paper. Most of it can be found, for example, in [8].

Let X be a nonempty set. A fuzzy set u in X is characterized by its membership function $u:X\rightarrow[0,1]$, where $u(x)$ is interpreted as the degree of membership of an element x in the fuzzy set u for each $x\in X$.

Definition 2.1

A fuzzy number is a function such as $u:\mathbb{R}\longrightarrow[0,1]$ satisfying the following properties:

• (i) u is normal, that is, there exists $x_{0}\in\mathbb{R}$ such that $u(x_{0})=1$;

• (ii) u is a fuzzy convex set, i.e., $u((1-\lambda)x+\lambda y) \geq \min\{u(x),u(y)\}, \forall x,y \in\mathbb{R},\lambda \in[0,1]$;

• (iii) u is upper semi-continuous;

• (iv) $[u]^{0}=cl\{x \in\mathbb{R};u(x)> 0 \}$ is compact.

The set of all fuzzy real numbers is denoted by $\mathbb{R}_{F}$. Given a fuzzy number $u\in \mathbb {R}_{F}$ and $0< r \leq1$, we obtain the r-level set of u by $[u]^{r}= \{s\in\mathbb{R}\: |\: u(s)\geq r \}$ and the support of u as $[u]^{0}=cl\{ s\in\mathbb{R} \: | \: u(s)>0 \}$. For any $r \in[0,1]$, due to the properties imposed on the set of fuzzy numbers, we have that $[u]^{r}$ is a bounded closed interval. The notation $[u]^{r}=[\underline{u}^{r}, \overline{u}^{r}]$ denotes explicitly the r-level set of u.

For given $u,v\in \mathbb {R}_{F}$ and $\lambda\in\mathbb{R}$, we define the sum $u+ v$ and the product λu by the standard level-set operations $[u+ v]^{r}=[u]^{r} +[v]^{r}$, $[\lambda u]^{r}=\lambda[u]^{r}$, $\forall r \in[0,1]$, where $[u]^{r} +[v]^{r}$ means the usual addition of two intervals (subsets) of $\mathbb {R}$ and $\lambda[u]^{r}$ means the usual product between a scalar and a subset of $\mathbb{R}$. The metric structure is given by the Hausdorff distance $D: \mathbb {R}_{F} \times \mathbb {R}_{F} \rightarrow\mathbb{R}_{+}\cup\{0\}$,

$$D[u,v]=\sup_{r\in [0,1]}\max\bigl\{ \bigl\vert \underline{u}^{r}-\underline{v}^{r} \bigr\vert , \bigl\vert \overline {u}^{r}-\overline{v}^{r} \bigr\vert \bigr\} ,\quad u,v\in \mathbb {R}_{F} . $$

Remark 2.2

The following properties are well known [8]:

• 1. $(\mathbb {R}_{F} ,D)$ is a complete metric space.

• 2. $D[u+w,v+w]=D[u,v]$, $\forall u,v,w\in\mathbb{R}_{F}$.

• 3. $D[k u,k v]= |k| D[u,v]$, $\forall k\in\mathbb{R}$.

• 4. $D[u+v,w+e]\leq D[u,w]+D[v,e]$, $\forall u,v,w,e\in\mathbb{R}_{F}$.

For $u,v\in \mathbb {R}_{F}$, if there exists $w\in \mathbb {R}_{F}$ such that $u=v+ w$, then w is called the H-difference of $u,v$ and it is denoted by $u\ominus v$. We use this notation $u\ominus v$ to represent the H-difference of u and v, which is different, in general, from $u-v=u+(-1)v$.

Definition 2.3

([9])

Let $F:(a,b)\longrightarrow\mathbb{R}_{F}$. Fix $t_{0}\in(a,b)$. We say that F is generalized differentiable at $t_{0}$ if there exists an element $F'(t_{0})\in\mathbb{R}_{F}$ such that either

• (i) for all $h>0$ sufficiently close to 0, the H-differences $F(t_{0}+h)\ominus F(t_{0})$, $F(t_{0})\ominus F(t_{0}-h)$ exist and the limits (in the metric D)

  $$ \lim_{h\rightarrow0^{+}}\frac{F(t_{0}+h)\ominus F(t_{0})}{h}=\lim_{h\rightarrow0^{+}} \frac{F(t_{0})\ominus F(t_{0}-h)}{h}=F'(t_{0}) $$

  or

• (ii) for all $h>0$ sufficiently close to 0, the H-differences $F(t_{0})\ominus F(t_{0}+h)$, $F(t_{0}-h)\ominus F(t_{0})$ exist and the limits (in the metric D)

  $$ \lim_{h\rightarrow0^{+}}\frac{F(t_{0})\ominus F(t_{0}+h)}{-h}=\lim_{h\rightarrow0^{+}} \frac{F(t_{0}-h)\ominus F(t_{0})}{-h}=F'(t_{0}). $$

In the previous definition, case (i) corresponds to the H-derivative introduced in [19], so this differentiability concept is a generalization of the Hukuhara derivative. In [9], the authors consider four cases for derivatives. Here we only consider the two first cases of Definition 5 in [9]. In the other cases, the derivative is trivial because it is reduced to a crisp element.

Definition 2.4

Let $F : (a,b)\longrightarrow\mathbb{R}_{F}$. We say that F is $(i)$-differentiable on $(a,b)$ if F is differentiable in the sense (i) of Definition 2.3 on $(a,b)$. Similarly, we say that F is $(ii)$-differentiable on $(a,b)$ if F is differentiable in the sense (ii) of Definition 2.3 on $(a,b)$.

Theorem 2.5

([8])

Let $F : (a,b)\longrightarrow\mathbb{R}_{F}$ and put $[F(t)]^{r}=[\underline{F}(t;r),\overline{F}(t;r)]$ for each $r\in[0,1]$.

• (i) If F is $(i)$-differentiable, then $\underline{F}$ and F̅ are differentiable functions and $[F'(t)]^{r}=[\underline {F}'(t;r),\overline{F}'(t;r)]$.

• (ii) If F is $(ii)$-differentiable, then $\underline{F}$ and F̅ are differentiable functions and $[F'(t)]^{r}=[\overline{F}'(t;r),\underline{F}'(t;r)]$.

Let $T\subset\mathbb{R}$ be an interval. We denote by $C(T,\mathbb{R}_{F})$ the space of all continuous fuzzy functions on T. Also, we denote by $L^{1}(T,\mathbb{R}_{F})$ the space of all fuzzy functions $f:T\longrightarrow\mathbb{R}_{F}$ which are Lebesgue integrable on the bounded interval T of $\mathbb{R}$.

Definition 2.6

([4])

If $F :[a,b]\longrightarrow\mathbb{R}_{F}$ is Riemann integrable on $[a,b]$, then the parametric representation of its integral is given by

$$ \int_{a}^{b}F(t;r)\,dt= \biggl( \int_{a}^{b}\underline{F}(t;r)\,dt, \int _{a}^{b}\overline{F}(t;r)\,dt \biggr),\quad r \in[0,1]. $$

Definition 2.7

([15])

Given $b>0, f\in H^{1}(0,b)$, and $0<\alpha<1$, the Caputo fractional derivative of f of order α is given by

$$ {}^{C}D^{\alpha}f(t)=\frac{1}{\Gamma(1-\alpha)} \int_{0}^{t}(t-s)^{-\alpha }f'(s) \,ds,\quad t\geq0. $$

By changing the kernel $(t-s)^{-\alpha}$ by the function $\exp (-\frac{\alpha}{1-\alpha}(t-s) )$ and $\frac{1}{\Gamma(1-\alpha)}$ by $\frac{1}{\sqrt{2\pi(1-\alpha^{2})}}$, one obtains the new Caputo–Fabrizio operator of order $0<\alpha<1$, which has been recently introduced by Caputo and Fabrizio in [10] as

$$ ^{CF}D^{\alpha}f(t)=\frac{(2-\alpha)M(\alpha)}{2(1-\alpha)} \int_{0}^{t}\exp \biggl(-\frac{\alpha}{1-\alpha}(t-s) \biggr)f'(s)\,ds,\quad t\geq0, $$

where $M(\alpha)$ is a normalization constant depending on α.

According to the new definition, it is clear that if f is a constant function, then $D^{\alpha}f=0$ as in the usual Caputo derivative. The main difference between the old and the new definition is that, contrary to the old definition, the new kernel has no singularity for $t=s$.

In [16], the authors have introduced the new associated fractional integral and then they obtained that $M(\alpha)=\frac{2}{2-\alpha}$, so they proposed a new definition as follows.

Definition 2.8

[16] Let $0<\alpha<1$. The fractional Caputo–Fabrizio operator of order α of a function f is given by

$$ D^{\alpha}f(t)=\frac{1}{(1-\alpha)} \int_{0}^{t}\exp \biggl(-\frac{\alpha }{1-\alpha}(t-s) \biggr)f'(s)\,ds,\quad t\geq0. $$

In the following, we introduce the definition of Caputo–Fabrizio operator for fuzzy number valued functions.

Definition 2.9

Let $f:[0,a]\longrightarrow\mathbb{R}_{F}$ be generalized differentiable with $f'\in C ((0,a],\mathbb{R}_{F} )\cap L^{1} ((0,a),\mathbb{R}_{F} )$. The generalized fuzzy Caputo–Fabrizio operator of the fuzzy-valued function f is defined as

$$ \bigl(D^{\alpha}f\bigr) (t)=\frac{1}{(1-\alpha)} \int_{0}^{t}\exp \biggl(-\frac{\alpha }{1-\alpha}(t-s) \biggr)f'(s)\,ds,\quad t\geq0, $$

(1)

where $0<\alpha<1$.

Definition 2.10

Let $f:[0,a]\longrightarrow\mathbb{R}_{F}$ be generalized differentiable with $f'\in$ $C ((0,a],\mathbb{R}_{F} )\cap L^{1} ((0,a),\mathbb{R}_{F} )$. We say that f is $(i,\alpha)$-differentiable if $(D^{\alpha}f )(t;r)= [ (D^{\alpha}\underline{f} )(t;r), (D^{\alpha}\overline{f} )(t;r) ]$ and is $(ii,\alpha)$-differentiable if $(D^{\alpha}f )(t;r)= [ (D^{\alpha}\overline{f} )(t;r), (D^{\alpha}\underline{f} )(t;r) ]$.

Theorem 2.11

Let $f:[0,a]\longrightarrow\mathbb{R}_{F}$ be generalized differentiable at $t_{0}$ with $f'\in C ((0,a], \mathbb{R}_{F} )\cap L^{1} ((0,a),\mathbb{R}_{F} )$. Then:

• (i) f is $(i)$-differentiable at $t_{0}$ iff f is $(i,\alpha)$-differentiable at $t_{0}$.

• (ii) f is $(ii)$-differentiable at $t_{0}$ iff f is $(ii,\alpha)$-differentiable at $t_{0}$.

Proof

Using Theorem 2.5 and Definitions 2.6, 2.9, and 2.10, the proof is straightforward. □

3 Linear fractional differential equation

Losada and Nieto in [16] studied the initial value problem

$$ \textstyle\begin{cases} D^{\alpha}f(t)=\sigma(t),\quad t\geq0, \\ f(0)=f_{0}\in\mathbb{R}, \end{cases} $$

(2)

using the Caputo–Fabrizio operator. The authors in [16] applied the Laplace transform to both sides of (2) to obtain the solution. In this paper, we suppose that the appropriate conditions for applying the Laplace transform hold. For example, in (2), this is possible if $f\in H^{1} (0,\infty), f\in C([0,\infty)), \sigma \in C([0,\infty))$ and $^{CF}D^{\alpha}f, \sigma$ are functions of exponential order. We recall the following result from [16].

Theorem 3.1

Let $0<\alpha<1$. Then the unique solution of the initial value problem (2) is given by

$$ f(t)=f_{0}+(1-\alpha) \bigl(\sigma(t)-\sigma(0)\bigr)+\alpha I^{1}\sigma(t),\quad t\geq0, $$

where $I^{1}\sigma(t)=\int_{0}^{t} \sigma(s) \,ds$.

Now, we consider the following linear fractional differential equation:

$$ D^{\alpha}_{*} f(t)=\lambda f(t)+u(t),\quad f(0)=f_{0}, t\geq0, $$

(3)

where $\lambda,f_{0}\in\mathbb{R}$ and u is differentiable for all $t\geq0$. From Theorem 3.1, we have [16]

$$ f(t)=f_{0}+(1-\alpha) \bigl[\lambda\bigl(f(t)-f(0) \bigr)+u(t)-u(0) \bigr]+\alpha \int_{0}^{t}[\lambda f+u](s)\,ds,\quad t\geq0. $$

(4)

So

$$ (1-p)f(t)-q I^{1}f(t)=(1-p)f_{0}+(1-\alpha) \bigl(u(t)-u(0) \bigr)+\alpha I^{1}u(t),\quad t\geq0, $$

(5)

where $p=\lambda(1-\alpha)$ and $q= \lambda\alpha$.

If $p=1$, then we have

$$ -q I^{1}f(t)=(1-\alpha) \bigl(u(t)-u(0) \bigr)+\alpha I^{1}u(t),\quad t\geq0, $$

so

$$ f(t)=\frac{1-\alpha}{-q}u'(t)-\frac{\alpha}{q}u(t),\quad t>0 . $$

(6)

If $p\neq1$, then we have

$$ f(t)-\frac{q}{1-p}I^{1}f(t)=\tilde{\sigma}(t), \quad t\geq0, $$

(7)

where

$$ \tilde{\sigma}(t)=f_{0}+\frac{1-\alpha}{1-p} \bigl(u(t)-u(0) \bigr)+ \frac{\alpha}{1-p}I^{1}u(t),\quad t\geq0. $$

The case $\lambda=0$ is trivial, since in this case $p=q=0$ and, from (7), we obtain

$$ f(t)=\tilde{\sigma}(t), $$

(8)

which coincides with the expression in Theorem 3.1 taking $\sigma=u$.

If $\lambda\neq0$, we have

$$ f(t)-\tilde{\lambda}I^{1}f(t)=\tilde{\sigma}(t), \quad t\geq0, $$

where $\tilde{\lambda}=\frac{q}{1-p}$, hence

$$ f'(t)=\tilde{\lambda}f(t)+\tilde{\sigma}'(t),\quad t \geq0. $$

Thus, we have obtained an ordinary differential equation, which has a unique solution if we consider an initial condition [16].

4 Linear fuzzy model with Caputo–Fabrizio operator

In this section, we consider the fuzzy initial value problem

$$ \textstyle\begin{cases} D^{\alpha}f(t)=\lambda f(t)+u(t),\\ f(0)=f_{0}, \end{cases} $$

(9)

where $f,u:I \rightarrow \mathbb {R}_{F}$ are continuous fuzzy functions, u is generalized differentiable on I, $f_{0} \in \mathbb {R}_{F}$ and $\lambda\in \mathbb{R}$, and in such a way that functions $\underline {f},\overline{f},\underline{u},\overline{u},D^{\alpha}\underline {f},D^{\alpha}\overline{f}$ have Laplace transform. For the rest of the paper, the interval I may be $[0,A]$ for some $A>0$ or $I=[0,\infty)$. Our approach is based on the integral form of solution (4) which is a convex combination of the right-hand side function $\lambda f(t)+u(t)$ and one of its primitives. We suppose that the solution of (9) is generalized differentiable, and then we transfer fuzzy initial value problem (9) to a system of classical initial value problems. Then using Theorem 2.11 and (4), we obtain the $(i,\alpha)$-differentiable and $(ii,\alpha)$-differentiable solutions to (9).

We study the existence of $(i,\alpha)$- and $(ii,\alpha)$-solutions to problem (9) by distinguishing three cases $\lambda>0$, $\lambda<0$, and $\lambda= 0$.

Case I. Let $\lambda>0$. Suppose that $f(t)$ is $(i,\alpha)$-differentiable. Then (9) is equivalent to

$$ \bigl(D^{\alpha}\underline{f}(t),D^{\alpha}\overline{f}(t) \bigr)= \bigl(\lambda\underline{f}(t)+\underline {u}(t),\lambda\overline{f}(t)+ \overline{u}(t) \bigr). $$

So, we have

$$ \textstyle\begin{cases} D^{\alpha}\underline{f}(t)=\lambda\underline{f}(t)+\underline{u}(t),\qquad \underline{f}(0)=\underline{f_{0}},\\ D^{\alpha}\overline{f}(t)=\lambda\overline{f}(t)+\overline {u}(t),\qquad \overline{f}(0)=\overline{f_{0}}. \end{cases} $$

Then, by equation (5), we have

$$ \textstyle\begin{cases} (1-p)\underline{f}(t)-q I^{1}\underline{f}(t)=(1-p)\underline{f_{0}}+(1-\alpha) (\underline {u}(t)-\underline{u}(0) )+\alpha I^{1}\underline{u}(t), \\ (1-p)\overline{f}(t)-q I^{1}\overline{f}(t)=(1-p)\overline{f_{0}}+(1-\alpha) (\overline {u}(t)-\overline{u}(0) )+\alpha I^{1}\overline{u}(t), \end{cases} $$

(10)

where $p=\lambda(1-\alpha)$ and $q=\lambda\alpha$.

If $p=1$, then, by differentiating both sides of (10), we have

$$ \underline{f}(t)=\frac{1-\alpha}{-q}\underline{u}'(t)- \frac{\alpha }{q}\underline{u}(t), $$

and similarly

$$ \overline{f}(t)=\frac{1-\alpha}{-q}\overline{u}'(t)- \frac{\alpha }{q}\overline{u}(t). $$

Then we obtain

$$ \bigl[\underline{f}(t),\overline{f}(t) \bigr]=\frac{1-\alpha }{-q} \bigl[ \overline{u}'(t),\underline{u}'(t) \bigr]\ominus \frac {\alpha}{q} \bigl[\underline{u}(t),\overline{u}(t) \bigr], $$

provided the level sets define a valid fuzzy function. So, if $u(t)$ is $(i)$-differentiable, then we do not find any fuzzy solution $f(t)$, unless $u(t)$ is a crisp function on I. In case that $u(t)$ is $(ii)$-differentiable, then $[u'(t)]= [\overline{u}'(t),\underline {u}'(t) ]$ and we have the solution as follows:

$$f(t)=\frac{1-\alpha}{-q}u'(t)\ominus\frac{\alpha}{q}u(t),\quad f(0)=f_{0}, $$

provided that the H-difference exists.

Remark 4.1

It is easy to see that if $\operatorname{diam}(u'(t))\geq\frac {\alpha}{1-\alpha}\operatorname{diam}(u(t))$, then $\underline {f}(t)\leq\overline{f}(t)$, $\forall t\geq0$. Indeed, in this case, $\operatorname{diam}(u'(t))=\underline{u}'(t)-\overline{u}'(t)$, so that we have $\overline{f}(t)- \underline{f}(t)=\frac{1-\alpha}{q}\operatorname {diam}(u'(t))-\frac{\alpha}{q}\operatorname{diam}(u(t))\geq0$.

If $p<1$, then using (7), we obtain

$$ \underline{f}(t)-\frac{q}{1-p}I^{1} \underline{f}(t)=\underline {f}(0)+\frac{1-\alpha}{1-p} \bigl(\underline{u}(t)- \underline {u}(0) \bigr)+\frac{\alpha}{1-p}I^{1}\underline{u}(t). $$

(11)

If we put $\tilde{\lambda}=\frac{q}{1-p}$, then

$$ \underline{f}(t)-\tilde{\lambda}I^{1}\underline{f}(t)= \underline {f}(0)+\frac{(1-\alpha)\tilde{\lambda}}{q} \bigl(\underline {u}(t)-\underline{u}(0) \bigr)+\frac{\tilde{\lambda}\alpha }{q}I^{1}\underline{u}(t). $$

(12)

By differentiating both sides of (12), we obtain

$$ \underline{f}'(t)-\tilde{\lambda}\underline{f}(t)= \frac{(1-\alpha )\tilde{\lambda}}{q}\underline{u}'(t)+\frac{\tilde{\lambda}\alpha }{q} \underline{u}(t). $$

(13)

So, considering $\underline{f}(0)=\underline{f_{0}}$, we have

$$\begin{aligned} \underline{f}(t) =&e^{\tilde{\lambda}t} \biggl[ \int_{0}^{t} e^{-\tilde {\lambda}s} \biggl[ \frac{(1-\alpha)\tilde{\lambda}}{q}\underline {u}'(s)+\frac{\tilde{\lambda}\alpha}{q} \underline{u}(s) \biggr]\,ds+\underline{f_{0}} \biggr] \\ =&e^{\tilde{\lambda}t} \biggl[\frac{(1-\alpha)\tilde{\lambda }}{q} \int_{0}^{t} e^{-\tilde{\lambda}s}\underline{u}'(s) \,ds+\frac {\tilde{\lambda}\alpha}{q} \int_{0}^{t} e^{-\tilde{\lambda }s}\underline{u}(s)\,ds+ \underline{f_{0}} \biggr] \\ =&\frac{(1-\alpha)\tilde{\lambda}}{q} \bigl(\underline {u}(t)-e^{\tilde{\lambda}t}\underline{u}(0) \bigr)+e^{\tilde {\lambda}t}\frac{(1-\alpha)\tilde{\lambda}^{2}+\alpha\tilde {\lambda}}{q} \int_{0}^{t} e^{-\tilde{\lambda}s}\underline {u}(s)\,ds+ \underline{f_{0}}e^{\tilde{\lambda}t}. \end{aligned}$$

Therefore,

$$ \underline{f}(t)=\frac{(1-\alpha)\tilde{\lambda}}{q} \bigl(\underline{u}(t)-e^{\tilde{\lambda}t} \underline{u}(0) \bigr)+e^{\tilde{\lambda}t}\frac{\tilde{\lambda}^{2}\alpha}{q^{2}} \int _{0}^{t}e^{-\tilde{\lambda}s}\underline{u}(s)\,ds+ \underline {f_{0}}e^{\tilde{\lambda}t}, $$

and similarly

$$ \overline{f}(t)=\frac{(1-\alpha)\tilde{\lambda}}{q} \bigl(\overline{u}(t)-e^{\tilde{\lambda}t} \overline{u}(0) \bigr)+e^{\tilde{\lambda}t}\frac{\tilde{\lambda}^{2}\alpha}{q^{2}} \int _{0}^{t}e^{-\tilde{\lambda}s}\overline{u}(s)\,ds+ \overline{f_{0}}e^{\tilde {\lambda}t}. $$

Since $p<1$ and $\tilde{\lambda}>0$, then the solution is

$$ f(t)=\frac{(1-\alpha)\tilde{\lambda}}{q} \bigl(u(t)\ominus e^{\tilde{\lambda}t}u(0) \bigr)+e^{\tilde{\lambda}t}\frac{\tilde {\lambda}^{2}\alpha}{q^{2}} \int_{0}^{t}e^{-\tilde{\lambda }s}u(s)\,ds+f_{0}e^{\tilde{\lambda}t}, $$

provided that the H-difference exists.

On the other hand, if we consider $p>1$, since $\tilde{\lambda}<0$, similarly to the case $p<1$, we obtain

$$ f(t)=-\frac{(1-\alpha)\tilde{\lambda}}{q} \bigl(e^{\tilde{\lambda }t}u(0)\ominus u(t) \bigr)+e^{\tilde{\lambda}t}\frac{\tilde{\lambda}^{2}\alpha }{q^{2}} \int_{0}^{t}e^{-\tilde{\lambda}s}u(s)\,ds+f_{0}e^{\tilde{\lambda}t}, $$

provided that the H-difference exists. Thus, we have proved the following result.

Theorem 4.2

Let $0<\alpha<1$. For $\lambda>0$, the $(i,\alpha)$-solution to problem (9) is calculated as follows:

• (i) If $p=1$ and $u(t)$ is $(ii)$-differentiable, then $f(t)=\frac{1-\alpha}{-q}u'(t)\ominus\frac{\alpha}{q}u(t)$, $f(0)=f_{0}$.

• (ii) If $p<1$, then $f(t)=\frac{(1-\alpha)\tilde{\lambda}}{q} (u(t)\ominus e^{\tilde{\lambda}t}u(0) )+e^{\tilde{\lambda}t}\frac{\tilde {\lambda}^{2}\alpha}{q^{2}}\int_{0}^{t}e^{-\tilde{\lambda }s}u(s)\,ds+f_{0}e^{\tilde{\lambda}t}$, provided that the H-difference exists.

• (iii) If $p>1$, then $f(t)=-\frac{(1-\alpha)\tilde{\lambda}}{q} (e^{\tilde{\lambda }t}u(0)\ominus u(t) )+e^{\tilde{\lambda}t}\frac{\tilde{\lambda }^{2}\alpha}{q^{2}}\int_{0}^{t}e^{-\tilde{\lambda}s}u(s)\,ds+f_{0}e^{\tilde {\lambda}t}$, provided that H-differences exist.

Now, suppose that $f(t)$ is $(ii,\alpha)$-differentiable. Then (9) is equivalent to

$$ \bigl(D^{\alpha}\overline{f}(t),D^{\alpha}\underline{f}(t) \bigr)= \bigl(\lambda\underline{f}(t)+\underline {u}(t),\lambda \overline{f}(t)+\overline{u}(t) \bigr). $$

(14)

So, we have

$$ \textstyle\begin{cases} D^{\alpha}\underline{f}(t)=\lambda\overline{f}(t)+\overline{u}(t),\qquad \underline{f}(0)=\underline{f_{0}} ,\\ D^{\alpha}\overline{f}(t)=\lambda\underline{f}(t)+\underline{u}(t),\qquad \overline{f}(0)=\overline{f_{0}}. \end{cases} $$

From Theorem 3.1, we have

$$ \textstyle\begin{cases} \underline{f}(t)=\underline{f}(0)+(1-\alpha) (\lambda\overline {f}(t)+\overline{u}(t)-\lambda\overline{f}(0)-\overline{u}(0) )+\alpha I^{1}(\lambda\overline{f}+\overline{u})(t),\\ \overline{f}(t)=\overline{f}(0)+(1-\alpha) (\lambda\underline {f}(t)+\underline{u}(t)-\lambda\underline{f}(0)-\underline {u}(0) )+\alpha I^{1}(\lambda\underline{f}+\underline{u})(t). \end{cases} $$

By hypothesis, since u is generalized differentiable on I, then $\underline{u}(t)$ and $\overline{u}(t)$ are differentiable on I. So differentiating both sides of the last equations, we obtain the systems of ordinary differential equations

$$ \textstyle\begin{cases} \underline{f}'(t)-p\overline{f}'(t)=(1-\alpha)\overline {u}'(t)+q\overline{f}(t)+\alpha\overline{u}(t),\\ \overline{f}'(t)-p\underline{f}'(t)=(1-\alpha)\underline {u}'(t)+q\underline{f}(t)+\alpha\underline{u}(t). \end{cases} $$

Then, by solving this system for $p\neq1$, it is easy to see that

$$ \textstyle\begin{cases} \underline{f}'(t)=\frac{pq}{1-p^{2}}\underline{f}(t)+\frac {q}{1-p^{2}}\overline{f}(t)+\frac{\alpha p^{2}}{q(1-p^{2})}\underline {u}'(t)+\frac{\alpha p}{1-p^{2}}\underline{u}(t) +\frac{\alpha p}{q(1-p^{2})}\overline{u}'(t)+\frac{\alpha }{1-p^{2}}\overline{u}(t),\\ \overline{f}'(t)=\frac{pq}{1-p^{2}}\overline{f}(t)+\frac {q}{1-p^{2}}\underline{f}(t)+\frac{\alpha p^{2}}{q(1-p^{2})}\overline {u}'(t)+\frac{\alpha p}{1-p^{2}}\overline{u}(t) +\frac{\alpha p}{q(1-p^{2})}\underline{u}'(t)+\frac{\alpha }{1-p^{2}}\underline{u}(t). \end{cases} $$

So,

$$ \begin{pmatrix} \underline{f}'(t) \\ \overline{f}'(t) \end{pmatrix} =m \begin{pmatrix} p & 1 \\ 1 & p \end{pmatrix} \begin{pmatrix} \underline{f}(t) \\ \overline{f}(t) \end{pmatrix} +\frac{m \alpha}{q} \begin{pmatrix} \frac{ p^{2}}{q}\underline{u}'(t)+p\underline{u}(t)+\frac {p}{q}\overline{u}'(t)+\overline{u}(t)\\ \frac{p^{2}}{q}\overline{u}'(t)+ p \overline{u}(t)+\frac {p}{q}\underline{u}'(t)+\underline{u}(t) \end{pmatrix} , $$

where $m=\frac{q}{1-p^{2}}$.

By the variation of constants formula for ordinary differential equations, we have

$$\begin{aligned} \begin{pmatrix} \underline{f}(t) \\ \overline{f}(t) \end{pmatrix} =& e^{pmt} \begin{pmatrix} \cosh(mt) & \sinh(mt) \\ \sinh(mt) & \cosh(mt) \end{pmatrix} \\ &{}\times \left \{ \begin{pmatrix} \underline{f}(0) \\ \overline{f}(0) \end{pmatrix} + \int_{0}^{t} e^{-pms} \begin{pmatrix} \cosh(ms) & -\sinh(ms) \\ -\sinh(ms) & \cosh(ms) \end{pmatrix} \begin{pmatrix} \underline{b}(s) \\ \overline{b}(s) \end{pmatrix} \,ds \right \}, \end{aligned}$$

where

$$ \underline{b}(t)=\frac{m \alpha}{q} \biggl( \frac{p^{2}}{q} \underline {u}'(t)+p \underline{u}(t)+\frac{p}{q} \overline{u}'(t)+\overline {u}(t) \biggr) $$

(15)

and

$$ \overline{b}(t)=\frac{m \alpha}{q} \biggl(\frac{ p^{2}}{q} \overline {u}'(t)+ p\overline{u}(t)+\frac{p}{q} \underline{u}'(t)+\underline {u}(t) \biggr). $$

(16)

Then we have

$$\begin{aligned} \begin{pmatrix} \underline{f}(t) \\ \overline{f}(t) \end{pmatrix} =& e^{pmt} \begin{pmatrix} \cosh(mt) & \sinh(mt) \\ \sinh(mt) & \cosh(mt) \end{pmatrix} \\ &{}\times \begin{pmatrix} \underline{f}(0)+\int_{0}^{t}e^{-pms}[\underline{b}(s)\cosh (ms)-\overline{b}(s)\sinh(ms)]\,ds\\ \overline{f}(0)+\int_{0}^{t}e^{-pms}[-\underline{b}(s)\sinh (ms)+\overline{b}(s)\cosh(ms)]\,ds \end{pmatrix} . \end{aligned}$$

So that

$$\begin{aligned} \underline{f}(t) =&e^{pmt}\cosh(mt) \biggl(\underline{f}(0)+ \int _{0}^{t}e^{-pms}\bigl[\underline{b}(s) \cosh(ms)-\overline{b}(s)\sinh (ms)\bigr]\,ds \biggr) \\ &{}+e^{pmt}\sinh(mt) \biggl(\overline{f}(0)+ \int_{0}^{t}e^{-pms}\bigl[\overline {b}(s) \cosh(ms)-\underline{b}(s)\sinh(ms)\bigr]\,ds \biggr) \end{aligned}$$

and

$$\begin{aligned} \overline{f}(t) =&e^{pmt}\cosh(mt) \biggl(\overline{f}(0)+ \int _{0}^{t}e^{-pms}\bigl[\overline{b}(s) \cosh(ms)-\underline{b}(s)\sinh (ms)\bigr]\,ds \biggr) \\ &{}+e^{pmt}\sinh(mt) \biggl(\underline{f}(0)+ \int _{0}^{t}e^{-pms}\bigl[\underline{b}(s) \cosh(ms)-\overline{b}(s)\sinh (ms)\bigr]\,ds \biggr). \end{aligned}$$

Remark 4.3

It is easy to check that for $p<1$, when $u(t)$ is $(ii)$-differentiable and $\operatorname{diam}(u'(t))\geq\frac{\alpha }{1-\alpha} \operatorname{diam}(u(t))$, then

$$ b(t)=\frac{m \alpha p}{q} \biggl(\frac{p}{q}u'(t)+u(t) \biggr)\ominus -\frac{m \alpha}{q} \biggl(\frac{p}{q}u'(t)+u(t) \biggr) $$

(17)

is such that level-wise H-difference exists. Since, in this case $\operatorname{diam}(u'(t))=\underline{u}'(t)-\overline{u}'(t)$, and by (15)–(16), we have

$$\begin{aligned} \overline{b}(t)-\underline{b}(t) =&-\frac{\alpha p^{2}m}{q^{2}}\operatorname{diam} \bigl(u'(t)\bigr)+\frac{\alpha pm}{q}\operatorname {diam}\bigl(u(t) \bigr) \\ &{}+\frac{\alpha pm}{q^{2}}\operatorname{diam}\bigl(u'(t)\bigr)- \frac{\alpha m}{q}\operatorname{diam}\bigl(u(t)\bigr) \\ =&\frac{1-\alpha}{1+p}\operatorname{diam}\bigl(u'(t)\bigr)- \frac{\alpha }{1+p}\operatorname{diam}\bigl(u(t)\bigr)\geq0. \end{aligned}$$

It is easy to check that, when $u(t)$ is $(i)$-differentiable, then $b(t)$ is not a fuzzy function, unless $u(t)$ and $u'(t)$ are crisp.

Therefore, if $p<1$ (or equivalently $m>0$), the $(ii,\alpha)$ solution to (9) is given by

$$\begin{aligned} f(t) =&e^{pmt}\cosh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[b(s)\cosh (ms)-b(s) \sinh(ms)\bigr]\,ds \biggr) \\ &{}\ominus-e^{pmt}\sinh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[b(s)\cosh (ms)-b(s) \sinh(ms)\bigr]\,ds \biggr), \end{aligned}$$

provided that the level-wise H-differences define a fuzzy interval for $t>0$, where $b(t)$ is defined in (17).

Remark 4.4

Since for $m>0$, $\cosh(mt)\geq\sinh(mt)$, then for every $C\in \mathbb{R}_{F}$, the H-difference $e^{pmt}\cosh(mt)C\ominus e^{pmt}\sinh(mt)C$ exists. Also the H-difference $e^{pmt}\cosh(mt)C\ominus- e^{pmt}\sinh(mt)C$ exists level-wise.

If $p>1$ (or equivalently $m<0$), similarly to the previous case, the $(ii,\alpha)$-solution is given by

$$\begin{aligned} f(t) =&e^{pmt}\cosh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[b(s)\cosh (ms) \ominus b(s)\sinh(ms)\bigr]\,ds \biggr) \\ &{}+e^{pmt}\sinh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[b(s)\cosh(ms) \ominus b(s)\sinh(ms)\bigr]\,ds \biggr). \end{aligned}$$

So, we have proved the following result.

Theorem 4.5

Let $\lambda>0$, $m=\frac{q}{1-p^{2}}$, $b(t)$ be a valid fuzzy function defined as in (17) and $u(t)$ be $(ii)$-differentiable with the property $\operatorname{diam}(u'(t))\geq \frac{\alpha}{1-\alpha} \operatorname{diam}(u(t))$ for $t>0$. Then the following assertions are valid:

• (i) If $p<1$, then the $(ii,\alpha)$-solution to (9) is given by

  $$\begin{aligned} &\begin{aligned} f(t)={}&e^{pmt}\cosh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[b(s)\cosh (ms)-b(s) \sinh(ms)\bigr]\,ds \biggr) \\ &{}\ominus-e^{pmt}\sinh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[b(s)\cosh (ms)-b(s) \sinh(ms)\bigr]\,ds \biggr), \end{aligned}\\ &\quad t\geq0, \end{aligned}$$

  provided that the level-wise differences define a fuzzy interval for $t>0$.

• (ii) If $p>1$, then the $(ii,\alpha)$-solution to (9) is given by

  $$\begin{aligned} &\begin{aligned} f(t)={}&e^{pmt}\cosh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[b(s)\cosh (ms) \ominus b(s)\sinh(ms)\bigr]\,ds \biggr) \\ &{}+e^{pmt}\sinh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[b(s)\cosh (ms) \ominus b(s)\sinh(ms)\bigr]\,ds \biggr), \end{aligned}\\ & \quad t\geq0, \end{aligned}$$

  provided that the level-wise differences define a fuzzy interval for $t>0$.

Case II. Let $\lambda<0$. Suppose that $f(t)$ is $(i,\alpha)$-differentiable. Then (9) is equivalent to the following system of ordinary differential equations:

$$ \textstyle\begin{cases} D^{\alpha}\underline{f}(t)=\lambda\overline{f}(t)+\underline{u}(t),\qquad \underline{f}(0)=\underline{f_{0}},\\ D^{\alpha}\overline{f}(t)=\lambda\underline{f}(t)+\overline {u}(t),\qquad \overline{f}(0)=\overline{f_{0}}. \end{cases} $$

Similarly to the second part of Case I, we have

$$\begin{aligned} \underline{f}(t) =&e^{pmt}\cosh(mt) \biggl( \underline{f}(0)+ \int _{0}^{t}e^{-pms}\bigl[\underline{ \tilde{b}}(s)\cosh(ms)-\overline{\tilde {b}}(s)\sinh(ms)\bigr]\,ds \biggr) \\ &{}+e^{pmt}\sinh(mt) \biggl(\overline{f}(0)+ \int _{0}^{t}e^{-pms}\bigl[\overline{ \tilde{b}}(s)\cosh(ms)-\underline{\tilde {b}}(s)\sinh(ms)\bigr]\,ds \biggr) \end{aligned}$$

(18)

and

$$\begin{aligned} \overline{f}(t) =&e^{pmt}\sinh(mt) \biggl( \underline{f}(0)+ \int _{0}^{t}e^{-pms}\bigl[\underline{ \tilde{b}}(s)\cosh(ms)-\overline{\tilde {b}}(s)\sinh(ms)\bigr]\,ds \biggr) \\ &{}+e^{pmt}\cosh(mt) \biggl(\overline{f}(0)+ \int _{0}^{t}e^{-pms}\bigl[\overline{ \tilde{b}}(s)\cosh(ms)-\underline{\tilde {b}}(s)\sinh(ms)\bigr]\,ds \biggr), \end{aligned}$$

(19)

where $m=\frac{q}{1-p^{2}}$ and

$$ \underline{\tilde{b}}(t)=\frac{m \alpha}{q} \biggl( \frac{ p^{2}}{q}\overline{u}'(t)+p\overline{u}(t)+ \frac{p}{q}\underline {u}'(t)+\underline{u}(t) \biggr) $$

(20)

and

$$ \overline{\tilde{b}}(t)=\frac{m \alpha}{q} \biggl( \frac {p^{2}}{q}\underline{u}'(t)+p \underline{u}(t)+ \frac{p}{q}\overline {u}'(t)+\overline{u}(t) \biggr). $$

(21)

First, we consider $p<-1$. It is easy to check that, when $u(t)$ is $(ii)$-differentiable and $\operatorname{diam}(u'(t))\geq\frac{\alpha }{1-\alpha} \operatorname{diam}(u(t))$, then

$$\begin{aligned} \tilde{b}(t) =& \biggl(\frac{\alpha p^{2}m}{q^{2}}u'(t)\ominus- \frac {\alpha pm}{q}u(t) \biggr) \\ &{}+ \biggl(\frac{\alpha pm}{q^{2}}u'(t)\ominus -\frac{\alpha m}{q}u(t) \biggr) \end{aligned}$$

(22)

is such that the corresponding level-wise H-differences exist. This fact is due to the following. In this case, $\operatorname {diam}(u'(t))=\underline{u}'(t)-\overline{u}'(t)$ and, using (20)–(21), we have

$$\begin{aligned} \overline{\tilde{b}}(t)-\underline{\tilde{b}}(t) =&\frac{\alpha p^{2}m}{q^{2}} \operatorname{diam}\bigl(u'(t)\bigr)-\frac{\alpha pm}{q}\operatorname {diam}\bigl(u(t)\bigr) \\ -&\frac{\alpha pm}{q^{2}}\operatorname{diam}\bigl(u'(t)\bigr)+ \frac{\alpha m}{q}\operatorname{diam}\bigl(u(t)\bigr) \\ =&\frac{\alpha-1}{1+p}\operatorname{diam}\bigl(u'(t)\bigr)+ \frac{\alpha }{1+p}\operatorname{diam}\bigl(u(t)\bigr)\\ \geq&0. \end{aligned}$$

Therefore, since we suppose $1+p<0$, so if $\operatorname {diam}(u'(t))\geq\frac{\alpha}{1-\alpha} \operatorname{diam}(u(t))$, then the level sets of $\tilde{b}(t)$ are valid intervals. It is easy to check that, when $u(t)$ is $(i)$-differentiable, $\tilde{b}(t)$ is not a fuzzy function, unless $u(t)$ is crisp for every t.

Thus, if $p<-1$, then $m>0$ and, by equations (18)–(19), we have the $(i,\alpha)$-solution as follows:

$$\begin{aligned} f(t) =&e^{pmt}\cosh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[\tilde {b}(s) \cosh(ms)-\tilde{b}(s)\sinh(ms)\bigr]\,ds \biggr) \\ &{}\ominus-e^{pmt}\sinh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[\tilde {b}(s) \cosh(ms)-\tilde{b}(s)\sinh(ms)\bigr]\,ds \biggr), \end{aligned}$$

provided level-wise differences define a fuzzy interval for $t>0$, where $\tilde{b}(t)$ is defined as in (22).

Now, suppose that $-1< p<0$ (or equivalently $m<0$). In this case, if $u(t)$ is $(i)$-differentiable, then, using (20)–(21), we can write $\tilde{b}(t)$ as a fuzzy function

$$ \tilde{b}(t)=\frac{\alpha m}{q}u(t)+\frac{\alpha pm}{q}u(t)+ \frac {\alpha pm}{q^{2}}u'(t)+\frac{\alpha p^{2}m}{q^{2}}u'(t). $$

(23)

On the other hand, if $u(t)$ is (2)-differentiable, then by (20)–(21)

$$ \tilde{b}(t)= \biggl(\frac{\alpha pm}{q}u(t)\ominus- \frac{\alpha p^{2}m}{q^{2}}u'(t) \biggr)+ \biggl(\frac{\alpha m}{q}u(t) \ominus-\frac {\alpha pm}{q^{2}}u'(t) \biggr), $$

(24)

where the level-wise H-differences exist when $\frac{\alpha}{1-\alpha} \operatorname{diam}(u(t))\geq\operatorname{diam}(u'(t))$.

Then, for $-1< p<0$, we obtain

$$\begin{aligned} f(t) =&e^{pmt}\cosh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[\tilde {b}(s) \cosh(ms)\ominus\tilde{b}(s)\sinh(ms)\bigr]\,ds \biggr) \\ &{}+e^{pmt}\sinh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[\tilde{b}(s)\cosh (ms)\ominus\tilde{b}(s)\sinh(ms)\bigr]\,ds \biggr), \end{aligned}$$

where $\tilde{b}(t)$ is defined by (23) or (24) (according to the type of differentiability of $u(t)$), provided that the level-wise H-differences define proper fuzzy functions. In consequence, we have proved the following result.

Theorem 4.6

Suppose that $\lambda<0$.

• (i) Let $p<-1$, $u(t)$ be $(ii)$-differentiable and satisfying $\operatorname{diam}(u'(t))\geq\frac{\alpha}{1-\alpha} \operatorname{diam}(u(t))$. Then the $(i,\alpha)$-solution to problem (9) is given by

  $$\begin{aligned} f(t) =&e^{pmt}\cosh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[\tilde {b}(s) \cosh(ms)-\tilde{b}(s)\sinh(ms)\bigr]\,ds \biggr) \\ &{}\ominus-e^{pmt}\sinh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[\tilde {b}(s) \cosh(ms)-\tilde{b}(s)\sinh(ms)\bigr]\,ds \biggr), \end{aligned}$$

  provided the H-difference exists, where $\tilde{b}(t)$ is given in (22).

• (ii) Let $-1< p<0$. If u is $(i)$-differentiable and $\tilde {b}(t)$ is defined in (23), or if u is $(ii)$-differentiable and satisfies condition $\frac{\alpha}{1-\alpha} \operatorname{diam}(u(t))\geq\operatorname{diam}(u'(t))$ such that $\tilde{b}(t)$ is a valid fuzzy function in (24), then the $(i,\alpha)$-solution to problem (9) is given by

  $$\begin{aligned} f(t) =&e^{pmt}\cosh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[\tilde {b}(s) \cosh(ms)\ominus\tilde{b}(s)\sinh(ms)\bigr]\,ds \biggr) \\ &{}+e^{pmt}\sinh(mt) \biggl(f(0)+ \int_{0}^{t}e^{-pms}\bigl[\tilde{b}(s)\cosh (ms)\ominus\tilde{b}(s)\sinh(ms)\bigr]\,ds \biggr), \end{aligned}$$

provided the H-difference exists.

Suppose that $\lambda<0$ and $f(t)$ is $(ii,\alpha )$-differentiable. Then (9) is equivalent to

$$ \textstyle\begin{cases} D^{\alpha}\underline{f}(t)=\lambda\underline{f}(t)+\overline{u}(t),\qquad \underline{f}(0)=\underline{f_{0}}, \\ D^{\alpha}\overline{f}(t)=\lambda\overline{f}(t)+\underline {u}(t),\qquad \overline{f}(0)=\overline{f_{0}}. \end{cases} $$

Then, using (5), we have

$$ (1-p )\underline{f}(t)-q I^{1}\underline{f}(t)= (1-p ) \underline{f_{0}}+(1-\alpha ) \bigl(\overline{u}(t)-\overline{u}(0) \bigr)+\alpha I^{1}\overline{u}(t), $$

(25)

and similarly for $\overline{f}(t)$. Since $\lambda<0$ and $0<\alpha <1$, then $1-p>1$, so that, using (7), we get

$$ \underline{f}(t)-\frac{q}{1-p}I^{1}\underline{f}(t)=\underline {f}(0)+\frac{1-\alpha}{1-p} \bigl(\overline{u}(t)-\overline {u}(0) \bigr)+ \frac{\alpha}{1-p}I^{1}\overline{u}(t). $$

Similarly to the previous case, proceeding analogously to (11), we obtain

$$ \underline{f}(t)=\frac{(1-\alpha)\tilde{\lambda}}{q} \bigl(\overline{u}(t)-e^{\tilde{\lambda}t} \overline{u}(0) \bigr)+e^{\tilde{\lambda}t}\frac{\tilde{\lambda}^{2}\alpha}{q^{2}} \int _{0}^{t}e^{-\tilde{\lambda}s}\overline{u}(s)\,ds+ \underline{f_{0}}e^{\tilde {\lambda}t}, $$

and similarly

$$ \overline{f}(t)=\frac{(1-\alpha)\tilde{\lambda}}{q} \bigl(\underline{u}(t)-e^{\tilde{\lambda}t} \underline{u}(0) \bigr)+e^{\tilde{\lambda}t}\frac{\tilde{\lambda}^{2}\alpha}{q^{2}} \int _{0}^{t}e^{-\tilde{\lambda}s}\underline{u}(s)\,ds+ \overline{f_{0}}e^{\tilde {\lambda}t}, $$

where $\tilde{\lambda}=\frac{q}{1-p}$. Hence we deduce

$$ f(t)= \biggl(f_{0}e^{\tilde{\lambda}t}-\frac{(1-\alpha)\tilde{\lambda }}{\lambda\alpha}e^{\tilde{\lambda}t}u(0) \biggr)\ominus- \biggl(\frac{(1-\alpha)\tilde{\lambda}}{\lambda\alpha}u(t)+e^{\tilde {\lambda}t}\frac{\tilde{\lambda}^{2}}{\lambda^{2}\alpha} \int _{0}^{t}e^{-\tilde{\lambda}s}u(s)\,ds \biggr), $$

provided that the H-differences exist. So, we have the following result.

Theorem 4.7

For $\lambda<0$, the $(ii,\alpha )$-solution to problem (9) is given by

$$ f(t)= \biggl(f_{0}e^{\tilde{\lambda}t}-\frac{(1-\alpha)\tilde{\lambda }}{\lambda\alpha}e^{\tilde{\lambda}t}u(0) \biggr)\ominus- \biggl(\frac{(1-\alpha)\tilde{\lambda}}{\lambda\alpha}u(t)+e^{\tilde {\lambda}t}\frac{\tilde{\lambda}^{2}}{\lambda^{2}\alpha} \int _{0}^{t}e^{-\tilde{\lambda}s}u(s)\,ds \biggr), $$

provided that the H-difference exists.

Case III. Let $\lambda= 0$. Let $f(t)$ be $(i,\alpha)$-differentiable. Then problem (9) is equivalent to

$$ \bigl(D^{\alpha}\underline{f}(t),D^{\alpha}\overline{f}(t) \bigr)= \bigl(\underline{u}(t),\overline{u}(t) \bigr),\quad \bigl(\underline{f}(0), \overline{f}(0) \bigr)= (\underline {f_{0}},\overline{f_{0}} ). $$

So, we have

$$ \textstyle\begin{cases} D^{\alpha}\underline{f}(t)=\underline{u}(t),\qquad \underline{f}(0)=\underline{f_{0}},\\ D^{\alpha}\overline{f}(t)=\overline{u}(t),\qquad \overline{f}(0)=\overline{f_{0}}. \end{cases} $$

So, by Theorem 3.1, we obtain

$$ \textstyle\begin{cases} \underline{f}(t)=\underline{f}(0)+(1-\alpha)(\underline {u}(t)-\underline{u}(0))+\alpha \int_{0}^{t}\underline{u}(s)\,ds,\\ \overline{f}(t)=\overline{f}(0)+(1-\alpha)(\overline {u}(t)-\overline{u}(0))+\alpha \int_{0}^{t}\overline{u}(s)\,ds. \end{cases} $$

So, the $(i,\alpha)$-solution to (9) is given by

$$ f(t)=f(0)+(1-\alpha) \bigl(u(t)\ominus u(0) \bigr)+\alpha \int_{0}^{t}u(s)\,ds, $$

provided that the H-differences exist. To obtain $(ii,\alpha )$-solution, we have

$$ \textstyle\begin{cases} \underline{f}(t)=\underline{f}(0)+(1-\alpha) (\overline {u}(t)-\overline{u}(0) )+\alpha \int_{0}^{t}\overline{u}(s)\,ds,\\ \overline{f}(t)=\overline{f}(0)+(1-\alpha) (\underline {u}(t)-\underline{u}(0) )+\alpha \int_{0}^{t}\underline{u}(s)\,ds. \end{cases} $$

So the $(ii,\alpha)$-solution to (9) is given by

$$ f(t)=f(0)\ominus- \biggl[(1-\alpha) \bigl(u(t)\ominus u(0) \bigr)+\alpha \int_{0}^{t}u(s)\,ds \biggr], $$

provided that the H-differences exist. So, we have the following result.

Theorem 4.8

The $(i,\alpha)$- and $(ii,\alpha)$-differentiable solutions to the problem

$$ \textstyle\begin{cases} D^{\alpha}f(t)=u(t),\quad t\geq0,\\ f(0)=f_{0}\in\mathbb{R}_{F} \end{cases} $$

are given by

$$ f(t)=f(0)+(1-\alpha) \bigl(u(t)\ominus u(0) \bigr)+\alpha \int_{0}^{t}u(s)\,ds $$

and

$$ f(t)=f(0)\ominus- \biggl[(1-\alpha) \bigl(u(t)\ominus u(0) \bigr)+\alpha \int_{0}^{t}u(s)\,ds \biggr], $$

respectively, provided that the corresponding H-differences exist.

5 Examples

In this section, we provide several examples to illustrate the main results.

Example 5.1

Let $\lambda=1$ and $u(t)=(-e^{t},0,e^{t})$ be a triangular fuzzy number valued function. Then $\tilde{\lambda}=1$ and we have $\underline{u}^{r}(t)=(r-1)e^{t}$ and $\overline{u}^{r}(t)=(1-r)e^{t}$. So, (9) is written as follows:

$$ \textstyle\begin{cases} {}^{CF}D_{*}^{\alpha}f(t)= f(t)+(-e^{t},0,e^{t}), \\ f(0)=(-1,0,1)\in\mathbb{R}_{F}. \end{cases} $$

(26)

We see that $p=1-\alpha<1$, so by Theorem 4.2-(ii), the $(i,\alpha)$-solution to (26) is

$$ f(t)=\frac{1}{\alpha}tu(t)+f(0)e^{t}= \biggl(\frac{t}{\alpha}+1 \biggr) \bigl(-e^{t},0,e^{t}\bigr). $$

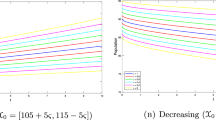
In this case H-difference $u(t)\ominus e^{t} u(0)$ exists trivially. For $\alpha=\frac{1}{2}$, the support of $(i,\alpha)$-solution is shown in Fig. 1. Since $u(t)$ is not $(ii)$-differentiable, we cannot use Theorem 4.5 to obtain $(ii,\alpha)$-solution.

Figure 1

The support of the $(i,\alpha)$-solution of Example 5.1, for $\alpha=\frac{1}{2}$

Example 5.2

Let $\lambda=-1$ and $u(t)=(-e^{t},0,e^{t})$ be a triangular fuzzy number valued function. Then $\tilde{\lambda}=\frac{-\alpha}{2-\alpha}<0$, $-1< p<0$, $m=\frac{-1}{2-\alpha}<0$, $\underline{u}^{r}(t)=(r-1)e^{t}$, and $\overline{u}^{r}(t)=(1-r)e^{t}$.

So, equation (9) is equivalent to

$$ \textstyle\begin{cases} {}^{CF}D_{*}^{\alpha}f(t)= -f(t)+(-e^{t},0,e^{t}), \\ f(0)=(-1,0,1)\in\mathbb{R}_{F}. \end{cases} $$

(27)

So, using Theorem 4.6, the $(i,\alpha)$-solution is

$$f(t)=\biggl(1+\frac{t}{\alpha}\biggr) \bigl(-e^{t},0,e^{t} \bigr), $$

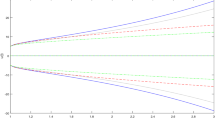
which, for $\alpha=\frac{1}{3}$, is shown in Fig. 2.

Figure 2

The support of the $(i,\alpha)$-solution of Example 5.2, for $\alpha=\frac{1}{3}$

For $(ii,\alpha)$-solution with $\alpha=\frac{1}{2}$ and $t\in [0,\frac{3}{4}ln3]$, by Theorem 4.7, we have

$$ f(t)= \biggl(\frac{3}{2}e^{\frac{-t}{3}}-\frac{1}{2}e^{t} \biggr) (-1,0,1), $$

whose support is shown in Fig. 3.

Figure 3

The support of the $(ii,\alpha)$-solution of Example 5.2, for $\alpha=\frac{1}{2}$