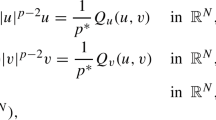A fixed point operator for systems of vector p-Laplacian with singular weights

Abstract

In this paper, after establishing a fixed point operator for a strongly coupled vector p-Laplacian with a singular and sign-changing weight function, which may not be integrable, we investigate the existence for the Dirichlet boundary value problems of strongly coupled vector p-Laplacian systems with a nonlinear term consisting of Hadamard product. The proofs are mainly based on topological degree arguments and the global continuation theorem.

1 Introduction

We are concerned with the existence of nontrivial solutions for strongly coupled nonlinear differential systems of the form

$$ (P_{\lambda})\quad \textstyle\begin{cases} -\Psi_{p}(u')'= \lambda h(t)\cdot f(u), \quad t\in(0,1),\\ u(0)= 0 = u(1), \end{cases} $$

where $p>1$, $\Psi_{p}: \mathbb{R}^{N} \to\mathbb{R}^{N}$ is defined by $\Psi _{p}(x)=|x|^{p-2}x$, $\lambda>0$ is a parameter, $h(t)=(h_{1}(t),\ldots ,h_{N}(t))$ with $h_{i} :(0,1) \to\mathbb{R}$, and $f(u)=(f_{1}(u),\ldots,f_{N}(u))$ with continuous $f_{i}: \mathbb{R}^{N}\to\mathbb{R}$. Here we denote $x \cdot y = (x_{1}y_{1}, x_{2}y_{2}, \ldots, x_{N}y_{N})$ the Hadamard product of x and y in $\mathbb{R}^{N}$. Thus, problem ($P_{\lambda}$) can be rewritten as

$$ \textstyle\begin{cases} -(|u'(t)|^{p-2}u'_{1}(t))'= \lambda h_{1}(t)f_{1}(u),\\ \vdots\\ -(|u'(t)|^{p-2}u'_{N}(t))'= \lambda h_{N}(t)f_{N}(u),\quad t\in(0,1),\\ u_{i}(0)=0=u_{i}(1), \quad i=1,\ldots,N. \end{cases} $$

Throughout the paper, we denote by $|\cdot|$ the absolute value on $\mathbb{R}$ or the Euclidean norm on $\mathbb{R}^{N}$ and by $\langle\cdot,\cdot\rangle$ the inner product on $\mathbb{R}^{N}$ and define $\varphi_{p}: \mathbb{R} \to\mathbb{R}$ by $\varphi _{p}(s)=|s|^{p-2}s$. For a weight function h, we assume that $h_{i} \in \mathcal{H}$, where

$$\mathcal{H}= \biggl\{ g\in L^{1}_{\mathrm{loc}}\bigl((0,1),\mathbb{R} \bigr) \Bigm| \int_{0}^{\frac{1}{2}}\varphi_{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}} \bigl|g(\tau)\bigr|\,d\tau \biggr)\,ds+ \int_{\frac{1}{2}}^{1} \varphi_{p}^{-1} \biggl( \int_{\frac{1}{2}}^{s} \bigl|g(\tau)\bigr|\,d\tau \biggr)\,ds< \infty \biggr\} . $$

It is well known that $L^{1} (0,1) \subsetneqq\mathcal{H}$. Thus, a function in $\mathcal{H}$ may have stronger singularity at the boundary than a function in $L^{1}(0,1)$ (see examples in Section 4). If $h_{i} \in\mathcal{H}$ for all $i=1,2,\ldots,N$, then $|h| \in \mathcal{H}$. In this sense, we shall denote $h \in\mathcal{H}$ whenever $h_{i} \in\mathcal{H}$ for all $i=1,2,\ldots,N$.

Scalar equations or systems of p-Laplacian-like problem ($P_{\lambda}$) appear in various applications, which describe reaction-diffusion systems, nonlinear elasticity, glaciology, population biology, combustion theory, and non-Newtonian fluids (see [1–4]). The study on the existence of solutions for p-Laplacian scalar equations or systems or more generalized Laplacian systems has attracted much attention recently (see [5–18] and the references therein).

Among their general setup, a solution operator for nonlinear p-Laplacian systems was introduced in the pioneering works of Manásevich and Mawhin [19, 20]. They applied the solution operator to study the existence of solutions for systems of strongly coupled vector p-Laplacian-like operators with $L^{1}$-Carathéodory nonlinear perturbations.

We see that the $L^{1}$-Carathéodory condition in problem ($P_{\lambda}$) corresponds to the condition $h \in L^{1}((0,1),\mathbb{R}^{N})$. As a generalization of the $L^{1}$-Carathéodory condition, it is interesting to consider the case $h \in\mathcal{H}$. Since our problem involves systems of strongly coupled differential operators and the weight function h may change sign, related studies are not known yet, as far as the authors know. Recently, for a scalar equation of ($P_{\lambda}$), Sim and Lee [21] established a new solution operator and proved an existence result by the global continuation theorem.

Thus, the goal of this paper is to get an existence result for ($P_{\lambda}$) where the differential operator is related to strongly coupled vector p-Laplacian and the weight function has stronger singularity at the boundary than $L^{1}$ and sign-changing. The novelty of the paper is providing a new solution operator, which is the most generalized so far.

This paper is organized as follows. In Section 2, we derive a solution operator for problem (W)+(D) with $g \in\mathcal{H}$. In Section 3, we prove the compactness of the solution operator for ($P_{\lambda}$) with $\lambda=1$. In Section 4, we show the existence of solutions and give some illustrative examples, which satisfy all assumptions in the paper and are not given in other studies.

2 A fixed point operator

In this section, we construct a solution operator for a strongly coupled vector p-Laplacian. Let us consider a problem of the form

$$\textstyle\begin{array}{@{}lll} &\displaystyle(W)&\quad {-}\Psi_{p}\bigl(w'\bigr)'= g(t),\quad t\in(0,1),\\ &\displaystyle(D)&\quad w(0)=0=w(1), \end{array} $$

where $g\in\mathcal{H}$. Since g may not be in $L^{1}((0,1),\mathbb{R}^{N})$, the solution of (W)+(D) may not be in $C^{1}([0,1],\mathbb{R}^{N})$. For an example of a simple scalar case, take $g(t) = (p-1) t^{-1}|1+ \ln t|^{p-2}$, $p>2$; then $g \notin L^{1}(0,1)$, but $g\in\mathcal{H}$, and the solution u is given by $u(t) = -t \ln t$, which is not in $C^{1}[0,1]$.

So by a solution to this problem we mean a function $w \in C([0,1],\mathbb{R}^{N}) \cap C^{1}((0,1),\mathbb{R}^{N})$ with $\Psi_{p}(w')$ absolutely continuous that satisfies equations (W)+(D).

We first give some remarks for calculations later on.

Remark 2.1

From the definition of $\Psi_{p}$ and $\varphi_{p}$ we get, for any $x, y\in\mathbb{R}^{N}$,

$$\bigl|\Psi_{p}^{-1}(x+y)\bigr|\leq\varphi_{p}^{-1} \bigl(|x|+|y| \bigr)\leq C_{p} \bigl(\varphi_{p}^{-1}\bigl(|x|\bigr)+ \varphi_{p}^{-1}\bigl(|y|\bigr) \bigr), $$

where

$$\begin{aligned} C_{p}= \textstyle\begin{cases} 1, & p>2,\\ 2^{\frac{2-p}{p-1}},& 1< p\leq2. \end{cases}\displaystyle \end{aligned}$$

Remark 2.2

By the homogeneity of $\varphi_{p}^{-1}$ we can deduce that if $h \in \mathcal{H}$, then $\alpha\cdot h \in\mathcal{H}$ for all $\alpha\in C([0,1],\mathbb{R}^{N})$.

Let w be a solution of (W)+(D). Then integrating both sides of $(W)$ on the intervals $[s,\frac{1}{2}]$ and $[\frac{1}{2},s]$ for $s\in(0,\frac {1}{2}]$ and $s\in[\frac{1}{2},1)$, respectively, we find that (W)+(D) is equivalent to

$$ \textstyle\begin{cases} w'(s)=\Psi_{p}^{-1} (a+\int_{s}^{\frac{1}{2}}g(\tau)\,d\tau ), \qquad w(0)=0, \quad s\in(0,\frac{1}{2}],\\ w'(s)=\Psi_{p}^{-1} (a-\int_{\frac{1}{2}}^{s}g(\tau)\,d\tau ), \qquad w(1)=0, \quad s\in[\frac{1}{2},1), \end{cases} $$

(2.1)

where $a=\Psi_{p}(w'(\frac{1}{2}))$. Applying Remark 2.1 with $x=a$ and $y=\int_{s}^{\frac{1}{2}}g(\tau)\,d\tau$, we get

$$\begin{aligned} \biggl\vert \Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr)\biggr\vert \leq& \varphi_{p}^{-1} \biggl(|a|+ \int_{s}^{\frac{1}{2}}\bigl|g(\tau)\bigr|\,d\tau \biggr) \\ \leq& C_{p}\varphi_{p}^{-1}\bigl(|a|\bigr)+ C_{p}\varphi_{p}^{-1} \biggl( \int_{s}^{\frac {1}{2}}\bigl|g(\tau)\bigr|\,d\tau \biggr). \end{aligned}$$

Since $g \in\mathcal{H}$, we know that

$$\Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr) \in L^{1} \biggl(\biggl(0,\frac{1}{2}\biggr]\biggr), \qquad \Psi_{p}^{-1} \biggl(a- \int_{\frac{1}{2}}^{s}g(\tau)\,d\tau \biggr) \in L^{1}\biggl(\biggl[\frac{1}{2},1\biggr)\biggr). $$

Thus, we may integrate both sides of (2.1) on the interval $[0,t]$ for $t\in[0,\frac{1}{2}]$ and on the interval $[t,1]$ for $t\in[\frac{1}{2},1]$, and we get

$$\begin{aligned} w(t)= \textstyle\begin{cases} \int_{0}^{t}\Psi_{p}^{-1} (a+\int_{s}^{\frac{1}{2}}g(\tau)\,d\tau )\,ds, & t\in[0,\frac{1}{2}],\\ \int_{t}^{1}\Psi_{p}^{-1} (-a+\int_{\frac{1}{2}}^{s}g(\tau)\,d\tau )\,ds, & t\in[\frac{1}{2},1]. \end{cases}\displaystyle \end{aligned}$$

We need to check that $w(\frac{1}{2}^{-})=w(\frac{1}{2}^{+})$. For $a \in\mathbb{R}^{N}$, define

$$ G_{g} (a)= \int_{0}^{\frac{1}{2}}\Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac {1}{2}}g(\tau)\,d\tau \biggr)\,ds- \int_{\frac{1}{2}}^{1}\Psi_{p}^{-1} \biggl(-a+ \int_{\frac{1}{2}}^{s}g(\tau )\,d\tau \biggr)\,ds. $$

(2.2)

Then the function $G_{g}: \mathbb{R}^{N}\rightarrow\mathbb{R}^{N}$ is well defined. If $G_{g}$ has a unique zero, then $w(\frac{1}{2}^{-})=w(\frac{1}{2}^{+})$. For this, we give the following lemma.

Lemma 2.3

For given $g \in\mathcal{H}$, the function $G_{g}$ defined in (2.2) has a unique zero $a=a(g)$ in  $\mathbb{R}^{N}$.

Proof

I. Existence. We claim that there exists $r>0$ such that $\langle G_{g} (a),a \rangle>0$ for all $a \in\partial B_{r}(0)\subset\mathbb{R}^{N}$. If the claim is valid, then we consider the homotopy

$$h(\lambda,a)=\lambda a+(1-\lambda)G_{g} (a) \quad\mbox{for } \lambda \in[0,1]. $$

By the claim,

$$ \bigl\langle h(\lambda,a),a\bigr\rangle =\lambda\langle a,a\rangle+(1- \lambda )\bigl\langle G_{g} (a),a\bigr\rangle >0 $$

for any $a\in\partial B_{r}(0)$, $\lambda\in[0,1]$. Taking $\Omega=B_{r}(0)$, we see that the Brouwer degree $d_{B}(h(\lambda,a), \Omega,0)$ is well defined, and by the homotopy invariance property we get

$$d_{B}\bigl(G_{g}(\cdot),\Omega,0\bigr)=d_{B} \bigl(h(0,a),\Omega,0\bigr)=d_{B}\bigl(h(1,a),\Omega ,0 \bigr)=d_{B}(id,\Omega,0)=1 $$

since $0\in\Omega$. This completes the proof of the existence of a zero of $G_{g}$. We now prove the claim. For convenience, we denote

$$\begin{aligned}& H_{g}(a)\triangleq \int_{0}^{\frac{1}{2}}\Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac {1}{2}}g(\tau)\,d\tau \biggr)\,ds, \qquad W_{g} (a) \triangleq \int_{\frac {1}{2}}^{1}\Psi_{p}^{-1} \biggl(-a+ \int_{\frac{1}{2}}^{s}g(\tau)\,d\tau \biggr)\,ds. \end{aligned}$$

Then it suffices to show that there exists $r>0$ such that $\langle H_{g} (a), a\rangle> 0$ and $\langle W_{g} (a), a \rangle< 0$ for all $a \in\partial B_{r}(0)\subset \mathbb{R}^{N}$. Indeed, we have

$$\begin{aligned} \bigl\langle H_{g}(a), a\bigr\rangle &= \int_{0}^{\frac{1}{2}}\biggl\langle \Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac {1}{2}}g(\tau)\,d\tau \biggr), a\biggr\rangle \,ds \\ & = \int_{0}^{\delta}\biggl\langle \Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac {1}{2}}g(\tau)\,d\tau \biggr), a\biggr\rangle \,ds+ \int_{\delta}^{\frac {1}{2}}\biggl\langle \Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr), a\biggr\rangle \,ds, \end{aligned}$$

where $\delta\in(0,\frac{1}{2})$ will be determined later. Since $g\in \mathcal{H}$, both integrations are well defined, and we denote

$$\begin{aligned}& H_{1,\delta} \triangleq \int_{0}^{\delta}\biggl\langle \Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr), a\biggr\rangle \,ds, \\& H_{2,\delta} \triangleq \int_{\delta}^{\frac{1}{2}}\biggl\langle \Psi _{p}^{-1} \biggl(a+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr), a\biggr\rangle \,ds. \end{aligned}$$

We first consider $H_{1,\delta}$. Since

$$\biggl| \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau\biggr|\leq \int_{s}^{\frac{1}{2}}\bigl|g(\tau )\bigr|\,d\tau, $$

applying Remark 2.1, we obtain

$$\begin{aligned} |H_{1,\delta}| &\leq \int_{0}^{\delta} \biggl|\biggl\langle \Psi_{p}^{-1}\biggl(a+ \int_{s}^{\frac {1}{2}}g(\tau)\,d\tau\biggr),a\biggr\rangle \biggr|\,ds \leq \int_{0}^{\delta} \biggl\vert \Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac {1}{2}}g(\tau)\,d\tau \biggr)\biggr\vert |a|\,ds \\ & \leq \int_{0}^{\delta} \varphi_{p}^{-1} \biggl(|a|+\biggl|\int_{s}^{\frac {1}{2}}g(\tau)\,d\tau\biggr| \biggr) |a|\,ds \leq \int_{0}^{\delta} \varphi_{p}^{-1} \biggl(|a|+ \int_{s}^{\frac {1}{2}}\bigl|g(\tau)\bigr|\,d\tau \biggr) |a|\,ds \\ &\leq \int_{0}^{\delta} C_{p} \biggl( \varphi_{p}^{-1}\bigl(|a|\bigr)+\varphi_{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}}\bigl|g(\tau)\bigr|\,d\tau \biggr) \biggr)|a|\,ds \\ & = C_{p} \delta|a|^{p^{\ast}} + C_{p} \biggl[ \int_{0}^{\delta}\varphi _{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}}\bigl|g(\tau)\bigr|\,d\tau \biggr)\,ds\biggr] |a|, \end{aligned}$$

where $p^{\ast}=\frac{p}{p-1}$. Thus, we get

$$\begin{aligned} H_{1,\delta}&\geq -C_{p} \delta|a|^{p^{\ast}} - C_{p} \biggl[ \int_{0}^{\delta }\varphi_{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}}\bigl|g(\tau)\bigr|\,d\tau \biggr)\,ds\biggr] |a| \\ & = |a|^{p^{\ast}} \biggl[-C_{p} \delta- C_{p} \biggl[ \int_{0}^{\delta}\varphi _{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}}\bigl|g(\tau)\bigr|\,d\tau \biggr)\,ds\biggr] \frac {1}{|a|^{p^{\ast}-1}} \biggr]. \end{aligned}$$

(2.3)

Now we consider $H_{2,\delta}$. Since $\langle\Psi_{p}(x),x\rangle =|x|^{p}$, $x \in\mathbb{R}^{N}$, we see that

$$\bigl\langle \Psi_{p}^{-1}(x),x\bigr\rangle =\bigl| \Psi_{p}^{-1}(x)\bigr|^{p}=|x|^{(p^{\ast }-1)p}=|x|^{p^{\ast}}. $$

Moreover, for $s\in[\delta,\frac{1}{2}]$, $|\int_{s}^{\frac{1}{2}}g(\tau )\,d\tau|\leq\int_{\delta}^{\frac{1}{2}}|g(\tau)|\,d\tau<\infty$; thus, denoting $\int_{\delta}^{\frac{1}{2}}|g(\tau)|\,d\tau\triangleq M_{\delta}$, we obtain

$$\begin{aligned} H_{2,\delta}={}& \int_{\delta}^{\frac{1}{2}}\biggl\langle \Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr),a + \int_{s}^{\frac {1}{2}}g(\tau)\,d\tau\biggr\rangle \,ds \\ &{}- \int_{\delta}^{\frac{1}{2}}\biggl\langle \Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr), \int_{s}^{\frac {1}{2}}g(\tau)\,d\tau\biggr\rangle \,ds \\ \geq{}& \int_{\delta}^{\frac{1}{2}}\biggl|a+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr|^{p^{\ast}}\,ds-M_{\delta} \int_{\delta}^{\frac{1}{2}}\biggl|\Psi_{p}^{-1} \biggl(a+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr)\biggr|\,ds. \end{aligned}$$

Since $p^{*} >1$ and

$$\biggl|a+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau\biggr|\ge|a|-\biggl| \int_{s}^{\frac {1}{2}}g(\tau)\,d\tau\biggr|\ge|a|-M_{\delta} $$

for $s\in[\delta,\frac{1}{2}]$, taking $|a|$ large enough to satisfy $|a|-M_{\delta}>0$, we get

$$\begin{aligned} H_{2,\delta} &\ge \int_{\delta}^{\frac{1}{2}}\bigl(|a|-M_{\delta}\bigr)^{p^{\ast }}\,ds-M_{\delta} \int_{\delta}^{\frac{1}{2}}\bigl(|a|+M_{\delta}\bigr)^{p^{\ast}-1}\,ds \\ & =\biggl(\frac{1}{2}-\delta\biggr) \bigl(|a|-M_{\delta}\bigr)^{p^{\ast}}-\frac{M_{\delta }}{2}\bigl(|a|+M_{\delta}\bigr)^{p^{\ast}-1} \\ & = |a|^{p^{\ast}} \biggl[\biggl(\frac{1}{2}-\delta\biggr) \biggl(1- \frac{M_{\delta }}{|a|}\biggr)^{p^{\ast}}-\frac{M_{\delta}}{2} \biggl(1+ \frac{M_{\delta}}{|a|}\biggr)^{p^{\ast}-1}\frac{1}{|a|} \biggr]. \end{aligned}$$

(2.4)

Combining (2.3) and (2.4), we get that

$$\begin{aligned} \bigl\langle H_{g}(a),a\bigr\rangle \geq{}&|a|^{p^{\ast}} \biggl[\biggl(\frac{1}{2}-\delta \biggr) \biggl(1-\frac{M_{\delta}}{|a|}\biggr)^{p^{\ast}} - \frac{M_{\delta}}{2}\cdot \biggl(1+\frac{M_{\delta}}{|a|}\biggr)^{p^{\ast}-1}\cdot\frac{1}{|a|} \\ &{} -C_{p}\delta -C_{p} \int_{0}^{\delta}\varphi_{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}}\bigl|g(\tau)\bigr|\,d\tau \biggr)\,ds\cdot \frac {1}{|a|^{p^{\ast}-1}} \biggr]. \end{aligned}$$

(2.5)

Since $g\in\mathcal{H}$, we have that $\varphi_{p}^{-1} (\int _{s}^{\frac{1}{2}}|g(\tau)|\,d\tau )\in L^{1}(0,\delta]$. Choosing $\delta>0$ sufficiently small and $|a|=r$ sufficiently large, we can make the right-hand side of (2.5) strictly greater than 0. This implies that there exists $r>0$ such that $\langle H_{g}(a),a \rangle>0$ for all $a \in\partial B_{r}(0)$. Applying a similar argument, we can show that $\langle W_{g} (a), -a \rangle> 0$ for all $a \in\partial B_{r}(0)$. Therefore, we conclude that there exists $r>0$ such that $\langle G_{g}(a),a \rangle>0$ for all $a \in\partial B_{r}(0)$, and the claim is proved.

II. Uniqueness. Suppose that $a_{1}$ and $a_{2}$ are two distinct zeros of $G_{g}$. Then

$$\bigl\langle G_{g}(a_{1})-G_{g}(a_{2}),a_{1}-a_{2} \bigr\rangle =0. $$

On the contrary,

$$\begin{aligned} & \bigl\langle G_{g}(a_{1})-G_{g}(a_{2}),a_{1}-a_{2} \bigr\rangle \\ & \quad= \bigl\langle H_{g}(a_{1})-H_{g}(a_{2}),a_{1}-a_{2} \bigr\rangle + \bigl\langle W(a_{2})-W(a_{1}),a_{1}-a_{2} \bigr\rangle \\ &\quad = \int_{0}^{\frac{1}{2}}\biggl\langle \Psi_{p}^{-1} \biggl(a_{1}+ \int _{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr)- \Psi_{p}^{-1} \biggl(a_{2}+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr),a_{1}-a_{2} \biggr\rangle \,ds \\ & \qquad{} + \int_{\frac{1}{2}}^{1}\biggl\langle \Psi_{p}^{-1} \biggl(-a_{2}+ \int _{\frac{1}{2}}^{s}g(\tau)\,d\tau \biggr)- \Psi_{p}^{-1} \biggl(-a_{1}+ \int_{\frac{1}{2}}^{s}g(\tau)\,d\tau \biggr),a_{1}-a_{2} \biggr\rangle \,ds. \end{aligned}$$

Therefore, we get

$$\begin{aligned} & \bigl\langle G_{g}(a_{1})-G_{g}(a_{2}),a_{1}-a_{2} \bigr\rangle \\ &\quad = \int_{0}^{\frac{1}{2}}\biggl\langle \Psi_{p}^{-1} \biggl(a_{1}+ \int _{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr)- \Psi_{p}^{-1} \biggl(a_{2}+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr), \\ & \qquad{} \biggl( a_{1}+ \int_{s}^{\frac{1}{2}}g(\tau )\,d\tau \biggr)- \biggl(a_{2}+ \int_{s}^{\frac{1}{2}}g(\tau)\,d\tau \biggr)\biggr\rangle \,ds \\ &\qquad{} + \int_{\frac{1}{2}}^{1}\biggl\langle \Psi_{p}^{-1} \biggl(-a_{2}+ \int _{\frac{1}{2}}^{s}g(\tau)\,d\tau \biggr)- \Psi_{p}^{-1} \biggl(-a_{1}+ \int_{\frac{1}{2}}^{s}g(\tau)\,d\tau \biggr), \\ & \qquad{} \biggl( -a_{2}+ \int_{\frac{1}{2}}^{s}g(\tau )\,d\tau \biggr) - \biggl(-a_{1}+ \int_{\frac{1}{2}}^{s}g(\tau)\,d\tau \biggr)\biggr\rangle \,ds>0 \end{aligned}$$

since $\langle\Psi_{p}^{-1}(x)-\Psi_{p}^{-1}(y),x-y\rangle>0$ for all $x,y\in\mathbb{R}^{N}$, $x\neq y$. This contradiction completes the proof of uniqueness. □

Lemma 2.3 implies that if $g\in\mathcal{H}$, then the solution w of (W)+(D) can be represented by

$$ w(t)= \textstyle\begin{cases} \int_{0}^{t}\Psi_{p}^{-1} (a(g)+\int_{s}^{\frac{1}{2}}g(\tau)\,d\tau )\,ds, & t\in[0,\frac{1}{2}],\\ \int_{t}^{1}\Psi_{p}^{-1} (-a(g)+\int_{\frac{1}{2}}^{s}g(\tau)\,d\tau )\,ds, & t\in[\frac{1}{2},1], \end{cases} $$

(2.6)

where $a(g)\in\mathbb{R}^{N}$ satisfies

$$ \int_{0}^{\frac{1}{2}}\Psi_{p}^{-1} \biggl(a(g)+ \int_{s}^{\frac{1}{2}}g(\tau )\,d\tau \biggr)\,ds= \int_{\frac{1}{2}}^{1}\Psi_{p}^{-1} \biggl(-a(g)+ \int_{\frac {1}{2}}^{s}g(\tau)\,d\tau \biggr)\,ds. $$

(2.7)

We note that $a(g)$ is determined uniquely up to g, and from this uniqueness property the following corollary is obvious.

Corollary 2.4

Let $g\in\mathcal{H}$, Then, as a function of g, a is homogeneous, that is,

$$a(\lambda g)=\lambda a(g) \quad\textit{for all } \lambda\in\mathbb{R}. $$

On the other hand, it is not hard to see that the function w defined in (2.6) satisfies $w\in C([0,1],\mathbb{R}^{N})\cap C^{1}((0,1),\mathbb{R}^{N})$, $\Psi_{p}(w')$ is absolutely continuous on $(0,1)$, and w satisfies (W)+(D). Therefore, we conclude that if $g\in \mathcal{H}$, then w is a solution of (W)+(D) if and only if w satisfies (2.6).

3 Compactness of the fixed point operator

Consider a nonlinear problem of the form

$$ (P)\quad\textstyle\begin{cases} -\Psi_{p}(u')'=h(t)\cdot f(u), \quad t\in(0,1),\\ u(0)= 0 = u(1), \end{cases} $$

where $h \in\mathcal{H}$ and $f \in C(\mathbb{R}^{N},\mathbb{R}^{N})$. We note that, by Remark 2.2, $h\cdot f(u)\in\mathcal{H}$. Let us apply the solution representation for (W)+(D) given in (2.6) replacing g with $h\cdot f(u)$. Then we may rewrite problem (P) equivalently as

$$u=T(u), $$

where $T: C([0,1],\mathbb{R}^{N}) \to C([0,1],\mathbb{R}^{N})$ is defined by

$$\begin{aligned} T(u) (t) = \textstyle\begin{cases} \int_{0}^{t} \Psi_{p}^{-1} (a( h\cdot f(u))+ \int_{s}^{\frac{1}{2}} h(\tau)\cdot f(u(\tau))\,d\tau )\,ds, & t\in[0,\frac{1}{2}],\\ \int_{t}^{1} \Psi_{p}^{-1} (-a( h\cdot f(u))+ \int_{\frac{1}{2}}^{s} h(\tau)\cdot f(u(\tau))\,d\tau )\,ds, & t\in[\frac{1}{2},1]. \end{cases}\displaystyle \end{aligned}$$

In this section, we prove that the solution operator T is completely continuous. For this, we need two lemmas about the properties of $a( h\cdot f(u))$. Since h and f are fixed, we regard $a( h\cdot f(u))$ as a function of $u\in C([0,1],\mathbb{R}^{N})$.

Lemma 3.1

The function a sends bounded sets in $C([0,1],\mathbb{R}^{N})$ into bounded sets in $\mathbb{R}^{N}$.

Proof

Assume that a sequence $\{u_{n}\}$ is bounded in $C([0,1],\mathbb {R}^{N})$. Let us denote $a_{n}\triangleq a(h\cdot f(u_{n}))$ and $G_{n} \triangleq G_{h\cdot f(u_{n})}$. Suppose that $\{a_{n}\}$ is unbounded in $\mathbb{R}^{N}$. Then there exists a subsequence $\{a_{n_{k}}\}$ such that $|a_{n_{k}}|\rightarrow \infty$ as $k\rightarrow\infty$. Since each $a_{n_{k}}$ is a zero of $G_{n_{k}}$, we see that $\langle G_{n_{k}}(a_{n_{k}}), a_{n_{k}}\rangle=0$ for all k. On the other hand, by the same calculation as in the proof of Lemma 2.3 we obtain

$$\begin{aligned} \bigl\langle H_{n_{k}} (a_{n_{k}}),a_{n_{k}} \bigr\rangle \geq{}& |a_{n_{k}}|^{p^{\ast}}\biggl[\biggl(\frac{1}{2}- \delta\biggr) \biggl(1-\frac{MH_{\delta }}{|a_{n_{k}}|}\biggr)^{p^{\ast}} - \frac{MH_{\delta}}{2}\cdot\biggl(1+\frac {MH_{\delta}}{|a_{n_{k}}|}\biggr)^{p^{\ast}-1}\cdot \frac{1}{|a_{n_{k}}|} \\ &{}-C_{p}\delta-C_{p}\varphi_{p}^{-1}(M) \int _{0}^{\delta}\varphi_{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}}\bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds\cdot \frac {1}{|a_{n_{k}}|^{p^{\ast}-1}}\biggr], \end{aligned}$$

where $M=\sup_{k\in\mathbb{N}} \|f(u_{n_{k}})\|_{\infty}$ and $H_{\delta} = \int_{\delta}^{\frac{1}{2}}|h(\tau)|\,d\tau$. Since $|a_{n_{k}}|\rightarrow\infty$ as $k\rightarrow\infty$, we may choose sufficiently large k and then $\delta>0$ small enough to satisfy $\langle H_{n_{k}} (a_{n_{k}}),a_{n_{k}} \rangle>0$. Applying a similar argument for $W_{n_{k}}$, we conclude that $\langle G_{n_{k}} (a_{n_{k}}),a_{n_{k}} \rangle>0$ for sufficiently large k, and this contradiction completes the proof. □

Remark 3.2

If B is a bounded set in $C([0,1],\mathbb{R}^{N})$, then $\{a(h\cdot v) | v\in B\}$ is also bounded in $\mathbb{R}^{N}$. The proof is similar to that of Lemma 3.1 by replacing M with $\sup_{v\in B}\|v\|_{\infty}$.

Lemma 3.3

The function $a: C([0,1],\mathbb{R}^{N})\rightarrow\mathbb{R}^{N}$ is continuous.

Proof

Assume that $u_{n} \to u$ in $C([0,1],\mathbb{R}^{N})$. Then for the continuity of a, we need to show that $a(h\cdot f(u_{n}))\rightarrow a(h\cdot f(u))$ in $\mathbb{R}^{N}$ as $n\rightarrow\infty$. Denote again $a_{n}\triangleq a(h\cdot f(u_{n}))$. We know that $\{a_{n}\}$ is bounded in $\mathbb{R}^{N}$ by Lemma 3.1; thus, it has a convergent subsequence $\{a_{n_{k}}\}$, which converges to, say, $\hat{a}\in\mathbb{R}^{N}$. We first claim that

$$\begin{aligned} & \int_{0}^{\frac{1}{2}}\Psi_{p}^{-1} \biggl(\hat{a}+ \int_{s}^{\frac {1}{2}}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds \\ &\quad = \int_{\frac{1}{2}}^{1}\Psi_{p}^{-1} \biggl(-\hat{a}+ \int_{\frac {1}{2}}^{s}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds. \end{aligned}$$

(3.1)

Indeed, let us take $K=\sup_{n\in\mathbb{N}} |a_{n}|$, $M=\sup_{n\in \mathbb{N}} \|f(u_{n})\|_{\infty}$ and fix $s\in(0, {\frac{1}{2}}]$. Then we get

$$\bigl|h(\tau)\cdot f\bigl(u_{n_{k}}(\tau)\bigr)\bigr|\le M\bigl|h(\tau)\bigr| $$

for all $\tau\in[s, {\frac{1}{2}}]$. Moreover, $h_{i} \in L^{1}_{\mathrm{loc}} (0,1)$ implies $|h|\in L^{1} [s, {\frac{1}{2}}]$. Thus, by the continuity of $\Psi _{p}^{-1}$ and applying the Lebesgue dominated convergence theorem componentwise, we get

$$\lim_{k\to\infty} \Psi_{p}^{-1} \biggl(a_{n_{k}}+ \int_{s}^{\frac {1}{2}}h(\tau)\cdot f\bigl(u_{n_{k}}( \tau)\bigr)\,d\tau \biggr) =\Psi_{p}^{-1} \biggl(\hat{a}+ \int_{s}^{\frac{1}{2}}h(\tau)\cdot f\bigl(u(\tau )\bigr)\,d\tau \biggr). $$

Similarly, for $k\in\mathbb{N}$,

$$\biggl|\Psi_{p}^{-1} \biggl(a_{n_{k}}+ \int_{s}^{\frac{1}{2}}h(\tau)\cdot f\bigl(u_{n_{k}}( \tau)\bigr)\,d\tau \biggr) \biggr| \leq A+B \varphi_{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}}\bigl|h(\tau)\bigr|\,d\tau \biggr), $$

where $A=C_{p}\varphi_{p}^{-1}(K)$ and $B=C_{p}\varphi_{p}^{-1}(M)$. Since $h\in\mathcal{H}$, the right-hand side of the last inequality is in $L^{1} (0, {\frac{1}{2}}]$. Thus, applying the Lebesgue dominated convergence theorem componentwise again, we have

$$\begin{aligned} &\lim_{k\to\infty} \int_{0}^{\frac{1}{2}}\Psi_{p}^{-1} \biggl(a_{n_{k}}+ \int_{s}^{\frac{1}{2}}h(\tau)\cdot f\bigl(u_{n_{k}}( \tau)\bigr)\,d\tau \biggr)\,ds \\ &\quad = \int_{0}^{\frac{1}{2}}\Psi_{p}^{-1} \biggl(\hat{a}+ \int_{s}^{\frac {1}{2}}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds. \end{aligned}$$

(3.2)

By the same argument, for fixed $s\in[{\frac{1}{2}}, 1)$, we also get

$$ \begin{aligned}[b] &\lim_{k\to\infty} \int_{\frac{1}{2}}^{1}\Psi_{p}^{-1} \biggl(-a_{n_{k}}+ \int_{\frac{1}{2}}^{s}h(\tau)\cdot f\bigl(u_{n_{k}}( \tau)\bigr)\,d\tau \biggr)\,ds \\ &\quad= \int_{\frac{1}{2}}^{1}\Psi_{p}^{-1} \biggl(-\hat{a}+ \int_{\frac {1}{2}}^{s}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds. \end{aligned} $$

(3.3)

Moreover, by the definition of $a_{n_{k}}$ given in (2.7), we know that

$$\begin{aligned} & \int_{0}^{\frac{1}{2}}\Psi_{p}^{-1} \biggl(a_{n_{k}}+ \int_{s}^{\frac {1}{2}}h(\tau)\cdot f\bigl(u_{n_{k}}( \tau)\bigr)\,d\tau \biggr)\,ds \\ & \quad= \int_{\frac{1}{2}}^{1}\Psi_{p}^{-1} \biggl(-a_{n_{k}}+ \int_{\frac {1}{2}}^{s}h(\tau)\cdot f\bigl(u_{n_{k}}( \tau)\bigr)\,d\tau \biggr)\,ds. \end{aligned}$$

This implies that both limits in (3.2) and (3.3) are the same, and thus (3.1) is valid. Equation (3.1) implies that $\hat{a}=a(h\cdot f(u))$ by the uniqueness of â. So we conclude that $\lim_{k\to\infty} a_{n_{k}} ( = a(h\cdot f(u_{n_{k}})) ) = a(h\cdot f(u))$ in $\mathbb{R}^{N}$. It is not hard to see by the standard subsequence argument that $\lim_{n\to\infty} a_{n} ( = a(h\cdot f(u_{n})) ) = a(h\cdot f(u))$, and the proof is done. □

Remark 3.4

If $v_{n} \in C([0,1],\mathbb{R}^{N})$ with $v_{n}\to v$ as $n\to\infty$, then $a(h\cdot v_{n})\to a(h\cdot v)$ as $n\to\infty$. In particular, if $v=0$, then $a(h\cdot v_{n})\to0$ as $n\to\infty$. The proof is similar to that of Lemma 3.3 by replacing M with $\sup_{v\in B}\|v\|_{\infty}$.

Lemma 3.5

The operator $T: C([0,1],\mathbb{R}^{N})\rightarrow C([0,1],\mathbb{R}^{N})$ is completely continuous.

Proof

The continuity of T is easily verified mainly by Lemma 3.1 and the Lebesgue dominated convergence theorem. Let B be a bounded subset of $C([0,1],\mathbb{R}^{N})$. Then by the Arzelà-Ascoli theorem, it suffices to show that $T(B)$ is uniformly bounded and equicontinuous. Take $M_{B}=\sup_{u\in B} \|f(u)\|_{\infty}$, $K_{B}=\sup_{u\in B} |a(h\cdot f(u))|$, and denote $a_{u}\triangleq a(h\cdot f(u))$. Then, for $t \in(0,\frac{1}{2}]$,

$$\begin{aligned} \bigl|T(u) (t)\bigr| \leq& \int_{0}^{t} \biggl|\Psi_{p}^{-1} \biggl(a_{u}+ \int_{s}^{\frac {1}{2}}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr) \biggr|\,ds \\ \leq& \int_{0}^{t}\varphi_{p}^{-1} \biggl(K_{B}+M_{B} \int_{s}^{\frac {1}{2}}\bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds \\ \leq& \frac{1}{2}C_{p}\varphi_{p}^{-1}(K_{B})+C_{p} \varphi _{p}^{-1}(M_{B}) \int_{0}^{\frac{1}{2}}\varphi_{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}}\bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds. \end{aligned}$$

Since $h\in\mathcal{H}$, we see that the last bound is independent of $u\in B$ and $t \in(0,\frac{1}{2}]$. The bound on the interval $[\frac{1}{2},1)$ can be obtained similarly, and thus $T(B)$ is uniformly bounded.

To show the equicontinuity of $T(B)$, let $t_{1}, t_{2}\in[0,1]$ with $t_{1}< t_{2}$.

Case 1. $t_{1},t_{2}\in[0,\frac{1}{2} ]$ or $t_{1},t_{2}\in[\frac{1}{2}, 1 ]$. We have

$$\begin{aligned} & \bigl|T(u) (t_{1})-T(u) (t_{2}) \bigr| \\ &\quad\leq \int_{t_{1}}^{t_{2}} \biggl|\Psi_{p}^{-1} \biggl(a_{u}+ \int_{s}^{\frac {1}{2}}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr) \biggr|\,ds \\ &\quad \leq C_{p} \varphi_{p}^{-1}(K_{B}) (t_{2}-t_{1})+C_{p} \varphi _{p}^{-1}(M_{B}) \int_{t_{1}}^{t_{2}}\varphi_{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}} \bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds. \end{aligned}$$

The bound is independent of $u\in B$ and $\varphi_{p}^{-1} (\int _{s}^{\frac{1}{2}} |h(\tau)|\,d\tau )\in L^{1} (0,\frac{1}{2} ]$ since $h \in\mathcal {H}$; thus, we see that the bound converges to 0 as $|t_{1}-t_{2}| \to0$. The case of $t_{1},t_{2}\in[\frac{1}{2},1]$ can be similarly proved.

Case 2. $0< t_{1}\leq\frac{1}{2}< t_{2}<1$. Since $t_{1}$ and $t_{2}$ can be considered sufficiently close, without loss of generality, we assume that $\frac{1}{4}\leq t_{1}\leq\frac {1}{2}< t_{2}\leq\frac{3}{4}$. Then, by the definition of T,

$$\begin{aligned} T(u) (t_{1}) ={}& \int_{0}^{t_{1}}\Psi_{p}^{-1} \biggl(a_{u}+ \int_{s}^{\frac {1}{2}}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds \\ ={}& \int_{0}^{\frac{1}{2}}\Psi_{p}^{-1} \biggl(a_{u}+ \int_{s}^{\frac {1}{2}}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds \\ &{}- \int_{t_{1}}^{\frac{1}{2}}\Psi_{p}^{-1} \biggl(a_{u}+ \int_{s}^{\frac {1}{2}}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds \end{aligned}$$

and

$$\begin{aligned} T(u) (t_{2}) ={}& \int_{t_{2}}^{1}\Psi_{p}^{-1} \biggl(-a_{u}+ \int_{\frac {1}{2}}^{s}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds \\ = {}& \int_{\frac{1}{2}}^{1}\Psi_{p}^{-1} \biggl(-a_{u}+ \int_{\frac {1}{2}}^{s}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds \\ &{}- \int_{\frac{1}{2}}^{t_{2}}\Psi_{p}^{-1} \biggl(-a_{u}+ \int_{\frac {1}{2}}^{s}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds. \end{aligned}$$

Since, by the definition of $a_{u}$,

$$\begin{aligned} &\int_{0}^{\frac{1}{2}}\Psi_{p}^{-1} \biggl(a_{u}+ \int_{s}^{\frac {1}{2}}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds \\ &\quad= \int_{\frac{1}{2}}^{1}\Psi_{p}^{-1} \biggl(-a_{u}+ \int_{\frac {1}{2}}^{s}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds, \end{aligned}$$

we get

$$\begin{aligned} & \bigl|T(u) (t_{1})-T(u) (t_{2})\bigr| \\ &\quad= \biggl| \int_{\frac{1}{2}}^{t_{2}}\Psi_{p}^{-1} \biggl(-a_{u}+ \int_{\frac {1}{2}}^{s}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds\\ &\qquad{} - \int_{t_{1}}^{\frac{1}{2}}\Psi_{p}^{-1} \biggl(a_{u}+ \int_{s}^{\frac {1}{2}}h(\tau)\cdot f\bigl(u(\tau)\bigr)\,d\tau \biggr)\,ds \biggr| \\ &\quad\leq \int_{\frac{1}{2}}^{t_{2}}\varphi_{p}^{-1} \biggl(K_{B}+M_{B} \int _{\frac{1}{2}}^{s}\bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds + \int_{t_{1}}^{\frac{1}{2}} \varphi_{p}^{-1} \biggl(K_{B}+M_{B} \int _{s}^{\frac{1}{2}}\bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds \\ &\quad\leq \int_{\frac{1}{2}}^{t_{2}}\varphi_{p}^{-1} \biggl(K_{B}+M_{B} \int _{\frac{1}{2}}^{\frac{3}{4}}\bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds + \int_{t_{1}}^{\frac{1}{2}} \varphi_{p}^{-1} \biggl(K_{B}+M_{B} \int_{\frac {1}{4}}^{\frac{1}{2}}\bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds. \end{aligned}$$

Thus, using Remark 2.1, we obtain

$$\begin{aligned} & \bigl|T(u) (t_{1})-T(u) (t_{2})\bigr| \\ &\quad\leq C_{p} \int_{\frac{1}{2}}^{t_{2}} \varphi_{p}^{-1}(K_{B})\,ds +C_{p} \int_{\frac{1}{2}}^{t_{2}} \varphi_{p}^{-1}(M_{B}) \varphi _{p}^{-1} \biggl( \int_{\frac{1}{2}}^{\frac{3}{4}}\bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds \\ &\qquad{}+C_{p} \int_{t_{1}}^{\frac{1}{2}} \varphi_{p}^{-1}(K_{B})\,ds +C_{p} \int_{t_{1}}^{\frac{1}{2}} \varphi_{p}^{-1}(M_{B}) \varphi _{p}^{-1} \biggl( \int_{\frac{1}{4}}^{\frac{1}{2}}\bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds \\ & \quad\leq \biggl[ C_{p}\varphi_{p}^{-1}(K_{B})+C_{p} \varphi_{p}^{-1}(M_{B}) \varphi_{p}^{-1} \biggl( \int_{\frac{1}{4}}^{\frac{3}{4}}\bigl|h(\tau)\bigr|\,d\tau \biggr) \biggr] (t_{2}-t_{1}). \end{aligned}$$

Since the coefficient at $t_{2} -t_{1}$ is a constant independent on $u\in B$, the proof of the equicontinuity of $T(B)$ is complete. □

4 Applications

In this section, we apply the solution operator obtained in Section 2 and use the compactness of the operator in Section 3 to show the existence of nontrivial solutions for the problem

$$ (P_{\lambda})\quad\textstyle\begin{cases} -\Psi_{p}(u')'= \lambda h(t) \cdot f(u), \quad t\in(0,1), \\ u(0)= 0 = u(1). \end{cases} $$

For this, we first give one assumption on f.

• (F) $f_{i}(0,\ldots,0)>0$ and $\lim_{|s|\to\infty} f_{i}(s)/|s|^{p-1}=0$ for $s\in\mathbb{R}^{N}$, $i=1,\ldots,N$.

Let X be a Banach space, and $G : \mathbb{R} \times X \to X$ be completely continuous with $G(0,u)=0$. Consider

$$ u= G(\lambda,u). $$

(4.1)

Denote by $\mathcal{S}$ the set of solutions of (4.1), $\mathbb{R}_{+}=[0,\infty)$, and $\mathbb{R}_{-}=(-\infty,0]$. As the basic tool for the proof of our main theorem, we introduce the following theorem known as the global continuation theorem.

Theorem 4.1

([22])

Let X be a Banach space, and $G : \mathbb{R} \times X \to X$ be continuous and compact with $G(0,u)=0$. Then $\mathcal{S}$ contains a pair of unbounded components $\mathcal{C}^{+}$ and $\mathcal{C}^{-}$ in $\mathbb{R}_{+} \times X$ and $\mathbb{R}_{-} \times X$, respectively, and $\mathcal{C}^{+} \cap\mathcal{C}^{-} = \{(0,0)\}$.

For our fitting, let us take $X = C([0,1],\mathbb{R}^{N})$. Then the usual norm for X to be a Banach space is defined by $\|u\|_{\infty}= \sum_{i=1}^{N} \|u_{i}\|_{\infty}$. In this paper, for the convenience of computation, we establish an equivalent norm, which is defined by

$$\|u\|_{X} = \max_{0\le t \le1} \bigl|\bigl(u_{1}(t), \ldots, u_{N}(t)\bigr)\bigr| = \max_{0\le t \le1} \bigl(u_{1}^{2}(t)+ \cdots+ u_{N}^{2}(t) \bigr)^{1/2}. $$

Indeed, it is easy to see that

$$\|u\|_{X} \le\|u\|_{\infty}\le N \|u\|_{X}. $$

We are ready to state our main existence theorem.

Theorem 4.2

Assume that $h \in\mathcal{H}$ and that (F) holds. Then ($P_{\lambda}$) has at least one nontrivial solution for all $\lambda>0$.

We know that to solve ($P_{\lambda}$) is equivalent to solve

$$u= G(\lambda,u), $$

where $G: (0,\infty) \times X \to X$ is defined by

$$\begin{aligned} G(\lambda,u) (t) = \textstyle\begin{cases} \int_{0}^{t} \Psi_{p}^{-1} (a(\lambda h\cdot f(u))+ \int_{s}^{\frac{1}{2}} \lambda h(\tau)\cdot f(u(\tau))\,d\tau )\,ds, & t\in[0,\frac{1}{2}],\\ \int_{t}^{1} \Psi_{p}^{-1} (-a(\lambda h\cdot f(u)) + \int_{\frac{1}{2}}^{s} \lambda h(\tau)\cdot f(u(\tau))\,d\tau )\,ds, & t \in[\frac{1}{2},1]. \end{cases}\displaystyle \end{aligned}$$

By Remark 2.2 and Lemma 3.5 we can easily show that G is continuous and compact with $G(0,u)=0$. Since Theorem 4.1 guarantees an unbounded continuum $\mathcal{C}^{+}$, if we provide the a priori boundedness of solutions for ($P_{\lambda}$), then the unbounded continuum allows the existence of solutions for all $\lambda>0$.

Lemma 4.3

Assume that $h \in\mathcal{H}$ and that f satisfies (F). Let any $\Lambda>0$ be given, and let $(\lambda,u)$ be a solution for ($P_{\lambda}$) with $\lambda\in(0,\Lambda]$. Then there exists a constant $C(\Lambda)>0$, depending only on Λ, such that $\|u\|_{X} \le C(\Lambda)$.

Proof

Assume that there exists a sequence $(\lambda_{n},u_{n})\in(0,\Lambda] \times X$ such that, for any $n\in\mathbb{N}$,

$$u_{n}=G(\lambda_{n}, u_{n}) $$

with $\|u_{n}\|_{X} \to\infty$ as $n\to\infty$.

By using Remark 2.1 with $x=a(\lambda_{n} h\cdot f(u_{n}))$, $y=\int_{s}^{\frac{1}{2}}\lambda_{n} h(\tau)\cdot f(u_{n}(\tau))\,d\tau$ and the homogeneity of $\varphi_{p}^{-1}$ and a we can estimate the solution $u_{n}$ as follows:

$$\begin{aligned} \bigl|u_{n}(t)\bigr| =& \biggl| \int_{0}^{t}\Psi_{p}^{-1} \biggl(a\bigl(\lambda_{n} h\cdot f(u_{n})\bigr)+ \int_{s}^{\frac{1}{2}} \lambda_{n} h(\tau)\cdot f \bigl(u_{n}(\tau)\bigr)\,d\tau \biggr)\,ds\biggr| \\ \le& \int_{0}^{t}\biggl|\Psi_{p}^{-1} \biggl(a\bigl(\lambda_{n} h\cdot f(u_{n})\bigr)+ \int_{s}^{\frac{1}{2}} \lambda_{n} h(\tau)\cdot f \bigl(u_{n}(\tau)\bigr)\,d\tau \biggr)\biggr|\,ds \\ \le& \int_{0}^{t}\varphi_{p}^{-1} \biggl(\bigl|a\bigl(\lambda_{n} h\cdot f(u_{n})\bigr)\bigr|+ \biggl| \int_{s}^{\frac{1}{2}} \lambda_{n} h(\tau)\cdot f \bigl(u_{n}(\tau)\bigr)\,d\tau\biggr| \biggr)\,ds \\ \le& \varphi_{p}^{-1}(\lambda_{n}) \int_{0}^{\frac{1}{2}}\varphi _{p}^{-1} \biggl(\bigl|a\bigl(h\cdot f(u_{n})\bigr)\bigr|+ \biggl| \int_{s}^{\frac{1}{2}} h(\tau)\cdot f\bigl(u_{n}( \tau)\bigr)\,d\tau\biggr| \biggr)\,ds \\ \le& \varphi_{p}^{-1}(\Lambda) \int_{0}^{\frac{1}{2}}\varphi_{p}^{-1} \biggl(\frac{|a(h\cdot f(u_{n}))|}{\|u_{n}\|_{X}^{p-1}}+ \frac{|\int_{s}^{\frac{1}{2}} h(\tau)\cdot f(u_{n}(\tau))\,d\tau|}{\|u_{n}\|_{X}^{p-1}} \biggr)\,ds\|u_{n} \|_{X} \end{aligned}$$

for all $t\in[0,\frac{1}{2}]$. By the homogeneity of a again, we get

$$\bigl|u_{n}(t)\bigr|\le \varphi_{p}^{-1}(\Lambda) \int_{0}^{\frac{1}{2}}\varphi _{p}^{-1} \biggl(\biggl|a\biggl(h\cdot\frac{f(u_{n})}{\|u_{n}\|_{X}^{p-1}}\biggr)\biggr|+ \int_{s}^{\frac{1}{2}} \bigl|h(\tau)\bigr| \frac{|f(u_{n}(\tau))|}{\|u_{n}\|_{X}^{p-1}}\,d\tau \biggr)\,ds\|u_{n}\|_{X}. $$

By (F), for any $\varepsilon>0$, there exists $l_{\epsilon}>0$ such that for all $s\in\mathbb{R}^{N}$ with $|s|\ge l_{\epsilon}$,

$$ \bigl|f_{i}(s)\bigr| \le\varepsilon|s|^{p-1} \quad \mbox{for } i=1,\ldots,N. $$

Since $f_{i}$ is continuous on $\{s \in\mathbb{R}^{N} \mid |s| \le l_{\epsilon}\}$, there exists a constant $M_{\epsilon}>0$ such that

$$ \bigl|f_{i}(s)\bigr| \le M_{\epsilon}$$

on $\{s \in\mathbb{R}^{N} \mid |s| \le l_{\epsilon}\}$ for $i=1,\ldots,N$. Thus, we have

$$ \bigl|f_{i}(s)\bigr| \le\varepsilon|s|^{p-1}+M_{\epsilon}\quad\mbox{for all } s \in \mathbb{R}^{N} , i=1,\ldots,N. $$

(4.2)

Since $\|u_{n}\|_{X} \to\infty$ as $n\to\infty$, there exists $n_{\epsilon}\in\mathbb{N}$ such that for any $n\geq n_{\epsilon}$, we have

$$\|u_{n}\|_{X}\geq\biggl(\frac{M_{\epsilon}}{\epsilon} \biggr)^{\frac{1}{p-1}}, $$

that is,

$$\frac{1}{\|u_{n}\|_{X}^{p-1}}\leq\frac{\epsilon}{M_{\epsilon}}. $$

Using (4.2), we get that, for any $n\geq n_{\epsilon}$ and $t\in[0,1/2]$,

$$\frac{|f_{i}(u_{n}(t))|}{\|u_{n}\|_{X}^{p-1}}\leq\epsilon\cdot\frac {|u_{n}(t)|^{p-1}}{\|u_{n}\|_{X}^{p-1}}+\frac{M_{\epsilon}}{\|u_{n}\| _{X}^{p-1}}\leq \epsilon+M_{\epsilon}\cdot\frac{\epsilon}{M_{\epsilon}}=2\epsilon $$

and

$$ \frac{\|f(u_{n})\|_{X}}{\|u_{n}\|_{X}^{p-1}}\leq\frac{\|f(u_{n})\|_{\infty}}{\| u_{n}\|_{X}^{p-1}}=\frac{\sum_{i=1}^{N}\|f_{i} (u_{n})\|_{\infty}}{\|u_{n}\| _{X}^{p-1}}\leq N \cdot2\epsilon=2\epsilon N. $$

(4.3)

Take

$$B=\biggl\{ \frac{f(u_{n})}{\|u_{n}\|_{X}^{p-1}}\biggr\} _{n\geq n_{\epsilon}}. $$

Then B is a bounded subset in X. Thus, by Remark 3.2 we see that the set $\{a(h\cdot v) \mid v\in B\}$ is bounded in $\mathbb{R}^{N}$. Moreover, by (4.3) and Remark 3.4 we may choose a constant $C_{\epsilon}=C_{\epsilon}(\epsilon N)>0$ satisfying $C_{\epsilon}\to0$ as $\epsilon\to0$ such that

$$\biggl|a\biggl(h\cdot\frac{f(u_{n})}{\|u_{n}\|_{X}^{p-1}}\biggr)\biggr| \leq C_{\epsilon}\quad\mbox{for any } n\geq n_{\epsilon}. $$

Therefore, for $t\in[0,\frac{1}{2}]$, we obtain

$$\begin{aligned} \bigl|u_{n}(t)\bigr| \leq{}&\biggl[\varphi_{p}^{-1}( \Lambda) \int_{0}^{\frac{1}{2}}\varphi _{p}^{-1} \biggl(C_{\epsilon}+2\epsilon \int_{s}^{\frac{1}{2}} \bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds\biggr] \|u_{n}\|_{X} \\ \leq{}& \biggl[\frac{1}{2}\varphi_{p}^{-1}( \Lambda)C_{p} \varphi_{p}^{-1}(C_{\epsilon}) \\ &{}+\varphi_{p}^{-1}(\Lambda)C_{p} \varphi_{p}^{-1}(2\epsilon) \int _{0}^{\frac{1}{2}}\varphi_{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}} \bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds\biggr] \|u_{n}\|_{X}. \end{aligned}$$

(4.4)

By similar arguments, for $t\in[\frac{1}{2},1]$, we obtain

$$\begin{aligned} \bigl|u_{n}(t)\bigr| \leq{}&\biggl[\varphi_{p}^{-1}( \Lambda) \int_{\frac{1}{2}}^{1}\varphi _{p}^{-1} \biggl(C_{\epsilon}+2\epsilon \int_{\frac{1}{2}}^{s} \bigl|h(\tau)\bigr|\,d\tau \biggr)\,ds\biggr] \|u_{n}\|_{X} \\ \leq{}& \biggl[\frac{1}{2}\varphi_{p}^{-1}( \Lambda)C_{p} \varphi_{p}^{-1}(C_{\epsilon}) \\ &{}+\varphi_{p}^{-1}(\Lambda)C_{p} \varphi_{p}^{-1}(2\epsilon) \int_{\frac {1}{2}}^{1}\varphi_{p}^{-1} \biggl( \int_{\frac{1}{2}}^{s} \bigl|h(\tau)\bigr|\,d\tau\biggr)\,ds\biggr]\| u_{n}\|_{X}. \end{aligned}$$

(4.5)

Denoting $C_{h} \triangleq\max\{ \int_{0}^{\frac{1}{2}}\varphi_{p}^{-1}(\int_{s}^{\frac{1}{2}} |h(\tau)|\,d\tau )\,ds,\int_{\frac{1}{2}}^{1}\varphi_{p}^{-1}(\int_{\frac{1}{2}}^{s} |h(\tau )|\,d\tau)\,ds\}$, we can choose $\epsilon>0$ small enough such that

$$\frac{1}{2}\varphi_{p}^{-1}(\Lambda)C_{p} \varphi_{p}^{-1}(C_{\epsilon}) +\varphi_{p}^{-1}( \Lambda)C_{p} \varphi_{p}^{-1}(2\epsilon) C_{h} \leq\frac{1}{2}. $$

Consequently, combining (4.4) and (4.5), we obtain, for $t\in[0,1]$,

$$\bigl|u_{n}(t)\bigr|\leq\frac{1}{2}\|u_{n}\|_{X}. $$

This implies that

$$\|u_{n}\|_{X}\leq0 \quad\mbox{for } n\geq n_{\epsilon}, $$

which contradicts

$$\|u_{n}\|_{X}\geq\biggl(\frac{M_{\epsilon}}{\epsilon} \biggr)^{\frac{1}{p-1}}>0 \quad\mbox{for } n\geq n_{\epsilon}$$

and this completes the proof. □

Example 1

Consider the following p-Laplacian system:

$$ (E_{1})\quad\textstyle\begin{cases} -(|\mathbf{u}|^{p-2}u')'= \lambda h_{1}(t)[ (u^{2}+v^{2})^{\frac {p-1}{4}}+1],\\ -(|\mathbf{u}|^{p-2}v')'= \lambda h_{2}(t)e^{-v^{2}}[1+(u^{2})^{\frac {p-1}{3}}],\quad t\in(0,1),\\ u(0)=v(0)= 0 = u(1)=v(1), \end{cases} $$

where $\mathbf{u}=(u,v)$, $\lambda>0$ is a parameter, and $h(t)=(h_{1}(t),h_{2}(t))$ is given by

$$\begin{aligned}& h_{1}(t)= \textstyle\begin{cases} t^{-\alpha}, & t\in(0,\frac{1}{2}],\\ -1, & t\in(\frac{1}{2},1), 1< \alpha< p, \end{cases}\displaystyle \qquad h_{2}(t)=-1, \quad t\in(0,1). \end{aligned}$$

We note that $h\in L^{1} _{\mathrm{loc}}$ but $h_{1}\notin L^{1}$. We now show that $h\in\mathcal{H}$. Indeed,

$$\begin{aligned} \int_{s}^{\frac{1}{2}}\tau^{-\alpha}\,d\tau = & - \frac{1}{\alpha-1}\tau^{-(\alpha-1)} \bigg|_{s}^{\frac {1}{2}}=- \frac{1}{\alpha-1} \biggl[\biggl(\frac{1}{2}\biggr)^{-(\alpha-1)}-s^{-(\alpha-1)} \biggr] \\ = & \frac{1}{\alpha-1} \bigl[s^{-(\alpha-1)}-2^{\alpha-1}\bigr]\le \frac{1}{\alpha-1}s^{-(\alpha-1)}. \end{aligned}$$

Since $1<\alpha<p$, we have $\frac{1}{\alpha-1}s^{-(\alpha-1)}>0$ for $s\in(0,1)$ and

$$\begin{aligned} \int_{0}^{\frac{1}{2}}\varphi_{p}^{-1} \biggl( \int_{s}^{\frac{1}{2}}\tau ^{-\alpha}\,d\tau \biggr)\,ds \le& \int_{0}^{\frac{1}{2}}\varphi_{p}^{-1} \biggl(\frac{1}{\alpha -1}s^{-(\alpha-1)} \biggr)\,ds = \int_{0}^{\frac{1}{2}} \biggl(\frac{s^{-(\alpha-1)}}{\alpha-1} \biggr)^{\frac{1}{p-1}}\,ds \\ = & \frac{p-1}{(\alpha-1)^{\frac{1}{p-1}}(p-\alpha)}s^{\frac{p-\alpha }{p-1}} \bigg|_{0}^{\frac{1}{2}} < \infty. \end{aligned}$$

In addition, since $h_{1}$ and $h_{2}$ are constants on $(\frac{1}{2},1)$ and $(0,1)$, respectively, by Remark 2.1 we get $h\in\mathcal{H}$.

Next, we need to check that both $f_{1}(u,v)=(u^{2}+v^{2})^{\frac {p-1}{4}}+1$ and $f_{2}(u,v)= e^{-v^{2}}[1+(u^{2})^{\frac{p-1}{3}}]$ satisfy assumption (F). In fact, $f_{1}(0,0)=f_{2}(0,0)=1>0$, and

$$\begin{aligned}& \begin{aligned}[b] \lim_{|(u,v)|\to\infty}\frac{f_{1}(u,v)}{|(u,v)|^{p-1}} &= \lim _{|(u,v)|\to\infty}\frac{(u^{2}+v^{2})^{\frac {p-1}{4}}+1}{(u^{2}+v^{2})^{\frac{p-1}{2}}} \\ &= \lim_{|(u,v)|\to\infty} \biggl(\frac{1}{(u^{2}+v^{2})^{\frac {p-1}{4}}}+\frac{1}{(u^{2}+v^{2})^{\frac{p-1}{2}}} \biggr)=0, \end{aligned} \\& \begin{aligned}[b] 0&\leq\lim_{|(u,v)|\to\infty}\frac{f_{2}(u,v)}{|(u,v)|^{p-1}} =\lim _{|(u,v)|\to\infty}\frac{e^{-v^{2}}[1+(u^{2})^{\frac {p-1}{3}}]}{(u^{2}+v^{2})^{\frac{p-1}{2}}} \\ &\leq \lim_{|(u,v)|\to\infty} \biggl(\frac {1}{e^{v^{2}}(u^{2}+v^{2})^{\frac{p-1}{2}}}+\frac {1}{e^{v^{2}}(u^{2}+v^{2})^{\frac{p-1}{6}}} \biggr)=0. \end{aligned} \end{aligned}$$

that is, $\lim_{|(u,v)|\to\infty}\frac{f_{2}(u,v)}{|(u,v)|^{p-1}}=0$. Consequently, by Theorem 4.2 we see that problem ($E_{1}$) has at least one nontrivial solution for all $\lambda>0$.

Example 2

Consider the following p-Laplacian system with $p=6$:

$$ (E_{2})\quad\textstyle\begin{cases} -(|\mathbf{u}|^{4}u')'= \lambda h_{1}(t)[ 1- (u^{2}+v^{2})^{\frac {5}{3}}],\\ -(|\mathbf{u}|^{4}v')'= \lambda h_{2}(t)[2-e^{-(u^{2}+v^{4})}], \quad t\in (0,1),\\ u(0)=v(0)= 0 = u(1)=v(1), \end{cases} $$

where $\mathbf{u}=(u,v)$, $\lambda>0$ is a parameter, and $h(t)=(h_{1}(t),h_{2}(t))$ is given by

$$ h_{1}(t)= \textstyle\begin{cases} t^{-2}, & t\in(0,\frac{1}{2}],\\ -1,& t\in(\frac{1}{2},1), \end{cases} $$

and

$$ h_{2}(t)= \textstyle\begin{cases} t^{-4},& t\in(0,\frac{1}{2}],\\ 1,& t\in(\frac{1}{2},1). \end{cases} $$

By similar arguments as in Example 1, we can easily check that $h\in \mathcal{H}$ and $f_{1}$, $f_{2}$ satisfy assumption (F). Consequently, by Theorem 4.2 we see that problem ($E_{2}$) has at least one nontrivial solution for all $\lambda>0$.

Example 3

Consider the following p-Laplacian system:

$$ (E_{3})\quad\textstyle\begin{cases} -(|\mathbf{u}|^{p-2}u_{1}')'= \lambda h_{1}(t)\ln ((u_{1}^{2}+\cdots +u_{N}^{2})^{\frac{1}{2}}+2 ),\\ \vdots\\ -(|\mathbf{u}|^{p-2}u_{N}')'= \lambda h_{N}(t)\ln ((u_{1}^{2}+\cdots +u_{N}^{2})^{\frac{1}{2}}+N+1 ),\quad t\in(0,1),\\ u_{i}(0)=0=u_{i}(1), \quad i=1,\ldots,N, \end{cases} $$

where $\mathbf{u}=(u_{1},\ldots,u_{N})$, $\lambda>0$ is a parameter, $h(t)=(h_{1}(t),\ldots,h_{N}(t))$ is defined by

$$ h_{i}(t)=\frac{1}{t^{\alpha}(1-t)^{\alpha}}-4^{p}, \quad t\in(0,1), 1< \alpha < p, i=1,\ldots,N, $$

and

$$f_{i}(u_{1},\ldots,u_{N})=\ln \bigl( \bigl(u_{1}^{2}+\cdots+u_{N}^{2} \bigr)^{\frac {1}{2}}+i+1 \bigr),\quad i=1,\ldots,N. $$

We note that each $h_{i}$ is not in $L^{1}(0,1)$, $h_{i}(\frac {1}{2})=4^{\alpha}-4^{p}<0$ for $1<\alpha<p$, and $h:(0,1)\to\mathbb {R}^{N}$ is locally integrable. By similar arguments as in Example 1, we can easily check that $h\in \mathcal{H}$.

Next, let us check (F) for $f_{i}(u_{1},\ldots,u_{N})=\ln ((u_{1}^{2}+\cdots+u_{N}^{2})^{\frac{1}{2}}+i+1 )$. In fact, $f_{i}(0,\ldots,0)= \ln(i+1)>0$, and setting $x :=(u_{1}^{2}+\cdots +u_{N}^{2})^{\frac{1}{2}}$, we have

$$\begin{aligned} 0 \leq&\lim_{|(u_{1},\ldots,u_{N})|\to\infty}\frac{f_{i}(u_{1},\ldots ,u_{N})}{|(u_{1},\ldots,u_{N})|^{p-1}} = \lim _{|(u_{1},\ldots,u_{N})|\to\infty}\frac{\ln ((u_{1}^{2}+\cdots +u_{N}^{2})^{\frac{1}{2}}+i+1 )}{(u_{1}^{2}+\cdots+u_{N}^{2})^{\frac {p-1}{2}}} \\ =& \lim_{x\to+\infty}\frac{\ln(x+i+1)}{x^{p-1}} \\ =& \lim_{x\to+\infty} \frac{1}{x+i+1}\cdot\frac{1}{(p-1)x^{p-2}} \\ \leq& \lim_{x\to+\infty} \frac{1}{(p-1)x^{p-1}}=0, \end{aligned}$$

that is, $\lim_{|(u_{1},\ldots,u_{N})|\to\infty}\frac{f_{i}(u_{1},\ldots ,u_{N})}{|(u_{1},\ldots,u_{N})|^{p-1}}=0$ for $i=1,\ldots,N$. Consequently, by Theorem 4.2 we see that problem ($E_{3}$) has at least one nontrivial solution for all $\lambda>0$.