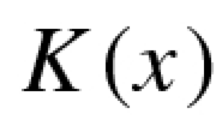Existence of a nontrivial solution for a $(p,q)$-Laplacian equation with p-critical exponent in ${\mathbb{R}}^N$

Abstract

In this paper we prove the existence of a nontrivial solution in ${\mathcal{D}}^{1,p}({\mathbb{R}}^N)\cap {\mathcal{D}}^{1,q}({\mathbb{R}}^N)$ for the following $(p,q)$-Laplacian problem:

$$\{\begin{array}{l}-{\mathrm{\Delta }}_{p}u-{\mathrm{\Delta }}_{q}u=\lambda g(x){|u|}^{r-1}u+{|u|}^{p^{\star }-2}u,\\ u(x)\ge 0,x\in {\mathbb{R}}^N,\end{array}$$

where $1<q\le p<r+1<p^{\star }:=\frac{Np}{N-p}$, $p<N$, $\lambda >0$ is a parameter, ${\mathrm{\Delta }}_{m}u:=div(|\mathrm{\nabla }u{|}^{m-2}\mathrm{\nabla }u)$ is the m-Laplacian operator and $g\in L^{\frac{p^{\star }}{p^{\star }-r-1}}({\mathbb{R}}^N)$ is positive in an open set.

MSC: 35J92, 47J30.

1 Introduction

In this paper we prove the existence of a nontrivial solution for the following problem involving the $(p,q)$-Laplacian and the p-critical exponent

$$\{\begin{array}{l}-{\mathrm{\Delta }}_{p}u-{\mathrm{\Delta }}_{q}u=\lambda g(x){|u|}^{r-1}u+{|u|}^{p^{\star }-2}u\text{in }{\mathbb{R}}^N,\\ u\ge 0,\end{array}$$

(1)

where $1<q\le p<r+1<p^{\star }:=\frac{Np}{N-p}$, $p<N$, $\lambda >0$ is a parameter, ${\mathrm{\Delta }}_{m}u:=div(|\mathrm{\nabla }u{|}^{m-2}\mathrm{\nabla }u)$ is the m-Laplacian operator and $g:{\mathbb{R}}^N\to \mathbb{R}$ is an integrable function satisfying

$$g\in L^{\gamma }\left({\mathbb{R}}^N\right)\text{with }\gamma =\frac{p^{\star }}{p^{\star }-r-1}$$

(2)

and

$$g(x)>0\text{for all }x\in {\mathrm{\Omega }}_g,$$

(3)

where ${\mathrm{\Omega }}_g$ is an open set of ${\mathbb{R}}^N$.

This kind of problem arises, for example, as the stationary version of the reaction-diffusion equation

$$u_t=div[D(u)\mathrm{\nabla }u]+f(x,u),$$

where u describes a concentration, $D(u):=({|\mathrm{\nabla }u|}^{p-2}+{|\mathrm{\nabla }u|}^{q-2})$ is the diffusion coefficient and $f(x,u)$ is the reaction term related to source and loss mechanisms (see [1]–[4]).

The differential operator ${\mathrm{\Delta }}_p+{\mathrm{\Delta }}_q$, known as the $(p,q)$-Laplacian operator when $p\ne q$, has deserved special attention in the last decade. It is not homogeneous and this feature turns out to impose some technical difficulties in applying usual elliptic methods for obtaining the existence and regularity of weak solutions of problems involving this operator.

When $p=q$, we have a single operator p-Laplacian. In this case, problem (1) can be reduced to

$$-{\mathrm{\Delta }}_{p}u=\lambda g(x){|u|}^{r-1}u+f(x){|u|}^{p^{\star }-2}u,x\in {\mathbb{R}}^N$$

(4)

with $f(x)=1$.

In the paper [5], Gonçalves and Alves showed the existence of a weak nonnegative solution for problem (4) with $\lambda =f(x)=1$, $p\ge 2$ and $g\ge 0$.

Drábek and Huang in [6], proved the existence of two positive solutions for problem (4) in the case where $r=p-1$, g and f change sign, $g^{+}\ne 0$, $f^{+}\ne 0$ (and other conditions).

Regarding specifically the $(p,q)$-Laplacian ($p\ne q$), Figueiredo proved, as a particular case of his main result in [1] (which was obtained for a problem involving a more general operator), the existence of a nontrivial weak solution for the following problem:

$$\{\begin{array}{l}-{\mathrm{\Delta }}_{p}u-{\mathrm{\Delta }}_{q}u+|u{|}^{p-2}u+|u{|}^{q-2}u=\lambda f(u)+{|u|}^{p^{\star }-2}u\text{in }{\mathbb{R}}^N,\\ u\ge 0,\end{array}$$

(5)

where f satisfies the Ambrosetti-Rabinowitz condition

$$0<F(t):={\int }_0^{t}f(s)ds\le \frac{1}{p+\theta }f(t)t,t>0$$

for some positive constant θ. In general, this condition not only ensures that the Euler-Lagrange functional associated with (5) has a mountain pass geometry, but also guarantees the boundedness of Palais-Smale sequences corresponding to the functional. We emphasize that the positiveness of $\lambda g(x){\int }_0^t|s{|}^{r-1}sds$ in problem (1) is not guaranteed since the function g can be negative in a large part of ${\mathbb{R}}^N$.

When Ω is a bounded domain of ${\mathbb{R}}^N$, variational methods have been employed for obtaining results of existence and multiplicity of solutions for the following problem with p-critical growth:

$$\{\begin{array}{ll}-{\mathrm{\Delta }}_{p}u-{\mathrm{\Delta }}_{q}u=\lambda g(x){|u|}^{r-2}u+{|u|}^{p^{\star }-2}u+\theta f(x,u)& \text{in }\mathrm{\Omega },\\ u=0& \text{on }\partial \mathrm{\Omega }.\end{array}$$

(6)

For $\theta =0$ and $g=1$, we refer to [7], where $1<r<q<p<N$, and to [8], where $1<q<p<r<p^{\star }$.

In [9], Yin and Yang established the existence of multiple weak solutions in $W_0^{1,p}(\mathrm{\Omega })$ for (6) where the nonlinearity $f(x,t)$ is of concave-convex type, $\lambda ,\theta >0$ are parameters, $g\in L^{\mathrm{\infty }}{(\mathrm{\Omega })}_{+}$ and $1<r<q<p<N$. They also obtained some results for the case $1<q<\frac{N(p-1)}{N-1}<p\le max\{p,p^{\star }-\frac{q}{p-1}\}<r<p^{\star }$.

The natural space to study $(p,q)$-Laplacian problems in a bounded domain Ω is $W_0^{1,p}(\mathrm{\Omega })$, thus taking advantage of the compact immersion $W_0^{1,p}(\mathrm{\Omega })\hookrightarrow L^s(\mathrm{\Omega })$ for $1\le s<p^{\star }$.

When the domain is the whole ${\mathbb{R}}^N$, Sobolev’s immersion is not compact. In order to overcome this issue, the concentration-compactness principle or constrained minimization methods (see [1], [3], [10] and [4], respectively) have been used to find weak solutions in $W^{1,p}({\mathbb{R}}^N)\cap W^{1,q}({\mathbb{R}}^N)$.

In this paper we prove an existence result for (1) in the reflexive Banach space

$$\mathbb{W}:={\mathcal{D}}^{1,p}\left({\mathbb{R}}^N\right)\cap {\mathcal{D}}^{1,q}\left({\mathbb{R}}^N\right),$$

where ${\mathcal{D}}^{1,m}({\mathbb{R}}^N)$ denotes the closure of $C_0^{\mathrm{\infty }}({\mathbb{R}}^N)$ with respect to the norm of $W^{1,m}({\mathbb{R}}^N)$. More precisely, our main result is stated as follows.

Theorem 1

Let g satisfy (2) and (3). There exists${\lambda }^{\ast }>0$such that for any$\lambda >{\lambda }^{\ast }$problem (1) has at least one nontrivial weak solution in$\mathbb{W}$.

Our nontrivial solution is obtained from the mountain pass theorem. We prove that $I_{\lambda }$, the Euler-Lagrange functional associated with nonnegative solutions of (1) in $\mathbb{W}$, satisfies a mountain pass geometry, circumventing the difficulties due to the fact that the $(p,q)$-Laplacian operator is not homogeneous. We also adapt standard arguments to prove the boundedness of Palais-Smale sequences. In order to overcome the lack of compactness of Sobolev’s immersion, we apply the concentration-compactness principle by making use of a suitable bounded measure and adapting arguments from [5], where a p-Laplacian problem involving critical exponents is considered. By following [7] and [8] we get a strict upper bound for $c_{\lambda }$, the level of the Palais-Smale sequence, valid for all λ large enough. Then, we use this fact and arguments derived from [5] to conclude that the nonnegative critical point for $I_{\lambda }$, obtained from the mountain pass theorem, is not the trivial one.

2 Preliminaries

In this section, we state some known results and notations that will be used to prove Theorem 1.

First, let us introduce the following version of the mountain pass theorem (see [11] or [12]).

Lemma 2

Let X be a real Banach space and$\mathrm{\Phi }\in C^1(X,\mathbb{R})$. Suppose that$\mathrm{\Phi }(0)=0$and that there exist$\alpha ,\rho >0$and$x_1\in X\setminus {\overline{B}}_{\rho }(0)$such that

♦ $\mathrm{\Phi }(u)\ge \alpha$for all$u\in X$with${\parallel u\parallel }_X=\rho$;

♦ $\mathrm{\Phi }(x_1)<\alpha$.

There exists a sequence $\{u_n\}\subset X$ satisfying

$$\mathrm{\Phi }(u_n)\to c\mathit{\text{and}}{\mathrm{\Phi }}^{\prime }(u_n)\to 0,$$

where c is the minimax level, defined by

$$c:=inf\{\underset{t\in [0,1]}{max}\mathrm{\Phi }(\gamma (t)):\gamma \in C([0,1],X),\gamma (0)=0\mathit{\text{ and }}\gamma (1)=x_1\}.$$

Let $1<m<N$ and denote by ${\mathcal{D}}^{1,m}({\mathbb{R}}^N)$ the closure of $C_0^{\mathrm{\infty }}({\mathbb{R}}^N)$ with respect to the norm of $W^{1,m}({\mathbb{R}}^N)$. We recall that ${\mathcal{D}}^{1,m}({\mathbb{R}}^N)$ is a reflexive Banach space that is also characterized by (see [13])

$${\mathcal{D}}^{1,m}\left({\mathbb{R}}^N\right)=\{u\in L^{m^{\star }}\left({\mathbb{R}}^N\right):\frac{\partial u}{\partial x_j}\in L^m\left({\mathbb{R}}^N\right),j=1,2,\dots ,N\},$$

where $m^{\star }:=\frac{Nm}{N-m}$, and that its original norm is equivalent to the gradient norm ${\parallel \mathrm{\nabla }\cdot \parallel }_{L^m({\mathbb{R}}^N)}$. Moreover, $W^{1,m}({\mathbb{R}}^N)⫋{\mathcal{D}}^{1,m}({\mathbb{R}}^N)\hookrightarrow L^{m^{\star }}({\mathbb{R}}^N)$.

The next result is a version of the concentration-compactness principle of Lions (see [14] and [15]).

Lemma 3

Let$v_n\in {\mathcal{D}}^{1,p}({\mathbb{R}}^N)$be a bounded sequence such that$v_n\rightharpoonup v$in$L^{p^{\star }}({\mathbb{R}}^N)$. If$v_n$is a subsequence such that${|v_n|}^{p^{\star }}dx\rightharpoonup \nu$for some measure ν, then there exist$x_i\in {\mathbb{R}}^N$and${\nu }_i>0$, $i=1,2,3,\dots$ , such that

$$\sum _{i=1}^{\mathrm{\infty }}{\nu }_i^{\frac{p}{p^{\star }}}<\mathrm{\infty }\mathit{\text{and}}{v}_n^{p^{\star }}\rightharpoonup {|v|}^{p^{\star }}+\sum _{i=1}^{\mathrm{\infty }}{\nu }_i{\delta }_{x_i}=\nu ,$$

where${\delta }_{x_i}$denotes the Dirac measure concentrated at$x_i$.

The next result follows from Theorem 1 of [16] combined with the Banach-Alaoglu theorem (see Remark (iii) of [16]).

Lemma 4

Let$1<p<\mathrm{\infty }$and let$\{u_n\}\subset L^p({\mathbb{R}}^N)$be a bounded sequence converging to u almost everywhere. Then$u_n\rightharpoonup u$ (weakly) in$L^p({\mathbb{R}}^N)$.

The following lemma can be found in [17], Lemma 2.7].

Lemma 5

Let$s>1$, Ω an open set in${\mathbb{R}}^N$and$u_n,u\in W^{1,s}(\mathrm{\Omega })$, $n=1,2,3,\dots$ . Let$a(x,\xi )\in C^0(\mathrm{\Omega }\times {\mathbb{R}}^N,{\mathbb{R}}^N)$satisfy, for positive numbers$\alpha ,\beta >0$, the following properties:

♦ $\alpha {|\xi |}^s\le a(x,\xi )\xi$for all$\xi \in {\mathbb{R}}^N$,

♦ $|a(x,\xi )|\le \beta {|\xi |}^{s-1}$for all$(x,\xi )\in \mathrm{\Omega }\times {\mathbb{R}}^N$,

♦ $[a(x,\xi )-a(x,\eta )][\xi -\eta ]>0$for all$(x,\xi )\in \mathrm{\Omega }\times {\mathbb{R}}^N$with$\xi \ne \eta$.

Then $\mathrm{\nabla }{u}_n\to \mathrm{\nabla }u$ in $L^s(\mathrm{\Omega })$ if and only if

$$\underset{n\to \mathrm{\infty }}{lim}{\int }_{\mathrm{\Omega }}[a(x,\mathrm{\nabla }{u}_n(x))-a(x,\mathrm{\nabla }u(x))][\mathrm{\nabla }{u}_n(x)-\mathrm{\nabla }u(x)]dx=0.$$

We denote by S the best Sobolev constant defined by

$$S:=inf\{\frac{{\parallel \mathrm{\nabla }u\parallel }_p^p}{{\parallel u\parallel }_{p^{\star }}^p}:u\in W^{1,p}\left({\mathbb{R}}^N\right)\setminus \{0\}\}.$$

(7)

3 The existence theorem

We deal with problem (1) in the reflexive Banach space

$$\mathbb{W}:={\mathcal{D}}^{1,p}\left({\mathbb{R}}^N\right)\cap {\mathcal{D}}^{1,q}\left({\mathbb{R}}^N\right),$$

endowed with the norm

$${\parallel u\parallel }_{\mathbb{W}}:={\parallel u\parallel }_{{\mathbb{E}}_p}+{\parallel u\parallel }_{{\mathbb{E}}_q},$$

where

$${\parallel u\parallel }_{{\mathbb{E}}_m}:={\left({\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{m}dx\right)}^{\frac{1}{m}}.$$

The Euler-Lagrange functional associated with (1) is

$$\begin{array}{rcl}{I}_{\lambda }(u)& :=& \frac{1}{p}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{p}dx+\frac{1}{q}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{q}dx-\frac{\lambda }{r+1}{\int }_{{\mathbb{R}}^N}g{u}_{+}^{r+1}dx\\ -\frac{1}{p^{\star }}{\int }_{{\mathbb{R}}^N}{u}_{+}^{p^{\star }}dx\text{for all }u\in \mathbb{W},\end{array}$$

(8)

where $u_{+}:=max\{0,u\}$. It is well defined in $\mathbb{W}$ and of class $C^1$ (as a consequence of hypothesis (2)).

In order to obtain a critical point for $I_{\lambda }$, we will find a Palais-Smale sequence for this functional, that is, a sequence $\{u_n\}\subset \mathbb{W}$ satisfying

$$I_{\lambda }(u_n)\to c\text{and}{\parallel I_{\lambda }^{\prime }(u_n)\parallel }_{{\mathbb{W}}^{\ast }}\to 0.$$

(9)

In the sequel we show that $I_{\lambda }$ satisfies a mountain pass geometry. In order to simplify the presentation, we denote, from now on, the norm of $\mathbb{W}$ by $\parallel \cdot \parallel$ instead of ${\parallel \cdot \parallel }_{\mathbb{W}}$.

Lemma 6

There exist$\eta ,\rho >0$and$u_0\in \mathbb{W}$satisfying: $\parallel u_0\parallel >\rho$, $I_{\lambda }(u_0)<0$and$I_{\lambda }(u)\ge \eta$for any$u\in \mathbb{W}$such that$\parallel u\parallel =\rho$.

Proof

The Hölder inequality implies that

$$\begin{array}{rl}\frac{\lambda }{r+1}{\int }_{{\mathbb{R}}^N}g{u}_{+}^{r+1}dx& \le \frac{\lambda }{S^{\frac{r+1}{p}}(r+1)}{\parallel g\parallel }_{\gamma }{\parallel u\parallel }_{{\mathbb{E}}_p}^{r+1}\\ \le \frac{\lambda }{S^{\frac{r+1}{p}}(r+1)}{\parallel g\parallel }_{\gamma }{[{\parallel u\parallel }_{{\mathbb{E}}_p}+{\parallel u\parallel }_{{\mathbb{E}}_q}]}^{r+1}\\ =:C_1{\parallel u\parallel }^{r+1},\end{array}$$

and (7) yields

$$\frac{1}{p^{\star }}{\int }_{{\mathbb{R}}^N}{u}_{+}^{p^{\star }}dx\le \frac{{\parallel u\parallel }_{{\mathbb{E}}_p}^{p^{\star }}}{S^{\frac{p^{\star }}{p}}{p}^{\star }}\le \frac{{({\parallel u\parallel }_{{\mathbb{E}}_p}+{\parallel u\parallel }_{{\mathbb{E}}_q})}^{p^{\star }}}{S^{\frac{p^{\star }}{p}}{p}^{\star }}=:C_2{\parallel u\parallel }^{p^{\star }}.$$

Let us suppose $\parallel u\parallel \le 1$. Then ${\parallel u\parallel }_{{\mathbb{E}}_q}\le \parallel u\parallel \le 1$ and

$$\begin{array}{rl}{I}_{\lambda }(u)& =\frac{1}{p}{\parallel u\parallel }_{{\mathbb{E}}_p}^p+\frac{1}{q}{\parallel u\parallel }_{{\mathbb{E}}_q}^q-\frac{\lambda }{r+1}{\int }_{{\mathbb{R}}^N}g{u}_{+}^{r+1}dx-\frac{1}{p^{\star }}{\int }_{{\mathbb{R}}^N}{u}_{+}^{p^{\star }}dx\\ \ge \frac{1}{p}({\parallel u\parallel }_{{\mathbb{E}}_p}^p+{\parallel u\parallel }_{{\mathbb{E}}_q}^q)-C_1{\parallel u\parallel }^{r+1}-C_2{\parallel u\parallel }^{p^{\star }}\\ \ge \frac{1}{p}({\parallel u\parallel }_{{\mathbb{E}}_p}^p+{\parallel u\parallel }_{{\mathbb{E}}_q}^p)-C_1{\parallel u\parallel }^{r+1}-C_2{\parallel u\parallel }^{p^{\star }}\\ \ge \frac{1}{2^{p-1}}{({\parallel u\parallel }_{{\mathbb{E}}_p}+{\parallel u\parallel }_{{\mathbb{E}}_q})}^p-C_1{\parallel u\parallel }^{r+1}-C_2{\parallel u\parallel }^{p^{\star }}=\frac{{\parallel u\parallel }^p}{p{2}^{p-1}}-C_1{\parallel u\parallel }^{r+1}-C_2{\parallel u\parallel }^{p^{\star }}.\end{array}$$

We have concluded that

$$I_{\lambda }(u)\ge {\parallel u\parallel }^p(\frac{1}{p{2}^{p-1}}-C_1{\parallel u\parallel }^{r+1-p}-C_2{\parallel u\parallel }^{p^{\star }-p}),\text{whenever }\parallel u\parallel \le 1.$$

(10)

Let us define $\varphi (t):=t^p(\frac{1}{p{2}^{p-1}}-C_1{t}^{r+1-p}-C_2{t}^{p^{\star }-p})$, $t\ge 0$. It is easy to see that there exists $0<t_1<1$ such that $\varphi (t)>0$ for all $t\in (0,t_1]$. Therefore, there exist $\eta >0$ and $0<\rho <1$ such that $I_{\lambda }(u)\ge \eta >0$ whenever $\parallel u\parallel =\rho$.

Now, let $v_0\in \mathbb{W}\setminus \{0\}$ such that $v_0\ge 0$. Then, for any $t>0$, one has

$$I_{\lambda }(t{v}_0)=\frac{t^p}{p}{\parallel v_0\parallel }_{{\mathbb{E}}_p}^p+\frac{t^q}{q}{\parallel v_0\parallel }_{{\mathbb{E}}_q}^q-\frac{t^{r+1}\lambda }{r+1}{\int }_{{\mathbb{R}}^N}g{v}_0^{r+1}dx-\frac{t^{p^{\star }}}{p^{\star }}{\int }_{{\mathbb{R}}^N}{v}_0^{p^{\star }}dx.$$

Since $I_{\lambda }(t{v}_0)\to -\mathrm{\infty }$ as $t\to \mathrm{\infty }$, there exists $u_0=t_0{v}_0\in \mathbb{W}$ such that $\parallel u_0\parallel >\rho$ and $I_{\lambda }(u_0)<0$. □

Lemma 7

Let$\{u_n\}\subset \mathbb{W}$be a Palais-Smale sequence. Then$\{u_n\}$is bounded in$\mathbb{W}$.

Proof

By hypothesis, $\{u_n\}$ satisfies (9). It follows that there exist positive constants $k_0$ and $k_1$ such that $I_{\lambda }(u_n)\le k_0$ and ${\parallel I_{\lambda }^{\prime }(u_n)\parallel }_{{\mathbb{W}}^{\ast }}\le k_1$ for all n large. Thus,

$$\begin{array}{rl}{k}_0+k_1\parallel u_n\parallel & \ge I_{\lambda }(u_n)-\frac{1}{r+1}〈I_{\lambda }^{\prime }(u_n),u_n〉\\ =(\frac{1}{p}-\frac{1}{r+1}){\parallel u_n\parallel }_{{\mathbb{E}}_p}^p+(\frac{1}{q}-\frac{1}{r+1}){\parallel u_n\parallel }_{{\mathbb{E}}_q}^q+(\frac{1}{r+1}-\frac{1}{p^{\star }}){\int }_{{\mathbb{R}}^N}{u}_{n_{+}}^{p^{\star }}dx\\ \ge (\frac{1}{p}-\frac{1}{r+1}){\parallel u_n\parallel }_{{\mathbb{E}}_p}^p+(\frac{1}{q}-\frac{1}{r+1}){\parallel u_n\parallel }_{{\mathbb{E}}_q}^q.\end{array}$$

That is, for all n large, we have

$$c_0(1+\parallel u_n\parallel )\ge c_1{\parallel u_n\parallel }_{{\mathbb{E}}_p}^p+c_2{\parallel u_n\parallel }_{{\mathbb{E}}_q}^q,$$

where $c_0$, $c_1$ and $c_2$ are positive constants that do not depend on n.

Suppose $\parallel u_n\parallel \to \mathrm{\infty }$. Then we have the three following cases to consider:

• 1. ${\parallel u_n\parallel }_{{\mathbb{E}}_p}\to \mathrm{\infty }$ and ${\parallel u_n\parallel }_{{\mathbb{E}}_q}\to \mathrm{\infty }$;

• 2. ${\parallel u_n\parallel }_{{\mathbb{E}}_p}\to \mathrm{\infty }$ and ${\parallel u_n\parallel }_{{\mathbb{E}}_q}$ is bounded;

• 3. ${\parallel u_n\parallel }_{{\mathbb{E}}_p}$ is bounded and ${\parallel u_n\parallel }_{{\mathbb{E}}_q}\to \mathrm{\infty }$.

The first case cannot occur. Indeed, it implies that ${\parallel u_n\parallel }_{{\mathbb{E}}_p}^p>{\parallel u_n\parallel }_{{\mathbb{E}}_p}^q$ for all n large, and thus

$$\begin{array}{rl}{c}_0(1+\parallel u_n\parallel )& \ge c_1{\parallel u_n\parallel }_{{\mathbb{E}}_p}^q+c_2{\parallel u_n\parallel }_{{\mathbb{E}}_q}^q\ge c_3({\parallel u_n\parallel }_{{\mathbb{E}}_p}^q+{\parallel u_n\parallel }_{{\mathbb{E}}_q}^q)\\ \ge \frac{c_3}{2^{q-1}}{({\parallel u_n\parallel }_{{\mathbb{E}}_p}+{\parallel u_n\parallel }_{{\mathbb{E}}_q})}^q=c_4{\parallel u_n\parallel }^q,\end{array}$$

which contradicts the fact that $\parallel u_n\parallel \to \mathrm{\infty }$.

If the second case occurs, we have, for all n large,

$$c_0(1+{\parallel u_n\parallel }_{{\mathbb{E}}_p}+{\parallel u_n\parallel }_{{\mathbb{E}}_q})\ge c_1{\parallel u_n\parallel }_{{\mathbb{E}}_p}^p+c_2{\parallel u_n\parallel }_{{\mathbb{E}}_q}^q\ge c_1{\parallel u_n\parallel }_{{\mathbb{E}}_p}^p,$$

and hence we arrive at the absurd

$$0<\frac{c_1}{c_0}\le \underset{n}{lim}(\frac{1}{{\parallel u_n\parallel }_{{\mathbb{E}}_p}^p}+\frac{1}{{\parallel u_n\parallel }_{{\mathbb{E}}_p}^{p-1}}+\frac{{\parallel u_n\parallel }_{{\mathbb{E}}_q}}{{\parallel u_n\parallel }_{{\mathbb{E}}_p}^p})=0.$$

Proceeding as in the second case, one can check that the third case cannot also happen. □

Lemma 8

Let$\{u_n\}\subset \mathbb{W}$be a Palais-Smale sequence. There exists a nonnegative function$u\in \mathbb{W}$such that, up to a subsequence,

$$\frac{\partial u_n}{\partial x_j}\to \frac{\partial u}{\partial x_j}\mathit{\text{a.e. }}{\mathbb{R}}^N,j\in \{1,2,\dots ,N\}.$$

Proof

We have

$$\begin{array}{rl}{\left({\int }_{{\mathbb{R}}^N}{|\phi v|}^{p^{\star }}dx\right)}^{\frac{1}{p^{\star }}}{S}^{\frac{1}{p}}& \le {\left({\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }(\phi v)|}^{p}dx\right)}^{\frac{1}{p}}\\ \le {\left({\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }\phi |}^p{|v|}^{p}dx\right)}^{\frac{1}{p}}+{\left({\int }_{{\mathbb{R}}^N}{|\phi |}^p{|\mathrm{\nabla }v|}^{p}dx\right)}^{\frac{1}{p}}\end{array}$$

for all $\phi \in C_0^{\mathrm{\infty }}({\mathbb{R}}^N)$ and $v\in {\mathcal{D}}^{1,p}({\mathbb{R}}^N)$, where the first inequality comes from (7). Hence,

$$\begin{array}{rcl}{\left({\int }_{{\mathbb{R}}^N}{|\phi |}^{p^{\star }}{|v|}^{p^{\star }}dx\right)}^{\frac{1}{p^{\star }}}{S}^{\frac{1}{p}}& \le & {\left({\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }\phi |}^p{|v|}^{p}dx\right)}^{\frac{1}{p}}\\ +{\left({\int }_{{\mathbb{R}}^N}{|\phi |}^p({|\mathrm{\nabla }v|}^p+{|\mathrm{\nabla }v|}^q)dx\right)}^{\frac{1}{p}}\end{array}$$

(11)

for all $\phi \in C_0^{\mathrm{\infty }}({\mathbb{R}}^N)$ and $v\in {\mathcal{D}}^{1,p}({\mathbb{R}}^N)\cap {\mathcal{D}}^{1,q}({\mathbb{R}}^N)$.

As a consequence of the boundedness of $\{u_n\}$, given by Lemma 7, there exists $u\in \mathbb{W}$ such that, up to a subsequence, $u_n\rightharpoonup u$ in $\mathbb{W}$. Since $I_{\lambda }^{\prime }(u_n)u_{n-}\to 0$, it follows that $u_{n-}\to 0$ in $\mathbb{W}$, so $u_{n+}\to u$ a.e. in ${\mathbb{R}}^N$.

Let $\mathrm{\Phi }\in C_0^{\mathrm{\infty }}({\mathbb{R}}^N)$ satisfy $0\le \mathrm{\Phi }\le 1$ and

$$\mathrm{\Phi }(x)=\{\begin{array}{ll}1& \text{if }x\in B_{\frac{1}{2}},\\ 0& \text{if }x\in {\mathbb{R}}^N\setminus B_1,\end{array}$$

where $B_{\tau }$ denotes the ball of ${\mathbb{R}}^N$ centered at the origin and with radius τ.

By applying Lemma 3 with $v_n=u_{n+}$ and $v=u$, we have

$$u_{n+}^{p^{\star }}\rightharpoonup u^{p^{\star }}+\sum _{i=1}^{\mathrm{\infty }}{\nu }_i{\delta }_{x_i}.$$

Define the measure $({|\mathrm{\nabla }{u}_{n+}|}^p+{|\mathrm{\nabla }{u}_{n+}|}^q)dx$. Since it is bounded, we have

$$({|\mathrm{\nabla }{u}_{n+}|}^p+{|\mathrm{\nabla }{u}_{n+}|}^q)dx\rightharpoonup \mu$$

for some measure μ. For each index i and each $\epsilon >0$, define

$${\phi }_{\epsilon }(x):=\mathrm{\Phi }\left(\frac{x-x_i}{\epsilon }\right).$$

It follows from inequality (11) that

$$\begin{array}{rcl}{\left({\int }_{{\mathbb{R}}^N}{|{\phi }_{\epsilon }|}^{p^{\star }}{u}_{+}^{p^{\star }}dx\right)}^{\frac{1}{p^{\star }}}{S}^{\frac{1}{p}}& \le & {\left({\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{\phi }_{\epsilon }|}^p{u}_{n+}^{p}dx\right)}^{\frac{1}{p}}\\ +{\left({\int }_{{\mathbb{R}}^N}{|{\phi }_{\epsilon }|}^p({|\mathrm{\nabla }{u}_{n+}|}^p+{|\mathrm{\nabla }{u}_{n+}|}^q)dx\right)}^{\frac{1}{p}}.\end{array}$$

By making $n\to \mathrm{\infty }$, we obtain

$${\left({\int }_{{\mathbb{R}}^N}{|{\phi }_{\epsilon }|}^{p^{\star }}d\nu \right)}^{\frac{1}{p^{\star }}}{S}^{\frac{1}{p}}\le {\left({\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{\phi }_{\epsilon }|}^p{|u|}^{p}dx\right)}^{\frac{1}{p}}+{\left({\int }_{{\mathbb{R}}^N}{|{\phi }_{\epsilon }|}^{p}d\mu \right)}^{\frac{1}{p}},$$

and then, by making $\epsilon \to 0$, we find

$${\left({\int }_{\{x_i\}}d\nu \right)}^{\frac{1}{p^{\star }}}{S}^{\frac{1}{p}}\le {\left({\int }_{\{x_i\}}d\mu \right)}^{\frac{1}{p}},$$

yielding

$$S{\nu }_i^{\frac{p}{p^{\star }}}\le {\mu }_i:={\int }_{\{x_i\}}d\mu .$$

(12)

On the other hand, from the fact that $I_{\lambda }^{\prime }(u_n){\phi }_{\epsilon }{u}_{n_{+}}\to 0$ we have

$$\begin{array}{c}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{p-2}{u}_{n+}\mathrm{\nabla }{\phi }_{\epsilon }\mathrm{\nabla }{u}_{n}dx+{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{q-2}{u}_{n+}\mathrm{\nabla }{\phi }_{\epsilon }\mathrm{\nabla }{u}_{n}dx\hfill \\ ={\int }_{{\mathbb{R}}^N}\lambda g{u}_{n+}^{r+1}{\phi }_{\epsilon }dx+{\int }_{{\mathbb{R}}^N}{u}_{n+}^{p^{\star }}{\phi }_{\epsilon }dx-{\int }_{{\mathbb{R}}^N}({|\mathrm{\nabla }{u}_{n+}|}^p+{|\mathrm{\nabla }{u}_{n+}|}^q){\phi }_{\epsilon }dx+o(1),\hfill \end{array}$$

and hence

$$\begin{array}{c}\underset{n}{lim}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{p-2}{u}_{n+}\mathrm{\nabla }{\phi }_{\epsilon }\mathrm{\nabla }{u}_{n}dx+\underset{n}{lim}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{q-2}{u}_{n+}\mathrm{\nabla }{\phi }_{\epsilon }\mathrm{\nabla }{u}_{n}dx\hfill \\ ={\int }_{{\mathbb{R}}^N}\lambda g{u}_{+}^{r+1}{\phi }_{\epsilon }dx+{\int }_{{\mathbb{R}}^N}{\phi }_{\epsilon }d\nu -{\int }_{{\mathbb{R}}^N}{\phi }_{\epsilon }d\mu .\hfill \end{array}$$

(13)

By Claim 1 in [5] and by the same argument replacing p with q, we obtain

$$\underset{n}{lim}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{p-2}{u}_{n+}\mathrm{\nabla }{\phi }_{\epsilon }\mathrm{\nabla }{u}_{n}dx=\underset{n}{lim}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{q-2}{u}_{n+}\mathrm{\nabla }{\phi }_{\epsilon }\mathrm{\nabla }{u}_{n}dx=o(\epsilon ).$$

Making $\epsilon \to 0$ in (13), we arrive at

$${\int }_{\{x_i\}}d\nu ={\int }_{\{x_i\}}d\mu ,$$

that is, ${\nu }_i={\mu }_i$. By combining this equality with (12), we obtain

$${\nu }_i\ge S^{\frac{N}{p}}.$$

Since ${\sum }_{i=1}^{\mathrm{\infty }}{({\nu }_i)}^{p/p^{\star }}<\mathrm{\infty }$, there exist at most a finite number s of indices i with ${\nu }_i>0$. Let us first consider the case where $s>0$. In this case we take ${\epsilon }_0>0$ such that

$$\{x_1,\dots ,x_s\}\subset B_{\frac{1}{2{\epsilon }_0}}(0)\text{and}{B}_{{\epsilon }_0}(x_i)\cap B_{{\epsilon }_0}(x_j)=\mathrm{\varnothing }\text{for }i\ne j.$$

We also define

$${\mathrm{\Psi }}_{\epsilon }(x):=\mathrm{\Phi }(\epsilon x)-\sum _{i=1}^s\mathrm{\Phi }\left(\frac{x-x_i}{\epsilon }\right)$$

for all $0<\epsilon <{\epsilon }_0$. Thus,

$${\mathrm{\Psi }}_{\epsilon }(x)=\{\begin{array}{ll}0& \text{if }x\in {\bigcup }_{i=1}^s{B}_{\frac{\epsilon }{2}}(x_i),\\ 1& \text{if }x\in A_{\epsilon }:=B_{\frac{1}{2\epsilon }}(0)\setminus {\bigcup }_{i=1}^s{B}_{\epsilon }(x_i).\end{array}$$

Now, let us define

$$P_n:=({|\mathrm{\nabla }{u}_n|}^{p-2}\mathrm{\nabla }{u}_n-{|\mathrm{\nabla }u|}^{p-2}\mathrm{\nabla }u+{|\mathrm{\nabla }{u}_n|}^{q-2}\mathrm{\nabla }{u}_n-{|\mathrm{\nabla }u|}^{q-2}\mathrm{\nabla }u)(\mathrm{\nabla }{u}_n-\mathrm{\nabla }u).$$

We claim that $P_n\ge 0$. Indeed, this is a consequence of the well-known fact: there exists $C(s)>0$ such that

$$〈{|x|}^{s-2}x-{|y|}^{s-2}y,x-y〉\ge C(s)\{\begin{array}{ll}\frac{{|x-y|}^2}{{(|x|+|y|)}^{2-s}}& \text{if }1\le s<2,\\ {|x-y|}^s& \text{if }s\ge 2\end{array}\text{for all }x,y\in {\mathbb{R}}^N.$$

(14)

Fix $\rho ,\epsilon >0$ with $0<\epsilon <\rho <{\epsilon }_0$. Then

$${\int }_{A_{\rho }}{P}_{n}dx\le {\int }_{A_{\rho }}{P}_n{\mathrm{\Psi }}_{\epsilon }dx\le {\int }_{{\mathbb{R}}^N}{P}_n{\mathrm{\Psi }}_{\epsilon }dx,$$

and thus

$$\begin{array}{rcl}{\int }_{A_{\rho }}{P}_{n}dx& \le & {\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^p{\mathrm{\Psi }}_{\epsilon }-{|\mathrm{\nabla }{u}_n|}^{p-2}{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }{u}_n\mathrm{\nabla }u\\ -{|\mathrm{\nabla }u|}^{p-2}{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }u\mathrm{\nabla }{u}_n+{|\mathrm{\nabla }u|}^p{\mathrm{\Psi }}_{\epsilon }dx\\ +{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^q{\mathrm{\Psi }}_{\epsilon }-{|\mathrm{\nabla }{u}_n|}^{q-2}{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }{u}_n\mathrm{\nabla }u\\ -{|\mathrm{\nabla }u|}^{q-2}{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }u\mathrm{\nabla }{u}_n+{|\mathrm{\nabla }u|}^q{\mathrm{\Psi }}_{\epsilon }dx\\ =& I_{\lambda }^{\prime }(u_n)(u_n{\mathrm{\Psi }}_{\epsilon })-{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{p-2}\mathrm{\nabla }{u}_n\mathrm{\nabla }{\mathrm{\Psi }}_{\epsilon }{u}_{n}dx\\ -{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{q-2}\mathrm{\nabla }{u}_n\mathrm{\nabla }{\mathrm{\Psi }}_{\epsilon }{u}_{n}dx\\ -I_{\lambda }^{\prime }(u_n)(u{\mathrm{\Psi }}_{\epsilon })+{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{p-2}\mathrm{\nabla }{u}_n\mathrm{\nabla }{\mathrm{\Psi }}_{\epsilon }udx\\ +{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{q-2}\mathrm{\nabla }{u}_n\mathrm{\nabla }{\mathrm{\Psi }}_{\epsilon }udx\\ -{\int }_{{\mathbb{R}}^N}\lambda g{u}_{n_{+}}^{r}u{\mathrm{\Psi }}_{\epsilon }dx-{\int }_{{\mathbb{R}}^N}{u}_{n_{+}}^{p^{\star }-1}u{\mathrm{\Psi }}_{\epsilon }dx+{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^p{\mathrm{\Psi }}_{\epsilon }dx\\ +{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^q{\mathrm{\Psi }}_{\epsilon }dx-{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{p-2}{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }{u}_n\mathrm{\nabla }udx\\ -{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{q-2}{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }{u}_n\mathrm{\nabla }udx\\ +{\int }_{{\mathbb{R}}^N}\lambda g{u}_{n_{+}}^{r+1}{\mathrm{\Psi }}_{\epsilon }dx+{\int }_{{\mathbb{R}}^N}{u}_{n_{+}}^{p^{\star }}{\mathrm{\Psi }}_{\epsilon }dx\\ -{\int }_{{\mathbb{R}}^N}\lambda g{u}_{n_{+}}^{r}u{\mathrm{\Psi }}_{\epsilon }dx-{\int }_{{\mathbb{R}}^N}{u}_{n_{+}}^{p^{\star }-1}u{\mathrm{\Psi }}_{\epsilon }dx.\end{array}$$

Since both $\{u{\mathrm{\Psi }}_{\epsilon }\}$ and $\{u_n{\mathrm{\Psi }}_{\epsilon }\}$ are bounded in $\mathbb{W}$, we have

$$I_{\lambda }^{\prime }(u_n)u{\mathrm{\Psi }}_{\epsilon },I_{\lambda }^{\prime }(u_n)u_n{\mathrm{\Psi }}_{\epsilon }\to 0.$$

(15)

By Claim 3 in [5] and by the same argument replacing p by q, we have

$$\underset{n}{lim}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{p-2}\mathrm{\nabla }{u}_n\mathrm{\nabla }{\mathrm{\Psi }}_{\epsilon }{u}_{n}dx=\underset{n}{lim}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{q-2}\mathrm{\nabla }{u}_n\mathrm{\nabla }{\mathrm{\Psi }}_{\epsilon }{u}_{n}dx=o(\epsilon )$$

and

$$\underset{n}{lim}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{p-2}\mathrm{\nabla }{u}_n\mathrm{\nabla }{\mathrm{\Psi }}_{\epsilon }udx=\underset{n}{lim}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{q-2}\mathrm{\nabla }{u}_n\mathrm{\nabla }{\mathrm{\Psi }}_{\epsilon }udx=o(\epsilon ).$$

(16)

Since the functional

$$f(v):={\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{p-2}\mathrm{\nabla }u{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }vdx+{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{q-2}\mathrm{\nabla }u{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }vdx$$

is bounded in $\mathbb{W}$, we have

$$\begin{array}{c}\underset{n}{lim}({\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{p-2}\mathrm{\nabla }u{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }{u}_{n}dx+{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{q-2}\mathrm{\nabla }u{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }{u}_{n}dx)\hfill \\ ={\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{p-2}\mathrm{\nabla }u{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }udx+{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{q-2}\mathrm{\nabla }u{\mathrm{\Psi }}_{\epsilon }\mathrm{\nabla }udx.\hfill \end{array}$$

(17)

It follows from Lemma 4 that

$$\{\begin{array}{ll}{u}_{n+}^{p^{\star }-1}\rightharpoonup u_{+}^{p^{\star }-1}& \text{in }{L}^{\frac{p^{\star }}{p^{\star }-1}}({\mathbb{R}}^N),\\ u_{n+}^r\rightharpoonup u_{+}^r& \text{in }{L}^{\frac{p^{\star }}{r}}({\mathbb{R}}^N),\\ u_{n+}^{r+1}\rightharpoonup u_{+}^{r+1}& \text{in }{L}^{\frac{p^{\star }}{r+1}}({\mathbb{R}}^N).\end{array}$$

Since $u\ge 0$, we have

$${\int }_{{\mathbb{R}}^N}g{u}_{n+}^{r+1}{\mathrm{\Psi }}_{\epsilon }dx\to {\int }_{{\mathbb{R}}^N}g{u}_{+}^{r+1}{\mathrm{\Psi }}_{\epsilon }dx,$$

(18)

$${\int }_{{\mathbb{R}}^N}g{u}_{n+}^{r}u{\mathrm{\Psi }}_{\epsilon }dx\to {\int }_{{\mathbb{R}}^N}g{u}_{+}^{r+1}{\mathrm{\Psi }}_{\epsilon }dx$$

(19)

and

$${\int }_{{\mathbb{R}}^N}{u}_{n+}^{p^{\star }-1}u{\mathrm{\Psi }}_{\epsilon }dx\to {\int }_{{\mathbb{R}}^N}{u}_{+}^{p^{\star }}{\mathrm{\Psi }}_{\epsilon }dx.$$

(20)

It follows from Lemma 3 that

$${\int }_{{\mathbb{R}}^N}{u}_{n+}^{p^{\star }}{\mathrm{\Psi }}_{\epsilon }dx\to {\int }_{{\mathbb{R}}^N}{u}_{+}^{p^{\star }}{\mathrm{\Psi }}_{\epsilon }dx.$$

(21)

We then conclude from (15)-(21) that

$$\underset{n}{lim}{\int }_{A_{\rho }}{P}_{n}dx=0.$$

Note that

$$\begin{array}{rcl}{P}_n& =& ({|\mathrm{\nabla }{u}_n|}^{p-2}\mathrm{\nabla }{u}_n-{|\mathrm{\nabla }u|}^{p-2}\mathrm{\nabla }u)(\mathrm{\nabla }{u}_n-\mathrm{\nabla }u)\\ +({|\mathrm{\nabla }{u}_n|}^{q-2}\mathrm{\nabla }{u}_n-{|\mathrm{\nabla }u|}^{q-2}\mathrm{\nabla }u)(\mathrm{\nabla }{u}_n-\mathrm{\nabla }u)\end{array}$$

and that (14) yields that each term above is nonnegative. Therefore,

$$\underset{n}{lim}{\int }_{A_{\rho }}({|\mathrm{\nabla }{u}_n|}^{p-2}\mathrm{\nabla }{u}_n-{|\mathrm{\nabla }u|}^{p-2}\mathrm{\nabla }u)(\mathrm{\nabla }{u}_n-\mathrm{\nabla }u)dx=0.$$

Lemma 5 with $a(x,\xi )={|\xi |}^{p-2}\xi$ then implies that $\mathrm{\nabla }{u}_n\to \mathrm{\nabla }u$ in $L^p(A_{\rho })$. Thus,

$$\frac{\partial u_n}{\partial x_j}\to \frac{\partial u}{\partial x_j}\text{a.e. in }{A}_{\rho }.$$

Since $\rho <{\epsilon }_0$ we have, in fact, that

$$\frac{\partial u_n}{\partial x_j}\to \frac{\partial u}{\partial x_j}\text{a.e. in }{\mathbb{R}}^N.$$

At last, in the case where $s=0$, that is, ${\nu }_i=0$ for all i, we just take ${\mathrm{\Psi }}_{\epsilon }(x):=\mathrm{\Phi }(\epsilon x)$ and $A_{\rho }:=B_{\frac{1}{2\rho }}$ and repeat the arguments above. □

From now on we denote, for each $\lambda >0$,

$${\tilde{c}}_{\lambda }:=\underset{u\in \mathbb{W}\setminus \{0\}}{inf}\underset{t\ge 0}{max}{I}_{\lambda }(tu).$$

(22)

Lemma 9

There exists ${\lambda }^{\ast }>0$ such that

$$0<{\tilde{c}}_{\lambda }<\frac{S^{\frac{N}{p}}}{N}\mathit{\text{for all }}\lambda >{\lambda }^{\ast }.$$

Proof

It follows from Lemma 6 that $I_{\lambda }(u)\ge \eta >0$ whenever $\parallel u\parallel =\rho$. Of course, this fact implies that ${\tilde{c}}_{\lambda }\ge \eta >0$. (We remark that η might depend on λ, but it is always positive.)

We recall that ${\mathrm{\Omega }}_g$ denotes the open set where g is positive. Let $u_0\in \mathbb{W}\setminus \{0\}$ with support in ${\mathrm{\Omega }}_g$ such that $u_0\ge 0$ and ${\parallel u_0\parallel }_{p^{\star }}=1$. Since

$$I_{\lambda }(t{u}_0)=\frac{t^p}{p}{\parallel u_0\parallel }_{{\mathbb{E}}_p}^p+\frac{t^q}{q}{\parallel u_0\parallel }_{{\mathbb{E}}_q}^q-\frac{t^{r+1}\lambda }{r+1}{\int }_{{\mathbb{R}}^N}g{u}_0^{r+1}dx-\frac{t^{p^{\star }}}{p^{\star }},t\ge 0,$$

we can see that $I_{\lambda }(t{u}_0)\to -\mathrm{\infty }$ as $t\to \mathrm{\infty }$ and that $I_{\lambda }(t{u}_0)\to 0^{+}$ as $t\to 0^{+}$. These facts imply that there exists $t_{\lambda }>0$ such that

$$\underset{t\ge 0}{max}{I}_{\lambda }(t{u}_0)=I_{\lambda }(t_{\lambda }{u}_0).$$

Since

$$\begin{array}{rcl}0& =& \frac{d}{dt}{[I_{\lambda }(t{u}_0)]}_{t=t_{\lambda }}\\ =& t_{\lambda }^{p-1}{\parallel u_0\parallel }_{{\mathbb{E}}_p}^p+t_{\lambda }^{q-1}{\parallel u_0\parallel }_{{\mathbb{E}}_q}^q-\lambda t_{\lambda }^r{\int }_{{\mathbb{R}}^N}g{u}_{0_{+}}^{r+1}dx-t_{\lambda }^{p^{\star }-1},\end{array}$$

we get

$$\lambda {\int }_{{\mathbb{R}}^N}g{u}_{0_{+}}^{r+1}dx=\frac{{\parallel u_0\parallel }_{{\mathbb{E}}_p}^p}{t_{\lambda }^{1+r-p}}+\frac{{\parallel u_0\parallel }_{{\mathbb{E}}_q}^q}{t_{\lambda }^{1+r-q}}-t_{\lambda }^{p^{\star }-1-r}\text{for all }\lambda >0,$$

(23)

where the left-hand side term is positive, since the support of $u_{0+}$ is contained in ${\mathrm{\Omega }}_g$. We can see from (23) that $t_{\lambda }\to 0$ as $\lambda \to \mathrm{\infty }$. Since $I_{\lambda }(t_{\lambda }{u}_0)\to 0^{+}$ as $t_{\lambda }\to 0^{+}$, there exists ${\lambda }^{\ast }>0$ such that

$$\underset{t\ge 0}{max}{I}_{\lambda }(t{u}_0)=I_{\lambda }(t_{\lambda }{u}_0)<\frac{S^{\frac{N}{p}}}{N}\text{for all }\lambda >{\lambda }^{\ast }.$$

Since ${\tilde{c}}_{\lambda }\le {max}_{t\ge 0}{I}_{\lambda }(t{u}_0)$, we conclude that

$${\tilde{c}}_{\lambda }<\frac{S^{\frac{N}{p}}}{N}\text{for all }\lambda >{\lambda }^{\ast }.$$

 □

Now we are in a position to prove Theorem 1.

Proof of Theorem 1

It follows from Lemmas 6 and 2 that there exists a sequence $\{u_n\}\subset \mathbb{W}$ such that

$$I_{\lambda }(u_n)\to c_{\lambda }\text{and}{I}_{\lambda }^{\prime }(u_n)\to 0,$$

where $c_{\lambda }$ is the minimax level of the mountain pass theorem associated with $I_{\lambda }$.

Arguing as in Lemma 2.2 of [18], one can check that

$$c_{\lambda }=\underset{u\in \mathbb{W}\setminus \{0\}}{inf}\underset{t\ge 0}{max}{I}_{\lambda }(tu):={\tilde{c}}_{\lambda }.$$

By Lemma 9 there exists ${\lambda }^{\ast }>0$ such that $0<c_{\lambda }<\frac{S^{\frac{N}{p}}}{N}$ for all $\lambda >{\lambda }^{\ast }$. Moreover, according to Lemmas 7 and 8, there exists a nonnegative function $u\in \mathbb{W}$ such that

$$\{\begin{array}{ll}{u}_n\rightharpoonup u& \text{in }\mathbb{W},\\ u_{n_{+}}\to u& \text{a.e. in }{\mathbb{R}}^N,\\ \frac{\partial u_n}{\partial x_i}(x)\to \frac{\partial u}{\partial x_i}(x)& \text{a.e. in }{\mathbb{R}}^N.\end{array}$$

It follows from Lemma 4 that

$$\{\begin{array}{ll}{|\mathrm{\nabla }{u}_n|}^{p-2}\frac{\partial u_n}{\partial x_i}\rightharpoonup {|\mathrm{\nabla }u|}^{p-2}\frac{\partial u}{\partial x_i}(x)& \text{in }{L}^{\frac{p}{p-1}}({\mathbb{R}}^N),\\ {|\mathrm{\nabla }{u}_n|}^{q-2}\frac{\partial u_n}{\partial x_i}\rightharpoonup {|\mathrm{\nabla }u|}^{q-2}\frac{\partial u}{\partial x_i}(x)& \text{in }{L}^{\frac{q}{q-1}}({\mathbb{R}}^N)\end{array}$$

and

$$\{\begin{array}{ll}{u}_{n_{+}}^{p^{\star }-1}\rightharpoonup u_{+}^{p^{\star }-1}& \text{in }{L}^{\frac{p^{\star }}{p^{\star }-1}}({\mathbb{R}}^N),\\ u_{n_{+}}^r\rightharpoonup u_{+}^r& \text{in }{L}^{\frac{p^{\star }}{r}}({\mathbb{R}}^N).\end{array}$$

Now, let $\varphi \in \mathbb{W}$. We have

$$\begin{array}{c}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{p-2}\mathrm{\nabla }{u}_n\mathrm{\nabla }\varphi dx\to {\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{p-2}\mathrm{\nabla }u\mathrm{\nabla }\varphi dx,\hfill \\ {\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{q-2}\mathrm{\nabla }{u}_n\mathrm{\nabla }\varphi dx\to {\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }u|}^{q-2}\mathrm{\nabla }u\mathrm{\nabla }\varphi dx,\hfill \\ {\int }_{{\mathbb{R}}^N}{u}_{n_{+}}^{p^{\star }-1}\varphi dx\to {\int }_{{\mathbb{R}}^N}{u}_{+}^{p^{\star }-1}\varphi dx\text{and}{\int }_{{\mathbb{R}}^N}g{u}_{n_{+}}^r\varphi dx\to {\int }_{{\mathbb{R}}^N}g{u}_{+}^r\varphi dx.\hfill \end{array}$$

Thus $I_{\lambda }^{\prime }(u)\varphi =0$, and we conclude that u is a solution of (1).

We know that $u\ge 0$. It remains to verify that $u\not\equiv 0$. Let

$$\underset{n\to \mathrm{\infty }}{lim}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{p}dx=:a\ge 0\text{and}\underset{n\to \mathrm{\infty }}{lim}{\int }_{{\mathbb{R}}^N}{|\mathrm{\nabla }{u}_n|}^{q}dx=:b\ge 0$$

and suppose that $u\equiv 0$.

Since $I_{\lambda }^{\prime }(u_n)u_n\to 0$, we also have

$${\parallel u_n\parallel }_{{\mathbb{E}}_p}^p+{\parallel u_n\parallel }_{{\mathbb{E}}_q}^q={\int }_{{\mathbb{R}}^N}\lambda g{u}_{n_{+}}^{r+1}dx+{\int }_{{\mathbb{R}}^N}{u}_{n_{+}}^{p^{\star }}dx+o(1).$$

Since ${\int }_{{\mathbb{R}}^N}\lambda g{u}_{n_{+}}^{r+1}dx\to 0$, we have

$${\parallel u_n\parallel }_{{\mathbb{E}}_p}^p=a+o(1),{\parallel u_n\parallel }_{{\mathbb{E}}_p}^q=b+o(1)\text{and}{\parallel u_{n_{+}}\parallel }_{p^{\star }}^{p^{\star }}=a+b+o(1).$$

By taking into account that $I_{\lambda }(u_n)\to c_{\lambda }$, we have

$$\frac{a}{p}+\frac{b}{q}-\frac{a+b}{p^{\star }}=c_{\lambda }>0.$$

Hence,

$$c_{\lambda }=\frac{a}{N}+b(\frac{1}{q}-\frac{1}{p^{\star }})\ge \frac{a}{N},$$

(24)

and we arrive at

$$c_{\lambda }N\ge a.$$

(25)

However, the equality in (24) shows that $a+b\ne 0$. By (7) and making $n\to \mathrm{\infty }$, we have

$$S{(a+b)}^{\frac{p}{p^{\star }}}\le a.$$

(26)

It follows that $a>0$. Thus

$$S{a}^{\frac{p}{p^{\star }}}\le S{(a+b)}^{\frac{p}{p^{\star }}}\le a,$$

that is,

$$a\ge S^{\frac{N}{p}}.$$

Then by (25) we have

$$c_{\lambda }N\ge S^{\frac{N}{p}},$$

which is a contradiction, because $c_{\lambda }<\frac{S^{\frac{N}{p}}}{N}$. □

Remark 10

By Theorems 1 and 2 of [2] it is easy to see that any solution of (1) is locally $C^{1,\alpha }$ if $g\in L^{\gamma }({\mathbb{R}}^N)\cap L^{\mathrm{\infty }}({\mathbb{R}}^N)$ and $1<q<p<r+1<p^{\star }$.