1 Introduction

The inertial neural networks model, which was first proposed by Babcock and Westerwelt [1, 2], is one of the other popular artificial neural network models used in a variety of application areas. This type of neural networks has received much attention by many researchers. In particular, numerous works have been devoted to study the dynamic behaviors on inertial neural networks with time-varying delays and some excellent results are reported, for example, stability [3–5], Hopf bifurcation [6–11], and synchronization [12–14]. To the best of our knowledge, the dynamics analysis on inertial neural networks is usually to convert them into a first-order differential system by reducing order variable substitution under the assumption that the activation functions are bounded [15–17]. However, the authors in [12, 18–21] pointed out that the above method not only raises the dimension in the inertial neural networks system, but also increases huge amount of computation which makes it difficult to realize in practice. For the above reasons, the authors of [19, 20] and [21], respectively, developed some non-reduced order techniques to investigate the stability and synchronization of inertial neural networks with different types of time delays.

On the other hand, in neural networks dynamics involving fields such as communication, economics, biology or ecology, the relevant state variables are usually considered as proteins and molecules, light intensity levels or electric charges, which are naturally anti-periodic [22–24]. Considering this factor, many recurrent neural network models involving time-varying delays and anti-periodic environments have been widely investigated in [16, 17, 24–26]. It is worth noting that the high-order Hopfield neural networks have the advantages of faster convergence speed, larger storage capacity and stronger fault tolerance than lower-order neural networks [27–29]. Consequently, Yao [30] studied the existence and global exponential stability of anti-periodic solutions for a class of proportional delayed high-order inertial Hopfield neural networks with time-varying delays.

In recent years, the authors in [21] have mentioned that many parallel routes with a series of different axon sizes and lengths appear in neural networks, and it is desired to explain the dynamics behaviors of neural networks by involving continuously distributed delays. Furthermore, the dynamic behaviors of many recurrent neural networks with continuously distributed delays have been revealed in [27, 31–35]. However, few articles have considered the anti-periodic problem for the following high-order inertial Hopfield neural networks (HIHNNs) involving time-varying delays and continuously distributed delays:

$$ \begin{aligned}[b] x_{i}''(t)=&-a_{i}(t)x_{i}'(t)-b_{i}(t)x_{i}(t)+ \sum_{j=1}^{n} c_{ij}(t)A_{j} \bigl(x_{j}(t)\bigr) \\ &\quad {}+\sum_{j=1}^{n} d_{ij}(t)B_{j}\bigl(x_{j}\bigl(t- q_{ij}( t)\bigr) \bigr) \\ &\quad {}+ \sum_{j=1}^{n}\sum _{l=1}^{n}\theta _{ijl}(t)Q_{j} \bigl(x_{j}\bigl( t-\eta _{ijl} (t) \bigr) \bigr)Q_{l}\bigl(x_{l}\bigl( t-\xi _{ijl}( t) \bigr)\bigr) \\ &\quad {}+ \sum_{j=1}^{n}h_{ij} (t) \int _{0}^{+\infty }\sigma _{ij}(u) K_{j}\bigl(x_{j}(t-u)\bigr)\,du \\ &\quad {}+ \sum_{j=1}^{n}\sum _{l=1}^{n}p_{ijl}(t) \int _{0}^{+ \infty }\hat{\sigma }_{ijl}(u) R_{j}\bigl(x_{j}(t-u)\bigr)\,du \\ &\quad {} \times \int _{0}^{+\infty } \bar{\sigma } _{ijl}(u) R_{l}\bigl(x_{l}(t-u)\bigr)\,du+J_{i}(t), \end{aligned} $$
(1.1)

and the initial value conditions:

$$ x_{i}(s)=\varphi _{i}(s),\qquad x_{i}'(0)= \psi _{i},\quad -\infty \leq s \leq 0, \varphi _{i} \in BC\bigl((- \infty , 0], \mathbb{R}\bigr), \psi _{i}\in \mathbb{R}, $$
(1.2)

where \(BC((-\infty ,0], \mathbb{R})\) is the set of all continuous and bounded functions from \((-\infty ,0]\) to \(\mathbb{R}\), \(J_{i}, c_{ij}, d_{ij}, \theta _{ijl}, h_{ij}, p_{ijl} :\mathbb{R} \rightarrow \mathbb{R}\), \(a_{i}, b_{i} : \mathbb{R}\rightarrow (0, +\infty )\) and \(q_{ij} , \eta _{ijl} , \xi _{ijl} :\mathbb{R}\rightarrow \mathbb{R}^{+}\) are bounded and continuous functions, \(a_{i}\), \(b_{i}\), \(q_{ij}\), \(\eta _{ijl}\), \(\xi _{ijl}\) are periodic functions with period \(T>0\), the input term \(J_{i}\) is T-anti-periodic (i.e. \(J_{i}(t+T)=-J_{i}(t)\) for all \(t\in \mathbb{R}\)), and \(i,j,l\in D= \{1,2,\ldots ,n\}\).

Motivated by the previous discussions, in this paper, without adopting the reduced order method, we shall install new results concerning the anti-periodic dynamics for HIHNNs with time-varying delays and continuously distributed delays. Some sufficient conditions ensuring the existence and global exponential stability on the anti-periodic solution of system (1.1) are established by using differential inequalities and the Lyapunov function method, which improve and complement some earlier publications [16, 17, 36–40].

We organize the paper as follows. In Sect. 2, some assumptions and an important lemmas are listed. Section 3 presents the main results and their detailed proof. Section 4 gives a numerical example to demonstrate the feasibility of the main results. Conclusions are drawn in Sect. 5.

2 Preliminary results

In this section, some assumptions and a key lemma are provided.

Assumptions

\((G_{1})\) :

There are nonnegative constants \(L^{A}_{j}\), \(L^{B}_{j}\), \(L^{Q}_{j}\), \(L^{K}_{j}\), \(L^{R}_{j}\), \(M^{Q}_{j}\) and \(M^{R}_{j}\) such that

$$\begin{aligned}& \textstyle\begin{cases} \vert A_{j}(u )-A_{j}(v ) \vert \leq L^{A} _{j} \vert u -v \vert , \qquad \vert B_{j}(u )-B_{j}(v ) \vert \leq L^{B}_{j} \vert u -v \vert , \\ \vert Q_{j}(u )-Q_{j}(v ) \vert \leq L^{Q}_{j} \vert u -v \vert , \qquad \vert K_{j}(u )-K_{j}(v ) \vert \leq L^{K} _{j} \vert u -v \vert , \\ \vert R_{j}(u )-R_{j}(v ) \vert \leq L^{R} _{j} \vert u -v \vert , \qquad \vert Q_{j}(u) \vert \leq M_{j}^{Q},\qquad \vert R_{j}(u) \vert \leq M_{j}^{R} , \end{cases}\displaystyle \\& \textstyle\begin{cases} c_{ij}(t+ T )A_{j}(u)=-c_{ij}(t)A_{j}(-u), \qquad d_{ij}(t+T)B_{j}(u)=-d_{ij}(t)B_{j}(-u), \\ \theta _{ijl}(t+T)Q_{j}(u)Q_{l}(v)=-\theta _{ijl}(t)Q_{j}(-u)Q_{l}(-v), \\ h_{ij}(t+T)\int _{0}^{+\infty }\sigma _{ij}(s)K_{j}(u)\,ds=- h_{ij}(t) \int _{0}^{+\infty }\sigma _{ij}(s)K_{j}(-u)\,ds, \end{cases}\displaystyle \end{aligned}$$

and

$$\begin{aligned}& p_{ijl}(t+T) \int _{0}^{+\infty }\hat{\sigma }_{ijl}(s)R_{j}(u) \,ds \int _{0}^{+ \infty }\bar{\sigma }_{ijl}(s)R_{l}(u) \,ds \\& \quad = -p_{ijl}(t) \int _{0}^{+\infty }\hat{\sigma }_{ijl}(s)R_{j}(-u) \,ds \int _{0}^{+\infty }\bar{\sigma }_{ijl}(s)R_{l}(-u) \,ds, \end{aligned}$$

for all \(u , v \in \mathbb{R} \), \(i, j, l \in D \).

\((G_{2})\) :

For \(i, j, l \in D \), \(|\sigma _{ij}(t)|e^{\mu t}\), \(|\hat{\sigma }_{ijl}(t)|e^{\mu t}\), \(|\bar{\sigma }_{ijl}(t)|e^{\mu t}\) are integrable on \([0, +\infty )\) for a positive constant μ.

\((G_{3})\) :

There are constants \(\beta _{i}>0\) and \(\alpha _{i}\geq 0\), \(\gamma _{i}\geq 0\) obeying

$$ C_{i} (t)< 0,\qquad 4C_{i}(t)D_{i }(t)> E_{i}^{2}(t),\quad \forall t \in \mathbb{R}, i\in D, $$
(2.1)

where

$$\begin{aligned}& \begin{aligned} C_{i}(t) ={}&\alpha _{i}\gamma _{i}-a_{i}(t) \alpha _{i}^{2} + \frac{1}{2}\alpha _{i}^{2}\sum_{j=1}^{n} \bigl( \bigl\vert c_{ij}(t) \bigr\vert L^{A}_{j} + \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j} \bigr) \\ &{} +\frac{1}{2} \alpha _{i}^{2}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l}+L^{Q}_{j}M^{Q}_{l} \bigr) \\ &{} +\frac{1}{2}\alpha _{i}^{2}\sum _{j=1}^{n} \bigl\vert h_{ij}(t) \bigr\vert L_{j}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \,du \\ &{} +\frac{1}{2}\alpha _{i}^{2}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl\vert p_{ijl}(t) \bigr\vert M_{j}^{R}L_{l}^{R} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \\ &{} +\frac{1}{2}\alpha _{i}^{2}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl\vert p_{ijl}(t) \bigr\vert M_{l}^{R}L_{j}^{R} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du, \end{aligned} \\& \begin{aligned} D_{i}(t) ={}& {-}b_{i}(t)\alpha _{i}\gamma _{i} +\frac{1}{2}\sum _{j=1}^{n}\bigl( \bigl\vert c_{ij}(t) \bigr\vert L^{A}_{j}+ \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j} \bigr) \vert \alpha _{i}\gamma _{i} \vert \\ &{}+\frac{1}{2}\sum_{j=1}^{n} \alpha _{j}^{2}\biggl( \bigl\vert c_{ji}(t) \bigr\vert L^{A}_{i} + d_{ji}^{+} L^{B}_{i}\frac{1}{1-\dot{q} _{ji} ^{+}}e^{2\lambda q_{ji}^{+}} \biggr) \\ &{}+\frac{1}{2}\sum_{j=1}^{n} \biggl( \bigl\vert c_{ji}(t) \bigr\vert L^{A}_{i} + d_{ji}^{+} L^{B}_{i} \frac{1}{1-\dot{q} _{ji} ^{+}}e^{2\lambda q_{ji}^{+}}\biggr) \vert \alpha _{j} \gamma _{j} \vert \\ &{}+\frac{1}{2} \sum_{j=1}^{n} \sum_{l=1}^{n} \vert \alpha _{i}\gamma _{i} \vert \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l}+L^{Q}_{j}M^{Q}_{l} \bigr) \\ &{}+\frac{1}{2} \sum_{l=1}^{n} \sum_{j=1}^{n}\bigl( \alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr) \theta _{lji} ^{+} M^{Q}_{j}L^{Q}_{i} e^{2\lambda \xi _{lji} ^{+}} \frac{1}{1-\dot{\xi } _{lji} ^{+}} \\ &{}+\frac{1}{2} \sum_{j=1}^{n} \sum_{l=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \theta _{jil} ^{+}L^{Q}_{i}M^{Q}_{l} e^{2 \lambda \eta _{jil} ^{+}} \frac{1}{1-\dot{\eta } _{jil} ^{+}} \\ &{}+\frac{1}{2}\sum_{j=1}^{n} \bigl(\alpha _{j}^{2} h_{ji}^{+}+ \vert \alpha _{j}\gamma _{j} \vert h_{ji}^{+}\bigr)L_{i}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ji}(u) \bigr\vert e^{2\lambda u}\,du \\ &{}+\frac{1}{2}\sum_{l=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{l}^{2} + \vert \alpha _{l}\gamma _{l} \vert \bigr)p_{lji}^{+} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{lji}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{lji}(u) \bigr\vert e^{2 \lambda u}\,duM_{j}^{R}L_{i}^{R} \\ &{}+\frac{1}{2}\sum_{j=1}^{n} \sum_{l=1}^{n}\bigl(\alpha _{j}^{2} + \vert \alpha _{j}\gamma _{j} \vert \bigr)p_{jil}^{+} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{jil}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{jil}(u) \bigr\vert e^{2 \lambda u}\,duM_{l}^{R}L_{i}^{R} \\ &{}+\frac{1}{2}\sum_{j=1}^{n} \vert \alpha _{i}\gamma _{i} \vert \bigl\vert h_{ij}(t) \bigr\vert L_{j}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \,du \\ &{}+\frac{1}{2}\sum_{j=1}^{n} \sum_{l=1}^{n} \vert \alpha _{i} \gamma _{i} \vert \bigl\vert p_{ijl}(t) \bigr\vert M_{j}^{R}L_{l}^{R} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \\ &{}+\frac{1}{2}\sum_{j=1}^{n} \sum_{l=1}^{n} \vert \alpha _{i} \gamma _{i} \vert \bigl\vert p_{ijl}(t) \bigr\vert M_{l}^{R}L_{j}^{R} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du , \end{aligned} \\& E_{i}(t) = \beta _{i}+\gamma _{i}^{2} -a_{i}(t)\alpha _{i}\gamma _{i}-b_{i}(t) \alpha _{i}^{2}, \qquad \dot{q}_{ij}^{+}= \max_{t\in [0, T]}q'_{ij}(t), \\& \dot{\eta }_{ijl}^{+}=\max_{t\in [0, T]}\eta '_{ijl}(t),\qquad \dot{\xi }_{ijl}^{+}= \max_{t\in [0, T]}\xi '_{ijl}(t), \\& q_{ij}^{+}=\max_{t\in [0, T]}q_{ij}(t),\qquad \eta _{ijl}^{+}= \max_{t\in [0, T]}\eta _{ijl}(t), \end{aligned}$$

and

$$\begin{aligned}& \xi _{ijl}^{+}=\max_{t\in [0, T]}\xi _{ijl}(t), \qquad c_{ij}^{+}=\sup _{t\in \mathbb{R}} \bigl\vert c_{ij}(t) \bigr\vert ,\qquad d_{ij}^{+}=\sup_{t\in \mathbb{R}} \bigl\vert d_{ij}(t) \bigr\vert , \\& \theta _{ijl}^{+}= \sup_{t\in \mathbb{R}} \bigl\vert \theta _{ijl}(t) \bigr\vert ,\quad i,j, l\in D . \end{aligned}$$
\((G_{4})\) :

For \(i, j, l\in D\), \(q_{ij}\), \(\eta _{ijl}\) and \(\xi _{ijl}\) are continuously differentiable, \(q_{ij}'(t)=\dot{q_{ij}} (t)< 1\), \(\eta _{ijl}'(t)=\dot{\eta _{ijl} }(t)< 1\) and \(\xi _{ijl}'(t)=\dot{\xi _{ijl}} (t)< 1\), for all \(t\in \mathbb{R}\).

Remark 2.1

According to \((G_{1})\) and the basic theory on functional differential equation with infinite delay in [41], one can show that all solutions of (1.1) and (1.2) exist in \([0, +\infty )\).

Lemma 2.1

Assume that\((G_{1})\), \((G_{2})\), \((G_{3})\)and\((G_{4})\)hold. Let\(x (t)=(x_{1}(t), x_{2}(t), \ldots , x_{n}(t))\)and\(y (t)=(y_{1}(t), y_{2}(t),\ldots , y_{n}(t))\)be two solutions of system (1.1) satisfying

$$ x_{i}(s)=\varphi ^{x}_{i}(s),\qquad x_{i}'(0) = \psi ^{x}_{i} ,\qquad y_{i}(s)= \varphi ^{y}_{i}(s),\qquad y_{i}'(0) = \psi ^{y}_{i}, $$
(2.2)

where\(i\in D\), \(\varphi ^{x}_{i}, \varphi ^{y}_{i} \in BC((-\infty , 0], \mathbb{R})\), \(\psi ^{x}_{i}, \psi ^{y}_{i}\in \mathbb{R} \). Then there are two positive constantsλand\(M=M(\varphi ^{x}, \psi ^{x},\varphi ^{y}, \psi ^{y})\)such that

$$ \bigl\vert x_{i}(t)- y_{i}(t) \bigr\vert \leq M e^{ -\lambda t},\qquad \bigl\vert x_{i}'(t)- y_{i}'(t) \bigr\vert \leq M e^{- \lambda t},\quad \textit{for all } t\geq 0, i\in D. $$
(2.3)

Proof

Denote \(z_{i}(t) =y_{i}(t)-x_{i}(t) \), then

$$\begin{aligned} &z_{i}''(t) \\ &\quad =-a_{i}(t)z_{i}'(t)-b_{i}(t)z_{i}(t) \\ &\qquad {}+\sum_{j=1}^{n} c_{ij}(t) \widetilde{A}_{j}\bigl(z_{j}(t)\bigr) +\sum _{j=1}^{n} d_{ij}(t) \widetilde{B}_{j}\bigl(z_{j}\bigl(t- q_{ij}( t)\bigr) \bigr) + \sum_{j=1}^{n}\sum _{l=1}^{n}\theta _{ijl}(t) \\ &\qquad {} \times \bigl[Q_{j}\bigl(y_{j}\bigl( t-\eta _{ijl} (t) \bigr)\bigr)Q_{l}\bigl(y_{l} \bigl( t-\xi _{ijl}( t) \bigr)\bigr)-Q_{j} \bigl(y_{j}\bigl( t-\eta _{ijl} (t) \bigr) \bigr)Q_{l}\bigl(x_{l}\bigl( t-\xi _{ijl}( t) \bigr)\bigr) \\ &\qquad {} + Q_{j}\bigl(y_{j}\bigl(t-\eta _{ijl} (t) \bigr)\bigr)Q_{l}\bigl(x_{l}\bigl( t-\xi _{ijl}( t) \bigr)\bigr)- Q_{j}\bigl(x_{j} \bigl(t- \eta _{ijl} (t) \bigr)\bigr)Q_{l} \bigl(x_{l}\bigl( t-\xi _{ijl}( t) \bigr)\bigr)\bigr] \\ &\qquad {} + \sum_{j=1}^{n}h_{ij} (t) \int _{0}^{+\infty }\sigma _{ij}(u) \widetilde{K}_{j}\bigl(z_{j}(t-u)\bigr)\,du + \sum _{j=1}^{n}\sum _{l=1}^{n}p_{ijl}(t) \\ &\qquad {} \times \biggl[ \int _{0}^{+\infty }\hat{\sigma }_{ijl}(u) R_{j}\bigl(y_{j}(t-u)\bigr)\,du \int _{0}^{+\infty } \bar{\sigma } _{ijl}(u) R_{l}\bigl(y_{l}(t-u)\bigr)\,du \\ &\qquad {} - \int _{0}^{+\infty }\hat{\sigma }_{ijl}(u) R_{j}\bigl(y_{j}(t-u)\bigr)\,du \int _{0}^{+ \infty } \bar{\sigma } _{ijl}(u) R_{l}\bigl(x_{l}(t-u)\bigr)\,du \\ &\qquad {} + \int _{0}^{+\infty }\hat{\sigma }_{ijl}(u) R_{j}\bigl(y_{j}(t-u)\bigr)\,du \int _{0}^{+ \infty } \bar{\sigma } _{ijl}(u) R_{l}\bigl(x_{l}(t-u)\bigr)\,du \\ &\qquad {} - \int _{0}^{+\infty }\hat{\sigma }_{ijl}(u) R_{j}\bigl(x_{j}(t-u)\bigr)\,du \int _{0}^{+ \infty } \bar{\sigma } _{ijl}(u) R_{l}\bigl(x_{l}(t-u)\bigr)\,du\biggr], \end{aligned}$$

where

$$ \textstyle\begin{cases} \widetilde{A}_{j}(z_{j}(t)) = A_{j}(y_{j}(t))- A_{j}(x_{j}(t)), \\ \widetilde{B}_{j}(z_{j}(t-q_{ij}(t)))= B_{j}(y_{j}(t-q_{ij}(t))) - B_{j}(x_{j}(t-q_{ij}(t))), \\ \widetilde{K}_{j}(z_{j}(t-u))=K_{j}(y_{j}(t-u))-K_{j}(x_{j}(t-u)), \end{cases} $$

and \(i, j\in D\).

According to \((G_{2})\) and the boundedness of (1.1), one can select a constant \(\lambda >0\) such that

$$ C_{i}^{\lambda }(t) < 0,\qquad 4C_{i}^{\lambda }(t)D_{i }^{\lambda }(t)> \bigl(E_{i}^{\lambda }(t)\bigr)^{2}, \quad \forall t\in \mathbb{R}, $$
(2.4)

where

$$\begin{aligned}& \begin{aligned} C_{i} ^{\lambda }(t) ={}& \lambda \alpha _{i}^{2}+ \alpha _{i}\gamma _{i}-a_{i}(t) \alpha _{i}^{2} +\frac{1}{2}\alpha _{i}^{2}\sum_{j=1}^{n} \bigl( \bigl\vert c_{ij}(t) \bigr\vert L^{A}_{j} + \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j} \bigr) \\ &{}+\frac{1}{2} \alpha _{i}^{2}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l}+L^{Q}_{j}M^{Q}_{l} \bigr) \\ &{}+\frac{1}{2}\alpha _{i}^{2}\sum _{j=1}^{n} \bigl\vert h_{ij}(t) \bigr\vert L_{j}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \,du \\ &{}+\frac{1}{2}\alpha _{i}^{2}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl\vert p_{ijl}(t) \bigr\vert M_{j}^{R}L_{l}^{R} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \\ &{}+\frac{1}{2}\alpha _{i}^{2}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl\vert p_{ijl}(t) \bigr\vert M_{l}^{R}L_{j}^{R} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du, \end{aligned} \\ & D_{i} ^{\lambda }(t) \\ & \quad =-b_{i}(t)\alpha _{i}\gamma _{i}+ \lambda \beta _{i}+\lambda \gamma _{i}^{2} +\frac{1}{2}\sum_{j=1}^{n} \bigl( \bigl\vert c_{ij}(t) \bigr\vert L^{A}_{j}+ \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j} \bigr) \vert \alpha _{i}\gamma _{i} \vert \\ & \qquad {}+\frac{1}{2}\sum_{j=1}^{n} \alpha _{j}^{2}\biggl( \bigl\vert c_{ji}(t) \bigr\vert L^{A}_{i} + d_{ji}^{+} L^{B}_{i}\frac{1}{1-\dot{q} _{ji} ^{+}}e^{2\lambda q_{ji}^{+}} \biggr) \\ & \qquad {}+\frac{1}{2}\sum_{j=1}^{n} \biggl( \bigl\vert c_{ji}(t) \bigr\vert L^{A}_{i} + d_{ji}^{+} L^{B}_{i} \frac{1}{1-\dot{q} _{ji} ^{+}}e^{2\lambda q_{ji}^{+}}\biggr) \vert \alpha _{j} \gamma _{j} \vert \\ & \qquad {}+\frac{1}{2} \sum_{j=1}^{n} \sum_{l=1}^{n} \vert \alpha _{i} \gamma _{i} \vert \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l}+L^{Q}_{j}M^{Q}_{l} \bigr) \\ & \qquad {}+\frac{1}{2} \sum_{l=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr) \theta _{lji} ^{+} M^{Q}_{j}L^{Q}_{i} e^{2 \lambda \xi _{lji} ^{+}} \frac{1}{1-\dot{\xi } _{lji} ^{+}} \\ & \qquad {}+\frac{1}{2} \sum_{j=1}^{n} \sum_{l=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \theta _{jil} ^{+}L^{Q}_{i}M^{Q}_{l} e^{2 \lambda \eta _{jil} ^{+}} \frac{1}{1-\dot{\eta } _{jil} ^{+}} \\ & \qquad {} +\frac{1}{2}\sum_{j=1}^{n} \bigl(\alpha _{j}^{2} h_{ji}^{+}+ \vert \alpha _{j}\gamma _{j} \vert h_{ji}^{+}\bigr)L_{i}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ji}(u) \bigr\vert e^{2\lambda u}\,du \\ & \qquad {} +\frac{1}{2}\sum_{l=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{l}^{2} + \vert \alpha _{l}\gamma _{l} \vert \bigr)p_{lji}^{+} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{lji}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{lji}(u) \bigr\vert e^{2 \lambda u}\,duM_{j}^{R}L_{i}^{R} \\ & \qquad {} +\frac{1}{2}\sum_{j=1}^{n} \sum_{l=1}^{n}\bigl(\alpha _{j}^{2} + \vert \alpha _{j}\gamma _{j} \vert \bigr)p_{jil}^{+} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{jil}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{jil}(u) \bigr\vert e^{2 \lambda u}\,duM_{l}^{R}L_{i}^{R} \\ & \qquad {}+\frac{1}{2}\sum_{j=1}^{n} \vert \alpha _{i}\gamma _{i} \vert \bigl\vert h_{ij}(t) \bigr\vert L_{j}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \,du \\ & \qquad {}+\frac{1}{2}\sum_{j=1}^{n} \sum_{l=1}^{n} \vert \alpha _{i} \gamma _{i} \vert \bigl\vert p_{ijl}(t) \bigr\vert M_{j}^{R}L_{l}^{R} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \\ & \qquad {}+\frac{1}{2}\sum_{j=1}^{n} \sum_{l=1}^{n} \vert \alpha _{i} \gamma _{i} \vert \bigl\vert p_{ijl}(t) \bigr\vert M_{l}^{R}L_{j}^{R} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du, \end{aligned}$$

and

$$ E_{i}^{\lambda }(t) = \beta _{i}+\gamma _{i}^{2}+2\lambda \alpha _{i} \gamma _{i} -a_{i}(t)\alpha _{i}\gamma _{i}-b_{i}(t)\alpha _{i}^{2},\quad i \in D . $$

Set

$$\begin{aligned} &W(t) \\ &\quad = \frac{1}{2}\sum_{i=1}^{n} \beta _{i}z_{i}^{2}(t)e^{2 \lambda t} + \frac{1}{2}\sum_{i=1}^{n}\bigl( \alpha _{i} z _{i}'(t)+ \gamma _{i}z_{i}(t)\bigr)^{2}e^{2\lambda t} \\ &\qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2} d_{ij} ^{+}+ \vert \alpha _{i}\gamma _{i} \vert d_{ij} ^{+}\bigr)e^{ 2\lambda q_{ij}^{+} }L^{B}_{j} \int _{t-q _{ij}(t)}^{t}z_{j}^{2}(s) \frac{1}{1-\dot{q} _{ij} ^{+}}e^{2\lambda s}\,ds \\ &\qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{l=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr) \theta _{lji} ^{+} M^{Q}_{j}L^{Q}_{i} e^{2\lambda \xi _{lji} ^{+}} \int _{t-\xi _{lji}( t) }^{t}z_{i}^{2}(s) \frac{1}{1-\dot{\xi } _{lji} ^{+}}e^{2\lambda s}\,ds \\ &\qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \theta _{jil} ^{+}L^{Q}_{i}M^{Q}_{l} e^{2\lambda \eta _{jil} ^{+}} \int _{t-\eta _{jil}( t) }^{t}z_{i}^{2}(s) \frac{1}{1-\dot{\eta } _{jil} ^{+}}e^{2\lambda s}\,ds \\ &\qquad {}+\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2} h_{ij}^{+}+ \vert \alpha _{i}\gamma _{i} \vert h_{ij}^{+} \bigr)L_{j}^{K} \int _{0}^{+ \infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \int _{t-u}^{t}z_{j}^{2}(s)e^{2\lambda (u+s)} \,ds\,du \\ &\qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{l=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr)p_{lji}^{+} M_{j}^{R}L_{i}^{R} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{lji}(u) \bigr\vert \,du \\ &\qquad {} \times \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{lji}(u) \bigr\vert \int _{t-u}^{t}z_{i}^{2}(s)e^{2 \lambda (u+s)} \,ds\,du \\ &\qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr)p_{jil}^{+} M_{l}^{R}L_{i}^{R} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{jil}(u) \bigr\vert \,du \\ &\qquad {} \times \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{jil}(u) \bigr\vert \int _{t-u}^{t}z_{i}^{2}(s)e^{2 \lambda (u+s)} \,ds\,du. \end{aligned}$$

A straightforward computation yields

$$\begin{aligned}& W'(t) \\ & \quad = 2\lambda \Biggl[\frac{1}{2}\sum_{i=1}^{n} \beta _{i}z_{i}^{2}(t)e^{2 \lambda t}+ \frac{1}{2}\sum_{i=1}^{n}\bigl( \alpha _{i}z '_{i}(t)+ \gamma _{i}z_{i}(t)\bigr)^{2}e^{2\lambda t} \Biggr] \\ & \qquad {} +\sum_{i=1}^{n}\bigl(\beta _{i}+\gamma _{i}^{2}\bigr)z_{i}(t)z '_{i}(t)e^{2 \lambda t}+\sum _{i=1}^{n}\alpha _{i}\bigl(\alpha _{i}z '_{i}(t)+ \gamma _{i}z_{i}(t)\bigr)e^{2\lambda t} \\ & \qquad {} \times \Biggl[-a_{i}(t)z '_{i}(t)-b_{i}(t)z_{i}(t)+ \sum_{j=1}^{n}c_{ij}(t) \widetilde{A}_{j}\bigl(z_{j}(t)\bigr) +\sum _{j=1}^{n}d_{ij}(t) \widetilde{B}_{j}\bigl(z_{j}\bigl(t-q_{ij}(t) \bigr)\bigr) \\ & \qquad {} +\sum_{j=1}^{n}\sum _{l=1}^{n}\theta _{ijl}(t) \bigl(Q_{j}\bigl(y_{j}\bigl(t- \eta _{ijl} (t) \bigr)\bigr)Q_{l}\bigl(y_{l}\bigl( t-\xi _{ijl} (t) \bigr)\bigr) \\ & \qquad {} -Q_{j}\bigl(y_{j}\bigl(t-\eta _{ijl} (t) \bigr)\bigr)Q_{l}\bigl(x_{l}\bigl( t-\xi _{ijl} (t) \bigr)\bigr)+Q_{j}\bigl(y_{j} \bigl( t-\eta _{ijl}( t) \bigr)\bigr)Q_{l} \bigl(x_{l}\bigl( t-\xi _{ijl} (t) \bigr)\bigr) \\ & \qquad {} -Q_{j}\bigl(x_{j}\bigl(t-\eta _{ijl}( t )\bigr)\bigr)Q_{l}\bigl(x_{l}\bigl(t- \xi _{ijl} (t )\bigr)\bigr)\bigr) \\ & \qquad {} + \sum_{j=1}^{n}h_{ij} (t) \int _{0}^{+\infty }\sigma _{ij}(u) \widetilde{K}_{j}\bigl(z_{j}(t-u)\bigr)\,du + \sum _{j=1}^{n}\sum _{l=1}^{n}p_{ijl}(t) \\ & \qquad {} \times \biggl( \int _{0}^{+\infty }\hat{\sigma }_{ijl}(u) R_{j}\bigl(y_{j}(t-u)\bigr)\,du \int _{0}^{+\infty } \bar{\sigma } _{ijl}(u) R_{l}\bigl(y_{l}(t-u)\bigr)\,du \\ & \qquad {} - \int _{0}^{+\infty }\hat{\sigma }_{ijl}(u) R_{j}\bigl(y_{j}(t-u)\bigr)\,du \int _{0}^{+ \infty } \bar{\sigma } _{ijl}(u) R_{l}\bigl(x_{l}(t-u)\bigr)\,du \\ & \qquad {} + \int _{0}^{+\infty }\hat{\sigma }_{ijl}(u) R_{j}\bigl(y_{j}(t-u)\bigr)\,du \int _{0}^{+ \infty } \bar{\sigma } _{ijl}(u) R_{l}\bigl(x_{l}(t-u)\bigr)\,du \\ & \qquad {} - \int _{0}^{+\infty }\hat{\sigma }_{ijl}(u) R_{j}\bigl(x_{j}(t-u)\bigr)\,du \int _{0}^{+ \infty } \bar{\sigma } _{ijl}(u) R_{l}\bigl(x_{l}(t-u)\bigr)\,du\biggr)\Biggr] \\ & \qquad {} +\sum_{i=1}^{n}\alpha _{i}\gamma _{i}\bigl(z '_{i} (t)\bigr)^{2}e^{2 \lambda t} +\frac{1}{2}\sum _{i=1}^{n}\sum_{j=1}^{n} \bigl( \alpha _{i}^{2}d_{ij} ^{+}+ \vert \alpha _{i}\gamma _{i} \vert d_{ij} ^{+}\bigr)e^{ 2 \lambda q_{ij}^{+} }L^{B}_{j} \\& \qquad {} \times \biggl[z_{j}^{2}(t)\frac{1}{1-\dot{q} _{ij} ^{+}}e^{2\lambda t}-z_{j}^{2} \bigl(t-q_{ij}(t)\bigr)e^{2 \lambda (t-q_{ij}(t))}\frac{ 1- q'_{ij}(t)}{1-\dot{q} _{ij} ^{+}} \biggr] \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{l=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr) \theta _{lji} ^{+} M^{Q}_{j}L^{Q}_{i} e^{2\lambda \xi _{lji} ^{+}} \\& \qquad {} \times \biggl[z_{i}^{2}(t)\frac{1}{1-\dot{\xi } _{lji} ^{+}} e^{2\lambda t}- z_{i}^{2}\bigl(t-\xi _{lji}( t)\bigr)e^{2\lambda (t-\xi _{lji}( t))} \frac{1- \xi _{lji}'( t) }{1-\dot{\xi } _{lji} ^{+}}\biggr] \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \theta _{jil} ^{+}L^{Q}_{i}M^{Q}_{l} e^{2\lambda \eta _{jil} ^{+}} \\& \qquad {} \times \biggl[z_{i}^{2}(t) \frac{1}{1-\dot{\eta } _{jil} ^{+}}e^{2 \lambda t}-z_{i}^{2} \bigl(t-\eta _{jil}( t)\bigr)e^{2\lambda (t-\eta _{jil}( t))} \frac{1-\eta _{jil}'( t)}{1-\dot{\eta } _{jil} ^{+}} \biggr] \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2} h_{ij}^{+}+ \vert \alpha _{i}\gamma _{i} \vert h_{ij}^{+} \bigr)L_{j}^{K} \\& \qquad {} \times \biggl[ \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert e^{2\lambda u}\,duz_{j}^{2}(t)e^{2 \lambda t}- \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert z_{j}^{2}(t-u) \,due^{2 \lambda t}\biggr] \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{l=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{l}^{2} + \vert \alpha _{l}\gamma _{l} \vert \bigr)p_{lji}^{+} M_{j}^{R}L_{i}^{R} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{lji}(u) \bigr\vert \,du \\& \qquad {} \times \biggl[ \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{lji}(u) \bigr\vert e^{2\lambda u}\,duz_{i}^{2}(t)e^{2 \lambda t} - \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{lji}(u) \bigr\vert z_{i}^{2}(t-u) \,due^{2 \lambda t}\biggr] \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2} + \vert \alpha _{j}\gamma _{j} \vert \bigr)p_{jil}^{+} M_{l}^{R}L_{i}^{R} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{jil}(u) \bigr\vert \,du \\& \qquad {} \times \biggl[ \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{jil}(u) \bigr\vert e^{2\lambda u}\,duz_{i}^{2}(t)e^{2 \lambda t} - \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{jil}(u) \bigr\vert z_{i}^{2}(t-u) \,due^{2 \lambda t}\biggr] \\& \quad \leq e^{2\lambda t}\Biggl\{ \sum_{i=1}^{n} \bigl(\beta _{i}+\gamma _{i}^{2}+2 \lambda \alpha _{i}\gamma _{i} -a_{i}(t)\alpha _{i}\gamma _{i}-b_{i}(t) \alpha _{i}^{2}\bigr)z_{i}(t)z '_{i}(t) \end{aligned}$$
$$\begin{aligned}& \qquad {} +\sum_{i=1}^{n}\bigl(\lambda \alpha _{i}^{2}+\alpha _{i} \gamma _{i}-a_{i}(t)\alpha _{i}^{2} \bigr) \bigl(z '_{i}(t)\bigr)^{2}-\sum _{i=1}^{n}\bigl(b_{i}(t) \alpha _{i}\gamma _{i}-\lambda \beta _{i}- \lambda \gamma _{i}^{2}\bigr)z_{i}^{2}(t) \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2}d_{ij} ^{+}+ \vert \alpha _{i}\gamma _{i} \vert d_{ij} ^{+}\bigr)L^{B}_{j}e^{2 \lambda q_{ij}^{+} }z_{j}^{2}(t) \frac{1}{1-\dot{q} _{ij}^{+}} \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{l=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr) \theta _{lji} ^{+} M^{Q}_{j}L^{Q}_{i} e^{2\lambda \xi _{lji} ^{+}} z_{i}^{2}(t) \frac{1}{1-\dot{\xi } _{lji} ^{+}} \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \theta _{jil} ^{+}L^{Q}_{i}M^{Q}_{l} e^{2\lambda \eta _{jil} ^{+}} z_{i}^{2}(t) \frac{1}{1-\dot{\eta } _{jil} ^{+}} \\& \qquad {}-\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2}d_{ij} ^{+}+ \vert \alpha _{i}\gamma _{i} \vert d_{ij} ^{+}\bigr) L^{B}_{j} z_{j}^{2} \bigl(t-q_{ij}(t)\bigr) \\& \qquad {} -\frac{1}{2}\sum_{i=1}^{n} \sum_{l=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr) \theta _{lji} ^{+} M^{Q}_{j}L^{Q}_{i} z_{i}^{2}\bigl(t-\xi _{lji}( t)\bigr) \\& \qquad {}- \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \theta _{jil} ^{+}L^{Q}_{i}M^{Q}_{l} z_{i}^{2}\bigl(t-\eta _{jil}( t)\bigr) \\& \qquad {} +\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert c_{ij}(t) \bigr\vert \bigl\vert \widetilde{A}_{j}\bigl(z_{j}(t) \bigr) \bigr\vert \\& \qquad {} +\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert d_{ij}(t) \bigr\vert \bigl\vert \widetilde{B}_{j}\bigl(z_{j} \bigl(t-q_{ij}(t)\bigr)\bigr) \bigr\vert \\& \qquad {} +\sum_{i=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha _{i} \gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \\& \qquad {}\times \sum_{j=1}^{n}\sum _{l=1}^{n} \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l} \bigl\vert z_{l}\bigl(t- \xi _{ijl} (t) \bigr) \bigr\vert +M^{Q}_{l}L^{Q}_{j} \bigl\vert z_{j}\bigl( t-\eta _{ijl} (t) \bigr) \bigr\vert \bigr) \\& \qquad {} +\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert h_{ij}(t) \bigr\vert \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \bigl\vert \widetilde{K}_{j} \bigl(z_{j}(t-u)\bigr) \bigr\vert \,du \\& \qquad {} +\sum_{i=1}^{n}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl( \alpha _{i}^{2} \bigl\vert z'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert p_{ijl}(t) \bigr\vert \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du \\& \qquad {} \times \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \bigl\vert z_{l}(t-u) \bigr\vert \,du M_{j}^{R}L_{l}^{R} \\& \qquad {} +\sum_{i=1}^{n}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl( \alpha _{i}^{2} \bigl\vert z'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert p_{ijl}(t) \bigr\vert \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \\& \qquad {} \times \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \bigl\vert z_{j}(t-u) \bigr\vert \,du M_{l}^{R}L_{j}^{R} \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2} h_{ij}^{+}+ \vert \alpha _{i}\gamma _{i} \vert h_{ij}^{+} \bigr)L_{j}^{K} \int _{0}^{+ \infty } \bigl\vert \sigma _{ij}(u) \bigr\vert e^{2\lambda u}\,du z_{j}^{2}(t) \\& \qquad {} -\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2} h_{ij}^{+}+ \vert \alpha _{i}\gamma _{i} \vert h_{ij}^{+} \bigr)L_{j}^{K} \int _{0}^{+ \infty } \bigl\vert \sigma _{ij}(u) \bigr\vert z_{j}^{2}(t-u)\,du \end{aligned}$$
$$\begin{aligned}& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{l=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{l}^{2} + \vert \alpha _{l}\gamma _{l} \vert \bigr)p_{lji}^{+} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{lji}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{lji}(u) \bigr\vert e^{2\lambda u}\,duz_{i}^{2}(t)M_{j}^{R}L_{i}^{R} \\& \qquad {} -\frac{1}{2}\sum_{i=1}^{n} \sum_{l=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{l}^{2} + \vert \alpha _{l}\gamma _{l} \vert \bigr)p_{lji}^{+} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{lji}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{lji}(u) \bigr\vert z_{i}^{2}(t-u) \,duM_{j}^{R}L_{i}^{R} \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2} + \vert \alpha _{j}\gamma _{j} \vert \bigr)p_{jil}^{+} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{jil}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{jil}(u) \bigr\vert e^{2\lambda u}\,duz_{i}^{2}(t)M_{l}^{R}L_{i}^{R} \\& \qquad {} -\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2} + \vert \alpha _{j}\gamma _{j} \vert \bigr)p_{jil}^{+} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{jil}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{jil}(u) \bigr\vert z_{i}^{2}(t-u) \,duM_{l}^{R}L_{i}^{R} \Biggr\} \\& \quad = e^{2\lambda t}\Biggl\{ \sum_{i=1}^{n} \bigl(\beta _{i}+\gamma _{i}^{2}+2 \lambda \alpha _{i}\gamma _{i} -a_{i}(t)\alpha _{i}\gamma _{i}-b_{i}(t) \alpha _{i}^{2}\bigr)z_{i}(t) z '_{i}(t) \\& \qquad {}+\sum_{i=1}^{n}\bigl(\lambda \alpha _{i}^{2}+\alpha _{i}\gamma _{i}-a_{i}(t) \alpha _{i}^{2} \bigr) \bigl(z '_{i}(t)\bigr)^{2} \\& \qquad {} +\sum_{i=1}^{n}\Biggl[-b_{i}(t) \alpha _{i}\gamma _{i}+\lambda \beta _{i}+ \lambda \gamma _{i}^{2} +\frac{1}{2}\sum _{j=1}^{n}\bigl( \alpha _{j}^{2} d_{ji} ^{+}+ \vert \alpha _{j}\gamma _{j} \vert d_{ji} ^{+}\bigr)L^{B}_{i}e^{ 2\lambda q_{ji}^{+} } \frac{1}{1-\dot{q} _{ji} ^{+}} \\& \qquad {} +\frac{1}{2} \sum_{l=1}^{n} \sum_{j=1}^{n}\bigl( \alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr) \theta _{lji} ^{+} M^{Q}_{j}L^{Q}_{i} e^{2\lambda \xi _{lji} ^{+}} \frac{1}{1-\dot{\xi } _{lji} ^{+}} \\& \qquad {} +\frac{1}{2} \sum_{j=1}^{n} \sum_{l=1}^{n}\bigl( \alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \theta _{jil} ^{+}L^{Q}_{i}M^{Q}_{l} e^{2\lambda \eta _{jil} ^{+}} \frac{1}{1-\dot{\eta } _{jil} ^{+}} \\& \qquad {} +\frac{1}{2}\sum_{j=1}^{n} \bigl(\alpha _{j}^{2} h_{ji}^{+}+ \vert \alpha _{j}\gamma _{j} \vert h_{ji}^{+}\bigr)L_{i}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ji}(u) \bigr\vert e^{2\lambda u}\,du \\& \qquad {} +\frac{1}{2}\sum_{l=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{l}^{2} + \vert \alpha _{l}\gamma _{l} \vert \bigr)p_{lji}^{+} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{lji}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{lji}(u) \bigr\vert e^{2 \lambda u}\,duM_{j}^{R}L_{i}^{R} \\& \qquad {} +\frac{1}{2}\sum_{j=1}^{n} \sum_{l=1}^{n}\bigl(\alpha _{j}^{2} + \vert \alpha _{j}\gamma _{j} \vert \bigr)p_{jil}^{+} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{jil}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{jil}(u) \bigr\vert e^{2 \lambda u}\,duM_{l}^{R}L_{i}^{R} \Biggr]z_{i}^{2}(t) \\& \qquad {} -\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2}d_{ij} ^{+}+ \vert \alpha _{i}\gamma _{i} \vert d_{ij} ^{+}\bigr) L^{B}_{j} z_{j}^{2} \bigl(t-q_{ij}(t)\bigr) \\& \qquad {} -\frac{1}{2}\sum_{i=1}^{n} \sum_{l=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr) \theta _{lji} ^{+} M^{Q}_{j}L^{Q}_{i} z_{i}^{2}\bigl(t-\xi _{lji}( t)\bigr) \\& \qquad {}-\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \theta _{jil} ^{+}L^{Q}_{i}M^{Q}_{l} z_{i}^{2}\bigl(t-\eta _{jil}( t)\bigr) \\& \qquad {} -\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2} h_{ij}^{+}+ \vert \alpha _{i}\gamma _{i} \vert h_{ij}^{+} \bigr)L_{j}^{K} \int _{0}^{+ \infty } \bigl\vert \sigma _{ij}(u) \bigr\vert z_{j}^{2}(t-u)\,du \\& \qquad {} -\frac{1}{2}\sum_{i=1}^{n} \sum_{l=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{l}^{2} + \vert \alpha _{l}\gamma _{l} \vert \bigr)p_{lji}^{+} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{lji}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{lji}(u) \bigr\vert z_{i}^{2}(t-u) \,duM_{j}^{R}L_{i}^{R} \end{aligned}$$
$$\begin{aligned}& \qquad {} -\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2} + \vert \alpha _{j}\gamma _{j} \vert \bigr)p_{jil}^{+} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{jil}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{jil}(u) \bigr\vert z_{i}^{2}(t-u) \,duM_{l}^{R}L_{i}^{R} \\& \qquad {} +\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert c_{ij}(t) \bigr\vert \bigl\vert \widetilde{A}_{j}\bigl(z_{j}(t) \bigr) \bigr\vert \\& \qquad {} +\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert d_{ij}(t) \bigr\vert \bigl\vert \widetilde{B}_{j}\bigl(z_{j} \bigl(t-q_{ij}(t)\bigr)\bigr) \bigr\vert \\& \qquad {} +\sum_{i=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha _{i} \gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \\& \qquad {}\times \sum_{j=1}^{n}\sum _{l=1}^{n} \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l} \bigl\vert z_{l}\bigl(t- \xi _{ijl} (t) \bigr) \bigr\vert +M^{Q}_{l}L^{Q}_{j} \bigl\vert z_{j}\bigl( t-\eta _{ijl} (t) \bigr) \bigr\vert \bigr) \\& \qquad {} +\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert h_{ij}(t) \bigr\vert \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \bigl\vert \widetilde{K} _{j} \bigl(z_{j}(t-u)\bigr) \bigr\vert \,du \\& \qquad {} +\sum_{i=1}^{n}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl( \alpha _{i}^{2} \bigl\vert z'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert p_{ijl}(t) \bigr\vert \\& \qquad {} \times \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+ \infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \bigl\vert z_{l}(t-u) \bigr\vert \,du M_{j}^{R}L_{l}^{R} \\& \qquad {} +\sum_{i=1}^{n}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl( \alpha _{i}^{2} \bigl\vert z'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert p_{ijl}(t) \bigr\vert \\& \qquad {} \times \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+ \infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \bigl\vert z_{j}(t-u) \bigr\vert \,du M_{l}^{R}L_{j}^{R} \Biggr\} ,\quad \forall t\in [0,+\infty ). \end{aligned}$$
(2.5)

It follows from \((G_{1})\) and \(PQ \leq \frac{1}{2} (P^{2} + Q^{2})\) (\(P, Q\in \mathbb{R}\)) that

$$\begin{aligned}& \sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert c_{ij}(t) \bigr\vert \bigl\vert \widetilde{A}_{j}\bigl(z_{j}(t )\bigr) \bigr\vert \\& \quad \leq \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \alpha _{i}^{2} \bigl\vert c_{ij}(t) \bigr\vert L^{A}_{j}\bigl( \bigl(z '_{i}(t) \bigr)^{2}+z_{j}^{2}(t)\bigr) \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \vert \alpha _{i} \gamma _{i} \vert \bigl\vert c_{ij}(t) \bigr\vert L^{A}_{j} \bigl(z_{i}^{2}(t)+z_{j}^{2}(t) \bigr) \\& \quad = \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\alpha _{i}^{2} \bigl\vert c_{ij}(t) \bigr\vert L^{A}_{j} \bigl(z'_{i}(t)\bigr)^{2} \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl( \vert \alpha _{i} \gamma _{i} \vert \bigl\vert c_{ij}(t) \bigr\vert L^{A}_{j} +\alpha _{j}^{2} \bigl\vert c_{ji}(t) \bigr\vert L^{A}_{i}+ \vert \alpha _{j}\gamma _{j} \vert \bigl\vert c_{ji}(t) \bigr\vert L^{A}_{i}\bigr)z_{i}^{2}(t), \\& \sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert d_{ij}(t) \bigr\vert \bigl\vert \widetilde{B}_{j}\bigl(z_{j} \bigl(t-q_{ij}(t)\bigr)\bigr) \bigr\vert \\& \quad \leq \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \alpha _{i}^{2} \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j}\bigl( \bigl(z' _{i}(t)\bigr)^{2}+z_{j}^{2} \bigl(t-q_{ij}(t)\bigr)\bigr) \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \vert \alpha _{i} \gamma _{i} \vert \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j} \bigl(z_{i}^{2}(t)+z_{j}^{2} \bigl(t-q_{ij}(t)\bigr)\bigr) \\& \quad = \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\alpha _{i}^{2} \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j} \bigl(z '_{i}(t)\bigr)^{2} + \frac{1}{2}\sum_{i=1}^{n}\sum _{j=1}^{n} \vert \alpha _{i}\gamma _{i} \vert \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j}z_{i}^{2}(t) \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j}+ \vert \alpha _{i}\gamma _{i} \vert \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j}\bigr)z_{j}^{2} \bigl(t-q_{ij}(t)\bigr), \\& \sum_{i=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha _{i} \gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \\& \qquad {} \times \sum_{j=1}^{n}\sum _{l=1}^{n} \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l} \bigl\vert z_{l}\bigl( t-\xi _{ijl} (t) \bigr) \bigr\vert +L^{Q}_{j} \bigl\vert z_{j} \bigl(t- \eta _{ijl} (t) \bigr) \bigr\vert M^{Q}_{l} \bigr) \\& \quad \leq \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\alpha _{i}^{2} \bigl\vert \theta _{ijl}(t) \bigr\vert M^{Q}_{j}L^{Q}_{l} \bigl( \bigl(z' _{i}(t)\bigr)^{2}+z_{l}^{2} \bigl(t-\xi _{ijl} (t) \bigr)\bigr) \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n} \vert \alpha _{i}\gamma _{i} \vert \bigl\vert \theta _{ijl}(t) \bigr\vert M^{Q}_{j}L^{Q}_{l} \bigl( \bigl(z _{i}(t)\bigr)^{2}+z_{l}^{2} \bigl(t-\xi _{ijl} (t) \bigr)\bigr) \\& \qquad {} + \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\alpha _{i}^{2} \bigl\vert \theta _{ijl}(t) \bigr\vert L^{Q}_{j}M^{Q}_{l} \bigl( \bigl(z' _{i}(t)\bigr)^{2}+z_{j}^{2} \bigl(t-\eta _{ijl}( t) \bigr)\bigr) \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n} \vert \alpha _{i}\gamma _{i} \vert \bigl\vert \theta _{ijl}(t) \bigr\vert L^{Q}_{j}M^{Q}_{l} \bigl( \bigl(z _{i}(t)\bigr)^{2}+z_{j}^{2} \bigl(t-\eta _{ijl} (t) \bigr)\bigr) \\& \quad = \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\alpha _{i}^{2} \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l}+L^{Q}_{j}M^{Q}_{l} \bigr) \bigl(z' _{i}(t)\bigr)^{2} \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n} \vert \alpha _{i}\gamma _{i} \vert \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l}+L^{Q}_{j}M^{Q}_{l} \bigr) \bigl(z _{i}(t)\bigr)^{2} \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \bigl\vert \theta _{ijl}(t) \bigr\vert M^{Q}_{j}L^{Q}_{l} z_{l}^{2}\bigl(t-\xi _{ijl} (t) \bigr) \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \bigl\vert \theta _{ijl}(t) \bigr\vert L^{Q}_{j}M^{Q}_{l} z_{j}^{2}\bigl(t-\eta _{ijl} (t) \bigr) \\& \quad = \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n}\alpha _{i}^{2} \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l}+L^{Q}_{j}M^{Q}_{l} \bigr) \bigl(z' _{i}(t)\bigr)^{2} \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n} \vert \alpha _{i}\gamma _{i} \vert \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l}+L^{Q}_{j}M^{Q}_{l} \bigr) \bigl(z _{i}(t)\bigr)^{2} \\& \qquad {} +\frac{1}{2}\sum_{l=1}^{n} \sum_{j=1}^{n}\sum _{i=1}^{n}\bigl(\alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr) \bigl\vert \theta _{lji}(t) \bigr\vert M^{Q}_{j}L^{Q}_{i} z_{i}^{2}\bigl(t-\xi _{lji} (t) \bigr) \\& \qquad {} +\frac{1}{2}\sum_{j=1}^{n} \sum_{i=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \bigl\vert \theta _{jil}(t) \bigr\vert L^{Q}_{i}M^{Q}_{l} z_{i}^{2}\bigl(t-\eta _{jil} (t) \bigr) , \\& \sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert z'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert h_{ij}(t) \bigr\vert \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \bigl\vert \widetilde{K}_{j} \bigl(z_{j}(t-u)\bigr) \bigr\vert \,du \\& \quad \leq \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \alpha _{i}^{2} \bigl\vert h_{ij}(t) \bigr\vert L_{j}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \,du\bigl(z'_{i}(t) \bigr)^{2} \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \vert \alpha _{i} \gamma _{i} \vert \bigl\vert h_{ij}(t) \bigr\vert L_{j}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \,duz_{i}^{2}(t) \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert h_{ij}(t) \bigr\vert L_{j}^{K}+ \vert \alpha _{i}\gamma _{i} \vert \bigl\vert h_{ij}(t) \bigr\vert L_{j}^{K}\bigr) \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert z_{j}^{2}(t-u)\,du, \\& \sum_{i=1}^{n}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl( \alpha _{i}^{2} \bigl\vert z'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert p_{ijl}(t) \bigr\vert \\& \qquad {} \times \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+ \infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \bigl\vert z_{l}(t-u) \bigr\vert \,du M_{j}^{R}L_{l}^{R} \\& \quad \leq \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \sum _{l=1}^{n}\alpha _{i}^{2} \bigl\vert p_{ijl}(t) \bigr\vert M_{j}^{R}L_{l}^{R} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du\bigl(z'_{i}(t) \bigr)^{2} \\& \qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n} \vert \alpha _{i}\gamma _{i} \vert \bigl\vert p_{ijl}(t) \bigr\vert M_{j}^{R}L_{l}^{R} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,duz^{2}_{i}(t) \\& \qquad {} +\frac{1}{2}\sum_{l=1}^{n} \sum_{j=1}^{n}\sum _{i=1}^{n}\bigl(\alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr) \bigl\vert p_{lji}(t) \bigr\vert M_{j}^{R}L_{i}^{R} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{lji}(u) \bigr\vert \,du \\& \qquad {} \times \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{lji}(u) \bigr\vert z^{2}_{i}(t-u)\,du, \end{aligned}$$

and

$$\begin{aligned} &\sum_{i=1}^{n}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl( \alpha _{i}^{2} \bigl\vert z'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert p_{ijl}(t) \bigr\vert \\ &\qquad {} \times \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+ \infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \bigl\vert z_{j}(t-u) \bigr\vert \,du M_{l}^{R}L_{j}^{R} \\ &\quad \leq \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \sum _{l=1}^{n}\alpha _{i}^{2} \bigl\vert p_{ijl}(t) \bigr\vert M_{l}^{R}L_{j}^{R} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du\bigl(z'_{i}(t) \bigr)^{2} \\ &\qquad {} +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\sum _{l=1}^{n} \vert \alpha _{i}\gamma _{i} \vert \bigl\vert p_{ijl}(t) \bigr\vert M_{l}^{R}L_{j}^{R} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,duz^{2}_{i}(t) \\ &\qquad {} +\frac{1}{2}\sum_{j=1}^{n} \sum_{i=1}^{n}\sum _{l=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \bigl\vert p_{jil}(t) \bigr\vert M_{l}^{R}L_{i}^{R} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{jil}(u) \bigr\vert \,du \\ &\qquad {} \times \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{jil}(u) \bigr\vert z^{2}_{i}(t-u)\,du, \end{aligned}$$

which, together with (2.4) and (2.5), entails

$$\begin{aligned} W'(t) \leq & e^{2\lambda t}\Biggl\{ \sum _{i=1}^{n}\bigl(\beta _{i}+ \gamma _{i}^{2}+2\lambda \alpha _{i}\gamma _{i} -a_{i}(t)\alpha _{i} \gamma _{i}-b_{i}(t)\alpha _{i}^{2} \bigr)z_{i}(t) z'_{i}(t) \\ &{}+\sum_{i=1}^{n}\Biggl[\lambda \alpha _{i}^{2}+\alpha _{i}\gamma _{i}-a_{i}(t) \alpha _{i}^{2} + \frac{1}{2}\alpha _{i}^{2}\sum _{j=1}^{n}\bigl( \bigl\vert c_{ij}(t) \bigr\vert L^{A}_{j} + \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j}\bigr) \\ &{} +\frac{1}{2} \alpha _{i}^{2}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l}+L^{Q}_{j}M^{Q}_{l} \bigr) \\ &{} +\frac{1}{2}\alpha _{i}^{2}\sum _{j=1}^{n} \bigl\vert h_{ij}(t) \bigr\vert L_{j}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \,du \\ &{} +\frac{1}{2}\alpha _{i}^{2}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl\vert p_{ijl}(t) \bigr\vert M_{j}^{R}L_{l}^{R} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \\ &{} +\frac{1}{2}\alpha _{i}^{2}\sum _{j=1}^{n}\sum_{l=1}^{n} \bigl\vert p_{ijl}(t) \bigr\vert M_{l}^{R}L_{j}^{R} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du\Biggr]\bigl(z'_{i}(t) \bigr)^{2} \\ &{}+\sum_{i=1}^{n}\Biggl[-b_{i}(t) \alpha _{i}\gamma _{i}+\lambda \beta _{i}+ \lambda \gamma _{i}^{2} +\frac{1}{2}\sum _{j=1}^{n}\bigl( \bigl\vert c_{ij}(t) \bigr\vert L^{A}_{j}+ \bigl\vert d_{ij}(t) \bigr\vert L^{B}_{j} \bigr) \vert \alpha _{i}\gamma _{i} \vert \\ &{}+\frac{1}{2}\sum_{j=1}^{n} \alpha _{j}^{2}\biggl( \bigl\vert c_{ji}(t) \bigr\vert L^{A}_{i} + d_{ji}^{+} L^{B}_{i}\frac{1}{1-\dot{q} _{ji} ^{+}}e^{2\lambda q_{ji}^{+}} \biggr) \\ &{}+\frac{1}{2}\sum_{j=1}^{n} \biggl( \bigl\vert c_{ji}(t) \bigr\vert L^{A}_{i} + d_{ji}^{+} L^{B}_{i} \frac{1}{1-\dot{q} _{ji} ^{+}}e^{2\lambda q_{ji}^{+}}\biggr) \vert \alpha _{j} \gamma _{j} \vert \\ &{} +\frac{1}{2} \sum_{j=1}^{n} \sum_{l=1}^{n} \vert \alpha _{i} \gamma _{i} \vert \bigl\vert \theta _{ijl}(t) \bigr\vert \bigl(M^{Q}_{j}L^{Q}_{l}+L^{Q}_{j}M^{Q}_{l} \bigr) \\ &{} +\frac{1}{2} \sum_{l=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{l}^{2}+ \vert \alpha _{l}\gamma _{l} \vert \bigr) \theta _{lji} ^{+} M^{Q}_{j}L^{Q}_{i} e^{2 \lambda \xi _{lji} ^{+}} \frac{1}{1-\dot{\xi } _{lji} ^{+}} \\ &{} +\frac{1}{2} \sum_{j=1}^{n} \sum_{l=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \theta _{jil} ^{+}L^{Q}_{i}M^{Q}_{l} e^{2 \lambda \eta _{jil} ^{+}} \frac{1}{1-\dot{\eta } _{jil} ^{+}} \\ &{} +\frac{1}{2}\sum_{j=1}^{n} \bigl(\alpha _{j}^{2} h_{ji}^{+}+ \vert \alpha _{j}\gamma _{j} \vert h_{ji}^{+}\bigr)L_{i}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ji}(u) \bigr\vert e^{2\lambda u}\,du \\ &{} +\frac{1}{2}\sum_{l=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{l}^{2} + \vert \alpha _{l}\gamma _{l} \vert \bigr)p_{lji}^{+} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{lji}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{lji}(u) \bigr\vert e^{2 \lambda u}\,duM_{j}^{R}L_{i}^{R} \\ &{} +\frac{1}{2}\sum_{j=1}^{n} \sum_{l=1}^{n}\bigl(\alpha _{j}^{2} + \vert \alpha _{j}\gamma _{j} \vert \bigr)p_{jil}^{+} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{jil}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{jil}(u) \bigr\vert e^{2 \lambda u}\,duM_{l}^{R}L_{i}^{R} \\ &{} +\frac{1}{2}\sum_{j=1}^{n} \vert \alpha _{i}\gamma _{i} \vert \bigl\vert h_{ij}(t) \bigr\vert L_{j}^{K} \int _{0}^{+\infty } \bigl\vert \sigma _{ij}(u) \bigr\vert \,du \\ &{} +\frac{1}{2}\sum_{j=1}^{n} \sum_{l=1}^{n} \vert \alpha _{i} \gamma _{i} \vert \bigl\vert p_{ijl}(t) \bigr\vert M_{j}^{R}L_{l}^{R} \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \\ &{} +\frac{1}{2}\sum_{j=1}^{n} \sum_{l=1}^{n} \vert \alpha _{i} \gamma _{i} \vert \bigl\vert p_{ijl}(t) \bigr\vert M_{l}^{R}L_{j}^{R} \int _{0}^{+\infty } \bigl\vert \bar{\sigma }_{ijl}(u) \bigr\vert \,du \int _{0}^{+\infty } \bigl\vert \hat{\sigma }_{ijl}(u) \bigr\vert \,du\Biggr]z_{i}^{2}(t) \Biggr\} \\ = & e^{2\lambda t}\Biggl\{ \sum_{i=1}^{n} \bigl(C^{\lambda }_{i} (t) \bigl(z'_{i}(t) \bigr)^{2}+D^{ \lambda }_{i}(t)z_{i}^{2}(t)+E^{\lambda }_{i}(t)z_{i}(t) z'_{i}(t)\bigr)\Biggr\} \\ = &e^{2\lambda t}\Biggl\{ \sum_{i=1}^{n}C_{i}^{\lambda }(t) \biggl( z '_{i}(t)+ \frac{E_{i}^{\lambda }(t)}{2C_{i}^{\lambda }(t)}z_{i}(t) \biggr)^{2} +\sum_{i=1}^{n} \biggl(D_{i}^{\lambda }(t)- \frac{(E^{\lambda }_{i}(t)) ^{2}}{4C_{i}^{\lambda }(t)}\biggr) z_{i}^{2}(t)\Biggr\} \\ \leq & 0,\quad \forall t \in [0, +\infty ). \end{aligned}$$

This indicates that \(W (t)\leq W (0)\) for all \(t \in [0, +\infty )\), and

$$ \frac{1}{2}\sum_{i=1}^{n} \beta _{i}z_{i}^{2}(t)e^{2\lambda t}+ \frac{1}{2}\sum_{i=1}^{n}\bigl( \alpha _{i} z '_{i}(t)+\gamma _{i}z_{i}(t)\bigr)^{2}e^{2 \lambda t} \leq W (0),\quad t \in [0, +\infty ). $$

Manifestly,

$$ \bigl(\alpha _{i} z'_{i}(t) e^{ \lambda t}+\gamma _{i}z_{i}(t)e^{ \lambda t} \bigr)^{2}=\bigl( \alpha _{i}z'_{i}(t)+ \gamma _{i}z_{i}(t)\bigr)^{2}e^{2\lambda t} $$

and

$$ \alpha _{i} \bigl\vert z'_{i}(t) \bigr\vert e^{ \lambda t}\leq \bigl\vert \alpha _{i} z'_{i}(t) e^{ \lambda t}+\gamma _{i}z_{i}(t)e^{ \lambda t} \bigr\vert + \bigl\vert \gamma _{i}z_{i}(t)e^{ \lambda t} \bigr\vert . $$

Combining with the Cauchy–Schwarz inequality, one can pick a constant \(M >0\) such that

$$ \bigl\vert z'_{i}(t) \bigr\vert \leq M e^{ -\lambda t},\qquad \bigl\vert z_{i}(t) \bigr\vert \leq M e^{- \lambda t},\quad t\geq 0, i\in D , $$

which proves Lemma 2.1. □

Remark 2.2

More precisely, according to Lemma 2.1, we know that, if \(y(t)\) is an equilibrium point or a T-anti-periodic solution of (1.1), then all solutions of the system (1.1) and their derivatives are exponentially convergent to \(y(t)\) and \(y'(t)\), respectively. Referring to the definition of stability adopted in [5, 18–21, 40, 42–45], this indicates that \(y(t)\) is globally exponentially stable.

3 Anti-periodicity of HIHNNs (1.1)

Now, we set out to present the main result of this paper as follows.

Theorem 3.1

Under conditions\((G_{1})\)–\((G_{4})\), system (1.1) has a globally exponentially stableT-anti-periodic solution.

Proof

Let \(v(t)=(v_{1}(t), v_{2}(t),\ldots , v_{n}(t))\) be a solution of system (1.1) with initial conditions:

$$ v_{i}(s)=\varphi ^{v}_{i}(s),\qquad v_{i}'(0)=\psi ^{v}_{i},\quad \varphi ^{v}_{i} \in BC\bigl( (-\infty , 0], \mathbb{R} \bigr), \psi ^{v}_{i}\in \mathbb{R}, i\in D. $$
(3.1)

Clearly, for any nonnegative integer m,

$$\begin{aligned} & \bigl((-1)^{m+1}v_{i} \bigl(t + (m+1) T\bigr) \bigr)'' \\ &\quad = -{a}_{i}(t) \bigl((-1)^{m+1}v_{i} \bigl(t + (m+1) T\bigr)\bigr)'-{b}_{i}(t) \bigl((-1)^{m+1}v_{i}\bigl(t+ (m+1) T\bigr)\bigr) \\ &\qquad {}+\sum_{j=1}^{n}{c}_{ij}(t)A_{j} \bigl((-1)^{m+1}v_{j}\bigl(t+ (m+1)T \bigr)\bigr) \\ &\qquad {} +\sum_{j=1}^{n}{d}_{ij}(t)B_{j} \bigl((-1)^{m+1}v_{j}\bigl( t+ (m+1)T-q_{ij}(t )\bigr) \bigr)+ \sum_{j=1}^{n}\sum _{l=1}^{n}\theta _{ijl}(t) \\ &\qquad {} \times Q_{j}\bigl((-1)^{m+1}v_{j}\bigl(t+ (m+1)T- \eta _{ijl} (t ) \bigr)\bigr) \\ &\qquad {} \times Q_{l}\bigl((-1)^{m+1}v_{l}\bigl( t+ (m+1)T-\xi _{ijl} (t ) \bigr)\bigr) \\ &\qquad {}+ \sum_{j=1}^{n}h_{ij} (t) \int _{0}^{+\infty }\sigma _{ij}(u) K_{j}\bigl((-1)^{m+1}v_{j}(t-u)\bigr)\,du \\ &\qquad {}+ \sum_{j=1}^{n}\sum _{l=1}^{n}p_{ijl}(t) \int _{0}^{+ \infty }\hat{\sigma }_{ijl}(u) R_{j}\bigl((-1)^{m+1}v_{j}(t-u)\bigr)\,du \\ &\qquad {} \times \int _{0}^{+\infty } \bar{\sigma } _{ijl}(u) R_{l}\bigl((-1)^{m+1}v_{l}(t-u)\bigr) \,du+J_{i}(t) , \end{aligned}$$
(3.2)

for all \(i\in D\), \(t+(m+1)T\geq 0 \). It is easy to see that \((-1)^{m+1} v (t + (m+1)T) \) is a solution of (1.1), and \(u(t)= -v (t + T)\) satisfies system (1.1) involving initial values:

$$ \varphi ^{u}_{i}(s)=-v_{i}(s+T),\qquad \psi ^{u}_{i} =-v_{i}'(T),\quad \mbox{for all } s\in (-\infty , 0], i\in D. $$

According to Lemma 2.1, we can take a constant \(N=N(\varphi ^{v}, \psi ^{v},\varphi ^{u}, \psi ^{u})\) satisfying

$$ \bigl\vert v_{i}(t)- u_{i}(t) \bigr\vert \leq N e^{-\lambda t} ,\qquad \bigl\vert v_{i}'(t)- u_{i}'(t) \bigr\vert \leq N e^{-\lambda t} ,\quad \mbox{for all } t\geq 0, i\in D. $$

Thus,

$$ \left . \textstyle\begin{array}{@{}l@{}} \vert (-1)^{p } v_{i}(t+pT)- (-1)^{p+1}v _{i}(t+(p+1)T) \vert \\ \quad = \vert v_{i}(t+pT )- u_{i}(t+pT) \vert \leq N e^{-\lambda (t+pT)} , \\ \vert ((-1)^{p }v_{i}(t+pT))'- ((-1)^{p+1}v_{i}(t+(p+1)T))' \vert \\ \quad = \vert v_{i}'(t+pT)- u_{i}'(t+pT) \vert \leq N e^{-\lambda (t+pT)} , \end{array}\displaystyle \right \}\quad \forall i\in D, t+pT\geq 0. $$

Thus, together with the facts that

$$\begin{aligned}& (-1)^{m+1}v_{i}\bigl(t+(m+1)T\bigr) \\ & \quad = v_{i} (t ) +\sum_{p=0}^{m }\bigl[ (-1)^{p+1}v _{i}\bigl(t + (p+1)T\bigr)- (-1)^{p }v_{i} (t + pT)\bigr]\quad (i\in D) \end{aligned}$$

and

$$\begin{aligned}& \bigl((-1)^{m+1}v_{i}\bigl(t+(m+1)T\bigr) \bigr)' \\ & \quad = v_{i} '(t ) +\sum_{p=0}^{m } \bigl[ \bigl((-1)^{p+1}v _{i}\bigl(t + (p+1)T\bigr) \bigr)'- \bigl((-1)^{p+1}v_{i} (t + pT) \bigr)'\bigr]\quad (i\in D), \end{aligned}$$

then, we can show that there exists a continuous differentiable function \(\kappa (t)=(\kappa _{1} (t), \kappa _{2} (t), \ldots ,\kappa _{n} (t)) \) such that \(\{ (-1)^{m }v (t + mT)\}_{m\geq 1}\) and \(\{ ((-1)^{m }v (t + mT))'\}_{m\geq 1}\) are uniformly convergent to \(\kappa (t) \) and \(\kappa '(t) \) on any compact set of \(\mathbb{R}\), respectively. Moreover,

$$\begin{aligned} \kappa (t+T)&=\lim_{m\rightarrow +\infty }(-1)^{m }v (t +T+ m T) \\ &= - \lim_{(m+1)\rightarrow +\infty }(-1)^{m +1} v \bigl(t + (m +1)T\bigr)=- \kappa (t ) \end{aligned}$$

involves that \(\kappa (t)\) is T-anti-periodic on \(\mathbb{R}\). It follows from \((G_{1})\)–\((G_{4})\) and the continuity on (3.2) that \(\{ v'' (t + (m+1)T) \}_{m\geq 1}\) uniformly converges to a continuous function on any compact set of \(\mathbb{R}\). Furthermore, for any compact set of \(\mathbb{R}\), setting \(m \longrightarrow +\infty \), we obtain

$$\begin{aligned} \kappa _{i}''(t)={}&{-}a_{i}(t) \kappa _{i}'(t)-b_{i}(t)\kappa _{i}(t)+ \sum_{j=1}^{n} c_{ij}(t)A_{j}\bigl(\kappa _{j}(t)\bigr) \\ &{}+\sum_{j=1}^{n} d_{ij}(t)B_{j} \bigl(\kappa _{j}\bigl(t- q_{ij}( t)\bigr) \bigr) \\ &{}+ \sum_{j=1}^{n}\sum _{l=1}^{n}\theta _{ijl}(t)Q_{j} \bigl( \kappa _{j}\bigl( t-\eta _{ijl} (t) \bigr) \bigr)Q_{l}\bigl(\kappa _{l}\bigl( t-\xi _{ijl}( t) \bigr)\bigr) \\ &{}+ \sum_{j=1}^{n}h_{ij} (t) \int _{0}^{+\infty }\sigma _{ij}(u) K_{j}\bigl( \kappa _{j}(t-u)\bigr)\,du \\ &{}+ \sum_{j=1}^{n}\sum _{l=1}^{n}p_{ijl}(t) \int _{0}^{+ \infty }\hat{\sigma }_{ijl}(u) R_{j}\bigl(\kappa _{j}(t-u)\bigr)\,du \\ &{} \times \int _{0}^{+\infty } \bar{\sigma } _{ijl}(u) R_{l}\bigl(\kappa _{l}(t-u)\bigr)\,du+J_{i}(t),\quad i\in D, \end{aligned}$$

which involves the fact that \(\kappa (t)\) is a T-anti-periodic solution of (1.1). With the aid of Lemma 2.1 and Remark 2.2, we find that \(\kappa (t)\) is globally exponentially stable. This completes the proof of Theorem 3.1. □

Remark 3.1

In this present paper, the exponential convergence on every solution and its derivative in system (1.1) is established. In particular, one can see that the results in [19–21, 30, 34] are a special case of Theorem 3.1. This indicates that our results generalize and improve the previous references.

4 A numerical example

In this section, we give an example with a simulation to demonstrate the feasibility and the validity of our theoretical results.

Example 4.1

Let \(n=2\), and let us regard the following high-order inertial Hopfield neural networks with mixed delays

$$ \textstyle\begin{cases} x_{1}''(t) = -(14.92+0.1 \vert \sin t \vert ) x_{1}'(t) -(27.89+0.2 \vert \sin t \vert )x_{1}(t) \\ \hphantom{x_{1}''(t) ={}}{}+ 2.28(\sin t) A_{1}(x_{1}(t))+ 2.19 (\cos t) A_{2}(x_{2}(t)) \\ \hphantom{x_{1}''(t) ={}}{}-0.84 (\cos 2t) B_{1}(x_{1}( t-0.2 \sin ^{2} t ))+2.41 (\cos 2t )B_{2}(x_{2}( t-0.3 \sin ^{2} t )) \\ \hphantom{x_{1}''(t) ={}}{}+4 (\sin t)Q_{1}(x_{1}(t-0.4 \sin ^{2} t)) Q_{2}(x_{2}(t-0.5 \sin ^{2} t)) \\ \hphantom{x_{1}''(t) ={}}{}-0.95(\cos 2t)\int _{0}^{+\infty }\sin (4u)e^{-0.5u}K_{1}(x_{1}(t-u))\,du \\ \hphantom{x_{1}''(t) ={}}{}+2.52(\sin 2t)\int _{0}^{+\infty }\sin (3u)e^{-u}K_{2}(x_{2}(t-u))\,du \\ \hphantom{x_{1}''(t) ={}}{}+3.8(\cos t)\int _{0}^{+\infty }\cos (2u)e^{-0.5u}R_{1}(x_{1}(t-u))\,du \\ \hphantom{x_{1}''(t) ={}}{}\times \int _{0}^{+\infty }\cos (2u)e^{-u}R_{2}(x_{2}(t-u))\,du +55\sin t , \\ x_{2}''(t) = -(15.11+0.1 \vert \cos t \vert ) x_{2}'(t) -(31.05- 0.1 \vert \sin t \vert )) x_{2}(t) \\ \hphantom{x_{2}''(t) ={}}{}-1.88 (\sin t) A_{1}(x_{1}(t)) - 2.33 (\cos t) A_{2}(x_{2}(t)) \\ \hphantom{x_{2}''(t) ={}}{}-2.18 (\sin 2t) B_{1}(x_{1}( t-0.2 \cos ^{2} t ))+3.18( \sin 2t) B_{2}(x_{2}( t-0.3 \cos ^{2} t )) \\ \hphantom{x_{2}''(t) ={}}{}+3.8 (\sin t)Q_{1}(x_{1}( t-0.4 \cos ^{2} t)) Q_{2}(x_{2}( t-0.5 \cos ^{2} t)) \\ \hphantom{x_{2}''(t) ={}}{}-2.28(\cos 2t)\int _{0}^{+\infty }\sin (2u)e^{-0.5u}K_{1}(x_{1}(t-u))\,du \\ \hphantom{x_{2}''(t) ={}}{}+3.28(\sin 2t)\int _{0}^{+\infty }\sin (5u)e^{-u}K_{2}(x_{2}(t-u))\,du \\ \hphantom{x_{2}''(t) ={}}{}+4(\cos t)\int _{0}^{+\infty }\cos (4u)e^{-0.5u}R_{1}(x_{1}(t-u))\,du \\ \hphantom{x_{2}''(t) ={}}{}\times \int _{0}^{+\infty }\cos (4u)e^{-u}R_{2}(x_{2}(t-u))\,du+48 \sin t, \end{cases} $$
(4.1)

where \(A_{1}(u) = A_{2}(u) =\frac{1}{35} |u | \), \(B_{1}(u) = B_{2}(u) = \frac{1}{48} u\), \(Q_{1}(u) = Q_{2}(u) = \frac{1}{110} (|u+1| -|u-1|)\), \(K_{1}(u)=K_{2}(u)=\frac{1}{4\pi }\arctan u\), \(R_{1}(u)=R_{2}(u)= \frac{1}{2\pi }|\arctan u| \).

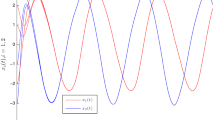
Obviously, one can take \(\lambda =0.01\), \(\alpha _{i}=\gamma _{i}=1.1\), \(\beta _{i}=5\), \(L_{i}^{A}=\frac{1}{35}\), \(L_{i}^{B}=\frac{1}{48}\), \(L_{i}^{Q}= \frac{1}{55}\), \(L_{i}^{K}= L_{i}^{R}=\frac{1}{2}\), \(M_{i}^{Q}=\frac{1}{55}\), \(M_{i}^{R}= \frac{1}{4}\), \(i=1,2\), such that (4.1) satisfies (2.4) and all the conditions assumed in Sect. 2. By Theorem 3.1, we know that system (4.1) has a globally exponentially stable π-anti-periodic solution \(x^{*}(t)\), and every solution of (4.1) and its derivative are exponentially convergent to \(x^{*}(t)\) and \((x^{*}(t))'\), respectively. Simulations in Figs. 1 and 2 reflect that the theoretical periodicity is in agreement with the numerically observed behavior.

Figure 1
figure 1

Numerical solutions \(x(t)\) to system (4.1) with initial values: \((\varphi _{1}(s),\varphi _{2}(s),\psi _{1}(s),\psi _{2}(s))\equiv ( 2 \sin t+1, -2\cos t-3 , 2, 0), (2\cos t+2, 3\sin t-1, 0, 3), (-3 \sin t-2, -4\sin t+3, -3, -4)\)

Full size image
Figure 2
figure 2

Numerical solutions \(x'(t)\) to system (4.1) with initial value \((\varphi _{1}(s),\varphi _{2}(s), \psi _{1}(s),\psi _{2}(s))\equiv ( 2\sin t+1, -2\cos t-3, 2, 0), (2\cos t+2, 3\sin t-1, 0, 3), (-3 \sin t-2, -4\sin t+3, -3, -4)\)

Full size image

Remark 4.1

By the way, there are many excellent results on inertial Hopfield neural networks with time-varying delays [18–21, 27, 29, 30]. However, the anti-periodicity on high-order inertial Hopfield neural networks with bounded time-varying delays and unbounded continuously distributed delays have never been touched upon by using the non-reduced order method. In addition, the corresponding results of [17–21, 27, 29, 30] and [46–95] cannot be used to reveal the convergence of the anti-periodic solution of the system (4.1).

5 Conclusions

In this paper, abandoning the traditional reduced order method, we explore the global convergence dynamics on a class of anti-periodic high-order inertial Hopfield neural networks with bounded time-varying delays and unbounded continuously distributed delays. Some sufficient conditions have been obtained to guarantee that every solution and its derivative of the addressed model is exponentially convergent to a anti-periodic solution and its derivative by combining differential inequality techniques with the Lyapunov function method. It should be mentioned that the results obtained in this manuscript are novel, and the method adopted provides a possible effective approach for studying other types high-order inertial neural networks with mixed delays.