1 Introduction

Consider the following unconstrained optimisation:

$$ \min f(x), \quad x\in \mathbb{R}^{n}, $$
(1)

where \(f:\mathbb{R}^{n} \rightarrow \mathbb{R}\) is continuously differentiable and bounded from below. Conjugate gradient method is one of the most effective line search methods for solving unconstrained optimisation problem (1) due to its features of low memory requirement and simple computation. Let \(x_{0}\) be an arbitrary initial approximate solution of problem (1). The iterative formula of conjugate gradient is given by

$$ x_{k+1}=x_{k}+\alpha _{k}d_{k}, \quad k\geq 0. $$
(2)

The search direction \(d_{k}\) is defined by

$$ d_{k}= \textstyle\begin{cases} -g_{0} ,& \text{if } k=0, \\ -g_{k}+\beta _{k} d_{k-1}, & \text{if } k\geq 1,\end{cases} $$
(3)

where \(g_{k}=\nabla f(x_{k})\) is the gradient of \(f(x)\) at \(x_{k}\) and \(\beta _{k}\) is a conjugate parameter. Different choices of \(\beta _{k}\) correspond to different conjugate gradient methods. Well-known formulas for \(\beta _{k}\) can be found in [8, 12–14, 17, 26]. The stepsize \(\alpha _{k}>0\) is usually obtained by the Wolfe line search

$$\begin{aligned}& f(x_{k}+\alpha _{k} d_{k}) \leq f(x_{k})+c_{1}\alpha _{k} g_{k}^{ \mathrm{T}}d_{k}, \end{aligned}$$
(4)
$$\begin{aligned}& g_{k+1}^{\mathrm{T}}d_{k} \geq c_{2}g_{k}^{\mathrm{T}}d_{k}, \end{aligned}$$
(5)

where \(0< c_{1}\leq c_{2}<1\). In order to exclude the points that are far from stationary points of \(f(x)\) along the direction \(d_{k}\), the strong Wolfe line search is used, which requires \(\alpha _{k}\) to satisfy (4) and

$$\begin{aligned} \bigl\vert g_{k+1}^{\mathrm{T}}d_{k} \bigr\vert \leq c_{2} \bigl\vert g_{k}^{\mathrm{T}}d_{k} \bigr\vert . \end{aligned}$$
(6)

Combining the conjugate gradient method and spectral gradient method [3], a spectral conjugate gradient method (SCG) was proposed by Bergin et al. [5]. Let \(s_{k-1}=x_{k}-x_{k-1}=\alpha _{k-1}d_{k-1}\) and \(y_{k-1}=g_{k}-g_{k-1}\). The direction \(d_{k}\) is termed as

$$ d_{k}= -\theta _{k}g_{k}+\beta _{k}s_{k-1}, $$
(7)

where the spectral parameter \(\theta _{k}\) and the conjugate parameter \(\beta _{k}\) are defined by

$$\begin{aligned} \theta _{k}= \frac{s_{k-1}^{\mathrm{T}}s_{k-1}}{s_{k-1}^{\mathrm{T}}y_{k-1}}, \qquad \beta _{k}= \frac{(\theta _{k}y_{k-1}-s_{k-1})^{\mathrm{T}}g_{k}}{d_{k-1}^{\mathrm{T}}y_{k-1}}, \end{aligned}$$

respectively. Obviously, if \(\theta _{k}=1\), the method is one of the classical conjugate gradient methods; if \(\beta _{k}=0\), the method is the spectral gradient method.

The SCG [5] was modified by Yu et al. [32] in order to achieve the descent directions. Moreover, there are other ways to determine \(\theta _{k}\) and \(\beta _{k}\). For instance, based on the descent condition, Wan et al. [29] and Zhang et al. [35] presented the modified PRP and FR spectral conjugate gradient method, respectively. Due to the strong convergence of the Newton method, Andrei [1] proposed an accelerated conjugate gradient method, which took advantage of the Newton method to improve the performance of the conjugate gradient method. Following this idea, Parvaneh et al. [24] proposed a new SCG, which is a modified version of the method suggested by Jian et al. [15]. Masoud [21] introduced a scaled conjugate gradient method which inherited the good properties of the classical conjugate gradient. More references in this field can be seen in [6, 10, 20, 28, 34].

Recently, Liu et al. [18, 19] introduced approximate optimal stepsizes (\(\alpha _{k}^{\mathrm{{AOS}}}\)) for gradient method. They constructed a quadratic approximation model of \(f(x_{k}-\alpha g_{k})\)

$$\begin{aligned} \varphi (\alpha )\equiv f(x_{k}-\alpha g_{k})=f(x_{k})- \alpha \Vert g_{k} \Vert ^{2}+\frac{1}{2}\alpha ^{2}g_{k}^{\mathrm{T}}B_{k}g_{k}, \end{aligned}$$

where the approximation Hessian matrix \(B_{k}\) is symmetric and positive definite. By minimising \(\varphi (\alpha )\), they obtained \(\alpha _{k}^{\mathrm{{AOS}}}=\frac{\|g_{k}\|^{2}}{g_{k}^{\mathrm{T}}B_{k}g_{k}}\) and proposed the approximate optimal gradient methods. If \(B_{k}=\frac{s_{k-1}^{\mathrm{T}}y_{k-1}}{\|s_{k-1}\|^{2}}I\) is selected, then the \(\alpha _{k}^{\mathrm{{AOS}}}\) reduces to \(\alpha _{k}^{\mathrm{{BB1}}}\), and the corresponding method is BB method [3]. If \(B_{k}=1/\bar{\alpha }_{k}^{\mathrm{{BB}}} I\) is chosen, where \(\bar{\alpha }_{k}^{\mathrm{{BB}}}\) is some modified BB stepsize, then the \(\alpha _{k}^{\mathrm{{AOS}}}\) reduces to \(\bar{\alpha }_{k}^{\mathrm{{BB}}}\), and the corresponding method is some modified BB method [4, 7, 30]. And if \(B_{k}=1/t I\), \(t>0\), then the \(\alpha _{k}^{\mathrm{{AOS}}}\) is the fixed stepsize t, and the corresponding method is the gradient method with fixed stepsize [16, 22, 33]. In this sense, the approximate optimal gradient method is a generalisation of the BB methods.

In this paper, we propose a new spectral conjugate gradient method based on the idea of the approximate optimal stepsize. Compared with the SCG method [5], the proposed method generates the sufficient descent direction per iteration and does not require more computation costs. Under some assumption conditions, the global convergence of the proposed method is established.

The rest of this paper is organised as follows. In Sect. 2, a new spectral conjugate gradient algorithm is presented and its computational costs are analysed. The global convergence of the proposed method is established in Sect. 3. In Sect. 4, some numerical experiments are used to show that the proposed method is superior to the SCG [5] and DY [8] methods. Conclusions are drawn in Sect. 5.

2 The new spectral conjugate gradient algorithm

In this section, we propose a new spectral conjugate gradient method with the form of (7). Let \(\bar{d_{k}}\) be a classical conjugate gradient direction. We firstly consider the approximate model of \(f(x_{k}+\alpha \bar{d_{k}})\)

$$ \psi (\alpha )\equiv f(x_{k}+\alpha \bar{d_{k}})=f(x_{k})+\alpha g_{k}^{ \mathrm{T}} \bar{d_{k}}+\frac{1}{2}\alpha ^{2}\bar{d_{k}}^{\mathrm{T}}B_{k} \bar{d_{k}} . $$
(8)

By \(\frac{d\psi }{d\alpha }=0\), we obtain the approximate optimal stepsize \(\alpha _{k}^{*}\) associated with \(\psi (\alpha )\)

$$ \alpha _{k}^{*}=- \frac{g_{k}^{\mathrm{T}}\bar{d_{k}}}{\bar{d_{k}}^{\mathrm{T}}B_{k}\bar{d_{k}}}. $$
(9)

Here, we choose BFGS update formula to generate \(B_{k}\), that is,

$$ B_{k}=B_{k-1}- \frac{B_{k-1}s_{k-1}s_{k-1}^{\mathrm{T}}B_{k-1}}{s_{k-1}^{\mathrm{T}}B_{k-1}s_{k-1}}+ \frac{y_{k-1}y_{k-1}^{\mathrm{T}}}{s_{k-1}^{\mathrm{T}}y_{k-1}}. $$
(10)

To reduce the computational and storage costs, the memoryless BFGS schemes are usually used to substitute \(B_{k}\), see [2, 23, 25]. In this paper, we choose \(B_{k-1}\) as a scalar matrix \(\xi \frac{\|y_{k-1}\|^{2}}{s_{k-1}^{\mathrm{T}}y_{k-1}}I\), \(\xi >0\). Then (10) can be rewritten as

$$ B_{k}=\xi \frac{ \Vert y_{k-1} \Vert ^{2}}{s_{k-1}^{\mathrm{T}}y_{k-1}}I-\xi \frac{ \Vert y_{k-1} \Vert ^{2}}{s_{k-1}^{\mathrm{T}}y_{k-1}} \frac{s_{k-1}s_{k-1}^{\mathrm{T}}}{s_{k-1}^{\mathrm{T}}s_{k-1}}+ \frac{y_{k-1}y_{k-1}^{\mathrm{T}}}{s_{k-1}^{\mathrm{T}}y_{k-1}}. $$
(11)

It is easy to prove that if \(s_{k-1}^{\mathrm{T}}y_{k-1}>0\), then \(B_{k}\) is symmetric and positive definite. If the direction \(\bar{d_{k}}\) is chosen as DY formula [8], i.e.,

$$ \bar{d_{k}}=d_{k}^{\mathrm{DY}}=-g_{k}+ \beta _{k}^{\mathrm{DY}}s_{k-1}, \qquad \beta _{k}^{\mathrm{DY}}= \frac{ \Vert g_{k} \Vert ^{2}}{s_{k-1}^{\mathrm{T}}y_{k-1}}. $$
(12)

Substituting (11) and (12) into (9), we have

$$ \alpha _{k}^{*}= \frac{-s_{k-1}^{\mathrm{T}}g_{k-1}}{{\xi \Vert y_{k-1} \Vert ^{2}p_{k}}}, $$
(13)

where

$$ p_{k}=1- \frac{(g_{k}^{\mathrm{T}}s_{k-1})^{2}}{ \Vert g_{k} \Vert ^{2} \Vert s_{k-1} \Vert ^{2}}+ \biggl( \frac{g_{k}^{\mathrm{T}}y_{k-1}}{ \Vert g_{k} \Vert \Vert y_{k-1} \Vert }+ \frac{ \Vert g_{k} \Vert }{ \Vert y_{k-1} \Vert } \biggr)^{2}. $$
(14)

To ensure the sufficient descent property of the direction and the bounded property of spectral parameter \(\theta _{k}\), the truncating technique in [19] is adopted to choose \(\theta _{k}\) and \(\beta _{k}\) as follows:

$$ \left \{ \textstyle\begin{array}{ll} \theta _{k}=\max \{\min \{\alpha _{k}^{*},\bar{\rho }_{k}\}, \rho _{k} \}, \\ \beta _{k}=\theta _{k}\beta _{k}^{\mathrm{DY}},\end{array}\displaystyle \right . $$
(15)

where \(\bar{\rho }_{k}=\frac{\|s_{k-1}\|^{2}}{s_{k-1}^{\mathrm{T}}y_{k-1}}\) and \(\rho _{k}=\frac{s_{k-1}^{\mathrm{T}}y_{k-1}}{\|y_{k-1}\|^{2}}\).

Based on the above analyses, we describe the following algorithm.

Algorithm 2.1

(NSCG)

Step 0.:

Let \(x_{0}\in \mathbb{R}^{n}\), \(\varepsilon >0\), \(0< c_{1} \leq c_{2}<1\) and \(1\leq \xi \leq 2\). Compute \(f_{0}=f(x_{0})\) and \(g_{0}=\nabla f(x_{0})\). Set \(d_{0}:=-g_{0}\) and \(k:=0\).

Step 1.:

If \(\|g_{k}\|\leq \varepsilon \), stop.

Step 2.:

Compute \(\alpha _{k}\) by (4) and (6).

Step 3.:

Set \(x_{k+1}=x_{k}+\alpha _{k}d_{k}\), and compute \(g_{k+1}\).

Step 4.:

Compute \(\theta _{k+1}\) and \(\beta _{k+1}\) by (15).

Step 5.:

Compute \(d_{k+1}\) by (7), set \(k:=k+1\). Return to Step 1.

Remark 1

By contrast with the SCG algorithm formula, the extra computational work of NSCG algorithm seems to require the inner products \(g_{k-1}^{\mathrm{T}}s_{k-1}\) per iteration. But \(g_{k-1}^{\mathrm{T}}s_{k-1}\) should be computed while implementing the Wolfe conditions. It implies that the extra computational work can be negligible.

Remark 2

It is well known that \(s_{k-1}^{\mathrm{T}}y_{k-1}>0\) can be guaranteed by the Wolfe line search. Since (11) implies a memoryless quasi-Newton update, from the references [27] and [31], it can be seen

$$\begin{aligned} m\leq \rho _{k} \leq \bar{\rho }_{k}\leq M, \end{aligned}$$

where m and M are positive constants. Together with (15), the parameter \(\theta _{k}\) satisfies that

$$ m \leq \theta _{k}\leq M. $$
(16)

The following theorem indicates that the search direction generated by NSCG algorithm satisfies the sufficient descent condition.

Theorem 2.1

The search direction\(d_{k}\)generated by NSCG algorithm is a sufficient descent direction, i.e.,

$$ g_{k}^{\mathrm{T}}d_{k}\leq -c \Vert g_{k} \Vert ^{2},\quad \textit{where } c=m/(1+c_{2})>0. $$
(17)

Proof

From (6), we have

$$\begin{aligned} l_{k}= \frac{g_{k}^{\mathrm{T}}s_{k-1}}{g_{k-1}^{\mathrm{T}}s_{k-1}}\in [-c_{2}, c_{2}]. \end{aligned}$$
(18)

Pre-multiplying (7) by \(g_{k}^{\mathrm{T}}\), from (15), (16) and (18), we have

$$\begin{aligned} g_{k}^{\mathrm{T}}d_{k} =&- \theta _{k} \Vert g_{k} \Vert ^{2}+\beta _{k}g_{k}^{\mathrm{T}}s_{k-1} \\ =&\theta _{k} \Vert g_{k} \Vert ^{2} \frac{1}{l_{k}-1} \\ \leq &-\frac{m}{1+c_{2}} \Vert g_{k} \Vert ^{2} \\ =&-c \Vert g_{k} \Vert ^{2}, \end{aligned}$$

where \(c=m/(1+c_{2})>0\). □

3 Convergence analysis

In this section, the convergence of NSCG algorithm is analysed. We consider that \(\|g_{k}\|\neq 0\) for all \(k\geq 0\), otherwise a stationary point is obtained. We make the following assumptions.

Assumption 3.1

  1. (i)

    The level set \(\varOmega =\{x| f(x)\leq f(x_{0})\}\) is bounded.

  2. (ii)

    In some open neighbourhood N of Ω, the function f is continuously differentiable and its gradient is Lipschitz continuous, i.e., there exists a constant \(L>0\) such that

    $$ \bigl\Vert g(x)-g(y) \bigr\Vert \leq L \Vert x-y \Vert \quad \text{for any } x,y\in N. $$
    (19)

Assumption 3.1 implies that there exists a constant \(\varGamma \geq 0\) such that

$$ \bigl\Vert g(x) \bigr\Vert \leq \varGamma \quad \text{for any } x\in \varOmega . $$
(20)

The following lemma called Zoutendijk condition [36] was originally given by Zoutendijk et al.

Lemma 3.1

Suppose that Assumption 3.1holds. Let the sequences\(\{d_{k}\}\)and\(\{\alpha _{k}\}\)be generated by NSCG algorithm. Then

$$ \sum_{k=0}^{\infty } \frac{(g_{k}^{\mathrm{T}}d_{k})^{2}}{ \Vert d_{k} \Vert ^{2}}< \infty . $$
(21)

From Assumption 3.1, Theorem 2.1 and Lemma 3.1, the following result can be proved.

Lemma 3.2

Suppose that Assumption 3.1holds. Let the sequences\(\{d_{k}\}\)and\(\{\alpha _{k}\}\)be generated by NSCG algorithm. Then either

$$ \liminf_{k\rightarrow \infty } \Vert g_{k} \Vert =0 $$
(22)

or

$$ \sum_{k=0}^{\infty } \frac{ \Vert g_{k} \Vert ^{4}}{ \Vert d_{k} \Vert ^{2}}< \infty . $$
(23)

Proof

It is sufficient to prove that if (22) is not true, then (23) holds. We use proofs by contradiction. Suppose that there exists \(\gamma >0\) such that

$$ \Vert g_{k} \Vert \geq \gamma \quad \text{for any } k\geq 0. $$
(24)

From (7) and Theorem 2.1, we have

$$\begin{aligned} \frac{ \Vert d_{k} \Vert ^{2}}{ \Vert d_{k-1} \Vert ^{2}} =&\frac{(\alpha _{k-1}\beta _{k})^{2} \Vert d_{k-1} \Vert ^{2} -\theta _{k}^{2} \Vert g_{k} \Vert ^{2}-2\theta _{k}d_{k}^{\mathrm{T}}g_{k}}{ \Vert d_{k-1} \Vert ^{2}} \\ \geq &(\alpha _{k-1}\beta _{k})^{2}-\theta _{k}^{2} \frac{ \Vert g_{k} \Vert ^{2}}{ \Vert d_{k-1} \Vert ^{2}}. \end{aligned}$$
(25)

Besides, pre-multiplying (7) by \(g_{k}^{\mathrm{T}}\), we have

$$\begin{aligned} g_{k}^{\mathrm{T}}d_{k}-\alpha _{k-1} \beta _{k}g_{k}^{\mathrm{T}}d_{k-1}=- \theta _{k} \Vert g_{k} \Vert ^{2}. \end{aligned}$$

By using the triangle inequality and (6), we get

$$ \bigl\vert g_{k}^{\mathrm{T}}d_{k} \bigr\vert +c_{2}\alpha _{k-1} \vert \beta _{k} \vert \bigl\vert g_{k-1}^{\mathrm{T}}d_{k-1} \bigr\vert \geq \theta _{k} \Vert g_{k} \Vert ^{2}. $$
(26)

Together with Cauchy’s inequality, (26) yields

$$\begin{aligned} \bigl(g_{k}^{\mathrm{T}}d_{k} \bigr)^{2}+(\alpha _{k-1}\beta _{k})^{2} \bigl(g_{k-1}^{\mathrm{T}}d_{k-1}\bigr)^{2} \geq \frac{\theta _{k}^{2}}{1+c_{2}^{2}} \Vert g_{k} \Vert ^{4}. \end{aligned}$$
(27)

Therefore, from (25) and (27), we obtain

$$\begin{aligned} &\frac{(g_{k}^{\mathrm{T}}d_{k})^{2}}{ \Vert d_{k} \Vert ^{2}}+ \frac{(g_{k-1}^{\mathrm{T}}d_{k-1})^{2}}{ \Vert d_{k-1} \Vert ^{2}} \\ &\quad =\frac{1}{ \Vert d_{k} \Vert ^{2}} \biggl[\bigl(g_{k}^{\mathrm{T}}d_{k} \bigr)^{2}+ \frac{ \Vert d_{k} \Vert ^{2}}{ \Vert d_{k-1} \Vert ^{2}}\bigl(g_{k-1}^{\mathrm{T}}d_{k-1} \bigr)^{2} \biggr] \\ &\quad \geq \frac{1}{ \Vert d_{k} \Vert ^{2}} \biggl[ \frac{\theta _{k}^{2}}{1+c_{2}^{2}} \Vert g_{k} \Vert ^{4}+\bigl(g_{k-1}^{\mathrm{T}}d_{k-1} \bigr)^{2} \biggl(\frac{ \Vert d_{k} \Vert ^{2}}{ \Vert d_{k-1} \Vert ^{2}}-(\alpha _{k-1}\beta _{k})^{2} \biggr) \biggr] \\ &\quad \geq \frac{ \Vert g_{k} \Vert ^{4}}{ \Vert d_{k} \Vert ^{2}} \biggl[ \frac{\theta _{k}^{2}}{1+c_{2}^{2}}-\theta _{k}^{2} \frac{(g_{k-1}^{\mathrm{T}}d_{k-1})^{2}}{ \Vert d_{k-1} \Vert ^{2}} \frac{1}{ \Vert g_{k} \Vert ^{2}} \biggr] \\ &\quad =\frac{ \Vert g_{k} \Vert ^{4}}{ \Vert d_{k} \Vert ^{2}}\theta _{k}^{2} \biggl[ \frac{1}{1+c_{2}^{2}}- \frac{(g_{k-1}^{\mathrm{T}}d_{k-1})^{2}}{ \Vert d_{k-1} \Vert ^{2}} \frac{1}{ \Vert g_{k} \Vert ^{2}} \biggr]. \end{aligned}$$
(28)

It follows from Lemma 3.1 that

$$\begin{aligned} \lim_{k\rightarrow \infty } \frac{(g_{k-1}^{\mathrm{T}}d_{k-1})^{2}}{ \Vert d_{k-1} \Vert ^{2}}=0. \end{aligned}$$

By use of (24) and \(\theta _{k}\geq m\), for all sufficiently large k, there exists a positive constant λ such that

$$ \theta _{k}^{2} \biggl[\frac{1}{1+c_{2}^{2}}- \frac{(g_{k-1}^{\mathrm{T}}d_{k-1})^{2}}{ \Vert d_{k-1} \Vert ^{2}} \frac{1}{ \Vert g_{k} \Vert ^{2}} \biggr]\geq \lambda . $$
(29)

Therefore, from (28) and (29) we have

$$\begin{aligned} \frac{(g_{k}^{\mathrm{T}}d_{k})^{2}}{ \Vert d_{k} \Vert ^{2}}+ \frac{(g_{k-1}^{\mathrm{T}}d_{k-1})^{2}}{ \Vert d_{k-1} \Vert ^{2}}\geq \lambda \frac{ \Vert g_{k} \Vert ^{4}}{ \Vert d_{k} \Vert ^{2}} \end{aligned}$$

holds for all sufficiently large k. Combining with the Zoutendijk condition, we deduce that inequality (23) holds. □

Corollary 3.1

Suppose that all the conditions of Lemma 3.2hold. If

$$ \sum_{k=0}^{\infty } \frac{1}{ \Vert d_{k} \Vert ^{2}}=+\infty , $$
(30)

then

$$\begin{aligned} \liminf_{k\rightarrow \infty } \Vert g_{k} \Vert =0. \end{aligned}$$

Proof

Suppose that there is a positive constant γ such that \(\|g_{k}\|\geq \gamma \) for all \(k\geq 0\). From Lemma 3.2, we have

$$\begin{aligned} \sum_{k=0}^{\infty }\frac{1}{ \Vert d_{k} \Vert ^{2}}\leq \frac{1}{\gamma ^{4}}\sum_{k=0}^{\infty } \frac{ \Vert g_{k} \Vert ^{4}}{ \Vert d_{k} \Vert ^{2}}\leq \infty , \end{aligned}$$

which contradicts (30), i.e., Corollary 3.1 is true. □

In the following, we establish the global convergence theorem of NSCG algorithm.

Theorem 3.1

Suppose that Assumption 3.1holds and the sequence\(\{x_{k}\}\)is generated by NSCG algorithm. If there exists a constant\(\gamma > 0\)such that\(\|g_{k}\|\geq \gamma \), then the algorithm satisfies

$$ \liminf_{k\rightarrow \infty } \Vert g_{k} \Vert =0. $$
(31)

Proof

From Theorem 2.1, we have

$$\begin{aligned} g_{k-1}^{\mathrm{T}}s_{k-1}\leq -c \Vert g_{k-1} \Vert \Vert s_{k-1} \Vert . \end{aligned}$$

Observe that \(y_{k-1}^{\mathrm{T}}s_{k-1}=g_{k}^{\mathrm{T}}s_{k-1}-g_{k-1}^{\mathrm{T}}s_{k-1} \geq (c_{2}-1)g_{k-1}^{\mathrm{T}}s_{k-1}\), we have

$$\begin{aligned} y_{k-1}^{\mathrm{T}}s_{k-1}\geq c(1-c_{2}) \Vert g_{k-1} \Vert \Vert s_{k-1} \Vert . \end{aligned}$$

Moreover, from (15), (17) and (20), we get

$$\begin{aligned} \beta _{k} \leq & M\frac{ \Vert g_{k} \Vert ^{2}}{y_{k-1}^{\mathrm{T}}s_{k-1}}\leq \frac{M}{c(1-c_{2})} \frac{ \Vert g_{k} \Vert ^{2}}{ \Vert g_{k-1} \Vert \Vert s_{k-1} \Vert } \\ \leq & \frac{M\varGamma ^{2}}{c\gamma (1-c_{2})}\frac{1}{ \Vert s_{k-1} \Vert }= \frac{\mu }{ \Vert s_{k-1} \Vert }, \end{aligned}$$

where \(\mu =M\varGamma ^{2}/c\gamma (1-c_{2})\). Thus

$$\begin{aligned} \Vert d_{k} \Vert \leq \vert \theta _{k} \vert \Vert g_{k} \Vert + \vert \beta _{k} \vert \Vert s_{k-1} \Vert \leq M \varGamma +\mu . \end{aligned}$$

This implies that \(\sum_{k=0}^{\infty }1/\|d_{k}\|^{2}=\infty \). By Corollary 3.1, (31) holds. □

4 Numerical results

In this section, we show the computational performance of NSCG algorithm. All codes are written in Matlab R2015b and run on PC with 2.50 GHz CPU processor and 4.00 GB RAM memory. Our test problems consist of 130 examples [9] from 100 to 5,000,000 variables.

We implement the same stopping criterion

$$ \Vert g_{k} \Vert \leq \varepsilon \quad \text{or} \quad \bigl\vert f(x_{k+1})-f(x_{k}) \bigr\vert \leq \varepsilon \max \bigl\{ 1.0, \bigl\vert f(x_{k}) \bigr\vert \bigr\} . $$
(32)

Set the parameters \(\varepsilon =10^{-6}\), \(\xi =1.0001\), \(c_{1}=0.0001\) and \(c_{2}=0.9\).

Liu et al. [19] proposed GM_AOS 1, GM_AOS 2 and GM_AOS 3 algorithms, and GM_AOS 2 algorithm was slightly better than the other algorithms. When the quadratic model is considered, the algorithm developed by [18] is identical with GM_AOS 1 algorithm. In a certain sense, our algorithm can be viewed as an extension of SCG algorithm [5] and a modification of DY algorithm[8]. Therefore, we adopt the performance profiles introduced by Dolan et al. [11] to display the numerical performances of NSCG, SCG, DY and GM_AOS 2 algorithms.

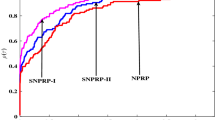
It is noticed that the number of iterations (Itr), the number of function evaluations (NF), the number of gradient evaluations (NG) and the CPU time (Tcpu) are important factors showing the numerical performance of an optimal method. In profiles, the top curve is the method that solved the most problems in a time that was within a factor of the best time. The horizontal axis gives the percentage \((\tau )\) of the test problems for which a method is the fastest (efficiency), while the vertical side gives the percentage \((\psi )\) of the test problems that are successfully solved by each of the methods. Moreover, we present the number of problems solved by the tested algorithms with a minimum number of Itr, NF and NG and the minimum Tcpu. If programme runs failure, we denote the number of Itr, NF, NG by a large positive integer, respectively, and denote the Tcpu by 1000 seconds. In this way, only NSCG algorithm can solve all test problems. However, SCG, DY and GM_AOS 2 algorithms do 98.5%, 93.8% and 92.3% of problems, respectively.

From Figs. 1–4, we can see that NSCG algorithm is the top performer, being more successful and more robust than SCG, DY and GM_AOS 2 algorithms. For example, in Fig. 1, subject to Itr, NSCG algorithm outperforms in 62 problems (i.e., it achieves the minimum number of iterations in 130 problems), SCG algorithm outperforms in 28 problems, DY algorithm outperforms in 23 problems, while GM_AOS 2 outperforms in 17 problems. Observe that NSCG algorithm is also the fastest of the three algorithms in Figs. 2, 3 and 4. To conclude, NSCG algorithm is more effective than other algorithms with respect to all the measures (Itr, NF, NG, Tcpu).

Figure 1
figure 1

Performance profiles for the number of iterations

Full size image
Figure 2
figure 2

Performance profiles for the number of function evaluations

Full size image
Figure 3
figure 3

Performance profiles for the number of gradient evaluations

Full size image
Figure 4
figure 4

Performance profiles for the CPU time

Full size image

5 Conclusions

In this paper, a new spectral conjugate gradient method is proposed based on the idea of approximate optimal stepsize. Besides, the memoryless BFGS formula is embedded in our algorithm to reduce the computational and storage costs. Under some assumptions, global convergence of the proposed method is established. Numerical results show that this method is efficient and competitive.