Weighted pseudo-almost periodic solutions and global exponential synchronization for delayed QVCNNs

Abstract

In this paper, we study the existence of weighted pseudo-almost periodic solutions and the global exponential synchronization of delayed quaternion-valued cellular neural networks (QVCNNs). Firstly, we use the Banach fixed point theorem to establish the existence of weighted pseudo-almost periodic solutions for this class of QVCNNs. Then, under the condition that the drive system has a unique weighted pseudo-almost periodic solution, by designing a state-feedback controller and constructing suitable Lyapunov functions, we see that the drive–response structure of delayed QVCNNs with weighted pseudo-almost periodic coefficients achieve global exponential synchronization. Finally, a numerical example is given to illustrate the feasibility of our results.

1 Introduction

Cellular neural networks (CNNs), which were originally proposed by Chua and Yang in [1, 2], have been widely used in signal processing, pattern recognition, associative memory, combinatorial optimization, intelligent robot control, and other new fields of application are constantly being discovered. In the past 30 years, many authors have considered the existence, uniqueness and stability of equilibrium points ([3]), periodic solutions ([4, 5]), almost periodic solutions ([6, 7]), pseudo-almost periodic solutions ([8, 9]) and weighted pseudo-almost periodic solutions ([10, 11]) of CNNs. In addition, as is well known, for artificial neural network systems and theoretical ecosystems, the dynamic behavior of the systems is the focus of great concern and interest. Stability, periodicity and almost periodicity are important dynamic characteristics of the systems. Therefore, these behaviors of neural network systems and ecosystems have been extensively studied (see [12,13,14,15,16,17,18,19,20,21,22,23,24]). In addition, we know that weighted pseudo-almost periodicity is an extension of pseudo-almost periodicity and pseudo-almost periodicity. However, to the best of our knowledge, the results of weighted pseudo-almost periodic solutions for CNNs are still rare.

On the one hand, synchronization is a common phenomenon in real world systems. This means that two or more systems are mutually regulated to reach a common dynamic behavior. Since Pecora and Carrol in [25] introduced the concept of drive–response synchronization for coupled chaotic systems, chaos synchronization has become a hot research topic due to its potential applications in secure communication, automatic control, biological systems, information science ([26, 27]). Also, the synchronization of neural networks has been the focus of scientific research and has been widely studied (see [28,29,30,31,32,33,34]).

On the other hand, it is well known that a quaternion consists of a real and three imaginary parts [35]. The three imaginary units i, j and k obey Hamilton’s multiplication rules:

$$ ij=-ji=k, \qquad jk=-kj=i, \qquad ki=-ik=j, \qquad i^{2}=j^{2}=k^{2}=ijk=-1. $$

The skew field of a quaternion is denoted by $\mathbb{H}:=\{h=h^{R}+ih ^{I}+jh^{J}+kh^{K}\}$, where $h^{R}, h^{I}, h^{J}, h^{K}\in \mathbb{R}$.

In recent years, quaternion-valued neural networks, which can be seen as a generic extension of complex-valued neural networks or real-valued neural networks, have been found many practical applications and have been widely concerned [36, 37]. Since the application of neural networks depends on their dynamics, some papers have been devoted to the study of the dynamical behaviors for quaternion-valued neural networks ([38,39,40,41,42,43]). However, up to now, there are still no results about weighted pseudo-almost periodic solutions and synchronization of QVCNNs. Therefore, it is very important and necessary to study the weighted pseudo-almost periodicity and synchronization of QVCNNs.

Motivated by the above discussion, in this paper, we consider the following delayed QVCNN:

$$ x_{p}'(t)=-c_{p}(t)x_{p}(t)+ \sum_{q=1}^{n}a_{pq}(t)f_{q} \bigl(x_{q}(t)\bigr)+ \sum_{q=1}^{n}b_{pq}(t)g_{q} \bigl(x_{q}\bigl(t-\tau _{pq}(t)\bigr) \bigr)+J_{p}(t), $$

(1)

where $p\in \{1,2,\ldots ,n\}:=S$, n corresponds to the number of units in the neural network; $x_{p}(t)$ is the state of the pth neuron at time t; $c_{p}(t)>0$ is the self-feedback connection weight; $a_{pq}(t)$, $b_{pq}(t)$ represent the connection weight and the delay connection weight between cell p and q at time t, respectively; $J_{p}(t)$ is an external input on the pth unit at time t; $f_{q}$ and $g_{q}$ are activation functions; $\tau _{pq}(t)$ represents the transmission delay at time t.

The initial value is given by

$$\begin{aligned} x_{p}(s)=\varphi _{p}(s),\quad s\in [-\tau ,0],p\in S, \end{aligned}$$

where $\tau =\max_{p,q\in S} \{\sup_{t\in \mathbb{R}}|\tau _{pq}(t)| \}$, $\varphi _{p}(s)=\varphi _{p}^{R}(s)+i \varphi _{p}^{I}(s)+j\varphi _{p}^{J}(s)+k\varphi _{p}^{K}(s)$ is a continuous function.

This paper is organized as follows: In Sect. 2, we introduce some definitions, preliminary lemmas. In Sect. 3, we establish some sufficient conditions for the existence of weighted pseudo-almost periodic solutions of (1). In Sect. 4, global exponential synchronization is investigated. In Sect. 5, we give an example to demonstrate the feasibility of our results. This paper ends with a brief conclusion in Sect. 6.

2 Preliminaries

Let $\mathit{BC}(\mathbb{R},\mathbb{R}^{n})$ be the set of all bounded and continuous functions from $\mathbb{R}$ to $\mathbb{R}^{n}$.

Definition 1

([44, 45])

A function $f\in \mathit{BC}(\mathbb{R},\mathbb{R} ^{n})$ is said to be almost periodic if, for any $\epsilon >0$, it is possible to find a real number $l=l(\epsilon )>0$, for any interval with length $l(\epsilon )$, there exists a number $\tau =\tau (\epsilon )$ in this interval such that $|f(t+\tau )-f(t)|<\epsilon$ for all $t\in \mathbb{R}$. The collection of such functions will be denoted by $\mathit{AP}(\mathbb{R},\mathbb{R}^{n})$.

Let $\mathbb{W}$ denote the collection of functions (weights) $\nu :\mathbb{R}\rightarrow (0,+\infty )$, which are locally integrable over $\mathbb{R}$ such that $\nu >0$ almost everywhere. If $\nu \in \mathbb{W}$ and for $r>0$, we set $Q_{r}:=[-r,r]$ and

$$ \nu (Q_{r}):= \int _{Q_{r}}\nu (x)\,\mathrm{d}x. $$

Let

$$\begin{aligned} \mathbb{W}_{\infty }= \Bigl\{ \nu \in \mathbb{W}:\inf_{x\in \mathbb{R}} \nu (x)=\nu _{0}>0, \lim_{r\rightarrow \infty }\nu (Q_{r})=\infty \Bigr\} . \end{aligned}$$

Definition 2

([46])

Fix $\nu \in \mathbb{W}_{\infty }$. A continuous function $f\in \mathit{BC}(\mathbb{R},\mathbb{X})$ is called weighted pseudo-almost periodic if it can be written as $f=g+h$ with $g\in \mathit{AP}( \mathbb{R},\mathbb{X})$ and $h\in \mathit{PAP}_{0}(\mathbb{R}, \mathbb{X},\nu )$, where the space $\mathit{PAP}_{0}(\mathbb{R}, \mathbb{X},\nu )$ is defined by

$$\begin{aligned} \mathit{PAP}_{0}(\mathbb{R},\mathbb{X},\nu )= \biggl\{ g\in \mathit{BC}(\mathbb{R},\mathbb{X}) : \lim_{r\rightarrow \infty } \frac{1}{ \nu (Q_{r})} \int _{Q_{r}} \bigl\Vert g(t) \bigr\Vert \nu (t) \,\mathrm{d}t=0 \biggr\} . \end{aligned}$$

The collection of all weighted pseudo-almost periodic functions $f:\mathbb{R}\rightarrow \mathbb{R}^{n}$ will be denoted by $\mathit{PAP}(\mathbb{R},\mathbb{R}^{n},\nu )$.

Lemma 1

([47])

If $f,g\in \mathit{PAP}(\mathbb{R},\mathbb{R},\nu )$, then $f+g, fg \in \mathit{PAP}(\mathbb{R},\mathbb{R},\nu )$; if $f\in \mathit{PAP}( \mathbb{R},\mathbb{R},\nu )$, $g\in \mathit{AP}(\mathbb{R},\mathbb{R})$, then $fg\in \mathit{PAP}(\mathbb{R},\mathbb{R},\nu )$.

Lemma 2

([47])

Fix $\nu \in \mathbb{W}_{\infty }$. Suppose that, for any $s\in \mathbb{R}$,

$$ \overline{\lim_{|t|\rightarrow \infty }}\frac{\nu (t+s)}{\nu (t)}< \infty . $$

Then $\mathit{PAP}_{0}(\mathbb{R},\mathbb{X},\nu )$ is translation-invariant.

Denote

$$\begin{aligned} \mathbb{W}_{\infty }^{\mathrm{Inv}}= \biggl\{ \nu \in \mathbb{W}_{ \infty }:\forall s\in \mathbb{R}, \overline{\lim _{|t|\rightarrow \infty }}\frac{\nu (t+s)}{\nu (t)}< \infty \biggr\} . \end{aligned}$$

Lemma 3

([10])

If $f\in C(\mathbb{R},\mathbb{R})$ satisfies the Lipschitz condition, $\varphi \in \mathit{PAP}(\mathbb{R},\mathbb{R},\nu )$ and $\delta \in C(\mathbb{R},\mathbb{R})$, then $f(\varphi (t-\delta (t)))\in \mathit{PAP}(\mathbb{R},\mathbb{R},\nu )$.

Definition 3

Fix $\nu \in \mathbb{W}_{\infty }$. Let $f=f^{R}+if^{I}+jf^{J}+kf ^{K}:\mathbb{R}\rightarrow \mathbb{H}$ where $f^{l}:\mathbb{R}\rightarrow \mathbb{R}, l\in \{R,I,J,K\}:=T$. f is said to be weighted pseudo-almost periodic if, for every $l\in T$, $f^{l}$ is weighted pseudo-almost periodic. The collection of such functions will be denoted by $\mathit{PAP}(\mathbb{R},\mathbb{H},\nu )$.

Let $x_{q}= x_{q}^{R}+ix_{q}^{I}+jx_{q}^{J}+k x_{q}^{K}\in \mathbb{H}$, where $x_{q}^{l}:\mathbb{R}\rightarrow \mathbb{R}, l \in T$. Then $f_{q}(x_{q})$ and $g_{q}(x_{q})$ of (1) can be expressed as

$$\begin{aligned}& \begin{aligned} f_{q}(x_{q}) ={}&f_{q}^{R} \bigl(x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr)+i f_{q}^{I} \bigl(x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr) \\ &{}+jf_{q}^{J} \bigl(x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr)+k f _{q}^{K} \bigl(x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr), \end{aligned} \\& \begin{aligned} g_{q}(x_{q}) ={}&g_{q}^{R} \bigl(x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr)+i g_{q}^{I} \bigl(x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr) \\ &{}+jg_{q}^{J} \bigl(x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr)+k g _{q}^{K} \bigl(x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr), \end{aligned} \end{aligned}$$

where $f_{q}^{l},g_{q}^{l}:\mathbb{R}^{4}\rightarrow \mathbb{R}$, $q\in S$, $l\in T$.

According to Hamilton rules, system (1) can be transformed into the following system:

$$\begin{aligned}& \begin{aligned} \bigl(x_{p}^{R} \bigr)'(t) ={}&{-}c_{p}(t)x_{p}^{R}(t)+\sum _{q=1}^{n} \bigl({a}_{pq}^{R}(s)f_{q}^{R} \{t,x\}- {a}_{pq}^{I}(s)f_{q}^{I} \{t,x\} \\ &{}-{a}_{pq}^{J}(s)f_{q}^{J} \{t,x\}-{a}_{pq}^{K}(s)f_{q}^{K} \{t,x\} \bigr)+\sum_{q=1}^{n} \bigl({b}_{pq}^{R}(s)g_{q}^{R} \{t,\tau ,x\} \\ &{}- {b}_{pq}^{I}(s)g_{q}^{I} \{t,\tau ,x\}-{b}_{pq}^{J}(s)g_{q}^{J} \{t, \tau ,x\} \\ &{}-{b}_{pq}^{K}(s)g_{q}^{K}\{t, \tau ,x\} \bigr)+J_{p}^{R}(t) \\ \triangleq {}& {-}c_{p}(t)x_{p}^{R}(t)+F_{p}^{R} \bigl(t,x(t)\bigr)+J_{p}^{R}(t), \quad q\in S, \end{aligned} \\& \begin{aligned} \bigl(x_{p}^{I} \bigr)'(t) ={}&{-}c_{p}(t)x_{p}^{I}(t)+\sum _{q=1}^{n} \bigl({a}_{pq}^{R}(s)f_{q}^{I} \{t,x\} + {a}_{pq}^{I}(s)f_{q}^{R} \{t,x \} \\ &{}+{a}_{pq}^{J}(s)f_{q}^{K} \{t,x\}-{a}_{pq}^{K}(s)f_{q}^{J} \{t,x\} \bigr)+\sum_{q=1}^{n} \bigl({b}_{pq}^{R}(s)g_{q}^{I} \{t,\tau ,x\} \\ &{}+ {b}_{pq}^{I}(s)g_{q}^{R} \{t,\tau ,x\}+{b}_{pq}^{J}(s)g_{q}^{K} \{t, \tau ,x\} \\ &{} -{b}_{pq}^{K}(s)g_{q}^{J} \{t,\tau ,x\} \bigr)+J_{p}^{I}(t) \\ \triangleq {}& {-}c_{p}(t)x_{p}^{I}(t)+F_{p}^{I} \bigl(t,x(t)\bigr)+J_{p}^{I}(t), \quad q\in S, \end{aligned} \\& \begin{aligned} \bigl(x_{p}^{J} \bigr)'(t) ={}&{-}c_{p}(t)x_{p}^{J}(t)+\sum _{q=1}^{n} \bigl({a}_{pq}^{R}(s)f_{q}^{J} \{t,x\}+ {a}_{pq}^{J}(s)f_{q}^{R} \{t,x\} \\ &{}-{a}_{pq}^{I}(s)f_{q}^{K} \{t,x\}+{a}_{pq}^{K}(s)f_{q}^{I} \{t,x\} \bigr)+\sum_{q=1}^{n} \bigl({b}_{pq}^{R}(s)g_{q}^{J} \{t,\tau ,x\} \\ &{}+ {b}_{pq}^{J}(s)g_{q}^{R} \{t,\tau ,x\}-{b}_{pq}^{I}(s)g_{q}^{K} \{t, \tau ,x\} \\ &{}+{b}_{pq}^{K}(s)g_{q}^{I}\{t, \tau ,x\} \bigr)+J_{p}^{J}(t) \\ \triangleq {}&{-}c_{p}(t)x_{p}^{J}(t)+F_{p}^{J} \bigl(t,x(t)\bigr)+J_{p}^{J}(t), \quad q\in S, \end{aligned} \\& \begin{aligned} \bigl(x_{p}^{K} \bigr)'(t) ={}&{-}c_{p}(t)x_{p}^{K}(t)+\sum _{q=1}^{n} \bigl({a}_{pq}^{R}(s)f_{q}^{K} \{t,x\}+ {a}_{pq}^{K}(s)f_{q}^{R} \{t,x\} \\ &{}+{a}_{pq}^{I}(s)f_{q}^{J} \{t,x\}-{a}_{pq}^{J}(s)f_{q}^{I} \{t,x\} \bigr)+\sum_{q=1}^{n} \bigl({b}_{pq}^{R}(s)g_{q}^{K} \{t,\tau ,x\} \\ &{}+ {b}_{pq}^{K}(s)g_{q}^{R} \{t,\tau ,x\}+{b}_{pq}^{I}(s)g_{q}^{J} \{t, \tau ,x\} \\ &{}-{b}_{pq}^{J}(s)g_{q}^{I}\{t, \tau ,x\} \bigr)+J_{p}^{K}(t) \\ \triangleq {}& {-}c_{p}(t)x_{p}^{K}(t)+F_{p}^{K} \bigl(t,x(t)\bigr)+J_{p}^{K}(t), \quad q\in S, \end{aligned} \end{aligned}$$

where

$$\begin{aligned}& f_{q}^{l}\{t,x\} \triangleq f_{q}^{l} \bigl(x_{q}^{R}(t),x_{q}^{I}(t),x _{q}^{J}(t),x_{q}^{K}(t) \bigr), \\& g_{q}^{l}\{t,\tau ,x\} \triangleq g_{q}^{l} \bigl(x_{q}^{R} \bigl(t-\tau _{pq}(t)\bigr),x_{q}^{I}\bigl(t- \tau _{pq}(t)\bigr), x_{q}^{J}\bigl(t-\tau _{pq}(t)\bigr),x_{q} ^{K}\bigl(t-\tau _{pq}(t)\bigr) \bigr). \end{aligned}$$

That is, system (1) is decomposed into the following system:

$$ \bigl(x_{p}^{l} \bigr)'(t)=-c_{p}(t)x_{p}^{l}(t)+F_{p}^{l} \bigl(t,x(t)\bigr)+J_{p} ^{l}(t), $$

(2)

where $p\in S$, $l\in T$. The initial condition associated with (2) is of the form

$$\begin{aligned} x_{p}^{l}(s)=\varphi _{p}^{l}(s), \quad s\in [-\tau ,0], p\in S, l\in T. \end{aligned}$$

Remark 1

If $x=(x_{1}^{R},x_{2}^{R},\ldots x_{n}^{R}, x_{1}^{I}, x_{2}^{I}, \ldots ,x_{n}^{I},x_{1}^{J}, x_{2}^{J}, \ldots ,x_{n}^{J},x_{1}^{K}, x _{2}^{K},\ldots ,x_{n}^{K})^{T}$ is a solution of system (2), then $z=(z_{1},z_{2},\ldots , z_{n})^{T}$ is a solution of (1), where $z_{p}=x_{p}^{R}+ix_{p}^{I}+jx_{p}^{J}+kx_{p}^{K}, p\in S$, and vice versa.

For the convenience, in the following, we introduce the following notation:

$$ f^{-}=\inf_{t\in \mathbb{R}} \bigl\vert f(t) \bigr\vert ,\qquad f^{+}=\sup_{t\in \mathbb{R}} \bigl\vert f(t) \bigr\vert , $$

where $f:\mathbb{R\rightarrow \mathbb{R}}$ is a bounded function.

Throughout the paper, we assume that the following conditions hold:

$(H_{1})$ :

For $p,q\in S$, $c_{p}\in C(\mathbb{R},\mathbb{R}^{+})$ with $c_{p}^{-}=\inf_{t\in \mathbb{R}}c_{p}(t)>0$, $a_{pq}, b _{pq}\in \mathit{PAP}(\mathbb{R},\mathbb{H},\mu )$, $\tau _{pq}\in \mathit{AP}(\mathbb{R},\mathbb{R}^{+})$, for fixed $\nu \in \mathbb{W}_{\infty }^{\mathrm{Inv}}$, and $J_{p}\in \mathit{PAP}( \mathbb{R},\mathbb{H})$.

$(H_{2})$ :

Functions $f_{q}^{l}, g_{q}^{l}\in C(\mathbb{R}^{4}, \mathbb{R})$ and, for any $x_{q}^{l}, y_{q}^{l}\in \mathbb{R}$, there exist positive constants $L_{f}^{l}$ and $L_{g}^{l}$ such that

$$\begin{aligned}& \bigl\vert f_{q}^{l} \bigl( y_{q}^{R},y_{q}^{I},y_{q}^{J},y_{q}^{K} \bigr)- f _{q}^{l} \bigl( x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr) \bigr\vert \\& \quad \leq L_{f}^{R} \bigl\vert y_{q}^{R}-x_{q}^{R} \bigr\vert +L_{f}^{I} \bigl\vert y_{q} ^{I}- x_{q}^{I} \bigr\vert +L_{f}^{J} \bigl\vert y_{q}^{J}-x_{q}^{J} \bigr\vert +L_{f} ^{K} \bigl\vert y_{q}^{K}-x_{q}^{K} \bigr\vert , \\& \bigl\vert g_{q}^{l} \bigl( y_{q}^{R},y_{q}^{I},y_{q}^{J},y_{q}^{K} \bigr)- g _{q}^{l} \bigl( x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr) \bigr\vert \\& \quad \leq L_{g}^{R} \bigl\vert y_{q}^{R}-x_{q}^{R} \bigr\vert +L_{g}^{I} \bigl\vert y_{q} ^{I}- x_{q}^{I} \bigr\vert +L_{g}^{J} \bigl\vert y_{q}^{J}-x_{q}^{J} \bigr\vert +L_{g} ^{K} \bigl\vert y_{q}^{K}-x_{q}^{K} \bigr\vert , \end{aligned}$$

and $f_{q}^{l}(\mathbf{0})=g_{q}^{l}(\mathbf{0})=0$, where $q\in S$, $l\in T$.

$(H_{3})$ :

$\rho =\max_{p\in S} \{ \frac{1}{c_{p}^{-}} (A_{p}+B_{p} ) \}<1$, where for $p\in S$,

$$\begin{aligned}& A_{p}=\sum_{q=1}^{n} \bigl(a_{pq}^{R^{+}}+a_{pq}^{I^{+}}+a_{pq} ^{J^{+}}+a_{pq}^{K^{+}} \bigr) \bigl(L_{f}^{R}+L_{f}^{I}+L_{f}^{J}+L_{f} ^{K} \bigr), \\& B_{p}=\sum_{q=1}^{n} \bigl(b_{pq}^{R^{+}}+b_{pq}^{I^{+}}+b_{pq} ^{J^{+}}+b_{pq}^{K^{+}} \bigr) \bigl(L_{g}^{R}+L_{g}^{I}+L_{g}^{J}+L_{g} ^{K} \bigr). \end{aligned}$$

3 The existence of weighted pseudo-almost periodic solutions

In this section, we will study the existence and global exponential stability of weighted pseudo-almost periodic solutions of system (2).

Let

$$\begin{aligned} \mathbb{B}={}& \bigl\{ \varphi =\bigl(\varphi _{1}^{R}, \ldots , \varphi _{n} ^{R}, \varphi _{1}^{I}, \ldots , \varphi _{n}^{I}, \varphi _{1}^{J}, \ldots , \varphi _{n}^{J},\varphi _{1}^{K}, \ldots , \\ & \varphi _{n}^{K}\bigr)^{T}:= (\varphi _{1},\varphi _{2},\ldots ,\varphi _{n})^{T} \in \mathit{PAP}\bigl(\mathbb{R},\mathbb{R}^{4n},\nu \bigr) \bigr\} \end{aligned}$$

with the norm $\|\varphi \|_{\mathbb{B}}=\max_{p\in S} \{ \max_{l\in T} \{\sup_{t\in \mathbb{R}}|\varphi _{p} ^{l}(t)| \} \}$, then $\mathbb{B}$ is a Banach space.

Let

$$\begin{aligned} \varphi ^{0}(t) ={}& \bigl(\bigl(\varphi ^{0} \bigr)_{1}^{R}(t),\ldots ,\bigl(\varphi ^{0} \bigr)_{n} ^{R}(t),\bigl(\varphi ^{0} \bigr)_{1}^{I}(t),\ldots , \bigl(\varphi ^{0}\bigr)_{n}^{I}(t), \\ &\bigl(\varphi ^{0}\bigr)_{1}^{J}(t), \ldots ,\bigl(\varphi ^{0}\bigr)_{n}^{J}(t), \bigl(\varphi ^{0}\bigr)_{1}^{K}(t),\ldots , \bigl(\varphi ^{0}\bigr)_{n}^{K}(t) \bigr)^{T}, \end{aligned} $$

where $(\varphi ^{0})_{p}^{l}(t)=\int _{-\infty }^{t}e^{-\int _{s}^{t}c _{p}(u)\,\mathrm{d}u}J_{p}^{l}(s)\,\mathrm{d}s$, $p\in S$, $l\in T$ and κ is a constant satisfying $\kappa \geq \|\varphi ^{0}\|_{ \mathbb{B}}$.

Lemma 4

Fix $\nu \in \mathbb{W}_{\infty }^{\mathrm{Inv}}$. Suppose that assumptions $(H_{1})$ and $(H_{2})$ hold. For each $\varphi =(\varphi _{1}^{R}, \ldots , \varphi _{n}^{R}, \varphi _{1}^{I}, \ldots , \varphi _{n}^{I}, \varphi _{1}^{J}, \ldots , \varphi _{n}^{J}, \varphi _{1}^{K}, \ldots , \varphi _{n}^{K})^{T}\in \mathbb{B}$, define a nonlinear operator Φ as follows:

$$\begin{aligned}& \bigl(\varphi _{1}^{R}, \ldots , \varphi _{n}^{R}, \varphi _{1}^{I}, \ldots , \varphi _{n}^{I}, \varphi _{1}^{J}, \ldots , \varphi _{n}^{J}, \varphi _{1}^{K}, \ldots , \varphi _{n}^{K}\bigr)^{T} \\& \quad \rightarrow \bigl(\bigl(x^{\varphi }\bigr)_{1}^{R}, \ldots ,\bigl(x^{\varphi }\bigr)_{n} ^{R}, \bigl(x^{\varphi }\bigr)_{1}^{I},\ldots , \bigl(x^{\varphi }\bigr)_{n}^{I}, \bigl(x^{ \varphi }\bigr)_{1}^{J}, \ldots , \bigl(x^{\varphi }\bigr)_{n}^{J}, \bigl(x^{\varphi }\bigr)_{1} ^{K},\ldots , \bigl(x^{\varphi }\bigr)_{n}^{K} \bigr)^{T}, \end{aligned}$$

where

$$\begin{aligned} \bigl(x^{\varphi }\bigr)^{l}_{p}(t)= \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{p}(u) \,\mathrm{d}u}\varOmega _{p}^{l}(s)\,\mathrm{d}s, \qquad \varOmega _{p}^{l}(t)=F_{p}^{l}\bigl(t, \varphi (t)\bigr)+J_{p}^{l}(t), \quad p\in S, l\in T, \end{aligned}$$

then Φ maps $\mathbb{B}$ into itself.

Proof

Let $\varphi \in \mathbb{B}$. By $(H_{2})$ and Lemma 3, we have $f_{q}^{l}[t,\varphi ]\in \mathit{PAP}(\mathbb{R},\mathbb{R},\nu )$ and by $(H_{1})$ and Lemma 3, we have $g_{q}^{l}[t,\tau ,\varphi ]\in \mathit{PAP}(\mathbb{R},\mathbb{R},\nu )$. Hence, from Lemma 1, we obtain $\varOmega _{p}^{l}\in \mathit{PAP}(\mathbb{R}, \mathbb{R},\nu )$ for all $p\in S$, $l\in T$. Consequently, $\varOmega _{p} ^{l}$ can be written as $\varOmega _{p}^{l}=\varOmega _{p1}^{l}+\varOmega _{p2} ^{l}$, where $\varOmega _{p1}^{l}\in \mathit{AP}(\mathbb{R},\mathbb{R})$, $\varOmega _{p2}^{l}\in \mathit{PAP}_{0}(\mathbb{R},\mathbb{R},\nu )$. Hence,

$$\begin{aligned} \bigl(x^{\varphi }\bigr)^{l}_{p}(t) &= \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{p}(u) \,\mathrm{d}u}\varOmega _{p1}^{l}(s)\,\mathrm{d}s + \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u}\varOmega _{p2}^{l}(s)\,\mathrm{d}s \\ &=:\varTheta _{p1}^{l}(t)+\varTheta _{p2}^{l}(t), \quad p\in S, l\in T. \end{aligned}$$

First, we will prove that $\varTheta _{p1}^{l}\in \mathit{AP}(\mathbb{R}, \mathbb{R})$ for all $p\in S$, $l\in T$. For every $\epsilon > 0$, since $\varOmega _{p1}^{l}, c_{p}\in \mathit{AP}(\mathbb{R},\mathbb{R})$, it is possible to find a real number $l=l(\epsilon )>0$, for each interval with length $l(\epsilon )$, there exists a number $\tau =\tau (\epsilon )$ in this interval such that $|\varOmega _{p1}^{l}(t+\tau )-\varOmega _{p1}^{l}(t)|<\epsilon$ and $|c_{p}(t+\tau )-c_{p}(t)|<\epsilon$, then

$$\begin{aligned}& \bigl\vert \varTheta _{p1}^{l}(t+ \tau )-\varTheta _{p1}^{l}(t) \bigr\vert \\& \quad = \biggl\vert \int _{-\infty }^{t+\tau }e^{-\int _{s}^{t+\tau }c_{p}(u) \,\mathrm{d}u}\varOmega _{p1}^{l}(s)\,\mathrm{d}s - \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u}\varOmega _{p1}^{l}(s)\,\mathrm{d}s \biggr\vert \\& \quad = \biggl\vert \int _{-\infty }^{t}e^{-\int _{s+\tau }^{t+\tau }c_{p}(u) \,\mathrm{d}u}\varOmega _{p1}^{l}(s+\tau )\,\mathrm{d}s - \int _{-\infty }^{t}e ^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u}\varOmega _{p1}^{l}(s)\,\mathrm{d}s \biggr\vert \\& \quad = \biggl\vert \int _{-\infty }^{t}e^{-\int _{s+\tau }^{t+\tau }c_{p}(u) \,\mathrm{d}u}\varOmega _{p1}^{l}(s+\tau )\,\mathrm{d}s - \int _{-\infty }^{t}e ^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u}\varOmega _{p1}^{l}(s+\tau )\,\mathrm{d}s \\& \qquad {}+ \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u}\varOmega _{p1} ^{l}(s+\tau )\,\mathrm{d}s - \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{p}(u) \,\mathrm{d}u}\varOmega _{p1}^{l}(s)\,\mathrm{d}s \biggr\vert \\& \quad \leq \int _{-\infty }^{t} \bigl\vert e^{-\int _{s+\tau }^{t+\tau }c_{p}(u) \,\mathrm{d}u}-e^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u} \bigr\vert \bigl\vert \varOmega _{p1}^{l}(s+\tau ) \bigr\vert \,\mathrm{d}s \\& \qquad {}+ \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u} \bigl\vert \varOmega _{p1}^{l}(s+\tau )-\varOmega _{p1}^{l}(s) \bigr\vert \,\mathrm{d}s. \end{aligned}$$

(3)

By $(e^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u} )_{t}'=-c_{p}(t)e ^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u}$, we have

$$\begin{aligned}& \bigl\vert e^{-\int _{s+\tau }^{t+\tau }c_{p}(u)\,\mathrm{d}u}-e^{-\int _{s} ^{t}c_{p}(u)\,\mathrm{d}u} \bigr\vert \\& \quad = \bigl\vert - \bigl(e^{-\int _{\theta }^{t}c_{p}(u)\,\mathrm{d}u}e^{- \int _{s+\tau }^{\theta +\tau }c_{p}(u)\,\mathrm{d}u} \bigr) \big|_{\theta =t}^{s} \bigr\vert \\& \quad = \biggl\vert - \biggl[ \int _{t}^{s}e^{-\int _{\theta }^{t}c_{p}(u)\,\mathrm{d}u} \bigl(e^{-\int _{s+\tau }^{\theta +\tau }c_{p}(u)\,\mathrm{d}u} \bigr)_{ \theta }'\,\mathrm{d}\theta \\& \qquad {}+ \int _{t}^{s} \bigl(e^{-\int _{\theta }^{t}c_{p}(u)\,\mathrm{d}u} \bigr)_{ \theta }' e^{-\int _{s+\tau }^{\theta +\tau }c_{p}(u)\,\mathrm{d}u} \,\mathrm{d}\theta \biggr] \biggr\vert \\& \quad = \biggl\vert \int _{t}^{s}e^{-\int _{\theta }^{t}c_{p}(u)\,\mathrm{d}u} \bigl(c _{p}(\theta +\tau )-c_{p}(\theta ) \bigr) e^{-\int _{s+\tau }^{\theta + \tau }c_{p}(u)\,\mathrm{d}u}\,\mathrm{d}\theta \biggr\vert \\& \quad \leq \int _{t}^{s}e^{-\int _{\theta }^{t}c_{p}(u)\,\mathrm{d}u} \bigl\vert c _{p}(\theta +\tau )-c_{p}(\theta ) \bigr\vert \,\mathrm{d}\theta \leq \frac{1}{c _{p}^{-}} e^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u}\epsilon . \end{aligned}$$

(4)

Since $\varOmega _{p1}^{l}\in \mathit{AP}(\mathbb{R},\mathbb{R})$, it is a uniformly continuous and bounded function. Denote $G(t):=\int _{- \infty }^{t} |\varOmega _{p1}^{l}(s) |\,\mathrm{d}s$ and substitute (4) into (3), we have

$$\begin{aligned} \bigl\vert \varTheta _{p1}^{l}(t+\tau )-\varTheta _{p1}^{l}(t) \bigr\vert \leq \frac{ \epsilon }{(c_{p}^{-})^{2}} \bigl(c_{p}^{-}+ \Vert G \Vert _{\mathbb{B}} \bigr), \end{aligned}$$

which implies that $\varTheta _{p1}^{l}\in \mathit{AP}(\mathbb{R}, \mathbb{R})$, $p\in S$, $l\in T$.

Next, for $p\in S$, $l\in T$, set

$$\begin{aligned} \varLambda _{p}^{l}=\frac{1}{\nu (Q_{r})} \int _{Q_{r}} \biggl\vert \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u} \varOmega _{p2}^{l}(s) \,\mathrm{d}s \biggr\vert \nu (t) \,\mathrm{d}t. \end{aligned}$$

To prove that $\varTheta _{p2}^{l}\in \mathit{PAP}_{0}(\mathbb{R}, \mathbb{R},\nu )$, we only need to show that $\lim_{r\rightarrow \infty }\varLambda _{p}^{l}=0$, $p\in S$, $l\in T$. By a similar argument as that in the proof of Lemma 3.4 in [47], one can see that $\varTheta _{p2}^{l}\in \mathit{PAP}_{0}( \mathbb{R},\mathbb{R},\nu )$, $p\in S$, $l\in T$. Therefore, we have $(x^{\varphi })^{l}_{p}\in \mathit{PAP}(\mathbb{R},\mathbb{R},\nu )$, that is, Φ maps $\mathbb{B}$ into itself. This completes the proof. □

Remark 2

It is easy to check that, for $p\in S$, $l\in T$,

$$\begin{aligned} \bigl(x^{\varphi }\bigr)^{l}_{p}(t)= \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{p}(u) \,\mathrm{d}u} \varOmega _{p}^{l}(s)\,\mathrm{d}s \end{aligned}$$

satisfy the following equations:

$$\begin{aligned} \bigl(x_{p}^{l} \bigr)'(t)=-c_{p}(t)x_{p}^{l}(t)+ \varOmega _{p}^{l}(t), \quad p\in S, l\in T. \end{aligned}$$

Theorem 1

Assume that $(H_{1})$–$(H_{3})$ hold, then system (2) has a unique weighted pseudo-almost periodic solution in $\mathbb{B}^{ \ast }= \{\varphi |\varphi \in \mathbb{B}, \|\varphi -\varphi ^{0} \|_{\mathbb{B}}\leq \frac{\rho \kappa }{1-\rho } \}$.

Proof

For any $\varphi \in \mathbb{B}$, by Lemma 4, Φ maps $\mathbb{B}$ into itself. Obviously,

$$\begin{aligned} \bigl\Vert \varphi ^{0} \bigr\Vert _{\mathbb{B}} =&\max _{1\leq p\leq n} \biggl\{ \sup_{t\in \mathbb{R}}\max _{l\in T} \biggl\vert \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{p}(u)\,\mathrm{d}u}J_{p}^{l}(s) \,\mathrm{d}s \biggr\vert \biggr\} \\ \leq & \max_{1\leq p\leq n} \biggl\{ \max_{l\in T} \biggl\{ \frac{J_{p}^{l^{+}}}{c_{p}^{-}} \biggr\} \biggr\} =\kappa . \end{aligned}$$

Hence, for all $\varphi \in \mathbb{B}^{\ast }= \{\varphi |\varphi \in \mathbb{B}, \|\varphi -\varphi ^{0}\|_{\mathbb{B}}\leq \frac{ \rho \kappa }{1-\rho } \}$, we have

$$\begin{aligned} \Vert \varphi \Vert _{\mathbb{B}} \leq \bigl\Vert \varphi -\varphi ^{0} \bigr\Vert _{\mathbb{B}}+ \bigl\Vert \varphi ^{0} \bigr\Vert _{\mathbb{B}} \leq \frac{\rho \kappa }{1-\rho }+ \kappa =\frac{\kappa }{1-\rho }. \end{aligned}$$

Next, we show that Φ maps $\mathbb{B}^{\ast }$ into itself. In fact, for any $\varphi \in \mathbb{B}^{\ast }$, by $(H_{2})$, we have

$$\begin{aligned}& \sup_{t\in \mathbb{R}} \bigl\vert (\varPhi \varphi )_{p}^{R}(t)-\bigl( \varphi ^{0} \bigr)_{p}^{R}(t) \bigr\vert \\& \quad = \sup_{t\in \mathbb{R}} \Biggl\vert \int _{-\infty }^{t}e^{-\int _{s} ^{t}c _{p} (u)\,\mathrm{d}u} \Biggl[\sum _{q=1}^{n} \bigl({a}_{pq} ^{R}(s)f_{q}^{R}[t,\varphi ]- {a}_{pq}^{I}(s)f_{q}^{I}[t, \varphi ] \\& \qquad {}-{a}_{pq}^{J}(s)f_{q}^{J}[t, \varphi ]-{a}_{pq}^{K}(s)f_{q}^{K}[t, \varphi ] \bigr) +\sum_{q=1}^{n} \bigl({b}_{pq}^{R}(s)g_{q}^{R}[t, \tau ,\varphi ] \\& \qquad {} -{b}_{pq}^{I}(s)g_{q}^{I}[t, \tau ,\varphi ]-{b}_{pq}^{J}(s)g_{q} ^{J}[t,\tau ,\varphi ] -{b}_{pq}^{K}(s)g_{q}^{K}[t, \tau ,\varphi ] \bigr) \Biggr]\,\mathrm{d}s \Biggr\vert \\& \quad \leq \sup_{t\in \mathbb{R}} \int _{-\infty }^{t}e^{-\int _{s} ^{t}c_{p} (u)\,\mathrm{d}u} \Biggl[\sum _{q=1}^{n} \bigl( \bigl\vert a_{pq} ^{R}(s) \bigr\vert \bigl\vert f_{q}^{R}[t,\varphi ] \bigr\vert + \bigl\vert a_{pq}^{I}(s) \bigr\vert \bigl\vert f_{q}^{I}[t,\varphi ] \bigr\vert \\& \qquad {}+ \bigl\vert a_{pq}^{J}(s) \bigr\vert \bigl\vert f_{q}^{J}[t,\varphi ] \bigr\vert + \bigl\vert a_{pq} ^{K}(s) \bigr\vert \bigl\vert f_{q}^{K}[t,\varphi ] \bigr\vert \bigr) +\sum _{q=1} ^{n} \bigl( \bigl\vert {b}_{pq}^{R}(s) \bigr\vert \bigl\vert g_{q}^{R}[t,\tau ,\varphi ] \bigr\vert \\& \qquad {} + \bigl\vert {b}_{pq}^{I}(s) \bigr\vert \bigl\vert g_{q}^{I}[t,\tau ,\varphi ] \bigr\vert + \bigl\vert {b}_{pq}^{J}(s) \bigr\vert \bigl\vert g_{q}^{J}[t,\tau ,\varphi ] \bigr\vert + \bigl\vert {b}_{pq}^{K}(s) \bigr\vert \bigl\vert g_{q}^{K}[t,\tau ,\varphi ] \bigr\vert \bigr) \Biggr] \,\mathrm{d}s \\& \quad \leq \sup_{t\in \mathbb{R}} \int _{-\infty }^{t}e^{-\int _{s} ^{t}c _{p} (u)\,\mathrm{d}u} \Biggl[\sum _{q=1}^{n} \bigl(a_{pq}^{R ^{+}}+a_{pq}^{I^{+}}+a_{pq}^{J^{+}} +a_{pq}^{K^{+}} \bigr) \\& \qquad {} \times \bigl(L_{f}^{R}+L_{f}^{I}+L_{f}^{J}+L_{f}^{K} \bigr) \Vert \varphi \Vert _{\mathbb{B}} +\sum _{q=1}^{n} \bigl(b_{pq}^{R^{+}}+b_{pq}^{I ^{+}}+b_{pq}^{J^{+}}+b_{pq}^{K^{+}} \bigr) \\& \qquad {} \times \bigl(L_{g}^{R}+L_{g}^{I} +L_{g}^{J}+L_{g}^{K} \bigr) \Vert \varphi \Vert _{\mathbb{B}} \Biggr]\,\mathrm{d}s \\& \quad \leq \frac{1}{c_{p}^{-}} (A_{p}+B_{p} ) \Vert \varphi \Vert _{ \mathbb{B}}, \quad p\in S. \end{aligned}$$

(5)

Similarly, we can obtain

$$ \sup_{t\in \mathbb{R}} \bigl\vert (\varPhi \varphi )_{p}^{l}(t)-\bigl(\varphi ^{0} \bigr)_{p}^{l}(t) \bigr\vert \leq \frac{1}{c_{p}^{-}} (A_{p}+B_{p} ) \Vert \varphi \Vert _{\mathbb{B}}, \quad p\in S, l=I,J,K. $$

(6)

It follows from (5) and (6) that

$$\begin{aligned} \bigl\Vert \varPhi \varphi -\varphi ^{0} \bigr\Vert _{\mathbb{B}}\leq \rho \Vert \varphi \Vert _{ \mathbb{B}}\leq \frac{\rho \kappa }{1-\rho }, \end{aligned}$$

which implies that $\varPhi \varphi \in \mathbb{B}^{\ast }$. So, the mapping Φ is a self mapping from $\mathbb{B}^{\ast }$ to $\mathbb{B}^{\ast }$. Finally, we prove that Φ is a contraction mapping. In fact, in view of $(H_{2})$, for any $\varphi ,\psi \in \mathbb{B }$, we have

$$\begin{aligned}& \sup_{t\in \mathbb{R}} \bigl\vert (\varPhi \varphi )_{p}^{R}(t)-( \varPhi \psi )_{p}^{R}(t) \bigr\vert \\ & \quad = \sup_{t\in \mathbb{R}} \Biggl\vert \int _{-\infty }^{t}e^{-\int _{s} ^{t} c _{p}(u)\,\mathrm{d}u} \Biggl[\sum _{q=1}^{n} \bigl({a}_{pq} ^{R}(s) \bigl(f_{q}^{R}\{t,\varphi \} -f_{q}^{R}\{t,\psi \} \bigr) \\ & \qquad {} -{a}_{pq}^{I}(s) \bigl(f_{q}^{I} \{t,\varphi \}-f_{q}^{I}\{t,\psi \} \bigr)-{a}_{pq}^{J}(s) \bigl(f_{q}^{J}\{t,\varphi \}-f_{q}^{J} \{t,\psi \} \bigr) \\ & \qquad {} -{a}_{pq}^{K}(s) \bigl(f_{q}^{K} \{t,\varphi \} -f_{q}^{K}\{t,\psi \} \bigr) \bigr)+\sum _{q=1}^{n} \bigl({b}_{pq}^{R}(s) \bigl(g_{q}^{R}\{t, \tau ,\varphi \} \\ & \qquad {}-g_{q}^{R}\{t,\tau ,\psi \} \bigr) -{b}_{pq}^{I}(s) \bigl(g_{q}^{I} \{t, \tau ,\varphi \}-g_{q}^{I}\{t,\tau ,\psi \} \bigr) \\ & \qquad {} -{b}_{pq}^{J}(s) \bigl(g_{q}^{J} \{t,\tau ,\varphi \}-g_{q}^{J}\{t, \tau ,\psi \} \bigr) -{b}_{pq}^{K}(s) \bigl(g_{q}^{K} \{t,\tau ,\varphi \} \\ & \qquad {}-g_{q}^{K}\{t,\tau ,\psi \} \bigr) \bigr) \Biggr] \,\mathrm{d}s \Biggr\vert \\ & \quad \leq \sup_{t\in \mathbb{R}} \int _{-\infty }^{t}e^{-\int _{s} ^{t} c _{p}(u)\,\mathrm{d}u} \Biggl[\sum _{q=1}^{n} \bigl( \bigl\vert {a} _{pq}^{R}(s) \bigr\vert \bigl\vert f_{q}^{R}\{t,\varphi \} -f_{q}^{R} \{t,\psi \} \bigr\vert \\ & \qquad {} + \bigl\vert {a}_{pq}^{I}(s) \bigr\vert \bigl\vert f_{q}^{I}\{t,\varphi \}-f_{q}^{I} \{t, \psi \} \bigr\vert + \bigl\vert {a}_{pq}^{J}(s) \bigr\vert \bigl\vert f_{q}^{J}\{t,\varphi \}-f _{q}^{J}\{t,\psi \} \bigr\vert \\ & \qquad {} + \bigl\vert {a}_{pq}^{K}(s) \bigr\vert \bigl\vert f_{q}^{K}\{t,\varphi \} -f_{q}^{K} \{t,\psi \} \bigr\vert \bigr)+\sum_{q=1}^{n} \bigl( \bigl\vert {b}_{pq}^{R}(s) \bigr\vert \bigl\vert g_{q}^{R}\{t,\tau ,\varphi \} \\ & \qquad {}-g_{q}^{R}\{t,\tau ,\psi \} \bigr\vert + \bigl\vert {b}_{pq}^{I}(s) \bigr\vert \bigl\vert g _{q}^{I}\{t,\tau ,\varphi \}-g_{q}^{I} \{t,\tau ,\psi \} \bigr\vert \\ & \qquad {}+ \bigl\vert {b}_{pq}^{J}(s) \bigr\vert \bigl\vert g_{q}^{J}\{t,\tau ,\varphi \}-g_{q} ^{J}\{t,\tau ,\psi \} \bigr\vert + \bigl\vert {b}_{pq}^{K}(s) \bigr\vert \bigl\vert g_{q}^{K}\{t, \tau ,\varphi \} \\ & \qquad {}-g_{q}^{K}\{t,\tau ,\psi \} \bigr\vert \bigr) \Biggr]\,\mathrm{d}s \\ & \quad \leq \sup_{t\in \mathbb{R}} \int _{-\infty }^{t}e^{-\int _{s} ^{t} c _{p}(u)\,\mathrm{d}u} \Biggl[\sum _{q=1}^{n} \bigl(a_{pq}^{R ^{+}}+a_{pq}^{I^{+}}+a_{pq}^{J^{+}} +a_{pq}^{K^{+}} \bigr) \\ & \qquad {} \times \bigl(L_{f}^{R}+L_{f}^{I}+L_{f}^{J}+L_{f}^{K} \bigr) \Vert \varphi -\psi \Vert _{\mathbb{B}} +\sum _{q=1}^{n} \bigl(b_{pq}^{R^{+}}+b_{pq} ^{I^{+}} \\ & \qquad {}+b_{pq}^{J^{+}}+b_{pq}^{K^{+}} \bigr) \bigl(L_{g}^{R}+L_{g}^{I} +L_{g} ^{J}+L_{g}^{K} \bigr) \Vert \varphi -\psi \Vert _{\mathbb{B}} \Biggr]\,\mathrm{d}s \\& \quad \leq \frac{1}{c_{p}^{-}} (A_{p}+B_{p} ) \Vert \varphi -\psi \Vert _{\mathbb{B}}, \quad p\in S. \end{aligned}$$

(7)

Similarly, we can get

$$ \sup_{t\in \mathbb{R}} \bigl\vert (\varPhi \varphi )_{p}^{R}(t)-(\varPhi \psi )_{p}^{R}(t) \bigr\vert \leq \frac{1}{c_{p}^{-}} (A_{p}+B_{p} ) \Vert \varphi -\psi \Vert _{\mathbb{B}}, \quad p\in S, l=I,J,K. $$

(8)

From (7) and (8), we obtain

$$\begin{aligned} \Vert \varPhi \varphi -\varPhi \psi \Vert _{\mathbb{B}}\leq \rho \Vert \varphi -\psi \Vert _{\mathbb{B}}. \end{aligned}$$

Since $(H_{3})$, Φ is a contraction mapping. Hence, Φ has a fixed point in $\mathbb{B}^{\ast }$. That is, system (2) has a unique weighted pseudo-almost periodic solution in $\mathbb{B}^{ \ast }$. This completes the proof. □

4 Global exponential synchronization

In this section, we consider system (1) as the drive system and design a response system as

$$\begin{aligned} y_{p}'(t) =&-c_{p}(t)y_{p}(t)+ \sum_{q=1}^{n}a_{pq}(t)f_{q} \bigl(y _{q}(t)\bigr) \\ &{} +\sum_{q=1}^{n}b_{pq}(t)g_{q} \bigl(y_{q}\bigl(t-\tau _{pq}(t)\bigr)\bigr) +J_{p}(t)+u _{p}(t), \end{aligned}$$

(9)

where $p\in S, u_{p}(t)$ is a controlled input.

Let signals $e_{p}(t)= y_{p}(t)-x_{p}(t)$, then we can obtain the following error system:

$$\begin{aligned} e_{p}'(t) =&-c_{p}(t)e_{p}(t)+ \sum_{q=1}^{n}a_{pq}(t) \bigl(f _{q}\bigl(y_{q}(t)\bigr) -f_{q} \bigl(x_{q}(t)\bigr) \bigr)+\sum_{q=1}^{n}b_{pq}(t) \\ &{}\times \bigl(g_{q}\bigl(y_{q}\bigl(t-\tau _{pq}(t)\bigr)\bigr)-g_{q}\bigl(x_{q} \bigl(t-\tau _{pq}(t)\bigr)\bigr) \bigr)+u_{p}(t), \quad p\in S. \end{aligned}$$

(10)

In order to realize the weighted pseudo-almost periodic synchronization of the drive–response system, we design the following state-feedback controller:

$$ u_{p}(t)=-d_{p}(t)e_{p}(t)+\sum _{q=1}^{n}p_{pq}(t)h_{q} \bigl(e_{q}(t)\bigr) +\sum_{q=1}^{n}q_{pq}(t) \bar{h}_{q}\bigl(e_{q}\bigl(t-\sigma _{pq}(t)\bigr)\bigr), \quad p\in S. $$

(11)

The initial condition of (9) is

$$\begin{aligned} y_{p}(s)=\psi _{p}(s), \quad s\in [-\xi ,0], p\in S, \end{aligned}$$

where $\xi =\max \{\tau ,\sigma \}$, $\sigma =\max_{p,q\in S} \{\sup_{t\in \mathbb{R}}\sigma _{pq}(t) \}$, $\psi _{p}(s)=\psi _{p}^{R}(s)+i\psi _{p}^{I}(s)+j\psi _{p}^{J}(s)+k\psi _{p}^{K}(s)$ is a continuous function.

System (10) can be decomposed into the following real-valued system:

$$\begin{aligned}& \bigl(e_{p}^{R} \bigr)'(t) = - \bigl(c_{p}(t)+d_{p}(t)\bigr)e_{p}^{R}(t) +\sum_{q=1}^{n} \bigl({a}_{pq}^{R}(t) \bigl(f_{q}^{R}\{t,y\} -f_{q} ^{R}\{t,x\} \bigr) \\& \hphantom{\bigl(e_{p}^{R} \bigr)'(t) =}{}-{a}_{pq}^{I}(t) \bigl(f_{q}^{I} \{t,y\}-f_{q}^{I}\{t,x\} \bigr) -{a} _{pq}^{J}(t) \bigl(f_{q}^{J}\{t,y\}-f_{q}^{J} \{t,x\} \bigr) \\& \hphantom{\bigl(e_{p}^{R} \bigr)'(t) =}{}-{a}_{pq}^{K}(t) \bigl(f_{q}^{K} \{t,y\}-f_{q}^{K}\{t,x\} \bigr) \bigr) + \sum _{q=1}^{n} \bigl({b}_{pq}^{R}(t) \bigl(g_{q}^{R}\{t,y\} \\& \hphantom{\bigl(e_{p}^{R} \bigr)'(t) =}{}-g_{q}^{R}\{t,x\} \bigr)-{b}_{pq}^{I}(t) \bigl(g_{q}^{I}\{t,y\}-g_{q} ^{I}\{t,x\} \bigr)-{b}_{pq}^{J}(t) \bigl(g_{q}^{J}\{t,y\} \\& \hphantom{\bigl(e_{p}^{R} \bigr)'(t) =}{}-g_{q}^{J}\{t,x\} \bigr)-{b}_{pq}^{K}(t) \bigl(g_{q}^{K}\{t,y\}-g_{q} ^{K}\{t,x\} \bigr) \bigr) \\& \hphantom{\bigl(e_{p}^{R} \bigr)'(t) =}{}+\sum_{q=1}^{n} \bigl({p}_{pq}^{R}(t)h_{q}^{R} \{t,e\}-{p}_{pq} ^{I}(t)h_{q}^{I} \{t,e\}-{p}_{pq}^{J}(t)h_{q}^{J} \{t,e\} \\& \hphantom{\bigl(e_{p}^{R} \bigr)'(t) =}{}-{p}_{pq}^{K}(t)h_{q}^{K} \{t,e\} \bigr)+\sum_{q=1}^{n} \bigl( {q}_{pq}^{R}(t)\bar{h}_{q}^{R} \{t,\sigma ,e\}-{q}_{pq}^{I}(t)\bar{h} _{q}^{I}\{t,\sigma ,e\} \\& \hphantom{\bigl(e_{p}^{R} \bigr)'(t) =}{}-{q}_{pq}^{J}(t)\bar{h}_{q}^{J} \{t,\sigma ,e\} -{q}_{pq}^{K}(t) \bar{h}_{q}^{K} \{t,\sigma ,e\} \bigr), \\& \bigl(e_{p}^{I} \bigr)'(t) = - \bigl(c_{p}(t)+d_{p}(t)\bigr)e_{p}^{I}(t) +\sum_{q=1}^{n} \bigl({a}_{pq}^{R}(t) \bigl(f_{q}^{I}\{t,y\}-f_{q}^{I} \{t,x\} \bigr) \\& \hphantom{\bigl(e_{p}^{I} \bigr)'(t) =}{}+{a}_{pq}^{I}(t) \bigl(f_{q}^{R} \{t,y\}-f_{q}^{R}\{t,x\} \bigr)+{a}_{pq} ^{J}(t) \bigl(f_{q}^{K}\{t,y \}-f_{q}^{K}\{t,x\} \bigr) \\& \hphantom{\bigl(e_{p}^{I} \bigr)'(t) =}{}-{a}_{pq}^{K}(t) \bigl(f_{q}^{J} \{t,y\}-f_{q}^{J}\{t,x\} \bigr) \bigr) + \sum _{q=1}^{n} \bigl({b}_{pq}^{R}(t) \bigl(g_{q}^{I}\{t,y\} \\& \hphantom{\bigl(e_{p}^{I} \bigr)'(t) =}{}-g_{q}^{I}\{t,x\} \bigr) +{b}_{pq}^{I}(t) \bigl(g_{q}^{R}\{t,y\}-g_{q} ^{R}\{t,x\} \bigr)+{b}_{pq}^{J}(t) \bigl(g_{q}^{K}\{t,y\} \\& \hphantom{\bigl(e_{p}^{I} \bigr)'(t) =}{}-g_{q}^{K}\{t,x\} \bigr)-{b}_{pq}^{K}(t) \bigl(g_{q}^{J}\{t,y\}-g_{q} ^{J}\{t,x\} \bigr) \bigr) \\& \hphantom{\bigl(e_{p}^{I} \bigr)'(t) =}{}+\sum_{q=1}^{n} \bigl({p}_{pq}^{R}(t)h_{q}^{I} \{t,e\}+{p}_{pq} ^{I}(t)h_{q}^{R} \{t,e\} +{p}_{pq}^{J}(t)h_{q}^{K} \{t,e\} \\& \hphantom{\bigl(e_{p}^{I} \bigr)'(t) =}{}-{p}_{pq}^{K}(t)h_{q}^{J} \{t,e\} \bigr) +\sum_{q=1}^{n} \bigl( {q}_{pq}^{R}(t)\bar{h}_{q}^{I} \{t,\sigma ,e\}+{q}_{pq}^{I}(t)\bar{h} _{q}^{R}\{t,\sigma ,e\} \\& \hphantom{\bigl(e_{p}^{I} \bigr)'(t) =}{}+{q}_{pq}^{J}(t)\bar{h}_{q}^{K} \{t,\sigma ,e\}-{q}_{pq}^{K}(t) \bar{h}_{q}^{J} \{t,\sigma ,e\} \bigr), \\& \bigl(e_{p}^{J} \bigr)'(t) = - \bigl(c_{p}(t)+d_{p}(t)\bigr)e_{p}^{J}(t) +\sum_{q=1}^{n} \bigl({a}_{pq}^{R}(t) \bigl(f_{q}^{J}\{t,y\}-f_{q}^{J} \{t,x\} \bigr) \\& \hphantom{\bigl(e_{p}^{J} \bigr)'(t) =}{}+{a}_{pq}^{J}(t) \bigl(f_{q}^{R} \{t,y\}-f_{q}^{R}\{t,x\} \bigr)-{a}_{pq} ^{I}(t) \bigl(f_{q}^{K}\{t,y \}-f_{q}^{K}\{t,x\} \bigr) \\& \hphantom{\bigl(e_{p}^{J} \bigr)'(t) =}{}+{a}_{pq}^{K}(t) \bigl(f_{q}^{I} \{t,y\}-f_{q}^{I}\{t,x\} \bigr) \bigr) + \sum _{q=1}^{n} \bigl({b}_{pq}^{R}(t) \bigl(g_{q}^{J}\{t,y\} \\& \hphantom{\bigl(e_{p}^{J} \bigr)'(t) =}{}-g_{q}^{J}\{t,x\} \bigr) +{b}_{pq}^{J}(t) \bigl(g_{q}^{R}\{t,y\}-g_{q} ^{R}\{t,x\} \bigr)-{b}_{pq}^{I}(t) \bigl(g_{q}^{K}\{t,y\} \\& \hphantom{\bigl(e_{p}^{J} \bigr)'(t) =}{}-g_{q}^{K}\{t,x\} \bigr) +{b}_{pq}^{K}(t) \bigl(g_{q}^{I}\{t,y\}-g_{q} ^{I}\{t,x\} \bigr) \bigr) \\& \hphantom{\bigl(e_{p}^{J} \bigr)'(t) =}{}+\sum_{q=1}^{n} \bigl({p}_{pq}^{R}(t)h_{q}^{J} \{t,e\}+{p}_{pq} ^{J}(t)h_{q}^{R} \{t,e\} -{p}_{pq}^{I}(t)h_{q}^{K} \{t,e\} \\& \hphantom{\bigl(e_{p}^{J} \bigr)'(t) =}{}+{p}_{pq}^{K}(t)h_{q}^{I} \{t,e\} \bigr) +\sum_{q=1}^{n} \bigl( {q}_{pq}^{R}(t)\bar{h}_{q}^{J} \{t,\sigma ,e\}+{q}_{pq}^{J}(t)\bar{h} _{q}^{R}\{t,\sigma ,e\} \\& \hphantom{\bigl(e_{p}^{J} \bigr)'(t) =}{}-{q}_{pq}^{I}(t)\bar{h}_{q}^{K} \{t,\sigma ,e\} +{q}_{pq}^{K}(t) \bar{h}_{q}^{I} \{t,\sigma ,e\} \bigr), \\& \bigl(e_{p}^{K} \bigr)'(t) = - \bigl(c_{p}(t)+d_{p}(t)\bigr)e_{p}^{K}(t) +\sum_{q=1}^{n} \bigl({a}_{pq}^{R}(t) \bigl(f_{q}^{K}\{t,y\}-f_{q}^{K} \{t,x\} \bigr) \\& \hphantom{\bigl(e_{p}^{K} \bigr)'(t) = }{}+{a}_{pq}^{K}(t) \bigl(f_{q}^{R} \{t,y\}-f_{q}^{R}\{t,x\} \bigr)+{a}_{pq} ^{I}(t) \bigl(f_{q}^{J}\{t,y \}-f_{q}^{J}\{t,x\} \bigr) \\& \hphantom{\bigl(e_{p}^{K} \bigr)'(t) = }{}-{a}_{pq}^{J}(t) \bigl(f_{q}^{I} \{t,y\}-f_{q}^{I}\{t,x\} \bigr) \bigr) + \sum _{q=1}^{n} \bigl({b}_{pq}^{R}(t) \bigl(g_{q}^{K}\{t,y\} \\& \hphantom{\bigl(e_{p}^{K} \bigr)'(t) = }{}-g_{q}^{K}\{t,x\} \bigr) +{b}_{pq}^{K}(t) \bigl(g_{q}^{R}\{t,y\}-g_{q} ^{R}\{t,x\} \bigr)+{b}_{pq}^{I}(t) \bigl(g_{q}^{J}\{t,y\} \\& \hphantom{\bigl(e_{p}^{K} \bigr)'(t) = }{}-g_{q}^{J}\{t,x\} \bigr) -{b}_{pq}^{J}(t) \bigl(g_{q}^{I}\{t,y\}-g_{q} ^{I}\{t,x\} \bigr) \bigr) \\& \hphantom{\bigl(e_{p}^{K} \bigr)'(t) = }{}+\sum_{q=1}^{n} \bigl({p}_{pq}^{R}(t)h_{q}^{K} \{t,e\}+{p}_{pq} ^{K}(t)h_{q}^{R} \{t,e\}+{p}_{pq}^{I}(t)h_{q}^{J} \{t,e\} \\& \hphantom{\bigl(e_{p}^{K} \bigr)'(t) = }{}-{p}_{pq}^{J}(t)h_{q}^{I} \{t,e\} \bigr) +\sum_{q=1}^{n} \bigl( {q}_{pq}^{R}(t)\bar{h}_{q}^{K} \{t,\sigma ,e\} +{q}_{pq}^{K}(t)\bar{h} _{q}^{R}\{t,\sigma ,e\} \\& \hphantom{\bigl(e_{p}^{K} \bigr)'(t) = }{}+{q}_{pq}^{I}(t)\bar{h}_{q}^{J} \{t,\sigma ,e\}-{q}_{pq}^{J}(t) \bar{h}_{q}^{I} \{t,\sigma ,e\} \bigr), \end{aligned}$$

where $h_{q}^{l}\{t,e\}\triangleq h_{q}^{l} (e_{q}^{R}(t),e_{q} ^{I}(t),e_{q}^{J}(t),e_{q}^{K}(t) ), \bar{h}_{q}^{l}\{t,\sigma ,e \}\triangleq \bar{h}_{q}^{l} (e_{q}^{R}(t-\sigma _{pq}(t)),e_{q} ^{I}(t-\sigma _{pq}(t)), e_{q}^{J}(t-\sigma _{pq}(t)),e_{q}^{K}(t - \sigma _{pq}(t)) ), p,q\in S, l\in T$.

Definition 4

Systems (9) and (1) are globally exponentially synchronized, if there exist positive constants M and λ such that

$$\begin{aligned} \bigl\Vert y(t)-x(t) \bigr\Vert \leq M \Vert \psi -\varphi \Vert _{0}e^{-\lambda t}, \quad t\geq 0, \end{aligned}$$

where $x=(x_{1}^{R},\ldots ,x_{n}^{R},x_{1}^{I},\ldots ,x_{n}^{I},x _{1}^{J},\ldots , x_{n}^{J}, x_{1}^{K},\ldots ,x_{n}^{K})$ and $y=(y_{1}^{R}, \ldots ,y_{n}^{R},y_{1}^{I}, \ldots ,y_{n}^{I}, y_{1}^{J}, \ldots , y_{n}^{J},y_{1}^{K},\ldots ,y _{n}^{K})$ are solutions of the corresponding real-valued systems of (1) and (9) with initial values $\varphi =(\varphi _{1} ^{R},\ldots ,\varphi _{n}^{R}, \varphi _{1}^{I},\ldots ,\varphi _{n}^{I}, \varphi _{1}^{J},\ldots ,\varphi _{n}^{J}, \varphi _{1}^{K}, \ldots ,\varphi _{n}^{K})$ and $\psi =(\psi _{1}^{R},\ldots ,\psi _{n} ^{R},\psi _{1}^{I}, \ldots , \psi _{n}^{I},\psi _{1}^{J},\ldots ,\psi _{n}^{J}, \psi _{1}^{K},\ldots ,\psi _{n}^{K})$, respectively,

$$ \bigl\Vert y(t)-x(t) \bigr\Vert =\max_{p\in S, l\in T} \bigl\{ \bigl\vert y_{p}^{l}(t) \bigr\vert - \bigl\vert x _{p}^{l}(t) \bigr\vert \bigr\} , \qquad \Vert \psi - \varphi \Vert _{0}=\max_{p\in S, l\in T} \Bigl\{ \sup _{t\in \mathbb{R}} \bigl\vert \psi _{p}^{l}(t) \bigr\vert - \bigl\vert \varphi _{p}^{l}(t) \bigr\vert \Bigr\} . $$

Theorem 2

Let $(H_{1})$–$(H_{3})$ hold. Suppose further that

$(H_{4})$ :

For $p,q\in S, d_{p}\in \mathit{AP}(\mathbb{R}, \mathbb{R}^{+})$, $p_{pq}, q_{pq}\in \mathit{PAP}(\mathbb{R}, \mathbb{H})$, $\sigma _{pq}\in \mathit{AP}(\mathbb{R},\mathbb{R}^{+})$.

$(H_{5})$ :

Functions $h_{q}^{l},\bar{h}_{q}^{l}\in C( \mathbb{R}^{4},\mathbb{R})$, for any $x_{q}^{l},y_{q}^{l}\in \mathbb{R}$, there exist positive constants $L_{h}^{l}, L_{\bar{h}} ^{l}$ such that, for $q\in S$, $l\in T$,

$$\begin{aligned}& \bigl\vert h_{q}^{l} \bigl( y_{q}^{R},y_{q}^{I},y_{q}^{J},y_{q}^{K} \bigr)- h _{q}^{l} \bigl( x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr) \bigr\vert \\& \quad \leq L_{h}^{R} \bigl\vert y_{q}^{R}-x_{q}^{R} \bigr\vert +L_{h}^{I} \bigl\vert y_{q} ^{I}- x_{q}^{I} \bigr\vert +L_{h}^{J} \bigl\vert y_{q}^{J}-x_{q}^{J} \bigr\vert +L_{h}^{K} \bigl\vert y_{q}^{K}-x_{q}^{K} \bigr\vert , \\& \bigl\vert \bar{h}_{q}^{l} \bigl( y_{q}^{R},y_{q}^{I},y_{q}^{J},y_{q}^{K} \bigr)- \bar{h}_{q}^{l} \bigl( x_{q}^{R},x_{q}^{I},x_{q}^{J},x_{q}^{K} \bigr) \bigr\vert \\& \quad \leq L_{\bar{h}}^{R} \bigl\vert y_{q}^{R}-x_{q}^{R} \bigr\vert +L_{\bar{h}} ^{I} \bigl\vert y_{q}^{I}- x_{q}^{I} \bigr\vert +L_{\bar{h}}^{J} \bigl\vert y_{q}^{J}-x _{q}^{J} \bigr\vert +L_{\bar{h}}^{K} \bigl\vert y_{q}^{K}-x_{q}^{K} \bigr\vert . \end{aligned}$$

$(H_{6})$ :

There exists a positive constant λ such that

$$\begin{aligned} \lambda -c_{p}^{-}-d_{p}^{-} +A_{p} +\frac{1}{\alpha } B_{p}e^{\lambda \tau } +P_{p}+ \frac{1}{\beta } Q_{p}e^{\lambda \sigma }< 0, \quad p\in S, \end{aligned}$$

where

$$\begin{aligned} P_{p}=\sum_{q=1}^{n} \bigl(p_{pq}^{R^{+}}+p_{pq}^{I^{+}}+p_{pq} ^{J^{+}}+p_{pq}^{K^{+}} \bigr) \bigl(L_{h}^{R}+L_{h}^{I}+L_{h}^{J}+L_{h} ^{K} \bigr), \\ Q_{p}=\sum_{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q_{pq}^{I^{+}}+q_{pq} ^{J^{+}}+q_{pq}^{K^{+}} \bigr) \bigl(L_{\bar{h}}^{R}+L_{\bar{h}}^{I}+L _{\bar{h}}^{J}+L_{\bar{h}}^{K} \bigr). \end{aligned}$$

Then (1) has a unique weighted pseudo-almost periodic solution. Moreover, (1) and (9) are globally exponentially synchronized.

Proof

By (10), for any $t>0$, $l\in T$, we have

$$\begin{aligned}& D^{+} \bigl\vert e_{p}^{l}(t) \bigr\vert \\& \quad \leq -\bigl(c_{p}^{-}+d_{p}^{-} \bigr) \bigl\vert e_{p}^{l}(t) \bigr\vert +\sum _{q=1}^{n} \bigl(a_{pq}^{R^{+}}+a_{pq}^{I^{+}}+a_{pq}^{J^{+}} +a_{pq}^{K^{+}} \bigr) \bigl(L_{f}^{R} \bigl\vert e_{q}^{R}(t) \bigr\vert \\& \qquad {}+L_{f}^{I} \bigl\vert e_{q}^{I}(t) \bigr\vert +L_{f}^{J} \bigl\vert e_{q}^{J}(t) \bigr\vert +L_{f}^{K} \bigl\vert e_{q} ^{K}(t) \bigr\vert \bigr) +\sum _{q=1}^{n} \bigl( b_{pq}^{R^{+}}+b_{pq}^{I ^{+}}+b_{pq}^{J^{+}} \\& \qquad {}+b_{pq}^{K^{+}} \bigr) \bigl(L_{g}^{R} \bigl\vert e_{q}^{R}\bigl(t-\tau _{pq}(t) \bigr) \bigr\vert +L _{g}^{I} \bigl\vert e_{q}^{I}\bigl(t-\tau _{pq}(t)\bigr) \bigr\vert +L_{g}^{J} \bigl\vert e_{q}^{J} \bigl(t-\tau _{pq}(t)\bigr) \bigr\vert \\& \qquad {}+L_{g}^{K} \bigl\vert e_{q}^{K} \bigl(t-\tau _{pq}(t)\bigr) \bigr\vert \bigr)+\sum _{q=1}^{n} \bigl(p_{pq}^{R^{+}}+p_{pq}^{I^{+}}+p_{pq}^{J^{+}}+p_{pq}^{K^{+}} \bigr) \bigl(L_{h}^{R} \bigl\vert e_{q}^{R}(t) \bigr\vert \\& \qquad {}+L_{h}^{I} \bigl\vert e_{q}^{I}(t) \bigr\vert +L_{h}^{J} \bigl\vert e_{q}^{J}(t) \bigr\vert +L_{h}^{K} \bigl\vert e_{q} ^{K}(t) \bigr\vert \bigr) +\sum _{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q_{pq}^{I ^{+}}+q_{pq}^{J^{+}} \\& \qquad {}+q_{pq}^{K^{+}} \bigr) \bigl(L_{\bar{h}}^{R} \bigl\vert e_{q}^{R}\bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert +L _{\bar{h}}^{I} \bigl\vert e_{q}^{I}\bigl(t-\sigma _{pq}(t) \bigr) \bigr\vert \\& \qquad {}+L_{\bar{h}}^{J} \bigl\vert e_{q}^{J} \bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert +L_{\bar{h}}^{K} \bigl\vert e_{q} ^{K}\bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert \bigr). \end{aligned}$$

Construct a Lyapunov function as follows:

$$ V(t)= V^{R}(t)+V^{I}(t)+V^{J}(t)+V^{K}(t), $$

where

$$\begin{aligned}& V^{l}(t)=\sum_{p=1}^{n} \bigl( \bigl\vert e_{p}^{l}(t) \bigr\vert e^{\lambda t}+\Delta _{p}(t) \bigr), \quad l\in T,\\& \begin{aligned} \Delta _{p}(t) ={}&\frac{1}{\alpha } \sum _{q=1}^{n} \bigl(b_{pq} ^{R^{+}}+b_{pq}^{I^{+}}+b_{pq}^{J^{+}}+b_{pq}^{K^{+}} \bigr) \int _{t-\tau _{pq}(t)}^{t} \bigl(L_{g}^{R} \bigl\vert e_{q}^{R}(s) \bigr\vert \\ &{}+L_{g}^{I} \bigl\vert e_{q}^{I}(s) \bigr\vert +L_{g}^{J} \bigl\vert e_{q}^{J}(s) \bigr\vert +L_{g}^{K} \bigl\vert e_{q} ^{K}(s) \bigr\vert \bigr)e^{\lambda ( s+\tau )}\,\mathrm{d}s \\ &{}+\frac{1}{\beta } \sum_{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q_{pq} ^{I^{+}}+q_{pq}^{J^{+}}+q_{pq}^{K^{+}} \bigr) \int _{t-\sigma _{pq}(t)} ^{t} \bigl(L_{\bar{h}}^{R} \bigl\vert e_{q}^{R}(s) \bigr\vert \\ &{}+L_{\bar{h}}^{I} \bigl\vert e_{q}^{I}(s) \bigr\vert +L_{\bar{h}}^{J} \bigl\vert e_{q}^{J}(s) \bigr\vert +L _{\bar{h}}^{K} \bigl\vert e_{q}^{K}(s) \bigr\vert \bigr)e^{\lambda ( s+\sigma )}\,\mathrm{d}s, \quad p\in S. \end{aligned} \end{aligned}$$

Computing the upper right derivative of $V(t)$ along the solutions of (10), we have

$$\begin{aligned}& D^{+}V^{R}(t) \\& \quad \leq \sum_{p=1}^{n} \Biggl\{ \lambda e^{\lambda t} \bigl\vert e_{p}^{R}(t) \bigr\vert + e^{\lambda t}D^{+} \bigl\vert e_{p} ^{R}(t) \bigr\vert +\frac{1}{\alpha } \sum _{q=1}^{n} \bigl(b_{pq}^{R^{+}} +b _{pq}^{I^{+}}+b_{pq}^{J^{+}}+b_{pq}^{K^{+}} \bigr) \\& \qquad {} \times \bigl(L_{g}^{R} \bigl\vert e_{q}^{R}(t) \bigr\vert +L_{g}^{I} \bigl\vert e_{q}^{I}(t) \bigr\vert +L_{g} ^{J} \bigl\vert e_{q}^{J}(t) \bigr\vert +L_{g}^{K} \bigl\vert e_{q}^{K}(t) \bigr\vert \bigr)e^{\lambda ( t+\tau )} \\& \qquad {}-\frac{1}{\alpha } \sum_{q=1}^{n} \bigl(b_{pq}^{R^{+}} +b_{pq} ^{I^{+}}+b_{pq}^{J^{+}}+b_{pq}^{K^{+}} \bigr) \bigl(L_{g}^{R} \bigl\vert e_{q}^{R} \bigl(t- \tau _{pq}(t)\bigr) \bigr\vert \\& \qquad {}+L_{g}^{I} \bigl\vert e_{q}^{I} \bigl(t-\tau _{pq}(t)\bigr) \bigr\vert +L_{g}^{J} \bigl\vert e_{q}^{J}\bigl(t-\tau _{pq}(t) \bigr) \bigr\vert +L_{g}^{K} \bigl\vert e_{q}^{K}\bigl(t-\tau _{pq}(t)\bigr) \bigr\vert \bigr) \\& \qquad {}\times e^{\lambda ( t-\tau _{pq}(t)+\tau )}\bigl(1-\tau _{pq}'(t) \bigr) + \frac{1}{ \beta } \sum_{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q_{pq}^{I^{+}}+q_{pq} ^{J^{+}}+q_{pq}^{K^{+}} \bigr) \\& \qquad {}\times \bigl(L_{\bar{h}}^{R} \bigl\vert e_{q}^{R}(t) \bigr\vert +L_{\bar{h}}^{I} \bigl\vert e_{q}^{I}(t) \bigr\vert +L _{\bar{h}}^{J} \bigl\vert e_{q}^{J}(t) \bigr\vert +L_{\bar{h}}^{K} \bigl\vert e_{q}^{K}(t) \bigr\vert \bigr)e^{ \lambda ( t+\sigma )} \\& \qquad {}-\frac{1}{\beta } \sum_{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q_{pq} ^{I^{+}}+q_{pq}^{J^{+}}+q_{pq}^{K^{+}} \bigr) \bigl(L_{\bar{h}}^{R} \bigl\vert e _{q}^{R}\bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert \\& \qquad {} +L_{\bar{h}}^{I} \bigl\vert e_{q}^{I} \bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert +L_{\bar{h}}^{J} \bigl\vert e _{q}^{J}\bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert \\& \qquad {} +L_{\bar{h}}^{K} \bigl\vert e_{q}^{K} \bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert \bigr)e^{\lambda ( t- \sigma _{pq}(t)+\sigma )} \bigl(1-\sigma _{pq}'(t)\bigr) \Biggr\} \\& \quad \leq \sum_{p=1}^{n} \Biggl\{ \bigl(\lambda -c_{p}^{-}-d_{p}^{-} \bigr)e ^{\lambda t} \bigl\vert e_{p}^{R}(t) \bigr\vert +\sum_{q=1}^{n} \bigl(a_{pq}^{R^{+}} +a _{pq}^{I^{+}}+a_{pq}^{J^{+}}+a_{pq}^{K^{+}} \bigr) \\& \qquad {}\times \bigl(L_{f}^{R} \bigl\vert e_{q}^{R}(t) \bigr\vert +L_{f}^{I} \bigl\vert e_{q}^{I}(t) \bigr\vert +L_{f}^{J} \bigl\vert e _{q}^{J}(t) \bigr\vert +L_{f}^{K} \bigl\vert e_{q}^{K}(t) \bigr\vert \bigr)e^{\lambda t} \\& \qquad {}+\sum_{q=1}^{n} \bigl( b_{pq}^{R^{+}} +b_{pq}^{I^{+}}+b_{pq} ^{J^{+}}+b_{pq}^{K^{+}} \bigr) \bigl(L_{g}^{R} \bigl\vert e_{q}^{R} \bigl(t-\tau _{pq}(t)\bigr) \bigr\vert \\& \qquad {}+L_{g}^{I} \bigl\vert e_{q}^{I} \bigl(t-\tau _{pq}(t)\bigr) \bigr\vert +L_{g}^{J} \bigl\vert e_{q}^{J}\bigl(t-\tau _{pq}(t) \bigr) \bigr\vert +L_{g}^{K} \bigl\vert e_{q}^{K}\bigl(t-\tau _{pq}(t)\bigr) \bigr\vert \bigr)e^{\lambda t} \\& \qquad {} +\sum_{q=1}^{n} \bigl(p_{pq}^{R^{+}}+p_{pq}^{I^{+}}+p_{pq} ^{J^{+}}+p_{pq}^{K^{+}} \bigr) \bigl(L_{h}^{R} \bigl\vert e_{q}^{R}(t) \bigr\vert +L_{h}^{I} \bigl\vert e _{q}^{I}(t) \bigr\vert \\& \qquad {}+L_{h}^{J} \bigl\vert e_{q}^{J}(t) \bigr\vert +L_{h}^{K} \bigl\vert e_{q}^{K}(t) \bigr\vert \bigr)e^{\lambda t} + \sum_{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q_{pq}^{I^{+}}+q_{pq}^{J ^{+}}+q_{pq}^{K^{+}} \bigr) \\& \qquad {}\times \bigl(L_{\bar{h}}^{R} \bigl\vert e_{q}^{R}\bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert +L_{ \bar{h}}^{I} \bigl\vert e_{q}^{I} \bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert +L_{\bar{h}}^{J} \bigl\vert e_{q}^{J}\bigl(t- \sigma _{pq}(t)\bigr) \bigr\vert \\ & \qquad {}+L_{\bar{h}}^{K} \bigl\vert e_{q}^{K} \bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert \bigr)e^{\lambda t}+ \frac{1}{ \alpha } \sum_{q=1}^{n} \bigl(b_{pq}^{R^{+}}+b_{pq}^{I^{+}}+b _{pq}^{J^{+}}+b_{pq}^{K^{+}} \bigr) \\ & \qquad {}\times \bigl(L_{g}^{R} \bigl\vert e_{q}^{R}(t) \bigr\vert +L_{g}^{I} \bigl\vert e_{q}^{I}(t) \bigr\vert +L_{g} ^{J} \bigl\vert e_{q}^{J}(t) \bigr\vert +L_{g}^{K} \bigl\vert e_{q}^{K}(t) \bigr\vert \bigr)e^{\lambda ( t+\tau )} \\ & \qquad {}-\sum_{q=1}^{n} \bigl(b_{pq}^{R^{+}}+b_{pq}^{I^{+}}+b_{pq}^{J ^{+}}+b_{pq}^{K^{+}} \bigr) \bigl(L_{g}^{R} \bigl\vert e_{q}^{R} \bigl(t-\tau _{pq}(t)\bigr) \bigr\vert \\ & \qquad {}+L_{g}^{I} \bigl\vert e_{q}^{I} \bigl(t-\tau _{pq}(t)\bigr) \bigr\vert +L_{g}^{J} \bigl\vert e_{q}^{J}\bigl(t-\tau _{pq}(t) \bigr) \bigr\vert +L_{g}^{K} \bigl\vert e_{q}^{K}\bigl(t-\tau _{pq}(t)\bigr) \bigr\vert \bigr)e^{\lambda t} \\ & \qquad {}+ \frac{1}{\beta } \sum_{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q_{pq} ^{I^{+}}+q_{pq}^{J^{+}}+q_{pq}^{K^{+}} \bigr) \bigl(L_{\bar{h}}^{R} \bigl\vert e_{q} ^{R}(t) \bigr\vert +L_{\bar{h}}^{I} \bigl\vert e_{q}^{I}(t) \bigr\vert \\ & \qquad {}+L_{\bar{h}}^{J} \bigl\vert e_{q}^{J}(t) \bigr\vert +L_{\bar{h}}^{K} \bigl\vert e_{q}^{K}(t) \bigr\vert \bigr)e ^{\lambda ( t+\sigma )} - \sum_{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q _{pq}^{I^{+}}+q_{pq}^{J^{+}}+q_{pq}^{K^{+}} \bigr) \\ & \qquad {}\times \bigl(L_{\bar{h}}^{R} \bigl\vert e_{q}^{R}\bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert +L_{ \bar{h}}^{I} \bigl\vert e_{q}^{I} \bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert +L_{\bar{h}}^{J} \bigl\vert e_{q}^{J}\bigl(t- \sigma _{pq}(t)\bigr) \bigr\vert \\ & \qquad {} +L_{\bar{h}}^{K} \bigl\vert e_{q}^{K} \bigl(t-\sigma _{pq}(t)\bigr) \bigr\vert \bigr)e^{\lambda t} \Biggr\} \\ & \quad \leq \sum_{p=1}^{n} \Biggl\{ \bigl(\lambda -c_{p}^{-}-d_{p}^{-} \bigr) \bigl\vert e _{p}^{R}(t) \bigr\vert +\sum _{q=1}^{n} \bigl(a_{pq}^{R^{+}} +a_{pq}^{I^{+}}+a _{pq}^{J^{+}}+a_{pq}^{K^{+}} \bigr) \\ & \qquad {}\times \bigl(L_{f}^{R} \bigl\vert e_{q}^{R}(t) \bigr\vert +L_{f}^{I} \bigl\vert e_{q}^{I}(t) \bigr\vert +L_{f} ^{J} \bigl\vert e_{q}^{J}(t) \bigr\vert +L_{f}^{K} \bigl\vert e_{q}^{K}(t) \bigr\vert \bigr) +\frac{1}{\alpha } \sum_{q=1}^{n} \bigl(b_{pq}^{R^{+}} \\ & \qquad {}+b_{pq}^{I^{+}}+b_{pq}^{J^{+}}+b_{pq}^{K^{+}} \bigr) \bigl(L_{g}^{R} \bigl\vert e _{q}^{R}(t) \bigr\vert +L_{g}^{I} \bigl\vert e_{q}^{I}(t) \bigr\vert +L_{g}^{J} \bigl\vert e_{q}^{J}(t) \bigr\vert \\ & \qquad {} +L_{g}^{K} \bigl\vert e_{q}^{K}(t) \bigr\vert \bigr)e^{\lambda \tau }+\sum_{q=1} ^{n} \bigl(p_{pq}^{R^{+}}+p_{pq}^{I^{+}}+p_{pq}^{J^{+}}+p_{pq}^{K^{+}} \bigr) \bigl(L_{h}^{R} \bigl\vert e_{q}^{R}(t) \bigr\vert \\ & \qquad {}+L_{h}^{I} \bigl\vert e_{q}^{I}(t) \bigr\vert +L_{h}^{J} \bigl\vert e_{q}^{J}(t) \bigr\vert +L_{h}^{K} \bigl\vert e_{q} ^{K}(t) \bigr\vert \bigr) \\ & \qquad {}+ \frac{1}{\beta } \sum_{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q_{pq} ^{I^{+}}+q_{pq}^{J^{+}}+q_{pq}^{K^{+}} \bigr) \bigl(L_{\bar{h}}^{R} \bigl\vert e _{q}^{R}(t) \bigr\vert +L_{\bar{h}}^{I} \bigl\vert e_{q}^{I}(t) \bigr\vert \\ & \qquad {}+L_{\bar{h}}^{J} \bigl\vert e_{q}^{J}(t) \bigr\vert +L_{\bar{h}}^{K} \bigl\vert e_{q}^{K}(t) \bigr\vert \bigr)e ^{\lambda \sigma } \Biggr\} e^{\lambda t} \\ & \quad \leq \sum_{p=1}^{n} \Biggl\{ \bigl(\lambda -c_{p}^{-}-d_{p}^{-} \bigr) + \sum_{q=1}^{n} \bigl(a_{pq}^{R^{+}}+a_{pq}^{I^{+}} +a_{pq}^{J ^{+}}+a_{pq}^{K^{+}} \bigr) \bigl(L_{f}^{R}+L_{f}^{I} \\ & \qquad {}+L_{f}^{J}+L_{f}^{K} \bigr) +\frac{1}{\alpha } \sum_{q=1}^{n} \bigl(b_{pq}^{R^{+}}+b_{pq}^{I^{+}}+b_{pq}^{J^{+}}+b_{pq}^{K^{+}} \bigr) \bigl(L_{g}^{R}+L_{g}^{I} \\ & \qquad {}+L_{g}^{J} +L_{g}^{K} \bigr)e^{\lambda \tau }+\sum_{q=1}^{n} \bigl(p_{pq}^{R^{+}}+p_{pq}^{I^{+}}+p_{pq}^{J^{+}}+p_{pq}^{K^{+}} \bigr) \bigl(L_{h}^{R}+L_{h}^{I} \\ & \qquad {}+L_{h}^{J}+L_{h}^{K} \bigr)+ \frac{1}{\beta } \sum_{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q_{pq}^{I^{+}}+q_{pq}^{J^{+}}+q_{pq}^{K^{+}} \bigr) \bigl(L_{\bar{h}}^{R}+L_{\bar{h}}^{I} \\ & \qquad {}+L_{\bar{h}}^{J}+L_{\bar{h}}^{K} \bigr)e^{\lambda \sigma } \Biggr\} e ^{\lambda t} \bigl\Vert e(t) \bigr\Vert \\ & \quad = \sum_{p=1}^{n} \biggl\{ \bigl( \lambda -c_{p}^{-}-d_{p}^{-} \bigr) +A _{p} +\frac{1}{\alpha } B_{p}e^{\lambda \tau }+P_{p}+ \frac{1}{\beta } Q_{p}e^{\lambda \sigma } \biggr\} e^{\lambda t} \bigl\Vert e(t) \bigr\Vert . \end{aligned}$$

(12)

Performing a similar calculation, we can obtain

$$ \begin{aligned} D^{+}V^{l}(t) \leq {}& \sum _{p=1}^{n} \biggl\{ \bigl(\lambda -c_{p} ^{-}-d_{p}^{-}\bigr) +A_{p} +\frac{1}{\alpha } B_{p}e^{\lambda \tau }+P _{p} \\ & {}+ \frac{1}{\beta } Q_{p}e^{\lambda \sigma } \biggr\} e^{\lambda t} \bigl\Vert e(t) \bigr\Vert , \quad l=I,J,K. \end{aligned} $$

(13)

In view of $(H_{6})$, (12) and (13), we have

$$\begin{aligned} D^{+}V(t)\leq 0. \end{aligned}$$

Hence, $V(t)\leq V(0)$ for all $t\geq 0$.

On the other hand, we have

$$\begin{aligned} V^{R}(0) =&\sum_{p=1}^{n} \Biggl\{ \bigl\vert e_{p}^{R}(0) \bigr\vert + \frac{1}{ \alpha } \sum_{q=1}^{n} \bigl(b_{pq}^{R^{+}}+b_{pq}^{I^{+}}+b _{pq}^{J^{+}} +b_{pq}^{K^{+}} \bigr) \\ &{}\times \int _{0-\tau _{pq}(0)}^{0} \bigl(L_{g}^{R} \bigl\vert e_{q}^{R}(s) \bigr\vert +L_{g} ^{I} \bigl\vert e_{q}^{I}(s) \bigr\vert +L_{g}^{J} \bigl\vert e_{q}^{J}(s) \bigr\vert \\ &{}+L_{g}^{K} \bigl\vert e_{q}^{K}(s) \bigr\vert \bigr)e^{\lambda ( s+\tau )}\,\mathrm{d}s+\frac{1}{ \beta } \sum _{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q_{pq}^{I^{+}}+q_{pq} ^{J^{+}} \\ &{}+q_{pq}^{K^{+}} \bigr) \int _{0-\sigma _{pq}(0)}^{0} \bigl(L_{\bar{h}}^{R} \bigl\vert e _{q}^{R}(s) \bigr\vert +L_{\bar{h}}^{I} \bigl\vert e_{q}^{I}(s) \bigr\vert \\ &{}+L_{\bar{h}}^{J} \bigl\vert e_{q}^{J}(s) \bigr\vert +L_{\bar{h}}^{K} \bigl\vert e_{q}^{K}(s) \bigr\vert \bigr) e ^{\lambda ( s+\sigma )} \,\mathrm{d}s \Biggr\} \\ \leq &\sum_{p=1}^{n} \Biggl\{ 1+ \frac{1}{\alpha } \sum_{q=1}^{n} \bigl(b_{pq}^{R^{+}}+b_{pq}^{I^{+}}+b_{pq}^{J^{+}}+b_{pq} ^{K^{+}} \bigr) \bigl(L_{g}^{R}+L_{g}^{I} \\ &{}+L_{g}^{J}+L_{g}^{K} \bigr) \frac{(e^{\lambda \tau }-1)}{\lambda }+\frac{1}{ \beta } \sum_{q=1}^{n} \bigl(q_{pq}^{R^{+}}+q_{pq}^{I^{+}}+q_{pq} ^{J^{+}}+q_{pq}^{K^{+}} \bigr) \\ &{}\times \bigl(L_{\bar{h}}^{R} +L_{\bar{h}}^{I}+L_{\bar{h}}^{J} +L_{ \bar{h}}^{K} \bigr)\frac{(e^{\lambda \sigma }-1)}{\lambda } \Biggr\} \Vert \psi -\varphi \Vert _{0} \\ =& \sum_{p=1}^{n} \biggl\{ 1+ \frac{(e^{\lambda \tau }-1)}{ \alpha \lambda }B_{p}+ \frac{(e^{\lambda \sigma }-1)}{\beta \lambda }Q _{p} \biggr\} \Vert \psi -\varphi \Vert _{0}. \end{aligned}$$

Similarly, we can get

$$\begin{aligned} V^{l}(0)\leq \sum_{p=1}^{n} \biggl\{ 1+ \frac{(e^{\lambda \tau }-1)}{\alpha \lambda }B_{p}+ \frac{(e^{\lambda \sigma }-1)}{ \beta \lambda }Q_{p} \biggr\} \Vert \psi -\varphi \Vert _{0}, \quad l=I,J,K. \end{aligned}$$

It is obvious that

$$\begin{aligned} \bigl\Vert y(t)-x(t) \bigr\Vert e^{\lambda t}= \bigl\Vert e(t) \bigr\Vert e^{\lambda t}\leq V(t), \quad t\geq 0. \end{aligned}$$

Hence, we have

$$\begin{aligned} \bigl\Vert y(t)-x(t) \bigr\Vert \leq V(t)e^{-\lambda t}\leq V(0)e^{-\lambda t} \leq M \Vert \psi -\varphi \Vert _{0}e^{-\lambda t}, \quad t\geq 0, \end{aligned}$$

where

$$\begin{aligned} M=\sum_{p=1}^{n} \biggl\{ 1+ \frac{(e^{\lambda \tau }-1)}{ \alpha \lambda }B_{p}+ \frac{(e^{\lambda \sigma }-1)}{\beta \lambda }Q _{p} \biggr\} >1. \end{aligned}$$

Therefore, system (1) and system (9) are globally exponentially synchronized. This completes the proof. □

5 A numerical example

In this section, we give two numerical examples to illustrate the effectiveness of our results.

Example 1

Consider the following drive system:

$$ x_{p}'(t)=-c_{p}(t)x_{p}(t)+ \sum_{q=1}^{2}a_{pq}(t)f_{q} \bigl(x_{q}(t)\bigr) +\sum_{q=1}^{2}b_{pq}(t)g_{q} \bigl(x_{q}\bigl(t-\tau _{pq}(t)\bigr) \bigr)+J_{p}(t), $$

(14)

where $p=1,2$, $\nu (t)=e^{|t|}$, and the coefficients are as follows:

$$\begin{aligned}& f_{q}(x_{q})=\frac{ \vert x^{R}+1 \vert - \vert x^{R}-1 \vert }{4}+ \frac{1}{2}k\sin \bigl(x^{I}+x ^{J}+x^{K} \bigr), \\& g_{q}(x_{q})=\frac{1}{4}\arctan x^{R}+\frac{1}{4}i\sin x^{K}+ \frac{1}{4}j\tanh \bigl(x_{q}^{I}+x_{q}^{J} \bigr), \\& c_{1}(t)=4+ \bigl\vert \sin (\sqrt{5}t)+\cos t \bigr\vert , \qquad c_{2}(t)=7-2\cos \sqrt{2}t,\qquad \tau _{pq}(t)= \frac{1}{2}(1+\sin 2t), \\& a_{11}(t)= a_{12}(t)=0.2\sin (\sqrt{2}t)+0.1i\bigl( \sin (\sqrt{2}t)+ \cos t\bigr)+0.1k\cos (\sqrt{7}t), \\& a_{21}(t)= a_{22}(t)=0.1\sin (\sqrt{5}t)+0.3j\sin t+0.2k(\sin t+ \cos \sqrt{3}t), \\& b_{11}(t)=b_{12}(t)=0.5\cos (\sqrt{7}t) +0.4k\bigl( \cos (\sqrt{3}t)+ \sin \sqrt{2}(t)\bigr), \\& b_{21}(t)=b_{22}(t)=0.3+0.4i\sin (\sqrt{3}t)+0.3j\sin \sqrt{2}t+0.1k, \\& J_{1}(t)=2\bigl(\sin t+\cos (2t)\bigr)+i2\sin (\sqrt{5}t) +j2\cos ( \sqrt{7}t) +k\bigl(1.9\cos \sqrt{3}t+0.1e^{-t}\bigr), \\& J_{2}(t)=1.9\cos \sqrt{3}t+0.1e^{-t}+i2\sin t +j \bigl(1.9\cos t+0.1e^{-t}\bigr) +k2\bigl(\sin (\sqrt{3}t)+\sin t \bigr). \end{aligned}$$

By a simple computation, for $p=1,2$, $l\in T$, we have

$$\begin{aligned}& c_{1}^{-}=4, \qquad c_{2}^{-}=5, \qquad J_{p}^{l^{+}}=2,\qquad L_{f}^{l}= \frac{1}{2},\qquad L_{g}^{l}= \frac{1}{4}, \\& A_{1}=1.6,\qquad B_{1}=1.8,\qquad A_{2}=2.4, \qquad B_{2}=2.2, \end{aligned}$$

and

$$\begin{aligned}& \kappa =\max \biggl\{ \frac{J_{1}^{l^{+}}}{c_{1}^{-}} , \frac{J_{2} ^{l^{+}}}{c_{2}^{-}} \biggr\} = \frac{1}{2}, \\& \rho =\max \biggl\{ \frac{1}{c_{1}^{-}} (A_{1}+B_{1} ) , \frac{1}{c _{2}^{-}} (A_{2}+B_{2} ) \biggr\} =\max \{0.85,0.92\}=0.92< 1. \end{aligned}$$

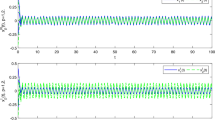
So, all the assumptions of Theorem 1 is satisfied. Therefore, by Theorem 1, we see that (14) has a unique weighted pseudo-almost periodic solution (see Fig. 1).

Figure 1

The states of four parts of $x_{1}(t)$ and $x_{2}(t)$

Example 2

Consider the following drive system:

$$ x_{p}'(t)=-c_{p}(t)x_{p}(t)+ \sum_{q=1}^{2}a_{pq}(t)f_{q} \bigl(x_{q}(t)\bigr) +\sum_{q=1}^{2}b_{pq}(t)g_{q} \bigl(x_{q}\bigl(t-\tau _{pq}(t)\bigr) \bigr)+J_{p}(t) $$

(15)

and the response system

$$\begin{aligned} y_{p}'(t) =&-c_{p}(t)y_{p}(t)+ \sum_{q=1}^{2}a_{pq}(t)f_{q} \bigl(y _{q}(t)\bigr) \\ &{} +\sum_{q=1}^{2}b_{pq}(t)g_{q} \bigl(y_{q}\bigl(t-\tau _{pq}(t)\bigr)\bigr) +J_{p}(t)+u _{p}(t), \end{aligned}$$

(16)

where $p=1,2$,

$$ u_{p}(t)=-d_{p}(t)e_{p}(t)+\sum _{q=1}^{2}p_{pq}(t)h_{q} \bigl(e_{q}(t)\bigr) +\sum_{q=1}^{2}q_{pq}(t) \bar{h}_{q}\bigl(e_{q}\bigl(t-\sigma _{pq}(t)\bigr)\bigr). $$

(17)

Consider the weight $\nu (t)=e^{|t|}$ and the coefficients are taken as follows:

$$\begin{aligned}& f_{q}(x_{q})=\frac{1}{5}\tanh x_{q}^{R}+\frac{1}{5}i \bigl\vert x_{q}^{I} +x_{q} ^{J}+x_{q}^{K} \bigr\vert +j\frac{1}{7}\sin x_{q}^{J}+ \frac{1}{5}k \bigl\vert x_{q}^{K} \bigr\vert , \\& g_{q}(x_{q})=\frac{1}{7}\sin \biggl(x_{q}^{R}+\frac{1}{4}x_{q}^{I} \biggr)+ \frac{1}{7}i \bigl\vert x_{q}^{J} +x_{q}^{K} \bigr\vert +\frac{1}{9}j\tanh x_{q}^{K}+ \frac{1}{7}k \sin x_{q}^{I}, \\& h_{q}(e_{q})=\frac{1}{5}\tanh e_{q}^{R}+\frac{1}{5}i \bigl\vert e_{q}^{R} +e_{q} ^{I}+e_{q}^{J}+e_{q}^{K} \bigr\vert +\frac{1}{8}j\sin ^{2} e_{q}^{K}+ \frac{1}{5}k \sin e_{q}^{I}, \\& \bar{h}_{q}(e_{q})=\frac{1}{7}\sin \bigl(e_{q}^{I}+e_{q}^{J}\bigr)+ \frac{1}{7}i \bigl\vert e _{q}^{J}+e_{q}^{K} \bigr\vert +\frac{1}{8}j\tanh \bigl(e_{q}^{R}+e_{q}^{K} \bigr)+ \frac{1}{7}k \sin ^{2} e_{q}^{I}, \\& a_{11}(t)=0.1\bigl(\cos (2t)+i\sin (2t)+j+k\sin (\sqrt{3}t)\bigr), \\& a_{12}(t)=0.1\bigl(\sin (\sqrt{2}t)+\cos (2t) +j\sin t+k\cos ( \sqrt{3}t)\bigr), \\& a_{21}(t)=0.1\bigl(\cos (\sqrt{2}t)+i\bigl(\sin (\sqrt{3}t)+\cos t \bigr)\bigr), \\& a_{22}(t)=0.1\bigl(\sin t+i\cos (\sqrt{3}t)+k\sin (\sqrt{2}t) \bigr), \\& b_{11}(t)=0.1\bigl(\sin t+\cos (\sqrt{2}t)+j\cos ^{2} t +k\cos (2t)\bigr), \\& b_{12}(t)=0.1\bigl(\sin (\sqrt{3}t) +k\bigl(\cos (2t)+\sin \sqrt{3}t\bigr)\bigr), \\& b_{21}(t)=0.1\bigl(\sin (2t)+j\sin (\sqrt{5}t)+k\cos (3t)\bigr), \\& b_{22}(t)=0.1\bigl(i\cos t+j\sin t+k\sin (\sqrt{3}t)\bigr), \\& p_{11}(t)=0.1+i0.1\cos t +k\bigl(0.09\cos t+0.01e^{-t} \bigr), \\& p_{12}(t)=0.1\cos (\sqrt{3}t) +i\bigl(0.09\sin t+0.01e^{-t} \bigr) +j\cos ^{2} t, \\& p_{21}(t)=0.09\sin (\sqrt{2}t)+0.01e^{-t} +j0.1\cos t+0.1k, \\& p_{22}(t)=i0.1\sin (3t)+k\bigl(0.09\bigl(\sin (\sqrt{3}t)+\cos (2t) \bigr)+0.01e ^{-t}\bigr), \\& q_{11}(t)=i0.1\sin \sqrt{3}t +j0.1\cos \sqrt{2}t +k\bigl(0.09+0.01e ^{-t}\bigr), \\& q_{12}(t)=0.1\cos (2t) +i\bigl(0.09\cos t+0.01e^{-t} \bigr)+j0.1\sin ^{2} t), \\& q_{21}(t)=0.1\bigl(\sin (\sqrt{2})+\cos (4t)\bigr) +k0.1\sin t , \\& q_{22}(t)=0.09\cos (\sqrt{2}t)+0.01e^{-t} +i0.1\sin \sqrt{2}t +k0.1 \sin (3t), \\& c_{1}(t)=2\sin (\sqrt{2}t) +4,\qquad c_{2}(t)=5-2\cos ( \sqrt{3}t), \\& d_{1}(t)=\bigl(\sin (\sqrt{2}t)+\cos t\bigr)+5,\qquad d_{2}(t)=6-2\cos ( \sqrt{5}t), \\& J_{1}(t)=0.9\sin t+0.1e^{-t}+i\cos (\sqrt{3}t) +j\sin ( \sqrt{3}t) +k\cos (2t), \\& J_{2}(t)=\sin t+i\bigl(\sin t+\cos (\sqrt{2}t)\bigr) +j\bigl(0.9\cos t +0.1e^{-t}\bigr)+k \sin (2t), \\& \tau _{11}(t)=\frac{1}{5},\qquad \tau _{12}(t)=\frac{1}{4} \bigl\vert \sin (2t) \bigr\vert , \qquad \tau _{21}(t)=\frac{1}{6} \bigl\vert \cos (2t) \bigr\vert ,\qquad \tau _{22}(t)= \frac{1}{4}, \\& \sigma _{11}(t)=\frac{1}{9} \vert \cos t \vert , \qquad \sigma _{12}(t)=\frac{1}{8}, \qquad \sigma _{21}(t)=\frac{1}{10} \bigl\vert \sin (2t) \bigr\vert , \qquad \sigma _{22}(t)= \frac{1}{8} \bigl\vert \sin (2t) \bigr\vert . \end{aligned}$$

By a simple computation, for $p=1,2$, $l\in T$, we have

$$\begin{aligned}& c_{1}^{-}=2, \qquad c_{2}^{-}=3, \qquad d_{1}^{-}=d_{2}^{-}=4, \qquad \tau =\frac{1}{4}, \\& \sigma =\frac{1}{8}, \qquad J_{p}^{l^{+}}=1, \qquad \alpha =\frac{3}{4}, \qquad \beta =\frac{7}{8}, \\& L_{f}^{l}= L_{h}^{l}= \frac{1}{5} , \qquad L_{g}^{l}= L_{\bar{h}}^{l}=\frac{1}{7}, \qquad A_{1}=1.12, \qquad B_{1}\approx 0.5714, \qquad P_{1}=0.96, \\& Q_{1}\approx 0.6857, \qquad A_{2}\approx 0.6857, \qquad B_{2}\approx 0.6857, \qquad P_{2}\approx 0.5714, \qquad Q_{2}\approx 0.5714, \end{aligned}$$

and

$$\begin{aligned}& \kappa =\max \biggl\{ \frac{J_{1}^{l^{+}}}{c_{1}^{-}} , \frac{J_{2} ^{l^{+}}}{c_{2}^{-}} \biggr\} = \frac{1}{2}, \\& \rho =\max \biggl\{ \frac{1}{c_{1}^{-}} (A_{1}+B_{1} ) , \frac{1}{c _{2}^{-}} (A_{2}+B_{2} ) \biggr\} =\max \{0.8457,0.4571\}=0.8457< 1. \end{aligned}$$

Take $\lambda =1$, then we have

$$\begin{aligned}& \bigl(\lambda -c_{1}^{-}-d_{1}^{-} \bigr) +A_{1} +\frac{1}{\alpha } B_{1}e^{ \lambda \tau }+P_{1} + \frac{1}{\beta } Q_{1}e^{\lambda \sigma } \approx -1.05374< 0, \\& \bigl(\lambda -c_{2}^{-}-d_{2}^{-} \bigr) +A_{2} +\frac{1}{\alpha } B_{2}e^{ \lambda \tau }+P_{2}+ \frac{1}{\beta } Q_{2}e^{\lambda \sigma } \approx -2.82898< 0. \end{aligned}$$

So, all the assumptions of Theorem 2 are satisfied. So by Theorem 2, system (15) has a unique weighted pseudo-almost periodic solution and system (15) and (16) are globally exponentially synchronized (see Figs. 2–4).

Figure 2

The states of four parts of $x_{1}(t)$ and $x_{2}(t)$

Figure 3

The states of four parts of $y_{1}(t)$ and $y_{2}(t)$

Figure 4

Synchronization

6 Conclusion

In this work, we studied the existence of weighted pseudo-almost periodic solutions of delayed QVCNNs. Moreover, when the drive system has a unique weighted pseudo-almost periodic solution, we investigated global exponential synchronization of the drive–response structure of delayed QVCNNs with weighted pseudo-almost periodic coefficients. The approach of this paper can be used to study the problem of the weighted pseudo-almost periodic solutions and synchronization for other types of neural networks.