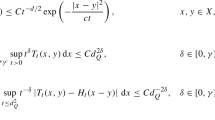Riesz transforms on the Hardy space associated with generalized Schrödinger operators

Abstract

Let $\mathcal{L}=-\Delta +\mu$ be a generalized Schrödinger operator, where the measure μ is a nonnegative Radon measure. In this paper, we establish the molecular characterization of the Hardy type space $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$ associated with $\mathcal{L}$. As applications, we obtain the $H^{1}_{\mathcal{L}}$-boundedness of Riesz transforms and the imaginary power related to $\mathcal{L}$.

1 Introduction

Consider the generalized Schrödinger operator

$$ \mathcal{L}=-\Delta +\mu\quad \text{in }\mathbb{R}^{n}, n\geq 3, $$

(1.1)

where μ is a nonnegative Radon measure on $\mathbb{R}^{n}$. Throughout this paper we assume that μ satisfies the following conditions: there exist positive constants $C_{0}$, $C_{1}$, and δ such that

$$ \mu \bigl(B(x,r) \bigr)\leq C_{0} \biggl( \frac{r}{R} \biggr)^{n-2+\delta }\mu \bigl(B(x,R) \bigr) $$

(1.2)

and

$$ \mu \bigl(B(x,2r) \bigr)\leq C_{1} \bigl\{ \mu \bigl(B(x,r) \bigr)+r^{n-2} \bigr\} $$

(1.3)

for all $x\in \mathbb{R}^{n}$ and $0< r< R$, where $B(x,r)$ denotes the open ball centered at x with radius r. Condition (1.2) may be regarded as scale-invariant Kato-condition, and (1.3) says that the measure μ is doubling on balls satisfying $\mu (B(x,r)) \geq c r^{n-2}$.

Hardy spaces are widely used various fields of analysis and partial differential equations. Let Δ be the Laplace operator on $\mathbb{R}^{n}$. It is well known that $H^{1}(\mathbb{R}^{n})$ can be characterized by the maximal function $\sup_{t>0}|e^{-t\Delta }f(x)|$. See Stein [14]. In a sense, $H^{1}(\mathbb{R}^{n})$ can be seen as the Hardy space associated with the operator −Δ. Let $\mathcal{L}$ be a general differential operator, such as second order elliptic self-adjoint operators in divergence form, degenerate Schrödinger operators with nonnegative potential, Schrödinger operators with nonnegative potential, and so on. In recent years, the Hardy spaces associated with $\mathcal{L}$ have become one of hot issues in harmonic analysis, see [2, 4,5,6,7,8,9,10] and the references therein.

Let $\mathcal{L}$ be a generalized Schrödinger operator. Denote by $\{T_{t}\}_{t>0}:=\{e^{-t\mathcal{L}}\}_{t>0}$ the heat semigroup generated by $-\mathcal{L}$. The kernel of $\{T_{t}\}$ is denoted by $K_{t}^{\mathcal{L}}(\cdot ,\cdot )$, that is,

$$ T_{t}f(x)= \int _{\mathbb{R}^{n}}{}K_{t}^{\mathcal{L}}(x,y)f(y)\,d\mu (y). $$

The maximal function associated with $\{T_{t}\}$ is defined as

$$ \mathcal{M}_{\mathcal{L}}(f) (x):=\sup_{t>0} \bigl\vert e^{-t\mathcal{L}}f(x) \bigr\vert \in L^{1} \bigl(\mathbb{R}^{n} \bigr). $$

In [15], Wu and Yan introduced the following Hardy type space associated with $\mathcal{L}$.

Definition 1.1

A Hardy type space $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$ related to $\mathcal{L}$ is defined as the set of all functions in $f\in L^{1}( \mathbb{R}^{n})$ satisfying $\mathcal{M}_{\mathcal{L}}(f)\in L^{1}( \mathbb{R}^{n})$. The norm of $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$ is defined as $\|f\|_{H^{1}_{\mathcal{L}}}:=\|\mathcal{M}_{\mathcal{L}}(f) \|_{L^{1}}$.

Let $\mathcal{L}=-\Delta$. $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$ goes back to the classical Hardy space $H^{1}(\mathbb{R}^{n})$. For a linear operator T, one of the methods to derive the $H^{1}$-boundedness is the so-called “atomic-molecular” method. In recent years, several authors used this method to investigate the boundedness on Hardy spaces associated with operators, see [3, 11, 13]. In Sect. 3.1, via a class of $(1, q)$-type atoms associated with $\mathcal{L}$, we obtain the corresponding atomic characterization of $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$, see Sect. 3.1. Further, in Sect. 3.2, we introduce the $(p,q,\varepsilon )$-moleculars associated with $\mathcal{L}$ and establish the molecular decomposition of $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$, see Theorem 3.6. In Sect. 4, let $R_{\mathcal{L}}$ and $\mathcal{L}^{i\gamma }$ denote the Riesz transforms and the imaginary power associated with $\mathcal{L}$, i.e.,

$$ \textstyle\begin{cases} R_{\mathcal{L}}:=\nabla (-\Delta +\mu )^{-1/2}; \\ \mathcal{L}^{\gamma }:=(-\Delta +\mu )^{i\gamma }. \end{cases} $$

By the aid of the regularities of the integral kernels, we can apply Theorems 3.3 & 3.6 to derive the $H^{1}_{ \mathcal{L}}$-boundedness of $R_{\mathcal{L}}$ and $\mathcal{L}^{i \gamma }$, see Theorems 4.4 & 4.6, respectively.

Throughout this article, we will use c and C to denote the positive constants, which are independent of the main parameters and may be different at each occurrence. By $B_{1} \sim B_{2}$, we mean that there exists a constant $C>1$ such that ${1}/{C} \leq {B_{1}}/{B_{2}}\leq C$.

2 Preliminaries

2.1 Generalized Schrödinger operators

Let μ be a Radon measure satisfying conditions (1.2) & (1.3). The auxiliary function $m(x, \mu )$ is defined by

$$ \frac{1}{m(x,\mu )}=:\sup \biggl\{ r>0: \frac{\mu (B(x,r))}{r^{n-2}} \leq C_{1} \biggr\} . $$

We begin by recalling some basic properties of the function $m(x,\mu )$.

Lemma 2.1

([12, Proposition 1.8 & Remark 1.9])

Suppose that μ satisfies (1.2) & (1.3). Then

• (i) $0< m(x,\mu )<\infty$ for every $x\in \mathbb{R}^{n}$.

• (ii) If $r=m(x,\mu )^{-1}$, then $r^{n-2}\leq \mu (B(x,r)) \leq C_{1}r^{n-2}$.

• (iii) If $|x-y|\leq Cm(x,\mu )^{-1}$, then $m(x,\mu ) \approx m(y,\mu )$.

• (iv) There exist constants $c, C>0$ such that, for $x,y\in \mathbb{R}^{n}$,

  $$ \frac{cm(y,\mu )}{\{1+ \vert x-y \vert m(y,\mu )\}^{k_{0}/(1+k_{0})}}\leq m(x, \mu )\leq Cm(y,\mu ) \bigl\{ 1+ \vert x-y \vert m(y,\mu ) \bigr\} ^{k_{0}} $$

  with $k_{0}=C_{2}/\delta >0$ and $C_{2}=\log _{2}(C_{1}+2^{n-2})$.

With the modified Agmon metric $ds^{2}=m(x,\mu )\{dx^{2}_{1}+\cdots +dx _{n}^{2}\}$, the distance function $d(x,y,\mu )$ is given by

$$ d(x,y,\mu )=\inf_{\gamma } \int ^{1}_{0}m \bigl(\gamma (\tau ),\mu \bigr) \bigl\vert \gamma '( \tau ) \bigr\vert \,d\tau , $$

(2.1)

where $\gamma :[0,1]\rightarrow \mathbb{R}^{n}$ is absolutely continuous and $\gamma (0)=x$, $\gamma (1)=y$.

A parabolic-type distance function associated with $m(x,\mu )$ is defined by

$$ d_{\mu }(x,y,t)=\inf_{\gamma } \int ^{1}_{0}m \bigl(\tilde{\gamma }(\tau ), \mu \bigr)\max \bigl\{ \bigl\vert (\tilde{\gamma })'(\tau ) \bigr\vert , \bigl\vert (\gamma _{n+1})'(\tau ) \bigr\vert \bigr\} \,d \tau , $$

(2.2)

where $\gamma (\tau )=(\gamma _{1}(\tau ),\ldots ,\gamma _{n}(\tau ))=( \tilde{\gamma }(\tau ),\gamma _{n+1}(\tau )):[0,1]\rightarrow \mathbb{R}^{n}\times \mathbb{R}_{+}$ is absolutely continuous with $\gamma (0)=(x,0)$, $\gamma (1)=(y,\sqrt{t})$.

Lemma 2.2

([15, Lemma 2.2])

For the distance function $d(x,y,\mu )$ in (2.1), we have

• (i) For every $x,y, z\in \mathbb{R}^{n}$,

  $$ d(x,y,\mu )\leq d(x,z,\mu )+d(z,y,\mu ). $$

• (ii) There are two positive constants c and C such that, for any $x,y\in \mathbb{R}^{n}$,

  $$ c \bigl\{ \bigl\{ 1+ \vert x-y \vert m(x,\mu ) \bigr\} ^{1/(k_{0}+1)}-1 \bigr\} \leq d(x,y,\mu ) \leq C \bigl\{ 1+ \vert x-y \vert m(x,\mu ) \bigr\} ^{k_{0}+1}. $$

Lemma 2.3

([15, Lemma 2.3])

For the distance function $d_{\mu }(x,y,t)$, there exist two positive constants c and C such that, for any $x,y\in \mathbb{R}^{n}$, $x\neq y$, and $t>0$,

$$ \textstyle\begin{cases} d_{\mu }(x,y,t)\geq c \{\{1+\max \{ \vert x-y \vert ,\sqrt{t}\}m(x,\mu )\} ^{1/(k_{0}+1)}-1 \}; \\ d_{\mu }(x,y,t)\leq C \{1+\max \{ \vert x-y \vert , \sqrt{t}\}m(x,\mu ) \}^{k_{0}+1}. \end{cases} $$

It follows from (1.2), (1.3), and Lemma 2.1 that there exists a constant $C>0$ such that, for every $x\in \mathbb{R}^{n}$,

$$ \mu \bigl(B(x,r) \bigr)\leq \textstyle\begin{cases} C (rm(x,\mu ) )^{\delta }r^{n-2},& r< m(x,\mu )^{-1}; \\ C (rm(x,\mu ) )^{C _{2}}m(x,\mu )^{2-n},& r< m(x,\mu )^{-1}, \end{cases} $$

(2.3)

see [15, (2.1)]. The above estimate implies the following.

Lemma 2.4

([15, (2.2)])

For every nonnegative Schwarz function ω,

$$ \int _{\mathbb{R}^{n}}t^{-n/2}\omega \biggl(\frac{x-y}{\sqrt{t}} \biggr)\,d\mu (y) \leq \textstyle\begin{cases} Ct^{-1} ( \sqrt{t}m(x,\mu ) )^{\delta },& t< m(x,\mu )^{-2}; \\ Ct ^{-1} (\sqrt{t}m(x,\mu ) )^{C_{2}-n+2},& t\geq m(x,\mu )^{-2}. \end{cases} $$

(2.4)

2.2 Function spaces associated with $\mathcal{L}$

In order to characterize $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$, Wu and Yan [15] introduced the following $H^{1}_{\mathcal{L}}$-atoms. For $j\in \mathbb{Z}$, define the sets $\mathcal{B}_{j}$ as

$$ \mathcal{B}_{j}= \bigl\{ x: 2^{j/2}\leq m(x,\mu )< 2^{(j+1)/2} \bigr\} . $$

Since $0< m(x,\mu )<\infty$, we have $\mathbb{R}^{n}=\bigcup_{j\in \mathbb{Z}}\mathcal{B}_{j}$.

Definition 2.5

A function a is a $(1,\infty )$-atom for $H^{1}_{\mathcal{L}}( \mathbb{R}^{n})$ associated with a ball $B(x_{0},r)$ if

• (i) $\operatorname{supp} a\subset B(x_{0},r)$;

• (ii) $\|a\|_{L^{\infty }}\leq |B(x_{0},r)|^{-1}$;

• (iii) if $x_{0}\in \mathcal{B}_{j}$, then $r\leq 2^{1-j/2}$;

• (iv) if $x_{0}\in \mathcal{ B}_{j}$ and $r\leq 2^{-1-j/2}$, then $\int a(x)\,dx=0$.

The atomic norm of $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$ is defined by $\|f\|_{\mathcal{L}\text{-}\mathrm{atom}}:=\inf \{\sum_{j}|\lambda _{j}|\}$, where the infimum is taken over all decompositions $f=\sum_{j}\lambda _{j}a_{j}$, where $\{a_{j}\}$ is a sequence of $(1,\infty )$-atoms and $\{\lambda _{j}\}$ is a sequence of scalars.

One of the main results of [15] is the following proposition.

Proposition 2.6

([15, Theorem 1.2])

Assume that μ is a nonnegative Radon measure on $\mathbb{R}^{n}$ satisfying (1.2) & (1.3) for some $\delta >0$. Then the norms $\|f\|_{H^{1}_{\mathcal{L}}}$ and $\|f\|_{\mathcal{L}\text{-}\mathrm{atom}}$ are equivalent, that is, there exists a constant $C>0$ such that

$$ \frac{1}{C} \Vert f \Vert _{H^{1}_{\mathcal{L}}}\leq \Vert f \Vert _{H_{\mathcal{L}}^{1}\text{-}\mathrm{atom}} \leq C \Vert f \Vert _{H^{1}_{\mathcal{L}}}. $$

At the end of this section, we state some regularity estimates for the kernel $K^{{\mathcal{L}}}_{t}(\cdot ,\cdot )$.

Proposition 2.7

([15, Lemma 3.7])

• (i) There exist positive constants C and c depending only on n and constants $C_{0}$, $C_{1}$ and δ in (1.2) & (1.3) such that

  $$ 0\leq K^{{\mathcal{L}}}_{t}(x,y)\leq C h_{t}(x-y)e^{-c d_{\mu }(x,y,t)}. $$

• (ii) For every $0<\delta '<\delta _{0}=\min \{\alpha , \delta , \nu \}$, there exists a constant C such that, for every $N^{\prime }>0$, there exists a constant $C>0$ such that, for $|h|<\sqrt{t}$, we have

  $$ \bigl\vert K^{\mathcal{L}}_{t}(x+h,y)-K^{\mathcal{L}}_{t}(x,y) \bigr\vert \leq C_{N^{\prime }} \biggl(\frac{ \vert h \vert }{\sqrt{t}} \biggr)^{\delta '}\frac{1}{t^{n/2}}e^{-c \vert x-y \vert ^{2}/t} \frac{C_{N}}{\{1+\sqrt{t}m(x,\mu )+\sqrt{t}m(y,\mu )\}^{N^{\prime }}}. $$

3 Molecular characterization of $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$

3.1 The $(1,q)$-atom decomposition

Now we introduce a new type of atoms.

Definition 3.1

A function a is a $(1,q)$-atom of $H^{1}_{\mathcal{L}}(\mathbb{R} ^{n})$ if

• (i) $\operatorname{supp}a\subset B(x_{0},r)$;

• (ii) $\|a\|_{q}\leq |B(x_{0},r)|^{1/q-1}$;

• (iii) if $r\leq \rho (x_{0})$, then $\int a(x)\,dx=0$.

Theorem 3.2

Any $(1,\infty )$-atom is a $(1,q)$-atom.

Proof

In fact, by Hölder’s inequality,

$$\begin{aligned} \Vert a \Vert _{q} \leq \Vert a \Vert _{\infty } \bigl\vert B(x_{0},r) \bigr\vert ^{1/q}\leq \bigl\vert B(x_{0},r) \bigr\vert ^{1/q-1}. \end{aligned}$$

 □

Theorem 3.3

Let $\mathcal{L}=-\triangle +\mu$ be a generalized Schrödinger operator, where $\mu \neq 0$ is a nonnegative Radon measure on ${\mathbb{R}}^{n}$ satisfying (1.2) & (1.3) for some $\delta >0$. Then $f\in {H^{1}_{\mathcal{L}}}(\mathbb{R}^{n})$ if and only if $f=\sum_{j}\lambda _{j}a_{j}$, where $\{{a_{j}}\}$ are $(1,q)$-atoms and $\{{\lambda _{j}}\}$ are scalars.

Proof

Because an $(1,\infty )$-atom is also an $(1,q)$-type atom, we only need to prove that there exists a constant c such that, for any $(1,q)$-atom a, ${\|{\mathcal{M}_{\mathcal{L}}}(a)\|_{1}}\leq c$. Suppose that a is a $(1,q)$-atom supported in $B(x_{0},r)$. We write ${\|{\mathcal{M}_{\mathcal{L}}}(a)\|_{1}}\leq I_{1}+I_{2}$, where

$$ \textstyle\begin{cases} I_{1}:=\int _{B(x_{0},4r)} \vert {\mathcal{M}_{\mathcal{L}}}a(x) \vert \,dx; \\ I_{2}:=\int _{B^{c}(x_{0},4r)} \vert {\mathcal{M}_{\mathcal{L}}}a(x) \vert \,dx. \end{cases} $$

By Hölder’s inequality and the $L^{q}$-boundedness of $\mathcal{M}_{\mathcal{L}}$, we can get

$$\begin{aligned} I_{1} \leq &{ \Vert {\mathcal{M}_{\mathcal{L}}}a \Vert _{q}} \bigl\vert B(x_{0},r) \bigr\vert ^{1- {1}/{q}} \leq {C \Vert a \Vert _{q}} \bigl\vert B(x_{0},r) \bigr\vert ^{1-{1}/{q}}\leq C. \end{aligned}$$

The estimation of $I_{2}$ is divided into two cases.

Case 1: $1/{m(x_{0},\mu )}\leq r\leq 1/{4 m(x_{0},\mu )}$. For this case, by (i) of Lemma 2.7, we have

$$\begin{aligned} {\mathcal{M}_{\mathcal{L}}}(a) (x) \leq &c\sup_{t>0} { \int _{B(x _{0},r)}} {t^{-n/2}} {e^{-{ \vert x-y \vert ^{2}}/t}} { \bigl(1+m(x,\mu )\sqrt{t} \bigr)^{-N}} \bigl\vert a(y) \bigr\vert \,dy \\ \leq &c\sup_{t>0} { \int _{B(x_{0},r)}} {t^{-n/2}} {e^{-{ \vert x-y \vert ^{2}}/t}} { \bigl(1+{ \vert x-y \vert ^{2}}/{\sqrt{t}} \bigr)^{-n-N}} { \bigl(1+m(x,\mu )\sqrt{t} \bigr)^{-N}} \bigl\vert a(y) \bigr\vert \,dy. \end{aligned}$$

If $y \in B(x_{0},r)$ and $|x-x_{0}|>4r$, then $|y-x_{0}|\leq |x-x _{0}|/4$ and $|y-x|\geq 3|x-x_{0}|/4$. We can apply Lemma 2.1 to obtain

$$\begin{aligned} \bigl\vert {\mathcal{M}_{\mathcal{L}}}(a) (x) \bigr\vert \leq & c\sup _{t>0}\frac{1}{t ^{n/2}}{ \int _{B(x_{0},r)}} { \bigl({ \vert x-x_{0} \vert }/{ \sqrt{t}} \bigr)^{-n-N}} { \bigl(m(x, \mu )\sqrt{t} \bigr)^{-N}} \bigl\vert a(y) \bigr\vert \,dy \\ \leq &c{ \vert x-x_{0} \vert ^{-n-N}} { \bigl[m(x,\mu ) \bigr]^{-N}} { \int _{B(x_{0},r)}} \bigl\vert a(y) \bigr\vert \,dy \\ \leq &c{ \vert x-x_{0} \vert ^{-n-{N}/{({k_{0}}+1})}} \bigl[m(x_{0},\mu ) \bigr]^{-{N}/( {{k_{0}}+1})}, \end{aligned}$$

which gives

$$\begin{aligned} { \int _{ \vert x-x_{0} \vert >4r}} \bigl\vert {\mathcal{M}_{\mathcal{L}}}a(x) \bigr\vert \,dx \leq &c{ \int _{ \vert x-x _{0} \vert >4r}} { \vert x-x_{0} \vert ^{-n-{N}/{({k_{0}}+1})}} \bigl[m(x_{0},\mu ) \bigr]^{-{N}/( {{k_{0}}+1})}\,dx \\ \leq &c{ \vert x-x_{0} \vert ^{-n-{N}/{({k_{0}}+1})}}r^{-{N}/({{k_{0}}+1})} \leq C, \end{aligned}$$

where in the last inequality we have used the fact that $1\leq r m(x _{0},\mu )\leq 4$.

Case2: $r<1/m(x_{0},\mu )$. By Proposition 2.7 and the symmetry of $K^{\mathcal{L}}_{t}(\cdot ,\cdot )$, we have

$$\begin{aligned} \bigl\vert K^{\mathcal{L}}_{t}(x,y+h)-K^{\mathcal{L}}_{t}(x,y) \bigr\vert \leq C_{N}{ \bigl( { \vert h \vert }/{\sqrt{t}} \bigr)^{\delta '}} {t^{-n/2}} {e^{-{ \vert x-y \vert ^{2}}/ct}} { \bigl\{ {1+ \sqrt{t}m(x,\mu )+\sqrt{t}m(y,\mu ) \bigr\} }^{-N}}. \end{aligned}$$

Notice that $|y-x_{0}|< r$, $|x-x_{0}|>4r\Rightarrow |x-y|\geq {3|x-x _{0}|}/{4}$. By the canceling condition of a, we can get

$$\begin{aligned} \bigl\vert {\mathcal{M}_{\mathcal{L}}}a(x) \bigr\vert \leq &\sup _{t>0} \biggl\vert { \int _{B(x_{0},r)}} \bigl[K^{\mathcal{L}}_{t}(x,y)-K^{\mathcal{L}}_{t}(x,x _{0}) \bigr]a(y)\,dy \biggr\vert \\ \leq &c\sup_{t>0} { \int _{B(x_{0},r)}} {t^{-n/2}} {e^{-{ \vert x-y \vert ^{2}}/ct}} { \bigl({ \vert y-x_{0} \vert }/{\sqrt{t}} \bigr)^{\delta '}} \bigl\vert a(y) \bigr\vert \,dy \\ \leq &c\sup_{t>0} \biggl\{ {t^{-n/2}} { \int _{B(x_{0},r)}} { \bigl(1+ { \vert x-y \vert }/{\sqrt{t}} \bigr)^{-n-\delta '}} { \vert y-x_{0} \vert ^{\delta '}}/{t^{\delta '/2}} \bigl\vert a(y) \bigr\vert \,dy \biggr\} \\ \leq &{cr^{\delta '}} { \vert x-x_{0} \vert ^{-n-\delta '}}, \end{aligned}$$

which gives

$$\begin{aligned} { \int _{ \vert x-x_{0} \vert \geq 4r}} \bigl\vert {\mathcal{M}_{\mathcal{L}}}a(x) \bigr\vert \,dx \leq &c { \int _{ \vert x-x_{0} \vert \geq 4r}} {r^{\delta '}} { \vert x-x_{0} \vert ^{-n-\delta '}}\,dx \leq C. \end{aligned}$$

 □

3.2 Molecular characterization of $H^{1}_{\mathcal{L}}( \mathbb{R}^{n})$

Now we introduce the molecular of $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$.

Definition 3.4

Let $1\leq q\leq \infty$, $\varepsilon >0$, $b=1-{1}/{q}+\varepsilon$. An $L^{q}$-function M is called a $(1,q,\varepsilon )$-molecular centered at $x_{0}$ if

• (i) $|x|^{nb}M(x)\in L^{q}(\mathbb{R}^{n})_{j}$;

• (ii) $\|M\|^{{\varepsilon }/{b}}_{q}\||x-x_{0}|^{nb}M(\cdot ) \|^{1-{\varepsilon }/{b}}_{q}\leq 1$;

• (iii) if $x_{0}\in B_{k}$ and $\|M\|_{q}^{\{n({1}/{q}-1)\}^{-1}} \leq m(x_{0},\mu )^{-1}$, $\int M(x)\,dx=0$.

Lemma 3.5

If a is a $(1,q)$-atom supported on $B(x_{0},r)$, a is also a $(1,q,\varepsilon )$-molecular centered at $x_{0}$.

Proof

Recall that $\|a\|_{q}\leq |B(x_{0},r)|^{{1}/{q}-1}$. It is easy to see that

$$\begin{aligned} \int _{\mathbb{R}^{n}} \bigl\vert \vert x-x_{0} \vert ^{nb}a(x) \bigr\vert ^{q}\,dx \leq & \bigl\vert B(x_{0},r) \bigr\vert ^{bq+1-q}, \end{aligned}$$

which indicates that $|\cdot -x_{0}|^{nb}a\in L^{q}(\mathbb{R}^{n})$ with $\||\cdot -x_{0}|^{nb}a\|_{q}\leq |B(x_{0},r)|^{q}$. Moreover, for $b=1-{1}/{q}+\varepsilon$,

$$\begin{aligned} \Vert a \Vert ^{{\varepsilon }/{b}}_{q} \bigl\Vert \vert \cdot -x_{0} \vert ^{nb}a(\cdot ) \bigr\Vert ^{1- {\varepsilon }/{b}}_{q} \leq \bigl\vert B(x_{0},r) \bigr\vert ^{({1}/{q}-1)({\varepsilon }/ {b})} \bigl\vert B(x_{0},r) \bigr\vert ^{\varepsilon (1-{\varepsilon }/{b})}\leq 1. \end{aligned}$$

We only need to verify the canceling condition, i.e., $\|a\|^{1/\{n( {1}/{q}-1)\}}_{q}\leq m(x_{0},\mu )^{-1}$. Denote by $\omega _{n}$ the volume of the unit ball in $\mathbb{R}^{n}$. It is clear that $\omega _{n}>1$ and $\|a\|_{q}\leq \omega ^{({1}/{q}-1)}_{n}r^{n({1}/ {q}-1)}\leq r^{n({1}/{q}-1)}$, equivalently,

$$ r\leq \Vert a \Vert ^{1/\{n({1}/{q}-1)\}}_{q}\leq m(x_{0}, \mu )^{-1}. $$

By the canceling condition of $(1,q)$-atoms, we can see that $\int _{\mathbb{R}^{n}}a(x)\,dx=0$. So a is a $(1,q,\varepsilon )$-molecular centered at $x_{0}$. □

Theorem 3.6

Let $1\leq q\leq \infty$, $\varepsilon >0$, $b=1-{1}/{q}+\varepsilon$. Then $f\in H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$ if and only if $f=\sum_{j}\lambda _{j}M_{j}$, where $\{M_{j}\}$ are $(1,q, \varepsilon )$-moleculars and $\{\lambda _{j}\}$ are scalars with $\inf \sum_{j}|\lambda _{j}|\sim \|f\|_{H^{1}_{\mathcal{L}}}$, where the infimum is taken over all decompositions.

Proof

We have known that any $(1,q)$-type atom is also a $(1,q,\varepsilon )$-type molecular. By Theorem 3.3, if $f\in H^{1}_{ \mathcal{L}}(\mathbb{R}^{n})$, then there exist a sequence of $(1,q)$-type atoms $\{a_{j}\}$ and a sequence of scalars $\{\lambda _{j}\}$ such that $f=\sum_{j}\lambda _{j}a_{j}$. This means that f can be represented as a linear combination of $(1,q,\varepsilon )$-moleculars. Conversely, we only need to verify that, for any $(1,q,\varepsilon )$-molecular, $\|M\|_{H^{1}_{ \mathcal{L}}}\leq C$. For simplicity, denote

$$ N_{\mathcal{L}}(M)=: \Vert M \Vert ^{{\varepsilon }/{b}}_{q} \bigl\Vert \vert \cdot -x_{0} \vert ^{nb}M( \cdot ) \bigr\Vert ^{1-{\varepsilon }/{b}}_{q}. $$

Without loss of generality, we assume that $N_{\mathcal{L}}(M)=1$ and $q=2$. Write $\sigma =\|M\|^{1/\{n({1}/{2}-1)\}}_{2}$. Let

$$ \textstyle\begin{cases} E_{0}=\{x: \vert x-x_{0} \vert \leq \sigma \}; \\ E_{k}=\{x:2^{k-1}\sigma < \vert x-x_{0} \vert \leq 2^{k}\sigma \},\quad k\in N; \\ B_{k}=\{x: \vert x-x_{0} \vert \leq 2^{k}\sigma \},\quad k=0,1,2,\ldots . \end{cases} $$

Denote by $\psi _{k}$ the characteristic function $\chi _{E_{k}}(x)$ and write $M(x)=\sum_{k}M_{k}(x)$, where $M_{k}:=M(x)\psi _{k}(x)$.

Case 1: $\sigma \leq 1/ m(x_{0},\mu )$. Then $\|M\|^{1/\{n( {1}/{2}-1)\}}_{2}\leq m(x_{0},\mu )^{-1}$ and $\int _{\mathbb{R}^{n}} M(x)\,dx=0$. The proof is similar to the classical case, and we omit it.

Case 2: $\sigma >1/m(x_{0},\mu )$. For this case, $\||\cdot -x _{0}|^{n({1}/{2}+\varepsilon )}M(\cdot )\|^{1-{\varepsilon }/{b}}_{2}= \|M\|^{-{\varepsilon }/{b}}_{2}$. Denote by σ the term $\|M\|^{1/\{n({1}/{2}-1)\}}_{2}$. Then $\||\cdot -x_{0}|^{n({1}/{2}+ \varepsilon )}M(\cdot )\|_{2}=\sigma ^{n\varepsilon }$ and

$$\begin{aligned} \frac{1}{ \vert B_{0} \vert } \int _{\mathbb{R}^{n}} \bigl\vert M_{0}(x) \bigr\vert ^{2}\,dx \leq &\frac{1}{ \sigma ^{n}} \Vert M \Vert ^{2}_{2}=\frac{1}{\sigma ^{2n}}, \end{aligned}$$

which implies that $\|M_{0}\|_{2}\leq |B_{0}|^{-{1}/{2}}$.

For the term $M_{k}$, we have

$$\begin{aligned} \frac{1}{ \vert B_{k} \vert } \int _{\mathbb{R}^{n}} \bigl\vert M_{k}(x) \bigr\vert ^{2}\,dx \leq &\frac{1}{(2^{k-1} \sigma )^{n}} \bigl\Vert \vert \cdot -x_{0} \vert ^{nb}M_{k}(\cdot ) \bigr\Vert ^{2}_{2} \bigl(2^{k-1} \sigma \bigr)^{-n(1+2\varepsilon )} \\ \leq & \bigl(2^{k-1}\sigma \bigr)^{-2n-2\varepsilon n}\sigma ^{2n\varepsilon } \\ \leq &C_{n,\varepsilon } \bigl(2^{k}\sigma \bigr)^{-2n}2^{-2k\varepsilon }, \end{aligned}$$

that is, $\|M\|_{2}\leq C|B_{k}|^{-{1}/{2}}2^{-k\varepsilon n}$. Let $a_{k}(x)=\lambda ^{-1}_{k}M_{k}(x)$, $k=0,1,2,\ldots$ , where $\lambda _{k}=2^{-2k\varepsilon n}$ and $a_{k}$, $k\in \mathbb{Z}_{+}$, are $(1,2)$-atoms. Hence $M(x)=\sum_{k}\lambda _{k}a_{k}(x)= \sum_{k}M_{k}(x)$ and $\sum_{k}|\lambda _{k}|=C\sum_{k}2^{-2k\varepsilon n}<\infty$. Repeating the procedure of [3, Theorem 4], we can prove that $M\in H^{1}_{\mathcal{L}}( \mathbb{R}^{n})$. We omit the details, and this completes the proof of Theorem 3.6. □

4 Operators on the Hardy type space $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$

4.1 The $H^{1}_{\mathcal{L}}$-boundedness of ${\mathcal{L}} ^{i\gamma }$

Let $q_{t}(\cdot ,\cdot )$ denote the kernel of $e^{-t\mathcal{L}}-e ^{-t(-\Delta )}$. We have

$$ q_{t}(x,y)=h_{t}(x-y)-K^{\mathcal{L}}_{t}(x-y)= \int ^{t}_{0} \int _{\mathbb{R}^{n}}K^{\mathcal{L}}_{s}(x,t)h_{t-s}(z-y) \,d\mu (z)\,ds. $$

The following estimate was obtained by Wu and Yan [15].

Lemma 4.1

([15, Lemma 3.6])

• (i) There exist constants C and c such that, for every $x,y\in \mathbb{R}^{n}$ and $t>0$,

  $$ q_{t}(x,y)\leq \textstyle\begin{cases} C( \sqrt{t}m(x, \mu ))^{\delta }t^{-{n}/{2}}e^{-{|x-y|^{2}}/{ct}} , & \sqrt{t}\leq m(x, \mu )^{-1}; \\ C( \sqrt{t}m(y, \mu ))^{\delta }t^{-{n}/{2}}e^{-{|x-y|^{2}}/{ct}} , & \sqrt{t}\leq m(y, \mu )^{-1}; \\ h_{t}(x-y), & \textit{elsewhere}. \end{cases} $$

• (ii) For every $0<\delta '<\min \{1,\delta \}$ and $C>0$, there exist constants $C'$ and c such that, for every $h,x,y\in \mathbb{R}^{n}$, $|h|\leq {|x-y|}/{4}$, $|h|\leq C m(y, \mu )^{-1}$, we have

  $$ \bigl\vert q_{t}(x,y+h)-q_{t}(x,y) \bigr\vert \leq C' \bigl( \vert h \vert m(x, \mu ) \bigr)^{\delta '}t^{-{n}/ {2}}e^{-{ \vert x-y \vert ^{2}}/{ct}}. $$

By the functional calculus, we can see that the kernel of $(-\Delta )^{i \gamma }-\mathcal{L}^{i\gamma }$ can be expressed as

$$ g(x,y):= \int ^{\infty }_{0}t^{-i\gamma }q_{t}(x,y) \frac{dt}{t}. $$

(4.1)

Lemma 4.2

Let $\mathcal{L}=-\Delta +\mu$ be a generalized Schrödinger operator, where $\mu \neq 0$ is a nonnegative Radon measure on $\mathbb{R}^{n}$ satisfying (1.2) & (1.3) for some $\delta >0$.

• (i) If $y\in B(x_{0}, r)$, then

  $$ \bigl\vert g(x,y) \bigr\vert \leq C m(x_{0}, \mu )^{\delta }{ \vert x-y \vert ^{\delta -n}}. $$

  (4.2)

• (ii) There exists $0<\delta '<\delta$ such that

  $$ \bigl\vert g(x,y)-g(x,x_{0}) \bigr\vert \leq {C} { \vert x-y \vert ^{-n}} \bigl( \vert y-x_{0} \vert m(x,\mu ) \bigr) ^{\delta '}. $$

Proof

(i). In fact, we can deduce (4.2) from Lemma 4.1. Precisely,

Case 1: $\sqrt{t}\leq 1/m(y, \mu )$. Because $y\in B$, then $|y-x_{0}|< r< {1}/{m(x_{0}, \mu )}$, $m(y, \mu )\thicksim m(x_{0}, \mu )$. By (i) of Lemma 4.1, we can get

$$\begin{aligned} \bigl\vert g(x,y) \bigr\vert \leq &Cm(x_{0}, \mu )^{\delta } \int ^{\infty }_{0}t^{-{n}/ {2}+{\delta }/{2}-1}e^{-{ \vert x-y \vert ^{2}}/{ct}}\,dt \leq C m(x_{0}, \mu )^{ \delta }{ \vert x-y \vert ^{\delta -n}}. \end{aligned}$$

Case 2: $\sqrt{t}>1/m(y, \mu )$. For this case, $\sqrt{t}m(y, \mu )>1$. Using Lemma 4.1 again, we can deduce that

$$\begin{aligned} \bigl\vert g(x,y) \bigr\vert \leq &C \int ^{\infty }_{0}t^{-{n}/{2}}e^{-{ \vert x-y \vert ^{2}}/{ct}} \bigl( \sqrt{t}m(y, \mu ) \bigr)^{\delta }\frac{dt}{t} \leq C m(x_{0}, \mu )^{ \delta }{ \vert x-y \vert ^{\delta -n}}. \end{aligned}$$

(ii). It follows from (4.1) that

$$\begin{aligned} \bigl\vert g(x,y)-g(x,x_{0}) \bigr\vert =& \biggl\vert \int ^{\infty }_{0}t^{-i\gamma }q_{t}(x,y) {dt}/{t}- \int ^{\infty }_{0}t^{-i\gamma }q_{t}(x,x_{0}) \frac{dt}{t} \biggr\vert \\ \leq & \int ^{\infty }_{0}t^{-i\gamma } \bigl\vert q_{t}(x,y)-q_{t}(x,x_{0}) \bigr\vert \frac{dt}{t}. \end{aligned}$$

By (ii) of Lemma 4.1 and a direct computation, we get

$$\begin{aligned} \bigl\vert g(x,y)-g(x,x_{0}) \bigr\vert \leq & \biggl\vert \int ^{\infty }_{0}t^{-i\gamma } \bigl[ \vert y-x _{0} \vert m(x,\mu ) \bigr]^{\delta '}t^{-{n}/{2}}e^{-{c \vert x-y \vert ^{2}}/{t}} \frac{dt}{t} \biggr\vert \\ \leq &C \bigl[ \vert y-x_{0} \vert m(x,\mu ) \bigr]^{\delta '} \int ^{\infty }_{0}t^{-{n}/ {2}}e^{-{c \vert x-y \vert ^{2}}/{t}} \frac{dt}{t} \\ \leq & C{ \vert x-y \vert ^{-n}} \bigl[ \vert y-x_{0} \vert m(x,\mu ) \bigr]^{\delta '}. \end{aligned}$$

This completes the proof of Lemma 4.2. □

We recall that an operator T taking $\mathcal{C}^{\infty }( \mathbb{R}^{n})$ into $L^{1}_{\mathrm{loc}}(\mathbb{R}^{n})$ is called a Calderón–Zygmund operator if

• (a) T extends to a bounded operator on $L^{2}(\mathbb{R}^{n},dx)$;

• (b) there exists a kernel K such that, for every $f\in L^{1} _{c}(\mathbb{R}^{n},dx)$,

  $$ Tf(x)= \int _{\mathbb{R}^{n}}K(x,y)f(y)\,dy\quad \text{a.e. on }\{\operatorname{supp} f\} ^{c}; $$

• (c) the kernel K satisfies

  $$ \textstyle\begin{cases} \vert K(x,y) \vert \leq {c}/{ \vert x-y \vert ^{n}}; \\ \vert K(x+h,y)-K(x,y) \vert \leq {c \vert h \vert ^{\delta }}/{ \vert x-y \vert ^{n+\delta }}; \\ \vert K(x,y+h)-K(x,y) \vert \leq {c \vert h \vert ^{\delta }}/{ \vert x-y \vert ^{n+\delta }}. \end{cases} $$

  (4.3)

In [12], Shen proved the following result.

Theorem 4.3

Let $\mathcal{L}=-\Delta +\mu$ be a generalized Schrödinger operator, where $\mu \neq 0$ is a nonnegative Radon measure on $\mathbb{R}^{n}$ satisfying (1.2) & (1.3) for some $\delta >0$. Then, for $\gamma \in \mathbb{R}^{n}$, $\mathcal{L}^{i\gamma }$ is a Calderón–Zygmund operator.

Now we prove the $H^{1}_{\mathcal{L}}$-boundedness of $\mathcal{L} ^{i\gamma }$.

Theorem 4.4

Let μ be a nonnegative Radon measure in $\mathbb{R}^{n}$, $n \geq 3$. Suppose that μ satisfies conditions (1.2) & (1.3) for some $\delta >0$. Then, for $\gamma \in \mathbb{R}^{n}$, $\mathcal{L}^{i\gamma }$ is bounded on $H^{1}_{\mathcal{L}}( \mathbb{R}^{n})$.

Proof

We only need to prove that, for any $(1,\infty )$ atom a, $\mathcal{L}^{i\gamma }(a)$ is a $(1,q, \varepsilon )$-molecular and $\|\mathcal{L}^{i\gamma }(a)\|_{H^{1}_{\mathcal{L}}}\leq C$. Let a be a $(1,\infty )$ atom supported on $B(x_{0},r)$. Then $\|a\|_{\infty } \leq {1}/{|B(x_{0},r)|}$. If $r< m(x_{0},\mu )^{-1}$, $\int a(x)\,dx=0$. Set $B^{\sharp }=B(x_{0}, {2}/{m(x_{0},\mu )})$ and $B^{*}=B(x_{0},2r)$. We divide the proof into three parts.

Part I: $\mathcal{L}^{i\gamma }a\in L^{q}(\mathbb{R}^{n}) \& |x|^{nb}L ^{i\gamma }(a)\in L^{q}(\mathbb{R}^{n})$.

$$\begin{aligned} \bigl\Vert \vert x \vert ^{nb}\mathcal{L}^{i\gamma }a \bigr\Vert _{q} \leq & \bigl\Vert x_{B^{*}} \vert \cdot \vert ^{nb} \mathcal{L}^{i\gamma }a \bigr\Vert _{q}+ \bigl\Vert x_{({B^{*}})^{c}} \vert \cdot \vert ^{nb} \mathcal{L}^{i\gamma }a \bigr\Vert _{q} \\ =& \biggl( \int _{B^{*}} \vert x \vert ^{qnb} \bigl\vert \mathcal{L}^{i\gamma }(a) \bigr\vert ^{q}\,dx \biggr)^{ {1}/{q}}+ \biggl( \int _{({B^{*}})^{c}} \vert x \vert ^{qnb} \bigl\vert \mathcal{L}^{i\gamma }(a) \bigr\vert ^{q}\,dx \biggr)^{{1}/{q}} \\ \leq & \bigl(r+ \vert x_{0} \vert \bigr)^{nb} \bigl\Vert \mathcal{L}^{i\gamma }a \bigr\Vert _{q}+ \biggl[ \int _{({B^{*}})^{c}} \vert x \vert ^{qnb} \biggl\vert \int _{\mathbb{R}^{n}}K^{\mathcal{L}} _{\gamma }(x,y)a(y)\,dy \biggr\vert ^{q}\,dx \biggr]^{{1}/{q}}. \end{aligned}$$

By the $L^{q}$-boundedness of $\mathcal{L}^{i\gamma }$ and Minkowski’s inequality, $\||x|^{nb}\mathcal{L}^{i\gamma }a\|_{q}\leq S_{1}+S_{2}$, where

$$ \textstyle\begin{cases} S_{1}:=(r+ \vert x_{0} \vert )^{nb} \Vert a \Vert _{q}; \\ S_{2}:=\int _{B(x_{0},r)} \vert a(y) \vert [\int _{({B^{*}})^{c}} \vert x \vert ^{qnb} \vert K ^{\mathcal{L}}_{\gamma }(x,y) \vert ^{q}\,dx ]^{{1}/{q}}. \end{cases} $$

Because $\|a\|_{q}\leq |B(x_{0},r)|^{{1}/{q}-1}$, then

$$ S_{1}= \bigl(r+ \vert x_{0} \vert \bigr)^{nb} \Vert a \Vert _{q}\leq \bigl(r+ \vert x_{0} \vert \bigr)^{nb}r^{n({1}/{q}-1)}. $$

For the term $S_{2}$, recall that

$$ K^{\mathcal{L}}_{\gamma }(x,y)= \int ^{\infty }_{0}t^{-i\gamma }K^{ \mathcal{L}}_{t}(x,y) \frac{dt}{t}. $$

Proposition 2.7 implies that

$$\begin{aligned} \bigl\vert K^{\mathcal{L}}_{\gamma }(x,y) \bigr\vert \leq &C_{N}{t^{-{n}/{2}}}\frac{e ^{-c{ \vert x-y \vert ^{2}}/{t}}}{\{1+ \vert x-y \vert [m(x,\mu )+m(y,\mu )]\}^{N}} \frac{dt}{t} \\ \leq &\frac{C_{N}}{\{1+ \vert x-y \vert [m(x,\mu )+m(y,\mu )]\}^{N}} \frac{1}{ \vert x-y \vert ^{n}}, \end{aligned}$$

which gives

$$\begin{aligned} S_{2}\leq C \int _{B} \bigl\vert a(y) \bigr\vert \biggl[ \int _{({B^{*}})^{c}} \vert x \vert ^{qnb}\frac{1}{ \{1+ \vert x-y \vert [m(x,\mu )+m(y,\mu )]\}^{qN}} \frac{dx}{ \vert x-y \vert ^{qn}} \biggr]^{ {1}/{q}}\,dy. \end{aligned}$$

For $x\in B$ and $y\in ({B^{*}})^{c}$, we can see that $|x-y|\geq {|x-x_{0}|}/{2}$. Notice that for $y\in B(x_{0},r)$, $|x_{0}-y|< r$ and

$$ m(y,\mu )^{N}\geq \biggl[\frac{cm(x_{0},\mu )}{\{1+ \vert x_{0}-y \vert m(x_{0}, \mu )\}^{{k_{0}}/{(k_{0}+1)}}} \biggr]^{N}. $$

Then, via a direct computation, we have

$$\begin{aligned} S_{2} \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \frac{1}{m(y,\mu )^{N}} \biggl\{ \int _{({B^{*}})^{c}}\frac{ \vert x \vert ^{qnb}\,dx}{ \vert x-x_{0} \vert ^{(n+N)q}} \biggr\} ^{ {1}/{q}}\,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \frac{1}{m(y,\mu )^{N}} \biggl\{ \biggl[ \int _{({B^{*}})^{c}}\frac{1}{ \vert x-x_{0} \vert ^{(n+N)q-qnb}}\,dx \biggr]^{{1}/ {q}} \\ &{}+ \biggl[ \int _{({B^{*}})^{c}} \frac{ \vert x_{0} \vert ^{qnb}}{ \vert x-x_{0} \vert ^{(n+N)q}}\,dx \biggr]^{{1}/{q}} \biggr\} \,dy \\ \leq &C \int _{B}\frac{ \vert a(y) \vert }{m(y,\mu )^{N}} \bigl\{ r^{n\varepsilon -N}+ \vert x _{0} \vert ^{nb}r^{-n-N+{n}/{q}} \bigr\} \,dy \\ \leq &C\frac{\{1+r m(x_{0},\mu )\}^{k_{0}N/(k_{0}+1)}}{m(x_{0}, \mu )^{N}} \bigl\{ r^{n\varepsilon -N}+ \vert x_{0} \vert ^{nb}r^{-n-N+{n}/{q}} \bigr\} \biggl( \int _{B} \bigl\vert a(y) \bigr\vert \,dy \biggr)< \infty . \end{aligned}$$

Part II: $N_{\mathcal{L}}(\mathcal{L}^{i\gamma }a)=\| \mathcal{L}^{i\gamma }a\|^{{\varepsilon }/{b}}_{q}\||\cdot -x_{0}|^{nb} \mathcal{L}^{i\gamma }a\|^{1-{\varepsilon }/{b}}_{q}\leq C$ .

Case I: $r\geq \rho (x_{0})$. Because $x\in ({B^{*}})^{c}$ and $y\in B$,

$$ \bigl\Vert \mathcal{L}^{i\gamma }a \bigr\Vert _{q}\leq \biggl( \int _{B^{*}} \bigl\vert \mathcal{L}^{i \gamma }a(y) \bigr\vert ^{q}\,dy \biggr)^{{1}/{q}}+ \biggl( \int _{({B^{*}})^{c}} \bigl\vert \mathcal{L}^{i\gamma }a(y) \bigr\vert ^{q}\,dy \biggr)^{{1}/{q}}. $$

Because $\mathcal{L}^{i\gamma }$ is bounded on $L^{q}(\mathbb{R}^{n})$, $q>1$, then

$$ \biggl( \int _{B^{*}} \bigl\vert \mathcal{L}^{i\gamma }a(y) \bigr\vert ^{q}\,dy \biggr)^{{1}/{q}} \leq \bigl\Vert \mathcal{L}^{i\gamma }a \bigr\Vert _{q}\leq C \Vert a \Vert _{q}\leq \vert B \vert ^{{1}/ {q}-1}. $$

For $y\in B$ and $x\in (B^{\ast })^{c}$, $|x-y|\geq |x-x_{0}|/2$. By Theorem 4.3, we can get

$$\begin{aligned} \biggl( \int _{({B^{*}})^{c}} \bigl\vert \mathcal{L}^{i\gamma }a(x) \bigr\vert ^{q}\,dx \biggr)^{ {1}/{q}} \leq & \int _{B} \bigl\vert a(y) \bigr\vert \biggl( \int _{({B^{*}})^{c}} \bigl\vert K^{ \mathcal{L}}_{\gamma }(x,y) \bigr\vert ^{q}\,dx \biggr)^{{1}/{q}}\,dy \\ \leq & \int _{B} \bigl\vert a(y) \bigr\vert \biggl( \int _{({B^{*}})^{c}}{ \vert x-y \vert ^{-nq}}\,dx \biggr)^{ {1}/{q}}\,dy \\ \leq & \int _{B} \bigl\vert a(y) \bigr\vert r^{{n}/{q}-n} \,dy\leq C r^{{n}/{q}-n}. \end{aligned}$$

Because $q>1 \& r\geq \rho (x_{0})$, the above estimates indicate that

$$ \bigl\Vert \mathcal{L}^{i\gamma }a(x) \bigr\Vert ^{1/\{{n}/{q}-n\}}\geq \rho (x_{0})^{( {n}/{q}-n)/\{{n}/{q}-n\}}=\rho (x_{0}), $$

which means that such $\mathcal{L}^{i\gamma }a$ need not satisfy the canceling condition.

On the other hand, we write $\||\cdot -x_{0}|^{nb}\mathcal{L}^{i \gamma }a\|_{q}\leq I_{1}+I_{2}$, where

$$ \textstyle\begin{cases} I_{1}:= \Vert \chi _{B^{*}} \vert \cdot -x_{0} \vert ^{nb}\mathcal{L}^{i\gamma }a \Vert _{q}; \\ I_{2}:= \Vert \chi _{({B^{*}})^{c}} \vert \cdot -x_{0} \vert ^{nb}\mathcal{L}^{i\gamma }a \Vert _{q}. \end{cases} $$

For $I_{1}$, by the $L^{q}$-boundedness of $\mathcal{L}^{i\gamma }$ and the fact that $\varepsilon -b={1}/{q}-1$, we have

$$\begin{aligned} I_{1} \leq &C \vert B \vert ^{b} \bigl\Vert \mathcal{L}^{i\gamma }a \bigr\Vert _{q} \leq C \vert B \vert ^{\varepsilon }. \end{aligned}$$

For $I_{2}$, because

$$ \bigl\vert K^{\mathcal{L}}_{\gamma }(x,y) \bigr\vert \leq \frac{C_{N}}{\{1+ \vert x-y \vert [m(x, \mu )+m(y,\mu )]\}^{N}}\frac{1}{ \vert x-y \vert ^{n}}, $$

we can use Lemma 2.1 and the fact that $r\geq {1}/{m(x_{0}, \mu )}$ to obtain

$$\begin{aligned} I_{2} \leq &C \int _{B}\frac{ \vert a(y) \vert }{m(y,\mu )^{N}} \biggl( \int _{({B^{*}})^{c}}\frac{ \vert x-x _{0} \vert ^{nbq}}{ \vert x-x_{0} \vert ^{(n+N)q}}\,dx \biggr)^{{1}/{q}}\,dy \\ \leq &C \int _{B}\frac{ \vert a(y) \vert }{m(y,\mu )^{N}}r^{nb+{n}/{q}-n-N}\,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \biggl\{ \frac{1}{m(x_{0},\mu )}+ \vert y-x_{0} \vert \biggr\} ^{N}r^{nb+ {n}/{q}-n-N}\,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert r^{N}r^{nb+{n}/{q}-n-N} \,dy \\ \leq &C \vert B \vert ^{\varepsilon }. \end{aligned}$$

The estimates for $I_{1}$ and $I_{2}$ imply that

$$\begin{aligned} N_{\mathcal{L}} \bigl(\mathcal{L}^{i\gamma }a \bigr) =& \bigl\Vert \mathcal{L}^{i\gamma }a \bigr\Vert ^{{\varepsilon }/{b}}_{q} \bigl\Vert \vert \cdot -x_{0} \vert \mathcal{L}^{i\gamma }a \bigr\Vert ^{1-{\varepsilon }/{b}}_{q}\leq C. \end{aligned}$$

Case 2: $r<{1}/{m(x_{0},\mu )}$. For this case, the atom a has the canceling property. There exists a positive integer m such that ${2^{-m-1}}/{m(x_{0},\mu )}\leq r< {2^{-m}}/{m(x_{0},\mu )}$. Let $B^{\sharp }=B(x_{0}, {2}/{m(x_{0},\mu )})$ and $B^{\ast }=B(x_{0},2r)$. We write

$$ \mathcal{L}^{i\gamma }a= \bigl(\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma } \bigr)a+(- \Delta )^{i\gamma }a. $$

We will prove that $(\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma })a$ and $(-\Delta )^{i\gamma }a$ are both moleculars. For $r<{1}/{m(x_{0}, \mu )}$, any $(1,q)$-atom is a classical atom. By Alverez–Milman [1], $(-\Delta )^{i\gamma }a$ is a $(1,q, \varepsilon )$-molecular. Hence, $(-\Delta )^{i\gamma }a$ is a molecular of $H^{1}_{\mathcal{L}}( \mathbb{R}^{n})$. We write $\|(\mathcal{L}^{i\gamma }-(-\Delta )^{i \gamma })a\|_{q}\leq I_{1}+I_{2}+I_{3}$, where

$$ \textstyle\begin{cases} I_{1}:= \Vert (\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma })a\chi _{B^{ \ast }} \Vert _{q}; \\ I_{2}:= \Vert (\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma })a \chi _{B^{\sharp }\backslash B^{\ast }} \Vert _{q}; \\ I_{3}:= \Vert (\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma })a \chi _{(B^{\sharp })^{c}} \Vert _{q}. \end{cases} $$

We first estimate the term $I_{1}$. Because $\delta \in (0,n)$, then ${n}/{q}-n+\delta >0$. Estimate (4.2) implies that

$$\begin{aligned} I_{1} \leq &C \int _{B} \biggl( \int _{B^{\ast }} \bigl\vert g(x,y) \bigr\vert ^{q} \,dx \biggr)^{{1}/ {q}} \bigl\vert a(y) \bigr\vert \,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert m(x_{0}, \mu )^{\delta } \biggl( \int _{B^{\ast }} { \vert x-y \vert ^{-q(n-\delta )}}\,dx \biggr)^{{1}/{q}}\,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert m(x_{0}, \mu )^{\delta }r^{{(n-qn+q\delta )}/ {q}}\,dy \\ \leq &Cm(x_{0}, \mu )^{\delta } \bigl[{2^{m}m(x_{0}, \mu )} \bigr]^{- {n}/{q}+n-\delta } \\ \leq &C{m(x_{0}, \mu )}^{{n}-n/{q}}. \end{aligned}$$

Now we deal with $I_{3}$. If $x\in (B^{\sharp })^{c}$ and $y\in B$, then $|y-x|\sim |x-x_{0}|$. By the canceling property of a, we have

$$\begin{aligned} \bigl\vert \bigl[\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma } \bigr](a) (x) \bigr\vert \leq & \biggl\vert \int _{B} \bigl[ K^{\mathcal{L}}_{\gamma }(x,y)-K_{\gamma }(x,y) \bigr]a(y)\,dy \biggr\vert \\ \leq & \biggl\vert \int _{B} \bigl[ K^{\mathcal{L}}_{\gamma }(x,x_{0})-K^{ \mathcal{L}}_{\gamma }(x,y) \bigr]a(y)\,dy \biggr\vert \\ &{} + \biggl\vert \int _{B} \bigl[K_{\gamma }(x,y)-K _{\gamma }(x,x_{0}) \bigr]a(y)\,dy \biggr\vert \\ \leq & \int _{B} \bigl\vert a(y) \bigr\vert \biggl[ \frac{ \vert y-x_{0} \vert ^{\delta }}{ \vert x-x_{0} \vert ^{n+ \delta }}+\frac{ \vert y-x_{0} \vert }{ \vert x-x_{0} \vert ^{n+1}} \biggr]\,dy \\ \leq &C \biggl(\frac{r^{\delta }}{ \vert x-x_{0} \vert ^{n+\delta }}+\frac{r}{ \vert x-x _{0} \vert ^{n+1}} \biggr). \end{aligned}$$

Then, since $r m(x_{0}, \mu )<1$, we obtain that

$$\begin{aligned} I_{3} \leq &C \biggl[ \int _{(B^{\sharp })^{c}} \biggl(\frac{r^{\delta }}{ \vert x-x _{0} \vert ^{n+\delta }}+\frac{r}{ \vert x-x_{0} \vert ^{n+1}} \biggr)^{q}\,dx \biggr]^{{1}/ {q}} \\ \leq &C \biggl\{ \biggl[ \int _{(B^{\sharp })^{c}}\frac{r^{q\delta }}{ \vert x-x _{0} \vert ^{q(n+\delta )}}\,dx \biggr]^{{1}/{q}} + \biggl[ \int _{(B^{\sharp })^{c}}\frac{r ^{q}}{ \vert x-x_{0} \vert ^{q(n+1)}}\,dx \biggr]^{{1}/{q}} \biggr\} \\ \leq &Cr^{\delta }m(x_{0}, \mu )^{\delta +n-{n}/{q}}+r m(x_{0}, \mu )^{\delta +1-{n}/{q}} \\ \leq &Cm(x_{0}, \mu )^{n-{n}/{q}}. \end{aligned}$$

At last, we estimate $I_{2}$. For this case, $x\in B^{\sharp }\backslash B^{\ast }$, then $2r<|x-x_{0}|<{2}/{m(x_{0}, \mu )}$ and $|x-y|\sim |x-x _{0}|$. Applying (4.2) and the canceling property of a again, we get

$$\begin{aligned} \bigl\vert \bigl[\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma } \bigr]a(x) \bigr\vert \leq &C \int _{B} { \bigl[ \vert y-x_{0} \vert m(x_{0}, \mu ) \bigr]^{\delta '}} { \vert x-x_{0} \vert ^{-n}} \bigl\vert a(y) \bigr\vert \,dy \\ \leq &C \bigl[m(x_{0}, \mu ) \bigr]^{\delta '}{r^{\delta '}} { \vert x-x_{0} \vert ^{-n}} \int _{B} \bigl\vert a(y) \bigr\vert \,dy \\ \leq &C \bigl[m(x_{0}, \mu ) \bigr]^{\delta '}{r^{\delta '}} { \vert x-x_{0} \vert ^{-n}} \\ \leq &C{2^{-m\delta '}} { \vert x-x_{0} \vert ^{-n}}, \end{aligned}$$

which implies that

$$\begin{aligned} I_{2} \leq &C \biggl[ \int _{B^{\sharp }\backslash B^{\ast }} \bigl\vert \bigl[\mathcal{L} ^{i\gamma }-(- \Delta )^{i\gamma } \bigr]a(x) \bigr\vert ^{q}\,dx \biggr]^{{1}/{q}} \\ \leq &C \biggl( \int _{B^{\sharp }\backslash B^{\ast }}{2^{-m\delta 'q}} { \vert x-x_{0} \vert ^{-nq}}\,dx \biggr)^{{1}/{q}} \\ \leq &C{m(x_{0}, \mu )}^{{n}-n/{q}}, \end{aligned}$$

where in the last inequality we have used the fact that $q<{n}/{(n- \delta ')}$.

Finally, it follows from the estimates for $I_{i}$, $i=1,2,3$, that

$$ \bigl\Vert \bigl[\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma } \bigr]a \bigr\Vert ^{1/({n}/{q}-n)} _{q}\geq {m(x_{0}, \mu )}^{-1}. $$

On the other hand, the $L^{q}$-boundedness of $\mathcal{L}^{i\gamma }-(- \Delta )^{i\gamma }$ gives

$$ \bigl\Vert \bigl[\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma } \bigr]a \bigr\Vert _{q}\leq \Vert a \Vert _{q}= \biggl( \int _{B} \bigl\vert a(y) \bigr\vert ^{q}\,dy \biggr)^{{1}/{q}}\leq r^{{n}/{q}-n}. $$

This means that for this case, $(\mathcal{L}^{i\gamma }-(-\Delta )^{i \gamma })a$ need not satisfy the canceling condition.

Part III: There exists a constant C such that, for any $(1,\infty )$-atom, uniformly,

$$ {N}_{\mathcal{L}} \bigl( \bigl[\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma } \bigr]a \bigr) \leq C. $$

We write $b=1-{1}/{q}+\varepsilon$, then $\varepsilon -b={1}/{q}-1$. We have proved that

$$\begin{aligned} \bigl\Vert \bigl(\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma } \bigr)a \bigr\Vert _{q} \leq &C\rho (x _{0})^{{n}/{q}-n}\leq \rho (x_{0})^{n(\varepsilon -b)}. \end{aligned}$$

Now we split: $\||\cdot -x_{0}|^{nb}(\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma })a\|_{q}\leq I_{1}+I_{2}$, where

$$ \textstyle\begin{cases} I_{1}:= \Vert \vert \cdot -x_{0} \vert ^{nb}(\mathcal{L}^{i\gamma }-(-\Delta )^{i \gamma })a \Vert _{L^{q}(B^{\sharp })}; \\ I_{2}:= \Vert \vert \cdot -x_{0} \vert ^{nb}(\mathcal{L}^{i\gamma }-(-\Delta )^{i \gamma })a \Vert _{L^{q}((B^{\sharp })^{c})}. \end{cases} $$

For $I_{1}$, because $B^{\sharp }=(x_{0},2\rho (x_{0}))$,

$$\begin{aligned} I_{1} \leq &C\rho (x_{0})^{nb} \biggl[ \int _{B^{\sharp }} \bigl\vert \bigl(\mathcal{L} ^{i\gamma }-(- \Delta )^{i\gamma } \bigr)a(x) \bigr\vert ^{q} \biggr]^{{1}/{q}} \leq C \rho (x_{0})^{nb}\rho (x_{0})^{n(\varepsilon -b)}\leq C\rho (x_{0})^{n \varepsilon }. \end{aligned}$$

For $I_{2}$, we further split $I_{2}$ into $I_{2,1}+I_{2,2}$, where

$$ \textstyle\begin{cases} I_{2,1}:= \Vert \vert \cdot -x_{0} \vert ^{nb}\mathcal{L}^{i\gamma }a \Vert _{L^{q}((B^{ \sharp })^{c})}; \\ I_{2,2}:= \Vert \vert \cdot -x_{0} \vert ^{nb}(-\Delta )^{i\gamma }a \Vert _{L^{q}((B^{ \sharp })^{c})}. \end{cases} $$

Notice that $\varepsilon <{\delta }/{n}$ and $nb-(n+\delta )+{n}/ {q}<0$. By Theorem 4.3, we have

$$\begin{aligned} I_{2,1} \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \biggl[ \int _{(B^{\sharp })^{c}} \vert x-x_{0} \vert ^{qnb}| \int _{B}{ \vert y-x_{0} \vert ^{q\delta }} { \vert x-x_{0} \vert ^{-q(n+\delta )}}\,dx \biggr]^{ {1}/{q}}\,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \vert y-x_{0} \vert ^{\delta } \biggl[ \int _{(B^{\sharp })^{c}} \vert x-x _{0} \vert ^{qnb-q(n+\delta )}\,dx \biggr]^{{1}/{q}}\,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert r^{\delta }\rho (x_{0})^{nb-(n+\delta )+{n}/ {q}}\,dy \\ \leq &C \rho (x_{0})^{n\varepsilon }. \end{aligned}$$

For $I_{2,2}$, similarly, we have

$$\begin{aligned} I_{2,2} \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \vert x-x_{0} \vert \biggl( \int _{ \vert x-x_{0} \vert \geq 2\rho (x_{0})}{ \vert x-x_{0} \vert ^{q(nb-n-1)}} \vert x-x_{0} \vert ^{n-1}\,d \vert x-x _{0} \vert \biggr)^{{1}/{q}}\,dy \\ \leq & C \int _{B} \bigl\vert a(y) \bigr\vert r\rho (x_{0})^{nb-(n+1)+{n}/{q}}\,dy \\ \leq &C \rho (x_{0})^{n\varepsilon }, \end{aligned}$$

where we have used the fact that $0<\varepsilon <\min \{{\delta }/ {n},{1}/{n}\}$. Finally, we get

$$ \bigl\Vert \vert \cdot -x_{0} \vert ^{nb} \bigl( \mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma } \bigr)a \bigr\Vert _{q}\leq \rho (x_{0})^{n\varepsilon }, $$

and, hence,

$$\begin{aligned}& \bigl\Vert \bigl(\mathcal{L}^{i\gamma }-(-\Delta )^{i\gamma } \bigr)a \bigr\Vert ^{{\varepsilon }/ {b}}_{q} \bigl\Vert \vert \cdot -x_{0} \vert ^{nb} \bigl(\mathcal{L}^{i\gamma }-(- \Delta )^{i \gamma } \bigr)a \bigr\Vert ^{(1-{\varepsilon }/{b})}_{q} \\& \quad \leq C\rho (x_{0})^{n( \varepsilon -b){\varepsilon }/{b}}\rho (x_{0})^{n\varepsilon (1-{\varepsilon }/ {b})} \leq C. \end{aligned}$$

Finally, we have proved that, for any $(1,\infty )$-atom, $\mathcal{L}^{i\gamma }a$ is a $(1,q,\varepsilon )$-molecular or the linear combination of finite $(1,q,\varepsilon )$-moleculars. □

4.2 The $H^{1}_{\mathcal{L}}$-boundedness of Riesz transforms $R_{\mathcal{L}}$

In this section, we prove that Riesz transforms $R_{\mathcal{L}}$ are bounded on $H^{1}_{\mathcal{L}}(\mathbb{R}^{n})$. The Riesz transforms associated with $\mathcal{L}$ are defined as

$$ R_{\mathcal{L}}:=\nabla (-\Delta +\mu )^{-1/2}, $$

where $(-\Delta +\mu )^{-{1}/{2}}=\frac{1}{\pi }\int ^{\infty }_{0} \lambda ^{-{1}/{2}}(-\Delta +\mu +\lambda )^{-1}\,d\lambda$. Shen proved the following estimate of $R_{\mathcal{L}}$. Assume that μ satisfies (1.2) & (1.3) for some $\delta >1$. Then $\nabla (- \Delta +\mu )^{-{1}/{2}}$ is a Calderón–Zygmund operator. Precisely,

$$ \nabla (-\Delta +\mu )^{-{1}/{2}}f(x)= \int _{\mathbb{R}^{n}}R_{ \mathcal{L}}(x,y)f(y)\,dy, $$

where

$$ R_{\mathcal{L}}(x,y):=\frac{1}{\pi } \int ^{\infty }_{0}\lambda ^{-{1}/ {2}}\nabla _{x}\varGamma _{\mu +\lambda }(x,y)\,d\lambda . $$

In [12], Shen proved the following results, see [12, (7.20), (7.26), (7.29)], respectively.

Lemma 4.5

The kernel $R_{\mathcal{L}}(\cdot ,\cdot )$ satisfies the following estimates:

$$ \textstyle\begin{cases} (1) \quad \vert R_{\mathcal{L}}(x,y) \vert \leq {Ce^{-cd(x,y,\mu )}}{ \vert x-y \vert ^{-n}}; \\ (2) \quad \vert R_{\mathcal{L}}(x+h,y)-R_{\mathcal{L}}(x,y) \vert \leq C ({ \vert h \vert }/ { \vert x-y \vert } )^{\delta -1}{ \vert x-y \vert ^{-n}}; \\ (3) \quad \vert R_{\mathcal{L}}(x,y+h)-R_{\mathcal{L}}(x,y) \vert \leq C ({ \vert h \vert }/ { \vert x-y \vert } )^{\delta _{1}}{ \vert x-y \vert ^{-n}},\quad \delta _{1}\in (0,1). \end{cases} $$

Theorem 4.6

Let $\mathcal{L}=-\Delta +\mu$ be a generalized Schrödinger operator, where $\mu \neq 0$ is a nonnegative Radon measure on $\mathbb{R}^{n}$ satisfying (1.2) & (1.3) for some $\delta >0$. The Riesz transform $R_{\mathcal{L}}$ is bounded on $H^{1}_{ \mathcal{L}}(\mathbb{R}^{n})$.

Proof

Similar to Theorem 4.4, the proof of this theorem is divided into three parts.

Part I: $\|{|\cdot |}^{nb}R_{\mathcal{L}}a\|_{q}<\infty$, uniformly. For any atom a and $B^{\ast }=B(x_{0},2r)$, we write $\|{|\cdot |}^{nb}R_{\mathcal{L}}a\|_{q}\leq I_{1}+I_{2}$, where $I_{1}:=\|{|\cdot |}^{nb}R_{\mathcal{L}}a\|_{L^{q}(B^{\ast })}$ and $I_{2}:=\|{|\cdot |}^{nb}R_{\mathcal{L}}a\|_{L^{q}((B^{\ast })^{c})}$.

By the $L^{q}$-boundedness of $R_{\mathcal{L}}$, we have

$$\begin{aligned} I_{1} \leq &r^{nb} \biggl( \int _{B^{\ast }} \bigl\vert R_{\mathcal{L}}a(x) \bigr\vert ^{q}\,dx \biggr)^{{1}/{q}}\leq r^{nb} \Vert a \Vert _{q} \leq r^{nb} \bigl\vert B(x_{0},r) \bigr\vert ^{{1}/ {q}-1} \leq r^{n\varepsilon }. \end{aligned}$$

By Lemma 4.5, for any positive $N>0$,

$$\begin{aligned} \bigl\vert R_{\mathcal{L}}(x,y) \bigr\vert \leq &C{ \vert x-y \vert ^{-n-N} \bigl[m(y,\mu ) \bigr]^{-N}}. \end{aligned}$$

On the other hand, for $y\in B$ and $x\in (B^{\ast })^{c}$, $|x-y|\geq {|x-x_{0}|}/{2}$. We can obtain that

$$\begin{aligned} I_{2} \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \biggl( \int _{(B^{\ast })^{c}} \vert x \vert ^{qnb} \bigl\vert R_{ \mathcal{L}}(x,y) \bigr\vert ^{q}\,dx \biggr)^{{1}/{q}} \,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \frac{1}{m(y,\mu )^{N}} \biggl( \int _{(B^{\ast })^{c}} \vert x \vert ^{qnb} \frac{1}{ \vert x-y \vert ^{(n+N)q}}\,dx \biggr)^{{1}/{q}}\,dy \\ \leq &C \biggl\{ \int _{B} \bigl\vert a(y) \bigr\vert \frac{ \vert x_{0} \vert ^{nb}}{m(y,\mu )^{N}} \biggl( \int _{(B^{\ast })^{c}}\frac{dx}{ \vert x-x_{0} \vert ^{(n+N)q}} \biggr)^{{1}/{q}}\,dy \\ &{}+ \int _{B} \bigl\vert a(y) \bigr\vert \frac{1}{m(y,\mu )^{N}} \biggl( \int _{(B^{\ast })^{c}}\frac{ \vert x-x _{0} \vert ^{qnb}}{ \vert x-x_{0} \vert ^{(n+N)q}}\,dx \biggr)^{{1}/{q}}\,dy \biggr\} \\ \leq &C \int _{B}\frac{ \vert a(y) \vert }{m(y,\mu )^{N}} \bigl\{ r^{n\epsilon -N}+ \vert x _{0} \vert ^{-n-N+{n}/{q}} \bigr\} \,dy. \end{aligned}$$

Because $y\in B(x_{0},r)$,

$$ m(y,\mu ) \geq \frac{Cm(x_{0},\mu )}{\{1+ \vert x-x_{0} \vert m(x_{0},\mu )\}^{ {k_{0}}/{(k_{0}+1)}}}, $$

which implies that $\|{|\cdot |}^{nb}a\|_{L^{q}((B^{\ast })^{c})}< \infty$.

Part II: $N_{\mathcal{L}}(R_{\mathcal{L}}(a))\leq C$. We divide the proof into two cases.

Case1: $r\geq {1}/{m(x_{0},\mu )}$. By the boundedness of the Riesz transform $R_{\mathcal{L}}$, we have

$$\begin{aligned} \Vert R_{\mathcal{L}}a \Vert _{q} \leq &C \bigl\{ \Vert R_{\mathcal{L}}a \Vert _{q}+ \Vert \chi _{(B^{\ast })^{c}}R_{\mathcal{L}}a \Vert _{q} \bigr\} \\ \leq &C \bigl\{ \Vert a \Vert _{q}+ \Vert \chi _{(B^{\ast })^{c}}R_{\mathcal{L}}a \Vert _{q} \bigr\} \\ \leq &C \biggl\{ \bigl\vert B(x_{0},r) \bigr\vert ^{{1}/{q}-1}+ \int _{B} \bigl\vert a(y) \bigr\vert \biggl( \int _{(B^{\sharp })^{c}} \bigl\vert R_{\mathcal{L}}(x,y) \bigr\vert ^{q}\,dx \biggr)^{{1}/{q}}\,dy \biggr\} . \end{aligned}$$

By Lemma 4.5, we can get

$$\begin{aligned} \int _{B} \bigl\vert a(y) \bigr\vert \biggl( \int _{(B^{\sharp })^{c}} \bigl\vert R_{\mathcal{L}}(x,y) \bigr\vert ^{q}\,dx \biggr)^{{1}/{q}}\,dy \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \biggl( \int ^{\infty }_{2r}s^{n-qn-1}\,ds \biggr)^{{1}/{q}}\,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \,dy \times r^{{n}/{q}-n} \\ \leq &C\rho (x_{0})^{{n}/{q}-n}, \end{aligned}$$

which means that $\|R_{\mathcal{L}}a\|^{1/({n}/{q}-n)}_{q}\geq \rho (x _{0})$, i.e., $R_{\mathcal{L}}a$ does not need the canceling condition for this case. Now we split $\||\cdot -x_{0}|^{nb}R_{\mathcal{L}}a\| _{q}\leq I_{1}+I_{2}$, where

$$ \textstyle\begin{cases} I_{1}:= (\int _{B^{\ast }} \vert x-x_{0} \vert ^{qnb} \vert R_{\mathcal{L}}a(x) \vert ^{q}\,dx )^{{1}/{q}}; \\ I_{2}:= (\int _{(B^{\ast })^{c}} \vert x-x_{0} \vert ^{qnb} \vert R_{\mathcal{L}}a(x) \vert ^{q}\,dx )^{{1}/{q}}. \end{cases} $$

It is easy to see that

$$\begin{aligned} I_{1}\leq r^{nb} \biggl( \int _{B^{\ast }} \bigl\vert R_{\mathcal{L}}a(x) \bigr\vert ^{q}\,dx \biggr)^{{1}/{q}} \leq r^{nb} \Vert R_{\mathcal{L}}a \Vert _{q} \leq r^{nb} \Vert a \Vert _{q} \leq r^{n\varepsilon }. \end{aligned}$$

For $I_{2}$, by Minkowski’s inequality,

$$\begin{aligned} I_{2} \leq &C \int _{B} \bigl\vert a(y) \bigr\vert {m(y,\mu )^{-N}} \biggl( \int _{B^{\ast }}{ \vert x-x _{0} \vert ^{qnb-q(n+N)}}\,dx \biggr)^{{1}/{q}}\,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert {m(y,\mu )^{-N}}r^{nb+{n}/{q}-n-N}\,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \bigl\{ {m(x_{0},\mu )^{-1}}+ \vert y-x_{0} \vert \bigr\} ^{N}r^{nb+{n}/{q}-n-N}\,dy \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert r^{N}r^{nb+{n}/{q}-n-N} \,dy \\ \leq &C \vert B \vert ^{(\varepsilon -b){\varepsilon }/{b}} \vert B \vert ^{\varepsilon (1- {\varepsilon }/{b})}, \end{aligned}$$

which gives $N_{\mathcal{L}}(R_{\mathcal{L}}a)=\|R_{\mathcal{L}}a\| ^{{\varepsilon }/{b}}_{q}\||\cdot -x_{0}|^{nb}R_{\mathcal{L}}a\|^{1- {\varepsilon }/{b}}_{q}\leq C$.

Case 2: $r\leq \rho (x_{0})$. Let $B^{\sharp }=B(x_{0},2\rho (x_{0}))$ and $B^{\ast }=B(x_{0},2r)$. So $R_{\mathcal{L}}a=R_{0}a+(R_{ \mathcal{L}}-R_{0})a$, where $R_{0}:=\nabla (-\Delta )^{-1/2}$. For any a with the canceling condition, $R_{0}a$ is a molecular. We only need to deal with $(R_{\mathcal{L}}-R_{0})a$. Split $\|(R_{\mathcal{L}}-R _{0})a\|_{q}\leq I_{1}+I_{2}+I_{3}$, where

$$ \textstyle\begin{cases} I_{1}:= (\int _{B^{\ast }} \vert (R_{\mathcal{L}}-R_{0})a(x) \vert ^{q}\,dx )^{ {1}/{q}}; \\ I_{2}:= (\int _{B^{\sharp } \backslash B^{\ast }} \vert (R_{\mathcal{L}}-R _{0})a(x) \vert ^{q}\,dx )^{{1}/{q}}; \\ I_{3}:= (\int _{(B^{\sharp })^{c}} \vert (R_{\mathcal{L}}-R_{0})a(x) \vert ^{q}\,dx )^{{1}/{q}}. \end{cases} $$

We first estimate $I_{3}$. For $x\in (B^{\sharp })^{c}$ and $y\in B$, $|x-y|\sim |x-x_{0}|$. Denote by $R_{0}(\cdot ,\cdot )$ the kernel of $\nabla (-\Delta )^{-1/2}$. We can get

$$\begin{aligned}& \bigl\vert (R_{\mathcal{L}}-R_{0}) (a) (x) \bigr\vert \\& \quad \leq C \biggl\{ \int _{B} \bigl\vert R_{ \mathcal{L}}(x,y)-R_{\mathcal{L}}(x,x_{0}) \bigr\vert \bigl\vert a(y) \bigr\vert \,dy+ \int _{B} \bigl\vert R_{0}(x,y)-R _{0}(x,x_{0}) \bigr\vert \bigl\vert a(y) \bigr\vert \,dy \biggr\} \\& \quad \leq C \Vert a \Vert _{\infty } \biggl( \int _{B}\frac{ \vert y-x_{0} \vert ^{\delta }}{ \vert x-x _{0} \vert ^{n+\delta }}\,dy+ \int _{B}\frac{ \vert y-x_{0} \vert }{ \vert x-x_{0} \vert ^{n+1}}\,dy \biggr) \\& \quad \leq C \Vert a \Vert _{\infty } \vert B \vert \biggl( \frac{r^{\delta }}{ \vert x-x_{0} \vert ^{n+\delta }}+\frac{r}{ \vert x-x_{0} \vert ^{n+1}} \biggr). \end{aligned}$$

It follows from the above estimate that

$$\begin{aligned} I_{3} \leq &C \biggl\{ \biggl( \int _{(B^{\sharp })^{c}}\frac{r^{q\delta }}{ \vert x-x _{0} \vert ^{q(n+\delta )}}\,dx \biggr)^{{1}/{q}} + \biggl( \int _{(B^{\sharp })^{c}}\frac{r ^{q}}{ \vert x-x_{0} \vert ^{q(n+1)}}\,dx \biggr)^{{1}/{q}} \biggr\} \\ \leq &C \bigl\{ r^{\delta }m(x_{0},\mu )^{n+\delta -{n}/{q}}+r \bigl[m(x_{0}, \mu ) \bigr]^{n+1-{n}/{q}} \bigr\} \\ \leq &C \bigl[m(x_{0},\mu ) \bigr]^{n-{n}/{q}}. \end{aligned}$$

For the estimates of $I_{1} \& I_{2}$, we need the following estimate:

$$ \bigl\vert R_{\mathcal{L}}(y,x)-R_{0}(y,x) \bigr\vert \leq C \biggl\{ \frac{1}{r^{n-1}} \int _{B(y,r)}\frac{d\mu (z)}{ \vert z-y \vert ^{n-1}}+\frac{(r m(x,\mu ))^{\delta }}{r^{n}} \biggr\} . $$

(4.4)

For $r={|x-y|}/{2}$,

$$ \bigl\vert R_{\mathcal{L}}(y,x)-R_{0}(y,x) \bigr\vert \leq C \biggl\{ \frac{1}{ \vert x-y \vert ^{n-1}} \int _{B(y, { \vert x-y \vert }/{2})}\frac{d\mu (z)}{ \vert z-y \vert ^{n-1}} +\frac{( \vert x-y \vert m(x, \mu ))^{\delta }}{ \vert x-y \vert ^{n}} \biggr\} . $$

We get $I_{1}\leq \int _{B}|a(y)|A_{1}(y)\,dy$, where

$$ A_{1}:= \biggl\{ \int _{B^{\ast }} \bigl\vert R_{\mathcal{L}}(x,y)-R_{0}(x,y) \bigr\vert ^{q}\,dx \biggr\} ^{{1}/{q}}. $$

Due to (4.4), we further obtain $A_{1}\leq U_{1}+U_{2}$, where

$$ \textstyle\begin{cases} U_{1}:= \{\int _{B^{\sharp }}{ \vert x-y \vert ^{q(1-n)}} ( \int _{B(x,{ \vert x-y \vert }/{2})}{ \vert z-x \vert ^{1-n}}\,d\mu (z) )^{q}\,dx \}^{{1}/ {q}}; \\ U_{2}:= \{\int _{B^{\sharp }}{( \vert x-y \vert m(y,\mu ))^{q\delta }}{ \vert x-y \vert ^{-qn}}\,dx \}^{{1}/{q}}. \end{cases} $$

For $U_{2}$, if $y\in B$, then $|y-x_{0}|< r<2\rho (x_{0})$ and $m(y,\mu )\sim m(x_{0},\mu )$. On the other hand, because $x\in B^{ \sharp }$, then $|x-y|<{3}/{m(x_{0},\mu )}$. We can get

$$\begin{aligned} U_{2} \leq & Cm(x_{0},\mu )^{\delta } \biggl( \int _{B^{\sharp }}{ \vert x-y \vert ^{q \delta -qn}}\,dx \biggr)^{{1}/{q}}\leq C m(x_{0},\mu )^{n-{n}/{q}}. \end{aligned}$$

Now we estimate the term $U_{1}$. Let $T_{j}=B(y,{2^{j+2}}/{ m(x_{0}, \mu )})$. If $y\in B$ and $x\in B^{\sharp }$, by the triangle inequality, it is easy to see that $B^{\sharp }\subset B(y,{4}/{ m(x _{0},\mu )})$. Also, for $x\in T_{j+1}\setminus T_{j}$, $|x-y|\geq {2^{j+2}}/{ m(x_{0},\mu )}$. On the other hand, $B(x,{|x-y|}/{2}) \subset B(y, {3|x-y|}/{2})$. Then

$$\begin{aligned} U_{1} \leq & C\sum^{0}_{j=-\infty } \biggl( \int _{T_{j+1}\setminus T_{j}} \frac{1}{ \vert x-y \vert ^{q(n-1)}} \biggl( \int _{B(x,{ \vert x-y \vert }/{2})} \frac{d\mu (z)}{ \vert z-x \vert ^{n-1}} \biggr)^{q}\,dx \biggr)^{{1}/{q}} \\ \leq & C\sum^{0}_{j=-\infty } \biggl[ \frac{m(x_{0},\mu )}{2^{j}} \biggr]^{n-1} \biggl( \int _{T_{j+1}\setminus T_{j}} \biggl( \int _{B(y,{ \vert x-y \vert }/{2})}\frac{d \mu (z)}{ \vert z-x \vert ^{n-1}} \biggr)^{q}\,dx \biggr)^{{1}/{q}} \\ \leq &C\sum^{0}_{j=-\infty } \biggl[ \frac{m(x_{0},\mu )}{2^{j}} \biggr]^{n-1} \biggl( \int _{T_{j+1}\setminus T_{j}} \biggl( \int _{B(y,{2^{j+2}}/{m(x_{0},\mu )})}\frac{d\mu (z)}{ \vert z-x \vert ^{n-1}} \biggr)^{q}\,dx \biggr)^{{1}/{q}} \\ \leq &C \sum^{0}_{j=-\infty } \biggl[ \frac{m(x_{0},\mu )}{2^{j}} \biggr]^{n-1}\frac{ \mu (3T_{j+1})}{2^{(j+2)(n-{n}/{q}-1)}} \bigl[m(x_{0}, \mu ) \bigr]^{n-{n}/{q}-1}. \end{aligned}$$

Notice that

$$ \mu (T_{j+1})=\mu \bigl(B \bigl(y,{2^{j+2}}/{m(x_{0}, \mu )} \bigr) \bigr)\leq \bigl(2^{j+2} \bigr)^{n-2+ \delta }{m(x_{0}, \mu )}^{2-n}. $$

A direct computation gives

$$\begin{aligned} U_{1} \leq &C \sum^{0}_{j=-\infty } \bigl[m(x_{0},\mu ) \bigr]^{n-{n}/{q}}2^{j(n-2+ \delta ')}{2^{-j(2n-{1}/{q}-2)}} \\ \leq &C \bigl[m(x_{0},\mu ) \bigr]^{n-{n}/{q}}\sum ^{0}_{j=-\infty }2^{j(n-2+ \delta '-2n+{n}/{q}+2)} \\ \leq &C \bigl[m(x_{0},\mu ) \bigr]^{n-{n}/{q}}, \end{aligned}$$

which implies that

$$\begin{aligned} I_{1}\leq C \int _{B} \bigl\vert a(y) \bigr\vert A_{1}(y) \,dy \leq C \Vert a \Vert _{1} \bigl[m(x_{0},\mu ) \bigr]^{n- {n}/{q}} \leq C \bigl[m(x_{0},\mu ) \bigr]^{n-{n}/{q}}. \end{aligned}$$

The estimate for $I_{2}$ is similar. Then we obtain $\|(R_{ \mathcal{L}}-R_{0})a\|^{1/\{{n}/{q}-n\}}_{q}\geq {C}/{m(x_{0},\mu )}$, which means $(R_{\mathcal{L}}-R_{0})a$ does not need the canceling condition. What is left to prove is the norm $\||\cdot -x_{0}|^{nb}(R _{\mathcal{L}}-R_{0})a\|_{q}$. We write $\||\cdot -x_{0}|^{nb}(R_{ \mathcal{L}}-R_{0})a\|_{q}\leq E_{1}+E_{2}$, where

$$ \textstyle\begin{cases} E_{1}:= (\int _{B^{\sharp }} \vert x-x_{0} \vert ^{qnb} \vert (R_{\mathcal{L}}-R_{0})a(x) \vert ^{q}\,dx )^{{1}/{q}}; \\ E_{2}:= (\int _{(B^{\sharp })^{c}} \vert x-x_{0} \vert ^{qnb} \vert (R_{\mathcal{L}}-R _{0})a(x) \vert ^{q}\,dx )^{{1}/{q}}. \end{cases} $$

By the $L^{p}$-boundedness of $R_{\mathcal{L}}$ and $R_{0}$, we get

$$\begin{aligned} E_{1} \leq &C{m(x_{0},\mu )}^{-nb} \bigl\Vert (R_{\mathcal{L}}-R_{0})a \bigr\Vert _{q} \leq C{m(x_{0},\mu )}^{-nb} \Vert a \Vert _{q} \leq C{m(x_{0},\mu )}^{-n\varepsilon }. \end{aligned}$$

For the term $E_{2}$, we have $E_{2}\leq E_{2,1}+E_{2,2}$, where

$$ \textstyle\begin{cases} E_{2,1}:= (\int _{(B^{\sharp })^{c}} \vert x-x_{0} \vert ^{qnb} \vert R_{\mathcal{L}}a(x) \vert ^{q}\,dx )^{{1}/{q}}; \\ E_{2,2}:= (\int _{(B^{\sharp })^{c}} \vert x-x_{0} \vert ^{qnb} \vert R_{0}a(x) \vert ^{q}\,dx )^{{1}/{q}}. \end{cases} $$

A direct computation gives

$$\begin{aligned} E_{2,1} \leq & C \int _{B} \bigl\vert a(y) \bigr\vert \,dy \biggl( \int _{(B^{\sharp })^{c}} \vert x-x_{0} \vert ^{qnb} \bigl\vert R _{\mathcal{L}}(x,y)-R_{\mathcal{L}}(x,x_{0}) \bigr\vert ^{q}\,dx \biggr)^{{1}/{q}} \\ \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \vert y-x_{0} \vert ^{\delta } \biggl( \int _{(B^{\sharp })^{c}}\frac{ \vert x-x _{0} \vert ^{qnb}}{ \vert x-x_{0} \vert ^{(n+\delta )q}}\,dx \biggr)^{{1}/{q}}\,dy \leq C{m(x _{0},\mu )}^{-n\varepsilon }. \end{aligned}$$

For $E_{2,2}$, because $R_{0}$ is a Calderón–Zygmund operator, the kernel $K_{0}(\cdot ,\cdot )$ satisfies

$$ \bigl\vert R_{0}(x,y)-R_{0}(x,x_{0}) \bigr\vert \leq C{ \vert y-x_{0} \vert } { \vert x-x_{0} \vert ^{-n-1}}. $$

We can get

$$\begin{aligned} E_{2,2} \leq &C \int _{B} \bigl\vert a(y) \bigr\vert \biggl( \int _{(B^{\sharp })^{c}} \vert x-x_{0} \vert ^{q(nb-n)}\,dx \biggr)^{{1}/{q}}\,dy \\ \leq &C r^{n+1-{n}/{q}} \biggl( \int ^{\infty }_{{2}/{m(x_{0},\mu )}}s ^{-(q-1)n-q+nbq-1}\,ds \biggr)^{{1}/{q}} \leq C{m(x_{0},\mu )}^{-n\varepsilon }. \end{aligned}$$

Finally, we obtain that

$$\begin{aligned} N_{L} \bigl((R_{\mathcal{L}}-R_{0})a \bigr) \leq &C{m(x_{0},\mu )}^{(n/{q}-{n})( {\varepsilon }/{b})}{m(x_{0},\mu )}^{n\varepsilon ({\varepsilon }/ {b}-1)}\leq C. \end{aligned}$$

 □