1 Introduction

More than sixty years ago, Lotka and Volterra laid the foundation for the science of competition between different species in [1, 2]. Over the several decades, considerable work has been done for N-species Lotka–Volterra (L-V) type systems to discuss their persistence, extinction, and global or local asymptotic behavior in [3,4,5,6,7,8,9,10,11,12,13,14,15,16]. For example,the interspecific competition has been observed based on the experiments in [4], partial persistence and extinction in N-dimensional competitive systems have been addressed in [6], and [7] shows a discrete delay decomposition approach to analyse stability of linear retarded and neutral systems. The permanence of stochastic L-V systems has been analyzed in [8,9,10,11,12]. In [13], sufficient and necessary conditions for permanence and extinction in a three-dimensional competitive L-V system have been proposed. In [14], a two species non-autonomous competitive phytoplankton system with Beddington–DeAngelis functional response has been proposed and sufficient conditions that guarantee the extinction of a species and global attractivity of the other one have been obtained. The stability analysis problem for competitive L-V system has also been one of the interesting research issues, and its global and local asymptotic stability problems have been sufficiently focused in [12, 14,15,16].

Considering the important influence of time delays on the system, there is considerable work on the persistence, extinction, and asymptotical stability of L-V competitive systems with delays in [3, 17,18,19,20,21,22,23,24]. For example, in [3] Teng has established the criteria under which a part of species is driven to extinction while other are persistent or all species are coexistent globally asymptotically stable. In [17], Oca and Pérez have extended the principle of competitive exclusion N-species nonautonomous L-V competition systems of differential equations with infinite delay, and in [18], Qiu and Deng have studied the optimal harvesting of a stochastic delay competitive L-V model with Lévy jumps systematically. For the stability analysis of time-delay systems, it has been identified that the Lyapunov–Krasovskii (L-K) theory based on the L-K functionals is less conservative than the Lyapunov–Razumikhin approach. By constructing some appropriate L-K functionals, the conditions for global or local asymptotic stability for competitive L-V systems with delays have been obtained in [3, 19,20,21,22,23,24]. By employing a linear matrix inequality (LMI) approach, a series of sufficient criteria which can ensure the stability of the positive equilibrium for the given L-V systems have been proposed in [22,23,24]. Specially, by using the LMI optimization approach, Park has obtained a stability criterion for the local stability of the positive equilibrium of the two-species L-V systems with discrete delays in [22]; Qiu and Cao have obtained sufficient criteria which guarantee the exponential stability of the same system in [23]; Sun and Meng have addressed the local asymptotic stability for the L-V system with time-varying delays in [24].

The integral terms are common in the derivative of L-K functionals, and the over-approximation methods are used to replace the integral terms with some more effective expressions. Unavoidably, the use of any inequalities will introduce some conservatism in the analysis and consequently in the resulting stability conditions. Over the past two decades, the inequality \(2ab\leq {a}^{2}+b^{2}\) has been used in [21], the inequality \(\sigma \int ^{\sigma }_{0}w(s)\,ds\geq [\int ^{\sigma } _{0}w(s)\,ds]^{2}\) has been adopted in [22] and [23], and Jensen’s inequality \([z(t)-z(t-\tau _{ij}(t))]^{T}W[z(t)-z(t-\tau _{ij}(t))] \leq {h}_{ij}\int ^{t}_{t-\tau _{ij}(t)}\dot{z}^{T}(s)W\dot{z}(s)\,ds\) has been employed in [24], respectively. The inherent conservative nature of these inequalities has led to some possible conservatism in the obtained conditions. Recently, the less conservative Wirtinger-based inequality has been proposed in [25, 26]. By incorporating augmented L-K functionals, some more effective stability conditions have been established for linear time-delay systems in [25, 26]. Unfortunately, for the competitive L-V system with time delays, the existing stability conditions are all based on the conservative inequalities and the simple L-K functionals. More importantly, the relationships between multiple delays are neglected in constructing the L-K functionals. Therefore, the existing results concerning the delayed L-V system are conservative to some extent, which motivates the present research.

In this paper, the following two-species competitive L-V system with time-varying delays is considered:

$$\begin{aligned} \textstyle\begin{cases} \frac{dx(t)}{dt}=x(t)[b_{1}-a_{11}x(t-\tau _{11}(t))-a_{12}y(t-\tau _{12}(t))], \\ \frac{dy(t)}{dt}=y(t)[b_{2}-a_{21}x(t-\tau _{21}(t))-a_{22}y(t-\tau _{22}(t))], \end{cases}\displaystyle \end{aligned}$$
(1)

where \(x(t)\) and \(y(t)\) stand for densities of both the populations at time t, respectively; \(b_{i}\), \(a_{ij}\) are positive scalars and \(0\leq \tau _{ij}(t)\leq {\tau }_{ij}\), \(\dot{\tau }_{ij}(t)\leq d_{ij}\) with \(d_{ij}\geq 0\), \(\tau _{ij}>0\) (\(i,j=1,2\)). The initial condition of system (1) is given as

$$\begin{aligned} \textstyle\begin{cases} x(s)=\phi _{1}(s)\geq 0,&-\tau \leq {s}\leq {0}, \phi _{1}(0)>0, \\ y(s)=\phi _{2}(s)\geq 0,&-\tau \leq {s}\leq {0}, \phi _{2}(0)>0, \end{cases}\displaystyle \end{aligned}$$
(2)

where \(\tau =\max_{1\leq i,j\leq 2}\{\tau _{ij}(t)\}\), and \(\phi _{1}(s)\), \(\phi _{2}(s)\) are assumed to be continuous.

If \({a_{11}/a_{21}}>b_{1}/b_{2}>a_{12}/a _{22}\), by denoting \(z^{*}=(x^{*},y^{*})\) with \(x^{*}=\frac{b_{1}a _{22}-b_{2}a_{12}}{a_{11}a_{22}-a_{12}a_{21}}\), \(y^{*}=\frac{b_{2}a _{11}-b_{1}a_{21}}{a_{11}a_{22}-a_{12}a_{21}}\), it is seen that \(x^{*},y^{*}\in (0,1)\). The four equilibrium points of system (1) are \((0,0)\), \((0,\frac{b_{2}}{a_{22}})\), \((\frac{b_{1}}{a_{11}},0)\), and \(z^{*}\) respectively. Define all positive solutions \(z(t)=(x(t),y(t))\) of system (1). The point \(z^{*}\) is the only one positive equilibrium point. The equilibrium point \(z^{*}\) indicates the coexistence of the two species.

In this paper, we are mainly concerned with the local stability problem of the positive equilibrium \(z^{*}\) of system (1). To reduce the possible conservatism in analyzing the stability of time-delay systems, this paper will choose the novel augmented L-K functionals and the less conservative integral inequalities in [26]. In particular, it should be pointed out that the second L-K functional proposed in this paper includes the cross terms between different time delays. The developed stability conditions in this paper are less conservative as compared with the existing ones in [22,23,24]. A numerical example shows the effectiveness and benefit of the proposed results.

Notation. The superscript “T” stands for the transpose of a matrix. The matrix \(R>0\) means that R is symmetric and positive definite, \(\mathbb{R}^{n}\) denotes the n-dimensional Euclidean space. In the paper, I and 0 are used to denote the identity and zero matrices with proper dimension. The symmetric terms in a symmetric matrix are denoted by ∗. In addition, we denote \(\mathbf{He}(A)=A+A^{T}\).

2 Preliminaries

Letting \(u(t)=x(t)-x^{*}\), \(v(t)=y(t)-y^{*}\), system (1) can be written as

$$\begin{aligned} \textstyle\begin{cases} \dot{u}(t)=[u(t)+{{x}^{*}}][-{{a}_{11}}u(t-{{\tau }_{11}(t)})-{{a} _{12}}v(t-{{\tau }_{12}(t)})], \\ \dot{v}(t)=[v(t)+{{y}^{*}}][-{{a} _{21}}u(t-{{\tau }_{21}(t)})-{{a}_{22}}v(t-{{\tau }_{22}(t)})], \end{cases}\displaystyle \end{aligned}$$
(3)

Correspondingly, the linearized model of (3) can be described by

$$\begin{aligned} \textstyle\begin{cases} \dot{u}(t)=-{{a}_{11}}{{x}^{*}}u(t-{{\tau }_{11}(t)})-{{a}_{12}}{{x} ^{*}}v(t-{{\tau }_{12}(t)}), \\ \dot{v}(t)=-{{a}_{21}}{{y} ^{*}}u(t-{{\tau }_{21}(t)})-{{a}_{22}}{{y}^{*}}v(t-{{\tau }_{22}(t)}). \end{cases}\displaystyle \end{aligned}$$
(4)

Let \({{z}^{T}}(t)=(u^{T}(t),v^{T}(t))\) and rewrite (4) in the following matrix form:

$$\begin{aligned} \dot{z}(t)&=-A_{11}z\bigl(t-\tau _{11}(t) \bigr)-A_{12}z\bigl(t-\tau _{12}(t)\bigr) \\ &\quad{}-A_{21}z\bigl(t-\tau _{21}(t)\bigr)-A_{22}z \bigl(t-\tau _{22}(t)\bigr), \end{aligned}$$
(5)

where

A 11 = [ a 11 x ∗ 0 0 0 ] , A 12 = [ 0 a 12 x ∗ 0 0 ] , A 21 = [ 0 0 a 21 y ∗ 0 ] , A 22 = [ 0 0 0 a 22 y ∗ ] .

The following lemma of Wirtinger-based integral inequality plays an important role in the proof of our main results

Lemma 1

([26])

For a given matrix \(R>0\), the following inequality holds for differentiable function \(w(t)\) in \([a,b]\rightarrow \)\({\mathbb{R}^{n}}\):

$$\begin{aligned} { \int ^{b}_{a}{\dot{w}}^{T}}(u)R{ \dot{w}}(u)\geq \frac{1}{b-a}\bigl(w(b)-w(a)\bigr)^{T}R \bigl(w(b)-w(a)\bigr)+ \frac{3}{b-a}\varOmega ^{T}R\varOmega , \end{aligned}$$
(6)

where \(\varOmega =w(b)+w(a)-\frac{2}{b-a}\int ^{b}_{a}w(u)\,du\).

3 Main results

In this section, by using the augmented L-K functionals and the Wirtinger-based integral inequality, one can obtain the following theorems for ensuring the local asymptotic stability of the L-V system (1). First of all, we will consider the case of constant delays, i.e., \(\tau _{ij}(t)=\tau _{ij}\) (\(t\geq 0\)).

Theorem 1

The positive equilibrium \({{z}^{*}}\) of the L-V system (1) with constant delays is locally asymptotically stable, if there exist \(10\times 10\)-dimensional matrix \(P_{1}>0\), \(2\times 2\)-dimensional matrices \({{Q}_{ij}}\ge 0\), \({{R}_{ij}}>0\), \(i,j=1,2\), such that the following LMI holds:

$$\begin{aligned} \psi _{1} =\mathbf{He} \bigl( F_{1}^{T}P_{1}{{F}_{0}} \bigr)+ \varGamma _{1}+\varUpsilon _{1}< 0, \end{aligned}$$
(7)

where \(\varGamma _{1}=\operatorname{diag} \{\sum_{i,j=1}^{2}{{{Q}_{ij}}},0,0,0,0,-Q _{11},-Q_{12},-Q_{21},-Q_{22} \}\) and

$$\begin{aligned} &{{F}_{1}}= \begin{bmatrix} I & 0&0&0&0 & 0&0&0&0 \\ 0 & I&0&0&0 & 0&0&0&0 \\ 0 & 0&I&0&0 & 0&0&0&0 \\ 0 & 0&0&I&0 & 0&0&0&0 \\ 0 & 0&0&0&I & 0&0&0&0 \end{bmatrix} , \\ &{{F}_{0}}= \begin{bmatrix} 0 & 0&0&0&0 & -A_{11}&-A_{12}&-A_{21}&-A_{22} \\ I & 0&0&0&0 & -I&0&0&0 \\ I & 0&0&0&0 & 0&-I&0&0\\ I & 0&0&0&0 & 0&0&-I&0\\ I & 0&0&0&0 & 0&0&0&-I \end{bmatrix} , \\ &\varUpsilon _{1}= \begin{bmatrix} \varLambda _{1}&\frac{6}{\tau _{11}}R_{11}&\frac{6}{\tau _{12}}R_{12}&\frac{6}{ \tau _{21}}R_{21}&\frac{6}{\tau _{22}}R_{22}&-2R_{11}&-2R_{12}&-2R_{21}&-2R _{22}\\ *&-\frac{12}{\tau _{11}^{2}}R_{11}&0&0&0&\frac{6}{\tau _{11}}R _{11}&0&0&0\\ *&*&-\frac{12}{\tau _{12}^{2}}R_{12}&0&0&0&\frac{6}{\tau _{12}}R_{12}&0&0\\ *&*&*&-\frac{12}{\tau _{21}^{2}}R_{21}&0&0&0&\frac{6}{ \tau _{21}}R_{21}&0\\ *&*&*&*&-\frac{12}{\tau _{22}^{2}}R_{22}&0&0&0&\frac{6}{ \tau _{22}}R_{22}\\ *&*&*&*&*&\varLambda _{2}&A_{12}^{T}\varSigma {A_{12}}&A _{21}^{T}\varSigma {A_{21}}&A_{22}^{T}\varSigma {A_{22}}\\ *&*&*&*&*&*& \varLambda _{3}&A_{21}^{T}\varSigma {A_{21}}&A_{22}^{T}\varSigma {A_{22}}\\ *&*&*&*&*&*&*& \varLambda _{4}&A_{22}^{T}\varSigma {A_{22}}\\ *&*&*&*&*&*&*&*&\varLambda _{5} \end{bmatrix} \end{aligned}$$

with

$$\begin{aligned} &\varLambda _{1}=-4(R_{11}+R_{12}+R_{21}+R_{22}), \qquad \varLambda _{2}=A_{11}^{T} \varSigma {A_{11}}-4R_{11}, \\ &\varLambda _{3}=A_{12}^{T}\varSigma {A_{12}}-4R_{12}, \qquad \varLambda _{4}=A_{21} ^{T}\varSigma {A_{21}}-4R_{21}, \\ &\varLambda _{5}=A_{22}^{T}\varSigma {A_{22}}-4R_{22}, \qquad \varSigma =\tau _{11} ^{2}R_{11}+\tau _{12}^{2}R_{12}+ \tau _{21}^{2}R_{21}+\tau _{22}^{2}R_{22}. \end{aligned}$$

Proof

Consider the following augmented L-K functional:

$$\begin{aligned} V(t)&= \bar{z}_{1}^{T}(t) P_{1} \bar{z}_{1}(t)+\sum_{i,j=1}^{2}{ \int ^{t}_{t- \tau _{ij}}}z^{T}(s){Q}_{ij}z(s)\,ds \\ &\quad{}+{\sum_{i,j=1}^{2}\tau _{ij}} { \int ^{t}_{t-\tau _{ij}}} { \int ^{t}_{ \theta }}\dot{z}^{T}(s)R_{ij} \dot{z}(s)\,ds \,d\theta , \end{aligned}$$
(8)

where \(\bar{z}_{1}(t)= [z^{T}(t),\int ^{t}_{t-\tau _{11}}z^{T}(s)\,ds,\int ^{t}_{t-\tau _{12}}z^{T}(s)\,ds,\int ^{t}_{t-\tau _{21}}z^{T}(s)\,ds,\int ^{t}_{t-\tau _{22}}z^{T}(s)\,ds ]^{T}\).

Clearly, functional (8) is positive since \(P_{1}>0\), \({{Q}_{ij}}>0\), and \({{R}_{ij}}>0\). Denoting that \(\xi _{1}(t)=[\bar{z}_{1}^{T}(t),z^{T}(t- \tau _{11}),z^{T}(t-\tau _{12}),z^{T}(t-\tau _{21}),z^{T}(t-\tau _{22})]^{T}\), we have

$$\begin{aligned} \bar{z}_{1}(t)={{F}_{1}}\xi _{1} ( t ), \qquad \dot{ \bar{z}}_{1}(t)= {{F}_{0}}\xi _{1} ( t ). \end{aligned}$$
(9)

Considering the derivative of \(V ( t )\) along system (5), we have

$$\begin{aligned} \dot{V}(t)&= \xi _{1}^{T}(t)\mathbf{He} \bigl(F^{T}_{1}P_{1}F_{0}\bigr)\xi _{1}(t)+ {{z}^{T}}(t) \Biggl( \sum _{i,j=1}^{2}{{{Q}_{ij}}} \Biggr)z(t) \\ & \quad {}-\sum_{i,j=1}^{2}{{{z}^{T}}( t-{{\tau }_{ij}} )} {{Q}_{ij}}z( t-{{\tau } _{ij}}) +\dot{z}^{T}(t) \Biggl(\sum^{2}_{i,j=1} \tau ^{2}_{ij}R_{ij} \Biggr)\dot{z}(t) \\ &\quad{}-\sum^{2}_{i,j=1}\tau _{ij} \int ^{t}_{t-\tau _{ij}}\dot{z}^{T}(s)R_{ij} \dot{z}(s)\,ds. \end{aligned}$$
(10)

By using Lemma 1, it follows that

$$\begin{aligned} \dot{V}(t)&\leq \xi _{1}^{T}(t)\mathbf{He} \bigl(F^{T}_{1}P_{1}F _{0}\bigr)\xi _{1}(t)+{{z}^{T}}(t) \Biggl( \sum _{i,j=1}^{2}{{{Q}_{ij}}} \Biggr)z(t) \\ &\quad{}-\sum_{i,j=1}^{2}{{{z}^{T}}( t-{{ \tau }_{ij}} )} {{Q}_{ij}}z( t- {{\tau }_{ij}}) \\ &\quad{}+ \Biggl[\sum^{2}_{i,j=1}A_{ij}z(t- \tau _{ij}) \Biggr]^{T} \Biggl(\sum ^{2} _{i,j=1}\tau _{ij}^{2}R_{ij} \Biggr) \Biggl[\sum^{2}_{i,j=1}A_{ij}z(t- \tau _{ij}) \Biggr] \\ &\quad{}-\sum^{2}_{i,j=1} \biggl\{ \bigl[z(t-\tau _{ij})-z(t) \bigr]^{T}R_{ij} \bigl[z(t-\tau _{ij})-z(t) \bigr] \\ &\quad{}-3 \biggl[z(t-\tau _{ij})+z(t)-\frac{2}{\tau _{ij}} \int ^{t}_{t-\tau _{ij}}z(s)\,ds \biggr]^{T}R_{ij} \\ &\quad {}\times \biggl[z(t-\tau _{ij})+z(t)-\frac{2}{\tau _{ij}} \int ^{t}_{t- \tau _{ij}}z(s)\,ds \biggr] \biggr\} \\ &=\xi _{1}^{T}(t)\psi _{1}\xi _{1}(t), \end{aligned}$$

where \(\psi _{1}\) is defined in (7). If LMI (7) is satisfied, we have \(\dot{V}(t)\leq {{\xi }_{1}^{T}} ( t )\psi _{1} \xi _{1} (t )<0\) and the proof of Theorem 1 is complete. □

Remark 1

Note that if LMI (7) is true, it follows that \(\dot{V} ( t )\le -\lambda {{ \Vert z ( t ) \Vert }^{2}}\), where \(\lambda >0\) is the minimal eigenvalue of the matrix \(-\psi _{1} \). This implies that system (5) is asymptotically stable. Then it can be concluded that the positive equilibrium \(z^{*}\) of the L-V system (1) is locally asymptotically stable.

Remark 2

In [22,23,24], an LMI-based approach has been used to address the stability problem of systems (1), and some significant results have been obtained. However, it is worth mentioning that the proposed conditions are conservative since the chosen L-K functional is simple and the adopted inequalities are conservative. Compared with the approaches used in [22,23,24], this paper has utilized more accurate Wirtinger inequality to estimate the upper bound of the derivative of L-K functional (8). In particular, it is noted that some augmented terms have been added in the L-K functional (8) to use Wirtinger inequality effectively.

Theorem 2

The positive equilibrium \({{z}^{*}}\) of the L-V system (1) with constant delays is locally asymptotically stable if there exist \(22\times 22\)-dimensional matrix \(P_{2}>0\), \(2\times 2\)-dimensional matrices \(Q_{ij}^{kl}\ge 0\) and \(R_{ij}^{kl}>0 \), (\(i,j,k,l=1,2\)) such that the following LMI holds:

$$\begin{aligned} \psi _{2}=\mathbf{He} \bigl( \tilde{F}_{1}^{T}P_{2}{{{ \tilde{F}}} _{0}} \bigr)+\varGamma _{2}+\varUpsilon _{2}< 0, \end{aligned}$$
(11)

where

$$\begin{aligned} &\tilde{F}_{1}= \begin{bmatrix} F_{1}&0_{10\times {12}}\\0_{12\times {18}}&\varXi \end{bmatrix} , \qquad \tilde{F}_{0}= \begin{bmatrix} F_{0}&0_{10\times {12}}\\\tilde{\varOmega }&\varXi \end{bmatrix} , \\ &\varGamma _{2}= \begin{bmatrix} \varGamma _{1}&0_{{18}\times {12}}\\0_{{12}\times {18}}&0_{12\times 12} \end{bmatrix} + \operatorname{diag}\{0_{10\times 10},\bar{Q},0_{12\times 12}\}, \\ &\varUpsilon _{2}= \begin{bmatrix} \varUpsilon _{1}&0_{18\times 12}\\0_{12\times 18}&0_{12\times 12} \end{bmatrix} + \begin{bmatrix} 0_{10\times 10}&0_{10\times 8}&0_{10\times 12}\\ *&\varPhi _{1}-2\varPhi _{2}&6 \varPhi _{3}\\ *&*&-12\varPhi _{4} \end{bmatrix} , \end{aligned}$$

with \(F_{0}\), \(F_{1}\), \(\varGamma _{1}\), \(\varUpsilon _{1}\) denoted in Theorem 1 and

$$\begin{aligned}& \tilde{\varOmega }= \begin{bmatrix} 0&0&0&0&0&-I&I&0&0\\ 0&0&0&0&0&-I&0&I&0\\ 0&0&0&0&0&-I&0&0&I\\ 0&0&0&0&0&0&-I&I&0 \\ 0&0&0&0&0&0&-I&0&I\\ 0&0&0&0&0&0&0&-I&I \end{bmatrix} , \\& \begin{aligned} \bar{Q}&=-\operatorname{diag} \Biggl\{ \sum_{k,l=1}^{2}({{ \tau }_{11}}-{{\tau } _{kl}})Q_{11}^{kl}, \sum_{k,l=1}^{2}( {{\tau }_{12}}-{{ \tau } _{kl}})Q_{12}^{kl}, \\ &\quad \sum_{k,l=1}^{2}( {{\tau }_{21}}-{{\tau }_{kl}})Q_{21}^{kl}, \sum _{k,l=1}^{2}( {{\tau }_{22}}-{{\tau }_{kl}} )Q_{22}^{kl} \Biggr\} , \end{aligned} \\& \begin{aligned} \varXi &=\operatorname{diag}\bigl\{ (\tau _{11}-\tau _{12})I,( \tau _{11}-\tau _{21})I,(\tau _{11}- \tau _{22})I, \\ &\quad (\tau _{12}-\tau _{21})I,(\tau _{12}-\tau _{22})I,(\tau _{21}-\tau _{22})I \bigr\} , \end{aligned} \\& \varPhi _{1}= \begin{bmatrix} A^{T}_{11}\tilde{\varSigma }A_{11}&A^{T}_{11}\tilde{\varSigma }A_{12}&A^{T} _{11}\tilde{\varSigma }A_{21}&A^{T}_{11}\tilde{\varSigma }A_{22}\\ *&A^{T} _{12}\tilde{\varSigma }A_{12}&A^{T}_{12}\tilde{\varSigma }A_{21}&A^{T}_{12} \tilde{\varSigma }A_{22}\\ *&*&A^{T}_{21}\tilde{\varSigma }A_{21}&A^{T}_{21} \tilde{\varSigma }A_{22}\\ *&*&*&A^{T}_{22}\tilde{\varSigma }A_{22} \end{bmatrix} , \\& \varPhi _{2}= \begin{bmatrix} \varPhi _{21}& R_{11}^{12} & R_{11}^{21} & R_{11}^{22} \\ * & \varPhi _{22} & R_{12}^{21} & R_{12}^{22} \\ * & * & \varPhi _{23}& R_{21}^{22} \\ * & * & * & \varPhi _{24} \end{bmatrix} , \\& \varPhi _{3}= \begin{bmatrix} R_{11}^{12} & R_{11}^{21} & R_{11}^{22} & 0 & 0 & 0 \\ R_{11}^{12} & 0 & 0 & R_{12}^{21} & R_{12}^{22} & 0 \\ 0 & R_{11}^{21} & 0 & R_{12} ^{21} & 0 & R_{21}^{22} \\ 0 & 0 & R_{11}^{22} & 0 & R_{12}^{22} & R _{21}^{22} \end{bmatrix} , \\& \varPhi _{4}=\operatorname{diag}\bigl\{ R_{11}^{12},R_{11}^{21},R_{11}^{22},R_{12}^{21},R _{12}^{22},R_{21}^{22}\bigr\} , \\& \tilde{\varSigma }=\sum_{i,j=1}^{2}\sum _{k,l=1}^{2}(\tau _{ij}-\tau _{kl})^{2}R^{kl}_{ij} \quad (10i+j< 10k+l), \\& \varPhi _{21}=2\bigl(R_{11}^{12}+R_{11}^{21}+R_{11}^{22} \bigr), \qquad \varPhi _{22}=2\bigl(R_{11} ^{12}+R_{12}^{21}+R_{12}^{22} \bigr), \\& \varPhi _{23}=2\bigl(R_{11}^{21}+R_{12}^{21}+R_{21}^{22} \bigr),\qquad \varPhi _{24}=2\bigl( R _{11}^{22}+R_{12}^{22}+R_{21}^{22} \bigr). \end{aligned}$$

Proof

Let us define the following novel augmented L-K functional:

$$\begin{aligned} \tilde{V} ( t )=V_{1}(t)+V_{2}(t)+V_{3}(t), \end{aligned}$$
(12)

where

$$\begin{aligned}& \begin{aligned} V_{1}(t)&= {\bar{z}_{2}^{T}}(t)P_{2} \bar{z}_{2}( t )+\sum_{i,j=1}^{2}{ \int ^{t} _{t-\tau _{ij}}}z^{T}(s){Q}_{ij}z(s)\,ds \\ &\quad{}+{\sum_{i,j=1}^{2}\tau _{ij}} { \int ^{t}_{t-\tau _{ij}}} { \int ^{t}_{ \theta }}\dot{z}^{T}(s)R_{ij} \dot{z}(s)\,ds \,d\theta , \end{aligned} \\& V_{2}(t)=\sum^{2}_{i,j=1}\sum ^{2}_{k,l=1}(\tau _{ij}-\tau _{kl}) \int ^{t-\tau _{kl}}_{t-\tau _{ij}}z^{T}(s)Q^{kl}_{ij}z(s)\,ds \quad (10i+j< 10k+l), \\& \begin{aligned} V_{3}(t)&= \sum^{2}_{i,j=1} \sum^{2}_{k,l=1}(\tau _{ij}-\tau _{kl}) \int ^{-\tau _{kl}} _{-\tau _{ij}} \int ^{t}_{t+\theta }\dot{z}^{T}(s)R^{kl}_{ij} \dot{z}(s)\,ds \,d \theta \\ & \quad (10i+j< 10k+l), \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \tilde{z}_{2}(t)&= \biggl[\bar{z}_{1}^{T}(t) ,\int ^{t-\tau _{12}}_{t-\tau _{11}}z^{T}(s)\,ds ,\int ^{t-\tau _{21}}_{t-\tau _{11}}z^{T}(s)\,ds ,\int ^{t-\tau _{22}}_{t-\tau _{11}}z^{T}(s)\,ds,\\ & \quad \int ^{t-\tau _{21}}_{t-\tau _{12}}z^{T}(s)\,ds ,\int ^{t-\tau _{22}}_{t-\tau _{12}}z^{T}(s)\,ds ,\int ^{t-\tau _{22}}_{t-\tau _{21}}z^{T}(s)\,ds \biggr]^{T}. \end{aligned}$$

Letting

$$\begin{aligned} {\xi }_{2}(t)&= \biggl[\xi _{1}^{T}(t) ,\frac{1}{\tau _{11}-\tau _{12}} \int ^{t-\tau _{12}}_{t-\tau _{11}}z^{T}(s)\,ds ,\frac{1}{\tau _{11}-\tau _{21}} \int ^{t-\tau _{21}}_{t-\tau _{11}}z^{T}(s)\,ds,\\ &\quad \frac{1}{\tau _{11}-\tau _{22}} \int ^{t-\tau _{22}}_{t-\tau _{11}}z^{T}(s)\,ds ,\frac{1}{\tau _{12}-\tau _{21}} \int ^{t-\tau _{21}}_{t-\tau _{12}}z^{T}(s)\,ds,\\ &\quad \frac{1}{\tau _{12}-\tau _{22}},\int ^{t-\tau _{22}}_{t-\tau _{12}}z^{T}(s)\,ds ,\frac{1}{\tau _{21}-\tau _{22}} \int ^{t-\tau _{22}}_{t-\tau _{21}}z^{T}(s)\,ds \biggr]^{T}, \end{aligned}$$

it is seen that \(\tilde{z}_{2}(t)={\tilde{{F}}_{1}}\xi _{2} ( t )\), \(\dot{\tilde{z}}_{2}(t)={\tilde{{F}}_{0}}\xi _{2} ( t )\). Computing the derivative of (12) along the solution of system (5), it follows that

$$\begin{aligned} &\begin{aligned}[b] \dot{V_{1}}(t)&= {\xi _{2}^{T}(t) \mathbf{He}}\bigl(\tilde{F}_{0}^{T}P_{2}\tilde{F} _{1}\bigr)\xi _{2}(t)+{{z}^{T}(t)} \Biggl( \sum _{i,j=1}^{2}{{{Q}_{ij}}} \Biggr)z(t) \\ & \quad {}-\sum_{i,j=1}^{2}{{{z}^{T}}( t-{{\tau }_{ij}} )} {{Q}_{ij}}z( t-{{\tau } _{ij}}) +\dot{z}^{T}(t) \Biggl(\sum^{2}_{i,j=1} \tau ^{2}_{ij}R_{ij} \Biggr)\dot{z}(t) \\ &\quad{}-\sum^{2}_{i,j=1}\tau _{ij} \int ^{t}_{t-\tau _{ij}}\dot{z}^{T}(s)R_{ij} \dot{z}(s)\,ds, \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned} &\begin{aligned}[b] \dot{V}_{2}(t)&= \sum^{2}_{i,j=1} \sum^{2}_{k,l=1}(\tau _{ij}-\tau _{kl}) \bigl[z^{T}(t- \tau _{kl})Q^{kl}_{ij}z(t- \tau _{kl}) \\ &\quad{}-z^{T}(t-\tau _{ij})Q^{kl}_{ij}z(t-\tau _{ij}) \bigr] \quad (10i+j< 10k+l), \end{aligned} \end{aligned}$$
(14)
$$\begin{aligned} &\begin{aligned}[b] \dot{V}_{3}(t)&= \sum^{2}_{i,j=1} \sum^{2}_{k,l=1}(\tau _{ij}-\tau _{kl}) \biggl[(\tau _{ij}- \tau _{kl}) \dot{z}^{T}(t)R^{kl}_{ij}\dot{z}(t) \\ &\quad{}- \int ^{t-\tau _{kl}}_{t-\tau _{ij}}\dot{z}^{T}(s)R^{kl}_{ij} \dot{z}(s)\,ds \biggr] \quad (10i+j< 10k+l). \end{aligned} \end{aligned}$$
(15)

Applying Lemma 1 to \(\dot{V}_{3}(t)\), it follows that

$$\begin{aligned} \dot{V}_{3}(t)&\leq \sum^{2}_{i,j=1} \sum^{2}_{k,l=1} \biggl\{ (\tau _{ij}- \tau _{kl})^{2} \dot{z}^{T}(t)R^{kl}_{ij} \dot{z}(t) \\ & \quad {}- \bigl[z(t-\tau _{kl})-z(t-\tau _{ij}) \bigr]^{T}{R}^{kl}_{ij} \bigl[z(t- \tau _{kl})-z(t-\tau _{ij}) \bigr] \\ & \quad {}-3 \biggl[z(t-\tau _{kl})+z(t-\tau _{ij})- \frac{2}{(\tau _{ij}-\tau _{kl})} \int ^{t-\tau _{kl}}_{t-\tau _{ij}}z(s)\,ds \biggr]^{T}R^{kl}_{ij} \\ & \quad {}\times \biggl[z(t-\tau _{kl})+z(t-\tau _{ij})- \frac{2}{(\tau _{ij}-\tau _{kl})} \int ^{t-\tau _{kl}}_{t-\tau _{ij}}z(s)\,ds \biggr] \biggr\} \\ & \quad (10i+j< 10k+l). \end{aligned}$$
(16)

Based on \({{\dot{V}}_{1}}(t)\), \({\dot{V}}_{2}(t)\), \({{\dot{V}}_{3}}(t)\), and inequality (16), we can eventually obtain

$$\begin{aligned} \dot{\tilde{V}}(t)=\dot{V}_{1}(t)+\dot{V}_{2}(t)+ \dot{V}_{3}(t)\le {\xi _{2}^{T}} ( t ){\psi _{2} }\xi _{2} ( t ). \end{aligned}$$
(17)

This implies that the positive equilibrium \({{z}^{*}}\) of the L-V system (1) is locally asymptotically stable if LMI (11) is satisfied. The proof of Theorem 2 is complete. □

Remark 3

Compared with the L-K functional (8) used in the proof of Theorem 1, some interconnected terms related to four time delays have been further incorporated in functional (12). By using such interconnected terms, the relationships between four time delays can be specifically reflected in the L-K functional (12). Then, a less conservative condition involving more slack variables is obtained for the case with different delays, which will be illustrated by a numerical example.

Next, we will address the L-V system (1) with time-varying delays.

Theorem 3

The positive equilibrium \({{z}^{*}}\) of the L-V system (1) with time-varying delays is locally asymptotically stable if there exist \(10\times 10\)-dimensional matrix \({P}_{1}>0\), \(2\times 2\)-dimensional matrices \({{Q}_{ij}}\ge 0\), \({{R}_{ij}}>0\), \(S_{ij}>0\), \(T_{ij}>0\), \(i,j=1,2\), such that the following LMI holds:

$$\begin{aligned} \psi _{3}&= \begin{bmatrix} \tilde{\psi _{1}}&0_{18\times {8}}\\ 0_{8\times {18}}&\varUpsilon _{3}\end{bmatrix}+\varGamma _{3}+ \mathbf{He}\bigl(\hat{F}^{T}_{1}P_{1} \hat{F}_{0}\bigr) \\ &\quad{}+ \begin{bmatrix} -\sum_{i,j=1}^{2}T_{ij}&0_{2\times 8}&0_{2\times 8}&\varPi _{1}\\ *&0_{8\times 8}&0_{8\times 8}&0_{8\times 8}\\ *&*&-\varPi _{2}&\varPi _{2}\\ *&*&*&-2\varPi _{2} \end{bmatrix} \\ &< 0, \end{aligned}$$
(18)

where

$$\begin{aligned} &\begin{aligned} \varGamma _{3}&=\operatorname{diag} \Biggl\{ \sum _{i,j=1}^{2}{S_{ij}},0_{16\times 16},-(1-d_{11})S_{11},-(1-d_{12})S_{12}, \\ &\quad{}-(1-d_{21})S_{21},-(1-d_{22})S_{22} \Biggr\} , \end{aligned} \\ &\hat{F}_{0}= \begin{bmatrix} 0_{2\times 2}&0_{2\times 8}&0_{2\times 8}&\hat{F}_{02}\\ \hat{F}_{01}&0_{8\times 8}&\hat{F}_{03}&0_{8\times 8}\end{bmatrix}, \qquad \hat{F}_{1}= \begin{bmatrix} {F}_{1}&0_{10\times 8}\end{bmatrix}, \\ &\tilde{\psi _{1}}=\psi _{1}- \mathbf{He} \bigl(F^{T}_{1}P_{1}F_{0}\bigr)- \begin{bmatrix} 0_{10\times 10}&0_{10\times 8}\\0_{8\times 10}&\varPi _{4} \end{bmatrix}, \\ &\varUpsilon _{3}= \begin{bmatrix} A^{T}_{11}\hat{\varSigma } A_{11}&A^{T}_{11}\hat{\varSigma } A_{12}&A^{T}_{11}\hat{\varSigma } A_{21}&A^{T}_{11}\hat{\varSigma } A_{22}\\ *&A^{T}_{12}\hat{\varSigma } A_{12}&A^{T}_{12}\hat{\varSigma } A_{21}&A^{T}_{12}\hat{\varSigma } A_{22}\\ *&*&A^{T}_{21}\hat{\varSigma } A_{21}&A^{T}_{21}\hat{\varSigma } A_{22}\\ *&*&*&A^{T}_{22}\hat{\varSigma } A_{22} \end{bmatrix}, \\ &\varPi _{1}= \begin{bmatrix} T_{11}&T_{12}&T_{21}&T_{22}\end{bmatrix}, \qquad \varPi _{2}= \operatorname{diag}\{T_{11},T_{12},T_{21},T_{22} \} \end{aligned}$$

with

$$\begin{aligned} &\hat{F}_{01}= \begin{bmatrix}I&I&I&I\end{bmatrix}^{T},\qquad \hat{F}_{02}= \begin{bmatrix}-A_{11}&-A_{12}&-A_{21}&-A_{11}\end{bmatrix}, \\ &\hat{F}_{03}=-\operatorname{diag}\{I,I,I,I\},\qquad \hat{\varSigma }=\sum _{i,j=1}^{2}\bigl[\tau ^{2}_{ij}({T_{ij}}+R_{ij}) \bigr], \\ &\varPi _{4}= \begin{bmatrix}A^{T}_{11}\varSigma A_{11}&A^{T}_{11}\varSigma A_{12}&A^{T}_{11}\varSigma A_{21}&A^{T}_{11}\varSigma A_{22}\\ *&A^{T}_{12}\varSigma A_{12}&A^{T}_{12}\varSigma A_{21}&A^{T}_{12}\varSigma A_{22}\\ *&*&A^{T}_{21}\varSigma A_{21}&A^{T}_{21}\varSigma A_{22}\\&*&*&A^{T}_{22}\varSigma A_{22}\end{bmatrix}. \end{aligned}$$

Proof

Consider the following augmented L-K functional:

$$\begin{aligned} \hat{V}(t)&= V(t)+\sum_{i,j=1}^{2} \int ^{t}_{t-\tau _{ij}(t)}z^{T}(s){S}_{ij}z(s)\,ds \\ &\quad{}+{\sum_{i,j=1}^{2}\tau _{ij}} \int ^{t}_{t-\tau _{ij}} \int ^{t}_{\theta }\dot{z}^{T}(s)T_{ij} \dot{z}(s)\,ds \,d\theta , \end{aligned}$$
(19)

where \(V(t)\) is denoted in (8). Considering the derivative of \(\hat{V}(t)\) and denoting \(\xi _{3}(t)=[\xi _{1}^{T}(t),z^{T}(t-\tau _{11}(t)),z^{T}(t-\tau _{12}(t)),z^{T}(t-\tau _{21}(t)),z^{T}(t-\tau _{22}(t))]^{T}\), we have

$$\begin{aligned} \dot{\hat{V}}(t)&\leq \xi _{3}^{T}(t)\mathbf{He} \bigl(\hat{F}^{T}_{1}{P}_{1}\hat{F}_{0} \bigr)\xi _{3}(t)+z^{T}(t)\sum_{i,j=1}^{2}(Q_{ij}+S_{ij})z(t) \\ & \quad {}+\dot{z}^{T}(t)\sum^{2}_{i,j=1} \tau ^{2}_{ij}(R_{ij}+T_{ij})\dot{z}(t)- \sum_{i,j=1}^{2}{{{z}^{T}}( t-{{\tau }_{ij}} )} {{Q}_{ij}}z( t-{{\tau }_{ij}}) \\ &\quad {} -\sum_{i,j=1}^{2}(1-d_{ij}){{{z}^{T}} \bigl( t-{{\tau }_{ij}(t)} \bigr)} {{S}_{ij}}z\bigl( t-{{\tau }_{ij}(t)}\bigr) \\ &\quad{}-\sum^{2}_{i,j=1}\tau _{ij} \int ^{t}_{t-\tau _{ij}}\dot{z}^{T}(s) (R_{ij}+T_{ij})\dot{z}(s)\,ds. \end{aligned}$$
(20)

For the term \(-\sum_{i,j=1}^{2}\tau _{ij}\int ^{t}_{t-\tau _{ij}}\dot{z}^{T}(s)R_{ij}\dot{z}(s)\,ds\), we use Lemma 1. While for the term \(-\sum_{i,j=1}^{2}\tau _{ij}\int ^{t}_{t-\tau _{ij}}\dot{z}^{T}(s)T_{ij}\dot{z}(s)\,ds\), by using Jensen’s inequality, it is seen that

$$\begin{aligned} & -\sum_{i,j=1}^{2}\tau _{ij} \int ^{t}_{t-\tau _{ij}}\dot{z}^{T}(s)T_{ij} \dot{z}(s)\,ds \\ &\quad \leq -\sum_{i,j=1}^{2} \biggl( \int ^{t}_{t-\tau _{ij}(t)}\dot{z}(s)\,ds \biggr)^{T} T_{ij} \biggl( \int ^{t}_{t-\tau _{ij}(t)}\dot{z}(s)\,ds \biggr) \\ & \qquad {}-\sum_{i,j=1}^{2} \biggl( \int ^{t-\tau _{ij}(t)}_{t-\tau _{ij}}\dot{z}(s)\,ds \biggr)^{T}T_{ij} \biggl( \int ^{t-\tau _{ij}(t)}_{t-\tau _{ij}}\dot{z}(s)\,ds \biggr) \\ &\quad \leq -\sum_{i,j=1}^{2}\bigl[z(t)-z \bigl(t-\tau _{ij}(t)\bigr)\bigr]^{T}T_{ij} \bigl[z(t)-z\bigl(t-\tau _{ij}(t)\bigr)\bigr] \\ &\qquad{}-\sum_{i,j=1}^{2}\bigl[z\bigl(t-\tau _{ij}(t)\bigr)-z(t-\tau _{ij})\bigr]^{T}T_{ij} \bigl[z\bigl(t-\tau _{ij}(t)\bigr)-z(t-\tau _{ij})\bigr]. \end{aligned}$$
(21)

Noting (20)–(21) and \(\psi _{3}\) defined in (18), it is easy to verify that if LMI (18) is satisfied, the inequality \(\dot{\hat{V}}(t)\leq {{\xi }_{3}^{T}}(t)\psi _{3}\xi _{3}(t)<0\) can be ensured, and this completes the proof. □

Corresponding to Theorem 2, the following improved condition is readily obtained.

Theorem 4

The positive equilibrium \(z^{*}\) of the L-V system (1) with time-varying delays is locally asymptotically stable if there exist \(22\times 22\)-dimensional matrix \({P}_{2}>0\), \(2\times 2\)-dimensional matrices \({{Q}_{ij}}\ge 0\), \({{R}_{ij}}>0\), \(S_{ij}>0\), \(T_{ij}>0\), \(i,j=1,2\), such that the following LMI holds:

$$\begin{aligned} \psi _{4}&= \begin{bmatrix}\tilde{\psi _{2}}&0_{30\times {8}}\\0_{8\times {30}}&\varUpsilon _{4}\end{bmatrix}+\varGamma _{4}+ \mathbf{He}\bigl(\vec{{F}}^{T}_{1}P_{2} \vec{{F}}_{0}\bigr) \\ &\quad{}+ \begin{bmatrix} 0_{2\times 2}&0_{2\times 8}&0_{2\times 8}&0_{2\times 12}&\varUpsilon _{5}\\ *&0_{8\times 8}&0_{8\times 8}&0_{8\times 12}&0_{8\times 8}\\ *&*&-\varUpsilon _{6}&0_{8\times 12}&\varUpsilon _{6}\\ *&*&*&0_{12\times 12}&0_{12\times 8}\\ *&*&*&*&-2\varUpsilon _{6} \end{bmatrix} \\ &< 0, \end{aligned}$$
(22)

where

$$\begin{aligned}& \begin{aligned} \varGamma _{4}&=\operatorname{diag} \Biggl\{ \sum_{i,j=1}^{2}({S_{ij}-T_{ij}}),0_{28\times 28},-(1-d_{11})S_{11}, \\ &\quad{}-(1-d_{12})S_{12},-(1-d_{21})S_{21},-(1-d_{22})S_{22} \Biggr\} , \end{aligned} \\& \vec{F}_{0}= \begin{bmatrix} 0_{2\times 2}&0_{2\times 8}&0_{2\times 8}&0_{2\times 12}&\hat{F}_{02}\\ \hat{F}_{01}&0_{8\times 8}&\hat{F}_{03}&0_{8\times 12}&0_{8\times 8}\\ 0_{12\times 2}&0_{12\times 8}&\hat{F}_{04}&\varXi &0_{12\times 8}\end{bmatrix}, \qquad \vec{F}_{1}= \begin{bmatrix}\tilde{F}_{1}&0_{22\times 8}\end{bmatrix}, \\& \tilde{\psi _{2}}=\psi _{2}-\mathbf{He}\bigl( \tilde{F}_{1}^{T}P_{2}\tilde{F}_{0} \bigr)- \begin{bmatrix} 0_{10\times 10}&0_{10\times 8}&0_{10\times 12}\\0_{8\times 10}&\varUpsilon _{7}&0_{8\times 12}\\0_{12\times 10}&0_{12\times 8}&0_{12\times 12} \end{bmatrix}, \\& \varUpsilon _{4}= \begin{bmatrix} A^{T}_{11}\vec{\varSigma }_{1}A_{11}&A^{T}_{11}\vec{\varSigma }_{1}A_{12}&A^{T}_{11}\vec{\varSigma }_{1}A_{21}&A^{T}_{11}\vec{\varSigma }_{1}A_{22}\\ *&A^{T}_{12}\vec{\varSigma }_{1}A_{12}&A^{T}_{12}\vec{\varSigma }_{1}A_{21}&A^{T}_{12}\vec{\varSigma }_{1}A_{22}\\ *&*&A^{T}_{21}\vec{\varSigma }_{1}A_{21}&A^{T}_{21}\vec{\varSigma }_{1}A_{22}\\ *&*&*&A^{T}_{22}\vec{\varSigma }_{1}A_{22}\end{bmatrix}, \\& \varUpsilon _{5}= \begin{bmatrix}T_{11}&T_{12}&T_{21}&T_{22} \end{bmatrix}, \qquad \varUpsilon _{6}= \operatorname{diag}\{T_{11},T_{12},T_{21},T_{22} \} \end{aligned}$$

with

$$\begin{aligned}& \hat{F}_{04}= \begin{bmatrix}-I&-I&-I&0&0&0\\I&0&0&-I&-I&0\\0&I&0&I&0&-I\\0&0&I&0&I&I\end{bmatrix}^{T}, \\& \varUpsilon _{7}= \begin{bmatrix} A^{T}_{11}\vec{\varSigma }_{2}A_{11}&A^{T}_{11}\vec{\varSigma }_{2}A_{12}&A^{T}_{11}\vec{\varSigma }_{2}A_{21}&A^{T}_{11}\vec{\varSigma }_{2}A_{22}\\ *&A^{T}_{12}\vec{\varSigma }_{2}A_{12}&A^{T}_{12}\vec{\varSigma }_{2}A_{21}&A^{T}_{12}\vec{\varSigma }_{2}A_{22}\\ *&*&A^{T}_{21}\vec{\varSigma }_{2}A_{21}&A^{T}_{21}\vec{\varSigma }_{2}A_{22}\\ *&*&*&A^{T}_{22}\vec{\varSigma }_{2}A_{22}\end{bmatrix}, \\& \vec{\varSigma }_{1}=\sum_{i,j=1}^{2} \tau ^{2}_{ij}(T_{ij}+R_{ij})+\sum _{i,j=1}^{2}\sum_{k,l=1}^{2}( \tau _{ij}-\tau _{kl})^{2}R_{ij}^{kl} \quad (10i+j< 10k+l), \\& \vec{\varSigma }_{2}=\sum_{i,j=1}^{2} \tau ^{2}_{ij}R_{ij}+\sum _{i,j=1}^{2}\sum_{k,l=1}^{2}( \tau _{ij}-\tau _{kl})^{2}R_{ij}^{kl} \quad (10i+j< 10k+l). \end{aligned}$$

Proof

Let us define the following novel augmented L-K functional:

$$\begin{aligned} \vec{V}(t)&=\tilde{V}(t)+\sum_{i,j=1}^{2}{ \int ^{t}_{t-\tau _{ij}(t)}}z^{T}(s){S}_{ij}z(s)\,ds \\ &\quad{}+{\sum_{i,j=1}^{2}\tau _{ij}} { \int ^{t}_{t-\tau _{ij}}} { \int ^{t}_{\theta }}\dot{z}^{T}(s)T_{ij} \dot{z}(s)\,ds \,d\theta , \end{aligned}$$
(23)

where \(\tilde{V}(t)\) is defined in functional (12). The subsequent arguments are similar to the proofs of Theorems 2–3 and thus are omitted here. □

4 Numerical example

In this section, let us consider the numerical example given in Zhen and Ma [21] and Park [22] to illustrate the effectiveness and the sharpness of our results.

Example

Consider the following system:

$$\begin{aligned} \textstyle\begin{cases} \frac{dx(t)}{dt}=x(t)[1-x(t-\tau _{11}(t))-0.5y(t-\tau _{12}(t))], \\ \frac{dy(t)}{dt}=y(t)[1-0.5x(t-\tau _{21}(t))-y(t-\tau _{22}(t))]. \end{cases}\displaystyle \end{aligned}$$
(24)

For the case that \(\tau _{ij}(t)\equiv \tau _{ij}\), according to the result of [21], the equilibrium \((2/3, 2/3)\) of system (24) is asymptotically stable if the following conditions hold:

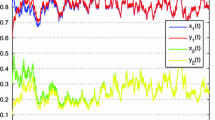
$$\begin{aligned} \begin{aligned} &28\tau _{11}+8\tau _{22}+5\tau _{12}+13\tau _{21}< 18, \\ &8\tau _{11}+28\tau _{22}+13\tau _{12}+5\tau _{21}< 18. \end{aligned} \end{aligned}$$
(25)

When \({{\tau }_{ij}}=\tau \), the upper bounds τ for local asymptotic stability obtained by the existing results and the theorems in this paper are listed in Table 1. For the case that \({{\tau }_{11}}= {{\tau }_{12}}={{\tau }_{21}}\), we can easily obtain the maximum upper bounds of \({{\tau }_{22}}\) for various τ, which are listed in Table 2. For the case of time-varying delay with \(\tau _{ij}(t)=\tau (t)\leq \tau \) and \(\dot{\tau }(t)\leq d\), by solving LMIs (18) and (22), the maximum admissible ranges of τ are obtained for different d, which are shown in Table 3. From Tables 1–3, it is seen that our proposed results can provide the larger delay bounds than those in [21, 22] and [24]. On the other hand, it is clear from Table 2 and Table 3 that Theorem 2 and Theorem 4 can provide larger delay bounds than Theorem 1 and Theorem 3, which means that the idea of using the relationships between four time delays is really effective in reducing the potential conservatism for the case with different delays. In the simulation, the state responses are plotted in Figs. 1–3. From Figs. 1–3, it is clear that the equilibrium \(( x*,y* )= ( 2/3,2/3 )\) of system (24) is asymptotically stable for the estimated ranges of time delays.

Figure 1
figure 1

State responses of system (24) (\({{\tau }_{ij}}=1.5\))

Full size image
Figure 2
figure 2

State responses of system (24) (\({{\tau }_{11}}={{\tau } _{12}}={{\tau }_{21}}=1.5\), \({{\tau }_{22}}=1.8\))

Full size image
Figure 3
figure 3

State responses of system (24) (\({{\tau }_{11}}={{\tau } _{12}}={{\tau }_{21}}=1.5\), \({{\tau }_{22}}=3.2\))

Full size image
Table 1 Maximum admissible ranges of the time delay τ
Full size table
Table 2 Maximum admissible upper bounds of \({{\tau }_{22}}\) for different τ
Full size table
Table 3 Maximum admissible ranges of τ for different d
Full size table

5 Conclusions

In this paper, we have addressed the local stability problem for a class of competitive L-V systems with time delays. By constructing some new quadratic L-K functionals and using the advanced Wirtinger integral inequality, four less conservative stability conditions have been obtained by means of LMIs. Different from most existing L-K functionals, some augmented terms have been introduced in our proposed L-K functionals. Moreover, the interconnected terms related to different time delays have been incorporated in the proposed L-K functional. Finally, a numerical example has been given to show the effectiveness and benefits of our obtained stability conditions. On the other hand, it is worth pointing out that the approach dealing with time-varying delays in this paper is standard. If some very recently developed techniques are employed [27,28,29,30,31,32,33], more effective conditions can be established.