1 Introduction

Applications of molecular structure descriptors are a standard procedure in the study of structure–property relations nowadays, especially in the field of QSAR/QSPR study. During the last century, theoretical chemists started working on the use of topological indices to obtain information of various properties of organic substances which depend upon their molecular structure. For this purpose, numerous topological indices were found and studied in the chemical literature [28]. Todeschini et al. used two zeroth-order and two first-order connectivity indices for the first time as descriptors in structure–property correlations in an optimization study. A set of new formulas for heat capacity, glass transition temperature, refractive index, cohesive energy and dielectric constant were introduced that were based on these descriptors. The Randić index has been used to parallel the boiling point and Kovats constants, and was closely correlated with many chemical properties.

A graph invariant that correlates the physico-chemical properties of a molecular graph with a number is called a topological index [18]. The first topological index was introduced by Wiener, a chemist, in 1947 to calculate the boiling points of paraffins in [29]. Zagreb indices, derived in 1972 by Gutman and Trinajstic [17], are used to study molecules and complexity of selected classes of molecules. Zagreb indices have found an interesting use in the QSPR/QSAR modeling and are useful in the study of anti-inflammatory activities of certain chemical instances. The harmonic index is one of the variants of degree-based topological indices which has also been studied in relationship with eigenvalues by Favaron et al. in [9]. The atom-bond connectivity \((\mathrm{ABC})\) index, introduced by Estrada et al. [4], gives a good model for the stability of linear and branched alkanes as well as the strain energy of cycloalkanes. The ABC index is used to predict the bioactivity of chemical compounds. The sum-connectivity index was proposed by Zhou et al. [31] and studied in relationship with the Randić index in [1]. Many topological indices have been studied in the literature [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27].

For the purpose of this article, we use the following standard notations: Given a graph \(G=(V,E)\) and for \(u,v\in V\), u being adjacent to v is denoted by \(u\sim v\) and \(\{u,v\} \in E\). The distance between any two vertices u and v of G is the minimum number of edges in the shortest \(u-v\) path and is denoted by \(d(u,v)\). The eccentricity \(\operatorname{ecc}(v)\) of a vertex v in G is the maximum distance between v and any of the other vertex of G, i.e. \(\operatorname{ecc}(v)=\max_{u\in V(G)}d(v,u)\). The diameter \(\operatorname{diam}(G)\) of G is the \(\operatorname{diam}(G)=\max_{v\in V(G)}\operatorname{ecc}(v)\) and the radius \(\operatorname{rad}(G)\) of G is the \(\operatorname{rad}(G)=\min_{v\in V(G)}\operatorname{ecc}(v)\). The number of adjacent vertices of v is called the degree of v in G, denoted by \(d_{G}(v)\). The maximum and minimum vertex degree in a graph G, are defined as \(\Delta (G)=\max \{d_{G}(u):u\in V(G)\}\) and \(\delta (G)= \min \{d_{G}(u):u\in V(G)\}\), respectively.

The generalized Sierpiński graph \(S(G,t)\) is a graph with \(V^{t}\) is the vertex set of \(S(G,t)\) and \(V=V(G)\). The vertex set \(V^{t}\) is the set of all words \(x_{1}x_{2}...x_{t}\) of length t where \(x_{r}\in V\), \(1\leq r\leq t\). \(\{x,y\}\in E(S(G,t))\) if and only if there exists \(i\in \{1,\ldots,n\}\) such that:

  1. 1.

    \(x_{j}=y_{j}\), if \(j< i\);

  2. 2.

    \(x_{i}\neq y_{i}\) and \(\{x_{i},y_{i}\}\in E(G)\);

  3. 3.

    \(x_{j}=y_{i}\) and \(y_{j}=x_{i}\) if \(j>i\).

The \(S(K_{n},3)\) are Tower of Hanoi graphs. The Sierpiński graph is a graph with \(G=K_{n}\), introduced in [23, 24]. Gravier et al. constructed the generalized Sierpiński graphs \(S(G,t)\) in [15].

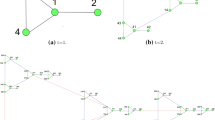
Notice that if \(\{x,y\}\) is an edge of \(S(G,t)\) then there is an edge \(\{u,v\}\) of G and a word w such that \(x=wuvv\cdots v\) and \(y=wvuu\cdots u\). Extreme vertices are the vertices of the form \(uu\cdots u\). Note that, for any graph G of order n and any integer \(t\geq 2\), \(S(G,t)\) has n extreme vertices and, if u has degree \(d_{G}(u)\), then the extreme vertex \(uu\cdots u\) of \(S(G,t)\) also has degree \(d_{G}(u)\). The degrees of vertices of the form \(vuu\cdots u\) and \(uvv\cdots v\) are equal to \(d_{G}(u) + 1\) and \(d_{G}(v) + 1\), respectively. For better understanding of \(S(G,t)\), please see Fig. 1.

Figure 1
figure 1

Generalized Sierpiński Graphs \(S(1,C_{4})\) and \(S(3,C_{4})\)

Full size image

It is clear that u as a vertex of \(V(S(G,t))\) has degree \(d_{S(G,t)}(u) \in \{d_{G}(u),d_{G}(u)+1\}\) where \(d_{G}(u)\) is degree of u in G. We use the terminology of [5]. \(\Im _{S(G, t)}(d_{G}(u),d _{G}(v))\) is the number of copies of \(\{u,v\}\) edge with degrees \(d_{G}(u)\) and \(d_{G}(v)\) in \(S(G,t)\). \(N(u)=\{s\in V:\{u,s\}\in E\}\) is the neighborhood of \(u\in V\). For \(u,v\in V\), the number of triangles of G containing u and v will be denoted by \(\tau (u,v)\) and the number of triangles of G will be denoted by \(\tau (G)\). For any pair of adjacent vertices \(u,v\in V\), we have \(|N(u)\cap N(v)|=\tau (u,v)\), \(|N(u)\cup N(v)|=d_{G}(u)+d_{G}(v)-\tau (u,v)\) and \(|N(u)-N(v)|=d_{G}(u)- \tau (u,v)\). From now onward, for a graph of order n, we will use the function \(\psi _{n}(t)=1+n+n^{2}+\cdots +n^{t-1}=\frac{n^{t}-1}{n-1}\).

Lemma 1

([5])

For any integer \(t\geq 2\) and any edge \(\{u,v\}\) of a graph G of order n,

  1. 1.

    \(\Im _{S(G, t)}(d_{G}(u),d_{G}(v))=n^{t-2}(n-d_{G}(u)-d _{G}(v)+\tau (u,v))\).

  2. 2.

    \(\Im _{S(G, t)}(d_{G}(u),d_{G}(v)+1)=n^{t-2}(d_{G}(v)- \tau (u,v))-\psi _{n}(t-2)d_{G}(u)\).

  3. 3.

    \(\Im _{S(G, t)}(d_{G}(u)+1,d_{G}(v))=n^{t-2}(d_{G}(u)- \tau (u,v))-\psi _{n}(t-2)d_{G}(v)\).

  4. 4.

    \(\Im _{S(G, t)}(d_{G}(u)+1,d_{G}(v)+1)=n^{t-2}(\tau (u,v)+1)+ \psi _{n}(t-2)(d_{G}(u)+d_{G}(v)+1)\).

Sierpiński graphs \(S(K_{n},t)\) originated from the topological study of the Lipscomb space. WK-recursive network is a class of graphs, which was introduced in computer science in [2, 11]. WK-recursive networks are structurally close to Sierpiński graphs, these can be obtained from Sierpiński graphs by adding an open edge to each of its extreme vertices. The graphs \(S(G,t)\) have been studied from different points of views. Colorings of these graphs have been found in [10, 21], crossing number and several metric invariants such as unique 1-perfect codes, average distance of these graphs have been studied in the literature. For more literature on Sierpiński graphs, please see [14, 19, 20, 24, 30].

In this paper, we study the topological indices of generalized Sierpiński and extended Sierpiński graphs with an arbitrary base graph. Bounds for the atom-bond connectivity index, harmonic index, Zagreb indices and sum-connectivity index for the generalized Sierpiński graphs and extended Sierpiński graphs have been determined. The atom-bond connectivity index, harmonic index, Zagreb indices and sum-connectivity index are the vertex-degree-based topological indices that can be studied in terms of topological indices of the base graph of a generalized Sierpiński graph, therefore we choose these indices for the study of topological indices of generalized Sierpiński and extended Sierpiński graphs.

2 Topological indices of generalized Sierpiński graphs

The atom-bond connectivity \((\mathrm{ABC})\) index, introduced by Estrada et al. [4], a degree based index, is defined as

$$ \operatorname{ABC}(G)=\sum_{u\sim v}\sqrt{ \frac{d_{G}(u)+d_{G}(v)-2}{d_{G}(u)d _{G}(v)}}. $$

In the following theorem, we present a lower bound for the atom-bond connectivity index for generalized Sierpiński graphs in terms of the atom-bond connectivity index of G.

Theorem 1

For any graph G of order \(n\geq 3\), \(\delta (G)\geq 2\) and any integer \(t\geq 2\),

$$ \operatorname{ABC}\bigl(S(G,t)\bigr)\leq \psi _{n}(t) \operatorname{ABC}(G). $$

Proof

The ABC index of \(S(G,t)\) can be expressed as

$$ \operatorname{ABC}\bigl(S(G,t)\bigr)=\sum_{{u\sim v}}\sum _{i=0}^{1}\sum_{j=0}^{1} \Im _{S(G,t)}\bigl(d_{G}(u)+i,d_{G}(v)+j\bigr)\sqrt{ \frac{(d_{G}(u)+i)+(d _{G}(v)+j)-2}{(d_{G}(u)+i)(d_{G}(v)+j)}} $$

by using Lemma 1:

$$ \begin{aligned} &=\sum_{u\sim v}\biggl\{ n^{t-2} \bigl(n-d_{G}(u)-d_{G}(v)+\tau (u,v)\bigr)\sqrt{ \frac{d _{G}(u)+d_{G}(v)-2}{d_{G}(u)d_{G}(v)}} \\ &\quad {}+n^{t-2}\bigl(d_{G}(v)-\tau (u,v)\bigr)- \psi _{n}(t-2)d_{G}(u)\sqrt{\frac{d_{G}(u)+d_{G}(v)-1}{d_{G}(u)(d _{G}(v)+1)}} \\ &\quad {}+n^{t-2}\bigl(d_{G}(u)-\tau (u,v)\bigr)-\psi _{n}(t-2)d_{G}(v)\sqrt{\frac{d _{G}(u)+d_{G}(v)-1}{(d_{G}(u)+1)d_{G}(v)}} \\ &\quad {}+n^{t-2}\bigl(\tau (u,v)+1\bigr)+ \psi _{n}(t-2) \bigl(d_{G}(u)+d_{G}(v)+1\bigr)\sqrt{\frac{d_{G}(u)+d_{G}(v)}{(d _{G}(u)+1)(d_{G}(v)+1)}} \biggr\} . \end{aligned} $$

We have \(\delta (G)\geq 2\), \(\sqrt{\frac{d_{G}(u)+d_{G}(v)-1}{d_{G}(u)(d _{G}(v)+1)}}\leq \sqrt{\frac{d_{G}(u)+d_{G}(v)-2}{d_{G}(u)d_{G}(v)}}\), \(\sqrt{\frac{d _{G}(u)+d_{G}(v)-1}{(d_{G}(u)+1)d_{G}(v)}}\leq \sqrt{\frac{d_{G}(u)+d _{G}(v)-2}{d_{G}(u)d_{G}(v)}}\) and \(\sqrt{\frac{d_{G}(u)+d_{G}(v)}{(d _{G}(u)+1)(d_{G}(v)+1)}}\leq \sqrt{\frac{d_{G}(u)+d_{G}(v)-2}{d_{G}(u)d _{G}(v)}}\). We deduce

$$ \begin{aligned} &\operatorname{ABC}\bigl(S(G,t)\bigr)\\ &\quad \leq \sum _{u\sim v}\bigl\{ n^{t-2}\bigl(n-d_{G}(u)-d_{G}(v)+ \tau (u,v)\bigr) +n^{t-2}\bigl(d_{G}(v)-\tau (u,v)\bigr)\\ &\qquad{}-\psi _{n}(t-2)d_{G}(u)+n^{t-2}\bigl(d _{G}(u)-\tau (u,v)\bigr)-\psi _{n}(t-2)d_{G}(v) \\ &\qquad {}+n^{t-2}\bigl(\tau (u,v)+1\bigr)+\psi _{n}(t-2) \bigl(d_{G}(u)+d_{G}(v)+1\bigr)\bigr\} \sqrt{ \frac{d _{G}(u)+d_{G}(v)-2}{d_{G}(u)d_{G}(v)}} \\ &\quad =\sum_{u\sim v}\bigl\{ n^{t-1}+n^{t-2}+ \psi _{n}(t-2)\bigr\} \sqrt{\frac{d _{G}(u)+d_{G}(v)-2}{d_{G}(u)d_{G}(v)}} \\ &\quad =\sum_{u\sim v}\psi _{n}(t)\sqrt{ \frac{d_{G}(u)+d_{G}(v)-2}{d _{G}(u)d_{G}(v)}}, \end{aligned} $$

which gives the desired result:

$$ \operatorname{ABC}\bigl(S(G,t)\bigr)\leq \psi _{n}(t) \operatorname{ABC}(G). $$

 □

The harmonic index, another variant of degree based topological indices, is defined as follows:

$$ H(G)=\sum_{u\sim v}\frac{2}{d_{G}(u)+d_{G}(v)}. $$

Now, we compute a lower bound for the harmonic index for generalized Sierpiński graphs.

Theorem 2

For any graph G of order \(n\geq 2\), size \(m\geq 1\) and any integer \(t\geq 2\),

$$ H\bigl(S(G,t)\bigr)\leq \psi _{n}(t)H(G). $$

Proof

The \(H(G)\) index of \(S(G,t)\) can be expressed as

$$ H\bigl(S(G,t)\bigr)=\sum_{u\sim v}\sum _{i=0}^{1}\sum_{j=0} ^{1}\Im _{S(G,t)}\bigl(d_{G}(u)+i,d_{G}(v)+j \bigr) \frac{2}{(d_{G}(u)+i)+(d_{G}(v)+j)}. $$

By using Lemma 1 and \(\frac{2}{d_{G}(u)+d_{G}(v)+j}\leq \frac{2}{d _{G}(u)+d_{G}(v)}\), for \(j=1,2\). We have

$$ \begin{aligned} H\bigl(S(G,t)\bigr)&\leq \sum_{u\sim v} \bigl\{ n^{t-2}\bigl(n-d_{G}(u)-d_{G}(v)+ \tau (u,v) \bigr) +n^{t-2}\bigl(d_{G}(v)-\tau (u,v)\bigr)\\&\quad{}-\psi _{n}(t-2)d_{G}(u)+n^{t-2}\bigl(d _{G}(u)-\tau (u,v)\bigr)-\psi _{n}(t-2)d_{G}(v) \\ &\quad {}+n^{t-2}\bigl(\tau (u,v)+1\bigr)+\psi _{n}(t-2) \bigl(d_{G}(u)+d_{G}(v)+1\bigr)\bigr\} \frac{2}{d _{G}(u)+d_{G}(v)} \\ &=\sum_{u\sim v}\bigl\{ n^{t-1}+n^{t-2}+ \psi _{n}(t-2)\bigr\} \frac{2}{d _{G}(u)+d_{G}(v)} \\ &=\sum_{u\sim v}\psi _{n}(t) \frac{2}{d_{G}(u)+d_{G}(v)}. \end{aligned} $$

We get the required result:

$$ H\bigl(S(G,t)\bigr)\leq \psi _{n}(t)H(G). $$

 □

Bounds on the Zagreb first and second indices, defined as

$$ Z_{1}(G)=\sum_{u\sim v}\bigl(d_{G}(u)+d_{G}(v) \bigr) $$

and

$$ Z_{2}(G)=\sum_{u\sim v}\bigl(d_{G}(u) \cdot d_{G}(v)\bigr) $$

for generalized Sierpiński graphs are presented in the following theorems.

Theorem 3

For any graph G of order \(n\geq 2\), size \(m\geq 1\) and any integer \(t\geq 2\),

$$ Z_{1}\bigl(S(G,t)\bigr)\leq 2m\psi _{n}(t) \bigl(n- \operatorname{rad}(G)+1\bigr). $$

Proof

The \(Z_{1}(G)\) index of \(S(G,t)\) can be expressed as

$$ Z_{1}\bigl(S(G,t)\bigr)=\sum_{u\sim v}\sum _{i=0}^{1}\sum_{j=0}^{1} \Im _{S(G,t)}\bigl(d_{G}(u)+i,d_{G}(v)+j\bigr) \bigl( \bigl(d_{G}(u)+i\bigr)+\bigl(d_{G}(v)+j\bigr)\bigr). $$

It is clear that \(d_{G}(u)+d_{G}(v)\leq d_{G}(u)+d_{G}(v)+1\leq d_{G}(u)+d _{G}(v)+2\). Using Lemma 1 and the above inequality we get

$$ \begin{aligned} Z_{1}\bigl(S(G,t)\bigr)&\leq \sum _{u\sim v}\bigl\{ n^{t-2}\bigl(n-d_{G}(u)-d_{G}(v)+ \tau (u,v)\bigr) \\ &\quad {}+n^{t-2}\bigl(d_{G}(v)-\tau (u,v)\bigr)-\psi _{n}(t-2)d_{G}(u) +n^{t-2}\bigl(d_{G}(u)- \tau (u,v)\bigr)\\&\quad{}-\psi _{n}(t-2)d_{G}(v)+n^{t-2} \bigl(\tau (u,v)+1\bigr)\\&\quad{}+\psi _{n}(t-2) \bigl(d _{G}(u)+d_{G}(v)+1 \bigr)\bigr\} \bigl(d_{G}(u)+d_{G}(v)+2\bigr) \\ &=\sum_{u\sim v}\bigl\{ n^{t-1}+n^{t-2}+ \psi _{n}(t-2)\bigr\} \bigl(d_{G}(u)+d _{G}(v)+2 \bigr) \\ &=\sum_{u\sim v}\psi _{n}(t) \bigl(d_{G}(u)+d_{G}(v)+2\bigr). \end{aligned} $$

By using \(d_{G}(u)\leq n-\operatorname{ecc}(u)\) and \(\operatorname{rad}(G)\leq \operatorname{ecc}(u)\), we get

$$ d_{G}(u)+d_{G}(v)+2\leq 2\bigl(n-\operatorname{rad}(G)+1 \bigr). $$

Using the above inequality, we get the required result:

$$ Z_{1}\bigl(S(G,t)\bigr)\leq 2m\psi _{n}(t) \bigl(n- \operatorname{rad}(G)+1\bigr). $$

 □

Theorem 4

For any graph G of order \(n\geq 2\), size \(m\geq 1\) and any integer \(t\geq 2\),

$$ Z_{2}\bigl(S(G,t)\bigr)\leq m\psi _{n}(t) \bigl(n- \operatorname{rad}(G)+1\bigr)^{2}. $$

Proof

The \(Z_{2}(G)\) index of \(S(G,t)\) can be expressed as

$$ Z_{2}\bigl(S(G,t)\bigr)=\sum_{u\sim v}\sum _{i=0}^{1}\sum_{j=0}^{1} \Im _{S(G,t)}\bigl(d_{G}(u)+i,d_{G}(v)+j\bigr) \bigl( \bigl(d_{G}(u)+i\bigr)\cdot \bigl(d _{G}(v)+j\bigr)\bigr). $$

It is clear that \(d_{G}(u)\cdot d_{G}(v)\leq d_{G}(u)\cdot (d_{G}(v)+1) \leq (d_{G}(u)+1)\cdot d_{G}(v)\leq (d_{G}(u)+1)\cdot {(d_{G}(v)+1)}\). Using Lemma 1 and the above inequality we get

$$\begin{aligned} &Z_{2}\bigl(S(G,t)\bigr)\\ &\quad \leq \sum _{u\sim v}\bigl\{ n^{t-2}\bigl(n-d_{G}(u)-d_{G}(v)+ \tau (u,v)\bigr) +n^{t-2}\bigl(d_{G}(v)-\tau (u,v)\bigr)\\ &\qquad{}-\psi _{n}(t-2)d_{G}(u)+n^{t-2}\bigl(d _{G}(u)-\tau (u,v)\bigr)-\psi _{n}(t-2)d_{G}(v) \\ &\qquad {}+n^{t-2}\bigl(\tau (u,v)+1\bigr)+\psi _{n}(t-2) \bigl(d_{G}(u)+d_{G}(v)+1\bigr)\bigr\} \bigl(d_{G}(u)+1 \bigr) \cdot \bigl(d_{G}(v)+1\bigr) \\ &\quad =\sum_{u\sim v}\bigl\{ n^{t-1}+n^{t-2}+ \psi _{n}(t-2)\bigr\} \bigl(d_{G}(u)+1\bigr) \cdot \bigl(d_{G}(v)+1\bigr) \\ &\quad =\sum_{u\sim v}\psi _{n}(t) \bigl(d_{G}(u)+1\bigr)\cdot \bigl(d_{G}(v)+1\bigr). \end{aligned}$$

We have \((d_{G}(u)+1)\cdot (d_{G}(v)+1)\leq (n-\operatorname{rad}(G)+1)^{2}\). Using the above inequality, we get the required result:

$$ Z_{2}\bigl(S(G,t)\bigr)\leq m\psi _{n}(t) \bigl(n- \operatorname{rad}(G)+1\bigr)^{2}. $$

 □

The sum-connectivity index was proposed by Zhou et al. [31]. The sum-connectivity index \(\chi (G)\) is defined as

$$ \chi (G)=\sum_{u\sim v}\frac{1}{\sqrt{d_{G}(u)+d_{G}(v)}}. $$

In the following result, we discuss the sum-connectivity index of generalized Sierpiński graphs.

Theorem 5

For any graph G of order \(n\geq 2\), size \(m\geq 1\) and any integer \(t\geq 2\),

$$ \chi \bigl(S(G,t)\bigr)\leq \psi _{n}(t)\chi (G). $$

Proof

The \(\chi (S(G,t))\) index of \(S(G,t)\) can be expressed as

$$ \chi \bigl(S(G,t)\bigr)=\sum_{u\sim v}\sum _{i=0}^{1}\sum_{j=0}^{1} \Im _{S(G,t)}\bigl(d_{G}(u)+i,d_{G}(v)+j\bigr) \frac{1}{(d_{G}(u)+i)+(d _{G}(v)+j)}. $$

We have \(\frac{1}{\sqrt{d_{G}(u)+d_{G}(v)+1}}\leq \frac{1}{\sqrt{d _{G}(u)+d_{G}(v)}}\) and \(\frac{1}{\sqrt{d_{G}(u)+d_{G}(v)+2}}\leq \frac{1}{\sqrt{d _{G}(u)+d_{G}(v)}}\). By using Lemma 1 and these inequalities, we have

$$ \begin{aligned} \chi \bigl(S(G,t)\bigr)&\leq \sum_{u\sim v} \bigl\{ n^{t-2}\bigl(n-d_{G}(u)-d_{G}(v)+ \tau (u,v) \bigr) +n^{t-2}\bigl(d_{G}(v)-\tau (u,v)\bigr)\\&\quad{}-\psi _{n}(t-2)d_{G}(u)+n^{t-2}\bigl(d _{G}(u)-\tau (u,v)\bigr)-\psi _{n}(t-2)d_{G}(v) \\ &\quad {}+n^{t-2}\bigl(\tau (u,v)+1\bigr)+\psi _{n}(t-2) \bigl(d_{G}(u)+d_{G}(v)+1\bigr)\bigr\} \frac{1}{\sqrt{d _{G}(u)+d_{G}(v)}} \\ &=\sum_{u\sim v}\bigl\{ n^{t-1}+n^{t-2}+ \psi _{n}(t-2)\bigr\} \frac{1}{\sqrt{d _{G}(u)+d_{G}(v)}} \\ &=\sum_{u\sim v}\psi _{n}(t) \frac{1}{\sqrt{d_{G}(u)+d_{G}(v)}}, \end{aligned} $$

which gives the desired result:

$$ \chi \bigl(S(G,t)\bigr)\leq \psi _{n}(t)\chi (G). $$

 □

3 Topological indices of extended Sierpiński graphs

The extended Sierpiński graph \(S(G,t^{+})\) was introduced by Klavžar et al. in [25]. The extended Sierpiński graph \(S(G,t^{+})\) is obtained from \(S(G,t)\) by adding a new vertex x, called the special vertex of \(S(G,t^{+})\), and edges joining x with all extreme vertices ϖ of \(S(G,t)\), as shown in Fig. 2. These edges are \(d_{S(G,t)}(s)\in \{d_{G}(s),d_{G}(s)+1\}\). The number of extreme vertices in \(S(G,t)\) is always the order of G. Therefore, in analogy to Lemma 1, we give the following result for extended Sierpiński graphs.

Figure 2
figure 2

Extended Sierpiński graph

Full size image

Lemma 2

For any integer \(t\geq 2\) and any edge \(\{u,v\}\) of a graph G of order n.

  1. 1.

    \(\Im _{S(G,t^{+})}(d_{G}(u),d_{G}(v))=n^{t-2}(n-d_{G}(u)-d _{G}(v)+\tau (u,v))\).

  2. 2.

    \(\Im _{S(G,t^{+})}(d_{G}(u),d_{G}(v)+1)=n^{t-2}(d_{G}(v)- \tau (u,v))-\psi _{n}(t-2)d_{G}(u)\).

  3. 3.

    \(\Im _{S(G,t^{+})}(d_{G}(u)+1,d_{G}(v))=n^{t-2}(d_{G}(u)- \tau (u,v))-\psi _{n}(t-2)d_{G}(v)\).

  4. 4.

    \(\Im _{S(G,t^{+})}(d_{G}(u)+1,d_{G}(v))=n^{t-2}(\tau (u,v)+1)+ \psi _{n}(t-2)(d_{G}(u)+d_{G}(v)+1)\).

  5. 5.

    \(\Im _{S(G,t^{+})}(d_{G}(\varpi ),d_{S(G,t^{+})}(x))=n\).

We use the above lemma to find topological indices for extended Sierpiński graphs \(S(G,t^{+})\).

Theorem 6

For any graph G of order \(n\geq 3\), \(\delta (G)\geq 2\) and any integer \(t\geq 2\),

$$ \operatorname{ABC}\bigl(S\bigl(G,t^{+}\bigr)\bigr)\leq \bigl(n +\psi _{n}(t)\bigr)\operatorname{ABC}(G). $$

Proof

The ABC index of \(S(G,t^{+})\) can be expressed as

$$ \begin{aligned} &\operatorname{ABC}\bigl(S\bigl(G,t^{+}\bigr)\bigr)\\ &\quad = \sum_{u\sim v}\sum_{i=0}^{1} \sum_{j=0}^{1}\Im _{S(G,t^{+})} \bigl(d_{G}(u)+i,d_{G}(v)+j\bigr)\sqrt{\frac{(d _{G}(u)+i)+(d_{G}(v)+j)-2}{(d_{G}(u)+i)(d_{G}(v)+j)}} \\ &\qquad {}+\Im _{S(G,t^{+})}\bigl(d_{G}(\varpi ),d_{S(G,t^{+})}(x) \bigr)\sqrt{\frac{d _{G}(\varpi )+d_{S(G,t^{+})}(x)-2}{d_{G}(\varpi )d_{S(G,t^{+})}(x)}}; \end{aligned} $$

by using Lemma 2

$$ \begin{aligned} &\operatorname{ABC}\bigl(S\bigl(G,t^{+}\bigr)\bigr)\\ &\quad = \sum_{u\sim v}\biggl\{ n^{t-2}\bigl(n-d_{G}(u)-d_{G}(v)+ \tau (u,v)\bigr)\sqrt{\frac{d_{G}(u)+d_{G}(v)-2}{d_{G}(u)d_{G}(v)}} \\ &\qquad {}+n^{t-2}\bigl(d_{G}(v)-\tau (u,v)\bigr)-\psi _{n}(t-2)d_{G}(u)\sqrt{\frac{d _{G}(u)+d_{G}(v)-1}{d_{G}(u)(d_{G}(v)+1)}} \\ &\qquad{}+n^{t-2}\bigl(d_{G}(u)-\tau (u,v)\bigr)- \psi _{n}(t-2)d_{G}(v)\sqrt{\frac{d_{G}(u)+d_{G}(v)-1}{(d_{G}(u)+1)d _{G}(v)}} \\ &\qquad {}+n^{t-2}\bigl(\tau (u,v)+1\bigr)+\psi _{n}(t-2) \bigl(d_{G}(u)+d_{G}(v)+1\bigr)\sqrt{\frac{d _{G}(u)+d_{G}(v)}{(d_{G}(u)+1)(d_{G}(v)+1)}} \\ &\qquad {}+n\sqrt{\frac{d_{G}( \varpi )+d_{S(G,t^{+})}(x)-2}{d_{G}(\varpi )d_{S(G,t^{+})}(x)}}\biggr\} . \end{aligned} $$

We have \(\delta (G)\geq 2\), \(\sqrt{\frac{d_{G}(u)+d_{G}(v)-1}{d_{G}(u)(d _{G}(v)+1)}}\leq \sqrt{\frac{d_{G}(u)+d_{G}(v)-2}{d_{G}(u)d_{G}(v)}}\), \(\sqrt{\frac{d _{G}(u)+d_{G}(v)-1}{(d_{G}(u)+1)d_{G}(v)}}\leq \sqrt{\frac{d_{G}(u)+d _{G}(v)-2}{d_{G}(u)d_{G}(v)}}\), \(\sqrt{\frac{d_{G}(u)+d_{G}(v)}{(d _{G}(u)+1)(d_{G}(v)+1)}}\leq \sqrt{\frac{d_{G}(u)+d_{G}(v)-2}{d_{G}(u)d _{G}(v)}}\) and \(\sqrt{\frac{d_{G}(\varpi )+d_{S(G,t^{+})}(x)-2}{d _{G}(\varpi )d_{S(G,t^{+})}(x)}}\leq \sqrt{\frac{d_{G}(u)+d_{G}(v)-2}{d _{G}(u)d_{G}(v)}}\). We have

$$ \begin{aligned} &\operatorname{ABC}\bigl(S\bigl(G,t^{+}\bigr)\bigr)\\ &\quad \leq \sum_{u\sim v}\bigl\{ n^{t-2} \bigl(n-d_{G}(u)-d_{G}(v)+ \tau (u,v)\bigr) +n^{t-2} \bigl(d_{G}(v)-\tau (u,v)\bigr)\\ &\qquad {}-\psi _{n}(t-2)d_{G}(u)+n^{t-2} \bigl(d _{G}(u)-\tau (u,v)\bigr)-\psi _{n}(t-2)d_{G}(v) \\ &\qquad {}+n^{t-2} \bigl(\tau (u,v)+1\bigr)+\psi _{n}(t-2) \bigl(d_{G}(u)+d_{G}(v)+1\bigr)+n\bigr\} \sqrt{ \frac{d _{G}(u)+d_{G}(v)-2}{d_{G}(u)d_{G}(v)}} \\ &\quad =\sum_{u\sim v}\bigl\{ n^{t-1}+n^{t-2}+ \psi _{n}(t-2)+n\bigr\} \sqrt{\frac{d _{G}(u)+d_{G}(v)-2}{d_{G}(u)d_{G}(v)}} \\ &\quad =\sum_{u\sim v}\bigl(n+\psi _{n}(t)\bigr) \sqrt{\frac{d_{G}(u)+d_{G}(v)-2}{d _{G}(u)d_{G}(v)}} \end{aligned} $$

and we get the required result:

$$ \operatorname{ABC}\bigl(S\bigl(G,t^{+}\bigr)\bigr)\leq \bigl(n +\psi _{n}(t)\bigr)\operatorname{ABC}(G). $$

 □

A lower bound for the harmonic index of extended Sierpiński graphs \(S(G,t^{+})\) is given in the following result.

Theorem 7

For any graph G of order \(n\geq 2\), size \(m\geq 1\) and any integer \(t\geq 2\),

$$ H\bigl(S\bigl(G,t^{+}\bigr)\bigr)\leq \bigl(n+\psi _{n}(t) \bigr)H(G). $$

Proof

The \(H(G)\) index of \(S(G,t^{+})\) can be expressed as

$$ \begin{aligned} H\bigl(S\bigl(G,t^{+}\bigr)\bigr)&=\sum _{u\sim v}\sum_{i=0}^{1}\sum _{j=0}^{1}\Im _{S(G,t^{+})} \bigl(d_{G}(u)+i,d_{G}(v)+j\bigr)\frac{2}{(d_{G}(u)+i)+(d _{G}(v)+j)} \\ &\quad {}+\Im _{S(G,t^{+})}\bigl(d_{G}(\varpi ),d_{S(G,t^{+})}(x) \bigr)\frac{2}{d _{G}(\varpi )+d_{S(G,t^{+})}(x)}. \end{aligned} $$

We have \(\frac{2}{d_{G}(u)+d_{G}(v)+j}\leq \frac{2}{d_{G}(u)+d_{G}(v)}\), for \(j=1,2\) and \(\frac{2}{d_{G}(\varpi )+d_{S(G,t^{+})}(x)}\leq \frac{2}{d_{G}(u)+d_{G}(v)}\). By using Lemma 2 and the above inequalities, we have

$$ \begin{aligned} H\bigl(S\bigl(G,t^{+}\bigr)\bigr)&\leq \sum _{u\sim v}\bigl\{ n^{t-2}\bigl(n-d_{G}(u)-d_{G}(v)+ \tau (u,v)\bigr) +n^{t-2}\bigl(d_{G}(v)-\tau (u,v)\bigr)\\&\quad{}-\psi _{n}(t-2)d_{G}(u)+n^{t-2}\bigl(d _{G}(u)-\tau (u,v)\bigr)-\psi _{n}(t-2)d_{G}(v) \\ &\quad {}+n^{t-2} \bigl(\tau (u,v)+1\bigr)+\psi _{n}(t-2) \bigl(d_{G}(u)+d_{G}(v)+1\bigr)+n\bigr\} \frac{2}{d _{G}(u)+d_{G}(v)} \\ &=\sum_{u\sim v}\bigr\{ n^{t-1}+n^{t-2}+\psi _{n}(t-2)+ n\bigr\} \frac{2}{d_{G}(u)+d_{G}(v)} \\ &=\sum_{u\sim v}\bigl(n+\psi _{n}(t)\bigr) \frac{2}{d_{G}(u)+d_{G}(v)}, \end{aligned} $$

which gives the desired result:

$$ H\bigl(S\bigl(G,t^{+}\bigr)\bigr)\leq \bigl(n+\psi _{n}(t) \bigr)H(G). $$

 □

Now, we discuss the Zagreb indices of extended Sierpiński graphs \(S(G,t^{+})\).

Theorem 8

For any graph G of order \(n\geq 2\), size \(m\geq 1\) and any integer \(t\geq 2\),

$$ Z_{1}\bigl(S\bigl(G,t^{+}\bigr)\bigr)\leq 2m\bigl(n+\psi _{n}(t)\bigr) \bigl(n-\operatorname{rad}(G)+1\bigr). $$

Proof

The \(Z_{1}\) index of \(S(G,t^{+})\) can be expressed as

$$ \begin{aligned} Z_{1}\bigl(S\bigl(G,t^{+}\bigr)\bigr)&=\sum _{u\sim v}\sum_{i=0}^{1} \sum_{j=0}^{1}\Im _{S(G,t)} \bigl(d_{G}(u)+i,d_{G}(v)+j\bigr) \bigl( \bigl(d_{G}(u)+i\bigr)+\bigl(d _{G}(v)+j\bigr)\bigr) \\ &\quad {}+\Im _{S(G,t^{+})}\bigl(d_{G}(\varpi ),d_{S(G,t^{+})}(x) \bigr) \bigl(d _{G}(\varpi )+d_{S(G,t^{+})}(x)\bigr). \end{aligned} $$

It is clear that \(d_{G}(u)+d_{G}(v)\leq d_{G}(u)+d_{G}(v)+1\leq d_{G}(u)+d _{G}(v)+2\) and similarly \((d_{G}(\varpi )+d_{S(G,t^{+})}(x))\leq d _{G}(u)+d_{G}(v)+2\). Using Lemma 2 and the above inequalities we get

$$ \begin{aligned} &Z_{1}\bigl(S\bigl(G,t^{+}\bigr)\bigr)\\ &\quad \leq \sum_{u\sim v}\bigl\{ n^{t-2}\bigl(n-d_{G}(u)-d _{G}(v)+\tau (u,v)\bigr) +n^{t-2}\bigl(d_{G}(v)- \tau (u,v)\bigr)\\ &\qquad{}-\psi _{n}(t-2)d_{G}(u)+n ^{t-2} \bigl(d_{G}(u)-\tau (u,v)\bigr)- \psi _{n}(t-2)d_{G}(v) \\ &\qquad {}+n^{t-2}\bigl(\tau (u,v)+1\bigr)+\psi _{n}(t-2) \bigl(d_{G}(u)+d_{G}(v)+1\bigr)+n\bigr\} \bigl(d_{G}(u)+d _{G}(v)+2\bigr) \\ &\quad =\sum_{u\sim v}\bigl\{ n^{t-1}+n^{t-2}+ \psi _{n}(t-2)+n\bigr\} \bigl(d_{G}(u)+d _{G}(v)+2 \bigr) \\ &\quad =\sum_{u\sim v}\bigl(n+\psi _{n}(t)\bigr) \bigl(d_{G}(u)+d_{G}(v)+2\bigr). \end{aligned} $$

We have \(d_{G}(u)+d_{G}(v)+2\leq 2(n-\operatorname{rad}(G)+1)\) Using the above inequality, we get the required result:

$$ Z_{1}\bigl(S\bigl(G,t^{+}\bigr)\bigr)\leq 2m\bigl(n+\psi _{n}(t)\bigr) \bigl(n-\operatorname{rad}(G)+1\bigr). $$

 □

Theorem 9

For any graph G of order \(n\geq 2\), size \(m\geq 1\) and any integer \(t\geq 2\),

$$ Z_{2}\bigl(S\bigl(G,t^{+}\bigr)\bigr)\leq m\bigl(n+\psi _{n}(t)\bigr) \bigl(n-\operatorname{rad}(G)+1\bigr)^{2}. $$

Proof

The \(Z_{2}\) index of \(S(G,t^{+})\) can be expressed as

$$ \begin{aligned} Z_{2}\bigl(S\bigl(G,t^{+}\bigr)\bigr)&=\sum _{u\sim v}\sum_{i=0}^{1} \sum_{j=0}^{1}\Im _{S(G,t^{+})} \bigl(d_{G}(u)+i,d_{G}(v)+j\bigr) \bigl( \bigl(d_{G}(u)+i\bigr) \cdot \bigl(d_{G}(v)+j\bigr)\bigr) \\ &\quad {}+\Im _{S(G,t^{+})}\bigl(d_{G}(\varpi ),d_{S(G,t^{+})}(x) \bigr) \bigl(d _{G}(\varpi )\bigr)\cdot \bigl(d_{S(G,t^{+})}(x) \bigr). \end{aligned} $$

It is clear that \(d_{G}(u)\cdot d_{G}(v)\leq d_{G}(u)\cdot (d_{G}(v)+1) \leq (d_{G}(u)+1)\cdot d_{G}(v)\leq (d_{G}(u)+1)\cdot (d_{G}(v)+1)\) and \(((d_{G}(\varpi ))\cdot (d_{S(G,t^{+})}(x)))\leq (d_{G}(u)+1)\cdot (d _{G}(v)+1)\). Using Lemma 2 and the above inequalities, we get

$$ \begin{aligned} Z_{2}\bigl(S\bigl(G,t^{+}\bigr)\bigr)&\leq \sum_{u\sim v}\bigl\{ n^{t-2}\bigl(n-d_{G}(u)-d _{G}(v)+\tau (u,v)\bigr) \\ &\quad {}+n^{t-2}\bigl(d_{G}(v)-\tau (u,v)\bigr)-\psi _{n}(t-2)d_{G}(u) +n^{t-2}\bigl(d_{G}(u)- \tau (u,v)\bigr)\\&\quad{}-\psi _{n}(t-2)d_{G}(v)+n^{t-2} \bigl(\tau (u,v)+1\bigr)\\&\quad{}+\psi _{n}(t-2) \bigl(d _{G}(u)+d_{G}(v)+1 \bigr)+n\bigr\} \bigl(d_{G}(u)+1\bigr)\cdot \bigl(d_{G}(v)+1 \bigr) \\ &=\sum_{u\sim v}\bigl\{ n^{t-1}+n^{t-2}+ \psi _{n}(t-2)+n\bigr\} \bigl(d_{G}(u)+1\bigr) \cdot \bigl(d_{G}(v)+1\bigr) \\ &=\sum_{u\sim v}\bigl(n+\psi _{n}(t)\bigr) \bigl(d_{G}(u)+1\bigr)\cdot \bigl(d_{G}(v)+1\bigr). \end{aligned} $$

We have \((d_{G}(u)+1)\cdot (d_{G}(v)+1)\leq (n-\operatorname{rad}(G)+1)^{2}\). Using this inequality, we get the required result:

$$ Z_{2}\bigl(S\bigl(G,t^{+}\bigr)\bigr)\leq m\bigl(n+\psi _{n}(t)\bigr) \bigl(n-\operatorname{rad}(G)+1\bigr)^{2}. $$

 □

The sum-connectivity index of extended Sierpiński graphs \(S(G,t^{+})\) is calculated in the following result.

Theorem 10

For any graph G of order \(n\geq 2\), size \(m\geq 1\) and any integer \(t\geq 2\),

$$ \chi \bigl(S\bigl(G,t^{+}\bigr)\bigr)\leq \bigl(n+\psi _{n}(t)\bigr)\chi (G). $$

Proof

The \(\chi (S(G,t^{+}))\) index of \(S(G,t^{+})\) can be expressed as

$$ \begin{aligned} \chi \bigl(S\bigl(G,t^{+}\bigr)\bigr)&=\sum _{u \sim v}\sum_{i=0}^{1}\sum _{j=0}^{1}\Im _{S(G,t)} \bigl(d_{G}(u)+i,d_{G}(v)+j\bigr)\frac{1}{\sqrt{(d _{G}(u)+i)+(d_{G}(v)+j)}} \\ &\quad {}+\Im _{S(G,t)}\bigl(d_{G}(\varpi ),d_{S(G,t^{+})}(x) \bigr)\frac{1}{\sqrt{d _{G}(\varpi )+d_{S(G,t^{+})}(x)}}. \end{aligned} $$

We have \(\frac{1}{\sqrt{d_{G}(u)+d_{G}(v)+1}}\leq \frac{1}{\sqrt{d _{G}(u)+d_{G}(v)}}\), \(\frac{1}{\sqrt{d_{G}(u)+d_{G}(v)+2}}\leq \frac{1}{\sqrt{d _{G}(u)+d_{G}(v)}}\) and \(\frac{1}{\sqrt{d_{G}(\varpi )+d_{S(G,t^{+})}(x)}}\leq \frac{1}{\sqrt{d _{G}(u)+d_{G}(v)}}\). By using Lemma 2 and these inequalities we have

$$ \begin{aligned} \chi \bigl(S\bigl(G,t^{+}\bigr)\bigr)&\leq \sum _{u\sim v}\bigl\{ n^{t-2}\bigl(n-d_{G}(u)-d _{G}(v)+\tau (u,v)\bigr) +n^{t-2}\bigl(d_{G}(v)- \tau (u,v)\bigr) \\ &\quad {}-\psi _{n}(t-2)d_{G}(u)+n ^{t-2} \bigl(d_{G}(u)-\tau (u,v)\bigr)- \psi _{n}(t-2)d_{G}(v) \\ &\quad {}+n^{t-2}\bigl(\tau (u,v)+1\bigr)+\psi _{n}(t-2) \bigl(d_{G}(u)+d_{G}(v)+1\bigr)+n\bigr\} \frac{1}{\sqrt{d _{G}(u)+d_{G}(v)}} \\ &=\sum_{u\sim v}\bigl\{ n^{t-1}+n^{t-2}+ \psi _{n}(t-2)+n\bigr\} \frac{1}{\sqrt{d _{G}(u)+d_{G}(v)}} \\ &=\sum_{u\sim v}\bigl(n+\psi _{n}(t)\bigr) \frac{1}{ \sqrt{d_{G}(u)+d_{G}(v)}}, \end{aligned} $$

which gives the desired result:

$$ \chi \bigl(S\bigl(G,t^{+}\bigr)\bigr)\leq \bigl(n+\psi _{n}(t)\bigr)\chi (G). $$

 □

4 Conclusion

In this paper, we have studied the topological indices of generalized Sierpiński and extended Sierpiński graphs with an arbitrary base graph. We have obtained some upper bounds in terms of some standard graph-theoretic parameters like order, size, radius and in terms of the topological indices of the base graph G. We have determined bounds for the atom-bond connectivity index, harmonic index, Zagreb indices and sum-connectivity index for the generalized Sierpiński graphs and extended Sierpiński graphs.