1 Introduction

In the past several decades, the dynamics of BAM neural networks has been widely investigated for their essential applications in classification, pattern recognition, optimization, signal and image processing, and so on [1–41]. In 1987, Kosko [42] proposed the following BAM neural network:

$$\begin{aligned} \textstyle\begin{cases} \frac{du_{i}(t)}{dt}=-a_{i}u_{i}(t)+\sum_{j=1}^{n}a_{ij}f_{j}(v_{j}(t-\sigma _{j}(t)))+I_{i},\\ \frac{dv_{i}(t)}{dt}=-b_{i}v_{i}(t)+\sum_{j=1}^{n}b_{ij}g_{j}(u_{j}(t-\tau_{j}(t)))+J_{i}, \end{cases}\displaystyle \end{aligned}$$
(1.1)

where \(i=1,2,\ldots,n,t>0\). Here, \(a_{i}>0,b_{i}>0\) denote the time scales of the respective layers of the network; \(-a_{i}u_{i}(t)\) and \(-b_{i}v_{i}(t)\) stand for the stabilizing negative feedback of the model. Noticing that the leakage delay often appears in the negative feedback term of neural networks (see [43–47]), Gopalsmay [48] studied the stability of the equilibrium and periodic solutions for the following BAM neural network:

$$\begin{aligned} \textstyle\begin{cases} \frac{dx_{i}(t)}{dt}=-a_{i}x_{i}(t-\tau_{i}^{(i)})+\sum_{j=1}^{n}a_{ij}f_{j}(y_{j}(t-\sigma_{j}^{(2)}))+I_{i},\\ \frac{dy_{i}(t)}{dt}=-b_{i}y_{i}(t-\tau_{i}^{(2)})+\sum_{j=1}^{n}b_{ij}g_{j}(x_{j}(t-\sigma_{j}^{(1)}))+J_{i}, \end{cases}\displaystyle \end{aligned}$$
(1.2)

where \(i=1,2,\ldots,n,t>0\). Since the delays in neural networks are usually time-varying in the real world, Liu [49] discussed the global exponential stability for the following general BAM neural network with time-varying leakage delays:

$$\begin{aligned} \textstyle\begin{cases} \frac{dx_{i}(t)}{dt}=-a_{i}x_{i}(t-\delta_{i}(t))+\sum_{j=1}^{n}a_{ij}f_{j}(y_{j}(t-\sigma_{ij}(t))+I_{i},\\ \frac{dy_{i}(t)}{dt}=-b_{i}y_{i}(t-\eta_{i}(t)+\sum_{j=1}^{n}b_{ij}g_{j}(x_{j}(t-\tau _{ij}(t))+J_{i}. \end{cases}\displaystyle \end{aligned}$$
(1.3)

However, so far, there have been rare reports on the existence and exponential stability of anti-periodic solutions of neural networks, especially for neural networks with leakage delays. Furthermore, the existence of anti-periodic solutions can be applied to help better describe the dynamical properties of nonlinear systems [49–65]. So we think that the investigation on the existence and stability of anti-periodic solutions for neural networks with leakage delays has significant value. Inspired by the ideas and considering the change of system parameters in time, we can modify neural network model (1.3) as follows:

$$\begin{aligned} \textstyle\begin{cases} \frac{dx_{i}(t)}{dt}=-a_{i}x_{i}(t-\delta_{i}(t))+\sum_{j=1}^{n}a_{ij}(t)f_{j}(y_{j}(t-\sigma_{ij}(t)))+I_{i}(t),\\ \frac{dy_{i}(t)}{dt}=-b_{i}y_{i}(t-\eta_{i}(t))+\sum_{j=1}^{n}b_{ij}(t)g_{j}(x_{j}(t-\tau_{ij}(t)))+J_{i}(t). \end{cases}\displaystyle \end{aligned}$$
(1.4)

The main objective of this article is to analyze the exponential stability behavior of anti-periodic oscillations of (1.4). Based on the fundamental solution matrix, Lyapunov function, and fundamental function sequences, we establish a sufficient condition ensuring the existence and global exponential stability of anti-periodic solutions of (1.4). The derived findings can be used directly to numerous specific networks. Besides, computer simulations are performed to support the obtained predictions. Our findings are a good complement to the work of Gopalsmay [48] and Liu [49].

The paper is planned as follows. In Sect. 2, several notations and preliminary results are prepared. In Sect. 3, we give a sufficient condition for the existence and global exponential stability of anti-periodic solution of (1.4). In Sect. 4, we present an example to show the correctness of the obtained analytic findings.

Remark 1.1

A time delay that exists in the negative feedback term (or called leakage term or forgetting term) of neural networks is called leakage delay. If there exists an anti-periodic solution in a dynamical system, then we can say that the system has anti-periodic oscillations.

2 Preliminary results

In this segment, several notations and lemmas will be given.

For any vector \(V=(v_{1},v_{2},\dots,v_{n})^{T}\) and matrix \(D=(d_{ij})_{n\times{n}}\), we define the norm as

$$\Vert V \Vert = \Biggl(\sum_{i=1}^{n}v_{i}^{2} \Biggr)^{\frac{1}{2}},\qquad \Vert D \Vert = \Biggl(\sum _{i=1}^{n}d_{ij}^{2} \Biggr)^{\frac{1}{2}}, $$

respectively. Let

$$\begin{aligned} &\tau=\Bigl\{ \sup_{t\in{R}}\max_{1\leq{i}\leq{n}} \delta_{i}(t),\sup_{t\in {R}}\max_{1\leq{i}\leq{n}} \eta_{i}(t), \sup_{t\in{R}}\max_{1\leq{i,j}\leq {n}} \sigma_{ij}(t),\sup_{t\in{R}}\max_{1\leq{i,j}\leq{n}} \tau_{ij}(t)\Bigr\} , \\ &\varphi(s)=\bigl(\varphi_{1}(s),\varphi_{2}(s),\ldots, \varphi_{n}(s)\bigr)^{T},\qquad \psi(s)=\bigl(\psi_{1}(s), \psi_{2}(s),\ldots,\psi_{n}(s)\bigr)^{T}, \end{aligned}$$

where \(\varphi_{i}(s)\in{C}([-\tau,0],R), \psi_{i}(s)\in{C}([-\tau,0],R),i=1,2,\ldots,n\), we define

$$\Vert \varphi \Vert =\sup_{-\tau\leq{s}\leq0} \Biggl(\sum _{i=1}^{n} \bigl\vert \varphi _{i}(s) \bigr\vert ^{2} \Biggr)^{\frac{1}{2}}, \qquad \Vert \psi \Vert =\sup _{-\tau\leq{s}\leq0} \Biggl(\sum_{i=1}^{n} \bigl\vert \psi_{i}(s) \bigr\vert ^{2} \Biggr)^{\frac{1}{2}}. $$

We assume that system (1.4) always satisfies the following initial conditions:

$$\begin{aligned} \textstyle\begin{cases} x_{i0}=\varphi_{i}(s),& s\in[-\tau,0],\\ y_{i0}=\psi_{i}(s),& s\in[-\tau,0]. \end{cases}\displaystyle \end{aligned}$$
(2.1)

Let \(x(t)=(x_{1}(t),x_{2}(t),\ldots,x_{n}(t))^{T}, y(t)=(y_{1}(t),y_{2}(t),\ldots,y_{n}(t))^{T}\) be the solution of system (1.4) with initial conditions (2.1). We say the solution \(x(t)=(x_{1}(t),x_{2}(t),\ldots,x_{n}(t))^{T}, y(t)=(y_{1}(t),y_{2}(t),\ldots,y_{n}(t))^{T}\) is T-anti-periodic on \(R^{2n}\) if \(x_{i}(t+T)=-x_{i}(t), y_{i}(t+T)=-y_{i}(t)\) for all \(t\in{R}\) and \(i=1,2,\dots,n\), where T is a positive constant.

Throughout this paper, for \(i,j=1,2,\ldots,n\), it will be assumed that there exist constants such that

$$\begin{aligned} &\delta_{i}^{+}=\sup_{t\in{R}} \delta_{i}(t), \qquad \eta_{i}^{+}=\sup _{t\in{R}}\eta_{i}(t),\qquad a_{ij}^{+}= \sup_{t\in{R}}a_{ij}(t), \\ & b_{ij}^{+}= \sup_{t\in{R}}b_{ij}(t),\qquad \tau_{ij}^{+}= \sup_{t\in{R}}\tau_{ij}(t), \qquad \sigma_{ij}^{+}= \sup_{t\in{R}}\sigma_{ij}(t) \end{aligned}$$

and \(t-\delta_{i}(t)>0, t-\eta_{i}(t)>0\).

We also assume that the following conditions hold.

(H1) For \(j=1,2,\ldots,n\), there exist constants \(L_{jf}>0, L_{jg}>0, M_{j}^{f}>0\), and \(M_{j}^{g}>0\) such that

$$\textstyle\begin{cases} \vert f_{j}(u )-f_{j}(v ) \vert \leq L_{jf} \vert u -v \vert , \quad \vert f_{j}(u) \vert < M_{j}^{f},\\ \vert g_{j}(u )-g_{j}(v ) \vert \leq L_{jg} \vert u -v \vert ,\quad \vert g_{j}(u) \vert < M_{j}^{g}, \end{cases} $$

for all \(u, v \in{R}\).

(H2) For all \(t,u\in{R}\) and \(i,j=1,2,\ldots,n\),

$$\textstyle\begin{cases} a_{ij}(t+T)f_{j}(u)=-a_{ij}(t)f_{j}(-u),\qquad b_{ij}(t+T)g_{j}(u)=-b_{ij}(t)g_{j}(-u),\\ \delta_{i}(t+T)=\delta_{i}(t),\qquad \eta_{i}(t+T)=\eta_{i}(t),\qquad \sigma_{ij}(t+T)=\sigma_{ij}(t),\\ \tau_{ij}(t+T)=\tau_{ij}(t),\qquad I_{i}(t+T)=-I_{i}(t),\qquad J_{i}(t+T)=-J_{i}(t), \end{cases} $$

where T is a positive constant.

It is clear that the conditions can be fulfilled; for example, let \(a_{ij}(t)=0.2 \vert \cos t \vert , f_{j}(u)=u^{2j-1},i,j=1,2,\ldots,n\), then we have \(a_{ij}(t+T)f_{j}(u)=-a_{ij}(t)f_{j}(-u)\).

(H3) The following inequality holds:

$$\frac{\sqrt{2}}{\alpha}\bigl(a_{i}\delta_{i}^{+}+b_{i} \eta_{i}^{+}\bigr)< 1, $$

where \(\alpha=\min_{1\leq{i}\leq{n}}\{a_{i},b_{i}\}, i=1,2,\dots,n\).

Definition 2.1

The solution \((x^{*}(t),y^{*}(t))^{T}\) of system (1.4) is said to globally exponentially stable if there exist constants \(\beta>0\) and \(M>1\) such that

$$\sum_{i=1}^{n} \bigl\vert x_{i}(t)-x_{i}^{*}(t) \bigr\vert ^{2}+\sum _{i=1}^{n} \bigl\vert y_{i}(t)-y_{i}^{*}(t) \bigr\vert ^{2}\leq {M}e^{-\beta t}\bigl( \bigl\Vert \varphi- \varphi^{*} \bigr\Vert ^{2}+ \bigl\Vert \psi-\psi^{*} \bigr\Vert ^{2}\bigr) $$

for each solution \((x(t),y(t))^{T}\) of system (1.4).

Next, we present three important lemmas which are necessary for proving our main results in Sect. 3.

Lemma 2.1

Let

$$A=\left ( \begin{matrix} -a_{i} & 0 \\ 0 & -b_{i} \end{matrix} \right ),\qquad \alpha=\min_{1\leq{i}\leq{n}}\{a_{i},b_{i} \}, $$

then we have

$$\Vert \exp A t \Vert \leq\sqrt{2}e^{-\alpha t} $$

for all \(t\geq0\).

Proof

Since

$$A=\left ( \begin{matrix} -a_{i} & 0 \\ 0 & -b_{i} \end{matrix} \right ), $$

it follows that

$$\exp A t=\left ( \begin{matrix} e^{-a_{i}t} & 0 \\ 0 & e^{-b_{i}t} \end{matrix} \right ). $$

By the definition of matrix norm, we get

$$\Vert \exp A t \Vert = \bigl(e^{ -2a_{i}t}+e^{ -2b_{i}t} \bigr)^{\frac{1}{2}}\leq\sqrt {2}e^{-\alpha t}. $$

 □

Lemma 2.2

Assume that

$$\mathrm{(H4)} \textstyle\begin{cases} -2a_{i}+a_{i}^{2}\delta_{i}^{+}+\sum_{j=1}^{n}a_{i}\delta _{i}^{+}a_{ij}^{+}L_{jf}^{2\xi_{j}}+\sum_{j=1}^{n}a_{ij}^{+}L_{jf}^{2\xi_{j}}\\ \quad{}+\sum_{i=1}^{n}a_{i}^{2}\delta_{i}^{+}+\sum_{j=1}^{n}b_{i}\eta _{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon _{j})}+b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})}< 0, \\ {-}2b_{i}+b_{i}^{2}\eta_{i}^{+}+\sum_{j=1}^{n}b_{i}\eta _{i}^{+}b_{ij}^{+}L_{jg}^{2\varepsilon_{j}}+\sum_{j=1}^{n}b_{ij}^{+}L_{jg}^{2\varepsilon_{j}}\\ \quad{} +\sum_{i=1}^{n}a_{i}^{2}\delta_{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi _{j})}+a_{ij}^{+}L_{jf}^{2(1-\xi_{j})}+b_{i}\eta_{i}^{+}< 0, \end{cases} $$

where \(0\leq\varepsilon_{i}\leq1\ (i=1,2,3,4,5,6)\) are any constants. Then there exists \(\beta>0\) such that

$$\begin{aligned} & \beta-2a_{i}+a_{i}^{2}\delta_{i}^{+}+ \sum_{j=1}^{n}a_{i}\delta _{i}^{+}a_{ij}^{+}L_{jf}^{2\xi_{j}}+ \sum_{j=1}^{n}a_{ij}^{+}L_{jf}^{2\xi _{j}} \\ & \quad{}+\sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+}e^{\beta \delta_{i}^{+}}+\sum _{j=1}^{n}b_{i}\eta_{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon _{j})}e^{\beta\tau_{ij}^{+}}+b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})}e^{\beta \tau_{ij}^{+}} \leq0, \\ & \beta-2b_{i}+b_{i}^{2}\eta_{i}^{+}+ \sum_{j=1}^{n}b_{i}\eta _{i}^{+}b_{ij}^{+}L_{jg}^{2\varepsilon_{j}}+ \sum_{j=1}^{n}b_{ij}^{+}L_{jg}^{2\varepsilon_{j}} \\ & \quad{}+\sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})}e^{\beta \delta_{ij}^{+}}+a_{ij}^{+}L_{jf}^{2(1-\xi_{j})}e^{\beta\delta _{ij}^{+}}+b_{i} \eta_{i}^{+}e^{\beta\eta_{i}^{+}}\leq0. \end{aligned}$$

Proof

Let

$$\begin{aligned} \varrho_{1i}(\beta)={}&\beta-2a_{i}+a_{i}^{2} \delta_{i}^{+}+\sum_{j=1}^{n}a_{i} \delta_{i}^{+}a_{ij}^{+}L_{jf}^{2\xi_{j}}+ \sum_{j=1}^{n}a_{ij}^{+}L_{jf}^{2\xi_{j}} \\ & {}+\sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+}e^{\beta \delta_{i}^{+}}+\sum _{j=1}^{n}b_{i}\eta_{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon _{j})}e^{\beta\tau_{ij}^{+}}+b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})}e^{\beta \tau_{ij}^{+}}, \\ \varrho_{2i}(\beta)={}&\beta-2b_{i}+b_{i}^{2} \eta_{i}^{+}+\sum_{j=1}^{n}b_{i} \eta _{i}^{+}b_{ij}^{+}L_{jg}^{2\varepsilon_{j}}+ \sum_{j=1}^{n}b_{ij}^{+}L_{jg}^{2\varepsilon_{j}} \\ & {}+\sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})}e^{\beta \delta_{ij}^{+}}+a_{ij}^{+}L_{jf}^{2(1-\xi_{j})}e^{\beta\delta _{ij}^{+}}+b_{i} \eta_{i}^{+}e^{\beta\eta_{i}^{+}}. \end{aligned}$$

Obviously, \(\varrho_{ji}(\beta)\ (j=1,2;i=1,2,\ldots,n)\) is a continuously differential function. We can easily check that

$$\textstyle\begin{cases} \frac{d\varrho_{1i}(\beta)}{d\beta}=1+\delta_{i}^{+}\sum_{i=1}^{n}a_{i}^{2}\delta_{i}^{+}e^{\beta \delta_{i}^{+}}+\tau_{ij}^{+}\sum_{j=1}^{n}b_{i}\eta _{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})}e^{\beta\tau_{ij}^{+}}+\tau _{ij}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})}e^{\beta\tau _{ij}^{+}}>0,\\ \lim_{\beta\rightarrow{+\infty}}\varrho_{1i}(\beta)=+\infty,\qquad \varrho _{1i}(0)< 0,\\ \frac{d\varrho_{2i}(\beta)}{d\beta}=1+\delta_{ij}^{+}\sum_{i=1}^{n}a_{i}^{2}\delta_{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})}e^{\beta \delta_{ij}^{+}}+\delta_{ij}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})}e^{\beta \delta_{ij}^{+}}+\eta_{i}^{+}b_{i}\eta_{i}^{+}e^{\beta\eta_{i}^{+}}>0,\\ \lim_{\beta\rightarrow{+\infty}}\varrho_{2i}(\beta)=+\infty,\qquad \varrho_{2i}(0)< 0. \end{cases} $$

By using the intermediate value theorem, we have that there exist constants \(\beta_{i}^{*}>0\ (i=1,2)\) such that

$$\varrho_{j}\bigl(\beta_{i}^{*}\bigr)=0,\quad j=1,2. $$

Let \(\beta_{0}=\min\{\beta_{1}^{*},\beta_{2}^{*}\}\), then it follows that \(\beta_{0}>0\) and

$$\varrho_{j}(\beta_{0})\leq0,\quad j=1,2. $$

This completes the proof of Lemma 2.2. □

Lemma 2.3

Assume that (H1), (H3), and (H4) are satisfied. Then, for any solution \((x_{1}(t),x_{2}(t),\ldots,x_{n}(t), y_{1},y_{2},\ldots, y_{n})^{T}\) of system (1.4), there exists a constant

$$\begin{aligned} \sigma^{*}={}& \biggl[1-\frac{\sqrt{2}}{\alpha}\bigl(a_{i} \delta_{i}^{+}+b_{i}\eta _{i}^{+} \bigr) \biggr]^{-1} \bigl[a_{i}\delta_{i}^{+} \bigl(a_{ij}^{+}M_{j}^{f}+I_{i}^{+} \bigr) \\ & {}+a_{ij}^{+}M_{j}^{f}+I_{i}^{+}+b_{i} \eta_{i}^{+} \bigl(b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr)+b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr] \end{aligned}$$

such that

$$\bigl\vert x_{i}(t) \bigr\vert \leq{\sigma^{*}},\qquad \bigl\vert y_{i}(t) \bigr\vert \leq{\sigma^{*}},\quad i=1,2,\ldots,n, $$

for all \(t>0\).

Proof

From (1.4), we have

$$\begin{aligned} \textstyle\begin{cases} \frac{dx_{i}(t)}{dt}=-a_{i}x_{i}(t)+a_{i}[x_{i}(t)-x_{i}(t-\delta_{i}(t))]+\sum_{j=1}^{n}a_{ij}(t)f_{j}(y_{j}(t-\sigma_{ij}(t)))+I_{i}(t),\\ \frac{dy_{i}(t)}{dt}=-b_{i}y_{i}(t)+b_{i}[y_{i}(t)-y_{i}(t-\eta_{i}(t))]+\sum_{j=1}^{n}b_{ij}(t)g_{j}(x_{j}(t-\tau_{ij}(t)))+J_{i}(t). \end{cases}\displaystyle \end{aligned}$$
(2.2)

Then we have

$$\begin{aligned} \textstyle\begin{cases} \frac{dx_{i}(t)}{dt}=-a_{i}x_{i}(t)+a_{i}\int_{t-\delta _{i}(t)}^{t}x_{i}^{\prime}(s)\,ds+\sum_{j=1}^{n}a_{ij}(t)f_{j}(y_{j}(t-\sigma _{ij}(t)))+I_{i}(t),\\ \frac{dy_{i}(t)}{dt}=-b_{i}y_{i}(t)+b_{i}\int_{t-\eta_{i}(t)}^{t}y_{i}^{\prime}(s)\,ds+\sum_{j=1}^{n}b_{ij}(t)g_{j}(x_{j}(t-\tau_{ij}(t)))+J_{i}(t). \end{cases}\displaystyle \end{aligned}$$
(2.3)

Thus

$$\begin{aligned} \textstyle\begin{cases} \frac{dx_{i}(t)}{dt}=-a_{i}x_{i}(t)+a_{i}\int_{t-\delta_{i}(t)}^{t} [-a_{i}x_{i}(s-\delta_{i}(s))\\ \phantom{\frac{dx_{i}(t)}{dt}=}{}+\sum_{j=1}^{n}a_{ij}(s)f_{j}(y_{j}(s-\sigma _{ij}(s)))+I_{i}(s) ]\,ds\\ \phantom{\frac{dx_{i}(t)}{dt}=}{}+\sum_{j=1}^{n}a_{ij}(t)f_{j}(y_{j}(t-\sigma_{ij}(t)))+I_{i}(t),\\ \frac{dy_{i}(t)}{dt}=-b_{i}y_{i}(t)+b_{i}\int_{t-\eta_{i}(t)}^{t} [-b_{i}y_{i}(s-\eta_{i}(s))\\ \phantom{\frac{dy_{i}(t)}{dt}=}{}+\sum_{j=1}^{n}b_{ij}(s)g_{j}(x_{j}(s-\tau _{ij}(s)))+J_{i}(s) ]\,ds\\ \phantom{\frac{dx_{i}(t)}{dt}=}{}+\sum_{j=1}^{n}b_{ij}(t)g_{j}(x_{j}(t-\tau_{ij}(t)))+J_{i}(t). \end{cases}\displaystyle \end{aligned}$$
(2.4)

Let

$$\begin{aligned} &z_{ii}(t)=\left ( \begin{matrix} x_{i}(t) \\ y_{i}(t) \end{matrix} \right ),\qquad A=\left ( \begin{matrix} -a_{i} & 0 \\ 0 & -b_{i} \end{matrix} \right ),\\ & f \bigl(x_{i}(t),y_{i}(t)\bigr)=\left ( \begin{matrix} f_{1}(x_{i}(t),y_{i}(t) \\ f_{2}(x_{i}(t),y_{i}(t) \end{matrix} \right),\qquad I_{ii}(t)= \left( \begin{matrix} I_{i}(t) \\ J_{i}(t) \end{matrix} \right), \end{aligned}$$

where

$$\begin{aligned} f_{1}(x_{i}(t),y_{i}(t)={}&a_{i} \int_{t-\delta_{i}(t)}^{t} \Biggl[-a_{i}x_{i} \bigl(s-\delta _{i}(s)\bigr)+\sum_{j=1}^{n}a_{ij}(s)f_{j} \bigl(y_{j}\bigl(s-\sigma_{ij}(s)\bigr)\bigr)+I_{i}(s) \Biggr]\,ds \\ & {}+\sum_{j=1}^{n}a_{ij}(t)f_{j} \bigl(y_{j}\bigl(t-\sigma_{ij}(t)\bigr)\bigr), \\ f_{2}(x_{i}(t),y_{i}(t)={}& b_{i} \int_{t-\eta_{i}(t)}^{t} \Biggl[-b_{i}y_{i} \bigl(s-\eta _{i}(s)\bigr)+\sum_{j=1}^{n}b_{ij}(s)g_{j} \bigl(x_{j}\bigl(s-\tau_{ij}(s)\bigr)\bigr)+J_{i}(s) \Biggr]\,ds \\ & {}+\sum_{j=1}^{n}b_{ij}(t)g_{j} \bigl(x_{j}\bigl(t-\tau_{ij}(t)\bigr)\bigr), \end{aligned}$$

then system (1.4) can be written in the following equivalent form:

$$\begin{aligned} z_{ii}^{\prime}(t)\leq{A}z_{ii}(t)+f \bigl(x_{i}(t),y_{i}(t)\bigr)+I_{ii}(t). \end{aligned}$$
(2.5)

Solving inequality (2.5), we have

$$z_{ii}(t)\leq{e^{At}}z_{ii}(0)+ \int_{0}^{t}e^{A(t-s)}\bigl[f \bigl(x_{i}(s),y_{i}(s)\bigr)+I_{ii}(t)\bigr]\,ds. $$

It follows from Lemma 2.1 that

$$\begin{aligned} \bigl\Vert z_{ii}(t) \bigr\Vert \leq {}&\sqrt{2}e^{-\alpha t} \bigl\Vert z_{ii}(0) \bigr\Vert +\sqrt{2} \int_{0}^{t}e^{\alpha (t-s)}\bigl[ \bigl\Vert f \bigl(x_{i}(s),y_{i}(s)\bigr) \bigr\Vert + \bigl\vert I_{ii}(s) \bigr\vert \bigr]\,ds \\ \leq{}& \sqrt{2} \Vert \varphi \Vert ^{2}+\frac{\sqrt{2}}{\alpha} \bigl(1-e^{-\alpha t} \bigr) \\ &{} \times \bigl[a_{i}\delta_{i}^{+} \bigl( \bigl\vert x_{i}\bigl(t-\delta _{i}(t)\bigr) \bigr\vert +a_{ij}^{+}M_{j}^{f}+I_{i}^{+} \bigr)+a_{ij}^{+}M_{j}^{f}+I_{i}^{+} \\ &{} +b_{i}\eta_{i}^{+} \bigl( \bigl\vert y_{i}\bigl(t-\eta _{i}(t)\bigr) \bigr\vert +b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr)+b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr] \\ \leq {}&\sqrt{2} \Vert \varphi \Vert ^{2}+\frac{\sqrt{2}}{\alpha} \bigl(1-e^{-\alpha t} \bigr) \\ &{} \times \bigl[a_{i}\delta_{i}^{+} \bigl( \bigl\Vert z_{ii}(t) \bigr\Vert +a_{ij}^{+}M_{j}^{f}+I_{i}^{+} \bigr)+a_{ij}^{+}M_{j}^{f}+I_{i}^{+} \\ &{} + b_{i}\eta_{i}^{+} \bigl(\Vert z_{ii}(t) \Vert +b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr)+b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr] \\ \leq{}& \sqrt{2} \Vert \varphi \Vert ^{2}+\frac{\sqrt{2}}{\alpha} \\ &{} \times \bigl[a_{i}\delta_{i}^{+} \bigl( \bigl\Vert z_{ii}(t) \bigr\Vert +a_{ij}^{+}M_{j}^{f}+I_{i}^{+} \bigr)+a_{ij}^{+}M_{j}^{f}+I_{i}^{+} \\ &{} + b_{i}\eta_{i}^{+} \bigl( \bigl\Vert z_{ii}(t) \bigr\Vert +b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr)+b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr]. \end{aligned}$$
(2.6)

Then

$$\begin{aligned} \bigl\Vert z_{ii}(t) \bigr\Vert \leq{}& \biggl[1- \frac{\sqrt{2}}{\alpha}\bigl(a_{i}\delta _{i}^{+}+b_{i} \eta_{i}^{+}\bigr) \biggr]^{-1} \bigl[a_{i}\delta_{i}^{+} \bigl(a_{ij}^{+}M_{j}^{f}+I_{i}^{+} \bigr) \\ & {}+a_{ij}^{+}M_{j}^{f}+I_{i}^{+}+b_{i} \eta_{i}^{+} \bigl(b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr)+b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr]. \end{aligned}$$

Let

$$\begin{aligned} \sigma^{*}={}& \biggl[1-\frac{\sqrt{2}}{\alpha}\bigl(a_{i} \delta_{i}^{+}+b_{i}\eta _{i}^{+} \bigr) \biggr]^{-1} \bigl[a_{i}\delta_{i}^{+} \bigl(a_{ij}^{+}M_{j}^{f}+I_{i}^{+} \bigr) \\ & {}+a_{ij}^{+}M_{j}^{f}+I_{i}^{+}+b_{i} \eta_{i}^{+} \bigl(b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr)+b_{ij}^{+}M_{j}^{g}+J_{i}^{+} \bigr]. \end{aligned}$$

Then it follows that \(\vert x_{i}(t) \vert \leq\sigma^{*}, \vert y_{i}(t) \vert \leq\sigma^{*}, i=1,2,\ldots,n\), for all \(t>0\). This completes the proof of Lemma 2.3. □

3 Main results

In this section, we present our main result that there exists an exponentially stable anti-periodic solution of (1.4).

Theorem 3.1

Assume that (H1)–(H4) hold true. Then any solution \((x^{*}(t),y^{*}(t))^{T}\) of system (1.4) is globally exponentially stable.

Proof

Let \(u_{i}(t)=x_{i}(t)-x_{i}^{*}(t), v_{i}(t)=y_{i}(t)-y_{i}^{*}(t), i=1,2,\ldots,n\). It follows from system (2.4) that

$$\begin{aligned} \textstyle\begin{cases} \frac{du_{i}(t)}{dt}=-a_{i}u_{i}(t)+a_{i}\int_{t-\delta_{i}(t)}^{t} [-a_{i}u_{i}(s-\delta_{i}(s))\\ \phantom{\frac{du_{i}(t)}{dt}=}{}+\sum_{j=1}^{n}a_{ij}(s)(f_{j}(y_{j}(s-\sigma_{ij}(s)))-f_{j}(y_{j}^{*}(s-\sigma _{ij}(s)))) ]\,ds\\ \phantom{\frac{du_{i}(t)}{dt}=}{}+\sum_{j=1}^{n}a_{ij}(t)(f_{j}(y_{j}(t-\sigma_{ij}(t)))-f_{j}(y_{j}^{*}(t-\sigma _{ij}(t)))),\\ \frac{dv_{i}(t)}{dt}=-b_{i}v_{i}(t)+b_{i}\int_{t-\eta_{i}(t)}^{t} [-b_{i}v_{i}(s-\eta_{i}(s))\\ \phantom{\frac{dv_{i}(t)}{dt}=}{}+\sum_{j=1}^{n}b_{ij}(s)(g_{j}(x_{j}(s-\tau_{ij}(s)))-g_{j}(x_{j}^{*}(s-\tau _{ij}(s)))) ]\,ds\\ \phantom{\frac{dv_{i}(t)}{dt}=}{}+\sum_{j=1}^{n}b_{ij}(t)(g_{j}(x_{j}(t-\tau_{ij}(t)))-g_{j}(x_{j}(t-\tau_{ij}(t)))), \end{cases}\displaystyle \end{aligned}$$
(3.1)

which leads to

$$\begin{aligned} \textstyle\begin{cases} \frac{1}{2}\frac{du_{i}^{2}(t)}{dt}=-a_{i}u_{i}^{2}(t)+a_{i}u_{i}(t)\int_{t-\delta _{i}(t)}^{t} [-a_{i}u_{i}(s-\delta_{i}(s))\\ \phantom{\frac{1}{2}\frac{du_{i}^{2}(t)}{dt}=}{}+\sum_{j=1}^{n}a_{ij}(s)(f_{j}(y_{j}(s-\sigma_{ij}(s)))-f_{j}(y_{j}^{*}(s-\sigma _{ij}(s)))) ]\,ds\\ \phantom{\frac{1}{2}\frac{du_{i}^{2}(t)}{dt}=}{}+u_{i}(t)\sum_{j=1}^{n}a_{ij}(t)(f_{j}(y_{j}(t-\sigma _{ij}(t)))-f_{j}(y_{j}^{*}(t-\sigma_{ij}(t)))),\\ \frac{1}{2}\frac{dv_{i}^{2}(t)}{dt}=-b_{i}v_{i}^{2}(t)+b_{i}v_{i}(t)\int_{t-\eta _{i}(t)}^{t} [-b_{i}v_{i}(s-\eta_{i}(s))\\ \phantom{\frac{1}{2}\frac{dv_{i}^{2}(t)}{dt}=}{}+\sum_{j=1}^{n}b_{ij}(s)(g_{j}(x_{j}(s-\tau_{ij}(s)))-g_{j}(x_{j}^{*}(s-\tau _{ij}(s)))) ]\,ds\\ \phantom{\frac{1}{2}\frac{dv_{i}^{2}(t)}{dt}=}{}+v_{i}(t)\sum_{j=1}^{n}b_{ij}(t)(g_{j}(x_{j}(t-\tau_{ij}(t)))-g_{j}(x_{j}(t-\tau_{ij}(t)))). \end{cases}\displaystyle \end{aligned}$$
(3.2)

In view of condition (H1), we get

$$\begin{aligned} \textstyle\begin{cases} \frac{du_{i}^{2}(t)}{dt}\leq-2a_{i}u_{i}^{2}(t)+a_{i}u_{i}(t)\int_{t-\delta _{i}(t)}^{t} [-a_{i}u_{i}(s-\delta_{i}(s))\\ \phantom{\frac{du_{i}^{2}(t)}{dt}\leq}{}+\sum_{j=1}^{n}a_{ij}(s)(f_{j}(y_{j}(s-\sigma_{ij}(s)))-f_{j}(y_{j}^{*}(s-\sigma _{ij}(s)))) ]\,ds\\ \phantom{\frac{du_{i}^{2}(t)}{dt}\leq}{}+u_{i}(t)\sum_{j=1}^{n}a_{ij}(t)(f_{j}(y_{j}(t-\sigma _{ij}(t)))-f_{j}(y_{j}^{*}(t-\sigma_{ij}(t)))),\\ \frac{dv_{i}^{2}(t)}{dt}\leq-2b_{i}v_{i}^{2}(t)+b_{i}v_{i}(t)\int_{t-\eta_{i}(t)}^{t} [-b_{i}v_{i}(s-\eta_{i}(s))\\ \phantom{\frac{dv_{i}^{2}(t)}{dt}\leq}{}+\sum_{j=1}^{n}b_{ij}(s)(g_{j}(x_{j}(s-\tau_{ij}(s)))-g_{j}(x_{j}^{*}(s-\tau _{ij}(s)))) ]\,ds\\ \phantom{\frac{dv_{i}^{2}(t)}{dt}\leq}{}+v_{i}(t)\sum_{j=1}^{n}b_{ij}(t)(g_{j}(x_{j}(t-\tau_{ij}(t)))-g_{j}(x_{j}(t-\tau_{ij}(t)))). \end{cases}\displaystyle \end{aligned}$$
(3.3)

Then

$$\begin{aligned} \textstyle\begin{cases} \frac{du_{i}^{2}(t)}{dt}\leq-2a_{i}u_{i}^{2}(t)+a_{i}\delta_{i}^{+} [a_{i}(u_{i}^{2}+u_{i}^{2}(t-\delta_{i}(t)))\\ \phantom{\frac{du_{i}^{2}(t)}{dt}\leq}{}+\sum_{j=1}^{n}a_{ij}^{+}(L_{jf}^{2\xi_{j}}u_{i}^{2}(t)+L_{jf}^{2(1-\xi _{j})}v_{j}^{2}(t-\delta_{ij}(t))) ]\\ \phantom{\frac{du_{i}^{2}(t)}{dt}\leq}{}+\sum_{j=1}^{n}a_{ij}^{+}(L_{jf}^{2\xi_{j}}u_{i}^{2}(t)+L_{jf}^{2(1-\xi _{j})}v_{j}^{2}(t-\delta_{ij}(t))),\\ \frac{dv_{i}^{2}(t)}{dt}\leq-2b_{i}v_{i}^{2}(t)+b_{i}\eta_{i}^{+} [b_{i}(v_{i}^{2}+v_{i}^{2}(t-\eta_{i}(t)))\\ \phantom{\frac{dv_{i}^{2}(t)}{dt}\leq}{}+\sum_{j=1}^{n}b_{ij}^{+}(L_{jg}^{2\varepsilon _{j}}v_{i}^{2}(t)+L_{jg}^{2(1-\varepsilon_{j})}u_{j}^{2}(t-\tau_{ij}(t))) ]\\ \phantom{\frac{dv_{i}^{2}(t)}{dt}\leq}{}+\sum_{j=1}^{n}b_{ij}^{+}(L_{jg}^{\varepsilon _{j}}v_{i}^{2}(t)+L_{jg}^{2(1-\varepsilon_{j})}u_{j}^{2}(t-\tau_{ij}(t))), \end{cases}\displaystyle \end{aligned}$$
(3.4)

where \(0\leq\xi_{j},\varepsilon_{j}\leq1,j=1,2,\ldots,n\).

Now we consider the following Lyapunov function:

$$\begin{aligned} V(t)={}&e^{\beta t}\sum_{i=1}^{n}u_{i}^{2}(t)+e^{\beta t} \sum_{i=1}^{n}v_{i}^{2}(t) \\ &{}+\sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+} \int_{t-\delta_{i}(t)}^{t}e^{\beta(s+\delta _{i}(t))}u_{i}^{2}(s)\,ds \\ & {}+\sum_{i=1}^{n}\sum _{j=1}^{n}a_{i}\delta_{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi _{j})} \int_{t-\delta_{ij}(t)}^{t}e^{\beta(s+\delta_{ij}(t))}v_{j}^{2}(s)\,ds \\ & {}+\sum_{i=1}^{n}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})} \int_{t-\delta _{ij}(t)}^{t}e^{\beta(s+\delta_{ij}(t))}v_{j}^{2}(s)\,ds \\ & {}+\sum_{i=1}^{n}b_{i}^{2} \eta_{i}^{+} \int_{t-\eta_{i}(t)}^{t}e^{\beta(s+\eta _{i}(t))}v_{i}^{2}(s)\,ds \\ & {}+\sum_{i=1}^{n}\sum _{j=1}^{n}b_{i}\eta _{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \int_{t-\tau _{ij}(t)}^{t}e^{\beta(s+\tau_{ij}(t))}u_{j}^{2}(s)\,ds \\ & {}+\sum_{i=1}^{n}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \int_{t-\tau _{ij}(t)}^{t}e^{\beta(s+\tau_{ij}(t))}u_{j}^{2}(s)\,ds, \end{aligned}$$
(3.5)

where β is given by Lemma 2.2. Differentiating \(V(t)\) along solutions to system (1.4), together with (3.3), we have

$$\begin{aligned} \frac{dV(t)}{dt}\leq{}&\beta{e^{\beta t}} \Biggl[\sum _{i=1}^{n}u_{i}^{2}(t)+\sum _{i=1}^{n}v_{i}^{2}(t) \Biggr] \\ & {}+e^{\beta t}\sum_{j=1}^{n} \Biggl\{ -2a_{i}u_{i}^{2}(t)+a_{i} \delta_{i}^{+} \Biggl[a_{i}\bigl(u_{i}^{2}+u_{i}^{2} \bigl(t-\delta_{i}(t)\bigr)\bigr) \\ & {}+\sum_{j=1}^{n}a_{ij}^{+} \bigl(L_{jf}^{2\xi_{j}}u_{i}^{2}(t)+L_{jf}^{2(1-\xi _{j})}v_{j}^{2} \bigl(t-\delta_{ij}(t)\bigr)\bigr) \Biggr] \\ & {}+\sum_{j=1}^{n}a_{ij}^{+} \bigl(L_{jf}^{2\xi_{j}}u_{i}^{2}(t)+L_{jf}^{2(1-\xi _{j})}v_{j}^{2} \bigl(t-\delta_{ij}(t)\bigr)\bigr) \Biggr\} \\ & {}+e^{\beta t}\sum_{j=1}^{n} \Biggl\{ -2b_{i}v_{i}^{2}(t)+b_{i} \eta_{i}^{+} \Biggl[b_{i}\bigl(v_{i}^{2}+v_{i}^{2} \bigl(t-\eta_{i}(t)\bigr)\bigr) \\ & {}+\sum_{j=1}^{n}b_{ij}^{+} \bigl(L_{jg}^{2\varepsilon _{j}}v_{i}^{2}(t)+L_{jg}^{2(1-\varepsilon_{j})}u_{j}^{2} \bigl(t-\tau_{ij}(t)\bigr)\bigr) \Biggr] \\ &{} +\sum_{j=1}^{n}b_{ij}^{+} \bigl(L_{jg}^{\varepsilon _{j}}v_{i}^{2}(t)+L_{jg}^{2(1-\varepsilon_{j})}u_{j}^{2} \bigl(t-\tau_{ij}(t)\bigr)\bigr) \Biggr\} \\ & {}+\sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+}\bigl[e^{\beta(t+\delta_{i}(t))} u_{i}^{2}(t)-e^{\beta t}u_{i}^{2} \bigl(t-\delta_{i}(t)\bigr)\bigr] \\ & {}+\sum_{i=1}^{n}\sum _{j=1}^{n}a_{i}\delta_{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi _{j})} \bigl[e^{\beta(t+\delta_{ij}(t))}v_{j}^{2}(t)-e^{\beta t}v_{j}^{2} \bigl(t-\delta _{ij}(t)\bigr)\bigr] \\ & {}+\sum_{i=1}^{n}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})} \bigl[e^{\beta(t+\delta _{ij}(t))}v_{j}^{2}(t)-e^{\beta(t)}v_{j}^{2} \bigl(t-\delta_{ij}(t)\bigr)\bigr] \\ & {}+\sum_{i=1}^{n}b_{i}^{2} \eta_{i}^{+}\bigl[e^{\beta(t+\eta_{i}(t))}v_{i}^{2}(t)-e^{\beta t}v_{i}^{2} \bigl(t-\eta_{i}(t)\bigr)\bigr] \\ & {}+\sum_{i=1}^{n}\sum _{j=1}^{n}b_{i}\eta _{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \bigl[e^{\beta(t+\tau _{ij}(t))}u_{j}^{2}(t)-e^{\beta t}u_{j}^{2} \bigl(t-\tau_{ij}(t)\bigr)\bigr] \\ & {}+\sum_{i=1}^{n}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \bigl[e^{\beta(t+\tau _{ij}(t))}u_{j}^{2}(t)-e^{\beta t}u_{j}^{2} \bigl(t-\tau_{ij}(t)\bigr)\bigr] \\ ={}&e^{\beta t} \Biggl[\beta-2a_{i}+a_{i}^{2} \delta_{i}^{+}+\sum_{j=1}^{n}a_{i} \delta _{i}^{+}a_{ij}^{+}L_{jf}^{2\xi_{j}}+ \sum_{j=1}^{n}a_{ij}^{+}L_{jf}^{2\xi _{j}}+ \sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+}e^{\beta\delta_{i}(t)} \\ & {}+\sum_{j=1}^{n}b_{i} \eta_{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon _{j})}e^{\beta\tau_{ij}(t)}+b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})}e^{\beta \tau_{ij}(t)} \Biggr]x_{i}^{2}(t) \\ & {}+e^{\beta t} \Biggl[\beta-2b_{i}+b_{i}^{2} \eta_{i}^{+}+\sum_{j=1}^{n}b_{i} \eta _{i}^{+}b_{ij}^{+}L_{jg}^{2\varepsilon_{j}}+ \sum_{j=1}^{n}b_{ij}^{+}L_{jg}^{2\varepsilon_{j}} \\ & {}+\sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})}e^{\beta \delta_{ij}(t)}+a_{ij}^{+}L_{jf}^{2(1-\xi_{j})}e^{\beta\delta _{ij}(t)}+b_{i} \eta_{i}^{+}e^{\beta\eta_{i}(t)} \Biggr]y_{i}^{2}(t) \\ \leq{}&e^{\beta t} \Biggl[\beta-2a_{i}+a_{i}^{2} \delta_{i}^{+}+\sum_{j=1}^{n}a_{i} \delta _{i}^{+}a_{ij}^{+}L_{jf}^{2\xi_{j}}+ \sum_{j=1}^{n}a_{ij}^{+}L_{jf}^{2\xi _{j}}+ \sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+}e^{\beta\delta_{i}^{+}} \\ & {}+\sum_{j=1}^{n}b_{i} \eta_{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon _{j})}e^{\beta\tau_{ij}^{+}}+b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})}e^{\beta \tau_{ij}^{+}} \Biggr]x_{i}^{2}(t) \\ & {}+e^{\beta t} \Biggl[\beta-2b_{i}+b_{i}^{2} \eta_{i}^{+}+\sum_{j=1}^{n}b_{i} \eta _{i}^{+}b_{ij}^{+}L_{jg}^{2\varepsilon_{j}}+ \sum_{j=1}^{n}b_{ij}^{+}L_{jg}^{2\varepsilon_{j}} \\ & {}+\sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})}e^{\beta \delta_{ij}^{+}}+a_{ij}^{+}L_{jf}^{2(1-\xi_{j})}e^{\beta\delta _{ij}^{+}}+b_{i} \eta_{i}^{+}e^{\beta\eta_{i}^{+}} \Biggr]y_{i}^{2}(t). \end{aligned}$$
(3.6)

It follows from Lemma 2.2 that \(\frac{dV(t)}{dt}\leq0\), which implies that \(V(t)\leq{V(0)}\) for all \(t>0\). Thus

$$\begin{aligned} & e^{\beta t} \Biggl[\sum_{i=1}^{n}u_{i}^{2}(t)+ \sum_{i=1}^{n}v_{i}^{2}(t) \Biggr] \\ &\quad \leq\sum_{i=1}^{n}u_{i}^{2}(0)+ \sum_{i=1}^{n}v_{i}^{2}(0) \\ & \qquad{}+\sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+} \int_{-\delta_{i}(0)}^{0}e^{\beta(s+\delta _{i}(0))}u_{i}^{2}(s)\,ds \\ & \qquad{}+\sum_{i=1}^{n}\sum _{j=1}^{n}a_{i}\delta_{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi _{j})} \int_{-\delta_{ij}(0)}^{0}e^{\beta(s+\delta_{ij}(0))}v_{j}^{2}(s)\,ds \\ & \qquad{}+\sum_{i=1}^{n}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})} \int_{-\delta _{ij}(0)}^{0}e^{\beta(s+\delta_{ij}(0))}v_{j}^{2}(s)\,ds \\ & \qquad{}+\sum_{i=1}^{n}b_{i}^{2} \eta_{i}^{+} \int_{-\eta_{i}(0)}^{0}e^{\beta(s+\eta _{i}(0))}v_{i}^{2}(s)\,ds \\ & \qquad{}+\sum_{i=1}^{n}\sum _{j=1}^{n}b_{i}\eta _{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \int_{-\tau _{ij}(0)}^{0}e^{\beta(s+\tau_{ij}(0))}u_{j}^{2}(s)\,ds \\ & \qquad{}+\sum_{i=1}^{n}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \int_{-\tau _{ij}(0)}^{t}e^{\beta(s+\tau_{ij}(0))}u_{j}^{2}(s)\,ds \\ &\quad \leq \bigl\Vert \varphi-\varphi^{*} \bigr\Vert ^{2}+ \bigl\Vert \psi-\psi^{*} \bigr\Vert ^{2}+\sum_{i=1}^{n}a_{i}^{2} \delta _{i}^{+}\frac{1}{\beta}e^{\beta\delta_{i}^{+}} \bigl\Vert \varphi-\varphi ^{*} \bigr\Vert ^{2} \\ & \qquad{}+\sum_{i=1}^{n}\sum _{j=1}^{n}a_{i}\delta_{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi _{j})} \frac{1}{\beta}e^{\beta\delta_{ij}^{+}} \bigl\Vert \psi-\psi^{*} \bigr\Vert ^{2} \\ & \qquad{}+\sum_{i=1}^{n}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})} \frac{1}{\beta}e^{\beta \delta_{ij}^{+}} \bigl\Vert \psi-\psi^{*} \bigr\Vert ^{2} \\ & \qquad{}+\sum_{i=1}^{n}b_{i}^{2} \eta_{i}^{+}\frac{1}{\beta}e^{\beta\eta _{i}^{+}} \bigl\Vert \psi-\psi^{*} \bigr\Vert ^{2} \\ & \qquad{}+\sum_{i=1}^{n}\sum _{j=1}^{n}b_{i}\eta _{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \frac{1}{\beta}e^{\beta\tau _{ij}^{+}} \bigl\Vert \varphi-\varphi^{*} \bigr\Vert ^{2} \\ & \qquad{}+\sum_{i=1}^{n}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \frac{1}{\beta }e^{\beta\tau_{ij}^{+}} \bigl\Vert \varphi-\varphi^{*} \bigr\Vert ^{2} \\ &\quad= \Biggl[1+\sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+}\frac{1}{\beta}e^{\beta\delta _{i}^{+}}+\sum _{i=1}^{n}\sum_{j=1}^{n}b_{i} \eta _{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \frac{1}{\beta}e^{\beta\tau _{ij}^{+}} \\ & \qquad{} +\sum_{i=1}^{n}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \frac {1}{\beta}e^{\beta\tau_{ij}^{+}} \Biggr] \bigl\Vert \varphi-\varphi^{*} \bigr\Vert ^{2} \\ & \qquad{}+ \Biggl[1+\sum_{i=1}^{n}\sum _{j=1}^{n}a_{i}\delta _{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})} \frac{1}{\beta}e^{\beta\delta _{ij}^{+}} \\ & \qquad{}+\sum_{i=1}^{n}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})} \frac{1}{\beta}e^{\beta \delta_{ij}^{+}}+\sum_{i=1}^{n}b_{i}^{2} \eta_{i}^{+}\frac{1}{\beta }e^{\beta\eta_{i}^{+}} \Biggr] \bigl\Vert \psi-\psi^{*} \bigr\Vert ^{2}. \end{aligned}$$
(3.7)

Let

$$\begin{aligned} &\theta_{1}=1+\sum_{i=1}^{n}a_{i}^{2} \delta_{i}^{+}\frac{1}{\beta}e^{\beta\delta _{i}^{+}}+\sum _{i=1}^{n}\sum_{j=1}^{n}b_{i} \eta _{i}^{+}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \frac{1}{\beta}e^{\beta\tau_{ij}^{+}} +\sum_{i=1}^{n}b_{ij}^{+}L_{jg}^{2(1-\varepsilon_{j})} \frac{1}{\beta }e^{\beta\tau_{ij}^{+}}, \\ &\theta_{2}=1+\sum_{i=1}^{n}\sum _{j=1}^{n}a_{i}\delta _{i}^{+}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})} \frac{1}{\beta}e^{\beta\delta _{ij}^{+}}+\sum_{i=1}^{n}a_{ij}^{+}L_{jf}^{2(1-\xi_{j})} \frac{1}{\beta }e^{\beta\delta_{ij}^{+}} \sum_{i=1}^{n}b_{i}^{2} \eta_{i}^{+}\frac{1}{\beta}e^{\beta\eta_{i}^{+}} \end{aligned}$$

and choose

$$M=\max\{\theta_{1},\theta_{2}\}>1. $$

Then Eq. (3.7) can be rewritten as

$$\sum_{i=1}^{n}u_{i}^{2}(t)+ \sum_{i=1}^{n}v_{i}^{2}(t) \leq{M}e^{-\beta t} \bigl[ \bigl\Vert \varphi-\varphi^{*} \bigr\Vert ^{2}+ \bigl\Vert \psi-\psi^{*} \bigr\Vert ^{2} \bigr] $$

for all \(t>0\). Then

$$\sum_{i=1}^{n} \bigl\vert x_{i}(t)-x_{i}^{*}(t) \bigr\vert ^{2}+\sum _{i=1}^{n} \bigl\vert y_{i}(t)-y_{i}^{*}(t) \bigr\vert ^{2}\leq {M}e^{-\beta t} \bigl[ \bigl\Vert \varphi- \varphi^{*} \bigr\Vert ^{2}+ \bigl\Vert \psi-\psi^{*} \bigr\Vert ^{2} \bigr] $$

for all \(t>0\). Thus the solution \((x(t),y(t))^{T}\) of system (1.4) is globally exponentially stable. □

Theorem 3.2

Assume that (H1)–(H4) are satisfied. Then system (1.4) has exactly one T-anti-periodic solution which is globally stable.

Proof

It follows from system (1.4) and (H2) that for each \(k\in{N}\), we have

$$\begin{aligned} & \frac{d}{dt} \bigl[(-1)^{k+1}x_{i}\bigl(t+(k+1)T \bigr) \bigr] \\ & \quad=(-1)^{k+1} [-a_{i}x_{i}\bigl(t+(k+1)T- \delta_{i}\bigl(t+(k+1)T\bigr)\bigr) \\ & \qquad{}+\sum_{j=1}^{n}a_{ij} \bigl(t+(k+1)T\bigr)f_{j}\bigl(y_{j}\bigl(t+(k+1)T-\sigma _{ij}\bigl(t+(k+1)T\bigr)\bigr)\bigr) \\ & \qquad{}+I_{i}\bigl(t+(k+1)T\bigr) \\ & \quad=-a_{i}(-1)^{k+1}x_{i}\bigl(t+(k+1)T- \delta_{i}(t)\bigr) \\ & \qquad{}+\sum_{j=1}^{n}a_{ij}(t)f_{j} \bigl((-1)^{k+1}y_{j}\bigl(t+(k+1)T-\sigma _{ij}(t) \bigr)\bigr)+I_{i}(t), \end{aligned}$$
(3.8)
$$\begin{aligned} & \frac{d}{dt} \bigl[(-1)^{k+1}y_{i} \bigl(t+(k+1)T\bigr) \bigr] \\ & \quad=(-1)^{k+1} \Biggl[-b_{i}y_{i}\bigl(t+(k+1)T- \eta_{i}\bigl(t+(k+1)T\bigr)\bigr) \\ & \qquad{}+\sum_{j=1}^{n}b_{ij} \bigl(t+(k+1)T\bigr)g_{j}\bigl(x_{j}\bigl(t+(k+1)T-\tau _{ij}\bigl(t+(k+1)T\bigr)\bigr)\bigr) \\ & \qquad{}+J_{i}\bigl(t+(k+1)T\bigr) \Biggr] \\ & \quad=-b_{i}(-1)^{k+1}y_{i}\bigl(t+(k+1)T- \eta_{i}(t)\bigr) \\ & \qquad{}+\sum_{j=1}^{n}b_{ij}(t)g_{j} \bigl((-1)^{k+1}x_{j}\bigl(t+(k+1)T-\tau _{ij}(t) \bigr)\bigr)+J_{i}(t). \end{aligned}$$
(3.9)

Let

$$\begin{aligned} &\bar{x}(t)=\bigl((-1)^{k+1}x_{1}\bigl(t+(k+1)T \bigr),(-1)^{k+1}x_{2}\bigl(t+(k+1)T\bigr),\ldots ,(-1)^{k+1}x_{n}\bigl(t+(k+1)T\bigr)\bigr)^{T}, \\ &\bar{y}(t)=\bigl((-1)^{k+1}y_{1}\bigl(t+(k+1)T \bigr),(-1)^{k+1}y_{2}\bigl(t+(k+1)T\bigr),\ldots ,(-1)^{k+1}y_{n}\bigl(t+(k+1)T\bigr)\bigr)^{T}. \end{aligned}$$

Obviously, for any \(k\in{N},(\bar{x}(t), \bar{y}(t))\) is also a solution of system (1.4). If the initial function \(\varphi_{i}(s), \psi_{i}(s)\ (i=1,2,\ldots,n)\) is bounded, it follows from Theorem 3.1 that there exists a constant \(\gamma>1\) such that

$$\begin{aligned} & \bigl\vert (-1)^{k+1}x_{i}\bigl(t+(k+1)T \bigr)-(-1)^{k}x_{i}(t+kT) \bigr\vert \\ & \quad \leq{M}e^{-\beta(t+kT)}\sup_{-\tau\leq{s}\leq0}\sum _{i=1}^{4} \bigl\vert x_{i}(t+T)+x_{i}(s) \bigr\vert ^{2} \\ & \quad \leq\gamma e^{-\beta(t+kT)}, \end{aligned}$$
(3.10)

where \(t+kT>0,i=1,2,\ldots,n\). Since for any \(k\in{N}\) we have

$$\begin{aligned} (-1)^{k+1} x_{i} \bigl(t + (k+1)T\bigr) = x_{i} (t ) +\sum_{j=0}^{k}\bigl[(-1)^{j+1} x _{i}\bigl(t + (j+1)T\bigr)-(-1)^{j} x_{i} (t + jT)\bigr], \end{aligned}$$
(3.11)

then

$$\begin{aligned} (-1)^{k+1} x_{i} \bigl(t + (k+1)T\bigr) \leq \bigl\vert x_{i} (t ) \bigr\vert +\sum_{j=0}^{k} \bigl\vert (-1)^{j+1} x _{i}\bigl(t + (j+1)T \bigr)-(-1)^{j} x_{i} (t + jT) \bigr\vert . \end{aligned}$$
(3.12)

By Lemma 2.3, we know that the solutions of system (1.4) are bounded. In view of (3.10) and (3.12), we can easily know that \(\{(-1)^{k+1} x_{i}(t + (k+1)T)\}\) uniformly converges to a continuous function \(x^{*}(t)=(x^{*}_{1}(t),x^{*}_{2}(t), \ldots, x^{*}_{n}(t))^{T}\) on any compact set of \({R^{n}}\). In a similar way, we can easily prove that \(\{(-1)^{k+1} y_{i}(t + (k+1)T)\}\) uniformly converges to a continuous function \(y^{*}(t)=(y^{*}_{1}(t),y^{*}_{2}(t), \ldots, y^{*}_{n}(t))^{T}\) on any compact set of \({R^{n}}\).

Now we show that \(x^{*}(t)\) is a T-anti-periodic solution of (1.4). Firstly, \(x^{*}(t)\) is T-anti-periodic since

$$\begin{aligned} x^{*}(t+T) &=\lim_{k\to\infty}(-1)^{k }x(t +T+ kT) \\ &=-\lim_{(k+1)\to\infty}(-1)^{k+1 } x\bigl(t +(k +1)T \bigr)=-x^{*}(t ). \end{aligned}$$
(3.13)

Then we can conclude that \(x_{i}^{*}(t)\) is T-anti-periodic on R. Similarly, \(y_{i}^{*}(t)\) is also T-anti-periodic on R. Thus we can conclude that \((x^{*}(t),y^{*}(t))^{T}\) is the solution of system (1.4).

In fact, together with the continuity of the right-hand side of system (1.4), let \(k\to\infty\), we can easily get

$$\begin{aligned} \textstyle\begin{cases} \frac{dx_{i}^{*}(t)}{dt}=-a_{i}x_{i}^{*}(t-\delta_{i}(t))+\sum_{j=1}^{n}a_{ij}(t)f_{j}(y_{j}^{*}(t-\sigma_{ij}(t)))+I_{i}(t),\\ \frac{dy_{i}^{*}(t)}{dt}=-b_{i}y_{i}^{*}(t-\eta_{i}(t))+\sum_{j=1}^{n}b_{ij}(t)g_{j}(x_{j}^{*}(t-\tau_{ij}(t)))+J_{i}(t). \end{cases}\displaystyle \end{aligned}$$
(3.14)

Therefore, \((x^{*}(t),y^{*}(t))^{T}\) is a solution of (1.4). Finally, by applying Theorem 3.1, it is easy to check that \((x^{*}(t),y^{*}(t))^{T}\) is globally exponentially stable. This completes the proof of Theorem 3.2. □

4 An example

In this section, we give an example to illustrate our main results derived in the previous sections. Consider the following BAM neural network with time-varying delays in the leakage terms:

$$\begin{aligned} \textstyle\begin{cases} \frac{dx_{1}(t)}{dt}=-a_{1}x_{1}(t-\delta_{1}(t))+\sum_{j=1}^{2}a_{1j}(t)f_{j}(y_{j}(t-\sigma_{1j}(t)))+I_{1}(t),\\ \frac{dx_{2}(t)}{dt}=-a_{2}x_{2}(t-\delta_{2}(t))+\sum_{j=1}^{2}a_{2j}(t)f_{j}(y_{j}(t-\sigma_{2j}(t)))+I_{2}(t),\\ \frac{dy_{1}(t)}{dt}=-b_{1}y_{1}(t-\eta_{1}(t))+\sum_{j=1}^{2}b_{1j}(t)g_{j}(x_{j}(t-\tau_{1j}(t)))+J_{1}(t),\\ \frac{dy_{2}(t)}{dt}=-b_{2}y_{2}(t-\eta_{2}(t))+\sum_{j=1}^{2}b_{2j}(t)g_{j}(x_{j}(t-\tau_{2j}(t)))+J_{2}(t), \end{cases}\displaystyle \end{aligned}$$
(4.1)

where

$$\begin{aligned} & \left [ \begin{matrix} \delta_{1}(t) & \delta_{2}(t) \\ \eta_{1}(t)& \eta_{2}(t) \end{matrix} \right ]=\left [ \begin{matrix} 0.05 \vert \sin t \vert & 0.05 \vert \sin t \vert \\ 0.04 \vert \cos t \vert & 0.04 \vert \cos t \vert \end{matrix} \right ], \\ & \left [ \begin{matrix} a_{11}(t) & a_{12}(t) \\ a_{21}(t)& a_{22}(t) \end{matrix} \right ]=\left [ \begin{matrix} 0.3 \vert \cos t \vert & 0.3 \vert \cos t \vert \\ 0.5 \vert \sin t \vert & 0.5 \vert \sin t \vert \end{matrix} \right ], \\ &\left [ \begin{matrix} b_{11}(t) & b_{12}(t) \\ b_{21}(t)& b_{22}(t) \end{matrix} \right ]=\left [ \begin{matrix} 0.03 \vert \cos t \vert & 0.03 \vert \cos t \vert \\ 0.05 \vert \sin t \vert & 0.05 \vert \sin t \vert \end{matrix} \right ], \\ & \left [ \begin{matrix} I_{1}(t) & I_{2}(t) \\ J_{1}(t)& J_{2}(t) \end{matrix} \right ]=\left [ \begin{matrix} 0.5\cos t& 0.5\cos t \\ 0.5\sin t & 0.5\sin t \end{matrix} \right ],\qquad \left [ \begin{matrix} a_{1} & a_{2} \\ b_{1}& b_{2} \end{matrix} \right ]=\left [ \begin{matrix} 2& 2 \\ 2 & 2 \end{matrix} \right ]. \end{aligned}$$

Set \(f_{j}(u)=g_{j}(u)=\frac{1}{2}( \vert u+1 \vert - \vert u-1 \vert ),j=1,2\). Then \(L_{jf}=g_{jg}=M_{j}^{f}=M_{j}^{g}=1, \delta_{1}^{+}=\delta_{2}^{+}=0.05, a_{1j}^{+}=0.3, a_{2j}^{+}=0.5, \eta_{1}^{+}=\eta_{2}^{+}=0.04, b_{1j}^{+}=0.03, b_{2j}^{+}=0.05, j=1,2\). It is easy to verify that

$$\frac{\sqrt{2}}{\alpha}\bigl(a_{i}\delta_{i}^{+}+b_{i} \eta_{i}^{+}\bigr)\approx0.12726< 1 $$

and

$$\begin{aligned} & {-}2a_{1}+a_{1}^{2}\delta_{1}^{+}+ \sum_{j=1}^{2}a_{1}\delta _{1}^{+}a_{1j}^{+}L_{jf}^{2\xi_{j}}+ \sum_{j=1}^{2}a_{1j}^{+}L_{jf}^{2\xi_{j}} \\ & \quad{}+\sum_{i=1}^{2}a_{i}^{2} \delta_{i}^{+}+\sum_{j=1}^{2}b_{1} \eta _{1}^{+}b_{1j}^{+}L_{jg}^{2(1-\varepsilon _{j})}+b_{1j}^{+}L_{jg}^{2(1-\varepsilon_{j})}=-2.862< 0, \\ & {-}2a_{2}+a_{2}^{2}\delta_{2}^{+}+ \sum_{j=1}^{2}a_{2}\delta _{2}^{+}a_{2j}^{+}L_{jf}^{2\xi_{j}}+ \sum_{j=1}^{2}a_{2j}^{+}L_{jf}^{2\xi_{j}} \\ & \quad{}+\sum_{i=1}^{2}a_{i}^{2} \delta_{i}^{+}+\sum_{j=1}^{2}b_{2} \eta _{2}^{+}b_{2j}^{+}L_{jg}^{2(1-\varepsilon _{j})}+b_{2j}^{+}L_{jg}^{2(1-\varepsilon_{j})}=-2.04< 0, \\ & {-}2b_{1}+b_{1}^{2}\eta_{1}^{+}+ \sum_{j=1}^{2}b_{1}\eta _{1}^{+}b_{1j}^{+}L_{jg}^{2\varepsilon_{j}}+ \sum_{j=1}^{2}b_{1j}^{+}L_{jg}^{2\varepsilon_{j}} \\ & \quad{}+\sum_{i=1}^{2}a_{1}^{2} \delta_{1}^{+}a_{1j}^{+}L_{jf}^{2(1-\xi _{j})}+a_{1j}^{+}L_{jf}^{2(1-\xi_{j})}+b_{1} \eta_{1}^{+}=-3.256< 0, \\ & {-}2b_{2}+b_{2}^{2}\eta_{2}^{+}+ \sum_{j=1}^{2}b_{2}\eta _{2}^{+}b_{2j}^{+}L_{jg}^{2\varepsilon_{j}}+ \sum_{j=1}^{2}b_{2j}^{+}L_{jg}^{2\varepsilon_{j}} \\ & \quad{}+\sum_{i=1}^{2}a_{2}^{2} \delta_{2}^{+}a_{2j}^{+}L_{jf}^{2(1-\xi _{j})}+a_{2j}^{+}L_{jf}^{2(1-\xi_{j})}+b_{2} \eta_{2}^{+}=-3.024< 0. \end{aligned}$$

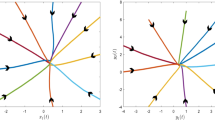
Then all the conditions (H1)–(H4) hold. Thus system (4.1) has exactly one π-anti-periodic solution which is globally exponentially stable. The results are illustrated in Fig. 1.

Figure 1
figure 1

Transient response of state variables \(x_{1}(t),x_{2}(t),y_{1}(t)\), and \(y_{2}(t)\)

Full size image

5 Conclusions

In this paper, we have investigated the asymptotic behavior of BAM neural networks with time-varying delays in the leakage terms. Applying the fundamental solution matrix of coefficient matrix, we obtained a series of new sufficient conditions to guarantee the existence and global exponential stability of an anti-periodic solution for the BAM neural networks with time-varying delays in the leakage terms. The obtained conditions are easy to check in practice. Finally, an example is included to illustrate the feasibility and effectiveness.