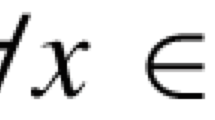Abstract
This paper introduces a new extragradient-type method to solve the multiple-sets split equality problem (MSSEP). Under some suitable conditions, the strong convergence of an algorithm can be verified in the infinite-dimensional Hilbert spaces. Moreover, several numerical results are given to show the effectiveness of our algorithm.
Similar content being viewed by others
1 Introduction
The split feasibility problem (SFP) was first presented by Censor et al. [1]; it is an inverse problem that arises in medical image reconstruction, phase retrieval, radiation therapy treatment, signal processing etc. The SFP can be mathematically characterized by finding a point x that satisfies the property
if such a point exists, where C and Q are nonempty closed convex subsets of Hilbert spaces \(H_{1}\) and \(H_{2}\), respectively, and \(A:H_{1}\rightarrow{H_{2}}\) is a bounded and linear operator.
There are various algorithms proposed to solve the SFP, see [2–4] and the references therein. In particular, Byrne [5, 6] introduced the CQ-algorithm motivated by the idea of an iterative scheme of fixed point theory. Moreover, Censor et al. [7] introduced an extension upon the form of SFP in 2005 with an intersection of a family of closed and convex sets instead of the convex set C, which is the original of the multiple-sets split feasibility problem (MSSFP).
Subsequently, an important extension, which goes by the name of split equality problem (SEP), was made by Moudafi [8]. It can be mathematically characterized by finding points \(x\in{C}\) and \(y\in{Q}\) that satisfy the property
if such points exist, where C and Q are nonempty closed convex subsets of Hilbert spaces \(H_{1}\) and \(H_{2}\), respectively, \(H_{3}\) is also a Hilbert space, \(A:H_{1}\rightarrow{H_{3}}\) and \(B:H_{2}\rightarrow{H_{3}}\) are two bounded and linear operators. When \(B=I\), the SEP reduces to SFP. For more information about the methods for solving SEP, see [9, 10].
This paper considers the multiple-sets split equality problem (MSSEP) which generalizes the MSSFP and SEP and can be mathematically characterized by finding points x and y that satisfy the property
where \(r, t\) are positive integers, \(\{C_{i}\}_{i=1}^{t}\in{H_{1}}\) and \(\{ Q_{j}\}_{j=1} ^{r}\in{H_{2}}\) are nonempty, closed and convex subsets of Hilbert spaces \(H_{1}\) and \(H_{2}\), respectively, \(H_{3}\) is also a Hilbert space, \(A:H_{1}\rightarrow{H_{3}}\), \(B:H_{2}\rightarrow{H_{3}}\) are two bounded and linear operators. Obviously, if \(B=I\), the MSSEP is just right MSSFP; if \(t=r=1\), the MSSEP changes into the SEP. Moreover, when \(B=I\) and \(t=r=1\), the MSSEP reduces to the SFP.
One of the most important methods for computing the solution of a variational inequality and showing the quick convergence is an extragradient algorithm, which was first introduced by Korpelevich [11]. Moreover, this method was applied for finding a common element of the set of solutions for a variational inequality and the set of fixed points of a nonexpansive mapping, see Nadezhkina et al. [12]. Subsequently, Ceng et al. in [13] presented an extragradient method, and Yao et al. in [14] proposed a subgradient extragradient method to solve the SFP. However, all these methods to solve the problem have only weak convergence in a Hilbert space. On the other hand, a variant extragradient-type method and a subgradient extragradient method introduced by Censor et al. [15, 16] possess strong convergence for solving the variational inequality.
Motivated and inspired by the above works, we introduce an extragradient-type method to solve the MSSEP in this paper. Under some suitable conditions, the strong convergence of an algorithm can be verified in the infinite-dimensional Hilbert spaces. Finally, several numerical results are given to show the feasibility of our algorithm.
2 Preliminaries
Let H be a real Hilbert space whose inner product and norm are denoted by \(\langle\cdot,\cdot\rangle\) and \(\Vert \cdot \Vert \), respectively. Let I denote the identity operator on H.
Next, we recall several definitions and basic results that will be available later.
Definition 2.1
A mapping \(T:H\rightarrow{H}\) goes by the name of
-
(i)
nonexpansive if
$$\Vert Tx-Ty\Vert \leq \Vert x-y\Vert , \quad \forall x,y\in{H}; $$ -
(ii)
firmly nonexpansive if
$$\Vert Tx-Ty\Vert \leq\langle{x-y,Tx-Ty}\rangle,\quad \forall x,y\in{H}; $$ -
(iii)
contractive on x if there exists \(0<\alpha<1\) such that
$$\Vert Tx-Ty\Vert \leq\alpha \Vert x-y\Vert ,\quad \forall x,y\in{H}; $$ -
(iv)
monotone if
$$\langle{Tx-Ty,x-y}\rangle\geq0,\quad \forall x,y\in{H}; $$ -
(v)
β-inverse strongly monotone if there exists \(\beta>0\) such that
$$\langle{Tx-Ty,x-y}\rangle\geq\beta \Vert Tx-Ty\Vert ^{2},\quad \forall x,y\in{H}. $$
The following properties of an orthogonal projection operator were introduced by Bauschke et al. in [17], and they will be powerful tools in our analysis.
Proposition 2.2
[17]
Let \(P_{C}\) be a mapping from H onto a closed, convex and nonempty subset C of H if
then \(P_{C}\) is called an orthogonal projection from H onto C. Furthermore, for any \(x,y\in{H}\) and \(z\in{C}\),
-
(i)
\(\langle{x-P_{C}x,z-P_{C}x}\rangle\leq0\);
-
(ii)
\(\Vert P_{C}x-P_{C}y\Vert ^{2}\leq\langle{P_{C}x-P_{C}y,x-y}\rangle\);
-
(iii)
\(\Vert P_{C}x-z\Vert ^{2}\leq \Vert x-z\Vert ^{2}-\Vert P_{C}x-x\Vert ^{2}\).
The following lemmas provide the main mathematical results in the sequel.
Lemma 2.3
[18]
Let C be a nonempty closed convex subset of a real Hilbert space H, let \(T:C\rightarrow{H}\) be α-inverse strongly monotone, and let \(r>0\) be a constant. Then, for any \(x,y\in{C}\),
Moreover, when \(0< r<2\alpha\), \(I-rT\) is nonexpansive.
Lemma 2.4
[19]
Let \(\{x^{k}\}\) and \(\{y^{k}\}\) be bounded sequences in a Hilbert space H, and let \(\{\beta_{k}\}\) be a sequence in \([0,1]\) which satisfies the condition \(0<\lim\inf_{k\rightarrow\infty}\beta_{k}\leq{\limsup_{k\rightarrow\infty}\beta_{k}}<1\). Suppose that \(x^{k+1}=(1-\beta_{k})y^{k}+\beta_{k}x^{k}\) for all \(k\geq0\) and \(\lim\sup_{k\rightarrow\infty}(\Vert y^{k+1}-y^{k}\Vert -\Vert x^{k+1}-x^{k}\Vert )\leq0\). Then \(\lim_{k\rightarrow\infty} \Vert y^{k}-x^{k}\Vert =0\).
The lemma below will be a powerful tool in our analysis.
Lemma 2.5
[20]
Let \(\{a_{k}\}\) be a sequence of nonnegative real numbers satisfying the condition \(a_{k+1}\leq(1-m_{k})a_{k}+m_{k}\delta_{k}, \forall{k\geq0,}\) where \(\{m_{k}\}\), \(\{\delta_{k}\}\) are sequences of real numbers such that
-
(i)
\(\{m_{k}\}\in[0,1]\) and \(\sum_{k=0}^{\infty}{m_{k}}=\infty\) or, equivalently,
$$\prod_{k=0}^{\infty}(1-m_{k})=\lim _{k\rightarrow\infty}\prod_{j=0}^{k}(1-m_{j})=0; $$ -
(ii)
\(\lim\sup_{k\rightarrow\infty}\delta_{k}\leq0\) or
-
(ii)’
\(\sum_{k=0}^{\infty}\delta_{k}m_{k}\) is convergent. Then \(\lim_{k\rightarrow\infty}a_{k}=0\).
3 Main results
In this section, we propose a formal statement of our present algorithm. Review the multiple-sets split equality problem (MSSEP), without loss of generality, suppose \(t>r\) in (1.3) and define \(Q_{r+1}=Q_{r+2}=\cdots =Q_{t}=H_{2}\). Hence, MSSEP (1.3) is equivalent to the following problem:
Moreover, set \(S_{i}=C_{i}\times{Q_{i}}\in{H}=H_{1}\times{H_{2}}\ (i=1,2,\ldots ,t)\), \(S={\bigcap_{i=1}^{t}}S_{i}\), \(G=[A,-B]:H\rightarrow{H_{3}}\), the adjoint operator of G is denoted by \(G^{*}\), then the original problem (3.1) reduces to
Theorem 3.1
Let \(\Omega\neq\emptyset\) be the solution set of MSSEP (3.2). For an arbitrary initial point \(w_{0}\in{S}\), the iterative sequence \(\{w_{n}\}\) can be given as follows:
where \(\{\alpha_{n}\}_{n=0}^{\infty}\) is a sequence in \([0,1]\) such that \(\lim_{n\rightarrow\infty}\alpha_{n}=0, and \sum_{n=1}^{\infty}\alpha _{n}=\infty\), and \(\{\gamma_{n}\}_{n=0}^{\infty}\), \(\{\lambda_{n}\}_{n=0}^{\infty}\), \(\{\mu_{n}\}_{n=0}^{\infty}\) are sequences in H satisfying the following conditions:
Then \(\{w_{n}\}\) converges strongly to a solution of MSSEP (3.2).
Proof
In view of the property of the projection, we infer \(\hat{w}=P_{S}(\hat {w}-tG^{*}G\hat{w})\) for any \(t>0\). Further, from the condition in (3.4), we get that \({\mu_{n}}\leq\frac{2}{\rho(G^{*}G)}\lambda_{n}\), it follows that \(I-\frac{\mu_{n}}{\lambda_{n}}G^{*}G\) is nonexpansive. Hence,
Since \(\alpha_{n}\rightarrow{0}\) as \(n\rightarrow\infty\) and from the condition in (3.4), \({\gamma_{n}}\in{(0,\frac{2}{\rho(G^{*}G)})}\), it follows that \(\alpha_{n}\leq{1-\frac{\gamma_{n}\rho(G^{*}G)}{2}}\) as \(n\rightarrow\infty\), that is, \(\frac{\gamma_{n}}{1-\alpha_{n}}\in{(0,\frac {2}{\rho{(G^{*}G)}})}\). We deduce that
which is equivalent to
Substituting (3.7) in (3.5), we obtain
By induction,
Consequently, \(\{w_{n}\}\) is bounded, and so is \(\{v_{n}\}\).
Let \(T=2P_{S}-I\). From Proposition 2.2, one can know that the projection operator \(P_{S}\) is monotone and nonexpansive, and \(2P_{S}-I\) is nonexpansive.
Therefore,
that is,
where \(b_{n}=\frac{\lambda_{n}(I-\frac{\mu_{n}}{\lambda _{n}}G^{*}G)v_{n}+T[(1-\lambda_{n})w_{n}+\lambda_{n}(I-\frac{\mu_{n}}{\lambda _{n}}G^{*}G)v_{n}]}{1+\lambda_{n}}\).
Indeed,
For convenience, let \(c_{n}=(I-\frac{\mu_{n}}{\lambda_{n}}G^{*}G)v_{n}\). By Lemma 2.5 in Shi et al. [1], it follows that \((I-\frac{\mu_{n}}{\lambda_{n}}G^{*}G)\) is nonexpansive and averaged. Hence,
Moreover,
Substituting (3.11) in (3.10), we infer that
By virtue of \(\lim_{n\rightarrow\infty}(\lambda_{n+1}-\lambda_{n})=0\), it follows that \(\lim_{n\rightarrow\infty} \vert \frac{\lambda_{n+1}}{1+\lambda_{n+1}}-\frac {\lambda_{n}}{1+\lambda_{n}}\vert =0\). Moreover, \(\{w_{n}\}\) and \(\{v_{n}\}\) are bounded, and so is \(\{c_{n}\}\). Therefore, (3.12) reduces to
Applying (3.13) and Lemma 2.4, we get
Combining (3.14) with (3.8), we obtain
Using the convexity of the norm and (3.5), we deduce that
which implies that
Since \(\lim\inf_{n\rightarrow\infty}\lambda_{n}\gamma_{n}(\frac{2}{\rho (G^{*}G)}-\frac{\gamma_{n}}{1-\alpha_{n}})>0\), \(\lim_{n\rightarrow\infty }\alpha_{n}=0\) and \(\lim_{n\rightarrow\infty} \Vert w_{n+1}-w_{n}\Vert =0\), we infer that
Applying Proposition 2.2 and the property of the projection \(P_{S}\), one can easily show that
where \(M>0\) satisfies
which means that
Since \(\lim_{n\rightarrow\infty}\alpha_{n}=0\), \(\lim_{n\rightarrow\infty }\Vert w_{n+1}-w_{n}\Vert =0\) and \(\lim_{n\rightarrow\infty} \Vert G^{*}Gw_{n}-G^{*}G\hat {w}\Vert =0\), we infer that
Finally, we show that \(w_{n}\rightarrow{\hat{w}}\). Using the property of the projection \(P_{S}\), we derive
which equals
It follows from (3.5) and (3.17) that
Since \(\frac{\gamma_{n}}{1-\alpha_{n}}\in{(0,\frac{2}{\rho(G^{*}G)})}\), we observe that \(\alpha_{n}\in{(0,1-\frac{\gamma_{n}\rho(G^{*}G)}{2})}\), then
that is to say,
By virtue of \(\sum_{n=1}^{\infty}(\frac{\lambda_{n}}{\gamma_{n}})<\infty\), \({\gamma_{n}}\in{(0,\frac{2}{\rho(G^{*}G)})}\) and \(\langle\hat{w},\hat {w}-v_{n}\rangle\) is bounded, we obtain \(\sum_{n=1}^{\infty}(\frac{2\lambda _{n}(2-\gamma_{n}\rho(G^{*}G))}{\gamma_{n}\rho_{n}(G^{*}G)})\langle\hat{w},\hat {w}-v_{n}\rangle<\infty\), which implies that
Moreover,
it follows that all the conditions of Lemma 2.5 are satisfied. Combining (3.18), (3.19) and Lemma 2.5, we can show that \(w_{n}\rightarrow \hat{w}\). This completes the proof. □
4 Numerical experiments
In this section, we provide several numerical results and compare them with Tian’s [21] algorithm (3.15)’ and Byrne’s [22] algorithm (1.2) to show the effectiveness of our proposed algorithm. Moreover, the sequence given by our algorithm in this paper has strong convergence for the multiple-sets split equality problem. The whole program was written in Wolfram Mathematica (version 9.0). All the numerical results were carried out on a personal Lenovo computer with Intel(R)Pentium(R) N3540 CPU 2.16 GHz and RAM 4.00 GB.
In the numerical results, \(A=(a_{ij})_{P\times{N}}\), \(B=(b_{ij})_{P\times{M}}\), where \(a_{ij}\in[0,1]\), \(b_{ij}\in[0,1]\) are all given randomly, \(P, M, N\) are positive integers. The initial point \(x_{0}=(1,1,\ldots,1)\), and \(y_{0}=(0,0,\ldots,0)\), \(\alpha_{n}=0.1\), \(\lambda _{n}=0.1\), \(\gamma_{n}=\frac{0.2}{\rho{(G^{*}G)}}\), \(\mu_{n}=\frac{0.2}{\rho {(G^{*}G)}}\) in Theorem 3.1, \(\rho_{1}^{n}=\rho_{2}^{n}=0.1\) in Tian’s (3.15)’ and \(\gamma_{n}=0.01\) in Byrne’s (1.2). The termination condition is \(\Vert Ax-By\Vert <\epsilon\). In Tables 1-4, the iterative steps and CPU are denoted by n and t, respectively.
References
Censor, Y, Elfving, T: A multiprojection algorithm using Bregman projections in a product space. Numer. Algorithms 8(2-4), 221-239 (1994)
Xu, HK: A variable Krasnosel’skii-Mann algorithm and the multiple-set split feasibility problem. Inverse Probl. 22(6), 2021-2034 (2006)
Lopez, G, Martin-Marqnez, V, Wang, F, Xu, HK: Solving the split feasibility problem without prior knowledge of matrix norms. Inverse Probl. 28, 085004 (2012)
Yang, Q: The relaxed CQ algorithm solving the split feasibility problem. Inverse Probl. 20(4), 1261-1266 (2004)
Byrne, C: Iterative oblique projection onto convex sets and the split feasibility problem. Inverse Probl. 18(2), 441-453 (2002)
Byrne, C: A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 20(1), 103-120 (2004)
Censor, Y, Elfving, T, Kopf, N, Bortfeld, T: The multiple-sets split feasibility problem and its applications for inverse problems. Inverse Probl. 21(6), 2071-2084 (2005)
Moudafi, A: Alternating CQ algorithm for convex feasibility and split fixed point problem. J. Nonlinear Convex Anal. 15(4), 809-818 (2013)
Shi, LY, Chen, RD, Wu, YJ: Strong convergence of iterative algorithms for solving the split equality problems. J. Inequal. Appl. 2014, Article ID 478 (2014)
Dong, QL, He, SN, Zhao, J: Solving the split equality problem without prior knowledge of operator norms. Optimization 64(9), 1887-1906 (2015)
Korpelevich, GM: An extragradient method for finding saddle points and for other problems. Ekonomikai Matematicheskie Metody 12(4), 747-756 (1976)
Nadezhkina, N, Takahashi, W: Weak convergence theorem by an extragradient method for nonexpansive mappings and monotone mappings. J. Optim. Theory Appl. 128(1), 191-201 (2006)
Ceng, LC, Ansari, QH, Yao, JC: An extragradient method for solving split feasibility and fixed point problems. Comput. Math. Appl. 64(4), 633-642 (2012)
Yao, Y, Postolache, M, Liou, YC: Variant extragradient-type method for monotone variational inequalities. Fixed Point Theory Appl. 2013, Article ID 185 (2013)
Censor, Y, Gibali, A, Reich, S: The subgradient extragradient method for solving variational inequalities in Hilbert space. J. Optim. Theory Appl. 148(2), 318-335 (2011)
Censor, Y, Gibali, A, Reich, S: Strong convergence of subgradient extragradient method for the variational inequalities in Hilbert space. Optim. Methods Softw. 26(4-5), 827-845 (2011)
Bauschke, HH, Combettes, PL: Convex Analysis and Monotone Operator Theory in Hilbert Space. Springer, London (2011)
Takahashi, W, Toyoda, M: Weak convergence theorems for nonexpansive mappings and monotone mappings. J. Optim. Theory Appl. 118(2), 417-428 (2003)
Suzuki, T: Strong convergence theorems for infinite families of nonexpansive mappings in general Banach spaces. Fixed Point Theory Appl. 2005 685918 (2005)
Xu, HK: Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 66(1), 240-256 (2002)
Tian, D, Shi, L, Chen, R: Iterative algorithm for solving the multiple-sets split equality problem with split self-adaptive step size in Hilbert spaces. Arch. Inequal. Appl. 2016(1), 1-9 (2016)
Byrne, C, Moudafi, A: Extensions of the CQ algorithm for feasibility and split equality problems. hal-00776640-version 1 (2013)
Acknowledgements
This research was supported by NSFC Grants No: 11226125; No: 11301379; No: 11671167.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that there are no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Ying Zhao and Luoyi Shi contributed equally to this work.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhao, Y., Shi, L. Strong convergence of an extragradient-type algorithm for the multiple-sets split equality problem. J Inequal Appl 2017, 52 (2017). https://doi.org/10.1186/s13660-017-1326-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-017-1326-y