1 Introduction

Let \(\mathbb{C}(\mathbb{R})\) denote the set of all complex (real) numbers, and \([n]:=\{1,2,\ldots,n\}\). An mth-order n-dimensional complex (real) tensor, denoted by \(\mathcal{A}\in\mathbb{C}^{[m,n]}(\mathbb{R}^{[m,n]})\), is a multidimensional array of \(n^{m}\) elements of the form

$$ \mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}}),\quad a_{i_{1}\cdots i_{m}}\in\mathbb {C}(\mathbb{R}), i_{j} \in[n], j\in[m]. $$

When \(m=2\), \(\mathcal{A}\) is an n-by-n matrix. A tensor \(\mathcal{A}=(a_{i_{1}\cdots i_{m}})\in\mathbb{R}^{[m,n]}\) is called nonnegative if each its entry is nonnegative, and it is called symmetric [2, 3] if

$$a_{i_{1}\cdots i_{m} }= a_{\pi(i_{1}\cdots i_{m} )},\quad \forall\pi\in\Pi_{m}, $$

where \(\Pi_{m}\) is the permutation group of m indices. Moreover, an mth-order n-dimensional tensor \(\mathcal{I}=(\delta_{i_{1}i_{2}\cdots i_{m}})\) is called the identity tensor [4] if

$$\delta_{i_{1}i_{2}\cdots i_{m}}= \left \{ \textstyle\begin{array}{l@{\quad}l} 1 &\mbox{if } i_{1}=i_{2}=\cdots=i_{m}, \\ 0 &\mbox{otherwise}. \end{array}\displaystyle \right . $$

For an n-dimensional vector \(x=(x_{1},x_{2},\ldots,x_{n})^{T}\), real or complex, we define the n-dimensional vector

$$\mathcal{A}x^{m-1}:= \biggl(\sum_{i_{2},\ldots,i_{m}\in[n]} a_{ii_{2}\cdots i_{m}}x_{i_{2}}\cdots x_{i_{m}} \biggr)_{1\leq i \leq n}, $$

and the n-dimensional vector

$$x^{[m-1]}:=\bigl(x_{i}^{m-1}\bigr)_{1\leq i \leq n}. $$

The following definition related to eigenvalues of tensors was first introduced and studied by Qi [3] and Lim [5].

Definition 1

[3, 5]

Let \(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{C}^{[m,n]}\). A pair \((\lambda,x)\in\mathbb{C}\times(\mathbb{C}^{n}\setminus\{0\})\) is called an eigenvalue-eigenvector (or simply eigenpair) of \(\mathcal{A}\) if satisfies the equation

$$ \mathcal{A}x^{m-1}=\lambda x^{[m-1]}. $$
(1)

We call \((\lambda,x)\) an H-eigenpair if they are both real.

In addition, the spectral radius of a tensor \(\mathcal{A}\) is defined as

$$\rho\mathcal{(A)} = \max\bigl\{ |\lambda|:\lambda \mbox{ is an eigenvalue of } \mathcal{A}\bigr\} . $$

Definition 2

A tensor \(\mathcal{A}\in\mathbb{C}^{[m,n]}\) is said to be nonsingular if zero is not an eigenvalue of \(\mathcal{A}\). Otherwise, it is called singular.

Tensor eigenvalue problems have gained special attention in the realm of numerical multilinear algebra, and they have a wide range in practice; see [3, 4, 6–16]. For instance, we can use the smallest H-eigenvalues of tensors to determine their positive (semi)definiteness, that is, for an even-order real symmetric tensor \(\mathcal{A}\), if its smallest H-eigenvalue is positive (nonnegative), then \(\mathcal{A}\) is positive (semi)definite; consequently, the multivariate homogeneous polynomial \(f(x)\) determined by \(\mathcal{A}\) is positive (semi)definite [3].

Most often, it is difficult to compute the smallest H-eigenvalue. Therefore, we always try to give a distribution range of eigenvalues of a given tensor in the complex plane. In particular, if this range is in the right-half complex plane, which means that the smallest H-eigenvalue is positive, then the corresponding tensor is positive definite.

Qi [3] generalized the Geršgorin eigenvalue inclusion theorem from matrices to real symmetric tensors, which can be easily extended to generic tensors; see [4, 17].

Theorem 1

Let \(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{C}^{[m,n]}\). Then

$$ \sigma(\mathcal{A})\subseteq\Gamma(\mathcal{A})=\bigcup _{i\in [n]}\Gamma_{i}(\mathcal{A}), $$

where \(\sigma(\mathcal{A})\) is the set of all the eigenvalues of \(\mathcal{A}\), and

$$ \Gamma_{i}(\mathcal{A})=\bigl\{ z\in\mathbb{C}:|z-a_{ii\cdots i}| \leq r_{i}(\mathcal{A})\bigr\} ,\quad r_{i}(\mathcal{A})=\sum _{\substack{i_{2},\ldots ,i_{m}\in[n],\\ \delta_{ii_{2}\cdots i_{m}}=0}}|a_{ii_{2}\cdots i_{m}}|. $$

Recently, as an extension of the theory in [18], Li et al. [1, 17, 19] proposed three new Brauer-type eigenvalue localization sets for tensors and showed tighter bounds than \(\Gamma(\mathcal{A})\) of Theorem 1. We list the latest Brauer-type eigenvalue localization set as follows. For convenience, we denote

$$\begin{aligned}& \Delta_{i}=\bigl\{ (i_{2},i_{3},\ldots, i_{m}):i_{j}=i \mbox{ for some } j\in\{2,3,\ldots , m\}, \mbox{where } i,i_{2},\ldots,i_{m}\in[n]\bigr\} , \\& \overline{\Delta}_{i}=\bigl\{ (i_{2},i_{3}, \ldots, i_{m}):i_{j}\neq i \mbox{ for any } j\in\{2,3,\ldots, m\}, \mbox{where } i,i_{2},\ldots,i_{m}\in[n]\bigr\} , \end{aligned}$$

and

$$ r_{i}^{\Delta_{i}}(\mathcal{A})=\sum_{\substack{(i_{2},\ldots,i_{m})\in\Delta _{i},\\ \delta_{ii_{2}\cdots i_{m}}=0}} |a_{ii_{2}\cdots i_{m}}|,\qquad r_{i}^{\overline{\Delta}_{i}}(\mathcal{A})=\sum _{(i_{2},\ldots,i_{m})\in\overline{\Delta}_{i}} |a_{ii_{2}\cdots i_{m}}|. $$

Theorem 2

[1]

Let \(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{C}^{[m,n]}\). Then

$$ \sigma(\mathcal{A})\subseteq\Omega(\mathcal{A})= \biggl(\bigcup _{i\in [n]}\hat{\Omega}_{i}(\mathcal{A}) \biggr)\cup \biggl(\bigcup_{\substack {i,j\in[n],\\ i\neq j}} \Bigl(\hat{\Omega}_{i,j}( \mathcal{A})\cap \Gamma_{i}(\mathcal{A}) \Bigr) \biggr), $$

where

$$ \hat{\Omega}_{i}(\mathcal{A})= \bigl\{ z\in\mathbb{C}:|z-a_{i\cdots i}| \leq r_{i}^{\Delta_{i}}(\mathcal{A}) \bigr\} $$

and

$$ \hat{\Omega}_{i,j}(\mathcal{A})= \bigl\{ z\in\mathbb{C}: \bigl(|z-a_{i\cdots i}|-r_{i}^{\Delta_{i}}(\mathcal{A}) \bigr) \bigl(|z-a_{j\cdots j}|-r_{j}^{\overline{\Delta}_{i}}(\mathcal{A}) \bigr)\leq r_{i}^{\overline{\Delta}_{i}}(\mathcal{A})r_{j}^{\Delta_{i}}( \mathcal {A}) \bigr\} . $$

Li et al. [1] proved that the set \(\Omega(\mathcal{A})\) in Theorem 2 is tighter than \(\Theta(\mathcal{A})\) in [19] and \(\mathcal{K}(\mathcal{A})\) in [17]; for details, see Theorem 2.3 in [1].

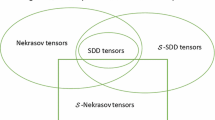
In this paper, we continue this research on the eigenvalue localization problem for tensors. A class of strictly diagonally dominant tensors that involve a parameter p in the interval \([1,\infty]\), denoted by p-norm SDD tensor, is introduced in Section 2. In Section 3, we discuss the relationships between p-norm SDD tensors and strong \(\mathcal{H}\)-tensors. A new eigenvalue inclusion set for tensors based on p-norm SDD tensors is obtained in Section 4, and numerical results show that the new set is tighter than \(\Omega(\mathcal{A})\) in Theorem 2 in some case. Finally, in Section 5, we give a checkable sufficient condition for the positive (semi)definiteness of even-order symmetric tensors.

2 p-Norm SDD tensors

In this section, we propose a new class of nonsingular tensors, namely p-norm strictly diagonally dominant tensors. First, some notation and the definition of strictly diagonally dominant tensors are given.

Given a tensor \(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{C}^{[m,n]}\) and a real number \(p\in[1,\infty]\), denote

$$ r_{i}^{p}(\mathcal{A}):= \biggl(\sum _{\substack{i_{2},\ldots,i_{m}\in[n],\\ \delta_{ii_{2}\cdots i_{m}}=0}}|a_{ii_{2}\cdots i_{m}}|^{p} \biggr)^{\frac {1}{p}} \quad \mbox{for all } i\in[n]. $$

In particular, if \(p=1\), then \(r_{i}^{1}(\mathcal{A})=r_{i}(\mathcal{A})\) for all \(i\in[n]\). If \(p=\infty\), then \(r_{i}^{\infty}(\mathcal{A})= \max_{\substack{i_{2},\ldots,i_{m}\in[n],\\ \delta{ii_{2}\cdots i_{m}}=0}}|a_{ii_{2}\cdots i_{m}}|\) for all \(i\in[n]\). For a vector \(x=(x_{1},x_{2},\ldots, x_{n})^{T}\in\mathbb{C}^{n}\), the \(l_{q}\)-norm on \(\mathbb{C}^{n}\) is

$$\|x\|_{q}:= \biggl(\sum_{i\in[n]}|x_{i}|^{q} \biggr)^{\frac{1}{q}}. $$

Definition 3

[16]

A tensor \(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{C}^{[m,n]}\) is diagonally dominant if

$$ |a_{ii\cdots i}|\geq r_{i}(\mathcal{A})\quad \mbox{for all } i\in[n], $$
(2)

and \(\mathcal{A}\) is strictly diagonally dominant if the strict inequality holds in (2) for all i.

Remark 1

\(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{C}^{[m,n]}\) is strictly diagonally dominant if and only if

$$ \max_{i\in[n]}\frac{r_{i}(\mathcal{A})}{|a_{ii\cdots i}|}< 1. $$

It is well known that strictly diagonally dominant tensors are nonsingular. An interesting problem arises: for a tensor \(\mathcal {A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{C}^{[m,n]}\) satisfying

$$\max_{i\in[n]}\frac{r_{i}^{p}(\mathcal{A})}{|a_{ii\cdots i}|}< 1, $$

is \(\mathcal{A}\) nonsingular or not? Certainly, when \(p=1\), \(\mathcal {A}\) is a strictly diagonally dominant tensor, which means that \(\mathcal{A}\) is nonsingular, but when \(p>1\), \(\mathcal{A}\) may be singular as the following simple example shows.

Example 1

Let \(\mathcal{A}=(a_{ijk})\in\mathbb{R}^{[3,2]}\), where

$$a_{111}=a_{222}=-3,\quad \mbox{and the remaining}\quad a_{ijk}=1. $$

Then, since \(\mathcal{A}e^{2}=0\), where \(e=(1,1,1)^{T}\), this implies \(0\in\sigma (\mathcal{A})\). However, for every \(p>1\), we have

$$\max_{i\in[2]}\frac{r_{i}^{p}(\mathcal{A})}{|a_{iii}|}=3^{\frac{1-p}{p}}< 1. $$

Therefore, something needs to be added in order to obtain a nonsingular \(\mathcal{A}\) for a real number \(p\in(1,\infty]\). We provide an answer further, but we first introduce a class of strictly diagonally dominant tensors that involve a parameter p in the interval \([1,\infty]\).

Definition 4

Let \(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{C}^{[m,n]}\) and \(p\in [1,\infty]\), \(\mathcal{A}\) is called a p-norm strictly diagonally dominant tensor (or, shortly, p-norm SDD tensor) if

$$ \bigl\Vert \delta_{p}(\mathcal{A})\bigr\Vert _{q}< 1, $$
(3)

where

$$\delta_{p}(\mathcal{A}):=(\delta_{1},\delta_{2}, \ldots,\delta_{n})^{T}, \qquad \delta_{i}:= \biggl( \frac{r_{i}^{p}(\mathcal{A})}{|a_{i\cdots i}|} \biggr)^{\frac{1}{m-1}}\quad \mbox{for all } i\in[n], $$

and q is Hölder’s complement of p, that is, \(\frac{1}{p}+\frac{1}{q}=1\).

Remark 2

Definition 4 extends the concept of \(\operatorname{SDD}(p)\) matrix given in [20] to tensors. Clearly, the \(\operatorname{SDD}(p)\) matrix is a 2nd-order p-norm SDD tensor.

Remark 3

Taking \(p=1\), \(\mathcal{A}\) is a 1-norm SDD tensor if and only if

$$\bigl\Vert \delta_{1}(\mathcal{A})\bigr\Vert _{\infty}=\max _{i\in[n]} \biggl(\frac {r_{i}(\mathcal{A})}{|a_{ii\cdots i}|} \biggr)^{\frac{1}{m-1}}< 1, $$

that is,

$$\max_{i\in[n]}\frac{r_{i}(\mathcal{A})}{|a_{ii\cdots i}|}< 1, $$

which is equivalent to the fact that \(\mathcal{A}\) is a strictly diagonally dominant tensor. The other extreme case is \(p=\infty\). \(\mathcal{A}\) is a ∞-norm SDD tensor if and only if

$$ \bigl\Vert \delta_{\infty}(\mathcal{A})\bigr\Vert _{1}=\sum _{i\in[n]} \biggl(\frac{\max_{\substack{i_{2},\ldots,i_{m}\in[n],\\\delta_{ii_{2}\cdots i_{m}}=0}}|a_{ii_{2}\cdots i_{m}}|}{|a_{ii\cdots i}|} \biggr)^{\frac{1}{m-1}}< 1. $$

The p-norm SDD tensors can also be characterized in the following way.

Proposition 1

Let \(\mathcal{A}\in\mathbb{C}^{[m,n]}\) and \(p\in[1,\infty]\). Then \(\mathcal{A}\) is a p-norm SDD tensor if and only if there exists an entrywise positive vector \(x=(x_{1},x_{2},\ldots,x_{n})^{T}\in\mathbb{R}^{n}\) such that \(\|x\|_{q}\leq1\), where q is Hölder’s complement of p such that

$$ x_{i}^{m-1}|a_{i\cdots i}|> r_{i}^{p}(\mathcal{A})\quad \textit{for all } i\in[n]. $$
(4)

Proof

Necessity. Suppose that \(\mathcal{A}\) is a p-norm SDD tensor. It follows from inequality (3) of Definition 4 that there exists a sufficiently small \(\varepsilon>0\) such that, for \(x_{i}:=\delta_{i}+\varepsilon>0\), where \(i\in[n]\), \(\|x\|_{q}\leq1\). Thus, \(x_{i}^{m-1}>\delta_{i}^{m-1}=\frac{r_{i}^{p}(\mathcal{A})}{|a_{i\cdots i}|}\), which implies inequality (4).

Sufficiency. Suppose that there exists an entrywise positive vector \(x>0\) such that \(\|x\|_{q}\leq1\) and inequality (4) holds. By inequality (4) we have

$$x_{i}^{m-1}>\frac{r_{i}^{p}(\mathcal{A})}{|a_{i\cdots i}|}=\delta_{i}^{m-1} \quad \mbox{for all } i\in[n], $$

which implies \(x_{i}>\delta_{i}\) for all \(i\in[n]\), which, together with \(\| x\|_{q}\leq1\), yields

$$\bigl\Vert \delta_{p}(\mathcal{A})\bigr\Vert _{q}< \|x \|_{q}\leq1. $$

Thus, \(\mathcal{A}\) is a p-norm SDD tensor. The proof is completed. □

The following result proves the nonsingular of p-norm SDD tensors.

Theorem 3

Let \(\mathcal{A}\in\mathbb{C}^{[m,n]}\) be a p-norm SDD tensor. Then \(\mathcal{A}\) is nonsingular.

Proof

Suppose that \(\mathcal{A}\) is singular, that is, \(0\in\sigma(\mathcal {A})\). It follows from equality (1) that there exists \(y\in \mathbb{C}^{n}\setminus\{0\}\), such that

$$ \mathcal{A}y^{m-1}=0. $$
(5)

Without the loss of generality, we can assume that \(\|y\|_{q}=1\). Then, equality (5) yields

$$a_{i\cdots i}y_{i}^{m-1}=-\sum _{\substack{i_{2},\ldots,i_{m}\in[n],\\ \delta _{ii_{2}\cdots i_{m}}=0}}a_{ii_{2}\cdots i_{m}}y_{i_{2}}\cdots y_{i_{m}} \quad \mbox{for all } i\in[n], $$

which implies that

$$ |a_{i\cdots i}||y_{i}|^{m-1}=\biggl\vert \sum_{\substack{i_{2},\ldots,i_{m}\in[n],\\ \delta_{ii_{2}\cdots i_{m}}=0}}a_{ii_{2}\cdots i_{m}}y_{i_{2}}\cdots y_{i_{m}}\biggr\vert \quad \mbox{for all } i\in[n]. $$
(6)

Then, applying the Hölder inequality to the right-hand side of equality (6), we obtain

$$\begin{aligned} |a_{i\cdots i}||y_{i}|^{m-1} \leq& \biggl( \sum_{\substack{i_{2},\ldots,i_{m}\in [n], \\ \delta_{ii_{2}\cdots i_{m}}=0}}|a_{ii_{2}\cdots i_{m}}|^{p} \biggr)^{\frac {1}{p}} \biggl(\sum_{\substack{i_{2},\ldots,i_{m}\in[n], \\ \delta _{ii_{2}\cdots i_{m}}=0}}|y_{i_{2}} \cdots y_{i_{m}}|^{q} \biggr)^{\frac {1}{q}} \\ =&r_{i}^{p}(\mathcal{A}) \Biggl[ \Biggl(\sum _{j=1}^{n}|y_{j}|^{q} \Biggr)^{m-1}-|y_{i}|^{(m-1)q} \Biggr]^{\frac{1}{q}} \\ =&r_{i}^{p}(\mathcal{A}) \bigl(\|y\|_{q}^{(m-1)q}-|y_{i}|^{(m-1)q} \bigr)^{\frac{1}{q}} \\ \leq&r_{i}^{p}(\mathcal{A})\|y\|_{q}^{m-1} \\ =&r_{i}^{p}(\mathcal{A}) \quad \mbox{for all } i\in[n]. \end{aligned}$$
(7)

Since \(\mathcal{A}\) is a p-norm SDD tenor, there exists an entrywise positive vector \(x>0\) such that \(\|x\|_{q}\leq1\) and inequality (4) holds. Combining inequality (4) with (7), we obtain

$$ |a_{i\cdots i}||y_{i}|^{m-1}\leq r_{i}^{p}( \mathcal {A})< x_{i}^{m-1}|a_{i\cdots i}|\quad \mbox{for all } i\in[n], $$

which means that

$$ |y_{i}|< x_{i} \quad \mbox{for all } i\in[n]. $$

Thus, \(\|x\|_{q}>\|y\|_{q}=1\), which contradicts \(\|x\|_{q}\leq1\). The proof is completed. □

3 Relationships between p-norm SDD tensors and strong \(\mathcal{H}\)-tensors

The following lemma shows that the strong \(\mathcal{H}\)-tensors play an important role in identifying the positive definiteness of even-order real symmetric tensors.

Lemma 1

[21]

Let \(\mathcal{A}=(a_{i_{1}\cdots i_{m}})\in\mathbb{R}^{[m,n]}\) be an even-order real symmetric tensor with \(a_{i\cdots i}>0\) for all \(i\in[n]\). If \(\mathcal{A}\) is a strong \(\mathcal{H}\)-tensor, then \(\mathcal{A}\) is positive definite.

It is known that the strictly diagonally dominant tensors are a subclass of strong \(\mathcal{H}\)-tensors. An interesting problem arises: whether the class of p-norm SDD tensors is a subclass of strong \(\mathcal{H}\)-tensors for an arbitrary \(p\in[1,\infty]\). In this section, we discuss this problem. We first recall the definition of strong \(\mathcal{H}\)-tensors.

Definition 5

[16]

A tenor \(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{R}^{[m,n]}\) is called an \(\mathcal {M}\)-tensor if there exist a nonnegative tensor \(\mathcal{B}\) and a positive real number \(\eta\geq\rho\mathcal{(B)}\) such that \(\mathcal{A}=\eta\mathcal{I}\)-\(\mathcal{B}\). If \(\eta>\rho\mathcal{(B)}\), then \(\mathcal{A}\) is called a strong \(\mathcal{M}\)-tensor.

Definition 6

[9]

Let \(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{C}^{[m,n]}\). We call another tensor \(\mathcal {M(A)}=(m_{i_{1}i_{2}\cdots i_{m}})\) the comparison tensor of \(\mathcal {A}\) if

$$m_{i_{1}i_{2}\cdots i_{m}}=\left \{ \textstyle\begin{array}{l@{\quad}l} +|a_{i_{1}i_{2}\cdots i_{m}}| &\mbox{if } (i_{2},i_{3},\ldots, i_{m})=(i_{1},i_{1},\ldots, i_{1}), \\ -|a_{i_{1}i_{2}\cdots i_{m}}| &\mbox{if } (i_{2},i_{3},\ldots, i_{m})\neq (i_{1},i_{1},\ldots, i_{1}). \end{array}\displaystyle \right . $$

Definition 7

[9]

We call a tensor an \(\mathcal{H}\)-tensor if its comparison tensor is an \(\mathcal{M}\)-tensor. We call it a strong \(\mathcal{H}\)-tensor if its comparison tensor is a strong \(\mathcal{M}\)-tensor.

Note that Li et al. [21] also provided an equivalent definition of strong \(\mathcal{H}\)-tensors; for details, see [21].

In [22], the multiplication of matrices has been extended to tensors. In the following, we state these results for reference.

Definition 8

[22]

Let \(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\) and \(\mathcal {B}=(b_{i_{1}i_{2}\cdots i_{k}})\) be n-dimensional tensors of orders \(m\geq 2\) and \(k\geq1\), respectively. The product \(\mathcal{AB}\) is the following n-dimensional tensor \(\mathcal{C}\) of order \((m-1)(k-1)+1\) with entries

$$ c_{i\alpha_{1}\alpha_{2}\cdots\alpha_{m-1}}=\sum_{i_{2},\ldots,i_{m}\in [n]}a_{ii_{2}\cdots i_{m}}b_{i_{2}\alpha_{1}} \cdots b_{i_{m}\alpha_{m-1}}, $$

where \(i\in[n]\) and \(\alpha_{1},\ldots,\alpha_{m-1}\in\{j_{2}j_{3}\cdots j_{k}:j_{l}\in[n],l=2,3,\ldots, k\}\).

Remark 4

When \(m=2\) and \(\mathcal{A}=(a_{ij})\) is a matrix of dimension n, then \(\mathcal{AB}\) is an mth-order n-dimensional tensor, and we have

$$(\mathcal{AB})_{i_{1}i_{2}\cdots i_{m}}=\sum_{l_{2}\in [n]}a_{i_{1}l_{2}}b_{l_{2}i_{2}\cdots i_{m}}, \quad i_{j}\in[n], j\in[m]. $$

In particular, the product of a diagonal matrix \(X=\operatorname{diag}(x_{1},x_{2},\ldots, x_{n})\) and the tensor \(\mathcal{A}\) is given by

$$(X\mathcal{A})_{i_{1}i_{2}\cdots i_{m}}=x_{i_{1}}a_{i_{1}i_{2}\cdots i_{m}}, \quad i_{j}\in [n], j\in[m]. $$

Remark 5

Given an n-by-n matrix X and two mth order n-dimensional tensors \(\mathcal{A}\), \(\mathcal{B}\), we have the right distributive law for tensors [22], that is,

$$ X\cdot\mathcal{A}+X\cdot\mathcal{B}=X\cdot(\mathcal{A}+\mathcal{B}). $$

Based on this multiplication of tensors, Kannan, Shaked-Monderer, and Berman [23] established a necessary and sufficient condition for a tensor to be a strong \(\mathcal{H}\)-tensor.

Lemma 2

[23]

Let \(\mathcal{A}\in\mathbb{C}^{[m,n]}\). Then \(\mathcal{A}\) is a strong \(\mathcal{H}\)-tensor if and only if \(a_{i\cdots i}\neq0\) for all \(i\in[n]\) and

$$\rho\bigl(\mathcal{I}-D_{\mathcal{M(A)}}^{-1}\mathcal{M(A)}\bigr)< 1, $$

where \(D_{\mathcal{M(A)}}\) is the diagonal matrix with the same diagonal entries as \(\mathcal{M(A)}\).

The following lemma is given by Qi [3].

Lemma 3

[3]

Let \(\mathcal{A}\in\mathbb{C}^{[m,n]}\) and \(\mathcal{B}=a(\mathcal {A}+b\mathcal{I})\), where a and b are two complex numbers. Then μ is an eigenvalue of \(\mathcal{B}\) if and only if \(\mu=a(\lambda+b)\) and λ is an eigenvalue of \(\mathcal{A}\). In this case, they have the same eigenvectors.

Next, we present an equivalence condition for singular tensors.

Lemma 4

Let \(\mathcal{A}\in\mathbb{C}^{[m,n]}\). Then \(\mathcal{A}\) is singular if and only if \(D\mathcal{A}\) is singular, where \(D=\operatorname{diag}(d_{1},d_{2},\ldots,d_{n})\) is a positive diagonal matrix.

Proof

Suppose that \(D\mathcal{A}\) is singular, that is, \(0\in\sigma (D\mathcal{A})\). Then there exists a vector \(x=(x_{1},x_{2},\ldots,x_{n})^{T}\neq0\) such that

$$\sum_{i_{2},\ldots,i_{m}\in[n]}d_{i}a_{ii_{2}\cdots i_{m}}x_{i_{2}} \cdots x_{i_{m}}=0\quad \mbox{for all } i\in[n], $$

which is equivalent to

$$\sum_{i_{2},\ldots,i_{m}\in[n]}a_{ii_{2}\cdots i_{m}}x_{i_{2}}\cdots x_{i_{m}}=0\quad \mbox{for all } i\in[n], $$

which implies \(0\in\sigma(\mathcal{A})\), that is, \(\mathcal{A}\) is singular. The proof is completed. □

By applying Lemmas 2, 3, and 4, we can now reveal the relationship of p-norm SDD tensors and strong \(\mathcal {H}\)-tensors.

Theorem 4

Let \(\mathcal{A}\in\mathbb{C}^{[m,n]}\). If \(\mathcal{A}\) is a p-norm SDD tensor, then \(\mathcal{A}\) is a strong \(\mathcal{H}\)-tensor.

Proof

By Lemma 2 the theorem will be proved if we can show that \(\rho (\mathcal{I}-D_{\mathcal{M(A)}}^{-1}\mathcal{M(A)})< 1\). Assume, on the contrary, that there exists \(\lambda\in\sigma(\mathcal{I}-D_{\mathcal {M(A)}}^{-1}\mathcal{M(A)})\) such that \(|\lambda|\geq1\). Then, by Lemma 3,

$$0\in\sigma\bigl(\lambda\mathcal{I}-\mathcal{I}+D_{\mathcal {M(A)}}^{-1} \mathcal{M(A)}\bigr). $$

According to the right distributive law for tensors, we have

$$ \lambda\mathcal{I}-\mathcal{I}+D_{\mathcal{M(A)}}^{-1}\mathcal {M(A)}=D_{\mathcal{M(A)}}^{-1} \bigl((\lambda-1)D_{\mathcal {M(A)}} \mathcal{I}+\mathcal{M(A)} \bigr), $$

which, together with Lemma 4, yields

$$ 0\in\sigma \bigl((\lambda-1)D_{\mathcal{M(A)}}\mathcal{I}+\mathcal {M(A)} \bigr). $$
(8)

However, there exists an entrywise positive vector \(x>0\) such that \(\| x\|_{q}\leq1\), and inequality (4) holds because \(\mathcal{A}\) is a p-norm SDD tensor. By inequality (4) we have

$$\begin{aligned} x_{i}^{m-1}\bigl\vert (\lambda-1)|a_{i\cdots i}|+|a_{i\cdots i}| \bigr\vert =&x_{i}^{m-1}|\lambda| |a_{i\cdots i}| \\ \geq&x_{i}^{m-1}|a_{i\cdots i}| \\ >&r_{i}^{p}(\mathcal{A}) \\ =&r_{i}^{p} \bigl((\lambda-1)D_{\mathcal{M(A)}}\mathcal{I}+ \mathcal {M(A)} \bigr), \end{aligned}$$

which implies that \((\lambda-1)D_{\mathcal{M(A)}}\mathcal{I}+\mathcal {M(A)}\) is a p-norm SDD tensor. By Theorem 3 we have

$$0\notin\sigma \bigl((\lambda-1)D_{\mathcal{M(A)}}\mathcal{I}+\mathcal {M(A)} \bigr), $$

which contradicts (8). The proof is completed. □

4 Eigenvalue localization

Similarly to matrices, a nonsingular class of tensors can lead to an eigenvalue localization result. In this section, we illustrate this fact with the class of p-norm SDD tensors.

Theorem 5

Let \(\mathcal{A}\in\mathbb{C}^{[m,n]}\) and \(p\in[1,\infty]\). Then

$$ \sigma(\mathcal{A})\subseteq\Phi^{p}(\mathcal{A}). $$

When \(p=1\), \(\Phi^{1}(\mathcal{A})=\Gamma(\mathcal{A})\). When \(p>1\),

$$\Phi^{p}(\mathcal{A})= \biggl\{ z\in\mathbb{C}:\sum _{i\in[n]} \biggl[\frac {r_{i}^{p}(\mathcal{A})}{|z-a_{i\cdots i}|} \biggr]^{\frac {p}{(m-1)(p-1)}}\geq1 \biggr\} . $$

Proof

Clearly, if \(p=1\), \(\sigma(\mathcal{A})\subseteq\Gamma(\mathcal{A})\) can be easily obtained from Theorem 1. If \(p>1\), suppose that there exists \(\lambda\in\sigma(\mathcal{A})\) such that \(\lambda\notin \Phi^{p}(\mathcal{A})\), that is,

$$ \sum_{i\in[n]} \biggl[\frac{r_{i}^{p}(\mathcal{A})}{|\lambda-a_{i\cdots i}|} \biggr]^{\frac{p}{(m-1)(p-1)}}< 1. $$
(9)

Let \(\mathcal{B}:=\lambda\mathcal{I}-\mathcal{A}=(b_{i_{1}i_{2}\cdots i_{m}})\). Since \(\lambda\in\sigma(\mathcal{A})\), this, together with Lemma 3, yields that \(\mathcal{B}\) is surely singular. On the other hand, by the definition of \(\mathcal{B}\) we obtain \(r_{i}^{p}(\mathcal{B})=r_{i}^{p}(\mathcal{A})\) and \(|b_{i\cdots i}|=|\lambda-a_{i\cdots i}|\) for all \(i\in[n]\), so that (9) becomes

$$\sum_{i\in[n]} \biggl[\frac{r_{i}^{p}(\mathcal{B})}{|b_{i\cdots i}|} \biggr]^{\frac{p}{(m-1)(p-1)}}< 1, $$

which implies

$$\bigl\Vert \delta_{p}(\mathcal{B})\bigr\Vert _{q}< 1, $$

where q is Hölder’s complement of p, which means that \(\mathcal{B}\) is a p-norm SDD tensor. By Theorem 3, \(\mathcal{B}\) is nonsingular. This leads to a contradiction. □

Remark 6

When \(m=2\), Theorem 5 reduces to the result of [20].

Remark 7

In particular, taking \(p=\infty\), we have

$$\Phi^{\infty}(\mathcal{A})= \biggl\{ z\in\mathbb{C}:\sum _{i\in[n]} \biggl[\frac{\max_{\substack{i_{2},\ldots,i_{m}\in[n],\\ \delta_{ii_{2}\cdots i_{m}}=0}}|a_{ii_{2}\cdots i_{m}}|}{|z-a_{i\cdots i}|} \biggr]^{\frac{1}{(m-1)}}\geq1 \biggr\} . $$

It follows from Theorem 5 that

$$ \sigma(\mathcal{A})\subseteq\Phi^{p}(\mathcal{A}), $$

but since this conclusion holds for any \(p\in[1,\infty]\), we immediately have the following theorem.

Theorem 6

Let \(\mathcal{A}\in\mathbb{C}^{[m,n]}\). Then

$$ \sigma(\mathcal{A})\subseteq\bigcap_{p\in[1,\infty]} \Phi^{p}(\mathcal{A}), $$

where \(\Phi^{p}(\mathcal{A})\) is defined as in Theorem  5.

The following example shows that \(\Phi^{\infty}(\mathcal{A})\) is tighter than \(\Omega(\mathcal{A})\) in some case.

Example 2

Let \(\mathcal{A}=(a_{ijk})\in\mathbb{R}^{[3,2]}\) and \(\mathcal {B}=(b_{ijk})\in\mathbb{R}^{[3,2]}\) with elements defined as follows:

$$\begin{aligned}& a_{111}=1.96, \qquad a_{222}=16, \quad \mbox{and the remaining}\quad a_{ijk}=1, \\& b_{111}=18,\qquad b_{222}=16,\quad \mbox{and the remaining}\quad b_{ijk}=1, \end{aligned}$$

respectively. The eigenvalue inclusion regions \(\Omega(\mathcal{A})\) (\(\Omega (\mathcal{B})\)), \(\Phi^{\infty}(\mathcal{A})\) (\(\Phi^{\infty}(\mathcal{B})\)) and the exact eigenvalues of \(\mathcal{A}\) (\(\mathcal{B}\)) are drawn in Figure 1A (Figure 1B), where \(\Omega (\mathcal{A})\) (\(\Omega(\mathcal{B})\)), \(\Phi^{\infty}(\mathcal{A})\) (\(\Phi^{\infty}(\mathcal{B})\)) and the exact eigenvalues of \(\mathcal{A}\) (\(\mathcal{B}\)) are respectively denoted by the blue area, the green area, and red asterisks. In addition, by Corollary 7.8 in [10] we have

$$\sigma(\mathcal{A})=\{ 15.6288, 16.7844, 1.7534+0.4687i, 1.7534-0.4687i\} $$

and

$$\sigma (\mathcal{B})=\{20.1811, 17.3673, 15.2258+0.5245i, 15.2258-0.5245i\}. $$

It is easy to see that \(\Phi^{\infty}(\mathcal{A})\subseteq\Omega (\mathcal{A})\), but \(\Omega(\mathcal{B})\subseteq\Phi^{\infty}(\mathcal{B})\).

Figure 1
figure 1

The eigenvalue inclusion sets of tensors \(\pmb{\mathcal {A}}\) and \(\pmb{\mathcal{B}}\) for Example 2 .

Full size image

5 Determining the positive (semi)definiteness for an even-order real symmetric tensor

By applying the results obtained in Sections 3 and 4 we give a sufficient condition for the positive (semi)definiteness of an even-order real symmetric tensor.

Theorem 7

Let \(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{R}^{[m,n]}\) be an even-order symmetric tensor with \(a_{i\cdots i}>0\) for all \(i\in[n]\). If \(\mathcal{A}\) is a p-norm SDD tensor, then \(\mathcal{A}\) is positive definite.

Proof

The theorem follows immediately from Lemma 1 and Theorem 4. □

Theorem 8

Let \(\mathcal{A}=(a_{i_{1}i_{2}\cdots i_{m}})\in\mathbb{R}^{[m,n]}\) be an even-order symmetric tensor with \(a_{i\cdots i}>0\) for all \(i\in[n]\), and \(p\in[1,\infty]\). If

$$ \bigl\Vert \delta_{p}(\mathcal{A})\bigr\Vert _{q}\leq1, $$

where q is Hölder’s complement of p. Then \(\mathcal{A}\) is positive semidefinite.

Proof

If \(p=1\), then

$$\bigl\Vert \delta_{1}(\mathcal{A})\bigr\Vert _{\infty}=\max _{i\in[n]} \biggl(\frac {r_{i}(\mathcal{A})}{|a_{ii\cdots i}|} \biggr)^{\frac{1}{m-1}}\leq1, $$

which implies that \(\mathcal{A}\) is diagonally dominant. By Theorem 3 of [24] it follows that \(\mathcal{A}\) is positive semidefinite.

If \(p>1\), then let λ be an H-eigenvalue of \(\mathcal{A}\), and \(\lambda<0\). By Theorem 5 we have \(\lambda\in\Phi^{p}(\mathcal {A})\), which implies that

$$\sum_{i\in[n]} \biggl[\frac{r_{i}^{p}(\mathcal{A})}{|\lambda-a_{i\cdots i}|} \biggr]^{\frac{p}{(m-1)(p-1)}}\geq1. $$

However, it follows from \(a_{ii\cdots i}>0\) for all \(i\in[n]\) that

$$\sum_{i\in[n]} \biggl[\frac{r_{i}^{p}(\mathcal{A})}{|a_{i\cdots i}|} \biggr]^{\frac{p}{(m-1)(p-1)}}> \sum_{i\in[n]} \biggl[ \frac{r_{i}^{p}(\mathcal{A})}{|\lambda-a_{i\cdots i}|} \biggr]^{\frac{p}{(m-1)(p-1)}}\geq1, $$

which implies

$$\bigl\Vert \delta_{p}(\mathcal{A})\bigr\Vert _{q}>1, $$

which contradicts \(\|\delta_{p}(\mathcal{A})\|_{q}\leq1\). This completes the proof. □

Example 3

Let \(\mathcal{A}\in\mathbb{R}^{[4,2]}\) be a symmetric tensor with elements defined as follows:

$$a_{1111}=21,\qquad a_{1222}=a_{2122}=a_{2212}=a_{2221}=-3, \qquad a_{2222}=8, $$

and the remaining \(a_{i_{1}i_{2}i_{3}i_{4}}=0\). By computation,

$$|a_{2222}|=8< 9=r_{2}^{\Delta_{2}}(\mathcal{A})=\sum _{\substack {(i_{2},i_{3},i_{4})\in\Delta_{2},\\ \delta_{2i_{2}i_{3} i_{4}}=0}}|a_{2i_{2}i_{3}i_{4}}|, $$

which means that the statement (I) of Proposition 2.4 in [1] does not hold, and hence we cannot use Proposition 2.4 in [1] to determine the positive definiteness of \(\mathcal{A}\). However, it is easy to verify that \(\mathcal{A}\) is a ∞-norm SDD tensor. By Theorem 7, \(\mathcal{A}\) is positive definite.

6 Conclusions

In this paper, we proposed a new class of nonsingular tensors (p-norm SDD tensors) and proved that the class of p-norm SDD tensors is a subclass of strong \(\mathcal{H}\)-tensors. Furthermore, we presented a new eigenvalue inclusion set, which is tighter than those provided by Li et al.[1] in some case. Based on this set, we presented a checkable sufficient condition for the positive (semi)definiteness of an even-order symmetric tensor.