Ordering non-bipartite unicyclic graphs with pendant vertices by the least Q-eigenvalue

Abstract

A unicyclic graph is a connected graph whose number of edges is equal to the number of vertices. Fan et al. (Discrete Math. 313:903-909, 2013) and Liu et al. (Electron. J. Linear Algebra 26:333-344, 2013) determined, independently, the unique unicyclic graph whose least Q-eigenvalue attains the minimum among all non-bipartite unicyclic graphs of order n with k pendant vertices. In this paper, we extend their results and determine the first three non-bipartite unicyclic graphs of order n with k pendant vertices ordering by least Q-eigenvalue.

1 Introduction

Let $G=(V, E)$ be a simple undirected graph with vertex set $V=V(G)= \{v_{1}, v_{2}, \ldots, v_{n}\}$ and edge set $E=E(G)$, where n is called the order of G. Let $A(G)$ be the adjacency matrix of a graph G and let $D(G)=\operatorname {diag}(d_{G}(v_{1}), d_{G}(v_{2}),\ldots, d_{G}(v_{n}))$ be the diagonal matrix of degrees of G, where $d_{G}(v)$ or simply $d(v)$ denotes the degree of a vertex v in G. The matrix $Q(G)=D(G)+ A(G)$ is called the signless Laplacian matrix (or Q-matrix) of G. Since $Q(G)$ is symmetric and positive semidefinite, it follows that its eigenvalues are real and nonnegative. We simply call the eigenvalues of $Q(G)$ as the signless Laplacian eigenvalues or Q-eigenvalues of G. As usual, we shall index the eigenvalues of $Q(G)$ in nonincreasing order and denote them as $q_{1}(G)\ge q_{2}(G)\ge\cdots\ge q_{n}(G)\ge 0$. Denote by $\kappa(G)$ the least Q-eigenvalue of G.

For a connected graph G, Desai and Rao [3] showed that $\kappa (G) = 0$ if and only if G is bipartite, and suggested that $\kappa (G)$ can be used as a measure of non-bipartiteness of G. For a connected non-bipartite graph G, how small can $\kappa(G)$ be? Cardoso et al. [4] proposed this problem and proved that the minimum value of $\kappa(G)$ of a connected non-bipartite graph G of order n is attained solely in the unicyclic graph that arises from a cycle of order 3 by attaching a path at one of its end vertices. Wang and Fan [5] investigated how the least Q-eigenvalue of a graph changes when a bipartite branch attached at one vertex is relocated to another vertex and proved a perturbation theorem on the least Q-eigenvalue. As an application, they minimized the least Q-eigenvalue among the class of connected graphs with fixed order which contains a given non-bipartite graph as an induced subgraph. Recently, the problem of finding all graphs with the minimal least Q-eigenvalue among a given class of graphs has been studied extensively. For related results, one may refer to [1, 2, 5–12].

A c-cyclic graph G is a connected graph with n vertices and $n+c-1$ edges. Specially, if $c = 0$, 1, or 2, then G is a tree, a unicyclic graph, or a bicyclic graph, respectively. Very recently, Fan et al. [1] and Liu et al. [2] determined, independently, the unique unicyclic graph whose least Q-eigenvalue attains the minimum among all non-bipartite unicyclic graphs of order n with k pendant vertices. In this paper, we extend their results and determine the first three non-bipartite unicyclic graphs of order n with k pendant vertices ordering by least Q-eigenvalue.

The rest of the paper is organized as follows. In Section 2, we recall some basic notions and lemmas used further, and prove two new lemmas. In Section 3, we order non-bipartite unicyclic graphs of order n with k pendant vertices. In Section 4, a conjecture is proposed.

2 Preliminaries

Denote by $C_{n}$ the cycle of order n. Let $G-uv$ denote the graph obtained from G by deleting the edge $uv\in E(G)$. Similarly, $G+uv$ is the graph obtained from G by adding an edge $uv\notin E(G)$, where $u, v\in V(G)$. We write $d_{G}(u, v)$ or simply $d(u, v)$ for the distance in G between vertices u and v. The diameter of a connected graph G is the maximum distance between pairs of vertices in $V(G)$. For $v\in V(G)$, $N_{G}(v)$ or simply $N(v)$ denotes the neighborhood of v in G. A pendant vertex of G is a vertex of degree 1. A pendant neighbor of G is a vertex adjacent to a pendant vertex.

Let $x=(x_{1}, x_{2}, \ldots, x_{n})^{T}$ be a column vector in $\mathbb {R}^{n}$. Then x can be considered as a function defined on $V(G)$, that is, each vertex $v_{i}$ is given by the value $x(v_{i})=x_{i}$. Then the quadratic form

$$x^{T}Q(G)x =\sum_{uv\in E(G)}\bigl(x(u) + x(v) \bigr)^{2}. $$

Let $\vert x(v)\vert$ denote the absolute value of $x(v)$. If x is an eigenvector corresponding to a Q-eigenvalue of G, then it defines on $V(G)$ naturally, i.e. $x(v)$ is the entry of x corresponding to v. For an arbitrary unit vector $x\in\mathbb{R}^{n}$, one can find in [5, 13]

$$ \kappa(G) \le x^{T}Q(G)x, $$

(1)

where equality holds if and only if x is an eigenvector corresponding to $\kappa(G)$.

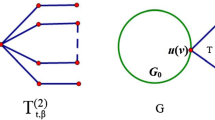
Let $G_{1}$ and $G_{2}$ be two vertex-disjoint graphs, and let $v_{1}\in V(G_{1})$, $v_{2}\in V(G_{2})$. $G_{1}(v_{1})\diamond G_{2}(v_{2})$ denotes the coalescence of $G_{1}$ and $G_{2}$, which arises from $G_{1}$, $G_{2}$ by identifying $v_{1}$ with $v_{2}$ and forming a new vertex u (see [5] for details). The graph $G_{1}(v_{1})\diamond G_{2}(v_{2})$ is also written as $G_{1}(u)\diamond G_{2}(u)$. If a graph G can be expressed in the form $G = G_{1}(u)\diamond G_{2}(u)$, where $G_{1}$ and $G_{2}$ are both connected and nontrivial, then $G_{i}$ is called a branch of G with root u for $i=1, 2$. Let x be a vector defined on $V(G)$. A branch H of G is called a zero branch with respect to x if $x(v) = 0$ for all $v \in V(H)$; otherwise it is called a nonzero branch with respect to x.

Lemma 2.1

([5])

Let G be a connected graph which contains a bipartite branch B with root v. Let x be an eigenvector of G corresponding to $\kappa(G)$.

• (i) If $x(v) = 0$, then B is a zero branch of G with respect to x.

• (ii) If $x(v)\neq0$, then $x(p)\neq0$ for every vertex $p\in V(B)$.

Lemma 2.2

([5])

Let G be a connected non-bipartite graph of order n, and let x be an eigenvector of G corresponding to $\kappa(G)$. Let T be a tree, which is a nonzero branch of G with respect to x and with root v. Then $\vert x(q)\vert < \vert x(p)\vert$ whenever p, q are vertices of T such that q lies on the unique path from v to p.

Lemma 2.3

([10])

Let $G = C(v_{0})\diamond B(v_{0})$ be a graph of order n, where $C=v_{0}v_{1}v_{2} \cdots v_{k} u_{k}u_{k-1} \cdots u_{1}v_{0}$ is a cycle of length $2k+1$, and B is a bipartite graph of order $n-2k>1$ (see Figure  1). Let $x=( x(v_{0}), x(v_{1}), x(v_{2}), \ldots, x(v_{k}), x(u_{1}), x(u_{2}), \ldots, x(u_{k}), \ldots )^{T}$ be an eigenvector corresponding to $\kappa(G)$. Then

• (i) $\vert x(v_{0})\vert =\max\{\vert x(w)\vert \mid w\in V(C)\}>0$;

• (ii) $x(v_{i})=x(u_{i})$ for $i=1, 2, \ldots, k$.

Figure 1

$\pmb{C(v_{0})\diamond B(v_{0})}$ .

Lemma 2.4

([10])

Let $G = G_{1}(v_{2}) \diamond T(u)$ and $G^{*} = G_{1}(v_{1})\diamond T(u)$, where $G_{1}$ is a non-bipartite connected graph containing two distinct vertices $v_{1}$, $v_{2}$, and T is a nontrivial tree. If there exists an eigenvector $x=( x(v_{1}), x(v_{2}), \ldots, x(v_{k}), \ldots)^{T}$ of G corresponding to $\kappa(G)$ such that $\vert x(v_{1})\vert > \vert x(v_{2})\vert$ or $\vert x(v_{1})\vert = \vert x(v_{2})\vert > 0$, then $\kappa(G^{*})<\kappa(G)$.

Lemma 2.5

([14])

Let G be a graph with n vertices and m edges. Then

$$\kappa(G)\le\frac{4m-4\operatorname {MaxCut}(G)}{n}, $$

where $\operatorname {MaxCut}(G)$ denotes, as usual, the size of the largest bipartite subgraph of G.

For a c-cyclic graph G, we have $\operatorname {MaxCut}(G)\ge n-1$. This implies the following lemma.

Lemma 2.6

Let G be a c-cyclic graph. Then $\kappa(G)\le\frac{4c}{n}$.

Lemma 2.7

([15])

Let G be a non-bipartite connected graph of order n with diameter D. Then $\kappa(G) \geq\frac{1}{n(D+1)}$.

$U_{n}^{k}(g)$, shown in Figure 2, denotes the unicyclic graph of order n with odd girth g and k pendant vertices, where $g+l+k=n$. $C_{3}^{ 1}(n-k-1)$, $C_{3}^{ 2}(n-k-1)$, and $C_{3}^{1}(n-k-2)$ are the unicyclic graphs of order n with k pendant vertices, shown in Figures 2 and 3, respectively.

Figure 2

$\pmb{U_{n}^{k}(g)}$ and $\pmb{C_{3}^{ 1}(n-k-1)}$ .

Figure 3

$\pmb{C_{3}^{ 2}(n-k-1)}$ and $\pmb{C_{3}^{1}(n-k-2)}$ .

Lemma 2.8

Let $3\le k \leq{(n-4)}/\sqrt{6}$. Then $\kappa(C_{3}^{ 2}(n-k-1))<\kappa(C_{3}^{1}(n-k-2))$.

Proof

Let $\kappa=\kappa(C_{3}^{1}(n-k-2))$, and $x=(x_{1}, x_{2}, \ldots, x_{n})^{T}$ be a unit eigenvector corresponding to κ. Then $\kappa =\sum_{v_{i}v_{j}\in E(C_{3}^{ 1}(n-k-2))}(x_{i}+x_{j})^{2}$ and $0<\kappa<1$ (by Lemma 2.6). From the eigenvalue equation $Q(C_{3}^{1}(n-k-2))x =\kappa x$, we have $x_{n-k+2}=\cdots=x_{n}$,

$$\begin{aligned}& x_{n-k} = (\kappa-1)x_{n}, \\& x_{n-k-1} = \bigl(\kappa^{2}-(k+1)\kappa+1\bigr)x_{n}, \\& x_{n-k-2} = \bigl(\kappa^{3}-(k+3)\kappa^{2}+(2k+2) \kappa-1\bigr)x_{n}, \\& x_{n-k+1} = \frac{1}{\kappa-1}\bigl(\kappa^{3}-(k+3) \kappa^{2}+(2k+2)\kappa-1\bigr)x_{n}, \end{aligned}$$

and $x_{n}\neq0$.

Let $y=(y_{1}, y_{2}, \ldots, y_{n})^{T}\in \mathbb{R}^{n}$, which is defined on $V(C_{3}^{ 2}(n-k-1))$, satisfy $y_{n-k+1}=-(x_{n-k-1}+x_{n-k-2}+x_{n-k+1})$, $y_{n-k+2}=-(x_{n-k-1}+x_{n-k+2}+x_{n-k})$, and $y_{i}=x_{i}$ for $i=1, 2, \ldots, n-k, n-k+3,\ldots, n$. Then

$$\sum_{v_{i}v_{j}\in E(C_{3}^{ 2}(n-k-1))}(y_{i}+y_{j})^{2}= \sum_{v_{i}v_{j}\in E(C_{3}^{1}(n-k-2))}(x_{i}+x_{j})^{2}= \kappa $$

and

$$\begin{aligned} \Vert y\Vert ^{2}-\Vert x\Vert ^{2} =&\sum _{i=1}^{n} y_{i}^{2}-\sum _{i=1}^{n} x_{i}^{2} \\ =&\kappa\bigl({\kappa^{5}}-(2k+2){\kappa^{4}}+ \bigl(k^{2}+2k-1\bigr){\kappa ^{3}}+(4k+6){ \kappa^{2}} \\ &{}-\bigl(2k^{2}+6k+3\bigr)\kappa+2 \bigr)x_{n}^{2}. \end{aligned}$$

Let $f(t)={t^{5}}-(2k+2){t^{4}}+(k^{2}+2k-1){t^{3}}+(4k+6){t^{2}}-(2k^{2}+6k+3)t+2$. It is not difficult to verify that $f(t)>0$ for $0 \le t \leq1/{(k^{2}+3k+2)}$.

Let $z=(z_{1}, z_{2}, \ldots, z_{n})^{T} \in \mathbb{R}^{n}$, which is defined on $V(C_{3}^{1}(n-k-2))$, satisfy $z_{1}=z_{2}=0$, $z_{n-k+1}=(-1)^{n-k+1}(n-k-3)$,

$$\begin{aligned}& z_{n-k-i} = (-1)^{n-k-i}(n-k-i-2)\quad\mbox{for } 0\le i\le n-k-3, \\& z_{n-k+i} = (-1)^{n-k+1}(n-k-1) \quad\mbox{for } i=2, 3, \ldots, k. \end{aligned}$$

Then, by (1) and $3\le k \leq{(n-4)}/\sqrt{6}$, we have

$$\begin{aligned} \kappa =&\kappa\bigl(C_{3}^{1}(n-k-2)\bigr)\le \frac{z^{T}Q(G)z}{z^{T}z} \\ =&\frac{n-1}{1^{2}+2^{2}+\cdots+(n-k-2)^{2}+(n-k-3)^{2}+(k-1)(n-k-1)^{2}} \\ =&\frac{6(n-1)}{2n^{3} - 9n^{2} -(6k^{2}-6k+11)n + 4k^{3} + 3k^{2} + 17k + 42}< \frac{1}{k^{2}+3k+2}. \end{aligned}$$

Therefore $f(\kappa)>0$, and so

$$\Vert y\Vert ^{2}-\Vert x\Vert ^{2}=\kappa f(\kappa) x_{n}^{2}>0. $$

Combining the above arguments, we have

$$\begin{aligned} \kappa\bigl(C_{3}^{2}(n-k-1)\bigr) \leq&\Vert y\Vert ^{-2}\sum_{v_{i}v_{j} \in E(C_{3}^{2}(n-k-1))}(y_{i}+y_{j})^{2}< \Vert x\Vert ^{-2} \sum_{v_{i}v_{j} \in E(C_{3}^{1}(n-k-2))}(x_{i}+x_{j})^{2} \\ =& \kappa. \end{aligned}$$

 □

Lemma 2.9

Let $n\ge120$, $k > \frac{-3+\sqrt{21}}{2}n$. Then $\kappa (C_{3}^{1}(n-k-2))< \kappa(C_{3}^{ 2}(n-k-1))$.

Proof

Let $\kappa=\kappa(C_{3}^{ 2}(n-k-1))$, and $x=(x_{1}, x_{2}, \ldots, x_{n})^{T}$ be a unit eigenvector corresponding to κ. Then $\kappa =\sum_{v_{i}v_{j}\in E(C_{3}^{ 2}(n-k-1))}(x_{i}+x_{j})^{2}$ and $0<\kappa<1$. From the eigenvalue equation $Q(C_{3}^{ 2}(n-k-1))x = \kappa x$, we have $x_{n-k+3}=\cdots=x_{n}$,

$$\begin{aligned}& x_{n-k} = (\kappa-1)x_{n}, \\& x_{n-k-1} = \bigl(\kappa^{2}-k\kappa+1\bigr)x_{n}, \\& x_{n-k+1} = x_{n-k+2}=\frac{1}{\kappa-1}\bigl(\kappa^{2}-k \kappa+1\bigr)x_{n}, \\& x_{n-k-2} = \frac{1}{\kappa-1}\bigl(\kappa^{4}-(k+5) \kappa^{3}+(5k+2)\kappa ^{2}-(2k+3)\kappa+1 \bigr)x_{n}, \end{aligned}$$

and $x_{n}\neq0$.

Let $y=(y_{1}, y_{2}, \ldots, y_{n})^{T}\in \mathbb{R}^{n}$, which is defined on $V(C_{3}^{1}(n-k-2))$, satisfy that $y_{n-k+1}=-(x_{n-k-1}+x_{n-k-2}+x_{n-k+1})$, $y_{n-k+2}=-(x_{n-k-1}+x_{n-k+2}+x_{n-k})$, and $y_{i}=x_{i}$ for $i=1, 2, \ldots, n-k, n-k+3, n-k+4, \ldots, n$. Then

$$\sum_{v_{i}v_{j}\in E(C_{3}^{1}(n-k-2))}(y_{i}+y_{j})^{2}= \sum_{v_{i}v_{j}\in E(C_{3}^{ 2}(n-k-1))}(x_{i}+x_{j})^{2}= \kappa $$

and

$$\begin{aligned} \Vert y\Vert ^{2}-\Vert x\Vert ^{2} =&\sum _{i=1}^{n} y_{i}^{2}-\sum _{i=1}^{n} x_{i}^{2} \\ =&\frac{\kappa}{\kappa-1}\bigl({\kappa^{6}}-(2k+7){\kappa ^{5}}+ \bigl(k^{2}+14k+14\bigr){\kappa^{4}}-\bigl(7k^{2}+28k+4 \bigr){\kappa^{3}} \\ &{} +\bigl(14k^{2}+6k+15\bigr)\kappa^{2}- \bigl(2k^{2}+14k+1\bigr)\kappa^{2}+6\bigr)x_{n}^{2}. \end{aligned}$$

Let

$$\begin{aligned} f(t) =&{t^{6}}-(2k+7){t^{5}}+\bigl(k^{2}+14k+14 \bigr){t^{4}}-\bigl(7k^{2}+28k+4\bigr){t^{3}}+ \bigl(14k^{2}+6k+15\bigr)t^{2} \\ &{}-\bigl(2k^{2}+14k+1 \bigr)t+6. \end{aligned}$$

Then $f(0)=6$. From $n\ge120$ and $k> \frac{-3+\sqrt{21}}{2}n$, we have $k > \frac{-3+\sqrt{21}}{2}n>94$, and

$$\begin{aligned}& k^{12}f\bigl(1/k^{2}\bigr) = 4k^{12}-14k^{11}+13k^{10}+6k^{9}+8k^{8}-28k^{7}-3k^{6}+14k^{5} \\& \hphantom{k^{12}f\bigl(1/k^{2}\bigr) =}{} +14k^{4}-2k^{3}-7k^{2}+1>0, \\& k^{12}f\bigl(3/k^{2}\bigr) = -42k^{11}+123k^{10}+54k^{9}-54k^{8}-756k^{7}-27k^{6} \\& \hphantom{k^{12}f\bigl(3/k^{2}\bigr) =}{} +1134k^{5}+1134k^{4}-486k^{3}-1701k^{2}+729< 0, \\& f'(t) = 6t^{5}-(10k+35)t^{4}+ \bigl(4k^{2}+56k+56\bigr)t^{3}-\bigl(21k^{2}+84k+12 \bigr)t^{2} \\& \hphantom{f'(t) =}{} +\bigl(28k^{2}+12k+30\bigr)t-\bigl(2k^{2}+14k+1\bigr)< 0, \end{aligned}$$

for $0\le t \leq1/30$. So $f(t)$ is strictly decreasing with respect to t in $[0,1/30]$. Recalling that $k > \frac{-3+\sqrt{21}}{2}n$, by Lemmas 2.6 and 2.7, we find that

$$\frac{3}{k^{2}}< \frac{1}{n(n-k)} \leq\kappa=\kappa\bigl(C_{3}^{2}(n-k-1) \bigr)\le \frac{4}{n}\le\frac{1}{30}. $$

This implies that $f(\kappa)<0$ and

$$\Vert y\Vert ^{2}-\Vert x\Vert ^{2}= \frac{\kappa}{\kappa-1}f(\kappa) x_{n}^{2}>0. $$

It follows that

$$\begin{aligned} \kappa\bigl(C_{3}^{1}(n-k-2)\bigr) \leq&\Vert y\Vert ^{-2} \sum_{v_{i}v_{j} \in E(C_{3}^{1}(n-k-2))}(y_{i}+y_{j})^{2}< \Vert x\Vert ^{-2} \sum_{v_{i}v_{j} \in E(C_{3}^{2}(n-k-1))}(x_{i}+x_{j})^{2} \\ =& \kappa. \end{aligned}$$

 □

3 Main results

Let $\mathcal{U}_{ n}^{k}$ be the set of non-bipartite unicyclic graphs of order n with k pendant vertices. From [1, 2], we know that $U_{n}^{k}(3)$ is the unique graph whose least Q-eigenvalue attains the minimum among all graphs in $\mathcal{U}_{ n}^{k}$. In this section, we will determine the first three graphs in $\mathcal{U}_{ n}^{k}$ ordered according to their least Q-eigenvalues.

For $k=1$, from [1], we know that $\kappa(U_{n}^{1}(3))<\kappa (U_{n}^{1}(5))<\kappa(U_{n}^{1}(7))<\cdots$ .

Theorem 3.1

Let $2\le k\le n-4$. Among all graphs in $\mathcal{U}_{ n}^{k}\backslash\{U_{n}^{k}(3)\}$, $C_{3}^{1}(n-k-1)$ is the unique graph whose least Q-eigenvalue attains the minimum.

Proof

Let G be a graph in $\mathcal{U}_{ n}^{k}\backslash\{ U_{n}^{k}(3)\}$ whose least Q-eigenvalue attains the minimum, and $C_{g}=v_{1}v_{2}\cdots v_{g}v_{1}$ be the unique cycle of G. Then g is odd, and G can be obtained by attaching rooted trees $T_{1}, \ldots, T_{g}$ to the vertices $v_{1}, \ldots, v_{g}$ of $C_{g}$, respectively, where $T_{i}$ contains the root vertex $v_{i}$. $\vert V(T_{i})\vert =1$ means that $V(T_{i})=\{v_{i}\}$ and in this case $T_{i}$ is a trivial tree. Let $x=(x_{1}, x_{2}, \ldots, x_{n})^{T}$ be a unit eigenvector corresponding to $\kappa(G)$.

First, we show that G is the cycle $C_{g}=v_{1}v_{2}\cdots v_{g}v_{1}$ with only one nontrivial tree attached. Otherwise, we assume that there are more than one nontrivial trees attached at two different vertices of the cycle $C_{g}$. Let $v_{t}$ be a vertex of the cycle $C_{g}$ such that $\vert x_{t}\vert \geq \vert x_{i}\vert$ for $i=1, 2, \ldots, g$. By Lemma 2.1, $x_{t}\neq0$. Let $v_{l}$ be another vertex of the cycle $C_{g}$ such that $\vert V(T_{l})\vert >1$, and let

$$G_{1}=G-\sum_{v\in N_{T_{l}}(v_{l})}v_{l}v+\sum _{v\in N_{T_{l}}(v_{l})}v_{t}v. $$

From $k\le n-4$, we have $G_{1}\in\mathcal{U}_{n}^{k} \backslash\{ U_{n}^{k}(3)\}$. By Lemma 2.4, we have $\kappa(G_{1})<\kappa(G)$, a contradiction. Therefore G is the cycle $C=v_{1}v_{2}\cdots v_{g}v_{1}$ with only one nontrivial tree attached. Without loss of generality, we may assume the nontrivial tree is $T_{g}$.

Second, we show that $g=3$. Otherwise, we assume that $g\ge5$. By Lemma 2.3, we have $x_{(g-3)/2}=x_{(g+3)/2}$. Let

$$G '=G-v_{(g-1)/2}v_{(g-3)/2}+v_{(g-1)/2}v_{(g+3)/2}. $$

Clearly, $G '\in\mathcal{U}_{ n}^{k+1}$, and from (1) we have

$$\kappa\bigl(G '\bigr)\le x^{T}Q\bigl(G ' \bigr)x=x^{T}Q(G)x=\kappa(G). $$

Let $v_{t}$ be a pendant vertex of G, and $y=(y_{1}, y_{2}, \ldots, y_{n})^{T}$ be a unit eigenvector corresponding to $\kappa(G ')$. By Lemma 2.2, we have $\vert y_{t}\vert > \vert y_{g}\vert >0$. Let $G ''=G '-v_{1}v_{g}+v_{1}v_{t}$. It is easy to see that $G ''\in\mathcal{U}_{ n}^{k}\backslash\{ U_{n}^{k}(3)\}$. By Lemma 2.4, we have $\kappa(G '')<\kappa(G ')$. Then we have $\kappa(G '')<\kappa(G)$, a contradiction. Therefore $g=3$.

Third, we show that G has two pendant neighbors exactly. Otherwise, suppose that G has $r\ge3$ pendant neighbors. Let $v_{a}$ be a pendant neighbor of G such that $d(v_{3}, v_{a})$ is as large as possible, $v_{s}$ and $v_{t}$ be two other pendant neighbors of G. Applying Lemma 2.4 to $v_{s}$ and $v_{t}$, we may obtain a graph $G '\in\mathcal{U}_{ n}^{k}\backslash\{U_{n}^{k}(3)\}$ or $G '\in \mathcal{U}_{ n}^{k+1}$ such that $\kappa(G ')<\kappa(G)$. If $G '\in\mathcal{U}_{ n}^{k}\backslash \{U_{n}^{k}(3)\}$, we have a contradiction. If $G '\in\mathcal{U}_{ n}^{k+1}$, without loss of generality, we may assume that $v_{s}$ is a pendant vertex of $G '$. Let u and w be two pendant vertices adjacent to $v_{t}$ of $G '$, and $G ''=G '-v_{t}w+uw$. Clearly, $G ''\in\mathcal{U}_{ n}^{k}\backslash\{U_{n}^{k}(3)\}$ and $\kappa(G '')<\kappa(G ')$. Then we have $\kappa(G '')<\kappa(G)$, a contradiction. Therefore G has two pendant neighbors exactly. Let $v_{a}$ be a pendant neighbor of G such that $d(v_{3}, v_{a})$ is as large as possible, and $v_{b}$ be another pendant neighbor of G.

Fourth, we show that $v_{b}$ is in path $v_{3}-v_{a}$. Otherwise, suppose that $v_{b}$ is not in path $v_{3}-v_{a}$. Employing Lemma 2.4 to vertices $v_{a}$ and $v_{b}$, we may obtain a graph $G '\in\mathcal {U}_{ n}^{k+1}$ such that $\kappa(G ')<\kappa(G)$. Without loss of generality, we may assume that $v_{b}$ is a pendant vertex of $G '$. Let u and w be two pendant vertices adjacent to $v_{a}$ of $G '$, and $G ''=G '-v_{a}w+uw$. Clearly, $G ''\in\mathcal{U}_{ n}^{k}\backslash\{U_{n}^{k}(3)\}$ and $\kappa(G '')<\kappa(G ')$. Then we have $\kappa(G '')<\kappa(G)$, a contradiction. Therefore $v_{b}$ is in path $v_{3}-v_{a}$.

Fifth, we show that $v_{a}$ and $v_{b}$ are adjacent. Otherwise, suppose that $v_{a}$ and $v_{b}$ are not adjacent. Let $v_{c}\in N(v_{b})$ be in path $v_{b}-v_{a}$, then, by Lemma 2.4, we have $\vert x_{c}\vert >\vert x_{b}\vert$. Let $v_{t}$ be the pendant vertex adjacent to $v_{b}$ and $G '=G-v_{b}v_{t}+v_{c}v_{t}$. Clearly, $G '\in\mathcal{U}_{ n}^{k}\backslash\{U_{n}^{k}(3)\}$ and by Lemma 2.4 we have $\kappa(G ')<\kappa(G)$, a contradiction. Therefore $v_{a}$ and $v_{b}$ are adjacent.

Sixth, we show that $d(v_{b})=3$. Otherwise, suppose that $d(v_{b})>3$. Let $v_{t}$ be the pendant vertex adjacent to $v_{b}$ and $G '=G-v_{b}v_{t}+v_{a}v_{t}$. Clearly, $G '\in\mathcal{U}_{ n}^{k}\backslash\{U_{n}^{k}(3)\}$. By Lemma 2.4, we have $\vert x_{a}\vert >\vert x_{b}\vert$, and by Lemma 2.4, we have $\kappa(G ')<\kappa(G)$, a contradiction. Therefore $d(v_{b})=3$.

From the above arguments, we have $G=C_{3}^{1}(n-k-1)$. □

For $k=n-3$, $\mathcal{U}_{ n}^{ n-3}=\{\Delta_{r, s, t} \mid r\ge s\ge t\ge0, r+s+t=n-3 \}$, where $\Delta_{r, s, t}$ is the graph obtained from the cycle $C_{3}$ by attaching r, s, t pendent edges to the vertices $v_{1}$, $v_{2}$, and $v_{3}$ of the cycle $C_{3}$, respectively. By a similar reasoning to that of Theorem 3.1, we can prove the following theorem.

Theorem 3.2

Let $n\ge8$, and $G\in\mathcal{U}_{ n}^{n-3}\backslash\{\Delta _{n-3, 0, 0}, \Delta_{n-4, 1, 0}, \Delta_{n-5, 2, 0}\}$. Then

$$\kappa(\Delta_{n-3, 0, 0})< \kappa(\Delta_{n-4, 1, 0})< \kappa ( \Delta_{n-5, 2, 0})< \kappa(G). $$

Next, we will determine the graph in $\mathcal{U}_{ n}^{k}\backslash\{ U_{n}^{k}(3), C_{3}^{1}(n-k-1)\}$ whose least Q-eigenvalue attains the minimum.

Theorem 3.3

Let $2\le k\le n-5$. Among all graphs in $\mathcal{U}_{ n}^{k}\backslash\{U_{n}^{k}(3), C_{3}^{1}(n-k-1)\}$, $C_{3}^{ 1}(n-k-2)$ or $C_{3}^{ 2}(n-k-1)$ is the graph whose least Q-eigenvalue attains the minimum.

Proof

Let G be a graph in $\mathcal{U}_{ n}^{k}\backslash\{ U_{n}^{k}(3), C_{3}^{1}(n-k-1)\}$ whose least Q-eigenvalue attains the minimum, and let $x=(x_{1}, x_{2}, \ldots, x_{n})^{T}$ be a unit eigenvector corresponding to $\kappa(G)$. By a similar reasoning to that of Theorem 3.1, we can prove that G is the cycle $C=v_{1}v_{2}v_{3}v_{1}$ with only one nontrivial tree $T_{3}$ attached at $v_{3}$, and G has two pendant neighbors exactly. Let $v_{a}$ be a pendant neighbor of G such that $d(v_{3}, v_{a})$ is as large as possible, and $v_{b}$ be another pendant neighbor of G. By a similar reasoning to that of Theorem 3.1, we can prove that $v_{b}$ is in path $v_{3}-v_{a}$.

Now we show that $d(v_{b}, v_{a})\le2$. Otherwise, suppose that $d(v_{b}, v_{a})\ge3$. Let $v_{t}$ be the pendant vertex adjacent to $v_{b}$ and $v_{c}\in N(v_{b})$ be in path $v_{b}-v_{a}$. Then, by Lemma 2.4, we have $\vert x_{c}\vert >\vert x_{b}\vert$. Let $G '=G-v_{b}v_{t}+v_{c}v_{t}$. Clearly, $G '\in\mathcal{U}_{ n}^{k}\backslash\{U_{n}^{k}(3), C_{3}^{1}(n-k-1)\}$ and $\kappa(G ')<\kappa(G)$, a contradiction. Therefore $d(v_{b}, v_{a})\le2$.

If $d(v_{b}, v_{a})=2$, then we declare $d(v_{b})=3$. Otherwise, suppose that $d(v_{b})\ge4$. Let $v_{t}$ be the pendant vertex adjacent to $v_{b}$ and let $G '=G-v_{b}v_{t}+v_{a}v_{t}$. Clearly, $G '\in\mathcal{U}_{ n}^{k}\backslash\{U_{n}^{k}(3), C_{3}^{1}(n-k-1)\}$ and $\kappa(G ')<\kappa(G)$, a contradiction. Therefore $d(v_{b})=3$ and $G=C_{3}^{1}(n-k-2)$.

If $d(v_{b}, v_{a})=1$, then we declare $d(v_{b})=4$. Otherwise, suppose that $d(v_{b})\ge5$. Let $v_{t}$ be the pendant vertex adjacent to $v_{b}$ and let $G '=G-v_{b}v_{t}+v_{a}v_{t}$. Clearly, $G '\in\mathcal{U}_{ n}^{k}\backslash\{U_{n}^{k}(3), C_{3}^{1}(n-k-1)\}$ and $\kappa(G ')<\kappa(G)$, a contradiction. Therefore $d(v_{b})=4$ and $G=C_{3}^{2}(n-k-1)$.

From the above arguments, we have $G=C_{3}^{1}(n-k-1)$ or $C_{3}^{2}(n-k-1)$. □

For $k=n-4$, $\mathcal{U}_{ n}^{ n-4}=\{C_{3}^{ r, s, t, l} \mid l\ge1, r\ge0, s\ge0, t\ge0, r+s+t+l=n-4 \}$, where $C_{3}^{ r, s, t, l}$, shown in Figure 4, denotes the unicyclic graph of order n with $n-4$ pendant vertices. $C_{3}^{ 1}(2)$ and $C_{3}^{ 2}(3)$, shown in Figure 4, are the unicyclic graphs of order n with $n-4$ pendant vertices.

Figure 4

$\pmb{C_{3}^{ r, s, t, l}}$ , $\pmb{C_{3}^{ 1}(2)}$ , and $\pmb{C_{3}^{ 2}(3)}$ .

Theorem 3.4

Let $n\ge7$. Among all graphs in $\mathcal{U}_{ n}^{ n-4}\backslash \{U_{n}^{ n-4}(3), C_{3}^{1}(3)\}$, $C_{3}^{ 1}(2)$ is the unique graph whose least Q-eigenvalue attains the minimum.

Proof

By a similar reasoning to that of Theorem 3.3, we can prove that $C_{3}^{ 2}(3)$ or $C_{3}^{ 1}(2)$ is the graph whose least Q-eigenvalue attains the minimum among all graphs in $\mathcal{U}_{ n}^{ n-4}\backslash\{U_{n}^{ n-4}(3), C_{3}^{1}(3)\}$. Let $\kappa=\kappa(C_{3}^{ 2}(3))$ and let $x=(x_{1}, x_{2}, \ldots, x_{n})^{T}$ be an eigenvector corresponding to κ. From the eigenvalue equations, we have $x_{1}=x_{2}$, $x_{5}=x_{6}$, $x_{7}=\cdots=x_{n}$,

$$\begin{aligned}& (\kappa-2)x_{1} = x_{1}+x_{3}, \\& (\kappa-5)x_{3} = 2x_{1}+x_{4}+2x_{5}, \\& (\kappa-n+5)x_{4} = x_{3}+(n-6)x_{7}, \\& (\kappa-1)x_{5} = x_{3}, \\& (\kappa-1)x_{7} = x_{4}. \end{aligned}$$

Since x is an eigenvector, it follows that $\kappa=\kappa(C_{3}^{ 2}(3))$ is the least root of the equation

$$f(x)\triangleq\left| \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} x-3 & -1 & 0 & 0 & 0 \\ -2 & x-5 & -1 & -2 & 0 \\ 0 & -1 & x-n+5 & 0 & -n+6 \\ 0 & -1 & 0 & x-1 & 0 \\ 0 & 0 & -1 & 0 & x-1 \end{array}\displaystyle \right| =0. $$

By an easy computation, we can obtain

$$f(x)=x^{5}-(n+5)x^{4}+(9n-17)x^{3}-(19n-65)x^{2}+(7n-16)x-4. $$

Similarly, from the eigenvalue equation, we can prove that $\kappa(C_{3}^{ 1}(2))$ is the least root of

$$g(x)\triangleq x^{6}-(n+6)x^{5}+(9n-2)x^{4}-(25n-48)x^{3}+(25n-58)x^{2}-(7n-8)x+4=0. $$

By Lemma 2.6, we have $0<\kappa(C_{3}^{ 2}(3)), \kappa (C_{3}^{ 1}(2))\le4/n$. Note that for $n\ge12$,

$$(x-1)f(x)-g(x)=x\bigl((n-10)x^{3}-(3n-34)x^{2}+(n-23)x+4 \bigr)>0 $$

for $0< x\le4/n$. It follows that $g(\kappa(C_{3}^{ 2}(3)))<0$. This implies that $\kappa(C_{3}^{ 1}(2))<\kappa(C_{3}^{ 2}(3))$.

For $7\le n\le11$, by computation, we can verify that $\kappa(C_{3}^{ 1}(2))<\kappa(C_{3}^{ 2}(3))$.

From the above arguments, we have $\kappa(C_{3}^{ 1}(2))<\kappa(C_{3}^{ 2}(3))$ for $n\ge7$. □

Combining Theorem 3.3 and Lemma 2.8, we have the following theorem.

Theorem 3.5

Let $3\le k \leq{(n-4)}/{\sqrt{6}}$. Among all graphs in $\mathcal {U}_{ n}^{k}\backslash\{U_{n}^{k}(3), C_{3}^{ 1}(n-k-1)\}$, $C_{3}^{ 2}(n-k-1)$ is the unique graph whose least Q-eigenvalue attains the minimum.

Combining Theorem 3.3 and Lemma 2.9, we have the following theorem.

Theorem 3.6

Let $n\ge120$, $k > \frac{-3+\sqrt{21}}{2}n$. Among all graphs in $\mathcal{U}_{ n}^{k}\backslash\{U_{n}^{k}(3), C_{3}^{1}(n-k-1)\}$, $C_{3}^{1}(n-k-2)$ is the unique graph whose least Q-eigenvalue attains the minimum.

4 Discussion

According to Lemmas 2.8 and 2.9, we propose the following conjecture.

Conjecture 4.1

There exists a real number α with $0<\alpha<1$ such that, for any $\varepsilon>0$, there exists a sufficiently large N such that

$$\kappa\bigl(C_{3}^{ 2}(n-k-1)\bigr)< \kappa \bigl(C_{3}^{1}(n-k-2)\bigr) $$

for all $n\ge N$ and all $3\le k \le(\alpha-\varepsilon) n$, and

$$\kappa\bigl(C_{3}^{ 2}(n-k-1)\bigr)>\kappa \bigl(C_{3}^{1}(n-k-2)\bigr) $$

for all $n\ge N$ and all $(\alpha+\varepsilon) n\le k \le n-5$.

If Conjecture 4.1 is true, then, by Lemmas 2.8 and 2.9, $\sqrt{6}/6\le\alpha\le(\sqrt{21}-3)/2$, where α is the same as in Conjecture 4.1.