1 Introduction

In this paper, we consider a smoothing Tikhonov regularization problem, which is an unconstrained minimization of the form [1]

$$ \min\| Ax-b\|^{2}+\delta\|\Delta x\| ^{2}+\eta \| x\|^{p}_{p}, $$
(1.1)

where \(A\in R^{m\times n}\), \(b\in R^{m}\), and \(x\in\mathcal{X} \subset R^{n} \), and \(\|\cdot\|\) denotes the Euclid norm. The parameters \(\delta \geq0\) and \(\eta\geq0\) are used to control the smoothness and size of the approximate solution. Matrix Δ is a (tridiagonal, Toeplitz) matrix, Δx represents a measure of the variation or smoothness of x, where

$$ \Delta=n^{2}\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 1 & -2 & 1 & 0 & \cdots& 0 & 0 &0 &0 \\ 0 & 1 &-2 & 1 & \cdots & 0 & 0 &0 &0 \\ 0 & 0 & 1 & -2 & \cdots& 0 & 0 &0 &0 \\ \vdots& \vdots& \vdots&\vdots& &\vdots&\vdots& \vdots&\vdots \\ 0 & 0 & 0 & 0 &\cdots&-2&1&0&0\\ 0 & 0 & 0 & 0 &\cdots&1&-2&1&0\\ 0 & 0 & 0 & 0 &\cdots& 0 &1&-2&1 \end{array}\displaystyle \right )\in R^{(n-2)\times n} . $$
(1.2)

The smoothing regularization problem (1.1) has numerous applications in many fields, including mathematical programs with vanishing constraints [2], maximum-likelihood estimation problem [3], language modeling [4], and so on.

The last term of the problem (1.1), \(\eta\|x\|^{p}_{p}\), is a regularization term. As a common regularization method, \(\ell_{1}\) regularization (\(p=1\)) problem has many good properties since it is a convex programming problem. In recent years, there has been an increasing interest in the \(\ell_{1}\) regularizer. The \(\ell_{1}\) regularization model can reconstruct the original signal with less observed signals, when the original signal is spare or the observed signal contains noise. Especially, the \(\ell_{1}\) formulation suits significantly better for denoising data containing so-called outliers, i.e., observations containing large measurement errors [5]. Therefore, mathematical models and large-scale fast algorithms associated with \(\ell_{1}\) regularization can be seen everywhere in compressed sensing, signal/image processing, machine learning, statistics, and many other fields [6–9].

By \(\ell_{1}\) regularization, the problem (1.1) reduces to

$$ \min\| Ax-b\|^{2}_{2}+\delta\|\Delta x\| ^{2}_{2}+\eta\| x\|_{1}. $$
(1.3)

It is identical to a separable convex minimization of the form

$$ \left \{ \textstyle\begin{array}{l} \min \frac{1}{2}\| Ax-b\|^{2}+ \frac {1}{2}\delta\|\Delta y\|^{2}+\eta\| z\|_{1}, \\ \quad \mbox{s.t. } x-y=0, \\ \hphantom{\quad \mbox{s.t. }}y-z=0. \end{array}\displaystyle \right . $$
(1.4)

The augmented Lagrangian function associated to the problem (1.4) is

$$\begin{aligned} L(x,y,\lambda,z,\mu) =&\frac{1}{2}\| Ax-b\|^{2}+ \frac{1}{2}\delta\|\Delta y\|^{2}-\lambda^{T}(x-y)+ \frac{\beta }{2}\|x-y\|^{2} \\ &{}-\mu^{T}(y-z)+\eta\|z\|_{1}+\frac{ \rho}{2}\|y-z \|^{2}. \end{aligned}$$
(1.5)

Indeed, there are many methods for solving the problem (1.4) in the literature. Among these methods, the parallel splitting augmented Lagrangian method and the alternating direction method of multipliers are two power tools. The recent research indicates that, due to the separable convex optimization with three block variables, the direct extension of the alternating direction method of multipliers is not necessarily convergent [10]. Thus, some hybrid splitting methods can be found in the literature. For example, see He [11], Peng and Wu [12], and Glowinski and Le Tallec [13].

The saddle point of a Lagrange function associated to the convex optimization problem (1.4), \(w^{*}=(x^{*},y^{*},\lambda^{*},z^{*},\mu^{*})\in{\mathcal{W}}\), satisfies the following variational inequalities:

$$ \left \{ \textstyle\begin{array}{l} (x'-x^{*})^{T}[A^{T}(Ax^{*}-b)-\lambda^{*}]\geq 0, \\ (y'-y^{*})^{T}[\delta\Delta^{T}\Delta{y^{*}}+\lambda^{*}-\mu^{*}]\geq0, \\ (\lambda'-\lambda^{*})^{T}(x^{*}-y^{*})\geq0, \\ \eta\|z'\|_{1}-\eta\|z^{*}\|_{1}+(z'-z^{*})^{T}[\mu^{*}]\geq0, \\ (\mu'-\mu^{*})^{T}(y^{*}-z^{*})\geq0, \end{array}\displaystyle \right .\quad \forall w'=\bigl(x', y', \lambda',z', \mu'\bigr)\in{\mathcal{W}}, $$
(1.6)

where

$$ {\mathcal{W}} = \mathcal{X}\times\mathcal{X}\times R^{n} \times \mathcal{X}\times R^{n}\subset R^{5\times n}. $$

In this paper, we will propose a new splitting method to solve the separable convex programming problem (1.4) as well as the structured variational inequalities (1.6). The proposed method, referred to as the hybrid splitting method (HSM), will combine a parallel splitting (augmented Lagrangian) method and an alternating directions method of multipliers. In the HSM, the predictor of the new iterate, \(\tilde{w}^{k}=(\tilde{x}^{k}, \tilde{y}^{k}, \tilde{\lambda }^{k}, \tilde{z}^{k}, \tilde{\mu}^{k} )\), is got in the following way: find \((\tilde{x}^{k},\tilde{y}^{k})\) in a parallel manner, and update \(\tilde{\lambda}^{k}\). Then compute \(\tilde{z}^{k}\) alternately with \((\tilde{x}^{k},\tilde{y}^{k})\), and update \(\tilde{\mu}^{k}\) at the last. The new iterate is produced by a correct operator. The global convergence of the HSM is proven under some wild assumptions.

The rest of this paper is organized as follows. In Section 2, we describe the proposed hybrid splitting method. Section 3 is devoted to showing that the sequence \(\{ w^{k} \}\) generated by the HSM is Fejér monotone with respect to the solution set. Then, the convergence of the HSM is proved. In Section 4, some preliminary numerical results are presented which indicate the feasibility and efficiency of the proposed method. Finally, some concluding remarks are made in Section 5.

2 The hybrid splitting method

In this section, we first propose a hybrid splitting method for the problem (1.6), and then we give some remarks on the described method.

Algorithm 2.1

(The hybrid splitting method (HSM))

For a given \(w^{k}=(x^{k}, y^{k}, \lambda^{k}, z^{k}, u^{k}) \in{\mathcal{W}}\), \(\beta_{k}>0 \), and \(\rho_{k}>0 \), the HSM produces the new iterate \({w}^{k+1}=(x^{k+1}, y^{k+1}, \lambda^{k+1} ,z^{k+1}, u^{k+1})\in {\mathcal{W}}\) by the following scheme:

  1. S1.

    Produce \(\tilde{w}^{k}=(\tilde{x}^{k},\tilde{y}^{k},\tilde{\lambda}^{k},\tilde {z}^{k},\tilde{\mu}^{k})\) by s1.1 to s1.5.

    1. s1.1.

      Find \(\tilde{x}^{k}\in\mathcal{X}\) (with fixed \(y^{k}\), \(\lambda^{k}\), \(z^{k}\), \(\mu^{k}\), \(\beta_{k}\), \(\rho_{k}\)) such that

      $$ \bigl(x'-\tilde{x}^{k}\bigr) \bigl\{ A^{T}\bigl(A\tilde{x}^{k}-b\bigr)-\lambda^{k}+ \beta_{k}\bigl(\tilde {x}^{k}-y^{k}\bigr) \bigr\} \geq 0, \quad \forall x'\in\mathcal{X}. $$
      (2.1)
    2. s1.2.

      Find \(\tilde{y}^{k}\in\mathcal{X}\) (with fixed \(x^{k}\), \(\lambda^{k}\), \(z^{k}\), \(\mu^{k}\), \(\beta_{k}\), \(\rho_{k}\)) such that

      $$ \bigl(y'-\tilde{y}^{k}\bigr) \bigl\{ \delta \Delta^{T}\Delta\tilde{y}^{k}+ \lambda^{k}- \mu^{k}-\beta_{k}\bigl(x^{k}-\tilde{y}^{k} \bigr)+\rho_{k}\bigl(\tilde {y}^{k}-z^{k}\bigr) \bigr\} \geq 0,\quad \forall y'\in\mathcal{X}. $$
      (2.2)
    3. s1.3.

      Update \(\tilde{\lambda}^{k}\) via

      $$ \tilde{\lambda}^{k}=\lambda^{k}- \beta _{k}\bigl(\tilde{x}^{k}-\tilde{y}^{k}\bigr). $$
      (2.3)
    4. s1.4.

      Find \(\tilde{z}^{k}\in\mathcal{X}\) (with fixed \(\tilde{x}^{k}\), \(\tilde{y}^{k}\), \(\tilde{\lambda}^{k}\), \(\mu^{k}\), \(\beta_{k}\), \(\rho_{k}\)) such that

      $$ \eta\bigl\Vert z'\bigr\Vert _{1}-\eta \bigl\Vert \tilde{z}^{k}\bigr\Vert _{1}+ \bigl(z'-\tilde{z}^{k}\bigr) \bigl\{ \mu^{k}-\rho _{k}\bigl(\tilde{y}^{k}-\tilde{z}^{k}\bigr) \bigr\} \geq 0,\quad \forall z'\in\mathcal{X}. $$
      (2.4)
    5. s1.5.

      Update \(\tilde{\mu}^{k}\) via

      $$ \tilde{\mu}^{k}=\mu^{k}- \rho_{k} \bigl(\tilde{y}^{k}-\tilde{z}^{k}\bigr). $$
      (2.5)
  2. S2.

    Convergence verification: for a given small \(\varepsilon >0\), if \(\| w^{k}-\tilde{w}^{k}\|_{\infty}<\varepsilon\) then stop, and accept \(w^{k}\) to be the approximate solution. Else, go to S3.

  3. S3.

    Produce the new iterate by

    $$ w^{k+1}=w^{k}-\alpha_{k}d \bigl(w^{k},\tilde{w}^{k}\bigr), $$
    (2.6)

    where

    $$\begin{aligned}& \alpha_{k}=\gamma\alpha^{*}_{k}, \quad \gamma\in(0, 2), \end{aligned}$$
    (2.7)
    $$\begin{aligned}& \alpha^{*}_{k}=\frac{\varphi(w^{k},\tilde{w}^{k})}{\| d(w^{k},\tilde{w}^{k})\|_{G}^{2}}, \end{aligned}$$
    (2.8)

    and

    $$\begin{aligned}& \varphi\bigl(w^{k},\tilde{w}^{k}\bigr)=\bigl\Vert w^{k}-\tilde{w}^{k}\bigr\Vert ^{2}_{G}, \qquad d\bigl(w^{k},\tilde{w}^{k}\bigr)=M \bigl(w^{k}-\tilde{w}^{k}\bigr), \\& G=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \frac{ \beta_{k}}{ 2} & 0 & 0 & 0 & 0 \\ 0 & \frac{ 2\beta_{k}+\rho_{k}}{ 4} &0 & 0 & 0 \\ 0 & 0 & \frac{ 1}{ \beta_{k}} & 0 & 0 \\ 0 & 0 & 0 &\frac{ \rho_{k}}{ 4} &0 \\ 0 & 0 & 0 & 0 &\frac{ 1}{ \rho_{k}} \end{array}\displaystyle \right ),\qquad M= \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \beta_{k} & 0 & 0 & 0 & 0 \\ 0 & \beta_{k}+\rho_{k} &-\frac{ \rho_{k}}{ 2} & 0& 0 \\ 0 & -\frac{ \rho_{k}}{ 2} & \frac { 2}{ \beta_{k}} & 0 & 0 \\ 0 & 0& 0 & \rho_{k} &0 \\ 0 & 0 & 0 & 0 &\frac{ 3}{ \rho_{k}} \end{array}\displaystyle \right ). \end{aligned}$$
    (2.9)

Remark 2.1

The parameters \(\beta_{k}\) and \(\rho_{k}\) are updated in the same style as proposed in He et al. [14]. By Remark 5.1 in [14], the sequences \(\{\beta _{k}\}\) and \(\{\rho_{k}\}\) are bounded and finally constants. Thus, there is a \(\kappa>0\) such that \(\|M\|^{2}_{G}:=\sum\|M(:, j)\| ^{2}_{G}\le\kappa\).

Remark 2.2

It is easy to show, \(\|M(w-\tilde{w})\|_{G}^{2}\le\| M\|_{G}^{2}\cdot\|w-\tilde{w}\|^{2}_{G}\). Thus by (2.8) we have

$$ \alpha_{k}^{*}\ge\frac{1}{\|M\| ^{2}_{G}}\ge\frac{1}{\kappa}, \quad \forall k. $$
(2.10)

For convenience in the analysis, the following notations are useful:

$$\begin{aligned}& F(w)=\left ( \textstyle\begin{array}{@{}c@{}} A^{T}(Ax-b)-\lambda\\ \sigma\Delta^{T}\Delta y+\lambda-\mu \\ x-y \\ \mu\\ y-z \end{array}\displaystyle \right ), \qquad H= \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} I & 0 & 0 & 0 & 0 \\ 0 & I & 0 & 0 & 0 \\ 0 & 0 & 2I & 0 & 0 \\ 0 & 0 & 0 & I & 0 \\ 0 & 0 & 0 & 0 & 3I \end{array}\displaystyle \right ), \\& g(w ,\tilde{w} )=\left ( \textstyle\begin{array}{@{}c@{}} \beta(x -\tilde{x} )-\beta(y -\tilde{y} ) \\ -\beta(x -\tilde{x} )+\beta(y -\tilde{y} )+\rho(y -\tilde{y} )-\rho(z -\tilde{z} ) \\ 0 \\ \rho(z -\tilde{z} )-\rho(y -\tilde{y} ) \\ 0 \end{array}\displaystyle \right ). \end{aligned}$$

By these notations, the variational inequalities (1.6) can be rewritten in a compact form: find \(w^{*}\in\mathcal{W}\) such that

$$ \bigl(w'-w^{*}\bigr)^{T} F\bigl(w^{*}\bigr) \ge0,\quad \forall w'\in\mathcal{W}. $$
(2.11)

In the HSM, (2.1)-(2.5) can be written in the compact form: find \(\tilde{w}^{k}\in\mathcal{W}\) such that

$$ \eta\bigl\Vert z'\bigr\Vert _{1}-\eta \bigl\Vert \tilde{z}^{k}\bigr\Vert _{1}+ \bigl(w'-\tilde{w}^{k}\bigr)^{T} \bigl[F\bigl( \tilde{w}^{k}\bigr)+g\bigl(w^{k},\tilde{w}^{k} \bigr)-M\bigl(w^{k}-\tilde {w}^{k}\bigr)\bigr]\ge0, \quad \forall w'\in\mathcal{W}. $$
(2.12)

3 The convergence

To prove the convergence of the HSM, we will show first in this section that the sequence \(\{w^{k}\}\) generated by the HSM is Fejér monotone with respect to the solution set \(\mathcal{W}^{*}\) of the problem (2.12).

Due to (1.6), multiplying both sides of the third inequality by 2, and multiplying both sides of the last inequality by 3, respectively, we get

$$ \left \{ \textstyle\begin{array}{l} (x'-x^{*})^{T}[A^{T}(Ax^{*}-b)-\lambda^{*}]\geq 0, \\ (y'-y^{*})^{T}[\delta\Delta^{T}\Delta{y^{*}}+\lambda^{*}-\mu^{*}]\geq0, \\ 2\times(\lambda'-\lambda^{*})^{T}(x^{*}-y^{*})\geq0, \\ \eta\|z'\|_{1}-\eta\|z^{*}\|_{1}+(z'-z^{*})^{T}[\mu^{*}]\geq0, \\ 3\times(\mu'-\mu^{*})^{T}(y^{*}-z^{*})\geq0, \end{array}\displaystyle \right .\quad \forall w'=\bigl(x', y', \lambda',z', \mu'\bigr)\in{\mathcal{W}}, $$
(3.1)

and (3.1) can be written as

$$ \bigl(w'-w^{*}\bigr)^{T} H F\bigl(w^{*}\bigr) \ge0,\quad \forall w'\in\mathcal{W}. $$
(3.2)

Lemma 3.1

For a given \(w^{k}=(x^{k},y^{k},\lambda^{k},z^{k},\mu^{k})\), if \(\tilde{w}^{k}=(\tilde{x}^{k},\tilde{y}^{k}, \tilde{\lambda}^{k},\tilde {z}^{k},\tilde{\mu}^{k})\) is generated by (2.1)-(2.5), then we have

$$ \bigl(\tilde{w}^{k}-w^{*}\bigr)^{T} F\bigl( \tilde {w}^{k}\bigr)\ge0 $$
(3.3)

and

$$ \bigl(\tilde{w}^{k}-w^{*}\bigr)^{T} H F\bigl( \tilde {w}^{k}\bigr)\ge0, $$
(3.4)

where \(w^{*}=(x^{*}, y^{*}, \lambda^{*},z^{*},\mu^{*})\in{\mathcal{W}}^{*}\) is a solution.

Proof

It is easy to show that \(F(w)\) is linear and consequently monotone. Indeed, let

$$Q=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} A^{T}A & 0 & -I & 0 & 0 \\ 0 & \delta\Delta^{T} \Delta& I & 0 & -I \\ I & -I & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & I \\ 0 & I & 0 & -I & 0 \end{array}\displaystyle \right ) \quad \mbox{and} \quad e= \left ( \textstyle\begin{array}{@{}c@{}} -A^{T} b \\ 0 \\ 0 \\ 0 \\ 0 \end{array}\displaystyle \right ), $$

then \(F(w)=Qw+e\). By the monotonicity of F and HF we have

$$\bigl(\tilde{w}^{k}-w^{*}\bigr)^{T} \bigl(F\bigl( \tilde{w}^{k}\bigr)-F\bigl(w^{*}\bigr)\bigr)\ge0 $$

and

$$\bigl(\tilde{w}^{k}-w^{*}\bigr)^{T} \bigl(HF\bigl( \tilde{w}^{k}\bigr)-HF\bigl(w^{*}\bigr)\bigr)\ge0, $$

respectively, which results in (by (2.11))

$$\bigl(\tilde{w}^{k}-w^{*}\bigr)^{T} F\bigl( \tilde{w}^{k}\bigr)\ge\bigl(\tilde{w}^{k}-w^{*} \bigr)^{T} F\bigl(w^{*}\bigr)\ge 0, $$

and by (3.2)

$$\bigl(\tilde{w}^{k}-w^{*}\bigr)^{T} HF\bigl( \tilde{w}^{k}\bigr)\ge\bigl(\tilde{w}^{k}-w^{*} \bigr)^{T} H F\bigl(w^{*}\bigr)\ge0. $$

 □

Lemma 3.2

For a given \(w^{k}=(x^{k},y^{k},\lambda^{k},z^{k},\mu^{k})\), if \(\tilde{w}^{k}=(\tilde {x}^{k},\tilde{y}^{k}, \tilde{\lambda}^{k},\tilde{z}^{k},\tilde{\mu}^{k})\) is generated by (2.1)-(2.5), then we have

$$\begin{aligned}& \bigl(\tilde{w}^{k}-w^{*}\bigr)^{T}\bigl[HF \bigl(\tilde{w}^{k}\bigr)+g\bigl(w^{k},\tilde{w}^{k} \bigr)\bigr] \\& \quad \ge \bigl(\lambda^{k}-\tilde{\lambda}^{k} \bigr)^{T}\bigl(x^{k}-\tilde{x}^{k}\bigr)-\bigl( \lambda ^{k}-\tilde{\lambda}^{k}\bigr)^{T} \bigl(y^{k}-\tilde{y}^{k}\bigr) \\& \qquad {} +\bigl(\mu^{k}-\tilde{\mu}^{k}\bigr)^{T} \bigl(y^{k}-\tilde{y}^{k}\bigr)-\bigl(\mu^{k}- \tilde{\mu }^{k}\bigr)^{T}\bigl(z^{k}- \tilde{z}^{k}\bigr). \end{aligned}$$
(3.5)

Proof

By a direct computation, we get

$$\begin{aligned}& \bigl(\tilde{w}^{k}-w^{*}\bigr)^{T}\bigl[HF\bigl( \tilde{w}^{k}\bigr)+g\bigl(w^{k},\tilde{w}^{k}\bigr) \bigr] \\& \quad = \bigl(\tilde{w}^{k}-w^{*}\bigr)^{T}HF\bigl( \tilde{w}^{k}\bigr)+\bigl(\tilde{w}^{k}-w^{*} \bigr)^{T} g\bigl(w^{k},\tilde{w}^{k}\bigr) \\& \quad \geq \bigl(\tilde{w}^{k}-w^{*}\bigr)^{T}g \bigl(w^{k},\tilde{w}^{k}\bigr) \\& \quad = \bigl(\tilde{x}^{k}-x^{*}\bigr)^{T}\beta_{k} \bigl(x^{k}-\tilde{x}^{k}\bigr)-\bigl(\tilde {x}^{k}-x^{*}\bigr)^{T}\beta_{k}\bigl(y^{k}- \tilde{y}^{k}\bigr)-\bigl(\tilde{y}^{k}-y^{*}\bigr)\beta _{k}\bigl(x^{k}-\tilde{x}^{k}\bigr) \\& \qquad {} +\bigl(\tilde{y}^{k}-y^{*}\bigr)^{T} \beta_{k}\bigl(y^{k}-\tilde{y}^{k}\bigr)+\bigl( \tilde {y}^{k}-y^{*}\bigr)\rho_{k}\bigl(y^{k}- \tilde{y}^{k}\bigr)-\bigl(\tilde{y}^{k}-y^{*}\bigr)\rho _{k}\bigl(z^{k}-\tilde{z}^{k}\bigr) \\& \qquad {} +\bigl(\tilde{z}^{k}-z^{*}\bigr)\rho_{k} \bigl(z^{k}-\tilde{z}^{k}\bigr)-\bigl(\tilde{z}^{k}-z^{*} \bigr)\rho _{k}\bigl(y^{k}-\tilde{y}^{k}\bigr) \\& \quad = \bigl[\bigl(\tilde{x}^{k}-\tilde{y}^{k}\bigr)- \bigl(x^{*}-y^{*}\bigr)\bigr]^{T}\beta_{k}\bigl(x^{k}- \tilde {x}^{k}\bigr)-\bigl[\bigl(\tilde{x}^{k}- \tilde{y}^{k}\bigr)-\bigl(x^{*}-y^{*}\bigr)\bigr]^{T} \beta_{k}\bigl(y^{k}-\tilde {y}^{k}\bigr) \\& \qquad {} +\bigl[\bigl(\tilde{y}^{k}-\tilde{z}^{k}\bigr)- \bigl(y^{*}-z^{*}\bigr)\bigr]^{T}\rho_{k}\bigl(y^{k}- \tilde {y}^{k}\bigr)-\bigl[\bigl(\tilde{y}^{k}- \tilde{z}^{k}\bigr)-\bigl(y^{*}-z^{*}\bigr)\bigr]^{T} \rho_{k}\bigl(z^{k}-\tilde {z}^{k}\bigr). \end{aligned}$$

Substituting \(x^{*}-y^{*}=0\), \(y^{*}-z^{*}=0\) into the last equation, we get

$$\begin{aligned}& \bigl(\tilde{w}^{k}-w^{*}\bigr)^{T}\bigl[HF \bigl(\tilde{w}^{k}\bigr)+g\bigl(w^{k},\tilde{w}^{k} \bigr)\bigr] \\& \quad \geq \bigl(\tilde{x}^{k}-\tilde{y}^{k}\bigr) \beta_{k}\bigl(x^{k}-\tilde{x}^{k}\bigr)-\bigl( \tilde {x}^{k}-\tilde{y}^{k}\bigr)\beta_{k} \bigl(y^{k}-\tilde{y}^{k}\bigr) \\& \qquad {}+\bigl(\tilde{y}^{k}-\tilde{z}^{k}\bigr) \rho_{k}\bigl(y^{k}-\tilde{y}^{k}\bigr)-\bigl(\tilde {y}^{k}-\tilde{z}^{k}\bigr)\rho_{k} \bigl(z^{k}-\tilde{z}^{k}\bigr). \end{aligned}$$
(3.6)

By (2.3) and (2.5), we get

$$\begin{aligned}& \bigl(\tilde{x}^{k}-\tilde{y}^{k}\bigr)= \frac {1}{\beta_{k}}\bigl(\lambda^{k}-\tilde{\lambda}^{k}\bigr), \end{aligned}$$
(3.7)
$$\begin{aligned}& \bigl(\tilde{y}^{k}-\tilde{z}^{k}\bigr)= \frac {1}{\rho_{k}}\bigl(\mu^{k}-\tilde{\mu}^{k}\bigr). \end{aligned}$$
(3.8)

Substituting (3.7) and (3.8) into the right-hand side of (3.6), we obtain

$$\begin{aligned}& \bigl(\tilde{w}^{k}-w^{*}\bigr)^{T}\bigl[HF\bigl( \tilde{w}^{k}\bigr)+g\bigl(w^{k},\tilde{w}^{k}\bigr) \bigr] \\& \quad \geq \bigl(\lambda^{k}-\tilde{\lambda}^{k}\bigr) \bigl(x^{k}-\tilde{x}^{k}\bigr)-\bigl(\lambda^{k}- \tilde {\lambda}^{k}\bigr) \bigl(y^{k}-\tilde{y}^{k} \bigr) \\& \qquad {}+\bigl(\mu^{k}-\tilde{\mu}^{k}\bigr) \bigl(y^{k}-\tilde{y}^{k}\bigr)-\bigl(\mu^{k}- \tilde{\mu }^{k}\bigr) \bigl(z^{k}-\tilde{z}^{k} \bigr). \end{aligned}$$

 □

Lemma 3.3

For a given \(w^{k}=(x^{k},y^{k},\lambda^{k},z^{k},\mu^{k})\), if \(\tilde{w}^{k}=(\tilde {x}^{k},\tilde{y}^{k}, \tilde{\lambda}^{k},\tilde{z}^{k},\tilde{\mu}^{k})\) is generated by (2.1)-(2.5), then we have

$$\begin{aligned}& \eta\bigl\Vert z'\bigr\Vert _{1}-\eta \bigl\Vert \tilde{z}^{k}\bigr\Vert _{1}+ \bigl(w'-\tilde{w}^{k}\bigr)^{T}\bigl[HF\bigl( \tilde {w}^{k}\bigr)+g\bigl(w^{k},\tilde{w}^{k} \bigr)-d\bigl(w^{k},\tilde{w}^{k}\bigr) \bigr] \\& \quad \ge0,\quad \forall z'\in\mathcal{X}, w'\in{ \mathcal{W}} . \end{aligned}$$
(3.9)

Proof

Combining (2.1)-(2.5) together, we have

$$\begin{aligned}& \eta\bigl\Vert z'\bigr\Vert _{1}-\eta\bigl\Vert \tilde{z}^{k}\bigr\Vert _{1}+\bigl(w'- \tilde{w}^{k}\bigr)^{T}\left ( \textstyle\begin{array}{@{}c@{}} A^{T}(A\tilde{x}^{k}-b)-\lambda^{k}+\beta_{k}(\tilde{x}^{k}-y^{k}) \\ \delta\Delta^{T}\Delta\tilde{y}^{k}+\lambda^{k}-\mu^{k} -\beta_{k}(x^{k}-\tilde{y}^{k})+\rho_{k}(\tilde{y}^{k}-z^{k}) \\ 2(\tilde{x}^{k}-\tilde{y}^{k})-\frac{1}{\beta_{k}} (\lambda^{k}-\tilde{\lambda}^{k}) \\ \mu^{k}-\rho_{k}(\tilde{y}^{k}-\tilde{z}^{k})\\ 3( \tilde{y}^{k}-\tilde{z}^{k})-\frac{1}{\rho_{k}}(\mu^{k}-\tilde{\mu }^{k}) \end{array}\displaystyle \right ) \\& \quad \geq0. \end{aligned}$$

By a manipulation, we get

$$\begin{aligned}& \eta\bigl\Vert z'\bigr\Vert _{1}-\eta \bigl\Vert \tilde{z}^{k}\bigr\Vert _{1}+ \bigl(w'-\tilde{w}^{k}\bigr)^{T}\left \{ \left ( \textstyle\begin{array}{@{}c@{}} A^{T}(A\tilde{x}^{k}-b)-\tilde{\lambda}^{k} \\ \delta\Delta^{T}\Delta\tilde{y}^{k}+\tilde{\lambda}^{k}-\tilde{\mu}^{k} \\ 2(\tilde{x}^{k}-\tilde{y}^{k})\\ \tilde{\mu}^{k}\\ 3(\tilde{y}^{k}-\tilde{z}^{k}) \end{array}\displaystyle \right )+g\bigl(w^{k}, \tilde{w}^{k}\bigr)-M\bigl(w^{k}-\tilde{w}^{k}\bigr) \right \} \\& \quad \geq0. \end{aligned}$$
(3.10)

The assertion (3.9) is just a compact form of (3.10). □

Theorem 3.1

For a given \(w^{k}=(x^{k},y^{k},\lambda^{k},z^{k},\mu^{k})\), if \(\tilde{w}^{k}=(\tilde {x}^{k},\tilde{y}^{k}, \tilde{\lambda}^{k},\tilde{z}^{k},\tilde{\mu}^{k})\) is generated by (2.1)-(2.5), then for any \(w^{*}=(x^{*}, y^{*}, \lambda^{*},z^{*},\mu^{*}) \in{\mathcal{W}}^{*}\) we have

$$ \bigl(\tilde{w}^{k}-w^{*}\bigr)^{T}\bigl[ H F \bigl(\tilde{w}^{k}\bigr)+g\bigl(w^{k},\tilde{w}^{k} \bigr)\bigr]\ge\varphi \bigl(w^{k},\tilde{w}^{k}\bigr)- \bigl(w^{k}-\tilde{w}^{k}\bigr)^{T}d \bigl(w^{k},\tilde{w}^{k}\bigr). $$
(3.11)

Proof

Note \(d(w^{k},\tilde{w}^{k})=M(w^{k}-\tilde{w}^{k})\), by (3.5) we get

$$\begin{aligned}& \bigl(\tilde{w}^{k}-w^{*}\bigr)^{T}\bigl[HF\bigl( \tilde{w}^{k}\bigr)+g\bigl(w^{k},\tilde{w}^{k}\bigr) \bigr] +\bigl(w^{k}-\tilde{w}^{k}\bigr)^{T}d \bigl(w^{k},\tilde{w}^{k}\bigr) \\& \quad \geq \bigl(\lambda^{k}-\tilde{\lambda}^{k} \bigr)^{T}\bigl(x^{k}-\tilde{x}^{k}\bigr) -\bigl( \lambda^{k}-\tilde{\lambda}^{k}\bigr)^{T} \bigl(y^{k}-\tilde{y}^{k}\bigr) \\& \qquad {}+\bigl(\mu^{k}- \tilde{\mu}^{k}\bigr)^{T}\bigl(y^{k}- \tilde{y}^{k}\bigr) -\bigl(\mu^{k}-\tilde{\mu}^{k} \bigr)^{T}\bigl(z^{k}-\tilde{z}^{k}\bigr) \\& \qquad {} +\beta_{k}\bigl\Vert x^{k}-\tilde{x}^{k} \bigr\Vert +\beta_{k}\bigl\Vert y^{k} - \tilde{y}^{k}\bigr\Vert +\rho_{k}\bigl\Vert y^{k}-\tilde{y}^{k}\bigr\Vert \\& \qquad {}-\frac{1}{2} \rho_{k}\bigl(y^{k}-\tilde{y}^{k} \bigr)^{T}\bigl(z^{k}-\tilde{z}^{k}\bigr) + \frac{2}{\beta_{k}}\bigl\Vert \lambda^{k}-\tilde{\lambda}^{k} \bigr\Vert ^{2} \\& \qquad {}-\frac{\rho_{k}}{2}\bigl(z^{k}-\tilde{z}^{k} \bigr)^{T}\bigl(y^{k}-\tilde{y}^{k}\bigr) + \rho_{k}\bigl\Vert z^{k}-\tilde{z}^{k}\bigr\Vert ^{2}+\frac{3}{\rho_{k}}\bigl\Vert \mu^{k} -\tilde{ \mu}^{k}\bigr\Vert ^{2} \\& \quad \geq \bigl(\lambda^{k}-\tilde{\lambda}^{k} \bigr)^{T}\bigl(x^{k}-\tilde{x}^{k}\bigr) -\bigl( \lambda^{k}-\tilde{\lambda}^{k}\bigr)^{T} \bigl(y^{k}-\tilde{y}^{k}\bigr) \\& \qquad {}+\bigl(\mu^{k}- \tilde{\mu}^{k}\bigr)^{T}\bigl(y^{k}- \tilde{y}^{k}\bigr) -\bigl(\mu^{k}-\tilde{\mu}^{k} \bigr)^{T}\bigl(z^{k}-\tilde{z}^{k}\bigr) \\ & \qquad {} -\rho_{k}\bigl(y^{k}-\tilde{y}^{k} \bigr)^{T}\bigl(z^{k}-\tilde{z}^{k}\bigr) + \beta_{k}\bigl\Vert x^{k}-\tilde{x}^{k}\bigr\Vert ^{2} \\ & \qquad {}+\beta_{k}\bigl\Vert y^{k} - \tilde{y}^{k}\bigr\Vert ^{2}+\rho_{k}\bigl\Vert y^{k}-\tilde{y}^{k}\bigr\Vert ^{2} + \rho_{k}\bigl\Vert z^{k}-\tilde{z}^{k}\bigr\Vert ^{2} \\ & \qquad {} +\frac{2}{\beta_{k}}\bigl\Vert \lambda^{k}-\tilde{ \lambda}^{k}\bigr\Vert ^{2} +\frac{3}{\rho_{k}}\bigl\Vert \mu^{k}-\tilde{\mu}^{k}\bigr\Vert ^{2} \\ & \quad = \biggl[\frac{1}{2}\beta_{k}\bigl\Vert x^{k}- \tilde{x}^{k}\bigr\Vert ^{2} +\bigl(\lambda^{k}- \tilde{\lambda}^{k}\bigr)^{T}\bigl(x^{k}- \tilde{x}^{k}\bigr) +\frac{1}{2\beta_{k}}\bigl\Vert \lambda^{k}-\tilde{\lambda}^{k}\bigr\Vert ^{2} \biggr] \\ & \qquad {} + \biggl[\frac{1}{2}\beta_{k}\bigl\Vert y^{k}-\tilde{y}^{k}\bigr\Vert ^{2} +\bigl( \lambda^{k}-\tilde{\lambda}^{k}\bigr)^{T} \bigl(y^{k}-\tilde{y}^{k}\bigr) +\frac{1}{2\beta_{k}}\bigl\Vert \lambda^{k}-\tilde{\lambda}^{k}\bigr\Vert ^{2} \biggr] \\ & \qquad {} + \biggl[\frac{1}{4}\rho_{k}\bigl\Vert y^{k}-\tilde{y}^{k}\bigr\Vert ^{2} +\bigl( \mu^{k}-\tilde{\mu}^{k}\bigr)^{T} \bigl(y^{k}-\tilde{y}^{k}\bigr)+\frac{1}{\rho_{k}}\bigl\Vert \mu^{k} -\tilde{\mu}^{k}\bigr\Vert ^{2} \biggr] \\ & \qquad {} + \biggl[\frac{1}{4}\rho_{k}\bigl\Vert z^{k}-\tilde{z}^{k}\bigr\Vert ^{2} +\bigl( \mu^{k}-\tilde{\mu}^{k}\bigr)^{T} \bigl(z^{k}-\tilde{z}^{k}\bigr)+\frac{1}{\rho_{k}}\bigl\Vert \mu^{k} -\tilde{\mu}^{k}\bigr\Vert ^{2} \biggr] \\ & \qquad {} + \biggl[\frac{1}{2}\rho_{k}\bigl\Vert y^{k}-\tilde{y}^{k}\bigr\Vert ^{2} - \rho_{k}\bigl(y^{k}-\tilde{y}\bigr)^{T} \bigl(z^{k}-\tilde{z}^{k}\bigr) +\frac{\rho_{k}}{2}\bigl\Vert z^{k}-\tilde{z}^{k}\bigr\Vert ^{2} \biggr] \\ & \qquad {} +\frac{1}{2}\beta_{k}\bigl\Vert x^{k}- \tilde{x}^{k}\bigr\Vert ^{2} +\frac{1}{2} \beta_{k}\bigl\Vert y^{k}-\tilde{y}^{k}\bigr\Vert ^{2} +\frac{1}{4}\rho_{k}\bigl\Vert y^{k}-\tilde{y}^{k}\bigr\Vert ^{2} \\ & \qquad {} +\frac{1}{\beta_{k}}\bigl\Vert \lambda^{k}-\tilde{ \lambda}^{k}\bigr\Vert ^{2} +\frac {1}{4} \rho_{k}\bigl\Vert z^{k}-\tilde{z}^{k}\bigr\Vert ^{2} +\frac{1}{\rho_{k}}\bigl\Vert \mu^{k}-\tilde{ \mu}^{k}\bigr\Vert ^{2} \\ & \quad = \frac{1}{2} \biggl[\sqrt{\beta_{k}}\bigl\Vert x^{k}-\tilde{x}^{k}\bigr\Vert +\frac{1}{\sqrt{\beta_{k}}}\bigl\Vert \lambda^{k}-\tilde{\lambda}^{k}\bigr\Vert \biggr]^{2} +\frac{1}{2} \biggl[\sqrt{\beta_{k}}\bigl\Vert y^{k}-\tilde{y}^{k}\bigr\Vert -\frac{1}{\sqrt{\beta_{k}}} \bigl\Vert \lambda^{k}-\tilde{\lambda}^{k}\bigr\Vert \biggr]^{2} \\ & \qquad {} + \biggl[\frac{\sqrt{\rho_{k}}}{2}\bigl\Vert y^{k}- \tilde{y}^{k}\bigr\Vert + \frac {1}{\sqrt{\rho_{k}}}\bigl\Vert \mu^{k}-\tilde{\mu}^{k}\bigr\Vert \biggr]^{2} + \biggl[\frac{\sqrt{\rho_{k}}}{2}\bigl\Vert z^{k}-\tilde{z}^{k}\bigr\Vert -\frac{1}{\sqrt{\rho_{k}}}\bigl\Vert \mu^{k}-\tilde{ \mu}^{k}\bigr\Vert \biggr]^{2} \\ & \qquad {} + \frac{1}{2} \bigl[\sqrt{\rho_{k}}\bigl\Vert y^{k}-\tilde{y}^{k}\bigr\Vert -\sqrt{\rho_{k}} \bigl\Vert z^{k}-\tilde{z}^{k}\bigr\Vert \bigr]^{2} \\ & \qquad {}+\frac{1}{2}\beta_{k}\bigl\Vert x^{k} -\tilde{x}^{k}\bigr\Vert ^{2}+ \frac{1}{2}\beta_{k}\bigl\Vert y^{k}- \tilde{y}^{k}\bigr\Vert ^{2} +\frac{1}{4} \rho_{k}\bigl\Vert y^{k}-\tilde{y}^{k}\bigr\Vert ^{2} \\ & \qquad {} + \frac{1}{\beta_{k}}\bigl\Vert \lambda^{k} -\tilde{ \lambda}^{k}\bigr\Vert ^{2} +\frac{1}{4} \rho_{k}\bigl\Vert z^{k}-\tilde{z}^{k}\bigr\Vert ^{2} +\frac{1}{\rho_{k}}\bigl\Vert \mu^{k}-\tilde{ \mu}^{k}\bigr\Vert ^{2} \\ & \quad \geq \frac{1}{2}\beta_{k}\bigl\Vert x^{k}- \tilde{x}^{k}\bigr\Vert ^{2} +\frac{1}{2} \beta_{k}\bigl\Vert y^{k}-\tilde{y}^{k}\bigr\Vert ^{2}+\frac{1}{4}\rho_{k}\bigl\Vert y^{k} -\tilde{y}^{k}\bigr\Vert ^{2}+ \frac{1}{\beta_{k}}\bigl\Vert \lambda^{k}-\tilde{\lambda}^{k} \bigr\Vert ^{2} \\ & \qquad {} +\frac{1}{4}\rho_{k}\bigl\Vert z^{k}- \tilde{z}^{k}\bigr\Vert ^{2}+\frac{1}{\rho_{k}}\bigl\Vert \mu^{k} -\tilde{\mu}^{k}\bigr\Vert ^{2} \\ & \quad = \bigl(w^{k}-\tilde{w}^{k}\bigr)^{T}G \bigl(w^{k}-\tilde{w}^{k}\bigr) , \end{aligned}$$

where

$$G= \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \frac{1}{2}\beta_{k} & & & & \\ & \frac{2\beta_{k}+\rho_{k}}{4} & & & \\ & & \frac{1}{\beta_{k}} & & \\ & & & \frac{1}{4}\rho_{k}& \\ & & & & \frac{1}{\rho_{k}} \end{array}\displaystyle \right ). $$

Thus, we have

$$\begin{aligned}& \bigl(\tilde{w}^{k}-w^{*}\bigr)^{T}\bigl[HF \bigl(\tilde{w}^{k}\bigr)+g\bigl(w^{k},\tilde{w}^{k} \bigr)\bigr] +\bigl(w^{k}-\tilde{w}^{k}\bigr)^{T}d \bigl(w^{k},\tilde{w}^{k}\bigr) \\& \quad \geq \bigl(w^{k}-\tilde{w}^{k}\bigr)^{T}G \bigl(w^{k}-\tilde{w}^{k}\bigr) = \bigl\Vert w^{k}-\tilde{w}^{k}\bigr\Vert ^{2}_{G }:= \varphi\bigl(w^{k},\tilde{w}^{k}\bigr). \end{aligned}$$
(3.12)

This theorem follows from (3.12) directly. □

Lemma 3.4

If \(\tilde{w}^{k}=(\tilde{x}^{k},\tilde {y}^{k}, \tilde{\lambda}^{k},\tilde{z}^{k},\tilde{\mu}^{k})\) is generated by (2.1)-(2.5) from a given \(w^{k}=(x^{k},y^{k}, \lambda^{k},z^{k},\mu^{k})\), then for any \(w^{*}=(x^{*}, y^{*}, \lambda^{*},z^{*},\mu^{*}) \in{\mathcal{W}}^{*}\), we have

$$ \bigl(w^{k}-w^{*}\bigr)^{T} G d \bigl(w^{k},\tilde{w}^{k}\bigr) \ge\varphi \bigl(w^{k},\tilde{w}^{k}\bigr). $$
(3.13)

Proof

We omit the proof of Lemma 3.4 here. A similar proof can be found in [15]. □

Theorem 3.2

For a given \(w^{k}=(x^{k},y^{k},\lambda^{k},z^{k},\mu^{k})\), if \(\tilde{w}^{k}=(\tilde {x}^{k},\tilde{y}^{k}, \tilde{\lambda}^{k},\tilde{z}^{k},\tilde{\mu}^{k})\) is generated by (2.1)-(2.5), then for any \(w^{*}=(x^{*}, y^{*}, \lambda^{*},z^{*},\mu^{*}) \in{\mathcal{W}}^{*}\) we have

$$ \bigl\Vert w^{k+1}-w^{*}\bigr\Vert ^{2}_{G} \leq\bigl\Vert w^{k}-w^{*}\bigr\Vert ^{2}_{G} - \gamma(2-\gamma)\frac{1}{\kappa}\bigl\Vert w^{k}- \tilde{w}^{k}\bigr\Vert ^{2}_{G}, $$
(3.14)

where \(0<\gamma<2\), \(\kappa>0 \).

Proof

By the iterative formula (2.6), and Lemma 3.4, we have

$$\begin{aligned} \bigl\Vert w^{k+1}-w^{*}\bigr\Vert ^{2}_{G} =& \bigl\Vert w^{k}-w^{*}-\alpha_{k} d\bigl(w^{k}, \tilde{w}^{k}\bigr)\bigr\Vert ^{2}_{G} \\ =&\bigl\Vert w^{k}-w^{*}\bigr\Vert ^{2}_{G}-2 \alpha_{k} \bigl\langle w^{k}-w^{*},Gd\bigl(w^{k}, \tilde{w}^{k}\bigr)\bigr\rangle +\alpha_{k} ^{2} \bigl\Vert d\bigl(w^{k},\tilde {w}^{k}\bigr)\bigr\Vert ^{2}_{G} \\ \leq&\bigl\Vert w^{k}-w^{*}\bigr\Vert ^{2}_{G}-2 \alpha_{k} \varphi\bigl(w^{k},\tilde{w}^{k}\bigr)+ \alpha ^{2}_{k}\bigl\Vert d\bigl(w^{k}, \tilde{w}^{k}\bigr)\bigr\Vert ^{2}_{G}. \end{aligned}$$

Following from (2.7) and (2.8), we have

$$\begin{aligned} \bigl\Vert w^{k+1}-w^{*}\bigr\Vert ^{2}_{G} \leq&\bigl\Vert w^{k}-w^{*}\bigr\Vert ^{2}_{G} -2\gamma\alpha^{*^{2}}_{k}\bigl\Vert d\bigl(w^{k}, \tilde{w}^{k}\bigr)\bigr\Vert ^{2}_{G} + \gamma^{2}\alpha^{*^{2}}_{k}\bigl\Vert d \bigl(w^{k},\tilde{w}^{k}\bigr)\bigr\Vert ^{2}_{G} \\ =&\bigl\Vert w^{k}-w^{*}\bigr\Vert ^{2}_{G} - \gamma(2-\gamma)\alpha^{*^{2}}_{k}\bigl\Vert d \bigl(w^{k},\tilde{w}^{k}\bigr)\bigr\Vert ^{2}_{G} \\ =& \bigl\Vert w^{k}-w^{*}\bigr\Vert ^{2}_{G} -\gamma(2-\gamma)\alpha^{*}_{k} \bigl\Vert w^{k}-\tilde {w}^{k}\bigr\Vert _{G}^{2} \\ \le& \bigl\Vert w^{k}-w^{*}\bigr\Vert ^{2}_{G} -\gamma(2-\gamma)\frac{1}{\kappa} \bigl\Vert w^{k}- \tilde{w}^{k}\bigr\Vert _{G}^{2}. \end{aligned}$$

The last inequality follows from (2.10). □

Theorem 3.2 claims the Fejér monotonicity of the sequence \(\{ w^{k}\}\) generated by the HSM. Adding (3.14) from 0 to ∞ with respect to k yields

$$ \gamma(2-\gamma)\frac{1}{\kappa}\sum_{k=0}^{\infty}\bigl\Vert w^{k}-\tilde{w}^{k}\bigr\Vert ^{2}_{G}\le\bigl\Vert w^{0}-w^{*}\bigr\Vert ^{2}_{G}-\lim_{k\rightarrow\infty}\bigl\Vert w^{k+1}-w^{*}\bigr\Vert ^{2}_{G}\le\bigl\Vert w^{0}-w^{*}\bigr\Vert ^{2}_{G}< \infty . $$

Thus we have

$$ \lim_{k \rightarrow\infty} \bigl\Vert w^{k}- \tilde{w}^{k}\bigr\Vert ^{2}_{G} =0, $$
(3.15)

which results in both \(\{w^{k}\}\) and \(\{\tilde{w}^{k}\}\) being bounded sequences and having cluster points. Let \(w^{\infty}\) be a cluster point of \(\{\tilde{w}^{k}\}\) and \(\{\tilde{w}^{k_{j}}\}\) be a subsequence converging to \(w^{\infty}\).

By the HSM, \(\tilde{w}^{k_{j}}\) is a solution of (2.12), thus

$$\begin{aligned}& \eta\bigl\Vert z'\bigr\Vert _{1}-\eta \bigl\Vert \tilde{z}^{k_{j}}\bigr\Vert _{1}+ \bigl(w'-\tilde{w}^{k_{j}}\bigr)^{T} \bigl[F\bigl( \tilde{w}^{k_{j}}\bigr)+g\bigl(w^{k_{j}},\tilde {w}^{k_{j}} \bigr)-M\bigl(w^{k_{j}}-\tilde{w}^{k_{j}}\bigr)\bigr] \\& \quad \ge0, \quad \forall w'\in \mathcal{W}. \end{aligned}$$
(3.16)

The limit (3.15) also results in \(\lim_{k_{j}\rightarrow \infty} g (w^{k_{j}}, \tilde{w}^{k_{j}})=0\) and \(\lim_{k_{j}\rightarrow\infty} d (w^{k_{j}}, \tilde{w}^{k_{j}})=M (w^{k_{j}}-\tilde{w}^{k_{j}})=0\) by positive-definiteness of G and M. Taking the limit on both sides of (3.16) we have

$$ \eta\bigl\Vert z'\bigr\Vert _{1}-\eta \bigl\Vert {z}^{\infty}\bigr\Vert _{1}+ \bigl(w'- {w}^{\infty}\bigr)^{T} F\bigl( {w}^{\infty}\bigr)\ge0, \quad \forall w'\in \mathcal{W}, $$
(3.17)

which implies \(w^{\infty}\) is a solution of the problem (1.4) by the optimality condition (2.11).

Note that (3.14) holds for all solutions of (1.4), we get

$$ \bigl\Vert w^{k+1}-w^{\infty}\bigr\Vert ^{2}_{G}\le\bigl\Vert w^{k}-w^{\infty}\bigr\Vert ^{2}_{G}, \quad \forall k. $$
(3.18)

Since \(\tilde{w}^{k_{j}} \rightarrow w^{\infty}\) and \(\|w^{k_{j}}-\tilde {w}^{k_{j}}\|^{2}_{G}\rightarrow0\) as \(k_{j} \rightarrow\infty\), for \(\forall\varepsilon>0\), there exists an integer \(k_{l}>0\) such that for all k and \(k_{j}\) larger than \(k_{l}\), we have

$$ \bigl\Vert \tilde{w}^{k_{j}}-w^{\infty}\bigr\Vert _{G}< \frac {\varepsilon}{2}, \qquad \bigl\Vert w^{k}- \tilde{w}^{k_{j}} \bigr\Vert _{G}< \frac{\varepsilon }{2}. $$
(3.19)

It follows from (3.18) and (3.19) that

$$\bigl\Vert w^{k}-w^{\infty}\bigr\Vert _{G}=\bigl\Vert w^{k}-\tilde{w}^{k_{j}}+\tilde{w}^{k_{j}}-w^{\infty}\bigr\Vert _{G}\le\bigl\Vert w^{k}-\tilde{w}^{k_{j}} \bigr\Vert _{G}+ \bigl\Vert \tilde{w}^{k_{j}}-w^{\infty}\bigr\Vert _{G}< \varepsilon. $$

Thus, the sequence \(\{w^{k}\}\) converges to \(w^{\infty}\), which is a solution of (1.4), or equivalently, of the problem (1.1).

4 Numerical results

The main computational cost of the HSM is in solving the subproblems (2.1)-(2.2) and (2.4). For generality of the HSM, we ignore the special structure of the matrices A and Δ, and employ the existing efficient method to solve those subproblems. In this paper, the subproblems (2.1) and (2.2) are solved by the projected Barzilai-Borwein method proposed by Dai and Fletcher [16], and the subproblem (2.4) is solved by a shrinkage-thresholding algorithm [17]. The test problems are discrete ill-posed problems selected from Hansen [18]. All tests are done on a laptop with Core(TM) i7 M620@D, 2.67 GHz, 4 GB RAM and Matlab R2009a.

A classical example of an ill-posed problem is a Fredholm integral equation of the first kind with a square integrable kernel, which has the form

$$ \int_{a}^{b} K(s, t) f(t)\, dt = g(s),\quad s\in [c, d], $$
(4.1)

where the right-hand side g and the kernel K are given, and f is unknown.

The following examples are used to test our algorithm.

Example 4.1

The kernel K is given by

$$K(s, t) = e^{-st}, $$

and the integration interval is \([0,\infty)\). The true solution f and the right-hand side g are given by

$$\begin{aligned} \begin{aligned} (\mathrm{a}) &\quad f(t)=e^{-\frac{t}{2}}, \qquad g(s)= \frac {1}{s+0.5}, \\ (\mathrm{b}) &\quad f(t) = 1- e^{-\frac{t}{2}}, \qquad g(s) = \frac{1}{s}- \frac{1}{s+0.5}, \\ (\mathrm{c}) &\quad f(t)= t^{2}\times e^{-\frac{t}{2}}, \qquad g(s) = \frac{2}{(s+0.5)^{3}}, \\ (\mathrm{d}) &\quad f(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} 0, & t\le2, \\ 1, & t>2, \end{array}\displaystyle \right . \qquad g(s)= \frac{e^{-2s}}{s}. \end{aligned} \end{aligned}$$

The numerical results are displayed in Figure 1.

Figure 1
figure 1

Numerical results on Example  4.1 : ‘∗’ is the true solution and ‘∘’ denotes the approximate solution.

Full size image

Example 4.2

Shaw test problem: one-dimensional image restoration model. We have the kernel K and the solution f, which are given by

$$K(s,t) = \bigl(\cos(s) + \cos(t)\bigr)\times\bigl(\sin(u)/u\bigr)^{2} $$

and

$$f(t) = a_{1}\times\exp\bigl(-c_{1}\times(t - t_{1})^{2}\bigr) + a_{2}\times\exp \bigl(-c_{2}\times(t - t_{2})^{2}\bigr), $$

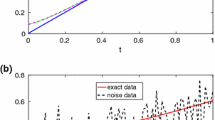
where \(u = \pi\times(\sin(s) + \sin(t))\). Both K and f are discretized by simple quadrature to produce A and x. Then the discrete right-hand side is produced as \(b = Ax\). In our test, the constants are assigned as follows: \(a_{1} = 2\), \(c_{1} = 6\), \(t_{1} = 0.8\); \(a_{2} = 1\), \(c_{2} = 2\), \(t_{2} = -0.5\). The numerical result is displayed in Figure 2(a).

Figure 2
figure 2

Numerical results on Examples 4.2 and 4.3 : ‘∗’ is the true solution and ‘∘’ denotes the approximate solution.

Full size image

Example 4.3

Baart test problem: the kernel K and right-hand side g of the discretization of a first-kind Fredholm integral equation are given by

$$K(s,t) = \exp\bigl(s\times\cos(t)\bigr),\qquad g(s) = 2\times\frac{\sinh(s)}{s}, $$

where \(s \in[0, \pi/2]\), \(t \in[0, \pi]\). The solution is given by \(f(t) = \sin(t)\). The numerical result is displayed in Figure 2(b).

We can draw the conclusion from the above computational results: the proposed hybrid splitting method is valid and efficient for the smoothing Tikhonov regularization problem.

5 Conclusions

We have proposed a hybrid splitting method for solving the smoothing Tikhonov regularization problem, which is to minimize the sum of three convex functions over a simple closed convex set. The problem can be reformulated as a convex minimization problem with three separable block variables, and we get the variational inequalities formulation by the KKT conditions of the separable convex minimization problem. By the convexity of the problem, the solution of the resulting variational inequalities is the same as the solution of the convex minimization problem. At each iteration of the proposed method, three subproblems are solved and two multipliers are updated. The former two subproblems are first solved in a parallel fashion, and immediately, the multipliers associated to these are updated; then the third subproblem is solved in the sense of an alternative fashion with the former two subproblems, and the multipliers associated to the last two block variables are updated. The proposed method is essentially to a hybrid splitting method since it combines the parallel splitting method and the alternating direction method, which are two power tools for the convex optimization problem with a separable structure. Under suitable assumptions, the global convergence of the hybrid splitting method is proved. The numerical results on the discrete ill-posed problems show that the proposed method has validity and efficiency.