1 Introduction

Among numerous non-stationary signals that arise in many radars [1] and communication [2, 3], instantaneous frequency (IF) signals, for instance, linear frequency modulated (LFM) signals, have obvious time-frequency characteristics which are continuous and decided the location. Similar to the time-frequency signatures, the spatial signature of the signal source also includes significant information about the signal source [4]. It ensures signal source identification due to the respective angle position received from a receiver antenna array, which is the directions-of-arrival. The characterization of DOA is viewed as steering vectors in which the source signal demonstrates a difference of the signal phase over every sensor antennas when electromagnetic wave covers the receiver antenna array [5]. Time-frequency (T-F) analysis plays important roles in the DOA estimation of the non-stationary signal [6].

Time-frequency analysis enables to process non-stationary signals overlying in both frequency and time domains in which windowing- and filtrating-based means cannot separate the different signal source components [7, 8]. For analyzing the non-stationary signals, such as LFM signals, time-frequency signal representations and analyses are necessary [9]. We engage in the class of signals where the instantaneous frequency particularly or basically determines the time-frequency signatures of the signal source. A successful application of time-frequency distribution desires prior knowledge for the signal source in order that the most advisable distribution is preferred [10]. In this article, Wigner-Ville distribution (WVD) is considered as the time-frequency distribution representation since it provides the most energy concentration in time-frequency domains, displays the non-stationary properties of the signal, and satisfies the marginal conditions [11]. Combining the time-frequency and spatial characteristic is accomplished into a framework named STFDs in time-frequency MUSIC (TF-MUSIC) [12]. This structure applies the signal location characteristic and energy concentration for increasing signal-to-noise ratio (SNR) and source signal identification before achieving the high-resolution direction-of-arrival estimation [13]. The framework desires the calculations of the WVD from the data obtained at each sensor, for instance, auto-terms of WVD and the cross terms of WVD between sensor antennas.

When the analyzed signal includes more than one signal source component, WVD performs signal auto-terms as positive magnitudes at their instantaneous frequency areas and the cross terms as oscillatory magnitudes along the geometrical middle point of auto-terms [14]. The cross-term problem of the WVD was first indicated in [15]. The suppression of cross terms is the core problem of bilinear time-frequency transformation. The references are abundant studies to suppress the cross terms and increase the time-frequency resolution. A method combined of the Hough transform (HT) and the Wigner-Ville distribution (WVD) performs cross term suppression [14, 16]. Another study researched the blind source separation approach based on the use of time-frequency analysis to eliminate cross terms in WVD [17]. The main purpose of research in [18] is to accomplish the high-resolution and the maximal cross-term contraction with the desirable diagonal or off-diagonal peculiarity of time-frequency distribution matrices in blind source separation applications. Researchers proposed a method named standardization of the pseud-quadratic form to suppress the cross terms in [19]. In order to suppress the cross term, Zuo et al. further propose a smoothed high-resolution time-frequency rate representation (SHR-TFRR) via utilizing an FR window to the high-resolution-time frequency rate representation, which is expressed in the convolution form [20, 21]. A pure idea is offered by Aiordachioaie and Popescu, as starting initial point to compose an approach to suppress the cross terms and to attain an exact image of WVD, including only the auto-terms [22]. A new method is offered by Wu and Li to suppress cross terms in the WVD of linear frequency modulation signals with multicomponent [23].

The existence of cross terms is difficult to be avoided. There are some researches in the references that take full use of cross terms in WVD in different research fields. Bird song syllable classification is realized using cross terms of Wigner-Ville ambiguity function in [24]. The Wigner distribution achieves artifacts well known as cross terms that are contemplated and undesirable in some situations; nevertheless, it can be utilized to ascertain the existence of greatly little signal source terms, in this case, VLPs terms [25]. Using the ambiguity domain interpretation, Jeong and Williams explored the theory of the cross terms (or interferences) in spectrograms [26]. A blind source separation technology applying both cross terms and auto-terms in the time-frequency distributions of the source signals was considered by Belouchrani et al. in [27]. As an application, Fadaili et al. showed that the source separation can be accomplished via exploiting one of these algorithms to a set of spatial quadratic time-frequency distribution matrices corresponding merely to the named cross terms and/or to the named auto-terms [28]. When the cross term is considered from different perspectives, the cross term accurately reflects the relationship between multiple signal components [29]. When the energy difference between non-stationary signals is large, specifically in the situation of low signal-to-noise ratio, a weak non-stationary signal may be buried in the noise. At this point, the weak non-stationary signal is the desired signal. It is difficult or almost impossible to extract the auto-term of the weak non-stationary signal. The cross-term amplitude of strong and weak non-stationary signal did not decrease significantly. In general, the cross terms contain sufficient information of weak non-stationary signal for its DOA estimation. Therefore, in the case that both strong and weak non-stationary signals existing simultaneously, the cross terms of STFDs are used to obtain DOA of the desired weak non-stationary signal in this paper.

This paper includes some sections. Section 2 reviews spatial time-frequency distribution in TF-MUSIC. In Section 3, cross-term selection procedures of STFDs are introduced. The analytical results are used in this section in order to examine the proposed method performance. Several simulations are offered in Section 4. Section 5 gives conclusions.

2 Related works

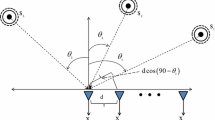
In narrowband signal array processing, because n source signals access on a m-element uniform linear array, the received data formula

$$ \mathbf{x}(t)=\mathbf{y}(t)+\mathbf{n}(t)=\mathbf{A}\left(\theta \right)\mathbf{d}(t)+\mathbf{n}(t) $$
(1)

is frequently presumed, where the m × n spatial matrix A(θ) = [a(θ1), a(θ2), …, a(θn)] implies the steering matrix. In the direction-of-arrival estimate situations, we expect A to be a well-known characteristic, and each column of matrix A associated with a single signal direction drives a distinct orientation. The analytical operation in this article does not rely upon any special matrix A structure characteristic. Because of the synthesis of the source signals at every antenna, the parts of the m × 1 data vector x(t) are multi-component source signals; nevertheless, every source signal di(t) of the source signal vector d(t) is often a single signal component. n(t) is an additive zero-mean white complex noise vector in which elements are presumed as temporal and spatial stationary random processes which are independent from the source signals.

In (1), it is presumed that the quantity m of sensors is more than the quantity n of source signals. Furthermore, matrix A has a column full rank because it involves that the steering vectors associated with n different directions of arrival have linear independence relationship. We furthermore presumed that the data covariance matrix

$$ {\mathbf{R}}_{\mathbf{x}\mathbf{x}}=\mathrm{E}\left[\mathbf{x}(t){\mathbf{x}}^{\mathrm{H}}(t)\right] $$
(2)

is not singular and that the processing duration includes N snapshots (N > m), where superscript H implies conjugate transpose, and E(·) implies the statistical expectation operator. From the above presumptions, the data correlation matrix is provided by

$$ {\mathbf{R}}_{\mathbf{x}\mathbf{x}}=\mathrm{E}\left[\mathbf{x}(t){\mathbf{x}}^{\mathrm{H}}(t)\right]={\mathbf{A}\mathbf{R}}_{\mathbf{dd}}{\mathbf{A}}^{\mathrm{H}}+{\sigma}^2\mathbf{I} $$
(3)

where Rdd = E[d(t)dH(t)] is the signal correlation matrix, σ2 is the noise power at every sensor antenna, and I implies the identity matrix. Let λ1 > λ2 > … > λn > λn + 1 = λn + 2 = … = λm = σ2 imply the characteristic values of Rxx. The λi, i = 1, …, n are individual. The eigenvectors corresponding to λ1, …, λn make up the columns of the matrix S = [s1, …, sn], and those associated with λn + 1, …, λm constitute the matrix G = [g1, …, gm − n]. Because the column vectors of A and S constitute their subspace, AHG = 0.

In effect, Rxx is not known and could be approximated via the applicable data snapshots x(i), i = 1, …, N. The approximated data covariance matrix is provided from

$$ {\hat{\mathbf{R}}}_{\mathbf{x}\mathbf{x}}=\frac{1}{N}\sum \limits_{i=1}^N\mathbf{x}(i){\mathbf{x}}^{\mathrm{H}}(i) $$
(4)

Let \( \left\{{\hat{\mathbf{s}}}_1,\dots, {\hat{\mathbf{s}}}_n,{\hat{\mathbf{g}}}_1,\dots, {\hat{\mathbf{g}}}_{m-n}\right\} \) imply the unit-norm eigenvectors of \( {\hat{\mathbf{R}}}_{\mathbf{xx}} \) that are arranged according to a descending order of the corresponding eigenvalues and make \( \hat{\mathbf{S}} \) and \( \hat{\mathbf{G}} \) imply the matrices determined by the set of vectors \( \left\{{\hat{\mathbf{s}}}_i\right\} \) and \( \left\{{\hat{\mathbf{g}}}_i\right\} \), severally. We retrospect that the DOAs can be evaluated by the traditional MUSIC approach via resolving the n values of θ for which the subsequent spatial spectrum is performed by maximization operation [30]:

$$ {f}_{\mathrm{MU}}\left(\theta \right)=\frac{1}{{\mathbf{a}}^{\mathrm{H}}\left(\theta \right){\hat{\mathbf{G}}\hat{\mathbf{G}}}^{\mathrm{H}}\mathbf{a}\left(\theta \right)} $$
(5)

where a(θ) is the steering vector associated with θ.

We then survey the concept and fundamental peculiarities of the STFDs. In this article, we straightforwardly examine a kind of Cohen’s class, specially, the Wigner-Ville distribution (WVD) as well as its characteristic. The discrete formula of WVD of a signal source x(t), via an odd length L rectangular window, is given by

$$ {D}_{xx}\left({k}_t,{k}_f\right)=\sum \limits_{k_{\tau }=-\left(L-1\right)/2}^{\left(L-1\right)/2}x\left({k}_t+{k}_{\tau}\right){x}^{\ast}\left({k}_t-{k}_{\tau}\right){e}^{-j4\pi {k}_f{k}_{\tau }} $$
(6)

where * implies complex conjugate. The integral of the product of the conjugate of the signal reflects the energy distribution of the signal in the time and frequency dimensions. Formula (6) reflects the details of the signal energy distribution. The spatial WVD matrix is attained via changing x(t) by the data snapshot vector x(t)

$$ {\mathbf{D}}_{\mathbf{x}\mathbf{x}}\left({k}_t,{k}_f\right)=\sum \limits_{k_{\tau }=-\left(L-1\right)/2}^{\left(L-1\right)/2}\mathbf{x}\left({k}_t+{k}_{\tau}\right){\mathbf{x}}^{\mathrm{H}}\left({k}_t-{k}_{\tau}\right){e}^{-j4\pi {k}_f{k}_{\tau }}. $$
(7)

Replacing (1) into (7), we attain

$$ {\mathbf{D}}_{\mathbf{xx}}\left({k}_t,{k}_f\right)={\mathbf{D}}_{\mathbf{yy}}\left({k}_t,{k}_f\right)+{\mathbf{D}}_{\mathbf{yn}}\left({k}_t,{k}_f\right)+{\mathbf{D}}_{\mathbf{ny}}\left({k}_t,{k}_f\right)+{\mathbf{D}}_{\mathbf{nn}}\left({k}_t,{k}_f\right). $$
(8)

We note that Dyy (kt,kf), Dyn (kt,kf), Dny (kt,kf), and Dnn (kt,kf) are matrices of m × m dimension. Due to the uncorrelated noise and signal presumption and the zero-mean noise property, the mathematic expectation of the cross-term STFD matrices between the noise and signal vectors equal to zero, such as E[Dyn(kt, kf)] = 0 and E[Dny(kt, kf)] = 0, and it pursues that

$$ {\displaystyle \begin{array}{c}\mathrm{E}\left[{\mathbf{D}}_{\mathbf{xx}}\left({k}_t,{k}_f\right)\right]=\mathrm{E}\left[{\mathbf{D}}_{\mathbf{yy}}\left({k}_t,{k}_f\right)\right]+\mathrm{E}\left[{\mathbf{D}}_{\mathbf{nn}}\left({k}_t,{k}_f\right)\right]\\ {}=\mathbf{A}\mathrm{E}\left[{\mathbf{D}}_{\mathbf{dd}}\left({k}_t,{k}_f\right)\right]{\mathbf{A}}^{\mathrm{H}}+{\sigma}^2\mathbf{I}\end{array}} $$
(9)

where the signal source time-frequency distribution matrix

$$ {\mathbf{D}}_{\mathbf{d}\mathbf{d}}\left({k}_t,{k}_f\right)=\sum \limits_{k_{\tau }=-\left(L-1\right)/2}^{\left(L-1\right)/2}\mathbf{d}\left({k}_t+{k}_{\tau}\right){\mathbf{d}}^{\mathrm{H}}\left({k}_t-{k}_{\tau}\right){e}^{-j4\pi {k}_f{k}_{\tau }} $$
(10)

is of n × n dimension matrix. For signal array processing researches, the hybrid matrix A includes the azimuth and projects the auto-terms and cross terms in time-frequency distributions of the source signals to the auto-terms and cross terms in time-frequency distributions of the received data.

Formula (9) is comparable to the other formula that has been generally utilized for direction finding problems, involving the source signal covariance matrix to the data spatial covariance matrix. From the above production, the covariance matrices are reestablished via the STFD matrices. The reestablished formulas for traditional array signal processing could be used, and core problems for various situations of array processing, especially those addressing non-stationary signal situations, can be addressed by bilinear transformations. It is prominent that (9) suits for every point. For reducing the noise influence and ensure the column full rank character for the involved matrix, many time-frequency points are used, contrary to a single one. Joint diagonalization [31] and the time-frequency averaging approach become the two key technologies that have been utilized for the objective [7, 13]. In this article, we merely use averaging operation for many time-frequency points.

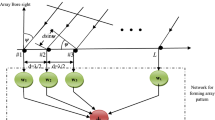
The time-frequency distribution transforms the one-dimensional time domain source signals into the two-dimensional time-frequency domain source signals. The time-frequency distribution characteristic of accumulating the incoming signal while widening the noise to the integrated time-frequency domain enhances the efficient SNR. Next, we calculate the signal subspace and noise subspace projection through a finite snapshot quantity of data. In the situation where the STFD matrices are averaged for the time-frequency signatures, we consider those N–L + 1 time-frequency distribution points. The result is provided via

$$ \hat{\mathbf{D}}=\frac{1}{\left(N-L+1\right)}\sum \limits_{i=1}^{N-L+1}{\mathbf{D}}_{\mathbf{xx}}\left({i}_t,{i}_f\right). $$
(11)

The unit-norm eigenvectors corresponding to \( {\hat{\lambda}}_1^{\mathrm{tf}},\dots, {\hat{\lambda}}_{n_0}^{\mathrm{tf}} \) are implied by the columns of \( {\hat{\mathbf{S}}}^{\mathrm{tf}}=\left[{\hat{\mathbf{s}}}_1^{\mathrm{tf}},\dots, {\hat{\mathbf{s}}}_{n_0}^{\mathrm{tf}}\right] \), and those associated with \( {\hat{\lambda}}_{n_0+1}^{\mathrm{tf}},\dots, {\hat{\lambda}}_m^{\mathrm{tf}} \) are implied by the columns of \( {\hat{\mathbf{G}}}^{\mathrm{tf}}=\left[{\hat{\mathbf{g}}}_1^{\mathrm{tf}},\dots, {\hat{\mathbf{g}}}_{m-{n}_0}^{\mathrm{tf}}\right] \). The superscript tf implies that the associated term is inferred from the matrix \( \hat{\mathbf{D}} \). Parallelly, for time-frequency MUSIC with n0 source signals considered, the DOAs are confirmed via confirming the n0 peaks of the spatial spectrum which are determined from the signals’ time-frequency domain:

$$ {f}_{\mathrm{MU}}^{\mathrm{tf}}\left(\theta \right)=\frac{1}{{\mathbf{a}}^{\mathrm{H}}\left(\theta \right){\hat{\mathbf{G}}}^{\mathrm{tf}}{\hat{\mathbf{G}}}^{\mathrm{tf}\mathrm{H}}\mathbf{a}\left(\theta \right)}. $$
(12)

3 Method

The virtues of time-frequency-based DOA estimation approach may merely be realized when suitable time-frequency points are considered in the STFD matrices. The key point of this kind of method is how to choose the suitable time-frequency points. The purpose of this paper is to estimate the DOA of weak non-stationary source signals based on cross terms of spatial time-frequency distribution in the presence of strong non-stationary signal interference. In the STFD framework, the source signal time-frequency characteristics should not be highly overlapping. The source STFD matrix is

$$ {\mathbf{D}}_{\mathbf{dd}}\left({k}_t,{k}_f\right)=\left(\begin{array}{cc}{D}_{d_1{d}_1}\left({k}_t,{k}_f\right)& {D}_{d_1{d}_2}\left({k}_t,{k}_f\right)\\ {}{D}_{d_2{d}_1}\left({k}_t,{k}_f\right)& {D}_{d_2{d}_2}\left({k}_t,{k}_f\right)\end{array}\right). $$
(13)

The two source signals, d1(kt) and d2(kt), are LFM signals. The following four types of time-frequency points are discussed. The first-type time-frequency points are associated with signal auto-terms merely. For those points, the source signal time-frequency distribution matrix has a rank-one diagonal mathematics structure. The second-type time-frequency points are associated with source signal cross-terms merely. For the points, the signal time-frequency distribution matrix is off-diagonal matrix. That is that the matrix is considered to be off-diagonal because their diagonal elements equal to zeros. The third-type time-frequency points are associated with both source signal auto-terms and cross terms. For the points, the signal time-frequency distribution matrix has no obvious algebraic specific structure which can be immediately used. The source signal cross terms and source signal auto-terms are inexistence in the fourth time-frequency points.

The diagonal and off-diagonal mathematics structures of the first- and second-type T-F points are frequently destroyed when the source signals are mixed. The first-, second-, and third-type T-F points are significant to the DOA estimation problem. The fourth should be abandoned because they do not have any effect in this situation. In this paper, we exploit cross terms of spatial time-frequency distribution to perform DOA estimation of weak non-stationary signals when there are both strong and weak non-stationary signals.

Because of the fact that in the first-type time-frequency points, Ddd(kt, kf) have a high outstanding algebraic structure which is a rank-one diagonal matrix, an outstanding mean to solve the direction-of-arrival estimation problem will become to utilize matrix decomposition technology, which is a traditional technology for DOA estimation. Yet, the procedure of the automatic time-frequency point’s selection, in the general situation, is difficult. Complicated time-frequency point selection technologies will be usually needed, as studied in the following.

Under the above condition, the STFDs have the structure as follows:

$$ {\mathbf{D}}_{\mathbf{xx}}\left({k}_t,{k}_f\right)={\mathbf{A}\mathbf{D}}_{\mathbf{dd}}\left({k}_t,{k}_f\right){\mathbf{A}}^{\mathrm{H}}+{\mathbf{D}}_{\mathbf{nn}}\left({k}_t,{k}_f\right), $$
(14)

Consider an n × m matrix W, named a whitening matrix, in order that WA implies a unitary matrix and implies U. It is

$$ \left(\mathbf{WA}\right){\left(\mathbf{WA}\right)}^{\mathrm{H}}={\mathbf{UU}}^{\mathrm{H}}=\mathbf{I}, $$
(15)

Pre- and post-multiplying Dxx(kt, kf) by W results in the whitened matrix, defined as

$$ {\underline {\mathbf{D}}}_{\mathbf{xx}}\left({k}_t,{k}_f\right)={\mathbf{W}\mathbf{D}}_{\mathbf{xx}}\left({k}_t,{k}_f\right){\mathbf{W}}^{\mathrm{H}}={\mathbf{U}\mathbf{D}}_{\mathbf{dd}}\left({k}_t,{k}_f\right){\mathbf{U}}^{\mathrm{H}}+{\mathbf{W}\mathbf{D}}_{\mathbf{nn}}\left({k}_t,{k}_f\right){\mathbf{W}}^{\mathrm{H}}, $$
(16)

where the second equation results from the W concept and (14). Distinctly, the whitening process results in a linear model in which a unitary mixed matrix is structured. In a whitened situation, some technologies use trace invariance in the matrix for unitary transform, taking it likely to judge the existence of signal cross terms. One technology [27] introduces that for the second-type T-F points, consider matrices that verify

$$ \frac{\mathrm{trace}\left\{{\underline {\mathbf{D}}}_{\mathbf{xx}}\left({k}_t,{k}_f\right)\right\}}{\left\Vert {\underline {\mathbf{D}}}_{\mathbf{xx}}\left({k}_t,{k}_f\right)\right\Vert }<\varepsilon $$
(17)

where trace {·} implies matrix mathematics trace, ||·|| implies mathematics Frobenius norm, and ε is a user-determined positive small value. For a noise condition, the selection procedure of time-frequency points of peak power (the first- and second-type time-frequency points) may develop a severe problem when the source signals are nearly submerged in noise. This is achieved by averaging the STFDs of cross terms to solve this problem.

4 Results and discussion

Assume an eight-sensor uniform linear array with a half wavelength separation between each element and an observation duration of 512 samples. The two linear frequency modulation signal components are transmitted from two source signals located at angles θ1 and θ2. The initiated and finished normalized frequencies of the source signal from θ1 = 30° are fs1 = 0 and fe1 = 0.3, whereas the homologous second frequencies for another source from θ2 = 40°are fs2 = 0.2 and fe2 = 0.5, severally. WVD is utilized to calculate the time-frequency distribution, and time-frequency averaging is utilized to build the noise subspace. The input SNR of θ1 is 5 dB, whereas the incoming SNR of θ2 is − 5 dB. Figure 1 shows the time-frequency spectrum of two LFM signals. From Fig. 1, the auto-term of the weak signal cannot be obtained on the time-frequency spectrum because of the submergence in noise. However, the cross terms in time-frequency plane can observe the normalized frequencies of which is approximately from 0.1 to 0.4. As shown in Fig. 2, the cross terms are extracted by the method mentioned above for the DOA estimation of the weak non-stationary signal. The DOA of strong and weak signals is estimated by cross terms in Fig. 3, which are approximately 30° and 40°, respectively.

Fig. 1
figure 1

T-F spectrum of two LFM signals

Full size image
Fig. 2
figure 2

Cross terms of T-F spectrum

Full size image
Fig. 3
figure 3

The estimated spatial spectrum

Full size image

If the SNR difference of the strong and weak signals increases further, the DOA of the weak signal cannot be directly obtained from the cross terms. The input SNR of θ1 is 10 dB, whereas the input SNR of θ2 is − 10 dB. The cross term is utilized from another perspective. Firstly, the position of the auto-terms of the strong signal and cross terms in the time-frequency domain is estimated. Then the position of the auto-terms of the weak signal is fitted according to the two positions in order to improve the SNR of the weak non-stationary signals. The spatial time-frequency distribution matrixes are extracted from the position of the weak signal for the DOA estimation. Figure 4 shows the T-F-spectrum of two linear frequency modulation signal components. Although the cross terms are no longer obvious on the time-frequency plane, they can also be extracted according to the characteristics of the matrix. In Fig. 5, the auto-terms of the weak non-stationary signal are fitted by the method mentioned above for the DOA estimation. The DOA of the strong and weak signals is simultaneously estimated in Fig. 6, which are approximately 30° and 40°, respectively. The time-frequency-MUSIC technology is realized respectively for two sets of time-frequency points, each one from one source signal.

Fig. 4
figure 4

T-F spectrum of two LFM signals

Full size image
Fig. 5
figure 5

Auto-terms of weak signal

Full size image
Fig. 6
figure 6

The estimated spatial spectrum

Full size image

When the incoming SNR of θ1 is 5 dB, the input SNR of θ2 is from − 8 dB to 0 dB. The results were calculated via averaging 100 Monte Carlo runs. Figure 7 shows the DOA estimation root-mean-square error with SNR for traditional MUSIC and time-frequency-MUSIC based on cross-terms. The RMSE of TF-MUSIC based on cross terms is less than that of the conventional MUSIC overall. The advantages of TF-MUSIC based on cross terms in poor SNR conditions become obvious from the figure.

Fig. 7
figure 7

The RMSE of DOA estimation versus input SNR of weak signal

Full size image

Next, the influence of snapshots on the algorithm is analyzed. With the other simulation conditions mentioned above unchanged, the number of snapshot is 256, 512, and 1024, respectively. From Fig. 8, the increase in the number of snapshots reduces the RMSE of DOA estimation. Then, the increase in that will also increase the calculation time. The impact of a small user-defined positive scalar ε on RMSE is also simulated. With the 512 snapshots, ε is 0.3, 0.5, and 0.7, respectively. From Fig. 9, different values of the same order have little influence on RMSE.

Fig. 8
figure 8

The RMSE at different snapshots

Full size image
Fig. 9
figure 9

The RMSE at different ε

Full size image

Figures 10 and 11 show the estimated spatial spectrum of TF-MUSIC based on cross terms and the traditional MUSIC where the direction separation is close (θ1 = 30°, θ2 = 33°). It is obvious that the source signals can be separated via the time-frequency-MUSIC based on cross terms whereas the conventional MUSIC fails. This is attributed to the combination of time-frequency analysis method and MUSIC algorithm. In the time-frequency MUSIC algorithm, for each signal energy distribution, the MUSIC algorithm is calculated separately, and only a single signal is included in the data covariance matrix. Therefore, two curves are generated and the target with an angle approaching can be distinguished.

Fig. 10
figure 10

The spatial spectra of TF-MUSIC

Full size image
Fig. 11
figure 11

The spatial spectra of MUSIC

Full size image

5 Conclusions

When the desired weak non-stationary signal may be buried in noise, especially in the condition of low signal-to-noise ratio, it is difficult or almost impossible to extract the auto-term of the weak non-stationary signal. However, the cross terms of the strong and weak non-stationary signal did not decrease significantly, which contain sufficient information of weak non-stationary signal for its DOA estimation. Therefore, in the case that both strong and weak non-stationary signals exist, meanwhile, the cross terms of STFDs are used to obtain DOA of the desired weak non-stationary signal in this paper. The DOA estimation root-mean-square error of TF-MUSIC based on cross terms is less than that of conventional MUSIC. The DOA of two closely spaced signals is resolved by the TF-MUSIC based on cross terms.