Spectral-energy efficiency maximization for wireless powered low-latency NOMA systems with full-duplex relaying

Abstract

This paper investigates a wireless powered communication system, where a base station (BS) and relay first harvest energy from the power beacon and use it for data transmission. Using non-orthogonal multiple access (NOMA), the BS delivers the messages to two NOMA users via a full-duplex (FD) relay to realize low-latency communication. As two important metrics in fifth-generation communication systems, spectral and energy efficiency are jointly analyzed in this paper. Under quality of service (QoS) requirement of two NOMA users and power constraints at the BS and relay, beamforming and time allocation ratio are jointly optimized so as to maximize sum data rate and energy efficiency of system. The formulated problems are hard to be solved directly due to its non-concave objective and non-convex constraints. To tackle these, one-dimensional search and path-following-based algorithms are proposed, which can iteratively obtain improved objectives with convergence guaranteed. With fast convergence and insensitivity to problem size, the proposed algorithm can reach at least local optimum. Numerical results verify the advantages of the proposed algorithms and the superiority of the proposed scheme.

1 Introduction

Being a state of the art, the exponential increment of traffic volume in wireless networks poses a formidable challenge to the design of modern wireless communication systems, which need to provide larger bandwidth, higher data rate, and lower communication delays. Non-orthogonal multiple access (NOMA) and full-duplex (FD) are recently recognized as two promising techniques to enlarge connections, improve spectral efficiency, balance user fairness, and support diverse services for the fifth-generation (5G) wireless communication networks [1, 2]. On the one hand, NOMA allows multiple users to access the same resources(frequency/time/code) via superposition coding in the power domain and separates interfered users by utilizing successive interference cancellation (SIC). NOMA can reach a balance between network throughput and user fairness by appropriately allocating the transmit power at the base station to multiple users according to their different channel conditions [3]. On the other hand, full-duplex technique enables the radios to simultaneously transmit and receive on the same frequency channel. Compared with conventional half-duplex (HD), FD mode can avoid processing delay so as to enhance spectral efficiency [4].

To take advantage of cooperative communication, many researchers combine cooperative communication with NOMA to further improve user fairness and communication reliability [5–7]. In cooperative NOMA, the relays are divided into two categories, i.e., user relay and dedicated relay. In [5], the authors proposed a novel cooperative NOMA scheme to enhance system capacity and user reception reliability. In the proposed scheme, some users in good channel conditions are regarded as relays to help the transmission between users in poor channel conditions and the BS. In addition, [6] adopted the dedicated relay to assist the BS to communicate with the far user. Ding [5] and Kim and Lee [6] showed the superiority of the proposed cooperative schemes by simulation. Different from [5] and [6], [7] investigated a scenario in which the BS communicates with two users with the help of a dedicated relay. However, the above works about cooperative NOMA mainly focus on half-duplex relay, which can only transmit or receive message at one time. To some extent, HD relay could lead to a reduction of spectral efficiency due to its extra time for cooperation.

Among all full-duplex transmission, full-duplex relaying is a typical application scenario, which has attracted significant attention in academia and industry [8–11]. In general, FD relay techniques are divided into two types, namely decode-and-forward (DF) relay and amplify-and-forward (AF) relay [12–15]. Since the transmit antenna at the relay is much closer to its receive antenna, FD relay easily suffers from self-interference (SI), which is the main challenge of FD relaying systems [16, 17]. To guarantee the feasibility of full-duplex relaying systems, many efforts have been made to degrade loop interference [18, 19]. Under the circumstances that self-interference is effectively suppressed, many literatures have paid much attention to full-duplex relay-assisted cooperative NOMA systems [20–22]. Zhong and Zhang [20] proposed FD NOMA transmission strategy, where a dedicated relay operates in FD mode to help the weak user. Zhang et al. [21] adopted the in-band relay to implement relaying, i.e., the near NOMA user acts as a FD relay to help far NOMA user and analyzed the proposed scheme from outage probability performance. Both [20] and [21] assumed imperfect SI cancellation. Aside from studying outage probability performance in in-band FD cooperative NOMA system with imperfect SI cancellation, [22] further took the user fairness into account so that minimum achievable rate of users is maximized.

The improvement on communication quality and the increased data processing complexity have imposed big challenges on the quality of power supply to wireless devices. Conventional wireless devices have limited lifetime. As a practical technique to realize battery-free wireless communication networks, energy harvesting has drawn wide attention [23–27]. To our best knowledge, conventional cooperative relaying technique requires extra power to support forwarding behavior, which would influence communication reliability due to its limited battery. Motivated by this, some literatures applied energy harvesting techniques to cooperative NOMA to enhance spectral and energy efficiency [28–30]. Liu et al. [28] proposed a novel simultaneous wireless information and power transfer (SWIPT) cooperative NOMA transmission schemes, where the near users first harvest energy from the received messages by means of power splitting architecture and then forward the decoded messages to the far users. Xu [29] maximized the data rate of the near users in SWIPT cooperative NOMA network by joint optimization of beamforming and power splitting ratio. To further extend [28] and [29], [30] implemented FD mode at the relay, which has demonstrated that the proposed scheme outperforms other existing schemes in terms of outage probability.

2 Method

In the aforementioned works, the energy source of relaying comes from the transmitter. However, considering that the location of the relay may be inconvenient to harvest energy from the transmitter, we deploy a dedicated power beacon (PB) for powering the BS and relay in this paper. Different from the above works, we assume that there are no direct links between the BS and two users. From the perspective of spectral and energy efficiency, two non-convex problems with joint optimization of beamforming and time allocation ratio are formulated subject to QoS requirements of two users and power constraints at the BS and relay. To cope with these, we propose two iterative algorithms based on one-dimensional search and path-following algorithm. With initial feasible points, the proposed algorithms can iteratively generate the improved feasible point and finally converge to at least local optimum within few steps by invoking the transformed convex problem. Simulation results verified the superiority of the proposed scheme compared with other existing strategies.

The contributions of this paper are summarized as follows:

∙ We consider a PB-assisted cooperative NOMA system with full-duplex relay by analyzing spectral and energy efficiency.

∙ Under QoS requirement of two users and power constraints at the BS as well as relay, we formulate the joint optimization of beamforming and time allocation ratio to maximize spectral and energy efficiency. To solve these, the iterative algorithms based on one-dimensional search and path-following algorithm are proposed to obtain at least local optimums, which can guarantee that the objective can converge to a KKT point within few steps.

∙ We show the convergence performance of the proposed algorithms and superiority of the proposed scheme over the other existing schemes by simulations and the impact of imperfect self-interference cancellation on the sum data rate performance.

The rest of this paper is structured as follows. In Section 2, the system model is briefly described and the optimization problems of spectral efficiency maximization and energy efficiency maximization are formulated in mathematical terms. Section 3 proposes joint optimization algorithm to find optimal solutions and analyzes its complexity and convergence behavior. Sections 4 and 5 present simulation results and conclusions, respectively.

Notations: Lower case, boldface lower case, and boldface upper letters represent scalars, vectors, and matrices, respectively. I and 0 denote an identity matrix and an all-zero vector or matrix, respectively. For matrix X, X^H and X^∗ denote its conjugate transpose and conjugate, respectively. For a vector x, ∥x∥ represents its Euclidean norm. 𝔼{∙} denotes the statistical expectation. R{∙} stands for the real part of a variable. |·| denotes the absolute value of a complex scalar. ℂ^m×n denotes the space of m×n complex matrices. $\mathcal {C}\mathcal {N}\left ({\mu,{\sigma ^{2}}} \right)$ denotes a circularly symmetric complex Gaussian RV x with mean μ and variance σ².

3 System model and problem formulation

3.1 System model

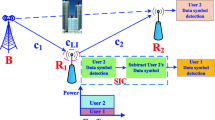
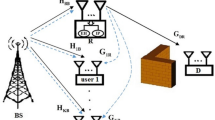
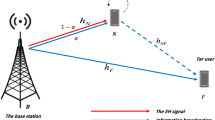
Consider a power beacon-based NOMA network, which consists of one base station, one full-duplex relay, and two NOMA users, as illustrated in Fig. 1. In proposed system, the power beacon is a signal-antenna device. Assume that M+1 antennas are employed at the BS, where one antenna is selected for receiving and M antenna is selected for transmission. Note that the allocation scheme of antennas at BS is fixed, which could be optimized. We assume that a direct link between the BS and two NOMA users is ignored due to the shadow fading [31]. $\;{h_{{\text {PB}}}} \sim {\mathcal {C}}{\mathcal {N}}\left ({0,d_{_{{\text {PB}}}}^{- \theta }} \right)$, $\;{h_{{\text {PR}}}} \sim {\mathcal {C}}{\mathcal {N}}\left ({0,d_{_{{\text {PR}}}}^{- \theta }} \right)$, $\;{\mathbf {h}_{{\text {BR}}}} \sim {\mathcal {C}}{\mathcal {N}}\left ({{\mathbf {0}},d_{_{{\text {BR}}}}^{- \theta }\mathbf {I}} \right)$, ${\mathbf {h}_{{\mathrm {RU1}}}} \sim {\mathcal {C}}{\mathcal {N}}\left ({{\mathbf {0}},d_{_{{\mathrm {RU1}}}}^{- \theta }\mathbf {I}} \right)$, and $\;{\mathbf {h}_{{\mathrm {RU2}}}} \sim {\mathcal {C}}{\mathcal {N}}\left ({{\mathbf {0}},d_{_{{\mathrm {RU2}}}}^{- \theta }\mathbf {I}} \right)$ represent the channel coefficients of PB to BS, PB to R, BS to R, R to U1, and R to U2 links, where θ is the path-loss exponent and d_ij is the distance between node i and node j. To perform full-duplex mode, the relay is equipped with one receive antenna and K>1 transmit antennas, which can efficiently focus its signal/energy on a target receive antenna [32, 33]. In addition, two NOMA users are single-antenna devices. In general, U1 has better channel state information (CSI) than U2, i.e., ∥h_RU1∥>∥h_RU2∥. In this paper, perfect CSI is assumed at all nodes [34].

Fig. 1

Power beacon-assisted NOMA system with full-duplex relay

As shown in Fig. 2, the whole communication duration T is divided into two parts. In the first interval time αT, the power beacon transfers the energy to the BS. Moreover, BS transfers the superposed signal w₁x₁+w₂x₂ to R while R transfers the decoded message r₁s₁+r₂s₂ to two users using NOMA in the second interval time (1−α)T. For simplicity, T is set as 1.

Fig. 2

An illustration of time diagram of the energy harvesting and information transmission in time block T

In proposed system, the BS and relay harvest energy from the PB in the first slot. The harvested energy at the BS and relay can be respectively written as

$$ {E_{\mathrm{b}}} = {\eta_{1}}\alpha TP{\left| {{h_{{\text{PB}}}}} \right|^{2}}, $$

(1)

$$ {E_{\mathrm{r}}} = {\eta_{2}}\alpha TP{\left| {{h_{{\text{PR}}}}} \right|^{2}}, $$

(2)

where η_i∈(0,1],i=1,2 represent the energy conversion efficiency which relies on rectification process and the energy harvesting circuitry. And 0≤α≤1 is denoted as time allocation ratio. Then, the average harvested energy at the BS and relay can be respectively expressed as

$$ {P_{\mathrm{b}}} = \frac{{{E_{\mathrm{b}}}}}{{\left({1 - \alpha} \right)T}} = \frac{{\eta \alpha P{{\left| {{h_{{\text{PB}}}}} \right|}^{2}}}}{{1 - \alpha }}, $$

(3)

$$ {P_{\mathrm{r}}} = \frac{{{E_{\mathrm{r}}}}}{{\left({1 - \alpha} \right)T}} = \frac{{\eta \alpha P{{\left| {{h_{{\text{PR}}}}} \right|}^{2}}}}{{1 - \alpha }}. $$

(4)

The received signal at R is denoted by

$$ {y_{\mathrm{r}}} = \sqrt {{P_{\mathrm{b}}}} \mathbf{h}_{{\text{BR}}}^{H}\left({{\mathbf{w}_{1}}{x_{1}} + {\mathbf{w}_{2}}{x_{2}}} \right) + \sqrt {u{P_{\mathrm{r}}}} \mathbf{h}_{{\text{LI}}}^{H}\left({{\mathbf{r}_{1}}{s_{1}} + {\mathbf{r}_{2}}{s_{2}}} \right) + {n_{\mathrm{r}}}, $$

(5)

where μ represents self-interference cancellation and ${n_{\mathrm {r}}} \sim {\mathcal {C}}{\mathcal {N}}\left ({0,{\sigma ^{2}}} \right)$ is the additive white Gaussian noise (AWGN) with complex Gaussian distribution of zero mean and covariance.

After receiving the superimposed signal from the BS, the relay first decodes x₂ by treating x₁ as noise, and then resorting to the SIC to decode x₁. Note that the relay is assumed to decode the received messages successfully [12]. Thus, the received signal-to-interference-plus-noise ratio (SINR) for decoding x₂ and x₁ are respectively written as

$$ {\gamma_{2}^{R}} = \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{2}}} \right|}^{2}}}}{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{1}}} \right|}^{2}} + \mu {P_{r}}\left({{{\left| {\mathbf{h}_{{\text{LI}}}^{H}{\mathbf{r}_{1}}} \right|}^{2}} + {{\left| {\mathbf{h}_{{\text{LI}}}^{H}{\mathbf{r}_{2}}} \right|}^{2}}} \right) + {\sigma^{2}}}} $$

(6)

and

$$ {\gamma_{1}^{R}} = \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{1}}} \right|}^{2}}}}{{\mu {P_{r}}\left({{{\left| {\mathbf{h}_{{\text{LI}}}^{H}{\mathbf{r}_{1}}} \right|}^{2}} + {{\left| {\mathbf{h}_{{\text{LI}}}^{H}{\mathbf{r}_{2}}} \right|}^{2}}} \right) + {\sigma^{2}}}}. $$

(7)

In the second phase, the relay transmits a superimposed signal $\mathbf {s} = \sqrt {{P_{\mathrm {r}}}} {\mathbf {r}_{1}}{s_{1}} + \sqrt {{P_{\mathrm {r}}}} {\mathbf {r}_{2}}{s_{2}}$ to two NOMA users. Then, the received message at U1 is denoted by

$$ {y_{1}} = \sqrt {{P_{\mathrm{r}}}} \mathbf{h}_{{\mathrm{RU1}}}^{H}\left({{\mathbf{r}_{1}}{s_{1}} + {\mathbf{r}_{2}}{s_{2}}} \right) + {n_{1}}. $$

(8)

And the received message at U2 is expressed as

$$ {y_{2}} = \sqrt {{P_{\mathrm{r}}}} \mathbf{h}_{{\mathrm{RU2}}}^{H}\left({{\mathbf{r}_{1}}{s_{1}} + {\mathbf{r}_{2}}{s_{2}}} \right) + {n_{2}}. $$

(9)

where ${n_{\mathrm {1}}} \sim {\mathcal {C}}{\mathcal {N}}\left ({0,{\sigma ^{2}}} \right)$ and ${n_{\mathrm {2}}} \sim {\mathcal C}{\mathcal {N}}\left ({0,{\sigma ^{2}}} \right)$ are the additive white Gaussian noise at U1 and U2, respectively.

Then, the received SINRs to detect x₂ and x₁ at U1 are respectively expressed as

$$ \gamma_{2}^{{\mathrm{U1}}} = \frac{{{P_{\mathrm{r}}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{2}}} \right|}^{2}}}}{{{P_{\mathrm{r}}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{1}}} \right|}^{2}} + {\sigma^{2}}}}, $$

(10)

$$ \gamma_{1}^{{\mathrm{U1}}} = \frac{{{P_{\mathrm{r}}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{1}}} \right|}^{2}}}}{{{\sigma^{2}}}}. $$

(11)

Further, the received SINR to detect x₂ at U2 are written as

$$ \gamma_{2}^{{\mathrm{U2}}} = \frac{{{P_{\mathrm{r}}}{{\left| {\mathbf{h}_{{\mathrm{RU2}}}^{H}{\mathbf{r}_{2}}} \right|}^{2}}}}{{{P_{\mathrm{r}}}{{\left| {\mathbf{h}_{{\mathrm{RU2}}}^{H}{\mathbf{r}_{1}}} \right|}^{2}} + {\sigma^{2}}}} $$

(12)

Hence, the available rate of U1 can be written as

$$ {R_{1}} = \min \left\{ {\ln \left({1 + {\gamma_{1}^{R}}} \right),\ln \left({1 + \gamma_{1}^{{\mathrm{U1}}}} \right)} \right\} $$

(13)

In addition, the data rate of U2 can be given by

$$ {R_{2}} = \min \left\{ {\ln \left({1 + {\gamma_{2}^{R}}} \right),\ln \left({1{\mathrm{ + }}\gamma_{2}^{{\mathrm{U1}}}} \right),\ln \left({1 + \gamma_{2}^{{\mathrm{U2}}}} \right)} \right\} $$

(14)

Then, the sum data rate of the whole system can be calculated as

$$ {R_{{\text{sum}}}} = {R_{1}} + {R_{2}} $$

(15)

3.2 Problem formulation

Given the transmission power P at the power beacon, the aim of this paper is to maximize spectral efficiency and energy efficiency by joint optimization of four beamforming vectors r₁,r₂,w₁,andw₂ and time allocation ratio α. Under QoS requirements of two NOMA users and power constraints at the BS and the relay, thus the corresponding optimization problems are respectively expressed as follows.

3.2.1 Spectral efficiency maximization

The formulated problem can be written as

$$ \mathop {\max }\limits_{\alpha,\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} {\mathrm{ }}{R_{{\text{sum}}}} $$

(16a)

$$ s.t.~~~~{\mathrm{ }}{R_{1}} \ge \bar R,{R_{2}} \ge \bar R $$

(16b)

$$ ~~~~~~~~{\left\| {{\mathbf{w}_{1}}} \right\|^{2}} + {\left\| {{\mathbf{w}_{2}}} \right\|^{2}} \le {P_{\mathrm{b}}} $$

(16c)

$$ ~~~~~~~~{\left\| {{\mathbf{r}_{1}}} \right\|^{2}} + {\left\| {{\mathbf{r}_{2}}} \right\|^{2}} \le {P_{\mathrm{r}}} $$

(16d)

$$ ~~~~~~~~0 < \alpha < 1 $$

(16e)

3.2.2 Energy efficiency maximization

Energy efficiency (EE) is defined as total throughput divided by the total power consumption [35], i.e., $\frac {{{R_{\text {sum}}}}}{{{P_{\text {sum}}}}}$. Herein, the total power consumption can be written as

$$ {P_{\text{sum}}} = {\left\| {{\mathbf{r}_{1}}} \right\|^{2}} + {\left\| {{\mathbf{r}_{2}}} \right\|^{2}} + {\left\| {{\mathbf{w}_{1}}} \right\|^{2}} + {\left\| {{\mathbf{w}_{2}}} \right\|^{2}} + {P_{c}} $$

(17)

where ∥w₁∥²+∥w₂∥² and ∥r₁∥²+∥r₂∥² represent the transmit power at the BS and relay, respectively, which is the constant power caused by signal processing and circuit consumption. The energy efficiency maximization problem can be expressed as

$$ \mathop {\max }\limits_{\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2},\alpha} \frac{{{R_{\text{sum}}}}}{{{P_{\text{sum}}}}} $$

(18a)

$$ s.t.\quad~\text{(16b)}-\text{(16e)} $$

(18b)

Herein, constraint (16b) stands for the target data rate of two NOMA users. Constraints (16c) and (16d) represent power constraints at power beacon and the base station, respectively. Finally, the time-switching ratio is characterized by constraint (16e). Note that problem (16) is non-convex due to its non-concave object (16a) and non-convex constraint (16b)-(16d). In the next section, we can convert the original problem into a convex form by employing one-dimensional search and path-following algorithm and find optimal solutions.

4 Proposed joint optimization

In this section, we propose a one-dimensional search and path-following-based iterative algorithm to solve spectral efficiency and energy efficiency maximization problem by jointly optimizing beamforming vectors and time allocation coefficient. The essence of the iterative algorithm is divided into two layers, i.e., the outer layer is to do one-dimensional search about and the inner layer is to execute path-following algorithm.

4.1 Sum rate maximization

To implement the path-following algorithm, we first fix the time allocation α. Firstly, let ${\gamma _{1}^{R}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},{\mathbf {w}_{1}}} \right)\! =\! \frac {{{P_{\mathrm {b}}}{{\left | {\mathbf {h}_{{\text {PR}}}^{H}{\mathbf {w}_{1}}} \right |}^{2}}}}{{{\varphi _{1}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},{\mathbf {w}_{1}}} \right)}}$, $\gamma _{2}^{{\mathrm {U1}}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2}} \right) \,=\, \frac {{{{\left | {\mathbf {h}_{{\mathrm {RU1}}}^{H}{\mathbf {r}_{2}}} \right |}^{2}}}}{{{\varphi _{2}}\left ({{\mathbf {r}_{1}}} \right)}}$, $\gamma _{2}^{{\mathrm {U2}}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2}} \right)\! =\! \frac {{{{\left | {\mathbf {h}_{{\mathrm {RU2}}}^{H}{\mathbf {r}_{2}}} \right |}^{2}}}}{{{\varphi _{3}}\left ({{\mathbf {r}_{1}}} \right)}}$ and ${\gamma _{2}^{R}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right) = \frac {{{P_{\mathrm {b}}}{{\left | {\mathbf {h}_{{\text {BR}}}^{H}{\mathbf {w}_{2}}} \right |}^{2}}}}{{{\varphi _{4}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},{\mathbf {w}_{1}}} \right)}}$, where ${\varphi _{1}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2}} \right)\! =\! \mu {P_{r}}\left ({{{\left | {\mathbf {h}_{{\text {LI}}}^{H}{\mathbf {r}_{1}}} \right |}^{2}} + {{\left | {\mathbf {h}_{{\text {LI}}}^{H}{\mathbf {r}_{2}}} \right |}^{2}}} \right) + {\sigma ^{2}}$, φ₂(r₁) = |hRU1Hr₁|²+σ², φ₃(r₁) = |hRU2Hr₁|² + σ² and ${\varphi _{4}}\left ({{\mathbf {w}_{1}},\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2}} \right) \,=\, {P_{\mathrm {b}}}{\left | {\mathbf {h}_{{\text {BR}}}^{H}{\mathbf {w}_{1}}} \right |^{2}} + \mu {P_{r}}\left ({{{\left | {\mathbf {h}_{{\text {LI}}}^{H}{\mathbf {r}_{1}}} \right |}^{2}} + {{\left | {\mathbf {h}_{{\text {LI}}}^{H}{\mathbf {r}_{2}}} \right |}^{2}}} \right) + {\sigma ^{2}}$.

Secondly, using equations (38) and (39), thus $\ln \left ({1 + {\gamma _{1}^{R}}} \right)$, $\ln \left ({1{\mathrm { + }}\gamma _{1}^{{\mathrm {U1}}}} \right)$, $\ln \left ({1 + \gamma _{2}^{{\mathrm {U1}}}} \right)$, $\ln \left ({1 + \gamma _{2}^{{\mathrm {U2}}}} \right)$, and $\ln \left ({1 + {\gamma _{2}^{R}}} \right)$ are respectively lower bounded by

$$ \begin{array}{l} \ln \left({1 + {\gamma_{1}^{R}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right)} \right)\\\quad \ge \ln \left({1 + \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{1}^{(k)}} \right|}^{2}}}}{{{\varphi_{1}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2}} \right)}}} \right) - \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{1}^{(k)}} \right|}^{2}}}}{{{\varphi_{1}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2}} \right)}}\\ + \frac{{2{P_{\mathrm{b}}}R\left\{ {{{\left({\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{1}^{(k)}} \right)}^{*}}\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{1}}} \right\}}}{{{\varphi_{1}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2}} \right)}} \\\quad- \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{1}^{(k)}} \right|}^{2}}\left({{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{1}^{(k)}} \right|}^{2}} + {\varphi_{1}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} \right)} \right)}}{{{\varphi_{1}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2}} \right)\left({{\varphi_{1}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2}} \right) + {P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{1}^{(k)}} \right|}^{2}}} \right)}}\\ = {\Pi_{1}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right) \end{array} $$

(19)

$$ \begin{array}{l} \ln \left({1{\mathrm{ + }}\gamma_{1}^{{\mathrm{U1}}}\left({{\mathbf{r}_{1}}} \right)} \right) \ge \ln \left({1 + \frac{{{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{\mathrm{1}}^{(k)}} \right|}^{2}}}}{{{\sigma^{2}}}}} \right) - \frac{{{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{1}^{(k)}} \right|}^{2}}}}{{{\sigma^{2}}}}\\ + \frac{{2{P_{r}}R\left\{ {{{\left({\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{1}^{(k)}} \right)}^{\mathrm{*}}}\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{\mathrm{1}}}} \right\}}}{{{\sigma^{2}}}}{\mathrm{ - }}\frac{{{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{1}^{(k)}} \right|}^{2}}\left({{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{1}}} \right|}^{2}}{\mathrm{ + }}{\sigma^{2}}} \right)}}{{{\sigma^{2}}\left({{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{1}^{(k)}} \right|}^{2}}{\mathrm{ + }}{\sigma^{2}}} \right)}}\\ {\mathrm{ = }}{\Pi_{\mathrm{2}}}\left({{\mathbf{r}_{\mathrm{1}}}} \right) \end{array} $$

(20)

$$ {{} \begin{aligned} \begin{array}{l} \ln \left({1 + \gamma_{2}^{{\mathrm{U1}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} \right)} \right) \!\ge\! \ln \left({1 \,+\, \frac{{{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}}}}{{{\varphi_{2}}\left({\mathbf{r}_{1}^{(k)}} \right)}}} \right) \,-\, \frac{{{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}}}}{{{\varphi_{2}}\left({\mathbf{r}_{1}^{(k)}} \right)}}\\ + \frac{{2{P_{r}}R\left\{ {{{\left({\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right|} \right)}^{*}}\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{2}}} \right\}}}{{{\varphi_{2}}\left({\mathbf{r}_{1}^{(k)}} \right)}} - \frac{{{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}}\left({{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}} + {\varphi_{2}}\left({{\mathbf{r}_{1}}} \right)} \right)}}{{{\varphi_{2}}\left({\mathbf{r}_{1}^{(k)}} \right)\left({{\varphi_{2}}\left({\mathbf{r}_{1}^{(k)}} \right) + {P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}}} \right)}}\\ = {\prod_{3}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} \right) \end{array} \end{aligned}} $$

(21)

$$ {{} \begin{aligned} \begin{array}{l} \ln \left({1 + \gamma_{2}^{{\mathrm{U2}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} \right)} \right) \!\ge\! \ln \left({1 + \frac{{{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU2}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}}}}{{{\varphi_{3}}\left({\mathbf{r}_{1}^{(k)}} \right)}}} \right) \,-\, \frac{{{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU2}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}}}}{{{\varphi_{3}}\left({\mathbf{r}_{1}^{(k)}} \right)}}\\ + \frac{{2{P_{r}}R\left\{ {{{\left({\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right)}^{*}}\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{2}}} \right\}}}{{{\varphi_{3}}\left({\mathbf{r}_{1}^{(k)}} \right)}} - \frac{{{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}}\left({{P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}} + {\varphi_{3}}\left({{\mathbf{r}_{1}}} \right)} \right)}}{{{\varphi_{3}}\left({\mathbf{r}_{1}^{(k)}} \right)\left({{\varphi_{3}}\left({\mathbf{r}_{1}^{(k)}} \right) + {P_{r}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}}} \right)}}\\ = {\prod_{4}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} \right) \end{array} \end{aligned}} $$

(22)

$$ {{}\begin{aligned} \begin{array}{l} \ln \left({1 \,+\, {\gamma_{2}^{R}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right)} \right) \\\quad \ge \ln \left({1 \,+\, \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{2}^{(k)}} \right|}^{2}}}}{{{\varphi_{4}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2},\mathbf{w}_{1}^{(k)}} \right)}}} \right)\! -\! \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{2}^{(k)}} \right|}^{2}}}}{{{\varphi_{4}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2},\mathbf{w}_{1}^{(k)}} \right)}}\\ \,+\, \frac{{2{P_{\mathrm{b}}}R\left\{ {{{\left({\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{2}^{(k)}} \right)}^{*}}\mathbf{h}_{{\text{PR}}}^{H}{\mathbf{w}_{2}}} \right\}}}{{{\varphi_{4}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2},\mathbf{w}_{1}^{(k)}} \right)}} \\\quad- \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{2}}} \right|}^{2}}\left({{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{2}}} \right|}^{2}} + {\varphi_{4}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right)} \right)}}{{{\varphi_{4}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2},\mathbf{w}_{1}^{(k)}} \right)\left({{\varphi_{4}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2},\mathbf{w}_{1}^{(k)}} \right) + {P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{2}}} \right|}^{2}}} \right)}}\\ = {\prod_{5}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) \end{array} \end{aligned}} $$

(23)

over the trust region

$$ \begin{array}{l} 2R\left\{ {{{\left({\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{j}^{(k)}} \right)}^{*}}\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{j}}} \right\}x - {\left| {\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{j}^{(k)}} \right|^{2}} > 0,{\mathrm{ }}j = 1,2\\ 2R\left\{ {{{\left({\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{i}^{(k)}} \right)}^{*}}\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{i}}} \right\}x - {\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{i}^{(k)}} \right|^{2}} > 0,{\mathrm{ }}i = 1,2\\ 2R\left\{ {{{\left({\mathbf{h}_{{\mathrm{RU2}}}^{H}\mathbf{r}_{2}^{(k)}} \right)}^{*}}\mathbf{h}_{{\mathrm{RU2}}}^{H}{\mathbf{r}_{2}}} \right\}x - {\left| {\mathbf{h}_{{\mathrm{RU2}}}^{H}\mathbf{r}_{2}^{(k)}} \right|^{2}} > 0\\ \end{array} $$

(24)

where ${\Pi _{1}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2}\!,\!{\mathbf {w}_{1}}} \right),{\Pi _{\mathrm {2}}}\left ({{\mathbf {r}_{\mathrm {1}}}} \right)$, ${\prod _{3}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2}} \right)$, ${\prod _{4}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2}} \right)$, and ${\prod _{5}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2}\!,\!\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right)$ are the inner approximation of $\ln \left ({1 + {\gamma _{1}^{R}}} \right),\ln \left ({1{\mathrm { + }}\gamma _{1}^{{\mathrm {U1}}}} \right),\ln \left ({1 + \gamma _{2}^{{\mathrm {U1}}}} \right),\ln \left ({1 + \gamma _{2}^{{\mathrm {U2}}}} \right)$, and $\ln \left ({1 + {\gamma _{2}^{R}}} \right)$ around feasible point $\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)$.

According to (19)–(23), the objective (16a) and non-convex constraint (16b) can be converted into convex one. The next feasible point $\left ({\left \{ {\mathbf {r}_{i}^{(k + 1)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k + 1)}} \right \}_{j = 1}^{2}} \right)$ of original problem (16) can be generated by solving the following problem at kth iteration

$$ \mathop {\max }\limits_{\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} {f_{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) $$

(25a)

$$ s.t.~~~~{R_{1}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right) \ge \bar R $$

(25b)

$$ ~~~~~~~~{R_{2}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) \ge \bar R $$

(25c)

$$ ~~~~~~~~\text{(16c)},\text{(16d)}, \text{(24)} $$

(25d)

where ${f_{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right) = {R_{1}^{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},{\mathbf {w}_{1}}} \right) + {R_{2}^{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right)$, ${R_{1}^{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},{\mathbf {w}_{1}}} \right) = \text {min}\left \{ {{\Pi _{1}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},{\mathbf {w}_{1}}} \right),{\Pi _{2}}\left ({{\mathbf {r}_{2}}} \right)} \right \}$, ${R_{2}^{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right) = \min \left \{ {\prod _{3}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2}} \right),{\prod _{4}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2}} \right),\right.\\ \left.{\prod _{5}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right) \right \}$ is the inner approximation of $f\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right) = {R_{{\text {sum}}}}$, ${R_{1}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},{\mathbf {w}_{1}}} \right)$, and ${R_{2}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right)$, respectively.

4.1.1 Convergence

It is easily found that $f\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right) \ge {f_{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right)$ and $f\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right) = {f_{k}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)$. Moreover, Algorithm 1 produces non-decreasing sequence provided that $\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right) \ne \left ({\left \{ {\mathbf {r}_{i}^{(k + 1)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k + 1)}} \right \}_{j = 1}^{2}} \right)$. That is to say, ${f_{k}}\left ({\left \{ {\mathbf {r}_{i}^{(k + 1)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k + 1)}} \right \}_{j = 1}^{2}} \right) > {f_{k}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)$. Thus, we can derive that the feasible point generated by Algorithm 1 can make objective value of (16) become bigger due to that and finally converge to the Karush-Kuhn-Tucker point of (16) after finitely many iterations [36].

4.1.2 Complexity

It is easily seen that the transformed convex problem (16) involves a=2M+2K+1 scalar real variables and b=5 quadratic and linear constraints. Hence, each iteration complexity of problem (16)is O(a²b^2.5+b^3.5) [37].

4.1.3 Initial feasible point generation

To find the initial feasible point satisfying the constraints (16b)–(16d), we should perform the following problem

$$ {{}\begin{aligned} \begin{array}{l} \mathop {\max }\limits_{\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}}\! \min \left\{ {{R_{1}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right),{R_{2}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right)} \right\}\!/\bar R\\ ~~~~~~s.t. ~~~~~~\text{(25d)} \end{array} \end{aligned}} $$

(26)

until $\min \left \{ {{R_{1}^{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},{\mathbf {w}_{1}}} \right),{R_{2}^{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right)} \right \}/\bar R \ge 1$ to generate a feasible point satisfying problem (16).

4.2 Energy efficiency maximization

Similar to operation in sum data maximization, only the objective (18a) and constraint (18b) still need to be tackled with fixed α. Before coping with the objective, we first resort to (38) such that

$$ {{} \begin{aligned} \begin{array}{l} \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{1}}} \right|}^{2}}}}{{{\varphi_{1}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right)}} \!\ge\!\! \frac{{2{P_{\mathrm{b}}}R\left\{ {{{\left({\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{1}^{(k)}}} \right)}^{*}}\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{1}}} \right\}}}{{{\varphi_{1}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2},\mathbf{w}_{1}^{(k)}} \right)}} \,-\, \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{1}^{(k)}} \right|}^{2}}{\varphi_{1}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right)}}{{{{\left[ {{\varphi_{1}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2},\mathbf{w}_{1}^{(k)}} \right)} \right]}^{2}}}} {\mathrm{ }} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\~~~~~~~~~~~~~~~~~~= {\chi_{1}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right), \end{array} \end{aligned}} $$

(27)

$$ {\begin{aligned} \frac{{{P_{\mathrm{r}}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{1}}} \right|}^{2}}}}{{{\sigma^{2}}}} &\ge \frac{{2{P_{\mathrm{r}}}R\left\{ {{{\left({\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{1}^{(k)}} \right)}^{*}}\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{1}}} \right\}}}{{{\sigma^{2}}}} \\&\quad- \frac{{{P_{\mathrm{r}}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{1}^{(k)}} \right|}^{2}}}}{{{\sigma^{2}}}} = {\chi_{2}^{k}}\left({{\mathbf{r}_{1}}} \right), \end{aligned}} $$

(28)

$$ {\begin{aligned} \frac{{{P_{\mathrm{r}}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{2}}} \right|}^{2}}}}{{{\varphi_{2}}\left({{\mathbf{r}_{1}}} \right)}} &\ge \frac{{2{P_{\mathrm{r}}}R\left\{ {{{\left({\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right)}^{*}}\mathbf{h}_{{\mathrm{RU1}}}^{H}{\mathbf{r}_{2}}} \right\}}}{{{\varphi_{2}}\left({{\mathbf{r}_{1}}} \right)}}\!\\& \quad-\! \frac{{{P_{\mathrm{r}}}{{\left| {\mathbf{h}_{{\mathrm{RU1}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}}{\varphi_{2}}\left({{\mathbf{r}_{1}}} \right)}}{{{{\left[ {{\varphi_{2}}\left({\mathbf{r}_{1}^{(k)}} \right)} \right]}^{2}}}} \,=\, {\chi_{3}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} \right), \end{aligned}} $$

(29)

$$ {{}\begin{aligned} \frac{{{P_{\mathrm{r}}}{{\left| {\mathbf{h}_{{\mathrm{RU2}}}^{H}{\mathbf{r}_{2}}} \right|}^{2}}}}{{{\varphi_{3}}\left({{\mathbf{r}_{1}}} \right)}} &\ge \frac{{2{P_{\mathrm{r}}}R\left\{ {{{\left({\mathbf{h}_{{\mathrm{RU2}}}^{H}\mathbf{r}_{2}^{(k)}} \right)}^{*}}\mathbf{h}_{{\mathrm{RU2}}}^{H}{\mathbf{r}_{2}}} \right\}}}{{{\varphi_{3}}\left({{\mathbf{r}_{1}}} \right)}}\! -\! \frac{{{P_{\mathrm{r}}}{{\left| {\mathbf{h}_{{\mathrm{RU2}}}^{H}\mathbf{r}_{2}^{(k)}} \right|}^{2}}{\varphi_{3}}\left({{\mathbf{r}_{1}}} \right)}}{{{{\left[ {{\varphi_{3}}\left({\mathbf{r}_{1}^{(k)}} \right)} \right]}^{2}}}} \\&\quad=\! {\chi_{4}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} \right), \end{aligned}} $$

(30)

$$ {{}\begin{aligned} \begin{array}{l} \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{2}}} \right|}^{2}}}}{{{\varphi_{4}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right)}} \!\ge\! \frac{{2{P_{\mathrm{b}}}R\left\{ {{{\left({\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{2}^{(k)}} \right)}^{*}}\mathbf{h}_{{\text{BR}}}^{H}{\mathbf{w}_{2}}} \right\}}}{{{\varphi_{4}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2},\mathbf{w}_{1}^{(k)}} \right)}} - \frac{{{P_{\mathrm{b}}}{{\left| {\mathbf{h}_{{\text{BR}}}^{H}\mathbf{w}_{2}^{(k)}} \right|}^{2}}{\varphi_{4}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right)}}{{{{\left[ {{\varphi_{4}}\left({\left\{ {\mathbf{r}_{i}^{(k)}} \right\}_{i = 1}^{2},\mathbf{w}_{1}^{(k)}} \right)} \right]}^{2}}}}\\ ~~~~~~~~~~~~~~~~~~= {\chi_{5}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right). \end{array} \end{aligned}} $$

(31)

over the trust region (24).

Next, utilizing Eq. (40), all the terms of energy efficiency can be approximated around $\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right)$ respectively by

$$ {{}\begin{aligned} \begin{array}{l} \frac{{\ln \left({1 + {\gamma_{1}^{R}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right)} \right)}}{{{P_{\text{sum}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right)}} \ge {a_{1}^{k}} - {b_{1}^{k}}{\left[ {{\chi_{1}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right)} \right]^{- 1}}\! \\\quad-\! {c_{1}^{k}}{P_{\text{sum}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2}} \right) {\mathrm{ = }}{\Phi_{1}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) \end{array} \end{aligned}} $$

(32)

$$ {\begin{aligned} \begin{array}{ll} \frac{{\ln \left({1{\mathrm{ + }}\gamma_{1}^{{\mathrm{U1}}}\left({{\mathbf{r}_{1}}} \right)} \right)}}{{{P_{\text{sum}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right)}} \ge {a_{2}^{k}} - {b_{2}^{k}}{\left[ {{\chi_{2}^{k}}\left({{\mathbf{r}_{1}}} \right)} \right]^{- 1}} &\\\quad- {c_{2}^{k}}{P_{\text{sum}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2}} \right) {\mathrm{ = }}{\Phi_{2}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) \end{array} \end{aligned}} $$

(33)

$$ {\begin{aligned} \begin{array}{ll} &\frac{{\ln \left({1{\mathrm{ + }}\gamma_{2}^{{\mathrm{U1}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} \right)} \right)}}{{{P_{\text{sum}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right)}} \ge {a_{3}^{k}}\! -\! {b_{3}^{k}}{\left[ {{\chi_{3}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} \right)} \right]^{- 1}}\! \\&-\! {c_{3}^{k}}{P_{\text{sum}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) {\mathrm{ = }}{\Phi_{3}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) \end{array} \end{aligned}} $$

(34)

$$ {\begin{aligned} \begin{array}{ll} &\frac{{\ln \left({1 + \gamma_{2}^{{\mathrm{U2}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} \right)} \right)}}{{{P_{\text{sum}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right)}} \ge {a_{4}^{k}}\! -\! {b_{4}^{k}}{\left[ {{\chi_{4}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2}} \right)} \right]^{- 1}} \\&- {c_{4}^{k}}{P_{\text{sum}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) {\mathrm{ = }}{\Phi_{4}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) \end{array} \end{aligned}} $$

(35)

$$ {{}\begin{aligned} \begin{array}{ll} \frac{{\ln \left({1 + {\gamma_{2}^{R}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right)} \right)}}{{{P_{\text{sum}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right)}} \ge {a_{5}^{k}} \,-\, {b_{5}^{k}}{\left[ {{\chi_{5}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right)} \right]^{- 1}} \\~~~~~~~~~~~~~~~~~~- {c_{5}^{k}}{P_{\text{sum}}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) {\mathrm{ = }}{\Phi_{5}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) \end{array} \end{aligned}} $$

(36)

where ${a_{1}^{k}} = \frac {{2\ln \left ({1 + {\gamma _{1}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\mathbf {w}_{1}^{(k)}} \right)} \right)}}{{{P_{\text {sum}}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right)}} + \frac {{2\ln \left ({1 + {\gamma _{1}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\mathbf {w}_{1}^{(k)}} \right)} \right)}}{{\left [ {{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right) + 1} \right ]\gamma _{1}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\mathbf {w}_{1}^{(k)}} \right)}$, ${b_{1}^{k}} = \frac {{{\gamma _{1}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\mathbf {w}_{1}^{(k)}} \right)}}{{\left [ {1 + {\gamma _{1}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\mathbf {w}_{1}^{(k)}} \right)} \right ]{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}}$, ${c_{1}^{k}} = \frac {{{\gamma _{1}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\mathbf {w}_{1}^{(k)}} \right)}}{{{{\left [ {{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)} \right ]}^{2}}}}$, ${a_{2}^{k}} = \frac {{2\ln \left ({1 + \gamma _{1}^{{\mathrm {U1}}}\left ({\mathbf {r}_{1}^{(k)}} \right)} \right)}}{{{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}} + \frac {{2\ln \left ({1 + \gamma _{1}^{{\mathrm {U1}}}\left ({\mathbf {r}_{1}^{(k)}} \right)} \right)}}{{\left [ {{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right) + 1} \right ]\gamma _{1}^{{\mathrm {U1}}}\left ({\mathbf {r}_{1}^{(k)}} \right)}}$, ${b_{2}^{k}} = \frac {{\gamma _{1}^{{\mathrm {U1}}}\left ({\mathbf {r}_{1}^{(k)}} \right)}}{{\left [ {1 + \gamma _{1}^{{\mathrm {U1}}}\left ({\mathbf {r}_{1}^{(k)}} \right)} \right ]{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}}$, ${c_{2}^{k}} = \frac {{\gamma _{1}^{{\mathrm {U1}}}\left ({\mathbf {r}_{1}^{(k)}} \right)}}{{{{\left [ {{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)} \right ]}^{2}}}}$, ${a_{3}^{k}} = \frac {{2\ln \left ({1 + \gamma _{2}^{{\mathrm {U1}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2}} \right)} \right)}}{{{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}} + \frac {{2\ln \left ({1 + \gamma _{2}^{{\mathrm {U1}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{j = 1}^{2}} \right)} \right)}}{{\left [ {{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right) + 1} \right ]\gamma _{2}^{{\mathrm {U1}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2}} \right)}}$, ${b_{3}^{k}} = \frac {{\gamma _{2}^{{\mathrm {U1}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2}} \right)}}{{\left [ {1 + \gamma _{2}^{{\mathrm {U1}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2}} \right)} \right ]{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}}$, ${c_{3}^{k}} = \frac {{\gamma _{2}^{{\mathrm {U1}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2}} \right)}}{{{{\left [ {{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)} \right ]}^{2}}}}$, ${a_{4}^{k}} = \frac {{2\ln \left ({1 + \gamma _{2}^{{\mathrm {U2}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2}} \right)} \right)}}{{{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}} + \frac {{2\ln \left ({1 + \gamma _{2}^{{\mathrm {U2}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2}} \right)} \right)}}{{\left [ {{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right) + 1} \right ]\gamma _{2}^{{\mathrm {U2}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2}} \right)}}$, ${b_{4}^{k}} = \frac {{\gamma _{2}^{{\mathrm {U2}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2}} \right)}}{{\left [ {1 + \gamma _{2}^{{\mathrm {U2}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2}} \right)} \right ]{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}}$, ${c_{4}^{k}} = \frac {{\gamma _{2}^{{\mathrm {U2}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2}} \right)}}{{{{\left [ {{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)} \right ]}^{2}}}}$, ${a_{5}^{k}}=\frac {{2\ln \left ({1 + {\gamma _{2}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)} \right)}}{{{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}} + \frac {{2\ln \left ({1 + {\gamma _{2}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)} \right)}}{{\left [ {{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right) + 1} \right ]\gamma _{2}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}$, ${b_{5}^{k}} \,=\, \frac {{{\gamma _{2}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}}{{\left [ {1 \,+\, {\gamma _{2}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)} \right ]{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}}$, ${c_{5}^{k}} \,=\, \frac {{{\gamma _{2}^{R}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)}}{{{{\left [ {{P_{\text {sum}}}\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)} \right ]}^{2}}}}$. In summary, the next feasible point $\left ({\left \{ {\mathbf {r}_{i}^{(k + 1)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k + 1)}} \right \}_{j = 1}^{2}} \right)$ of original problem (18) can be generated by solving the following problem at kth iteration

$$ \mathop {\max }\limits_{\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} {f_{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) $$

(37a)

$$ s.t.~~~~{R_{1}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},{\mathbf{w}_{1}}} \right) \ge \bar R $$

(37b)

$$ ~~~~~~~~{R_{2}^{k}}\left({\left\{ {{\mathbf{r}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{w}_{j}}} \right\}_{j = 1}^{2}} \right) \ge \bar R $$

(37c)

$$ ~~~~~~~~\text{(25d)} $$

(37d)

where ${g_{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right) \,=\, \min \left \{ {\Phi _{1}^{k}}\left (\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\right.\right.$$\left.\left.\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2} \right), {\Phi _{2}^{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right) \right \}$$+ \min \left \{ {\Phi _{3}^{k}}\left (\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\right.\right.$$\left.\left.\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2} \right),{\Phi _{4}^{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right), {\Phi _{5}^{k}}\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right) \right \}$ is the inner approximation of $g\left ({\left \{ {{\mathbf {r}_{i}}} \right \}_{i = 1}^{2},\left \{ {{\mathbf {w}_{j}}} \right \}_{j = 1}^{2}} \right) = \frac {{{R_{\text {sum}}}}}{{{P_{\text {sum}}}}}$ around feasible point $\left ({\left \{ {\mathbf {r}_{i}^{(k)}} \right \}_{i = 1}^{2},\left \{ {\mathbf {w}_{j}^{(k)}} \right \}_{j = 1}^{2}} \right)$.

Algorithm 2 can guarantee that the objective (18a) converges to a KKT point by iterating the convex problem (37). In addition, the computational cost of problem (37) at each iteration is O(c²d^2.5+d^3.5) due to its c=2M+2K+1 scalar real values and b=5 quadratic and linear constraints. The convergence and generation of initial feasible point of Algorithm 2 can refer to Algorithm 1 (Appendix).

5 Numerical results and discussions

This section presents the performance study of the proposed scheme, as compared to three alternative schemes.

∙ “HD NOMA-WPT” scheme: different from the proposed scheme, the relay adopts HD mode in this scheme, i.e., the relay first receives the superimposed signal from the BS in the first time slot and then transmit the messages to U1 and U2. Note that here the time block means the BS to two user transmission block.

∙ “FD NOMA-WPT with fixed α=0.5” scheme: the scheme adopts fixed time-switching coefficient α, which indicates that equal time is allocated for the BS to harvest energy and transmit signal respectively instead of optimizing.

∙ “OMA-WPT” scheme: the bandwidth is equally divided between link BS-R-U1 and BS-R-U2.

In the simulations, the system bandwidth is 1M and the pass-loss exponent is set as θ=4. For simplicity, distances between all nodes are assumed to be d_PB=5 m, d_BR=8 m, d_RU1=8 m, and d_RU2=16 m. What is more, the value of d_PR depends on d_BR and d_PR, i.e., ${d_{{\text {PR}}}} = \sqrt {d_{{\text {BR}}}^{2} + d_{{\text {PB}}}^{2}}$. Without loss of generality, assume that the number of transmit antennas at the BS and relay is set as M=K=4. The energy conversion efficiency is assumed to be η=0.8. The noise power is identical to be σ²=−80 dBm. Additionally, the minimum data rate of two NOMA users is set by $\bar R = 1$ Mbits. The constant power consumption is assumed to be P_c=45 dBm. The numerical results are obtained by average over 2000 randomized channel realizations. Without a specific station, the default parameters setting in the simulation are described as above.

The convergence performance of the proposed Algorithm 1 and Algorithm 2 is illustrated in Figs. 3 and 4, respectively. Obviously, the sum data rate and energy efficiency can reach at local optimum within 15 steps. Moreover, with the increase of the size of transmit antenna at the BS, sum data rate and energy efficiency are improved, but the convergence rates of the two proposed algorithms remain unchanged, which indicates the two proposed algorithms are insensitive to problem size.

Fig. 3

Convergence of the proposed Algorithm 1 under different number of transmit antennas at the BS

Fig. 4

Convergence of the proposed Algorithm2 under different number of transmit antennas at the BS

Figure 5 shows the sum data rate of system with the change of the transmit power at the power beacon. As shown in this figure, the sum data rate of all schemes increases with the increase of transmit power at the power beacon. Moreover, the proposed scheme yields the best among all strategies. It is observed that NOMA systems deliver more sum data rate than OMA systems and FD mode brings more sum data rate performance gain.

Fig. 5

The sum data rate of system versus transmit power at the power beacon

Figure 6 depicts the average energy efficiency versus the transmit power at power beacon. Different from sum data rate, performance gain would reach at a fixed value with the increase of transmit power at power beacon. Clearly, when transmit power at power beacon is 35 dBm, all schemes achieve an optimal balance between energy efficiency and energy consumption. In addition, performance gain in NOMA systems is superior to OMA from the perspective of energy efficiency.

Fig. 6

The average energy efficiency versus transmit power at the power beacon

Figure 7 presents the impact of self-interference level on sum data rate of system for M=4 and M=2. As shown, sum data rate of the FD scheme decreases with the increase of self-interference level, which demonstrates the necessity of self-interference cancellation. However, performance gain in FD scheme is still higher than that in HD one in terms of sum data rate.

Fig. 7

Sum data of system versus self-interference level

Figure 8 displays the location of the relay on average energy efficiency. Herein, assume that the BS is collinear with the far NOMA user U2 and the distance between the BS and U2 is fixed, i.e., 24 m. It is observed that the average energy efficiency first increases with the increase in the distance between relay and the BS and then decreases with the increase in the distance between relay and the BS. Apparently, when the relay is located in the middle of the BS and relay, energy efficiency performance can arrive at its maximum.

Fig. 8

Average energy efficiency versus distance between relay and the BS

6 Conclusion

This paper studies spectral and energy efficiency of cooperative NOMA system, where the BS and FD relay are powered by a power beacon. The transmit beamforming at the BS and relay and time allocation ratio are jointly optimized to maximize the sum data rate and energy efficiency. We propose iterative algorithms to solve the non-convex problems and analyzed the convergence of the proposed algorithms to make sure that the objectives of original problem converge to a KKT point. Simulation results have demonstrated the correctness and superiority of the proposed scheme.

7 Appendix

Since $\varphi \left ({x,y} \right) = \frac {{{x^{2}}}}{y}$ is convex, thus it is true that

$$ \frac{{{x^{2}}}}{y} \ge 2\frac{{{{\bar x}^{*}}x}}{{\bar y}} - \frac{{{{\left| {\bar x} \right|}^{2}}}}{{{{\bar y}^{2}}}}y $$

(38)

Following from [38], we have the below inequalities

$$ {{}\begin{aligned} \ln \left({1 + \frac{{{{\left| x \right|}^{2}}}}{y}} \right) \ge \ln \left({1{\mathrm{ + }}\frac{{{{\left| {\bar x} \right|}^{2}}}}{{\bar y}}} \right){\mathrm{ - }}\frac{{{{\left| {\bar x} \right|}^{2}}}}{{\bar y}}{\mathrm{ + }}\frac{{2R\left\{ {{{\bar x}^{*}}x} \right\}}}{{\bar y}} - \frac{{{{\left| {\bar x} \right|}^{2}}\left({{{\left| {\bar x} \right|}^{2}} + y} \right)}}{{\bar y\left({\bar y + {{\left| {\bar x} \right|}^{2}}} \right)}} \end{aligned}} $$

(39)

$$ {{}\begin{aligned} \frac{{\ln \left({1 + \omega} \right)}}{v} \ge \frac{{2\ln \left({1 + \bar \omega} \right)}}{{\bar v}} + \frac{{\bar \omega }}{{\left({\bar \omega + 1} \right)\bar v}} - \frac{{{{\bar \omega }^{2}}}}{{\left({\bar \omega + 1} \right)\bar v}}\frac{1}{\omega} - \frac{{\ln \left({1 + \bar \omega} \right)}}{{{{\bar v}^{2}}}}v \end{aligned}} $$

(40)

for all x∈ℂ, $\bar x \in {\Bbb C}$, y>0, and $\bar y > 0$, and over the trust region 2x^∗x−|x^∗|²>0.