1 Introduction

With the development of wireless communication, spectrum resources have become increasingly scarce, but most of the existing spectrum resources have not been fully utilized. Cognitive radio (CR) technology allows secondary users (SUs) to access the spectrum when the authorized primary user (PU) is idle, thus effectively alleviating the spectrum scarcity problem [1]. In CR, spectrum sensing is a key step that is mainly used to sense the existence of the PU [2].

1.1 Related work

Classical spectrum sensing methods include energy detection, matched filter detection, and cyclic eigenvalue detection [3]. As the simplest spectrum sensing algorithm, energy detection has low computational complexity and does not require prior information from the PU. Therefore, this method has been widely used. However, the algorithm is susceptible to noise uncertainty, which will greatly reduce detection performance [4, 5]. Matching filter detection is the optimal signal detection algorithm when all the information of the PU is known. However, the disadvantages of this method are also very obvious, because it requires prior knowledge of the PU that include the packet format and sequence, and the modulation type [6, 7]. The calculation of cyclic eigenvalue detection is relatively complicated, so it cannot be detected in real time; therefore, rapid detection is not possible [8].

The application of random matrix theory to spectrum sensing has attracted the interest of many researchers [9, 10]. By acquiring the sensing data of multiple SUs and composing the sampling signal matrix, and then calculating the covariance matrix, the corresponding eigenvalue is finally calculated as the decision statistic. Nowadays, many cooperative spectrum sensing algorithms based on random matrices have been proposed. Liu et al. proposed a maximum to minimum eigenvalue (MME) spectrum sensing method. The modified method uses the extracted MME feature value as a statistical feature of the signal and compares with a preset threshold to determine whether the PU exists [11]. However, when the number of sampling points is insufficient, the detection performance is obviously degraded. Liu et al. proposed a spectrum sensing method for the difference between the maximum eigenvalue and the average energy (DMEAE). The method uses the DMEAE feature as a statistical feature of the signal and then compares it with a preset threshold to achieve spectrum sensing [12]. Tulino et al. proposed a spectrum sensing method based on the difference between the maximum eigenvalue and the minimum feature (DMM) [13]. Similar to the above method, the DMM feature is also used as a statistical feature, and spectrum sensing is implemented by comparing with a preset threshold. However, this method has poor perceived performance when the number of cooperative SUs is small and the signal-to-noise ratio (SNR) is low. A statistical feature extraction method based on decomposition and recombination (DAR) is proposed. To logically increase the number of cooperative users, the method firstly splits and reorganizes the signal matrix, thereby effectively improving the spectrum sensing performance [14]. From the above analysis, it can be known that the traditional spectrum sensing based on random matrix needs to derive and calculate the threshold of the decision in advance. The whole process is complex, and there are problems such as inaccurate thresholds.

With the rapid development of information geometry theory, the concept of statistical manifolds is used to transform signal detection problems into geometric problems on manifolds, and then geometric tools can be used to visually analyze detection problems. Liu et al. used information geometry theory to detect radar signals. At the same time, a matrix constant false alarm rata (CFAR) and a distance detector based on geodesic were proposed [15]. Chen applied the information geometry method to spectrum sensing, increased the measurement of manifolds, and obtained the decision threshold through simulation [16]. Lu et al. used the matching method to obtain the closed expression of the decision threshold, which has higher computational complexity [17]. However, in spectrum sensing, the derivation of the threshold is not only complicated, but there is always some deviation in using the fixed decision threshold to determine whether the PU exists.

In recent years, machine learning has developed rapidly, which also provides a new idea for spectrum sensing. Spectrum sensing can be considered as a problem of two classifications that is whether the PU exists [18–20]. Kumar proposed a spectrum sensing method based on K-means clustering algorithm and energy feature. The method takes the energy value of the signal as the feature and then uses K-means clustering algorithm to classify these features [21]. Zhang et al. proposed a spectrum sensing method based on K-means and signal features that combines the feature extraction methods in the random matrix and selects MME, DMM, and DMEAE as the characteristics of training and classification [22]. Thilina et al. used K-means, Gaussian mixture model (GMM) in unsupervised learning, and neural network (NN) and support vector machine (SVM) in supervised learning to study spectrum perception [23]. Xue et al. proposed a cooperative spectrum sensing algorithm based on unsupervised learning. The dominant features and the maximum and minimum eigenvalues are used as features. K-means clustering and GMM are selected as the learning framework [24]. Compared with the traditional spectrum sensing method, spectrum sensing based on machine learning can effectively eliminate the cumbersome threshold calculation and has better adaptability. Similarly, the method does not need to know the priori information of the PU.

1.2 Contributions

Based on the above researches, this paper proposes a cooperative spectrum sensing method based on information geometry and fuzzy c-means (FCM) clustering algorithm (IGFCM). In the feature extraction process, the order-DAR (O-DAR) and interval-DAR (I-DAR) are introduced to obtain two new matrices, then two covariance matrices of two new matrices are calculated separately, and then two covariance matrices are mapped to the manifold using information geometry theory. Then, use the geodesic distance to calculate the distance on the manifold and use it as a feature. Finally, the FCM clustering algorithm is used to implement spectrum sensing. The spectrum sensing method proposed in this paper does not require any prior information about the communication system, and the unmarked training data is more easily obtained. In the experiment, the spectrum sensing performance of IGFCM was further analyzed. The simulation results show that the method effectively improves the spectrum sensing performance.

1.3 Methods or experimental

The main structure and arrangement of this paper are as follows. Section 2 mainly introduces the system model of cooperative spectrum sensing. Section 3 is to improve the spectrum sensing performance in the case of a small number of cooperative users and to analyze the spectrum sensing problem more intuitively. A signal feature extraction method based on split recombination and information geometry is proposed. Section 4 uses FCM clustering algorithm to achieve spectrum sensing. Section 5 uses the amplitude modulation signal to verify the proposed method.

2 Cooperative spectrum sensing system model

According to the perception of PU by a single SU in a cognitive radio network (CRN), the following binary hypothesis [25] about PU can be obtained. H0 indicates that the PU signal does not exist, and H1 indicates that the PU signal exists.

$$\begin{array}{@{}rcl@{}} x(n)=\left\{\begin{array}{l}w(n) \;H_{0}\\ s(n)+w(n) \;H_{1} \end{array}\right. \end{array} $$
(1)

where s(n) represents the signal transmitted by the PU and w(n) is the ambient noise. Since CR is primarily used for relatively fixed networks, the actual channel model is similar to additive white Gaussian noise (AWGN). The systems false alarm probability (Pf) and detection probability (Pd) can be defined as:

$$\begin{array}{@{}rcl@{}} P_{f}=P\lbrack H_{1}\vert H_{0}\rbrack \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} P_{d}=P\lbrack H_{1}\vert H_{1}\rbrack \end{array} $$
(3)

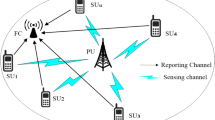
In CRN, spectrum sensing is often done in complex environments. Therefore, the SU needs to consider peripheral multi-path fading, shadow effects, and hidden terminals in the process of sensing the PU [26, 27]. Cooperative spectrum sensing reduces the impact of environmental factors by increasing the diversity of SUs. Therefore, to improve the performance of the spectrum sensing system, the method of multi-SU cooperative spectrum sensing is adopted. First, SUs collect information about the authorized channel and then transmits the information to a fusion center (FC) through the reporting channel; finally, the unified processing by the FC and the final decision is made. Cooperative spectrum sensing system model is shown in Fig. 1.

Fig. 1
figure 1

Cooperative spectrum sensing system model

Full size image

Assuming that there are M SUs in a CRN, the signals collected by the M SUs can form a signal vector matrix xi=[xi(1),xi(2),…,xi(N)], where X=[x1,x2,…,xM]T represents the signal sample value of the ith SU. Therefore, X is a matrix of M×N dimensions.

$$\begin{array}{@{}rcl@{}} {\mathbf{X}} = {\left[ {{x_{1}},{x_{2}},\ldots,{x_{M}}} \right]^{T}} = \left[ {\begin{array}{*{20}{c}} {{x_{1}}(1)}&{{x_{1}}(2)}& \cdots &{{x_{1}}(N)}\\ {{x_{2}}(1)}&{{x_{2}}(2)}& \cdots &{{x_{2}}(N)}\\ \vdots & \vdots & \ddots & \vdots \\ {{x_{M}}(1)}&{{x_{M}}(2)}& \cdots &{{x_{M}}(N)} \end{array}} \right] \end{array} $$
(4)

For ease of reference, the symbols and notations used in this paper are summarized in Table 1.

Table 1 Summary symbols and notations
Full size table

3 Feature extraction based on decomposition and recombination and information geometry

3.1 Feature extraction model

In the feature extraction process, the noise environment needs to be estimated first, and two covariance matrices are obtained by splitting and recombining the noise signal matrix in sequence and interval. The model of feature extraction based on decomposition and recombination and information geometry is shown in Fig. 2. In order to accurately estimate the noise environment, collect enough noise signal matrices and perform O-DAR and I-DAR and covariance transformation (as shown in the box in Fig. 2). Then, use the Riemann mean calculation method to solve the Riemann mean of these covariance matrices. Similarly, the signal matrix with the perception is also subjected to two kinds of split recombination, and the covariance matrix is transformed. Finally, the distance from the covariance matrix obtained from the environment to be perceived to the Riemann mean is calculated. Then, use this distance as a statistical feature of the signal.

Fig. 2
figure 2

Feature extraction model

Full size image

3.2 Information geometry overview

According to the matrix X, the corresponding covariance matrix can be calculated as shown in Eq. 5.

$$\begin{array}{@{}rcl@{}} {\mathbf{R}} = \frac{1}{N}{\mathbf{X}}{{\mathbf{X}}^{T}} \end{array} $$
(5)

From the theory of information geometry, we assume a set of probability density functions p(x|θ), where x is an n-dimensional sample belonging to the random variable Ω, x∈Ω∈Cn. θ is an m-dimensional parameter vector, θ∈Θ⊆Cm. Therefore, the probability distribution space can be described by parameter set Θ. The probability distribution function family S is as shown in Eq. 6.

$$\begin{array}{@{}rcl@{}} S = \left\{{p(x|{\theta})|{\theta} \in \Theta \subseteq {C^{m}}} \right\} \end{array} $$
(6)

Under a certain topological structure, S can form a microscopic manifold, called a statistical manifold, and θ is the coordinate of the manifold. From the perspective of information geometry, the probability density function can be parameterized by the corresponding covariance matrix. Under the two hypotheses H0 and H1 of spectrum sensing, the signal can be mapped to a point that is Rw or Rs+Rw, on the manifold. Rw and Rs+Rw are respectively the covariance calculated from the noise matrix and the signal matrix. In particular, both Rw and Rs+Rw are Toeplitz Hermitian positive definite matrices [17]. Therefore, a symmetric positive definite (SPD) matrix space composed of a covariance matrix can be defined as an SPD manifold.

3.3 Decomposition and recombination

In this section, we first split and reorganize the signal matrix for SU to logically increase the number of cooperative SUs. The DAR is divided into O-DAR and I-DAR. At the same time, the O-DAR and I-DAR are used to process the signal vector perceived by the SU. The specific algorithm is as follows [14]:

In the process of O-DAR, xi will be sequentially split into sub-signal vectors of q(q>0) segment s=N/q long. Then, the result of splitting xi is as follows:

$$ {{} \begin{aligned} {x_{i}}\left\{\begin{array}{l} {x_{i1}} = \left[ {{x_{i}}(1),{x_{i}}(2),\ldots,{x_{i}}(s)} \right]\\ {x_{i2}} \,=\, \left[ {{x_{i}}(s + 1),{x_{i}}(s + 2),\ldots,{x_{i}}(2s)} \right]\\ \vdots \\ {x_{iq}} = \left[ {{x_{i}}((q - 1)s + 1),{x_{i}}((q - 1)s + 2),\ldots,{x_{i}}(qs)} \right] \end{array}\right. \end{aligned}} $$
(7)

The signal vector in Eq. 4 is split according to Eq. 7, and then, the split sub-signal vector is recombined to obtain a qM×s dimensional signal matrix YO−DAR.

$$ {\begin{aligned} {{\mathbf{Y}}_{O - DAR}} = \left[ \begin{array}{l} {x_{11}}\\ \vdots \\ {x_{1q}}\\ \vdots \\ {x_{im}}\\ \vdots \\ {x_{Mq}} \end{array} \right] = \left[ {\begin{array}{cccc} {{x_{1}}(1)}&{{x_{1}}(2)}& \cdots &{{x_{1}}(s)}\\ \vdots &{}&{}&{}\\ {{x_{1}}((q - 1)s + 1)}&{{x_{1}}((q - 1)s + 2)}& \cdots &{{x_{1}}(qs)}\\ \vdots &{}&{}&{}\\ {{x_{i}}((m - 1)s + 1)}&{{x_{i}}((m - 1)s + 2)}& \cdots &{{x_{i}}(ms)}\\ \vdots &{}&{}&{}\\ {{x_{M}}((q - 1)s + 1)}&{{x_{M}}((q - 1)s + 2)}& \cdots &{{x_{M}}(qs)} \end{array}} \right] \end{aligned}} $$
(8)

In the process of I-DAR, select sampling points in the sampled data every q−1 units and then recombine the signal matrix X. The sampled data is separated by q−1 units, the sample points are reselected, and the signal matrix is recombined. According to I-DAR, the sampled data can be split into sub-signal vectors of q(q>0) segment s=N/q long. Then, the result of splitting xi is as follows:

$$\begin{array}{@{}rcl@{}} {x_{i}}\left\{\begin{array}{l} {x_{i1}} = \left[ {{x_{i}}(1),{x_{i}}(q + 1),\ldots,{x_{i}}((s - 1)q + 1)} \right]\\ {x_{i2}} = \left[ {{x_{i}}(2),{x_{i}}(q + 2),\ldots,{x_{i}}((s - 1)q + 2)} \right]\\ \vdots \\ {x_{iq}} = \left[ {{x_{i}}(q),{x_{i}}(q + q),\ldots,{x_{i}}((s - 1)q + q)} \right] \end{array} \right. \end{array} $$
(9)

The signal vector in Eq. 4 is split according to Eq. 9, and then, the split sub-signal vector is recombined to obtain a qM×s dimensional signal matrix YI−DAR.

$$ {\begin{aligned} {{\mathbf{Y}}_{I - DAR}} = \left[ \begin{array}{l} {x_{11}}\\ \vdots \\ {x_{1q}}\\ \vdots \\ {x_{im}}\\ \vdots \\ {x_{Mq}} \end{array} \right] = \left[ {\begin{array}{llll} {{x_{1}}(1)}&{{x_{1}}(q + 1)}& \cdots &{{x_{1}}((s - 1)q + 1)}\\ \vdots &{}&{}&{}\\ {{x_{1}}(q)}&{{x_{1}}(q + q)}& \cdots &{{x_{1}}((s - 1)q + q)}\\ \vdots &{}&{}&{}\\ {{x_{i}}(m)}&{{x_{i}}(q + m)}& \cdots &{{x_{i}}((s - 1)q + m)}\\ \vdots &{}&{}&{}\\ {{x_{M}}(q)}&{{x_{M}}(q + q)}& \cdots &{{x_{M}}((s - 1)q + q)} \end{array}} \right] \end{aligned}} $$
(10)

According to YO−DAR and YI−DAR, the corresponding covariance matrices RO and RI can be calculated.

$$\begin{array}{@{}rcl@{}} {{\mathbf{R}}^{O}} = \frac{1}{s}{{\mathbf{Y}}_{O - DAR}}{{\mathbf{Y}}_{O - DAR}}^{T} \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} {{\mathbf{R}}^{I}} = \frac{1}{s}{{\mathbf{Y}}_{I - DAR}}{{\mathbf{Y}}_{I - DAR}}^{T} \end{array} $$
(12)

3.4 Riemann mean

First, SUs collect P environmental noise matrices. These noise matrices are then processed using O-DAR and I-DAR, and the covariance matrix will be calculated. Thus, we can obtain \({\mathbf {R}}_{k}^{O}(k = 1,2,\ldots,P)\) and \({\mathbf {R}}_{k}^{I}(k = 1,2,\ldots,P)\) matrices. Their Riemann mean objective functions are shown in Eqs. 13 and 14, respectively.

$$\begin{array}{@{}rcl@{}} \Phi \left({\overline {\mathbf{R}}^{O}}\right) = \frac{1}{P}\sum\limits_{k = 1}^{P} {\mathrm{D}} \left({\mathbf{R}}_{k}^{O},{\overline {\mathbf{R}}^{O}}\right)\end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} \Phi \left({\overline {\mathbf{R}}^{I}}\right) = \frac{1}{P}\sum\limits_{k = 1}^{P} {\mathrm{D}} \left({\mathbf{R}}_{k}^{I},{\overline {\mathbf{R}}^{I}}\right)\end{array} $$
(14)

\({\overline {\mathbf {R}}^{O}}\) and \({\overline {\mathbf {R}}^{I}}\) are the matrix when Φ(∙) takes the minimum value, where D(∙,∙) is the geodesic distance of two points on the manifold described below.

$$\begin{array}{@{}rcl@{}} {\overline {\mathbf{R}}^{O}} = {\arg\min}\ \Phi \left({\overline {\mathbf{R}}^{O}}\right) \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} {\overline {\mathbf{R}}^{I}} = {\arg\min}\ \Phi \left({\overline {\mathbf{R}}^{I}}\right) \end{array} $$
(16)

Assume that for the case where there are two points R1 and R2 on the matrix manifold, \(\overline {\mathbf {R}}\) is located at the midpoint of the geodesic line connecting the two points R1 and R2 on the manifold. Its expression is as shown in Eq. 17.

$$\begin{array}{@{}rcl@{}} \overline {\mathbf{R}} = {\mathbf{R}}_{1}^{1/2}{\left({\mathbf{R}}_{1}^{- 1/2}{{\mathbf{R}}_{2}}{\mathbf{R}}_{1}^{- 1/2}\right)^{1/2}}{\mathbf{R}}_{2}^{1/2} \end{array} $$
(17)

If P>2, the Riemann mean will be difficult to calculate. Literatures [28, 29] give a method of iteratively calculating \(\overline {\mathbf {R}}\) using the gradient descent algorithm, and finally obtain the Riemann mean calculation formula as shown in Eq. 18.

$$\begin{array}{@{}rcl@{}} {\overline {\mathbf{R}}_{l + 1}} \!= \overline {\mathbf{R}}_{l}^{1/2}{e^{-\frac{\tau}{P}{\sum}_{k = 1}^{P} {\log \left(\overline {\mathbf{R}}_{l}^{- 1/2}{{\mathbf{R}}_{k}}\overline {\mathbf{R}}_{l}^{- 1/2}\right)}}}\overline {\mathbf{R}}_{l}^{1/2},\;\;\;0 \!\le\! \tau \!\le\! 1 \end{array} $$
(18)

where τ is the step size of iteration and l indicates the number of iteration steps. Therefore, we use the gradient descent algorithm to calculate the Riemann matrix, and get \({\overline {\mathbf {R}}^{O}}\) and \({\overline {\mathbf {R}}^{I}}\).

3.5 Geodesic distance

The study of a geometric structure is mainly to study some properties such as distance, tangent, and curvature on the structure. There are many ways to measure the distance between two probability distributions on a statistical manifold. The most common is the geodesic distance.

Assuming θ is a point on the manifold, the metric on the statistical manifold can be defined by G(θ) of the following equation, called the Fisher information matrix.

$$\begin{array}{@{}rcl@{}} {\text{G}({\theta}) = \text{E}} \left[ {\frac{{\partial \ln p(x|{\theta})}}{{\partial {{\theta}_{i}}}} \cdot \frac{{\partial \ln p(x|{\theta})}}{{\partial {{\theta}_{j}}}}} \right] \end{array} $$
(19)

Due to the nature of the manifold curvature, we determine the distance between the two points by defining the length of the curve connecting the two points on the manifold. Consider an arbitrary curve θ(t)(t1≤t≤t2) between two points θ1 and θ2 on an arbitrary manifold, where θ(t1)=θ1, θ(t2)=θ2. Then, the distance between θ1 and θ2 can be obtained along the curve θ(t) [30].

$$\begin{array}{@{}rcl@{}} {\text{D}({{\theta}_{1}}{{,}}{{\theta}_{2}})} \buildrel \Delta \over = \int_{{t_{1}}}^{{t_{2}}} {\sqrt {{{\left({\frac{{d{\theta}}}{{dt}}} \right)}^{T}}{\mathrm{G}({\theta})}\left({\frac{{d{\theta}}}{{dt}}} \right)dt}} \end{array} $$
(20)

It can be seen that the distance between θ1 and θ2 depends on the selection of the curve θ(t). We call the curve that makes Eq. 20 have the smallest distance as the geodesic, and call the corresponding distance as the geodesic distance.

For any probability distribution, the calculation of geodesic distance is more complicated, which has some adverse effects on its application. For a multivariate Gaussian distribution family with the same mean but different covariance matrices, consider the two members of R1 and R2 in the covariance matrix. The geodesic distance between them is shown in the following Eq. 21 [31].

$$ {\begin{aligned} {\mathrm{D}}({{\mathbf{R}}_{1}},{{\mathbf{R}}_{2}}) &\buildrel \Delta \over = \sqrt {\frac{1}{2}tr{{\log}^{2}}\left({{\mathbf{R}}_{1}^{- 1/2}{{\mathbf{R}}_{2}}{\mathbf{R}}_{1}^{- 1/2}} \right)} \\[-4pt]&= \sqrt {\frac{1}{2}\sum\limits_{i = 1}^{n} {{{\log}^{2}}{\eta_{i}}}} \end{aligned}} $$
(21)

where ηi is the i eigenvalues of the matrix \({\mathbf {R}}_{1}^{- 1/2}{{\mathbf {R}}_{2}}{\mathbf {R}}_{1}^{- 1/2}\).

According to the feature extraction process and the above analysis, the signal matrix to be perceived is split and recombined in sequence and interval, and the covariance matrix is transformed to obtain RO and RI. Then, we use Eq. 21 to solve the corresponding geodesic distance.

$$ {{} \begin{aligned} {d_{1}}={\mathrm{D}}\left({{\mathbf{R}}^{O}}{\mathrm{,}}{\overline {\mathbf{R}}^{O}}\right) &\buildrel \Delta \over = \sqrt {\frac{1}{2}tr{{\log}^{2}}\left({{{\left({{\mathbf{R}}^{O}}\right)}^{- 1/2}}{{\overline {\mathbf{R}}}^{O}}{{\left({{\mathbf{R}}^{O}}\right)}^{- 1/2}}} \right)} \\&= \sqrt {\frac{1}{2}\sum\limits_{i = 1}^{qM} {{{\log}^{2}}{\eta_{i}}}} \end{aligned}} $$
(22)
$$ {\begin{aligned} {d_{2}}&={\mathrm{D}}\left({{\mathbf{R}}^{I}}{\mathrm{,}}{\overline {\mathbf{R}}^{I}}\right) \buildrel \Delta \over = \sqrt {\frac{1}{2}tr{{\log}^{2}}\left({{{\left({{\mathbf{R}}^{I}}\right)}^{- 1/2}}{{\overline {\mathbf{R}}}^{I}}{{\left({{\mathbf{R}}^{I}}\right)}^{- 1/2}}} \right)} \\&= \sqrt {\frac{1}{2}\sum\limits_{i = 1}^{qM} {{{\log}^{2}}{\eta_{i}}}} \end{aligned}} $$
(23)

According to the geodesic d1 and d1, a two-dimensional feature vector D=[d1,d2] is used to represent the signal sensed by the SU. Finally, the feature vector D is used for spectrum sensing.

4 Cooperative spectrum sensing based on FCM clustering algorithm

The FCM clustering algorithm is based on the partitioning method to obtain the clustering result.The basic idea is to divide similar samples into the same class as much as possible. The FCM clustering algorithm is an improvement of the common K-means clustering algorithm. The common K-means clustering algorithm is hard to divide the data, and the FCM clustering algorithm is a flexible fuzzy partitioning [32].Compared with traditional spectrum sensing methods, cooperative spectrum sensing based on FCM clustering algorithm not only eliminates complex threshold derivation but also has adaptability. The overall flow of the IGFCM method described in this paper is shown in Fig. 3.

Fig. 3
figure 3

The overall flow of the IGFCM method

Full size image

The method of IGFCM is divided into two parts. In the first part, the red box indicates the training process. In the second part, the spectrum sensing process is represented in the green box.

4.1 Training process based on FCM

Before training, we need to prepare a training set \(\overline {\mathrm {D}}\):

$$\begin{array}{@{}rcl@{}} \overline {\mathrm{D}} = \left[{{{\mathbf{D}}_{1}},{{\mathbf{D}}_{2}},\ldots,{{\mathbf{D}}_{J}}} \right] \end{array} $$
(24)

Among them, Dj is the feature vector extracted in the third section and J represents the number of training feature vectors. The clustering algorithm divides the unlabeled training feature vectors into C non-overlapping clusters. Let Zc denote the set of training feature vectors belonging to class c, where c=1,2,…,C, then

$$\begin{array}{@{}rcl@{}} {Z_{c}} = \left\{{{{\mathbf{D}}_{j}}|{{\mathbf{D}}_{j}} \in Cluster\;c\;\forall \;j} \right\} \end{array} $$
(25)

The class Zc has a corresponding center Ψc, and each sample Dj belongs to Ψc with a membership degree of ucj and 0<ucj<1. The objective function Γ of the FCM clustering algorithm is shown in Eq. 26, and the constraint condition is shown in Eq. 27.

$$\begin{array}{@{}rcl@{}} \Gamma = {\sum}_{c = 1}^{C} {{\sum}_{j = 1}^{J} {u_{cj}^{m}}} {\left\| {{{\mathbf{D}}_{j}} - {\Psi_{c}}} \right\|^{2}} \end{array} $$
(26)
$$\begin{array}{@{}rcl@{}} {\sum}_{c = 1}^{C} {{u_{cj}} = 1},\;\;\;\;\forall \;j = 1,2,\ldots,J \end{array} $$
(27)

where ∥Dj−Ψc∥2 is an error metric and m is a weighted power exponent of the membership degree ucj, which may also be referred to as a smoothness index or a fuzzy weighted index, and m>1.

Using Lagrange to collate the objective function Γ and constraints, the objective function shown in Eq. 28 is obtained.

$$\begin{array}{@{}rcl@{}} \begin{array}{l} \Gamma \,=\, {\sum}_{c = 1}^{C} {{\sum}_{j = 1}^{J} {u_{cj}^{m}}} {\left\| {{{\mathbf{D}}_{j}} - {\Psi_{c}}} \right\|^{2}} \,+\, {\lambda_{1}}\left({{\sum}_{c = 1}^{C} {{u_{c1}} - 1}} \right) \\ \quad+ \ldots \,+\, {\lambda_{j}}\left({{\sum}_{c = 1}^{C} {{u_{cj}} - 1}} \right) \,+\, \ldots \,+\, {\lambda_{J}}\!\left({{\sum}_{c = 1}^{C} {{u_{cJ}} \,-\, 1}} \right) \end{array} \end{array} $$
(28)

Then, the membership degree ucj and the cluster center Ψc are respectively derived, and the constraint condition is substituted [33, 34], thereby obtaining the calculation formulas of ucj and Ψc, as shown in the Eqs. 29 and 30.

$$\begin{array}{@{}rcl@{}} {u_{cj}} = \frac{1}{{{\sum}_{k = 1}^{C} {{{\left({\frac{{\left\| {{{\mathbf{D}}_{j}} - {\Psi_{c}}} \right\|}}{{\left\| {{{\mathbf{D}}_{j}} - {\Psi_{k}}} \right\|}}} \right)}^{\frac{2}{{m - 1}}}}}}} \end{array} $$
(29)
$$\begin{array}{@{}rcl@{}} {\Psi_{c}} = \frac{{{\sum}_{j = 1}^{J} {\left({{{\mathbf{D}}_{j}}u_{cj}^{m}} \right)}}}{{{\sum}_{j = 1}^{J} {u_{cj}^{m}}}} \end{array} $$
(30)

The training process based on the FCM clustering algorithm is as follows:

Step 1 Input training data set \(\overline {\mathrm {D}}\), number of clusters C, smoothing index m, initialization membership ucj, and fault tolerance factor ε

Step 2 Calculate the class center Ψc by Eq. 30

Step 3 Calculate ν=∥Dj−Ψc∥2, if ν<ε, the algorithm stops; otherwise, continue to step 4

Step 4 Recalculate the membership degree ucj according to Eq. 29, return to step 2

Step 5 Output class center point Ψc

4.2 Spectrum sensing process based on FCM

After the training is successful, we can get a classifier for spectrum sensing, as shown in Eq. 31.

$$\begin{array}{@{}rcl@{}} \frac{{\left\| {\overline{\overline {\mathbf{D}}} - {\Psi_{1}}} \right\|}}{{\mathop {\min}\limits_{c = 2,3,\ldots,C} \left\| {\overline{\overline {\mathbf{D}}} - {\Psi_{c}}} \right\|}} > \xi \end{array} $$
(31)

In Eq. 31, \({\overline {\overline {\mathbf {D}}}}\) denotes an unknown perceptual signal feature vector. If Eq. 31 is satisfied, it indicates that the PU signal exists and the channel is not available; otherwise, the PU signal does not exist and the channel can be used. The parameter ξ is used to control the probability of missed detection and false alarm probability in the sensing process [21].

5 Simulation results and performance analysis

The cooperative spectrum sensing algorithm based on fuzzy c-means clustering algorithm is simulated and analyzed in this section. The simulation PU signal is the amplitude modulation (AM) signal, and the noise is Gaussian white noise. In order to ensure the accuracy of the experiment, according to the feature extraction method described in Section 4, 2000 signal feature vectors were extracted, of which 1000 are training samples and 1000 are used as test samples.

Firstly, we analyze the clustering effect of FCM clustering algorithm under this feature. Set the simulation parameters: cooperative SU M=2, sampling points N=1000, SNR=−11 dB. Figure 4 shows the signal and noise feature training samples obtained by the feature extraction method of split recombination combined with information geometry as the training input of the classifier.

Fig. 4
figure 4

Unclassified feature vectors

Full size image

Figure 5 shows the clustering data after using the fuzzy c-means clustering algorithm. The blue dot in Fig. 5 represents the noise feature vector, and the red dot represents the signal feature vector. Black dots and black triangles represent the center of the noise class and the PU signal class, respectively.

Fig. 5
figure 5

Classified feature vectors

Full size image

Further, we compare and analyze the performance of IGFCM and other methods, which are respectively characterized by energy (ED), and the IQMME, IQDMM, IQDMEAE methods are proposed in literature [22]. Given the simulation parameters, the cooperative SU number M=2, the number of sampling points N=1000, and the simulation diagrams when the SNR=− 13 dB and SNR=− 11 dB respectively are shown in Figs. 6 and 7. Compared with other methods, the IGFCM has better spectrum sensing performance.

Fig. 6
figure 6

ROC curves for different algorithms at SNR=− 13 dB and M=2

Full size image
Fig. 7
figure 7

ROC curves for different algorithms at SNR=− 11 dB and M=2

Full size image

Given the number of sampling points N=1000, the SNR=− 15 dB. The simulation results obtained when the number of SUs is 2, 4, 6, 8, and 10 respectively are as shown in Fig. 8. As can be seen from Fig. 8, the number of cooperative SUs M has a great relationship with the detection probability of the algorithm. As M increases, the detection probabilities of several algorithms increase to varying degrees.

Fig. 8
figure 8

ROC curve at different number of SU with SNR=− 15 dB

Full size image

As the number of sampling points increases, the perceived signal information is more comprehensive, so the extracted features are more representative. In order to observe the spectral sensing performance of the IGFCM method under different sampling points, keep the simulation parameters M=2 and SNR=− 13 dB unchanged. The IGFCM algorithm simulation diagram obtained when the number of sampling points is 1000, 1400, 1800, 2200, or 2600 respectively. As can be seen from Fig. 9, the spectrum sensing performance increases as the number of sampling points increases.

Fig. 9
figure 9

ROC curve at different sampling points with SNR=− 13 dB

Full size image

6 Conclusion

In this paper, a spectrum sensing method based on information geometry and FCM clustering is proposed. In the feature extraction process, a feature extraction method combining split recombination and information geometry is proposed to transform complex signal detection problems into manifolds. Geometric problems on the indirect analysis of signal detection problems using geometric tools. Finally, the FCM clustering algorithm is used to train the extracted features to obtain a classifier for spectrum sensing to realize spectrum sensing. The perceptual performance of the method described in this paper is further analyzed in the experimental part. The experimental results show that the method improves the spectrum sensing performance to some extent. In the future work, we will continue to study the application of clustering algorithms in spectrum sensing, such as kernel fuzzy c-means clustering (KFCM) and the scope of possibilistic fuzzy c-means (PFCM). It is hoped that the spectrum sensing performance can be further effectively improved.