1 Introduction

In recent years, turbo codes have been adopted as the channel coding scheme by some advanced communication standards [1, 2]. To improve the reliability in wireless data transmission, this family of error correction code also steps into some energy resource-constrained wireless applications [3]. In some scenarios, such as wireless sensor networks (WSNs), the sensor nodes only have limited weight of batteries, almost 80% of the overall power dissipation in the nodes is accounted for wireless data communication, and lifetime of the sensor nodes is dominated by the power dissipation of the communication module [4–6]. To reduce the transmission power and to decrease the number of data frame retransmission in the sensor nodes as much as possible, the research of turbo decoder with low power consumption and near optimal bit error rate (BER) is a key topic. However, in the engineering implementation of turbo code decoder, the maximum a posteriori (MAP) decoding algorithm is iteratively performed; the decoder requires large capacity memory and frequent memory accessing, which lead to high power dissipation of the turbo decoder [7]. Therefore, conventional turbo decoder is not suitable for power resource limited WSNs scenarios. Consequently, the energy issue of turbo decoder has become a bottleneck constraint that should be seriously concerned.

To address this deficiency of the conventional turbo decoder, researchers have proposed different decoding architectures. These techniques include stopping the iteration under certain criteria [8], replacing the memory accessing with reverse calculation [9], and recently reducing the memory capacity of state metrics cache (SMC). Among these techniques, the memory-reduced decoding scheme decrease the overall power dissipation by a larger margin. Moreover, since a lower memory capacity is required, this technique is effective for the design of turbo decoder with smaller chip area. According to this strategy, the traceback decoding scheme stores different metrics and sign bits in the SMC; the SMC size is 20% reduced [10]. In [11], the Walsh-Hadamard transform is introduced to represent the forward state metrics with a smaller word width of the SMC memory. Cost of this simplification is the increased dummy decoding complexity. In order to further reduce the SMC capacity and maintain a low dummy decoding complexity, this paper proposes to insert two modules in the turbo decoding architecture: in the compression module, the forward state metrics are iteratively compressed to be the metrics with smaller values. In the decompression module, the compressed metrics are used to estimate the forward state metrics. Furthermore, only simple operations such as addition, shifting, and compare are applied in the compression and decompression modules. Theoretically, there are errors in this proposed technique. But simulation results still show that the introduced errors have little impact on the decoding performance, as compared with the optimal decoding algorithm.

The rest of this paper is organized as follows. Section 2 gives a brief introduction of the MAP decoding algorithm and the derived variants. Section 3 addresses the proposed technique in detail, which include the compression and the decompression modules. In Section 4, the introduced dummy decoding complexity, the SMC capacity, and the BER performance of the proposed technique are discussed with clear analysis. At last, this paper is concluded in Section 5.

2 Turbo decoding algorithm

To simplify the decoding complexity, the MAP algorithm in logarithmic domain (Log-MAP) and its derivatives are widely used [12]. For the single binary convolutional turbo code that was defined in the LTE-Advanced standard [1], by assuming the encoded sequence is transmitted through an additive white Gaussian noise (AWGN) channel, the Log-MAP decoding algorithm is shown by Eq. (1).

$$ \tilde{\gamma }_{k}^{\left(z \right)}\left({{s}_{{{j}_{1}},k-1}},{{s}_{{{j}_{2}},k}} \right)=\frac{{{L}_{c}}}{2}\left(x_{k}^{s}y_{k}^{s}+x_{k}^{p}y_{k}^{p} \right)+\Lambda_{apr,k}^{\left(z \right)}\left({{u}_{k}} \right) $$
(1a)
$$ {{\tilde{\alpha }}_{k}}\left({{s}_{{{j}_{2}},k}} \right)=\underset{{{s}_{{{j}_{1}},k-1}}}{{ma{{x}^{*}}}}\,\left[ {{{\tilde{\alpha }}}_{k-1}}\left({{s}_{{{j}_{1}},k-1}} \right)+\tilde{\gamma }_{k}^{\left(z \right)}\left({{s}_{{{j}_{1}},k-1}},{{s}_{{{j}_{2}},k}} \right) \right] $$
(1b)
$$ {{\tilde{\beta }}_{k}}\left({{s}_{{{j}_{1}},k}} \right)=\underset{{{s}_{{{j}_{2}},k+1}}}{{ma{{x}^{*}}}}\,\left[ {{{\tilde{\beta }}}_{k+1}}\left({{s}_{{{j}_{2}},k+1}} \right)+\tilde{\gamma }_{k+1}^{\left(z \right)}\left({{s}_{{{j}_{1}},k}},{{s}_{{{j}_{2}},k+1}} \right) \right] $$
(1c)
$$ {{} \begin{aligned} & \Lambda_{apo,k}^{\left(z \right)}\left({{u}_{k}} \right)= \\ & \ \ \ \underset{\left({{u}_{k}}=z \right)}{{ma{{x}^{*}}}}\,\left[ {{{\tilde{\alpha }}}_{k-1}}\left({{s}_{{{j}_{1}},k-1}} \right)+\tilde{\gamma }_{k}^{\left(z \right)}\left({{s}_{{{j}_{1}},k-1}},{{s}_{{{j}_{2}},k}} \right)+{{{\tilde{\beta }}}_{k}}\left({{s}_{{{j}_{2}},k}} \right) \right] \\ & -\underset{\left({{u}_{k}}=0 \right)}{{ma{{x}^{*}}}}\,\left[ {{{\tilde{\alpha }}}_{k-1}}\left({{s}_{{{j}_{1}},k-1}} \right)+\tilde{\gamma }_{k}^{\left(z \right)}\left({{s}_{{{j}_{1}},k-1}},{{s}_{{{j}_{2}},k}} \right)+{{{\tilde{\beta }}}_{k}}\left({{s}_{{{j}_{2}},k}} \right) \right] \\ \end{aligned}} $$
(1d)
$$ \begin{aligned} & \Lambda_{ex,k}^{\left(z \right)}\left({{u}_{k}} \right)=\Lambda_{apo,k}^{\left(z \right)}\left({{u}_{k}} \right)-\Lambda_{apr,k}^{\left(z \right)}\left({{u}_{k}} \right)-\Lambda_{in,k}^{\left(z \right)}\left({{u}_{k}} \right) \\ & \left\{ \begin{array}{ll} & \Lambda_{in,k}^{\left(0 \right)}\left({{u}_{k}} \right)=0 \\ & \Lambda_{in,k}^{\left(1 \right)}\left({{u}_{k}} \right)={{L}_{c}}y_{k}^{s} \\ \end{array} \right. \\ \end{aligned} $$
(1e)

In Eq. (1), z belongs to {0, 1}, L c =2/σ2 (σ2 is the noise variance of the AWGN channel), k is the decoding time slot, \(x_{k}^{s}\) and \(\ x_{k}^{p}\) are the transmitted codewords, \(y_{k}^{s}\) and \(\ y_{k}^{p}\) are the received codewords, where s and p denote the systematic and parity bits. j∈{0,⋯,7} is the index of the state metrics, sj,k is the jth state at the decoding time slot k, \(\tilde {\gamma }_{k}^{\left (z \right)}\) is the branch metric, \({{\tilde {\alpha }}_{k}}\) is the forward state metric, and \({{\tilde {\beta }}_{k}}\) is the backward state metric. For u k =z, \(\Lambda _{apr,k}^{\left (z \right)}\left ({{u}_{k}} \right)\), \(\Lambda _{apo,k}^{\left (z \right)}\left ({{u}_{k}} \right)\) and \(\Lambda _{ex,k}^{\left (z \right)}\left ({{u}_{k}} \right)\) are the a priori log-likelihood ratio (LLR), the a posteriori LLR and the extrinsic information, respectively.

Note that the max∗ operator in Eq. (1) is defined and simplified as follows [13]:

$$ {{} \begin{aligned} & max*\left({{x}_{1}},{{x}_{2}} \right)=\ln \left(\exp \left({{x}_{1}} \right)+\exp \left({{x}_{2}} \right) \right) \\ & \approx \min \left\{ {{x}_{1}},{{x}_{2}} \right\}+\max \left\{ {{x}_{1}}-{{x}_{2}},0.75\left({{x}_{1}}-{{x}_{2}} \right)+0.625 \right\} \\ \end{aligned}} $$
(2)

For a max∗ operator with more than two operands, Eq. (2) can be recursively applied. However, this recursion processing is not necessary in practical. By using Eq. (3), the decoding complexity can be significantly reduced, which is shown as follows [13].

$$ {{} \begin{aligned} & {{\max }^{*}}\left({{x}_{1}},{{x}_{2}},\cdots,{{x}_{n}} \right)\approx {{\max }^{*}}\left({{y}_{1}},{{y}_{2}} \right) \\ & \approx \min \left\{ {{y}_{1}},{{y}_{2}} \right\}+\max \left\{ {{y}_{1}}-{{y}_{2}},0.75\left({{y}_{1}}-{{y}_{2}} \right)+0.625 \right\} \\ \end{aligned}} $$
(3)

where y1 and y2 are the maximum two variables among {x1,x2,⋯,x n }. In this research, Eq. (3) is adopted by Eq. (1) to calculate the forward state metrics \({{\tilde {\alpha }}_{k}}\), the backward state metrics \({{\tilde {\beta }}_{k}}\), and the a posteriori LLR \(\Lambda _{apo,k}^{\left (z \right)}\left ({{u}_{k}} \right)\).

3 Method of proposed compression/decompression technique

3.1 Compression of the state metrics

In the hardware implementation of turbo decoder, the state metrics are stored in the last in and first out (LIFO) SMC. Existing researches have shown that the (10,3) quantization scheme is suitable for getting satisfactory BER performance (10 is the total bits, 3 is the fractional bits) [9, 10]. To reduce the SMC capacity, we propose to compress the state metrics and to employ a (5,3) quantization scheme in this research.

Seen from Eq. (1b), for each decoding time slot k, there are eight forward state metrics \({{\tilde {\alpha }}_{k}}\left ({{s}_{{{j}_{2}},k}} \right),{{j}_{2}}\in \left \{ 0,\cdots,7 \right \}\). To facilitate the compression of these metrics, Eq. (4) is used for normalization. Since the decoding algorithm is performed in the logarithmic domain, when the same value is subtracted from the eight forward state metrics at time slot k, value of the a posteriori LLR \(\Lambda _{apo,k+1}^{\left (z \right)}\left ({{u}_{k+1}} \right)\) is not affected by replacing \(\phantom {\dot {i}\!}{{\tilde {\alpha }}_{k}}\left ({{s}_{{{j}_{2}},k}} \right)\) with \({{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right)\phantom {\dot {i}\!}\).

$$ {{{\alpha }'}_{k}}\left({{s}_{{{j}_{2}},k}} \right)={{\tilde{\alpha }}_{k}}\left({{s}_{{{j}_{2}},k}} \right)-{{\tilde{\alpha }}_{k}}\left({{s}_{0,k}} \right) $$
(4)

Subsequently, \({{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right),{{j}_{2}}\in \left \{ 1,\cdots,7 \right \}\phantom {\dot {i}\!}\) are recursively compressed by using Eq. (5) and noted that the value of α′ k (s0,k) is zero as implied by Eq. (4).

$$ {{{{\alpha }'}}_{k}}\left({{s}_{{{j}_{2}},k}} \right)=\frac{{{{{\alpha }'}}_{k}}\left({{s}_{{{j}_{2}},k}} \right)-{{{{\alpha }'}}_{k}}\left({{s}_{{{j}_{2}}-1,k}} \right)}{4} $$
(5)

In Eq. (5), 1/4 is the compression coefficient, and this division operation can be realized by using one 2-bits right shifting in hardware implementation. Considering that the values of \({{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right),{{j}_{2}}\in \left \{ 1,\cdots,7 \right \}\phantom {\dot {i}\!}\) may be positive or negative, when the (5,3) quantization scheme is adopted, the most significant bit represents the sign bit, while the rest bits represent the absolute value of the compressed forward state metrics. However, when \(\phantom {\dot {i}\!}\left | {{{{\alpha }'}}_{k}}\left ({{s}_{{{j}_{2}},k}} \right) \right |\) is larger than 1.875, the (5,3) scheme is not sufficient to quantize the compressed metrics. Therefore, a compare unit is employed to decide whether the next round of iterative compression should be performed: (i) if \(\max \left (\left | {{{{\alpha }'}}_{k}}\left ({{s}_{{{j}_{2}},k}} \right) \right | \right)>1.875\phantom {\dot {i}\!}\), \(\phantom {\dot {i}\!}{{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right)\) are feedback to the compression module, where Eq. (4) is applied for the next round of compression; (ii) if \(\phantom {\dot {i}\!}\max \left (\left | {{{{\alpha }'}}_{k}}\left ({{s}_{{{j}_{2}},k}} \right) \right | \right)\le 1.875, {{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right)\) are output and then are stored in the LIFO SMC. Since \(\phantom {\dot {i}\!}{{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right)\) are 10 bits quantized, and 7 bits are assigned for the integer part, at most 4 times of iterative compression is enough to guarantee \(\max \left (\left | {{{{\alpha }'}}_{k}}\left ({{s}_{{{j}_{2}},k}} \right) \right | \right)\) is no more than 1.875. So, the number of iterative compression times I k is an important parameter for the decompression, where 00, 01, 10, and 11 in binary denote the number of iterative compression times of 1, 2, 3, and 4 in decimal, respectively. As a result, when the compression procedure is finished, the number of iterative compression times and the compressed state metrics will be stored in the SMC. Furthermore, since α′ k (s0,k) equals to zero for each decoding time slot k, it is not necessary to store this metric in the SMC. For clear illustration, the word structure of the SMC is shown by Fig. 1 as below.

Fig. 1
figure 1

Word structure of the state metrics cache

Full size image

3.2 Decompression of the state metrics

In the backward direction, I k and \(\phantom {\dot {i}\!}{{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right)\) are read out from the LIFO SMC to estimate their original values, which is performed in the decompression module. Noted that α′ k (s0,k)=0, we propose to decompress \({{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right),\ {{j}_{2}}\in \left \{7,\cdots,1\right \}\phantom {\dot {i}\!}\) by using Eq. (6).

$$ {{{{\alpha }'}}_{k}}\left({{s}_{{{j}_{2}},k}} \right)=4{{{{\alpha }'}}_{k}}\left({{s}_{{{j}_{2}},k}} \right)+{{{{\alpha }'}}_{k}}\left({{s}_{{{j}_{2}}-1,k}} \right),{{j}_{2}}\in \left\{7,\cdots,1 \right\} $$
(6)

Equation (6) is the inverse calculation of Eq. (5), and I k is used to decide how many times Eq. (6) should be recursively performed. For example, if I k =10 in binary, Eq. (6) is 3 times recursively performed, and then the decompressed state metrics are output to the a posteriori LLR calculation module. It should be noted that, \(\phantom {\dot {i}\!}{{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right)\) in Eq. (4) are 10 bits quantized, when they are compressed by using Eq. (5), they will be 5 bits stored in the SMC. Considering the finite word length effect, when these metrics are used for decompression, errors will be introduced during the decompression procedure, which have negative effect on the decoding performance. As it can be seen from the simulation results in Fig. 6, the BER is slightly lost as compared with the Log-MAP algorithm.

3.3 State metrics compression based decoding architecture

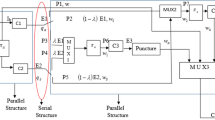
Based on the above described compression and decompression processes, two modules are inserted into the conventional decoding architecture. Assuming N denotes the decoding window length, the proposed decoding architecture is presented in Fig. 2, while Fig. 3 is the corresponded timing chart.

Fig. 2
figure 2

State metrics compressed turbo decoding architecture

Full size image
Fig. 3
figure 3

Timing chart of the proposed decoding architecture

Full size image

As shown in Fig. 2, in the forward direction, \(\tilde {\gamma }_{k}^{(z)}\) are calculated in the branch metrics unit (BMU), and then are input to the forward recursion module, where \({{\tilde {\alpha }}_{k}}\left ({{s}_{{{j}_{2}},k}} \right)\) are recursively calculated. Instead of been stored in the LIFO SMC, \({{\tilde {\alpha }}_{k}}\left ({{s}_{{{j}_{2}},k}} \right)\) are input to the compression module. In this module, the output control unit (OCU) is applied to enable the compression, and the compare unit (CU) provides the trigger signal. At first, the buffer is initialized as \({{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right)\phantom {\dot {i}\!}\), one adder and one 2-bits right shifting unit (RSU) are used to perform the compression. The compressed metrics are feedback to the adder, the buffer and the compare unit (CU). If \(\phantom {\dot {i}\!}\max \left (\left | {{{{\alpha }'}}_{k}}\left ({{s}_{{{j}_{2}},k}} \right) \right | \right)>1.875\) is true, the OCU is triggered to enable the next round of compression, while the addition counter unit (ACU) increases I k by 1 in decimal. Otherwise, the compression procedure is completed. Subsequently, the metrics in the buffer and the counting result in the ACU will be stored in the LIFO SMC. For the decompression module in the backward direction, I k is input to the subtraction counter unit (SCU), by which the OCU is triggered to enable the decompression. Note that a delay unit (DU) is applied to adjust the time slot, and one 2-bits left shifting unit (LSU) is used to realize the multiply operation.

4 Results and discussion

As presented in Fig. 2, two modules are embedded in the conventional turbo decoder architecture. To demonstrate the effectiveness of this technique, a set of MATLAB scripts is developed for verification, as the improved decoding algorithm detailed in Section 2 is used to construct the state metrics compressed decoding architecture. Build on this software platform, the introduced dummy decoding complexity, the SMC capacity, and the BER performance are discussed in this section.

4.1 Dummy decoding complexity

For the compression module, Eq. (4) shows seven addition operations are performed before the compression. When the OCU is enabled, one adder and one 2-bits RSU are employed to calculate \({{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right),\ {{j}_{2}}\in \left \{ 1,\cdots,7 \right \}\phantom {\dot {i}\!}\) recursively. Subsequently, seven compare operations are performed in the CU to decide whether the next round of compression should be enabled, and the ACU should increase I k by 1 or not. Similarly, in the decompression module, the SCU decides how many times the decompression procedure should be performed. By Eq. (6) and Fig. 2, the I k in OCU is used to enable the decompression module, in which one DU, one 2-bits LSU and one addition operation are performed to estimate the state metrics for each round of decompression. Therefore, I k is the key parameter to analyze the dummy decoding complexity of the proposed technique.

In Section 3, the described compression procedure shows I k is a variable that depend on if \(\max \left (\left | {{{{\alpha }'}}_{k}}\left ({{s}_{{{j}_{2}},k}} \right) \right | \right)>1.875\phantom {\dot {i}\!}\) is true, which means the difference between \({{{\alpha }'}_{k}}\left ({{s}_{{{j}_{2}},k}} \right),\ {{j}_{2}}\in \left \{ 1,\cdots,7 \right \}\phantom {\dot {i}\!}\) is the most important factor. As a result, I k may take different values with the same signal to noise ratio (SNR) but with different iteration number, or with the same iteration number but with different SNR. To this purpose, we define \(\phantom {\dot {i}\!}{{D}_{{{I}_{k}}}}\) as the total amount for I k equals to 1, 2, 3, and 4 in decimal, respectively. Consequently, the percentage \(\phantom {\dot {i}\!}{{E}_{{{I}_{k}}}}\) for \(\phantom {\dot {i}\!}{{D}_{{{I}_{k}}}}\) are calculated as:

$$ {{E}_{{{I}_{k}}}}=\frac{{{D}_{{{I}_{k}}}}}{\sum\limits_{{{I}_{k}}=1}^{4}{{{D}_{{{I}_{k}}}}}}\times 100 $$
(7)

Assuming the frame length is 1440, the statistical distribution of \({{E}_{{{I}_{k}}}}\phantom {\dot {i}\!}\) with the same SNR but with different iteration number is presented in Fig. 4. Although SNR = 0.9 dB is a special case, the results illustrated in Fig. 4 still represent a generic tendency: as the iteration goes on, more rounds of compression/decompression will be performed.

Fig. 4
figure 4

Statistical distribution of \(\protect {{E}_{{{I}_{k}}}}\) with SNR = 0.9 dB for different iteration number

Full size image

Similarly, the statistical distribution of \(\phantom {\dot {i}\!}{{E}_{{{I}_{k}}}}\) with 8 iterations but with different SNR is presented in Fig. 5. As SNR increases, the difference among the forward state metrics \(\phantom {\dot {i}\!}{{\tilde {\alpha }}_{k}}\left ({{s}_{{{j}_{2}},k}} \right), {{j}_{2}}\in \left \{0,\cdots,7 \right \}\) becomes larger, i.e., the probability for I k to represent a larger value will increase accordingly.

Fig. 5
figure 5

Statistical distribution of \(\protect \phantom {\dot {i}\!}{{E}_{{{I}_{k}}}}\) with eight iterations for different SNR

Full size image
Fig. 6
figure 6

BER performance comparison

Full size image

4.2 SMC capacity

At the cost of dummy decoding complexity that performed in the compression and decompression modules, the compressed state metrics can be 5 bits quantized. As presented in Fig. 1, one I k (2-bits represented) and seven compressed metrics should be stored in the SMC for each time slot (1×2+7×5=37 bits). Compared with the conventional decoding architecture, where the quantization scheme is (10,3) and eight state metrics should be stored in the SMC (8×10=80 bits), the proposed technique have reduced the SMC capacity by 53.75%. To summarize, the SMC organization and capacity comparison are illustrated in Table 1.

Table 1 Comparison of SMC organization and capacity
Full size table

4.3 BER simulation

To investigate the decoding performance of the proposed technique, the simulation environment is set as follows: for the LTE-Advanced standard defined turbo code [1], two kinds of frame length are used for demonstration (800 and 1440 bits, respectively), the code rate is 1/3, and the encoded sequences are transmitted through an AWGN channel. Three decoding algorithms, i.e., the optimal Log-MAP algorithm, the state metrics compressed decoding technique (the near optimal decoding algorithm detailed in Section 2 is implemented), and the maximum Log-MAP (Max-Log-MAP) algorithm, are used for comparison. For each frame, the employed decoding algorithm is 8 times performed iteratively. Moreover, the quantization schemes in Table 2 are adopted [9–11], and δ is the scaling factor [14].

Table 2 Quantization schemes adopted in the simulation
Full size table

Seen from Fig. 6, the Log-MAP algorithm gets the best BER performance, about 0.2 dB superior to the Max-Log-MAP algorithm, but only slightly outperforms that of the state metrics compressed decoding technique. Thanks for the simplified max∗ operator in Section 2, although the inserted compression and decompression modules have introduced some errors, the resulted BER loss is limited, about 0.05 dB at BER of 10−2 and then becomes smaller as SNR increase.

5 Conclusions

In the energy resource-limited applications where turbo code is adopted for data transmission, memory-reduced turbo decoder is an effective solution to reduce the overall power dissipation. In this paper, a state metrics compressed turbo decoding technique is proposed. It has been shown that, by inserting one compression and one decompression modules in the conventional decoding architecture, a quantization scheme with smaller SMC word length can be applied, and the SMC capacity is reduced by 53.75%. Dummy decoding complexity in the compression and decompression modules is analyzed in detail. In most cases of different iteration number but with the same SNR, and of different SNR with the same iteration number, one or two rounds of compression/decompression are implemented. For the LTE-Advanced standard defined turbo code, the proposed decoding technique clearly outperforms the Max-Log-MAP algorithm in BER performance, and only slightly degraded as compared with the optimal Log-MAP algorithm.