1 Introduction

Multi-domain signal processing can improve the array performance by exploiting space, time, polarization, frequency resources [1–3]. Nevertheless, the range domain information has not been sufficiently explored in literature. Although existing interference suppression approaches can be employed to exploit the angle as well as polarization domain information for polarization sensitive array (PSA), the joint information between range domain and other domains are rarely explored [4].

Recently, a new kind of array named frequency diverse array (FDA), which applies a small frequency increment between contiguous two elements, has gained substantial interest [5–8]. This small frequency increment, as compared to the carrier frequency, results in a angle-range-polarization-dependent beampattern [9–12] that is different from conventional phased-array providing only angle-dependent beampattern and frequency scanning array whose beam pointing angle changes with working frequency. These characteristics make the FDA attractive for a wide range of applications in target imaging [13], localization [14], and bistatic radar [15–18]. Instead of using a fixed frequency offset, W. Khan et al. presented a variational frequency offset scheme to achieve time-independent but angle-range-dependent beampattern [19, 20]. In [21], the authors derived the FDA Cramér-Rao lower bounds for estimating target direction, range and velocity. The work about the joint applications of FDA and multi-input and multi-output (MIMO) radar can be found in [16], where the FDA elements radiate coherent waveforms, rather than orthogonal waveforms like an MIMO radar. Additionally, an analytical investigation of FDA multipath characteristics was carried out in [22]. The authors of [23] extended the linear FDA to planar array.

In this paper, to further enhance the interference mitigation capability, we propose a PSFDA by combining the PSA and the FDA. A angle-range and polarization-dependent beamforming algorithm is also proposed by jointly using the norm-function constraint theory [24] and convex optimization [25]. The proposed method can effectively suppress both clutter and interference that is not accessible for the conventional phased-array systems. The new contributions of this work is different from our previous work [26] in at least two aspects: One is that, a more general signal model is presented for the PSFDA: the PSFDA considered in [26] is just arranged with uniformly spaced orthogonal dipole, while the PSFDA considered in this work is constituted by distributed collocated electromagnetic vector sensor (EMVS), and the antenna elements in each EMVS with 2≤P≤6 dipole elements, which contains the special case in [26]. Therefore, the signal model of the PSFDA in this work is more general when compared to the one in [26]; The second is that the output SINR performance of the high-dimensional PSFDAs are analyzed and simulated in a much more extensive way.

Note that, [·]T and [·]H denote the transpose and conjugate transpose operators, respectively. ∥·∥1, ∥·∥2, and ∥·∥∞ indicate the ℓ1-norm, ℓ2-norm, and ℓ∞-norm of a vector or matrix.

The remainder of this paper is organized as follows. Section 2 introduces the PSFDA, along with its measurement model. Section 3 proposes the angle-range and polarization dependent beamforming algorithm. Next, numerical simulation results and discussions are given in Section 4. Finally, conclusions are drawn in Section 5.

2 PSFDA and its signal model

2.1 Frequency diverse array

Consider a uniform M-element linear FDA with the element spacing d. The radiated frequency of the m-th element is given by [5]

$$ f_{m}=f_{0}+\Delta f_{m},~ m=1,2,\ldots,M, $$
(1)

where the frequency offset between the m-th element and the reference element is Δfm=(m−1)·Δf, f0, and Δf represent the carrier frequency and the frequency increment, respectively. Taking the first element as the reference for the array, then the phase difference between the m-th element and the reference element can be expressed as

$$ {\begin{aligned} \Delta \psi_{m-1}&=\psi_{m}-\psi_{1} \\ &\approx -\frac{2 \pi f_{0} (m-1) d {\sin}\theta}{c}+\frac{2 \pi r (m-1)\Delta f }{c} \\ &\quad-\frac{2 \pi (m-1)^{2} \Delta f d {\sin}\theta}{c} \end{aligned}} $$
(2)

where the approximation rm≈r−(m−1)d sinθ, where θ, r, and c are the direction and range of the given far-field point and the speed of light, respectively. The steering vector of a standard FDA can be expressed as (3), if the third term of (2) is ignored due to the fact that f0≫Δf and r≫dsinθ, we can obtain the steering vector of FDA as

$$ {} {\begin{aligned} &\mathbf{a}_{fda}{(\theta,r)}=\\ &\quad\left[\!1 \quad e^{-j\left(\frac{2 \pi f_{0} d {\sin}\theta}{c}\,-\,\frac{2 \pi r \Delta f }{c} \right)} \!\cdots\! e^{-j\left(\frac{2 \pi f_{0}(M-1)d {\sin}\theta}{c}-\frac{2 \pi r (M-1)\Delta f }{c} \right)}\! \right]^{T}. \end{aligned}} $$
(3)

It is seen that the FDA generates a range-dependent beampattern that is different from a phased-array. Therefore, FDA provides a more flexible beam scan option in either transmission or receive mode. The FDA beam direction will vary as a function of range r and angle θ, even for a fixed Δf. Specifically, the FDA is just a conventional phased-array when Δf=0Hz. If the range r is fixed, the beam direction will vary as a function of Δf. Therefore, the angle-range-dependent beampattern of FDA provides a potential to focus transmit energy in the desired range-angle section. More importantly, additional degrees of freedom can be provided if polarized sensors are adopted.

2.2 Polarization sensitive array

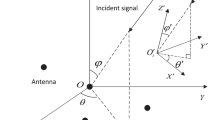
Considering a right-hand spherical coordinate system with the orthogonal basis defined by orthogonal components v1 and v2 (see Figs. 1 and 2), the measurement model of the vector sensor is given by [27]

$$ \left[ \begin{array}{c} \mathbf{y}_{E}(t) \\ \mathbf{y}_{H}(t) \end{array} \right]= \left[ \begin{array}{c} \mathbf{I}_{3} \\ (\mathbf{u} \times) \end{array} \right] \mathbf{V} \mathbf{Q} \mathbf{h} \mathbf{s}(t) + \left[ \begin{array}{c} \mathbf{e}_{E}(t) \\ \mathbf{e}_{H}(t) \end{array} \right], $$
(4)
Fig. 1
figure 1

Orthogonal vector triad (u,v1,v2)

Full size image
Fig. 2
figure 2

Electric polarization ellipse

Full size image

where I3 is the third order identity matrix, \((\mathbf {u}\times)=\left [ \begin {array}{ccc} \ \ 0 \ \ \ \ -u_{z} \ \ \ \ u_{y} \\ \ \ u_{z} \ \ \ \ \ 0 \ \ \ -u_{x} \\ -u_{y} \ \ \ \ u_{x} \ \ \ \ 0 \end {array} \right ]\), with ux,uy,uz being the x,y,z components of the unit direction for the propagation vector u=[cosθcosϕ,sinθcosϕ,sinϕ]T. The real-valued matrices \(\mathbf {V}\in \mathcal {R}^{{3\times 2}}\), \(\mathbf {Q}\in \mathcal {R}^{{2\times 2}}\) and complex vector \(\mathbf {h} \in {\mathcal {C}^{2\times 1}}\) are given, respectively, by

$$ \mathbf{V}=\left[ \begin{array}{c} \mathbf{V}^{(E)}_{x} \\ \mathbf{V}^{(E)}_{y} \\ \mathbf{V}^{(E)}_{z} \end{array} \right]=\left[ \begin{array}{cc} -\text{sin}\theta \ \ -\text{cos}\theta \text{sin}\phi \\ \text{cos}\theta \ \ -\text{sin}\theta \text{sin}\phi \\ 0 \ \ \text{cos}\phi \end{array} \right], $$
(5)
$$ \mathbf{Q}=\left[ \begin{array}{cc} \text{cos}\alpha \ \ \text{sin}\alpha \\ -\text{sin}\alpha \ \ \text{cos}\alpha \end{array} \right], \mathbf{h}=\left[ \begin{array}{c} \text{cos}\beta \\ j \text{sin}\beta \end{array} \right], $$
(6)

where θ∈[0,2π),ϕ∈[−π/2,π/2],α∈(−π/2,π/2] and β∈[−π/4,π/4] are the azimuth, elevation, polarized ellipse’s orientation and eccentricity angles, respectively. s(t) denotes the complex envelope of the transmitted signal. eE(t) and eH(t) are the noise components of electric and magnetic fields. \(\mathbf {V}^{(E)}_{x}\), \(\mathbf {V}^{(E)}_{y}\), and \(\mathbf {V}^{(E)}_{z}\) denote the response of the three electric dipoles along the x-, y-, and z-axis, respectively. Similarly, the definitions for the three magnetic dipoles along the x-, y-, and z-axis are given by

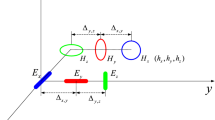
$$ \left[ \begin{array}{c} \mathbf{V}^{(M)}_{x} \\ \mathbf{V}^{(M)}_{y} \\ \mathbf{V}^{(M)}_{z} \end{array} \right]\,=\,\left[ \mathbf{u} \times \right] \left[ \begin{array}{c} \mathbf{V}^{(E)}_{x} \\ \mathbf{V}^{(E)}_{y} \\ \mathbf{V}^{(E)}_{z} \end{array} \right]=\left[ \begin{array}{cc} -\text{cos}\theta \text{sin}\phi \ \ \text{sin}\theta \\ -\text{sin}\theta \text{sin}\phi \ \ \ -\text{cos}\theta \\ \text{cos}\phi \ \ \ 0 \end{array} \right]. $$
(7)

Consider a general model of (4), the measurement formulation of a distributed electromagnetic vector sensor (DEMVS), which is also named as distributed electromagnetic component sensor array (see Fig. 3), can be expressed as [28]

$$ \underbrace{\left[ \begin{array}{c} \mathbf{y}_{E}(t)\\ \mathbf{y}_{H}(t) \end{array} \right]}_{\mathbf{y}(t)}=\sum_{k=1}^{K}{\mathbf{a}(\mathbf{\Lambda}_{k}) \mathbf{s}_{k}(t)}+\underbrace{\left[ \begin{array}{c} \mathbf{e}_{E}(t) \\ \mathbf{e}_{H}(t) \end{array} \right]}_{\mathbf{n}(t)}, $$
(8)
Fig. 3
figure 3

Distributed electromagnetic vector sensor, where Ex(Hx), Ey(Hy), and Ez(Hz) are the electric (magnetic) component sensors, respectively

Full size image
$$ \mathbf{a}(\mathbf{\Lambda}_{k})=\mathbf{\Gamma}(\theta_{k}, \phi_{k}) \mathbf{\Omega} \left[ \begin{array}{c} \mathbf{I}_{3} \\ (\mathbf{u}_{k} \times) \end{array} \right]\mathbf{V}_{k} \mathbf{Q}_{k}\mathbf{h}_{k}, $$
(9)

where Λk=[θk,ϕk,αk,βk] denotes the direction and polarization parameters of the k-th source signal. Γ(θk,ϕk) is a diagonal matrix with the n-th diagonal entry being \(\left [\mathbf {\Gamma }(\theta _{k}, \phi _{k}) \right ]_{n}=e^{j2\pi \mathbf {q}^{T}_{n}\mathbf {u}_{k}/\lambda } \ \ (n=1,2,\ldots,N,~(N\leq 6)\), where λ being the wavelength and N is the number of array elements constituting the DEMVS), which provides the phase shift between the DEMVS center and the position qn of the n-th element of the DEMVS, Ω is an N×6 selection matrix with elements of “1” and “0,” indicating the component of the electromagnetic field measured by the n-th sensor.

Extending (7) to an array with M-DEMVS, we can define the array directional response as b(θk,ϕk)⊗d(θk,ϕk), where \({\mathbf {d}(\theta _{k}, \phi _{k})}=\mathbf {\Gamma }(\theta _{k}, \phi _{k}) \mathbf {\Omega } \left [ \begin {array}{c} \mathbf {I}_{3} \\ (\mathbf {u}_{k} \times) \end {array} \right ]\mathbf {V}_{k}\) embeds all the directional information of the electromagnetic sources, \(\mathbf {b}(\theta _{k}, \phi _{k})=\left [ e^{j2 \pi \mathbf {p}^{T}_{1} \mathbf {u}_{k} / \lambda }, e^{j2 \pi \mathbf {p}^{T}_{2} \mathbf {u}_{k} / \lambda }, \ldots, e^{j2 \pi \mathbf {p}^{T}_{M} \mathbf {u}_{k}/ \lambda } \right ]^{T}\) represents the phase of the planewave at the position pi of the i-th DEMVS center (i=1,…,M), and the ⊗ is the Kronecker Product. Then, the measurements can be expressed as

$$ \mathbf{y}(t)=\sum_{k=1}^{K}\left[{\mathbf{b}(\theta_{k}, \phi_{k})} {\otimes} {\mathbf{d}(\theta_{k}, \phi_{k})}\right]{\mathbf{Q}_{k}}{\mathbf{h}_{k}}\mathbf{s}_{k}(t)+{\mathbf{n}(t)}. $$
(10)

According to Kronecker Product relationship (a⊗b)c=a⊗(bc), where a is a column vector, the number of columns in b is the same as the number of rows in c. (10) can be rewritten as

$$\begin{array}{@{}rcl@{}} \mathbf{y}(t)&=&\sum_{k=1}^{K}{\mathbf{b}(\theta_{k}, \phi_{k})} {\otimes} \left[{\mathbf{d}(\theta_{k}, \phi_{k})}{\mathbf{Q}_{k}}{\mathbf{h}_{k}}\right]\mathbf{s}_{k}(t)+{\mathbf{n}(t)} \\ &=&\sum_{k=1}^{K}{\mathbf{b}(\theta_{k}, \phi_{k})} {\otimes} {\mathbf{a}(\mathbf{\Lambda}_{k})}\mathbf{s}_{k}(t)+{\mathbf{n}(t)}, \\ \end{array} $$
(11)

where a(Λk)=d(θk,ϕk)Qkhk.

Different from the DEMVS, for the EMVS, the dipole elements of the EMVS are collocated, so both Γ and Ω are an 6×6 identity matrix I6, the d(θk,ϕk) can be simplified to \({\mathbf {d}(\theta _{k}, \phi _{k})}=\left [ \begin {array}{c} \mathbf {I}_{3} \\ (\mathbf {u}_{k} \times) \end {array} \right ]\mathbf {V}_{k}\).

2.3 Signal model of PSFDA

For the array constituted by M collocated EMVS, where each vector located at y-axis transmits a different frequency. That is, the radiated frequency from the m-th EMVS is taken as the same of Eq. 1. Similarly, the phase difference between the m-th EMVS and the first EMVS is

$$ {{} \begin{aligned} \Delta \psi_{m-1} &= \psi_{m}-\psi_{1} \\ &=-\frac{2 \pi f_{0} (m-1) d {\sin}\theta {\cos}\phi}{c}+\frac{2 \pi r (m-1)\Delta f }{c}\\ & -\frac{2 \pi (m-1)^{2} \Delta f d {\sin}\theta {\cos}\phi}{c}\\ &\approx -\frac{2 \pi f_{0} (m-1) d {\sin}\theta {\cos}\phi}{c}+\frac{2 \pi r (m-1)\Delta f }{c}. \end{aligned}} $$
(12)

Accordingly, the PSFDA signal model can be reformulated as

$$ \begin{aligned} \mathbf{Z}(t) &= \sum_{k=1}^{K}{\mathbf{c}(\mathbf{\Lambda}_{k})}{\otimes} {\mathbf{b}_{a,r}(\theta_{k}, \phi_{k}, r_{k})} \mathbf{s}_{k}(t)+{\mathbf{n}(t)}\\ &\,=\,\sum_{k=1}^{K}{\mathbf{c}(\mathbf{\Lambda}_{k})}{\otimes} \left[{\mathbf{b}_{a,k}(\theta_{k}, \phi_{k})}\odot {\mathbf{b}_{r,k}(r_{k})} \right]\mathbf{s}_{k}(t)\,+\,{\mathbf{n}(t)}\\ &=\sum_{k=1}^{K}{\mathbf{g}(\vartheta_{k})}\mathbf{s}_{k}(t)+{\mathbf{n}(t)}, \end{aligned} $$
(13)

where c(Λk)=

$${} \left[ \begin{array}{cc} -\text{sin}\theta_{k} \ \ \ \ -\text{cos}\theta_{k} \text{sin}\phi_{k} \\ \text{cos}\theta_{k} \ \ \ \ -\text{sin}\theta_{k} \text{sin}\phi_{k} \\ 0 \ \ \ \ \ \text{cos}\phi_{k} \\ -\text{cos}\theta_{k} \text{sin}\phi_{k} \ \ \ \ \ \ \text{sin}\theta_{k} \\ -\text{sin}\theta_{k} \text{sin}\phi_{k} \ \ \ \ -\text{cos}\theta_{k} \\ \text{cos}\phi_{k} \ \ \ 0 \end{array} \right] \left[ \begin{array}{cc} \text{cos}\alpha_{k} \ \ \text{sin}\alpha_{k} \\ -\text{sin}\alpha_{k} \ \ \text{cos}\alpha_{k} \end{array} \right] \left[ \begin{array}{c} \text{cos}\beta_{k} \\ j \text{sin}\beta_{k} \end{array} \right],\\ $$

\({\mathbf {b}_{a,k}(\theta _{k}, \phi _{k})}=\left [1~~e^{-j\varphi _{a,k}}~~\cdots ~~e^{-j(M-1)\varphi _{a,k}} \right ]^{T}\) with φa,k=2πf0dsinθkcosϕk/c, \({\mathbf {b}_{r,k}(r_{k})}=\left [1~~e^{j\psi _{r,k}}~~\cdots ~~e^{j(M-1)\psi _{r,k}} \right ]^{T}\) with ψr,k=2πrkΔf/c, and the ⊙is the Khatri-Rao product. In doing so, we get a spatio-polarized-range manifold g(𝜗k), denoting the spatio-polarized-range information 𝜗k=(θk,ϕk,αk,βk,rk) of the k-th signal. Assume an x-electric-component sensor and a y-electric-component sensor are used for each vector sensor, namely, the PSFDA array arrangement with uniformly spaced orthogonal dipoles as shown in Fig. 4. In this case, then we have

$${{} \begin{aligned} &\mathbf{c}(\mathbf{\Lambda}_{k})=\\&\quad\left[ \begin{array}{cc} -\text{sin}\theta_{k} \ \ -\text{cos}\theta_{k} \text{sin}\phi_{k} \\ \text{cos}\theta_{k} \ \ -\text{sin}\theta_{k} \text{sin}\phi_{k} \end{array} \right] \left[ \begin{array}{cc} \text{cos}\alpha_{k} \ \ \text{sin}\alpha_{k} \\ -\text{sin}\alpha_{k} \ \ \text{cos}\alpha_{k} \end{array} \right] \left[ \begin{array}{c} \text{cos}\beta_{k} \\ j \text{sin}\beta_{k} \end{array} \right]. \end{aligned}} $$
Fig. 4
figure 4

Polarization sensitive FDA

Full size image

Similarly, the signal models for the FDA and a conventional uniform linear phased-array (ULA) can be described, respectively, as

$$ \mathbf{Z}_{fda}(t)=\sum_{k=1}^{K} {\mathbf{b}_{a,k}(\theta_{k}, \phi_{k})}\odot {\mathbf{b}_{r,k}(r_{k})} \mathbf{s}_{k}(t)+{\mathbf{n}(t)}, $$
(14)
$$ \mathbf{Z}_{ula}(t)=\sum_{k=1}^{K}{\mathbf{b}_{a,k}(\theta_{k}, \phi_{k})}\mathbf{s}_{k}(t)+{\mathbf{n}(t)}. $$
(15)

The steering vector of PSFDA depends on the angle, range, frequency and polarization, which means the PSFDA has potential advantage in terms of discriminating the targets from interferences.

3 Proposed adaptive angle, range, and polarization beamformer

The PSFDA measurement model for the M collocated EMVS can be expressed as

$$ \begin{array}{l} \mathbf{Z}(t) ={\mathbf{g}(\vartheta_{s})}\mathbf{s}(t)+{\sum \limits_{j=1}^{J}} \mathbf{g}(\mathbf{\vartheta}_{j})\mathbf{i}_{j}(t) +\mathbf{n}(t),~ t=1,\dots, T \end{array} $$
(16)

where g(𝜗s) and g(𝜗j) (j=1,…,J=K−1) are the steering vectors for signal and interference, respectively. In the following, we assume that the signal of interest is s(t), interferences is ij(t) (j=1,…,J) and n(t) is a zero mean white Gaussian process.

According to the minimum-noise-variance beamformer for PSA [29], we can get the classical minimum variance for the angle-polarization-range sensitive (MVAPRS) beamformer as

$$ \mathbf{w}_{d}=\frac{\mathbf{R}_{z}^{-1}\mathbf{g}(\mathbf{\vartheta}_{s})}{\mathbf{g}^{H}(\mathbf{\vartheta}_{s})\mathbf{R}_{z}^{-1}\mathbf{g}(\mathbf{\vartheta}_{s})}, $$
(17)

where Rz=E{Z(t)ZH(t)} denotes the 2M×2M covariance matrix of the array snapshot vectors, and (·)−1 indicates the matrix inversion operator. To further enhance the interference mitigation capability, we propose an adaptive angle-range-polarization-dependent beamforming method. For a small number of interferences in the sidelobe domain, and non-sparse array gains in the main-lobe, to make the sidelobe of beampattern sparse, we sample the whole observation domain and form a overcomplete basis \({\mathbf {G}}_{s}= \left [\mathbf {g}\left (\bar {\mathbf {\vartheta }}_{1}\right), \mathbf {g}\left (\bar {\mathbf {\vartheta }}_{2}\right), \dots, \mathbf {g}\left (\bar {\mathbf {\vartheta }}_{s-q}\right), \mathbf {g}\left (\bar {\mathbf {\vartheta }}_{s+q}\right)\right.\), \(\left.\dots \,\mathbf {g}(\bar {\mathbf {\vartheta }}_{L_{0}})\right ] ({L_{0}} \gg K)\) corresponding to the sidelobe region of 𝜗s, where q is an integer associate with the bounds between the mainlobe and sidelobes of the beampattern, and we add the ℓ1-norm penalization on the array gains Gs. To further suppress the sidelobe level and interference, the ℓ∞-norm penalization is further imposed on the Gs. In doing so, the proposed beamformer w can be recast as,

$$ \begin{array}{l} {\underset{\mathbf{w}}{\mathrm{minimize~~}}} \mathbf{w}^{H}{\mathbf{R}_{z}}\mathbf{w} + \xi \|\mathbf{w}^{H} {\mathbf{G}}_{s} \|_{1} \\ {\mathrm{subject~to~}}{\| {\mathbf{w}^{H} \mathbf{g}(\mathbf{\varphi}_{s}) - 1} \|_{\infty}} \leq \varepsilon \\ \quad{\| \mathbf{w}^{H} {\mathbf{G}}_{s} \|_{\infty}} \leq \eta \end{array} $$
(18)

where the weighting factor ξ makes a tradeoff between the minimum variance constraint on total output energy and the sparse constraint on the sidelobe of beampattern, the parameters ε and η are designed according to the desired array performance. So the array gain including both sidelobes and interferences can be suppressed by ∥wHGs∥∞≤η. The ∥wHg(φs)−1∥∞≤ε in (Eq. 18) aims to maintain the signal of interest. \(\left \| \mathbf {c} \right \|_{\hbar }^{\hbar } = {\sum \nolimits }_{i} {{{\left | {{c_{i}}} \right |}^{\hbar }}}\) is \({\ell _{\hbar }}\)-norm of the vector c, \(\hbar \le 1\) leads to sparse solutions, while \(\hbar =2\) is the ℓ2-norm criterion. Due to the sparsity of the beam pattern,and to make the optimization problem (Eq. 18) be an easy-to-handle convex problem, we choose \(\hbar =1\), that is ∥wHGs∥1. Compared with the ℓ2-norm criterion that favors solutions with many nonzero entries, this sparse constraint has advantages for the cases with few nonzero elements for interference suppression and sidelobe reduction. The validity of our proposed method will be further demonstrated via numerical analysis in Section 4.

4 Simulation Results and Discussions

We first analyze the PSFDA performance by examing its spatial domain beampattern, spatial-polarization beampattern and spatial-range beampattern. Statistical simulations are carried out in an ideal scenario without steering vector mismatches.

In the following simulations, we consider a PSFDA with M=8 orthogonal dipole pairs and d=0.5m as shown in the Fig. 4. Suppose there are one signal of interest and one interference with fixed signal-to-interference ratio (SIR) equal to -20dB, 100 independent runs in spatially white gaussian noise. We assume that the powers of the polarized signal, interference and noise are \({\sigma _{s}^{2}}\), \({\sigma _{j}^{2}}\) and \({\sigma _{n}^{2}}\), respectively. The average SINR is determined by:

$$ \mathbf{{SINR}}=\frac{{\sigma_{s}^{2}} \mathbf{w}^{H} \mathbf{g}(\mathbf{\vartheta}_{s})\mathbf{g}^{H}(\mathbf{\vartheta}_{s})\mathbf{w}}{\sum \limits_{j=1}^{J} {\sigma_{j}^{2}} \mathbf{g}(\mathbf{\vartheta}_{j})\mathbf{g}^{H}(\mathbf{\vartheta}_{j}) +{\sigma_{n}^{2}} \mathbf{I}}. $$
(19)

where \(\mathbf {I} \in \mathcal {C}^{2M \times 2M}\).

4.1 Beampattern

4.1.1 Angle-range-dependent beampattern

Suppose the signal and interference have the angle-range-polarization characteristics (θs,ϕs,αs,βs,rs)=(20∘,60∘,−20∘,30∘,10km) and (θj,ϕj,αj,βj,rj)=(20∘,60∘,−20∘,30∘,8km), respectively. For an ideal scenario with the exact knowledge of the steering vector, Fig. 5 compares the PSA and PSFDA beampatterns. The angle-range-dependent S-shaped PSFDA beampattern has additional degrees of freedom and potential applications in suppressing the range interference and ambiguous clutter with same angle but different range from the target, while the range-independent PSA beampattern has no such advantages. Besides, compared with PSFDA, the FDA does not provide the polarization information.

Fig. 5
figure 5

Comparative beampattern between PSA and PSFDA, where Δf=30kHz,M=8,andf0=2GHz. a PSA beampattern. b PSFDA beampattern

Full size image

We also compare the block-shaped angle-range-dependent beampattern obtained by the MVAPRS beamformer and our proposed beamformer for the PSFDA with the frequency offsets as Δfm=(m−1)2·Δf,m=1,2,…,M. The results given in Fig. 6 demonstrate that our proposed algorithm can successfully suppress the interference as well as the MVAPRS.

Fig. 6
figure 6

Angle-range-dependent block-shaped beampattern: a MVAPRS beampattern, b Ours beampattern

Full size image

4.1.2 Spatio-polarized beampattern

We compare the PSFDA angle-polarization-dependent beampattern and the angle-elevation-dependent beampattern like that of a PSA beampattern, as shown in the Figs. 7 and 8, respectively. From Fig. 7, It is seen that the angle-polarization-dependent beampattern can keep the maximum energy at the target positions (20∘,60∘,20∘,30∘,10km) and suppress simultaneously the interference from (40∘,60∘,−40∘,30∘,10km). Similarly, the angle-elevation-dependent beampattern effectively suppresses the interference from (40∘,60∘,−20∘,30∘,10km), without reducing energy at the target (20∘,30∘,−20∘,30∘,10km). Moreover, the PSFDA not only has the same performance as that of PSA, but the former also outperforms the latter in range-dimension, as shown in Fig. 5.

Fig. 7
figure 7

Angle-polarization-dependent beampattern: a Angle dimension. b Polarization dimension

Full size image
Fig. 8
figure 8

Azimuth-elevation-dependent beampattern: a Azimuth dimension. b Elevation dimension

Full size image

In addition, we consider the statistical results for the angle-range-dependent block-shaped beampattern. Fig. 9 displays the output SINRs versus signal-to-interference ratio (SNR) for T=500. For a fixed SNR=0dB, the SINRs versus the number of snapshots T are shown in Fig. 10. The results clearly demonstrate that our proposed beamformer substantially outperforms the MVAPRS for SNR >0dB. Since the proposed algorithm is a convex optimization problem, it can be efficiently resolved by the openly CVX software [30].

Fig. 9
figure 9

SINR versus SNR

Full size image
Fig. 10
figure 10

SINR versus number of snapshots

Full size image

4.2 High-dimensional arrays

Finally, we analyze the performance of the optimal output SINR for high-dimensional arrays. The angle-range-polarization characteristics are same as that of Fig. 5. In each antenna, we consider the antenna elements with 2≤p≤6. For each p, the dipole elements are chosen according to Table 1. Note that at each row, the symbol “ √” denotes that a certain dipole element is selected in the antenna. For example, when p=2, two electric dipoles at the x-axis and y-axis are selected, respectively. Accordingly, the antenna response is \(\left [\begin {array} {cc} \mathbf {V}^{(E)}_{x} \\ \mathbf {V}^{(E)}_{y} \end {array} \right ]\).

Table 1 Vector antenna dipole elements for 2≤p≤6 used in the simulations in the Section 4.2
Full size table

The simulated optimal output SINRs versus SNR for p=2,3,4,5,6, under the angle-range-dependent block-shaped beampattern, are given in Fig. 11. For fixed SNR=0dB and SIR=-20dB, the optimal SINRs versus T for p=2,3,4,5,6 are shown in Fig. 12. It is noticed along with the increase of the sensor dimensionality p, the output SINRs will increase even under the same SNR (or number of snapshots). Figures 13 and 14 show that the optimal output SINR is approximately linearly proportional to p. This verify that the electromagnetic vector array has the advantage of enabling the control of beampattern polarization, which achieves more degrees of freedom.

Fig. 11
figure 11

Optimal SINR versus SNR for antenna dimensionality p

Full size image
Fig. 12
figure 12

Optimal SINR versus number of snapshots for antenna dimensionality p

Full size image
Fig. 13
figure 13

Optimal SINR versus antenna dimensionality p for SNR

Full size image
Fig. 14
figure 14

Optimal SINR versus antenna dimensionality p for number of snapshots

Full size image

5 Conclusions

In this paper, we formulated the PSFDA signal model and proposed a corresponding beamformer based on the MVAPRS, ℓ1-norm minimization and ℓ∞-norm constraint. The proposed adaptive beamformer is superior to the conventional MVAPRS on maintaining array gain for the signal of interest, and PSA beamformers in terms of both nulling interferences and maintaining signal of interest. In addition, the performance of the optimal output SINR is also analyzed for the high-dimensional arrays. Simulation results demonstrate that the electromagnetic vector array has the advantage of enabling the control of beampattern polarization and virtually increasing the array size.