1 Introduction

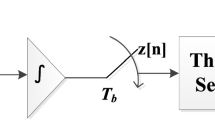
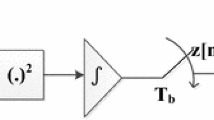
Accurate estimation of the time of arrival (TOA) in wireless systems is a challenging problem due to inter-symbol interference and multipath fading. Sixty gigahertz millimeter wave (MMW) is a promising technology for accurate TOA estimation due to its unique advantages which include high time resolution [1], high multipath resolution [2], and robustness to interference [3]. In the 60-GHz frequency band, an energy detector (ED) receiver is preferred for TOA estimation because it can be implemented easily in hardware and does not require precise channel estimation and synchronization as with a matched filter (MF) [4]. As shown in Fig. 1, a conventional ED only consists of a band-pass filter (BPF), a squaring operator, an integrator, and a decision device.

Fig. 1
figure 1

Block diagram of a conventional energy detector receiver

Full size image

The TOA can be estimated based on the first energy sample to exceed a threshold. Various ED-based TOA estimation methods have been proposed [5,6,7,8,9,10,11]. Guvenc first proposed a TOA estimation method via analyzing the kurtosis characteristics of the energy of the received pulses [6]. To account for signal variations, a normalized threshold was employed in [7], which is based on the maximum and minimum energy values. In [8], a fixed threshold based on the maximum energy value was used. The cell averaging constant false alarm rate (CA-CFAR) method is developed for the TOA estimate by employing the ED receiver in [9].A weighted ED receiver was proposed in [10] to reduce the effects of noise. Although an extreme learning machine was used to obtain the threshold [11], this algorithm performs poorly with a conventional ED in low signal-to-noise ratio (SNR) environments, particularly when there are noise-only energy values. We can see all of these algorithms perform poorly in low SNR environments because of the sensitivity of the threshold to noise. Using a conventional ED, these obtained energy samples are only noise which will have a significant effect on the TOA estimation \( {\widehat{\tau}}_{\mathrm{TOA}} \).

To reduce the effects of noise and improve the estimation accuracy, in this paper, (1) an improved ED receiver was presented for TOA estimation which employs impulse radio (IR) 60 GHz MMW signals. The received signals were processed based on empirical mode decomposition (EMD) [12]. This method has been used to analyze non-stationary and nonlinear signals [13]. EMD adaptively decomposes a signal into a series of intrinsic mode functions (IMFs) in descending order of frequency and a residual trend mode [13]. The IMFs and residual trend mode can be used to represent the noise which can then be deleted, resulting in an improved SNR [14]. (2) An ED-based TOA estimation technique was proposed which employs extreme learning machine (ELM). ELM was used to resolve a regression problem with the characteristics of the received ED values as inputs and the detector threshold as the output. Results are presented which show that this de-noising approach provides superior performance with the IEEE 802.15.3c channel models compared to several well-known techniques. And the simulation results were presented which show that ELM can provide robust and reliable TOA estimates. Further, the proposed approach can be used with other wireless systems.

The remainder of this paper is organized as follows: Section 2 presents the system model. An improved ED receiver was discussed using EMD in Section 3. Section 4 discusses the signal characteristics, and the proposed ED-based TOA estimation technique is introduced in Section 5. Some performance results are given in Section 6, and Section 7 provides some conclusions.

2 System model

The IEEE 802.15.3c Line of Sight (LOS) and Non-line of Sight (NLOS) channel models have been proposed by the TG3c group for 60 GHz indoor residential, office, and library environments [21]. Several types of signals have been considered for 60 GHz systems [18]. Pulse position modulation (PPM) with a truncated sinc pulse has been shown to better conform to the Federal Communications Commission (FCC) regulations and provide a lower error probability than other signals. Thus, PPM with a truncated sinc pulse is considered here.

The received 60-GHz MMW signal can be expressed as:

$$ r(t)=\left(\sqrt{\frac{E_b}{N_s}}\sum \limits_{j=\hbox{-} \infty}^{+\infty }p\left(t-{jT}_s-{c}_j{T}_c-{a}_j\beta \right)\cos \left(2\pi {f}_ct\right)\right)\ast h\left(t,\phi \right)+n(t), $$
(1)

where E b is the energy per bit, (*) denotes convolution, N s is the number of pulses transmitted per data symbol, j is the frame index, and T s is the frame duration. The time-hopping codes are c j  ∈ (0, 1, .…, N h  − 1), where N h   = T s /T c is the number of chip positions in a frame and the chip duration is T c , β is the PPM time shift employed when a j   =  1 and there is no shift when a j   =  0, n(t) is the additive white Gaussian noise (AWGN) with zero mean and two-sided power spectral density N 0/2, and h(t, ϕ) is the channel realization from the triple Saleh-Valenzuela model in the IEEE 802.15.3c standard.

The transmitted pulse sequence in (1) is:

$$ s(t)=\sqrt{\frac{E_b}{N_s}}\sum \limits_{j=-\infty}^{+\infty }p\left(t-{jT}_s-{c}_j{T}_c-{a}_j\beta \right)\cos \left(2\pi {f}_ct\right), $$
(2)

where p(t) is the Gaussian pulse and f c is the carrier frequency.

The channel realization can be given by:

$$ h\left(t,\phi \right)={\alpha}_{\mathrm{LOS}}\delta \left(t,\phi \right)+\sum \limits_{l=0}^L\sum \limits_{k=0}^{K_l}{\alpha}_{k,l}\delta \left(t-{T}_l-{\tau}_{k,l}\right)\delta \left(\phi -{\Theta}_l-{\omega}_{k,l}\right) $$
(3)

where δ(⋅) denotes the Dirac delta function, L denotes the cluster number, and K l denotes the rays number in thelth lth cluster. The scalar α k, l denotes the complex amplitude, α k, l and τ k, l denote the TOA, and ω k, l denotes the azimuth of the kth ray in the lth cluster. The average TOA and the average AOA of the lth cluster can be expressed as T l and Θ l , respectively.

The first term in (4) denotes the LOS component with

$$ {\alpha}_{\mathrm{LOS}}=20{\log}_{10}\left[\left(\frac{\mu_d}{d}\right)\left|\sqrt{G_{t1}{G}_{r1}}+\sqrt{G_{t2}{G}_{r2}}{\Gamma}_0\exp \left[j\frac{4\pi {h}_1{h}_2}{\lambda d}\right]\right|\right]-{PL}_d\left({\mu}_d\right)\kern0.36em \left[\mathrm{dB}\right] $$
(4)

where

$$ {PL}_d\left({\mu}_d\right)={PL}_d\left({d}_0\right)+10\cdot {n}_d\cdot {\log}_{10}\left(\frac{d}{d_0}\right)\kern0.36em \left[\mathrm{dB}\right] $$
(5)
$$ {PL}_d\left({d}_0\right)=20{\log}_{10}\left(\frac{4\pi {d}_0}{\lambda}\right)+{A}_{\mathrm{NLOS}}\kern0.36em \left[\mathrm{dB}\right] $$
(6)

and PL d denotes the path loss, λ denotes the wavelength, A NLOS denotes the attenuation caused due to the NLOS propagation, μ d denotes the average range, Γ0 denotes the reflection coefficient, and h 1 and h 2 denote the heights of the transmitted antenna and the received antenna, respectively. G t1, G t2, G r1, and G r2 denote the gains of the transmitted antenna for the path 1 and path 2 and the gains of the received antenna for the path 1 and path 2, respectively.

The ED integrator output for a received signal r(t) can be expressed as:

$$ z\left[n\right]\kern0.5em =\kern0.5em \sum \limits_{j=1}^{N_s}\kern0.5em {\int}_{\left(j\kern0.5em -\kern0.5em 1\right)\kern0.5em {T}_s\kern0.5em +\kern0.5em \left(\kern0.5em {c}_j\kern0.5em +\kern0.5em n\kern0.5em -\kern0.5em 1\right)\kern0.5em {T}_b}^{\left(j\kern0.5em -\kern0.5em 1\right)\kern0.5em {T}_s\kern0.5em +\kern0.5em \left(\kern0.5em {c}_j\kern0.5em +\kern0.5em n\kern0.5em \right)\kern0.5em {T}_b}{\left|r(t)\right|}^2\kern0.5em dt $$
(7)

where N s is the number of pulses per symbol, T b is the integration duration, 3 T s /2 is the integration interval, N b   = 3 T s /2 T b is the number of samples, j is the frame index, and the frame duration is T s . The TOA estimate can be expressed as:

$$ \widehat{\tau}\kern0.5em =\kern0.5em \left[\underset{1\le n\le {N}_b}{\arg \min}\kern0.5em \left\{\kern0.5em n\kern0.5em |z\left[n\right]\kern0.5em \ge \kern0.5em \eta \right\}\kern0.5em -\kern0.5em 0.5\right]\kern0.5em {T}_b $$
(8)

where η is the threshold which is based on a normalized threshold η norm given by:

$$ {\eta}_{\mathrm{norm}}\kern0.5em =\kern0.5em \frac{\eta \kern0.5em -\kern0.5em \min \left(z(n)\right)}{\max \left(z(n)\right)\kern0.5em -\kern0.5em \min \left(z(n)\right)} $$
(9)

As min(z[n]) is typically the integration of only noise, this can have a detrimental effect on the receiver performance due to it is sensitivity to noise. In this paper, an extended threshold crossing (ETC) algorithm is proposed where the threshold η can be expressed as:

$$ \eta ={\eta}_{\mathrm{norm}}\times \left\{\max \left(z\left[n\right]\right)\kern0.5em -\frac{1}{N_b}\sum \limits_{n=1}^{N_b}z\left[n\right]\right\}+\frac{1}{N_b}\sum \limits_{n=1}^{N_b}z\left[n\right] $$
(10)

The problem is then how to obtain η norm. Both curve-fitting and fixed threshold (FT) have been employed, but these methods cannot provide precise TOA estimates because the first arriving signal component cannot be accurately determined. The simplest threshold selection was the maximum energy selection (MES) method, i.e., the maximum energy was considered as the threshold. As shown in Fig. 2, the actual TOA locates before the maximum energy, which is challenging to acquire due to the first arriving path which cannot be detected. As a result, the MES method cannot achieve precise TOA estimations as shown in Fig. 2.

Fig. 2
figure 2

The relationship between the actual TOA and the maximum energy

Full size image

3 Proposed ED receiver

Figure 3 shows the energy values for a 60-GHz MMW signal (1) with the 3c CM1.1 model for an SNR of 10 dB and the signal without noise. These results indicate that many energy values are only noise which will have a significant effect on \( {\widehat{\tau}}_{\mathrm{TOA}} \). To reduce the effects of noise and improve the estimation accuracy, an improved ED receiver based on EMD will be presented in this section.

Fig. 3
figure 3

The energy values for a 60-GHz signal with the CM1.1 channel model. a 60 GHz signal without noise and b 60 GHz signal with AWGN and SNR = 10 dB

Full size image

Figure 4 shows the proposed receiver with signal de-noising using EMD. EMD adaptively decomposes the received signal into N IMFs, i.e., IMF1, ..., IMF N , in descending frequency order and a residual trend mode. The residual trend mode is the difference between the signal and the IMFs. The noise can be estimated using the first few IMFs and the residual trend mode [17, 18].

Fig. 4
figure 4

Block diagram of the new energy detector receiver

Full size image

To obtain the IMFs of a signal using EMD, let r(t) be the received signal, α(t) the residual component, m(t) the shifted component, IMF v (t) the vth IMF, and r u (t) (r l (t)) the upper (lower) envelope using a cubic spline function according to the local extrema.

The EMD algorithm is as follows [13]:

  1. 1)

    Set v = 0 and α(t)  =  r(t);

  2. 2)

    Let m(t)  =  α(t);

  3. 3)

    Determine the local extrema (maximum and minimum) of m(t);

  4. 4)

    Construct the upper and lower envelopes of the extrema using cubic spline functions;

  5. 5)

    Determine the average envelope given by [14]:

$$ u(t)=\frac{r_u(t)+{r}_l(t)}{2} $$
(11)
  1. 6)

    If the average envelope is zero or has only one extrema or zero crossing, go to step 7. Otherwise, calculate [15]:

$$ m(t)=m(t)-u(t) $$
(12)

and go to step 3.

  1. 7)

    If α(t) is monotonic, stop. Otherwise, set v = v + 1, IMF v (t) = m(t), and α(t)  =  r(t) − IMF v (t) and go to step 2 [16].

A 60-GHz MMW signal (1) with the 3c CM1.1 model and an SNR of 10 dB was decomposed using EMD into 11 IMFs and a residual trend mode. The first eight IMFs are shown in Fig. 5.

Fig. 5
figure 5

The first seven IMFs of a received 60 MMW signal with the 3c CM1.1 model and AWGN with SNR = 10 dB. The other parameters are the same as those in Section 4

Full size image

The boundary between the noise and signal components is determined as:

$$ {RP}_v=\left|\frac{P_v-\frac{1}{v-1}\sum \limits_{i=1}^{v-1}{P}_i}{\frac{1}{v-1}\sum \limits_{i=1}^{v-1}{P}_i}\right|,\kern1.5em v\ge 2 $$
(13)

where

$$ {P}_v={E}_v{\overline{T}}_v $$
(14)
$$ {E}_v=\frac{1}{N_v}\sum \limits_{j=1}^{N_e}{\left|{C}_v(j)\right|}^2 $$
(15)
$$ {\overline{T}}_v=\frac{2{N}_v}{O_v} $$
(16)

and N v is the number of values in IMF v , C v is the maximum value in IMF v , and O v is the number of local extrema in IMF v .

For a signal in AWGN, (14) is approximately a constant [17, 18]. As a result, IMF v can be regarded as noise when RP v  < 1 [18]. It was determined by simulation that IMFs 1 to 3 can be considered as noise. The histograms of the first three IMFs of white Gaussian noise and the 60-GHz signal (1) with the CM1.1 model and SNR = 10 dB are shown in Fig. 6. IMF1 for the 60-GHz MMW and AWGN follow the bimodal distribution, and the other IMFs follow the Gaussian distribution. The corresponding histograms are presented in Fig. 7. These results indicate that the first three IMFs have similar distributions in both cases. Table 1 shows the means and standard deviations of the first four IMFs, which confirm that the first three can be considered as noise [18]. Note that when v > 3 the IMFs differ significantly.

Fig. 6
figure 6

Histograms of the IMFs for AWGN and a 60-GHz signal plus noise with the CM1.1 model and SNR =10 dB. The other parameters are the same as those in Section 4. The superimposed red lines are the Gaussian line fits for each IMF

Full size image
Fig. 7
figure 7

Histograms of the energy value distributions for IMFs 1–3 of the AWGN and the 60-GHz signal plus noise in with the CM1.1 and SNR = 10 dB. The other parameters are the same as those in Section 4

Full size image
Table 1 The parameters for the acquired IMFs
Full size table

The received signal can be approximated as:

$$ \widehat{r}(t)=\sum \limits_{v=4}^{11}{\mathrm{IMF}}_v(t) $$
(17)

And the noise estimated as:

$$ \widehat{n}(t)=\sum \limits_{v=1}^3{\mathrm{IMF}}_v(t)+h(t) $$
(18)

Thus, the noise energy is estimated in part B in Fig. 4 as:

$$ {z}_2\left[n\right]\kern0.5em =\kern0.5em \sum \limits_{m=1}^M\kern0.5em {\int}_{\left(m-1\right){T}_s+\left({c}_m+n-1\right){T}_b}^{\left(m-1\right){T}_s+\left({c}_m+n\right){T}_b}\kern0.5em {\left|\sum \limits_{v=1}^3{\mathrm{IMF}}_v(t)+h(t)\right|}^2\kern0.5em dt $$
(19)

And the signal energy values obtained in part C of Fig. 4 as:

$$ z\left[n\right]\kern0.5em ={z}_1\left[n\right]-{z}_2\left[n\right] $$
(20)

Figure 8 shows the energy values after de-noising using EMD with the 3c CM1.1 model and an SNR of 10 dB. The similarity, i.e., the energy values with strong amplitude between these results in Fig. 8 and Fig. 3a, confirms the effectiveness of EMD de-noising.

Fig. 8
figure 8

The energy values of the received signal after de-noising with the CM1.1 and SNR = 10 dB. The other parameters are the same as those in Section 4

Full size image

4 Energy signal characteristics

In this section, the curl of the energy values is considered. The other characteristics including the kurtosis, skewness, maximum slope, and the standard deviation have been discussed in [11] in our previous work. However, the proposed threshold selection method cannot achieve accurate TOA estimations in low SNR values.

4.1 Curl

In vector calculus, the curl is an operator that describes the infinitesimal rotation of a vector field. The maximum curl of the received energy values is obtained as follows. Let (U, V) be a 2D vector field with U = V and

$$ U=\left[z\left[1\right],\kern0.5em z\left[2\right],\kern0.5em z\left[3\right],\kern0.5em \dots, \kern0.5em z\left[{N}_b-1\right],\kern0.5em z\left[{N}_b\right]\right] $$
(21)

The arrays X U and Y V are the coordinates of U and V, respectively, and X U is an N b  × N b dimensional array given by:

$$ {X}_U=\left[\begin{array}{l}1,\kern0.5em 2,\kern0.5em 3,\kern0.5em \dots, \kern0.5em {N}_b-1,\kern0.5em {N}_b\\ {}1,\kern0.5em 2,\kern0.5em 3,\kern0.5em \dots, {N}_b-1,\kern0.5em {N}_b\\ {}\kern1.24em \vdots \kern2.639999em \vdots \kern2.5em \\ {}1,\kern0.5em 2,\kern0.5em 3,\kern0.5em \dots, {N}_b-1,\kern0.5em {N}_b\\ {}1,\kern0.5em 2,\kern0.5em 3,\kern0.5em \dots, {N}_b-1,\kern0.5em {N}_b\end{array}\right] $$
(22)

Y V is also an N b  × N b dimensional array with Y V  = (X U )T. Let the γth difference of the matrix U in the Y V (:,  γ) direction be ℜ(γ) and the γth difference of the matrix V in the X U (γ,  :) direction be ℑ(γ). The curl is then given by:

$$ C\left(\gamma \right)\kern0.5em =\kern0.5em \Im \left(\gamma \right)\kern0.5em -\kern0.5em \Re \left(\gamma \right) $$
(23)

The maximum curl is the maximum of C(γ).

4.2 Signal parameter characteristics

In this section, the characteristics of the parameters of the energy values are investigated in indoor residential LOS and NLOS scenarios for SNR within 4–30 dB. For each SNR, 1000 channels were generated and the received signals sampled at 10 GHz. The system parameters are T s   =  200ns, T b   =  4ns, T c   =  1ns and \( \widehat{\tau}\sim U\left(0,{T}_f\right) \), where U(0, T f ) denotes the uniform distribution.

Figure 9 shows the skewness and maximum curl of the energy values. This figure also shows the kurtosis, maximum slope, standard deviation, the ratios of the kurtosis to the skewness (K/S), the ratios of the maximum slope to the standard, and the products of the maximum slope and the standard deviation (MSD). These results show that the skewness and kurtosis increase as SNR increases, but the skewness changes more quickly. Conversely, the maximum curl, maximum slope, and standard deviation decrease as SNR increases, but the maximum curl changes more quickly. Moreover, the skewness changes little while the maximum curl changes quickly when SNR < 8 dB. On the other hand, when SNR > 8 dB, the skewness changes rapidly but the maximum curl has little change. As a result, these parameters cannot reflect a wide range of SNRs.

Fig. 9
figure 9

The normalized parameters with respect to SNR

Full size image

5 TOA estimation using machine learning

In this section, a new metric was proposed using the skewness and maximum curl of the energy samples. This metric can provide a better indication of the changes in SNR than the parameters considered in the previous section. Then, ELM is used to determine the relationship between this metric and the threshold values.

5.1 The new metric

The parameters presented in Section 3 are not sufficiently sensitive to changes over a wide range of SNRs. Thus, a new matric is presented in this section. The mean absolute error (MAE) of the TOA estimates is used to evaluate the TOA algorithms and is given by:

$$ {\tau}_{\mathrm{MAE}}=\frac{1}{N_m}\sum \limits_{m=1}^{N_m}\left[{\tau}_m-{\widehat{\tau}}_m\right] $$
(24)

where τ m and \( {\widehat{\tau}}_m \) are the mth propagation time and TOA estimate, respectively, and N m is the number of TOA estimates.

The MAE of the TOA estimation presented in [7] is less than that in [6] because the skewness changes more rapidly than the kurtosis when SNR > 12 dB. However, neither of these approaches can provide good performance over a wide range of SNRs. Thus, a new metric is proposed which is given by:

$$ J=\frac{\left(K/S\right)-{\left(K/S\right)}_{\mathrm{min}}}{{\left(K/S\right)}_{\mathrm{max}}-{\left(K/S\right)}_{\mathrm{min}}}\times Q-\frac{C-{C}_{\mathrm{min}}}{C_{\mathrm{max}}-{C}_{\mathrm{min}}}\times R $$
(25)

where S is the skewness of the energy values and C is the maximum curl of these values. S max and S min are the maximum and minimum values of the skewness and C max and C min are the maximum and minimum values of the curl, respectively. Based on the extensive simulation results, Q and R should be less than 20 and satisfy Q  ≥  3 R. In this paper, Q = 20 and R = 2.

To test the sensitivity of J with respect to SNR, the average value of J was determined for the CM1.1 and CM1.2 channel models with T b  = 1 and 4 ns. Figure 10 shows that J is a monotonic function of SNR and is more sensitive to SNR than the other parameters over the range of SNRs.

Fig. 10
figure 10

Average metric values with respect to SNR

Full size image

5.2 Threshold determination

To find the best normalized threshold η best, the relationship between MAE and η norm with respect to J, the channel, and the integration period are examined. Except for small values of J, the MAE decreases with increasing J and the minimum MAE decreases with increasing J. Figure 11 shows the relationship between the normalized threshold and the MAEs. Usually, the normalized threshold with the minimum MAE was referred as the best normalized threshold. The value of η norm for the minimum MAE is defined as the best normalized threshold η best. As shown in Fig. 12, the average η best is defined as:

$$ {\eta}_{\mathrm{opt}}(J)\kern0.5em =\kern0.5em \frac{1}{N_i}\kern0.5em \sum \limits_{i=1}^{N_i}{\eta}_{\mathrm{opt}}^{\left({T}_b\kern0.5em =\kern0.5em i\kern0.5em ns\right)}\kern0.5em (J) $$
(26)

where

$$ {\eta}_{\mathrm{opt}}^{T_b=i\kern0.24em ns}(J)\kern0.5em =\kern0.5em \frac{\eta_{\mathrm{best}}^{\left( CM1.1,\kern0.5em {T}_b=i\kern0.24em ns\right)}\kern0.5em (J)\kern0.5em +\kern0.5em {\eta}_{\mathrm{best}}^{\left( CM2.1,{T}_b=i\kern0.24em ns\right)}\kern0.5em (J)}{2} $$
(27)
Fig. 11
figure 11

The MAEs of TOA estimations with respect to the normalized threshold. The arrow denotes the direction of the metric decreases

Full size image
Fig. 12
figure 12

Optimum threshold with respect to the best threshold with different models and T b

Full size image

N i is the number of integration periods and i is the integration period in nanosecond.

The integration periods considered are 1 and 4 ns, so that

$$ {\eta}_{\mathrm{opt}}(J)\kern0.5em =\kern0.5em \frac{\eta_{\mathrm{opt}}^{\left({T}_b=1\;\mathrm{ns}\right)}\kern0.5em (J)\kern0.5em +\kern0.5em {\eta}_{\mathrm{opt}}^{\left({T}_b=4\;\mathrm{ns}\right)}\kern0.5em (J)}{2} $$
(28)

where

$$ {\eta}_{\mathrm{opt}}^{T_b=i\;\mathrm{ns}}\kern0.5em (J)=\frac{\eta_{\mathrm{best}}^{\left( CM1.1,\kern0.5em {T}_b=i\;\mathrm{ns}\right)}\kern0.5em (J)\kern0.5em +\kern0.5em {\eta}_{\mathrm{best}}^{\left( CM2.1,{T}_b=i\;\mathrm{ns}\right)}\kern0.5em (J)}{2} $$
(29)

5.3 ELM-assisted TOA estimation

Artificial neural networks (ANN) such as the support vector machine (SVM) and back propagation neural network (BPNN) has been widely employed to solve regression problems [18,19,20,22]. ELM is a new and efficient method to train a single-hidden-layer feedforward neural networks (SLFNs) [23]. ELM has been applied in many fields such as signal and information processing due to the good general performance and fast learning with minimal human intervention [23,24,25,26,27,28,29,30,33]. ELM has been shown to provide better results than SVM and require less training time than BPNN. The most important property is that the parameters in the hidden layers can be automatically determined and a simple generalized inverse operation can be used to obtain the output weight. Further, the only parameter that needs to be specified is the number of nodes in the hidden layer [24]. Due to the complexity of the indoor channel environment, it is very difficult to estimate TOA accurately using traditional curve-fitting methods. ELM can be used to resolve this problem by determining the relationship between the input and output parameters according to the training results.

In ANN and SVM, the parameters in different layers need to be tuned which can consume significant time. Further, the learning rate and learning epochs must be tuned through an iterative procedure which makes it difficult to obtain optimal values [23, 24]. Different from NN and SVM solutions, ELM is a tuning-free algorithm. The input weights and hidden bias can be generated randomly before training the SLFN based on the sample set.

In this paper, ELM is used to determine the relationship between J and η opt. The number of nodes in the hidden layer is determined based on the training accuracy. The root mean square error (RMSE) was calculated for 1000 training trials for each number of nodes. The results obtained show that the RMSE is a decreasing function of the number of nodes, but when this number is 30, the RMSE is approximately constant. As a result, the number of node in the hidden layer is set to 30. The values J are rounded to the nearest integer or half integer, and these rounded values are used in training the ELM. As η opt varies from 0 to 1, the sigmoid function is used as the activation function which is given by:

$$ r=\frac{1}{1+{e}^{-x}} $$
(30)

6 Results and discussion

In this section, the MAEs of several well-known TC methods were examined for SNRs in the range 4 to 30 dB with the IEEE 802.15.3c channel models. Figure 13a shows the calculated MAEs of the obtained TOA estimations with the LOS propagation including the channel models CM 1.1 and CM 3.1, while the MAEs of the obtained TOA over the channel models CM 2.1 and CM 4.1 were shown in Fig. 13b.

Fig. 13
figure 13

The MAEs of several well-known methods with respect to SNR. a LOS scenes. b NLOS scene

Full size image

Based on the obtained results, the following conclusions can be obtained:

  1. (1)

    The obtained MAEs of the new proposed ED receiver with respect to each given SNR within 4–30 dB indicate the excellent capability of removing the AWGN and show better performances on TOA estimations compared with several well-known algorithms based on the ED receiver whether in LOS or NLOS scene for each given integration period as shown in Fig. 14.

  2. (2)

    The obtained MAEs of the improved ED received indicate that the ability to achieve TOA estimations in LOS models is better than that in NLOS models with regard to each given SNR within 4–30 dB. The difference is 15 ns at best.

  3. (3)

    Integration periods usually can cause bad effects on TOA accuracy; the TOA estimation accuracy increases with the increasing integration period regardless of the propagation environment as shown in Fig. 15. In the majority of cases, the MAEs with T b  = 1 ns is less than that with T b  = 4 ns and the difference is at most 2 ns.

  4. (4)

    It was turned out that the new ED receiver was independent of the propagation models and integration periods.

Fig. 14
figure 14

MAEs of the improved ED receiver over different propagation scenes with T b  = 4 ns

Full size image
Fig. 15
figure 15

MAEs of TOA estimation with respect to T b

Full size image

Here, ELM denotes the new ED method with the optimum thresholds acquired with the ELM algorithm, MES denotes the maximum energy selection method, K denotes the kurtosis based method, and FT denotes the fixed normalized threshold. In all cases, the average MAE of the improved ED receiver with the ELM algorithm is the lowest among the above algorithms.

7 Conclusions

In this paper, an improved energy detector (ED)-based TOA estimation method for impulse radio (IR) 60 GHz wireless system was presented using the empirical mode decomposition (EMD). The proposed solution employs the curl, the kurtosis, and the skewness of the energy values with an extreme learning machine (ELM). The optimum thresholds were determined for the IEEE 802.15.3c channel models in both LOS and NLOS environments. Results were presented which show that the proposed ELM approach provides better performance than other ED-based TOA estimation methods.