Introduction

Length of stay (LOS) is one of the most important outcomes in clinical epidemiology since it is directly linked to patients’ morbidity and economic costs [1]. It is easy to measure and often routinely collected in surveillance data bases. During the stay in hospital, patients are at risk to acquire nosocomial infections (NI) which belong to the major common adverse events in hospitals. Many observational reports have studied the impact of NI on length of stay by using different statistical methods. When evaluating the prolonged LOS of NI, the timing of NI plays an important role to distinguish between pre-infection time and consequence of NI. Several methodological papers showed the magnitude of the so-called time-dependent (aka immortal-time) bias which occurs if the timing of infection is not adequately addressed or rather ignored in the analysis [2, 3]. Multi-state models or time-dependent matching techniques account for the timing of NI to avoid the time-dependent bias [2–4]. However, there exist fundamentally different estimands to quantify this prolonged LOS associated with NI. In this article, we describe four different approaches and estimands in a simple multi-state framework [5], display their mathematical relationships in a multiplicative as well as additive way and apply them to a real cohort study.

Methods

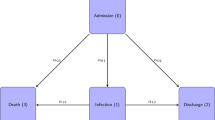
We consider a time-homogeneous multi-state model (Fig. 1) with the three states 0=admission, 1=nosocomial infection, 2=discharge/death and assume constant hazard rates λ01,λ02 and λ12 between the corresponding states. The hazards λij are interpreted as the daily risk of moving from state i to state j.

Fig. 1
figure 1

Multi-state model

Full size image

The infection hazard λ01, also denoted as the incidence density of NI, is estimated by dividing the number of NI events by the number of summed patient-days in state 0 [5]. Analogously, the event densities λ02 and λ12 are estimated by dividing the discharge/death events by the number of summed patient-days in state 0 and 1, respectively [5]. These estimates are formally obtained via maximum likelihood estimation [6]. Since the hazard rates are assumed to be time-constant, the time to leave state 0 follows an exponential distribution with the hazard rate λ01+λ02. Thus, the average sojourn time in state 0 is \(\frac {1}{\lambda _{01}+\lambda _{02}}\). Analogously, the time to leave state 1 follows an exponential distribution with the hazard rate λ12 leading to an average sojourn time in state 1 of \(\frac {1}{\lambda _{12}}\). The probability to acquire a NI is equal to \(\frac {\lambda _{01}}{\lambda _{01}+\lambda _{02}}\).

We can write the average LOS in terms of the hazards from the multi-state model, which is the sum of the sojourn time in state 0 and the sojourn time in state 1 multiplied with the probability to acquire a NI:

$$\begin{array}{*{20}l} \overline{LOS}=\frac{1}{\lambda_{01}+\lambda_{02}} + \frac{\lambda_{01}}{\lambda_{01}+\lambda_{02}} \times \frac{1}{\lambda_{12}} \end{array} $$

If we assume the common case that NI reduce the discharge hazard, i.e. \(\frac {\lambda _{12}}{\lambda _{02}}<1\), we can use some algebra to derive following relationship:

$$\begin{array}{*{20}l} \frac{1}{\lambda_{02}} < \overline{LOS} < \frac{1}{\lambda_{12}} \end{array} $$

where \(\frac {1}{\lambda _{02}}\) is interpreted as the average LOS in a hypothetical world without NI. The first inequality is shown as \(\frac {1}{\lambda _{0}2}<\overline {LOS} \Leftrightarrow \lambda _{12}(\lambda _{01}+\lambda _{02})<\lambda _{02}(\lambda _{12}+\lambda _{01}) \Leftrightarrow \lambda _{12}\lambda _{01}<\lambda _{02}\lambda _{01} \Leftrightarrow \lambda _{12}<\lambda _{02}\). The second inequality is shown as \(\overline {LOS}=(\lambda _{12}+\lambda _{01})/((\lambda _{01}+\lambda _{02})\lambda _{12})<(\lambda _{02}+\lambda _{01})/((\lambda _{01}+\lambda _{02})\lambda _{12}=1/\lambda _{12}\)

These inequalities mean that the mean LOS in a world without NI is smaller than the mean LOS in a real world and this is smaller than the mean sojourn time in state 1. Based on the multi-state model, four different approaches to quantify the LOS associated with NI can be derived.

Restrospective stratification of eventually infected and uninfected

The most common approach (A1) is to compare the average overall LOS of eventually infected patients with the average overall LOS of eventually uninfected patients. It addresses the following medical question of interest (see Table 1): ’How many days do patients with NI stay, on average, eventually longer in hospital than patients who will never acquire a NI?’. In terms of the multi-state model, the average overall LOS of eventually infected patients is the sum of the average sojourn times of state 0 and state 1, \(\frac {1}{\lambda _{01}+\lambda _{02}}+\frac {1}{\lambda _{12}}\). The average overall LOS of eventually uninfected patients is the sojourn time in state 0, \(\frac {1}{\lambda _{01}+\lambda _{02}}\). Thus, approach A1 is mathematically expressed by

$$\begin{array}{*{20}l} A_{1}&=\left(\frac{1}{\lambda_{01}+\lambda_{02}}+\frac{1}{\lambda_{12}}\right)-\left(\frac{1}{\lambda_{01}+\lambda_{02}}\right)=\frac{1}{\lambda_{12}}\\ &=\text{LOS difference of eventually infected and} \\&\quad\quad\quad \text{eventually uninfected} \end{array} $$
Table 1 Medical question of interest
Full size table

which is the average sojourn time in state 1, given the patient has reached this state, i.e., has acquired a NI. In this approach, the classification of infected and uninfected is done retrospectively at the end of hospital stay.

This approach does not distinguish between pre- and post-infection LOS and thus does not allow a prospective associational (or even causal) interpretation. The limitation is that the LOS before NI which is included in the LOS of eventually infected patients can not be interpreted as LOS attributed due to NI. Instead, the LOS before NI (which is per-se not attributable to NI) should count as uninfected LOS. Therefore, the following approaches have been developed.

Differentiating between pre- and post-infection length of stay

In contrast to the previous approach, the following approaches will differentiate between the pre-infection time and consequence of NI in terms of LOS.

The second approach A2, termed as attributable LOS [7, 8], compares the average sojourn time in state 1 \(\left (\frac {1}{\lambda _{12}}\right)\) with the average sojourn time in state 0 in a hypothetical world without NI \(\left (\frac {1}{\lambda _{02}}\right)\). The medical question of interest (see Table 1) is ’How many hospital days, on average, would a patient have stayed shorter if he/she would not have acquired a NI?’.

This is quantified by

$$\begin{array}{*{20}l} A_{2}&=\frac{1} {\lambda_{12}} - \frac{1}{\lambda_{02}} \\ &= \text{Attributable length of stay} \end{array} $$

In contrast to approach A1, the left part of the difference in approach \(A_{2} \left (\frac {1} {\lambda _{12}}\right)\) considers only the post-infection LOS of infected patients. Moreover, the right part \(\left (\frac {1}{\lambda _{02}}\right)\) considers a longer LOS than the one of approach A1 as \(\frac {1}{\lambda _{02}}> \frac {1}{\lambda _{01}+\lambda _{02}}\). This corrects for the limitations of approach A1. However, the limitation of approach A2 is that \(\frac {1}{\lambda _{02}}\) is not a real world mean time and is therefore a hypothetical quantity for LOS of uninfected patients.

In the third approach A3, we substract the average LOS in a hypothetical world from the one in a real world addressing the medical question ’How many hospital days would the average length of stay be shorter if all NI in the population would be eliminated?’. Algebraically, it is

$$\begin{array}{*{20}l} A_{3}&=\overline{LOS}-\frac{1}{\lambda_{02}}\\ &= \frac{\lambda_{01}}{\lambda_{01}+\lambda_{02}} \times \frac{1}{\lambda_{12}} \times \frac{(\lambda_{02}-\lambda_{12})} {\lambda_{02}}\\ &=\text{Population-attributable length of stay} \end{array} $$

This estimand is called the population-attributable LOS [8, 9], which is a population measure of extra LOS and compares the average LOS of a population in a world with NI with a population in a hypothetical world without NI.

In the fourth approach A4, we subtract the average length of stay from the sojourn time in state 1 which aims to answer the medical question ’How many days does a patient with NI stay, on average, longer in hospital?’ (see Table 1). It is

$$\begin{array}{*{20}l} A_{4}&= \left(\frac{\lambda_{02}} {\lambda_{12}}-1 \right) \times \frac{1}{\lambda_{01}+\lambda_{02}} \\ &=\text{Residual LOS of currently infected vs.}\\ &\quad\quad \text{currently uninfected } \end{array} $$

This estimand, also called the change of length of stay, is the established multi-state approach [10] and compares mean residual LOS between currently infected and uninfected patients using landmarking on each day in the hospital, it is a difference per infected patient.

Basic properties related to the hazard ratio \(\frac {\lambda _{12}}{\lambda _{02}}\)

In this section we consider basic relationships to the hazard ratio \(\frac {\lambda _{12}}{\lambda _{02}}\). The hazard ratio \(\frac {\lambda _{12}}{\lambda _{02}}\) is often calculated and it describes in a multiplicative way if and how NI prolongs LOS. A hazard ratio of 1 means that the daily chance to be discharged does not change if the patient acquires a NI meaning that NI does not prolong the LOS. It is more often the case that the hazard ratio is smaller than 1 indicating a prolonged LOS associated with NI. It is rarely the case that the hazard ratio is greater than 1 which would mean a shortened LOS associated with NI. It is obvious that approach A1 is always larger than 0 (A1>0) as λ12>0. Since it further does not depend on λ02, A1 always means that NI patients stay eventually longer than patients who never acquired NI, even if \(\frac {\lambda _{12}}{\lambda _{02}}=1\) or \(\frac {\lambda _{12}}{\lambda _{02}}>1\) which is not a required property. For the other approaches we have: \(\frac {\lambda _{12}}{\lambda _{02}}=1 \Leftrightarrow A_{2}=0 \Leftrightarrow A_{3}=0 \Leftrightarrow A_{4}=0\). It is also easily shown that \(\frac {\lambda _{12}}{\lambda _{02}}<1 \Leftrightarrow A_{2}>0 \Leftrightarrow A_{3}>0 \Leftrightarrow A_{4}>0\) and \(\frac {\lambda _{12}}{\lambda _{02}}>1 \Leftrightarrow A_{2}<0 \Leftrightarrow A_{3}<0 \Leftrightarrow A_{4}<0\). Thus, approaches A2, A3 and A4 have the required mathematically equivalent properties regarding the direction of the hazard ratio \(\frac {\lambda _{12}}{\lambda _{02}}\) whereas approach A1 does not.

In Table 2, the properties of all approaches are displayed, summarized and contrasted to each other.

Table 2 Approaches and their properties
Full size table

Additive and multiplicative comparisons of approaches

Before we compare the approaches in a additive and multiplicative way, we note that approaches A1 and A2 do not depend on infection hazard λ01 whereas approaches A3 and A4 do. Further, approaches A1, A2 and A4 are at the patient-individual level and therefore directly comparable whereas A3 is at the population-level. All approaches are displayed in the Table 3. We further note that there is also following relationship: A3+A4=A2.

Table 3 Overview and relationships of approaches to quantify prolonged hospital stay associated with nosocomial infections
Full size table

Comparing approaches A 1 and A 2

The additive relationship between approaches A1 and A2 is just the average length of stay of a population in a hypothetical world without NI \(\left (\frac {1}{\lambda _{02}}\right)\). The multiplicative relationship is \(\frac {A_{1}}{A_{2}}=\frac {\lambda _{02}}{\lambda _{02}-\lambda _{12}}\).

Comparing approaches A 1 and A 3

As before, the relationship between approaches A1 and A3 is best described and communicable in an additive way. The difference between A1 and A3 is \(A_{1}-A_{3}=\frac {1}{\lambda _{02}} \times \frac {\lambda _{02}^{2}+\lambda _{12}\lambda _{01}} {\lambda _{12}\lambda _{02}+\lambda _{12}\lambda _{01}}\) (Table 3). It is mainly the average length of stay of a population in a hypothetical world without NI \(\left (\frac {1}{\lambda _{02}}\right)\); multiplied with the factor \(\frac {\lambda _{02}^{2}+\lambda _{12}\lambda _{01}} {\lambda _{12}\lambda _{02}+\lambda _{12}\lambda _{01}}\) which is often larger than 1 as λ02 is often larger than λ12. In contrast, the multiplicative relationship is \(\frac {A_{1}}{A_{3}}=\frac {\lambda _{02}(\lambda _{01}+\lambda _{02})} {\lambda _{01}(\lambda _{02}-\lambda _{12})}\).

Comparing approaches A 1 and A 4

The relationship between approaches A1 and A4 is best described in an additive way. The difference is \(A_{1}-A_{4}=\frac {1}{\lambda _{12}} \times \frac {\lambda _{01}+\lambda _{12}}{\lambda _{01}+\lambda _{02}}=\overline {LOS}\) (Table 3). Thus, it mainly depends on the average sojourn time of state 1 which is \(\frac {1}{\lambda _{12}}\); the factor \(\frac {\lambda _{01}+\lambda _{12}}{\lambda _{01}+\lambda _{02}}\) is usually lower than 1 as λ02 is often larger than λ12. The multiplicative relationship is \(\frac {A_{1}}{A_{4}}=\frac {\lambda _{01}+\lambda _{02}}{\lambda _{02}-\lambda _{12}}\).

Comparing approaches A 2 and A 3

Approaches A3 and A2 are best compared in a multiplicative way: \(\frac {A_{3}}{A_{2}}=\frac {\lambda _{01}}{\lambda _{01}+\lambda _{02}}=\text {risk(NI)}\). The additive comparison is \(A_{2}-A_{3}=A_{4}=\frac {\lambda _{02}-\lambda _{12}}{\lambda _{12}(\lambda _{01}+\lambda _{02})}\).

Comparing approaches A 2 and A 4

Approach A2 is linked to approach A4 with \(\frac {A_{2}}{A_{4}}=\frac {\lambda _{01}+\lambda _{02}}{\lambda _{02}}=\frac {\text {odds(NI)}}{\text {risk(NI)}}\). Based on this formula, it follows that both approaches give similar results if the nosocomial infection is rare (risk is smaller than 10%). The additive comparison is \(A_{2} - A_{4}=A_{3}=\frac {\lambda _{01}}{\lambda _{02}}\times \frac {\lambda _{02}-\lambda _{12}}{\lambda _{12}(\lambda _{01}+\lambda _{02})}\).

Comparing approaches A 3 and A 4

In contrast to the previous comparisons to approach A1, approaches A3 and A4 are best compared in a multiplicative way. There is the following simple relationship: \(\frac {A_{3}}{A_{4}}=\frac {\lambda _{01}}{\lambda _{02}}= \text {odds(NI)}\). Thus, the factor odds(NI) links the population-level approach A3 to the individual-level approach A4. The additive relationship is rather complex: \(A_{4}-A_{3}=\frac {\lambda _{02}-\lambda _{01}}{\lambda _{02}} \times \frac {\lambda _{02}-\lambda _{12}}{\lambda _{12}(\lambda _{01}+\lambda _{02})}\).

Real data example

We use publicly available data from the R-package etm [11]. This is an observational prospectively collected cohort study including 756 intensive care patients from Germany of whom 124 patients acquired a nosocomial pneumonia (NI) during their stay in the intensive care unit (ICU). The data used here is a random sample from a larger cohort which is described in detail elsewhere [12].

Results

The cohort study followed 756 patients during their stay at the intensive-care unit. Of these patients, 124 patients acquired a NI during their stay in the ICU. The summed patient-days without NI was 6442 and with NI 1527. Thus, the constant hazards can be estimated as follows: \(\hat {\lambda }_{01}=124/6442=0.0192\), \(\hat {\lambda }_{02}=632/6442=0.0981\), and \(\hat {\lambda }_{12}=124/1527=0.0812\). The average length of stay of this cohort is \(\overline {LOS}=10.54\) days; the sojourn time in state 0 is \(\frac {1}{\hat {\lambda }_{01}+\hat {\lambda }_{02}}=8.52\) days and \(\frac {1}{\hat {\lambda }_{12}}=12.31\) days in state 1, respectively. The results of the different approaches are diverse, however, with different interpretation. As expected, A1 provides a exaggerated value of 12.31 days which just means that patients with NI stay eventually 12.31 days longer at ICU then eventually uninfected patients. In contrast, A4 yields that a NI prolongs the LOS by mean 1.77 ICU days per infected patient. The population-attributable LOS (A3) is 0.35 days meaning that there are on average 0.35 additional ICU days attributable to NI at the population level. The attributable LOS (A2) is 2.12 ICU days, interpreted as the average LOS which is attributable to NI for an infected patient.

Discussion

A multi-state model was used to mathematically derive four fundamentally different approaches to quantify the prolonged length of stay associated with nosocomial infections or other adverse events [13]. The relationships were displayed in an additive as well as a multiplicative way.

As in previous articles [2, 4], we encourage researchers to not retrospectively stratify by infection status and, consequently, to avoid the use of approach A1 because it does not differentiate between pre- and post-infection time and thus does not allow a causal interpretation.

The other approaches are suitable because they implicitly distinguish between the pre-infection time (which might be a risk factor) and post-infection time (which might be a consequence) of nosocomial infections. The main difference is the interpretation and we showed mathematical formulas how they are linked to each other. Thus, this knowledge can be used to better understand apparent discrepancies in the literature and transfer published values from one approach to the other.

The question whether nosocomial infections prolong hospital stay is - from the methodological point of view - related to ’life years lost among patients with a given disease’ [14] by replacing discharge with death and length of stay with age. Andersen [14] considered also a multistate model, the classical illness-death model, in order to study different statistical variants and extensions of our approach A4 including time-inhomogeneous Markov models, censoring and semi-Markov models. Approaches A1- A3 are not considered by Andersen and complement his considerations.

This study has following limitations. First, we focused on the basic approaches and did not consider any other covariates such as characteristics from the patient-, hospital- or even country-level (for instance, as in Stewardson et al. [15]). Even though there exists regression models [16] which allows for adjusting the change of length of stay (approach A4), we believe that the choice of the fundamental approach has a much stronger impact on the results than the adjustment for covariates. For instance, previous studies indicated that the time-dependent bias could not be redeemed by adjustment of several patient-level covariates [4]. Second, the hazard rates are often not time-homogeneous in real-data settings. Even though time-inhomogeneous approaches exist, we are convinced that this simplification is required to provide a clear transparency which leads to a better understanding of basic distinctions. Third, we combined the diametrically opposed endpoints discharge (alive) and death. We think that this combination is reasonable if the focus is on length of stay and their related economic costs, the topic of this paper. However, as rapid death results in shorter LOS, a length-of-stay analysis should always be accompanied with an analysis with respect to mortality. This can be done by using an extended multi-state model that distinguishes between inpatient death and discharge alive [5, 6].

Conclusion

We conclude that a clear distinction between different estimands is needed to better understand apparently large discrepancies in the literature. We recommend the use of approaches which differentiates between pre- and post-infection time.