1 Introduction

The Von Mises yield function is the most widely used isotropic yield function for its simple mathematical expression. It is convenient for use in theoretical derivation and finite element (FE) calculation. However, based on the isotropic hypothesis, the Von Mises yield function cannot describe anisotropic materials, especially for sheet metal. After several repetitions of rolling and heat treatment, sheet metals, which have a texture formed by the fibrous structure and preferred orientation of crystallization, exhibit obvious anisotropy [1,2,3,4].

Various anisotropic yield functions have been proposed to describe the anisotropic deformation behavior of materials. Among them, the quadratic anisotropic yield function (Hill48 yield function) proposed by Hill [5] is the most famous and is widely used because of its simple mathematical expression [6,7,8,9,10,11,12]. However, the Hill48 quadratic yield function can only explain four test results, and the results of the “abnormal” yield behavior observed in some processes involving rolled sheet metals cannot be reasonably described. Hence, this model is not always sufficient to represent real physical processes if we use the traditional method to obtain the parameters. Using a different parameter solving method may, however, have a different effect on the accuracy of the yield criteria [1, 13,14,15].

Besides Hill’s quadratic yield model, many other anisotropic yield models have been developed. For example, the famous plane stress yield function, Yld2000-2d, was proposed by Barlat et al. [16] to describe the anisotropic plastic deformation of sheet metals, especially for aluminum alloy. The Yld2000-2d yield function involves eight parameters which can be determined by the yield stresses and r-values along 0°, 45°, and 90°, and the equi-biaxial tension direction [16,17,18,19,20]. However, the solid element, which is necessary for some thick sheet metals especially when the stress along normal direction in the sheet plane cannot be ignored, in FE simulation cannot be used with the Yld2000-2d yield function because only plane stress variants are considered. The Yld2004 yield function with 18 parameters proposed by Barlat et al. [21], can predict six or eight earings [22,23,24,25,26,27]. Vegter et al. [28] proposed an anisotropic plane stress yield function based on a yield locus description that applies second order Bezier interpolations. Vegter’s yield function requires 17 independent parameters, which is expected to predict six or eight earings [28, 29]. Although some of the above yield functions can take into account more experimental results and predict complex anisotropic behavior, the mathematical expression or the solutions of the parameters are quite complicated, which is inconvenient for engineering application. Besides, a user subroutine is needed to implement the needed yield function into the FE (FE) software, which will increase the cost of FE simulation and cause slow convergence or non-convergence. As mentioned above, Hill’s quadratic yield function is the simplest of all the anisotropic yield functions. It involves only four parameters, making it convenient for use in the study. For an isotropic material, the function reduces to the Von Mises yield function. Hence, many researchers still prefer to use Hill’s yield model to develop new theories [30,31,32,33,34,35].

The parameters of the Hill48 yield function can be solved using the yield stress or r-value under different loading conditions [1, 14]. Existing studies have shown that both the yield stress and r-value have some effect on the earing phenomenon in deep drawing. However, the number and shape of the earing defects in deep drawing cannot be described accurately by the Hill48 yield function if the parameters are solved with yield stresses or r-values alone [1, 33].

In this study, a new method that takes the yield stress and r-value together into consideration to obtain the parameters of the Hill48 yield function is proposed. The anisotropic behavior of the 5754O aluminum alloy sheet is discussed and FE simulations of the deep drawing test are performed based on different yield functions to predict the earing phenomenon. The proposed method that uses the Hill48 yield function to predict the formation of eight earings in the deep drawing of 575O aluminum alloy sheet is validated using experimental results. This work forms the prerequisite for the deep drawing process optimization including blank shape optimization. It also lays the foundation for the accurate engineering analysis of the anisotropic sheet-forming problem and the realization of an effective FE analysis.

2 Hill48 Yield Function (Using the Associated Flow Rule)

The expression of the Hill48 yield function is shown in Eq. (1):

$$ \begin{gathered} f = F\left( {\sigma _{{yy}} - \sigma _{{xx}} } \right)^{2} + G\left( {\sigma _{{zz}} - \sigma _{{xx}} } \right)^{2} + H\left( {\sigma _{{xx}} - \sigma _{{yy}} } \right)^{2} \hfill \\ \quad \quad + 2L\sigma _{{yz}}^{2} + 2M\sigma _{{zx}}^{2} + 2\sigma _{{xy}}^{2} = \bar{\sigma }^{2} , \hfill \\ \end{gathered} $$
(1)

where x, y, z represent the orthotropic anisotropic direction. F, G, H, L, M, and N are independent anisotropic characteristic parameters determined from different material tests. \( \bar{\sigma } \) is the equivalent stress. When 3F = 3G = 3H = L = M = N, Eq. (1) will transform the Von Mises yield function for describing an isotropic material. Eq. (1) is appropriate for the FE simulation of sheet metal forming where a solid element should be used so that the stress along the normal direction of sheet is not ignored.

The metal sheet is often in a plane stress state during the forming process, that is, \( \sigma_{zz} \), \( \sigma_{xz} \), \( \sigma_{yz} \) is 0 and then, Eq. (1) can be simplified to

$$ f = \left( {G + H} \right)\sigma_{xx}^{2} - 2H\sigma_{xx} \sigma_{yy} + \left( {H + F} \right)\sigma_{yy}^{2} + 2N\sigma_{xy}^{2} = \bar{\sigma }^{2} . $$
(2)

Eq. (2) is appropriate for the FE simulation with shell- type elements in which only the plane stress is considered, but is not appropriate for that with solid elements where the stress along the normal direction should be considered.

3 Determination of the Parameters of Hill48 Yield Function

3.1 General Formula for Yield Stress and Anisotropy along Different Directions

According to the expression of the Hill48 yield function (Eq. (2)) in the plane stress state, the x and y directions are assumed to be the rolling direction and the transverse direction. The rolling direction is taken as the reference direction, that is, the yield stress in the rolling direction \( \sigma_{0} \) is taken as the reference stress. Therefore, we have

$$ \sigma_{xx} = \sigma_{0} = \bar{\sigma }. $$
(3)

According to the stress transformation formula, the stresses are expressed as:

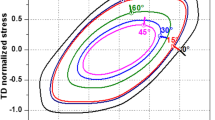
$$ \left\{ {\begin{array}{*{20}l} {\sigma _{x} = \sigma _{1} \cos ^{2} \alpha + \sigma _{2} \sin ^{2} \alpha - 2\tau _{{xy}} \cos \alpha \sin \alpha ,} \\ {\sigma _{y} = \sigma _{1} \sin ^{2} \alpha + \sigma _{2} \cos ^{2} \alpha + 2\tau _{{xy}} \cos \alpha \sin \alpha ,} \\ {\sigma _{{xy}} = \left( {\sigma _{1} - \sigma _{2} } \right)\cos \alpha \sin \alpha + \tau _{{xy}} \left( {\cos ^{2} \alpha - \sin ^{2} \alpha } \right),} \\ \end{array} } \right.$$
(4)

where \( \sigma_{1} \) is the stress along the angle α with respect to the reference direction, \( \sigma_{2} \) is the stress perpendicular to \( \sigma_{1} \) direction, and \( \tau_{xy} \) is the shear stress along the direction having the angle α. These stresses and the corresponding directions are shown in Figure 1.

Figure 1
figure 1

Stresses and corresponding directions at the angle α of the rolling direction

Full size image

The uniaxial tensile stress at an angle α to the rolling direction is set as \( \sigma_{\alpha } \) and then, we have \( \sigma_{1} = \sigma_{\alpha } \), \( \sigma_{2} = 0 \), \( \tau_{xy} = 0 \). Consequently, from Eq. (4), the stress component in the xoy plane is [36].

$$ \left\{ \begin{array}{l} \sigma_{xx} = \sigma_{\alpha } \cos^{2} \alpha , \hfill \\ \sigma_{yy} = \sigma_{\alpha } \sin^{2} \alpha , \hfill \\ \sigma_{xy} = \sigma_{\alpha } \sin \alpha \cos \alpha . \hfill \\ \end{array} \right. $$
(5)

The uniaxial tensile yield stress at the angle α to the rolling direction can be derived based on Eqs. (2), (3), and (5):

$$ \left\{ \begin{array}{l} \sigma_{\alpha } { = }\frac{{\sigma_{0} }}{{\sqrt {A + B + C} }}, \hfill \\ A = \left( {G + H} \right)\cos^{4} \alpha , \hfill \\ B = \left( {F + H} \right)\sin^{4} \alpha , \hfill \\ C = 2\left( {N - H} \right)\sin^{2} \alpha \cos^{2} \alpha . \hfill \\ \end{array} \right. $$
(6)

According to the associated flow criterion, the yield function in Eq. (2) is also a plastic potential function. The plastic strain increments \( {\text{d}}\varepsilon_{x} \), \( {\text{d}}\varepsilon_{y} \), and \( {\text{d}}\gamma_{xy} \) based on the Hill48 yield function can be obtained according to Drucker’s formula [37]:

$$ \left\{ \begin{array}{l} {\text{d}}\varepsilon_{xx} = {\text{d}}\lambda \left[ {2\left( {G + H} \right)\sigma_{xx} - 2H\sigma_{yy} } \right], \hfill \\ {\text{d}}\varepsilon_{yy} = {\text{d}}\lambda \left[ {2\left( {F + H} \right)\sigma_{yy} - 2H\sigma_{xx} } \right], \hfill \\ {\text{d}}\gamma_{xy} = 4{\text{d}}\lambda N\sigma_{xy} . \hfill \\ \end{array} \right. $$
(7)

Then, with Eqs. (5) and (7) we have

$$ \left\{ \begin{array}{l} {\text{d}}\varepsilon_{xx} = {\text{d}}\lambda \left[ {2\left( {G + H} \right)\sigma_{\alpha } \cos^{2} \alpha - 2H\sigma_{\alpha } \sin^{2} \alpha } \right], \hfill \\ {\text{d}}\varepsilon_{yy} = {\text{d}}\lambda \left[ {2\left( {F + H} \right)\sigma_{\alpha } \sin^{2} \alpha - 2H\sigma_{\alpha } \cos^{2} \alpha } \right], \hfill \\ {\text{d}}\gamma_{xy} = 4{\text{d}}\lambda N\sigma_{\alpha } \sin \alpha \cos \alpha . \hfill \\ \end{array} \right. $$
(8)

According to the Mohr circle rule for strains, we have,

$$ \varepsilon_{\alpha } { = }\frac{{\varepsilon_{x} + \varepsilon_{y} }}{2} + \frac{{\varepsilon_{x} - \varepsilon_{y} }}{2}\cos 2\alpha + \frac{{\gamma_{xy} }}{2}\sin 2\alpha . $$
(9)

Then, the strain increments \( {\text{d}}\varepsilon_{\alpha } \) in the loading direction and \( {\text{d}}\varepsilon_{\alpha + 90^\circ } \) in the width direction [33] are

$$ \left\{ \begin{array}{l} {\text{d}}\varepsilon_{\alpha } = {\text{d}}\varepsilon_{xx} \cos^{2} \alpha + {\text{d}}\varepsilon_{yy} \sin^{2} \alpha + {\text{d}}\gamma_{xy} \sin \alpha \cos \alpha , \hfill \\ {\text{d}}\varepsilon_{\alpha + 90^\circ } = {\text{d}}\varepsilon_{xx} \sin^{2} \alpha + {\text{d}}\varepsilon_{yy} \cos^{2} \alpha - {\text{d}}\gamma_{xy} \sin \alpha \cos \alpha . \hfill \\ \end{array} \right. $$
(10)

Based on the assumption that the plastic volume is constant, we have

$$ {\text{d}}\varepsilon_{x} + {\text{d}}\varepsilon_{y} + {\text{d}}\varepsilon_{z} = 0 , $$
(11)
$$ {\text{d}}\varepsilon_{z} = - \left( {{\text{d}}\varepsilon_{x} + {\text{d}}\varepsilon_{y} } \right){ = } - 2\left( {G\cos^{2} \alpha + F\sin^{2} \alpha } \right)\sigma_{\alpha } {\text{d}}\lambda . $$
(12)

According to the definition of anisotropy index, the anisotropy index under uniaxial tension along the angle α can be obtained

$$ r_{\alpha } = \frac{{{\text{d}}\varepsilon_{\alpha + 90^\circ } }}{{{\text{d}}\varepsilon_{z} }} = \frac{{H + \left( {2N - F - G - 4H} \right)\sin^{2} \alpha \cos^{2} \alpha }}{{F\sin^{2} \alpha + G\cos^{2} \alpha }}. $$
(13)

3.2 Solution of Regional Parameters

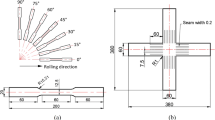
The uniaxial tensile yield stresses of 0°, 22.5°, 45°, 67.5°, and 90° direction are set as \( \sigma_{0} \), \( \sigma_{22.5} \), \( \sigma_{45} \), \( \sigma_{67.5} \), and \( \sigma_{90} \), and the anisotropy indexes (r-values) are set as r0, r22.5, r45, r67.5, and r90, respectively. The divisions on the sheet metal are shown in Figure 2, where X is the 0° direction (rolling direction), and Y is the 90° direction (transverse direction).

Figure 2
figure 2

Partitioning of the circular blank sheet (only one quarter of the divided model is displayed, and the four parts are marked I, II, III, and IV)

Full size image

Because of the anisotropy of the materials, the materials properties will vary from the loading directions. In addition, both stress anisotropy and deformation anisotropy play an important role in describing the anisotropic deformation behavior [1]. However, only one class of anisotropy from these can be incorporated in the Hill48 yield function when the parameters are determined using the traditional method. Based on the partitions shown above, more material data will be considered and the simulation results are expected to be more accurate. For example, the boundary of the first region extends from 0° to 22.5°. Both the stresses and r-values along the 0° and 22.5° directions (\( \sigma_{0} \), \( \sigma_{22.5} \), r0, r22.5) will be adopted to determine the parameters of the Hill48 yield function. The material properties along the 22.5° direction will be adopted to solve the parameters of the Hill48 yield function for both Parts I and II.

3.2.1 Yield Stress and Anisotropy Index Along Different Directions

In Sect. 3.1, the relationship between the uniaxial material properties (\( \sigma \) and r-value) and the loading direction (α) are obtained.

That is, the yield stress \( \sigma \) and r-value along any direction can be calculated. Then, let α be equal to 0°, 22.5°, 45°, 67.5°, and 90°, respectively. The relation between the parameters of the Hill48 yield function and the uniaxial material properties (yield stresses and r-values) can be obtained as follows.

(1) When α = 0°,

$$ G + H = 1 , $$
(14)
$$ r_{0} = \frac{H}{G}. $$
(15)

(2) When α = 22.5°,

$$ \left( {3 - 2\sqrt 2 } \right)F + \left( {3 + 2\sqrt 2 } \right)G + 4H + 2N = \frac{{8\sigma_{0}^{2} }}{{\sigma_{22.5}^{2} }} , $$
(16)
$$ r_{22.5} = - \frac{F + G - 4H - 2N}{{\left( {4 - 2\sqrt 2 } \right)F + \left( {4 + 2\sqrt 2 } \right)G}}. $$
(17)

(3) When α = 45°,

$$ F + G + 2N = \frac{{4\sigma_{0}^{2} }}{{\sigma_{45}^{2} }} , $$
(18)
$$ r_{45} = - \frac{F + G - 2N}{{2\left( {F + G} \right)}}. $$
(19)

(4) When α = 67.5°,

$$ \left( {3 + 2\sqrt 2 } \right)F + \left( {3 - 2\sqrt 2 } \right)G + 4H + 2N = \frac{{8\sigma_{0}^{2} }}{{\sigma_{67.5}^{2} }} , $$
(20)
$$ r_{67.5} = - \frac{F + G - 4H - 2N}{{\left( {4 + 2\sqrt 2 } \right)F + \left( {4 - 2\sqrt 2 } \right)G}}. $$
(21)

(5) When α = 90°,

$$ F + H = \frac{{\sigma_{0}^{2} }}{{\sigma_{90}^{2} }} , $$
(22)
$$ r_{90} = \frac{H}{F}. $$
(23)

3.2.2 Calculation of the Parameters of Hill48 Yield Function for Each Region

(1) Part I (0°‒22.5°)

For part I, the tensile properties (both yield stresses and r-values) along 0° and 22.5° directions are adopted since the direction of tensile deformation in part I is between 0° and 22.5°. According to Eqs. (14)‒(17),

$$ F = \frac{{\left( {4 + 2\sqrt 2 } \right)\sigma_{0}^{2} }}{{\left( {r_{22.5} + 1} \right)\sigma_{22.5}^{2} }} - \frac{3 + 2\sqrt 2 }{{r_{0} + 1}} , $$
(24)
$$ G = \frac{1}{{r_{0} + 1}} , $$
(25)
$$ H = \frac{{r_{0} }}{{r_{0} + 1}} , $$
(26)
$$ N = \frac{{\left( {4r_{22.5} + 2 + \sqrt 2 } \right)\sigma_{0}^{2} }}{{\left( {r_{22.5} + 1} \right)\sigma_{22.5}^{2} }} - \frac{{2r_{0} + \sqrt 2 + 1}}{{r_{0} + 1}}. $$
(27)

(2) Part II (22.5°‒45°)

Similarly, according to Eqs. (16)‒(19),

$$ F = \frac{{\left( {\sqrt 2 + 1} \right)\sigma_{0}^{2} }}{{\left( {r_{45} + 1} \right)\sigma_{45}^{2} }} + \frac{{\sqrt 2 \sigma_{0}^{2} }}{{\left( {r_{22.5} + 1} \right)\sigma_{22.5}^{2} }} , $$
(28)
$$ G = \frac{{\left( {\sqrt 2 + 1} \right)\sigma_{0}^{2} }}{{\left( {r_{45} + 1} \right)\sigma_{45}^{2} }} + \frac{{\sqrt 2 \sigma_{0}^{2} }}{{\left( {r_{22.5} + 1} \right)\sigma_{22.5}^{2} }} , $$
(29)
$$ H = \frac{{2r_{22.5} \sigma_{0}^{2} }}{{\left( {r_{22.5} + 1} \right)\sigma_{22.5}^{2} }} - \frac{{\left( {2r_{45} + 1} \right)\sigma_{0}^{2} }}{{\left( {r_{45} + 1} \right)\sigma_{45}^{2} }} , $$
(30)
$$ N = \frac{{\left( {2r_{45} + 1} \right)\sigma_{0}^{2} }}{{\left( {r_{45} + 1} \right)\sigma_{45}^{2} }} . $$
(31)

(3) Part III (45°‒67.5°)

From Eqs. (18)‒(21),

$$ F = \frac{{\left( {1 - \sqrt 2 } \right)\sigma_{0}^{2} }}{{\left( {r_{45} + 1} \right)\sigma_{45}^{2} }} + \frac{{\sqrt 2 \sigma_{0}^{2} }}{{\left( {r_{67.5} + 1} \right)\sigma_{67.5}^{2} }} , $$
(32)
$$ G = \frac{{\left( {\sqrt 2 + 1} \right)\sigma_{0}^{2} }}{{\left( {r_{45} + 1} \right)\sigma_{45}^{2} }} - \frac{{\sqrt 2 \sigma_{0}^{2} }}{{\left( {r_{67.5} + 1} \right)\sigma_{67.5}^{2} }} , $$
(33)
$$ H = \frac{{2r_{67.5} \sigma_{0}^{2} }}{{\left( {r_{67.5} + 1} \right)\sigma_{67.5}^{2} }} - \frac{{\left( {2r_{45} + 1} \right)\sigma_{0}^{2} }}{{\left( {r_{45} + 1} \right)\sigma_{45}^{2} }} , $$
(34)
$$ N = \frac{{\left( {2r_{45} + 1} \right)\sigma_{0}^{2} }}{{\left( {r_{45} + 1} \right)\sigma_{45}^{2} }} . $$
(35)

(4) Part IV (67.5°‒90°)

From Eqs. (20)‒(23),

$$ F = \frac{{\sigma_{0}^{2} }}{{\left( {r_{90} + 1} \right)\sigma_{90}^{2} }} , $$
(36)
$$ G = \frac{{\left( {4 + 2\sqrt 2 } \right)\sigma_{0}^{2} }}{{\left( {r_{67.5} + 1} \right)\sigma_{67.5}^{2} }} - \frac{{\left( {3 + 2\sqrt 2 } \right)\sigma_{0}^{2} }}{{\left( {r_{90} + 1} \right)\sigma_{90}^{2} }} , $$
(37)
$$ H = \frac{{r_{90} \sigma_{0}^{2} }}{{\left( {r_{90} + 1} \right)\sigma_{90}^{2} }} , $$
(38)
$$ N = \frac{{\left( {4r_{67.5} + 2 + \sqrt 2 } \right)\sigma_{0}^{2} }}{{\left( {r_{67.5} + 1} \right)\sigma_{67.5}^{2} }} - \frac{{\left( {2r_{90} + 1 + \sqrt 2 } \right)\sigma_{0}^{2} }}{{\left( {r_{90} + 1} \right)\sigma_{90}^{2} }} . $$
(39)

4 Performance of Different Yield Functions in Predicting Earing

4.1 Solution for Stress and Strain

The 5754O aluminum alloy sheet was used as sample for the uniaxial tensile test. The material constants of the sheet are shown in Table 1 [38].

Table 1 Material constants of 5754O aluminum alloy sheet
Full size table

The stress-strain values are calculated using the Voce-shaped stress-strain relationship. The expression is given by [38]

$$ \bar{\sigma } = \sigma_{0} + q\left( {1 - \exp \left( { - b\bar{\varepsilon }_{\text{p}} } \right)} \right) , $$
(40)

where \( \bar{\sigma } \) is the equivalent stress, \( \sigma_{0} \) is the initial yield strength, \( \bar{\varepsilon }_{\text{p}} \) is the equivalent plastic strain, q and b are the fitted material constants; the parameter values are shown in Table 2 [1].

Table 2 Material constants for the Voce-shaped stress-strain relationship
Full size table

4.2 Solution for Anisotropic Parameters

The anisotropy parameters of the Hill48 yield function are obtained using Eqs. (24)‒(39) and the values in Table 1 and Table 2, and the region-specific parameters are shown in Table 3.

Table 3 Anisotropic parameters of the Hill48 yield function
Full size table

In Abaqus, anisotropic yield behavior is defined based on the Hill48 yield function and six specific parameters are required to characterize the anisotropic properties of materials. However, only four specific parameters need to be calculated under the plane stress state.

The four coefficients of the Hill48 yield function under the plane stress state are defined as Eq. (41) [14]:

$$ \left\{ \begin{array}{l} F = \frac{1}{{2R_{22}^{2} }} + \frac{1}{{2R_{33}^{2} }} - \frac{1}{{2R_{11}^{2} }}, \\ G = \frac{1}{{2R_{11}^{2} }} + \frac{1}{{2R_{33}^{2} }} - \frac{1}{{2R_{22}^{2} }}, \\ H = \frac{1}{{2R_{11}^{2} }} + \frac{1}{{2R_{22}^{2} }} - \frac{1}{{2R_{33}^{2} }}, \\ N = \frac{3}{{2R_{12}^{2} }}. \\ \end{array} \right. $$
(41)

where \( R_{11} \), \( R_{22} \), \( R_{33} \) and \( R_{12} \) are four specified material parameters for using the Hill48 yield function in Abaqus. There are two other parameters, \( R_{13} \) and \( R_{23} \), whose values are assumed as \( R_{13} = R_{23} { = }1 \). Then, according to Eq. (41), \( R_{ij} \) can be written as Eq. (42). The calculation results are shown in Table 4.

Table 4 Four specified material parameters for using the Hill48 yield function in Abaqus
Full size table
$$ \left\{ \begin{array}{l} R_{11} = \sqrt {\frac{1}{G + H}} , \\ R_{22} = \sqrt {\frac{1}{F + H}} , \\ R_{33} = \sqrt {\frac{1}{F + G}} , \\ R_{12} = \sqrt {\frac{3}{2N}} . \\ \end{array} \right. $$
(42)

4.3 FE Simulation of Deep Drawing Test

Based on the above data, the FE simulation of the 5754O aluminum alloy sheet is performed. A deep drawing test was carried out on the sheet metal test machine. The process parameters are shown in Table 5. The schematic diagram of the deep drawing test is shown in Figure 3 [1].

Table 5 Deep drawing process parameters (mm)
Full size table
Figure 3
figure 3

Schematic diagram of deep drawing

Full size image

We take four nodes located in different locations from the edge to the center along the radial direction, followed by the node 1, the node 2, the node 3, and the node 4, as is shown in Figure 4. Figure 5 shows the strain-time curves of the four nodes. It can be seen from Figure 5 that strain of four points does not increase until a certain time. The closer to center the point is, the smaller the plastic deformation is, and the quicker the strain is to reach the maximum value. The greater the plastic deformation at the point near the edge, the later the strain reaches its maximum value. When the blank enters the cup wall, the plastic deformation no longer increases obviously. Therefore, we can speculate that the main deformation process of earings is before the material enters the cup wall.

Figure 4
figure 4

Location of four nodes along the radial direction

Full size image
Figure 5
figure 5

Strain-time curves of nodes from the edge to the center in the radial direction

Full size image

Three yield functions, namely, Yld2000-2d (implemented into ABAQUS by coding UMAT subroutine), Von Mises, and Hill48, are adopted to carry out the deep drawing simulations. The Hill48 parameters are determined using the traditional method and the proposed method shown above. Figure 6(a) shows the final shape of the part as obtained from the simulation based on Hill48 where the parameters are determined by the method proposed in this study. Figure 6(b) shows the experimental results and Figure 6(c) shows the comparison of experimental and simulation results. We compared the simulation results and the experimental results in terms of the part port height as shown in Figure 7. The simulation results based on the Hill48 yield function along with the parameter determination method proposed in this study can almost accurately predict the number and shape of the earings. The simulation results are in good agreement with the experimental results in the range of 0°‒360°.

Figure 6
figure 6

Comparison of the simulation results for each method with the experimental results

Full size image
Figure 7
figure 7

Comparison of simulation results and experimental results based on shell element

Full size image

When conditions other than the method are the same, and the step time is 1 s, it can be seen from Figure 8 that the computation time is the longest for Yld2000, which is much longer than that required for the other three methods. The other three methods have similar computation times, which are shorter. The computation time based on the new method proposed in this paper is slightly less than that based on the original Hill48 yield criterion, which saves time and increases efficiency.

Figure 8
figure 8

Computation time for different methods

Full size image

4.4 Discussions

As shown in Figure 7, we can see that, for the 5754O aluminum alloy sheet, different yield functions have a great influence on the prediction of earing. The Yld2000-2d yield criterion not only involves a large number of parameters and computations, but also can only predict up to four earings. The results obtained based on the original Hill48 yield criterion also cannot accurately describe the earings when compared with experimental result. The proposed new method combined with the FE simulation successfully predicted the eight earings, which can describe the experimental results more accurately. The simulated earing shape and trend are in good agreement with the experimental results. It can be seen from Figure 6(c) and Figure 7 that the results obtained using the new method are in good agreement with the experimental results. The above conclusions are applicable to other sheet metals as well. Shell type elements (S4R) are adopted in the simulated results shown in Figure 6. Similar results can be obtained with solid elements (e.g., C3D8R), which will not be demonstrated in this study.

The two traditional methods of the Hill48 yield function cannot accurately describe the stress anisotropy and the deformation anisotropy in different directions at the same time, while only one method can be used to solve the anisotropic parameters in practical applications [1]. With the method proposed in this study, which takes into account the stress anisotropy and deformation anisotropy simultaneously, the theoretical calculation and the simulation accuracy can be improved. As can be surmised from the general expression for the yield stress and anisotropy index at any angle in Sect. 3.1, the yield stress and anisotropy index in the direction of the boundary in a certain region can be obtained. Then, the anisotropic characteristic parameters are determined and the corresponding simulated results coincide with the experimental results. Besides, this avoids complex calculations when using other specialized yield functions to solve the parameters and does not increase the corresponding FE simulation costs.

5 Conclusions

  1. (1)

    A brand new method to predict eight earings that may occur during the deep drawing process is proposed. We divide a quarter-circular blank into four equal sectorial regions, and use the yield stress and anisotropy index simultaneously to solve for the parameters in each region.

  2. (2)

    Based on the theories of elastic-plastic mechanics, the Hill48 quadratic yield model is taken as the research object of study for solution, and obtain a general expression for the material property parameters - yield stress and anisotropy index at any angle.

  3. (3)

    Based on the new method, the FEFE simulation of the deep drawing process of a 5754O aluminum alloy sheet are carried out, and eight earings are successfully predicted, which is in good agreement with the experimental results.

  4. (4)

    In practical applications, the new method of solving parameters takes into account the stress anisotropy and deformation anisotropy at the same time, which provides a new method for solving for the parameters, thus making the Hill48 yield function convenient to use. This method will lay the foundation for blank shape optimization procedures in the future. It is also expected to be helpful in accurate engineering analysis and effective FE analysis of anisotropic sheet metal forming problems.