1 Introduction

Noise and vibration reductions are attractive topics in planetary gear trains (PGT), especially for those induced by the mesh and planet-pass excitations. The typical vibrations of a spur ring gear were analytically examined, and the relationships between mesh phase and in-plane elastic vibrations were identified based on symmetry [1]. While similar symmetry is held in helical PGT, the elastic vibration can be more complex to analyze. A question that can possibly be encountered during analysis is how the vibrations change.

Published studies directly or indirectly use the structure and excitation symmetries to capture vibration nature. The studies can be roughly considered in three groups: typical vibration modes [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21], planet phasing [1, 3, 22,23,24,25,26,27,28,29,30,31,32,33,34,35], and sideband [35,36,37,38,39,40,41,42,43,44], where the first group relates free vibration, but the last two link forced and parametric ones induced by the mesh or planet-pass excitations. Regardless of excitation patterns, free or forced, rigid or elastic, or even rigid-elastic coupling vibrations, motivations on the problem-solution method or physical explanations on the vibrations can be gained because the symmetric structure and excitation account for the distinctive vibrations.

Existing studies on the distinctive vibrations are generally based on spur PGT with the exception of Refs. [3, 8, 17, 21, 24], etc. The results imply that the vibrations can be classified into rotational, translational, and planet modes for spur PGT [5], but for helical one, it can be categorized as in phase, sequential phase, and counter phase [3], or rotational-axial, translational-tilting, and planet modes [8, 19]. As an extended research, Shi et al. [45] identified the typical vibration in centrifugal pendulum vibration absorbers. Qin et al. [20] examined the vibration modes of a horizontal wind turbine drive train, and they also studied the effect of bearing stiffness on these modes. Bu et al. [21] investigated the herringbone PGT and found the rotational and axial modes, translational modes, planet modes, rotational and axial ring modes, and translational ring modes. The above studies are generally based on rigid body assumption.

The typical vibration modes also arise if the elastic components such as the thin ring gear are considered [11, 12]. Wu and Parker [11] examined the PGT with elastic ring gear and identified the rigid-elastic vibration modes, and later Parker and Wu [12] proved the vibration modes of the PGT with unequally-spaced planets and elastic ring gear. Tanna and Lim [15, 16] examined the ring gear’s free vibration and proved the elastic vibration modes, including in-plane extensional, radial inextensional, out-of-plane bending, and torsional deformations. It seems that similar modes to those in Refs. [11, 12] can be found for the helical planetary ring gear even when considering various deformations owing to the symmetries. However, it could be a challenge to develop an analytical model incorporating many deformations. Even so, the theoretical analysis is another difficulty to be overcome.

Planet phasing is also a typical vibration, which has been well examined based on spur and helical PGT. Kahraman et al. [3, 24] addressed it and obtained general results governing the occurrence or suppression of the forced vibration for arbitrary number of planets. Parker et al. [25] proved the three forced vibration modes induced by the mesh excitation using superposition method, and then they extended it to helical PGT [19]. The phasing behaviors of the spur and helical PGT are in essence the same except for the specific excitations and vibration patterns. Canchi and Parker [28] studied the influence of mesh phase on parametric instability of the planetary ring gear and closed-form results were obtained. Yang and Dai [33] formulated the effect of mesh phase on primary and combination resonances by Multiple Scale method. As a common feature, most of the above studies employ the excitation superposition, through which the resulting response can be obtained and typical vibrations are identified.

Alternatively, Wang et al. [1] used the response instead of the excitation superposition to predict vibration of an elastic spur ring gear and found the phasing effect of basic parameters on typical flexural-extensional vibrations. The results imply that if the wavenumber is zero or unity, the rigid vibration modes are identical with those in Ref. [25]. While the responses of the helical ring gear can be more complex, typical vibrations could remain due to the mechanics similarities in their common symmetries, and the correspondence between the rigid and elastic vibrations could exist in helical PGT. These are the primary concerns of this work.

Another phasing is the mesh sideband associated with the instance where the principal spectrum component is slightly moved from the meshing frequency. Mcfadden and Smith [38] addressed the asymmetry of modulation sideband. To precisely predict the amplitudes of the dominant components, Mcnames [39] generalized their work using continuous-time Fourier series and presented more thorough and intuitive explanations on the observed spectrum. Zhang et al. [41] studied the relationships between tooth count, planet count, and sideband orders. Kahraman [35] asserted that sorting and aligning the planet run-out error in an in-phase configuration during assembly can minimize and in some cases even eliminate the errors effect on the dynamic load sharing. Then Inalpolat and Kahraman [36, 37] proposed a simplified model to describe the modulation sideband, and they developed an experimental PGT set-up to demonstrate the sideband from ring gear radial acceleration measurements. Based on the structure and mesh phase configurations, Vicuña [44] also obtained the analytical expressions governing the sideband. Aiming at the main excitation source, Singh [46, 47] presented a general physical understanding on the basic mechanism causing unequal load sharing. Gu and Velex [48] developed an original lumped parameter model and studied the influence of planet position errors. These researches gained valuable insights into the dynamic behaviors.

Among the aforementioned studies, Inalpolat and Kahraman [36], Mcfadden and Smith [38], Mcnames [39], Keller and Grabill [40], and Vicuña [44] introduced the assumption that the resulting vibration is equal to the sum of those at the ring-planet mesh positions. They found that the mesh frequency cannot be a component in response unless the ring gear tooth count is an integer multiple of planet count. Physically, it is the planet’s motion relative to the transducer that causes the transmitted vibration to vary and thus the mesh vibration to be modulated. Further, it is the mesh phases of the planets that cause the sideband occurrence, asymmetry, or even suppression. Like the vibration modes and planet phasing, the sideband and its asymmetry are both determined by the timing-relation between the inner excitations at different mesh positions. Based on these, more findings can be achieved when fully incorporating the structure and force symmetries of the helical PGT.

Since the two types of phasing phenomena link symmetry, a correspondence can exist between them. As a case in point, they share identical exciting rules [1, 38, 39, 41]. Wang et al. [1] employed the superposition principle to deal with the occurrence of spur planetary ring gear vibrations, and found that they are simply determined by lZr ± n = qN, where l, Zr, N, and q are the mesh excitation harmonic, ring gear tooth count, planet count, and arbitrary integer. n denotes wavenumber, which is associated with bending and extensional deformations instead of only the former. Mcfedden and Smith [38], Mcnames [39], and Zhang et al. [41] utilized the signal modulation principle to address elastic vibration and obtained the same expression. This expression governs the mesh sideband as the same notation n, but it designates modulating signal order. To gain more physical insights into the two typical vibrations, further work is much needed. This is another focus of this work.

The ring gear vibration is of a classical traveling-load dynamic problem. Such problem has been well studied by many researchers [49]. Compared with those of asymmetric dynamic problems, the vibrations of the helical PGT bear their own distinctions because of the symmetry and timing-relation between the mesh excitations. Based on the prior study [1], the present work analyzes the unique forced vibration with dual-frequency superposition and modulation methods. To facilitate the analysis, the scope is limited to the helical ring gear, though the three-dimensional mesh and sideband vibrations, including the in-plane bending and extensional, out-of-plane bending and torsional deformations, and especially their relationships, are all incorporated. Main results are verified by numerical calculation and comparisons with the results in the open literature.

2 Methods for Mesh and Sideband Vibrations

2.1 Superposition and Modulation Methods

The prediction on the mesh and sideband vibrations can be difficult when using differential equations to describe the physical laws because the three-dimensional excitations create various deformations. Other treatments include the Finite Element and experimental methods, which are sometimes employed as verification tools. Motivated by the previous studies [25, 50, 51], authors of this work uses superposition and modulation methods to address the rigid and elastic vibrations of symmetric power-transmission systems [1, 52,53,54]. It is not based on an ordinary or partial differential equation but on the structure, force, and deformation symmetries.

In the previous work [1], the elastic mesh-phasing vibrations of spur planetary ring gears were addressed by the superposition method, which was motivated by the ultrasonic motors [50] and PGT [25], but only in-plane bending and extensional deformations were incorporated. Practically, whatever the deformations are, the various free vibrations are of elastic waves definitely with periodicity due to the ring gear’s closed shape. Since the vibrations at different mesh positions are identical except for a phase lag, the resulting vibration can be obtained via a simple superposition either for bending or extensional deformation. The same can be true for the helical planetary ring gears.

As another point of view, since there exist two types of excitations with mesh and planet-pass frequencies on the ring and planet sides for each and every type of deformation, the resulting response can be explained as a type of modulation. As a result, the same predictions can be made by the superposition and modulation treatments such that insights into the phasing behaviors especially the excitation harmonics can be gained. Authors of this work examined the elastic vibration of permanent magnet motors and obtained complementary results [52]. In another study [54], the rigid-elastic vibrations incorporating the frequency splitting and mode contamination were also analyzed by fully considering mechanical and magnetic symmetries. However, the above two studies are limited to the in-plane vibration. Following the similar procedure, various vibrations of the helical ring gears can be examined analytically.

This work examines the mesh and planet-pass excitations and vibrations of helical ring gears in order to clarify the structure-excitation-vibration relation. To obtain more general results and avoid a specific mathematical model, this work employs the model-free dual-frequency superposition and modulation methods. No over restriction is imposed during the analyses except for the symmetries.

2.2 Periodic Excitations of Gear Meshing

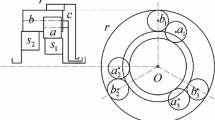
As well known, the PGT generally has excitations with mesh and planet-pass frequencies, which affect the system through the superposition or modulation via mechanical contact. Compared with the existing literature, the mesh frequency here is the same as that in the existing studies, but the meaning of the planet-pass frequency is different. To demonstrate these, Figure 1 depicts six typical instantaneous relative positions between ring gear teeth and planets, schematically showing the transition effect that naturally leads to two typical excitations with distinct frequencies. The two-dimensional case is used here for clarity purpose, but similar behaviors can be found in the axial direction.

Figure 1
figure 1

Typical excitations, where a–c imply the mesh excitation on a planet, and d–f show  the planet-pass excitation on a ring gear tooth

Full size image

Figure 1(a)‒(c) illustrate the planet P passes over ring teeth T1 and T2. During this process, the time-variant mesh excitation occurs. By contrast, Figure 1(d)‒(f) show the process between ring gear tooth T and planets P1 and P2, where planet-pass excitation is produced. Symmetry ensures that the excitations on each planet and tooth are the same except for phase lags. The two types of excitations can co-exist even in healthy PGT, and consequently the mesh and planet-pass phasings arise simultaneously. Compared with the mesh-frequency phasing in spur PGT, those in the helical one are more complicated.

2.3 Mesh and Planet-Pass Vibrations

Figure 2 illustrates a helical ring gear with equally-spaced N planets and Zr teeth, where the elastic vibrations are excited by the mesh and planet-pass excitations. Only the elstic waves traveling in an anti-clockwise direction are given for clarity purpose. In Figure 2(a), the rotating frame \(\{O_{\text{c}} - r_{\text{c}} ,\;\theta_{\text{c}} \}\) is attached on the carrier, where the polar axis is directed towards the first planet center such that the spatial initial phase \(\psi_{1}^{\text{c}}\) is zero. \(V_{i}^{{l_{\text{m}} + }}\) is the lmth harmonic of the traveling wave excited by the ith (\(i = 1, \, 2, \, 3, \ldots , \, N\)) mesh excitation. \(\varphi_{i}^{\text{c}}\) and \(A_{i}^{{l_{\text{m}} }}\) are the time initial phase and amplitude, respectively.

Figure 2
figure 2

Elastic vibrations around helical ring gear excited by a mesh frequency excitation and b planet-pass frequency excitation

Full size image

In Figure 2(b), \(\{ O_{\text{r}} - r_{\text{r}} ,\;\theta_{\text{r}} \}\) is a ring-fixed frame, where the polar axis is also directed towards the first tooth center such that the spatial initial phase \(\psi_{1}^{\text{r}}\) is zero. \(W_{j}^{{l_{\text{s}} + }}\) is the lsth harmonic of the traveling wave excited by the excitation on the jth (\(j = 1, \, 2, \, 3, \ldots ,\,\,Z_{\text{r}}\)) ring gear tooth. Similarly, \(\varphi_{j}^{\text{r}}\) and \(B_{j}^{{l_{\text{s}} }}\) are the initial phase and amplitude, respectively. Note that Figure 2 only presents the in-plane bending deformation, but the following analyses also apply to the out-of-plane case.

2.3.1 Mesh-Frequency Vibration

The deformations induced by the mesh excitation in the carrier-fixed frame are periodic with distinct time and position phases, the superposition of which results in the mesh-frequency response. Following the similar steps to those in the previous work [1], analytical results on the relationships between basic parameters and wave vibration can be formulated. However, as an important distinction, the vibrations here include more possibilities, including the in-plane bending and extensional, out-of-plane bending and torsional deformations. They are all characterized as geometrically closed shape and can be expressed by Fourier series as a general form. For instance, the elastic vibration in Figure 2(a) induced by the lmth harmonic excitation at the ith mesh position can be written as

$$V_{i}^{{l_{\text{m}} }} = A_{i}^{{l_{\text{m}} }} \cos m\left( {\theta_{\text{m}} + \gamma_{\uptheta}^{\text{c}} + \psi_{i}^{\text{c}} } \right)\cos l_{\text{m}} \left( {Z_{\text{r}} \omega_{\text{f}} t + \gamma_{\text{t}}^{\text{c}} + \varphi_{i}^{\text{c}} } \right),$$
(1)

where \(A_{i}^{{l_{\text{m}} }}\), \(m\), \(\theta_{\text{m}}\), and \(\omega_{\text{f}}\) are amplitude, wavenumber (depicting the deformation’s period), position angle and rotating speed of planet, respectively. \(\gamma_{\uptheta}^{\text{c}}\) and \(\gamma_{\text{t}}^{\text{c}}\) are introduced to demonstrate the position and time lags between the excitation and response. Equation (1) describes a wave response excited by the ith mesh excitation, which is given in the carried-fixed frame.

Symmetry leads to \(A_{i}^{{l_{\text{m}} }} = A_{1}^{{l_{\text{m}} }}\). Although the coefficients and lags are unknown, they do not affect the final results except for amplitude (this work does not care about it). Since the first planet is at \(\psi_{1}^{\text{c}} = 0\), the ith planet’s position is

$$\psi_{i}^{\text{c}} = {{2\pi \left( {i - 1} \right)} \mathord{\left/ {\vphantom {{2\pi \left( {i - 1} \right)} N}} \right. \kern-0pt} N}.$$
(2)

The time initial phase of the ith mesh position is [27]

$$\varphi_{i}^{\text{c}} = \psi_{i}^{\text{c}} Z_{\text{r}} .$$
(3)

Eq. (3) and the subsequent Eq. (8) are crucial for the superposition analysis. The net response can be obtained by superposition as

$$V^{{l_{\text{m}} }} = \sum\limits_{i = 1}^{N} {V_{i}^{{l_{\text{m}} }} } .$$
(4)

The following identities hold for integer values of G [25]

$$\left\{ \begin{array}{l} \sum\limits_{i = 1}^{N} {\sin \left[ {{{2{{\pi }}\left( {i - 1} \right)G} \mathord{\left/ {\vphantom {{2{{\pi }}\left( {i - 1} \right)G} N}} \right. \kern-0pt} N}} \right]} = 0, \hfill \\ \sum\limits_{i = 1}^{N} {\cos \left[ {{{2{{\pi }}\left( {i - 1} \right)G} \mathord{\left/ {\vphantom {{2{{\pi }}\left( {i - 1} \right)G} N}} \right. \kern-0pt} N}} \right]} = \left\{ \begin{array}{l} 0\quad {{\;\;G} \mathord{\left/ {\vphantom {{\;\;G} {N \ne {\text{integer,}}}}} \right. \kern-0pt} {N \ne {\text{integer,}}}} \hfill \\ N\quad \,{G \mathord{\left/ {\vphantom {G {N\,\, = {\text{integer}} .}}} \right. \kern-0pt} {N\,\, = {\text{integer}} .}} \hfill \\ \end{array} \right. \hfill \\ \end{array} \right.$$
(5)

According to Eqs. (1)‒(5), the relationships between the tooth count, planet count, mesh harmonic order, and elastic vibration order can be identified, as summarized in Table 1. While the results are identical with those of spur ring gear [1], they describe more deformations because the wavenumber designates the period only. Namely, the superposition method is only concerned about the deformation’s period no matter what the excitation patterns and specific deformations are.

Table 1 Exciting conditions for elastic mesh-frequency phasing
Full size table

2.3.2 Planet-Pass Frequency Vibration

The deformation induced by the planet-pass frequency excitation under the ring-fixed frame can be described as an elastic vibration with unique time and spatial lags, as shown in Figure 2(b). The vibration caused by the lsth harmonic excitation on the jth ring gear tooth is assumed as

$$W_{j}^{{l_{\text{s}} }} = B_{j}^{{l_{\text{s}} }} \cos n\left( {\theta_{\text{s}} + \gamma_{\theta }^{\text{r}} + \psi_{j}^{\text{r}} } \right)\cos l_{\text{s}} \left( {N\omega_{\text{f}} t + \gamma_{\text{t}}^{\text{r}} + \varphi_{j}^{\text{r}} } \right),$$
(6)

where \(B_{j}^{{l_{\text{s}} }}\), n, and \(\theta_{\text{s}}\) are amplitude, wavenumber (also depicting the deformation’s period), and position angle, respectively. The notations \(\gamma_{{{\theta}}}^{\text{r}}\) and \(\gamma_{\text{t}}^{\text{r}}\) imply the position and time lags between the excitation and response. With the same principle as Eq. (1), Eq. (6) also describes a wave response but excited by the planet-pass frequency excitation at the jth ring gear tooth.

Similarly, symmetry leads to \(B_{j}^{{l_{\text{s}} }} = B_{1}^{{l_{\text{s}} }}\). The vibration here is different from the previous work [1] in the physical meaning due to the difference in excitations.

Since the first tooth is at \(\psi_{1}^{\text{r}} = 0\), the position angle of the jth tooth becomes

$$\psi_{j}^{\text{r}} = {{2\pi \left( {j - 1} \right)} \mathord{\left/ {\vphantom {{2\pi \left( {j - 1} \right)} {Z_{\text{r}} }}} \right. \kern-0pt} {Z_{\text{r}} }},$$
(7)

thus the time initial angle becomes [55]

$$\varphi_{j}^{\text{r}} = \psi_{j}^{\text{r}} N.$$
(8)

The net response is obtained by the superposition as

$$W^{{l_{\text{s}} }} = \sum\limits_{j = 1}^{{Z_{\text{r}} }} {W_{j}^{{l_{\text{s}} }} } ,$$
(9)

Eqs. (6)‒(9) present the connections between the tooth count, planet count, planet-pass frequency harmonic order, and elastic vibration, as summarized in Table 2. Various deformations are included here, just as the above mesh-frequency response. Comparison between Tables 1 and 2 implies that there can be certain correspondence between the physical meanings of the harmonic excitation orders.

Table 2 Exciting conditions for elastic planet-pass phasing
Full size table

2.3.3 Transition between Ring and Planets

This section addresses the correlation between the mesh and planet-pass vibrations using the modulation principle. As mentioned above, the two types of excitations are on the ring and planet sides, respectively, and thus the net response is obtained by the excitations’ interaction, which is embodied as a modulation process. Without any loss of generality, the harmonic excitations in the carrier- and ring-fixed frames can be, respectively, expressed by the Fourier series as

$$f_{\text{m}} \left( {\theta_{\text{m}} ,\;t} \right) = C_{\text{c}}^{{l_{\text{m}} }} \cos \left( {l_{\text{m}} Z_{\text{r}} \theta_{\text{m}} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma _{\text{t}}^{\text{c}}} } \right),$$
(10)

and

$$f_{\text{s}} \left( {\theta_{\text{s}} ,\;t} \right) = D_{\text{r}}^{{l_{\text{s}} }} \cos \left( {l_{\text{s}} N\theta_{\text{s}} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma _{\text{t}}^{\text{r}}} } \right).$$
(11)

where \(l_{\tau 1}\), \(\theta_{\tau 1}\) (\(\tau 1 = {\text{m}},\,{\text{s}}\)) and \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma _{\text{t}}^{\tau 2}}\) (\(\tau 2 = {\text{c}},\,{\text{r}}\)) imply the harmonic order, position angle, and time phase, respectively, and \(C_{\text{c}}^{{l_{\text{m}} }}\) and \(D_{\text{r}}^{{l_{\text{s}} }}\) are the amplitudes. With Eqs. (10) and (11), the resulting excitation becomes

$$f_{{{\text{m}},{\text{s}}}}^{{l_{\text{m}} ,l_{\text{s}} }} \left( {\theta_{\text{m}} ,\;\theta_{\text{s}} ,\;t} \right) =\, E_{{{\text{c}},{\text{r}}}}^{{l_{\text{m}} ,l_{\text{s}} }} \cos \left( {l_{\text{m}} Z_{\text{r}} \theta_{\text{m}} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma_{\text{t}}^{\text{c}} } } \right)\cos \left( {l_{\text{s}} N\theta_{\text{s}} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma_{\text{t}}^{\text{r}} } } \right),$$
(12)

where \(E_{{{\text{c}},{\text{r}}}}^{{l_{\text{m}} ,l_{\text{s}} }}\) (\(E_{{{\text{c}},{\text{r}}}}^{{l_{\text{m}} ,l_{\text{s}} }} = C_{\text{c}}^{{l_{\text{m}} }} D_{\text{r}}^{{l_{\text{s}} }}\)) is a combined coefficient.

Eq. (12) is rewritten by the trigonometric identity as

$$\begin{aligned} f_{\text{m},\text{s}}^{{l_{\text{m}} ,l_{\text{s}} }} \left( {\theta_{\text{m}} ,\;\theta_{\text{s}} ,\;t} \right)& = \frac{{E_{\text{c},\text{r}}^{{l_{\text{m}} ,l_{\text{s}} }} }}{2}\left[ {\cos \left( {l_{\text{m}} Z_{\text{r}} \theta_{\text{m}} + l_{\text{s}} N\theta_{\text{s}} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma _{\text{t}}^{\text{c}}} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma _{\text{t}}^{\text{r}}} } \right)} \right. \\ & \left. { \, + \cos \left( {l_{\text{m}} Z_{\text{r}} \theta_{\text{m}} - l_{\text{s}} N\theta_{\text{s}} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma _{\text{t}}^{\text{c}}} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma_{\text{t}}^{\text{r}}} } \right)} \right]. \\ \end{aligned}$$
(13)

Since the position angles are satisfied with \(\theta_{\text{m}} = \theta_{\text{s}} - \Omega_{\text{f}} t\), where \(\Omega_{\text{f}}\) is the rotation speed of the carrier, with this knowledge, Eq. (13) becomes

$$\begin{aligned} f_{{{\text{m}},{\text{s}}}}^{{l_{{\text{m}}} ,l_{{\text{s}}} }} \left( {\theta _{{\text{m}}} ,\;\theta _{{\text{s}}} ,\;t} \right) & = \frac{{E_{{{\text{c}},{\text{r}}}}^{{l_{{\text{m}}} ,l_{{\text{s}}} }} }}{2}\left\{ { \cos \left[ {l_{{\text{m}}} Z_{{\text{r}}} \Omega _{{\text{f}}} t - \left( {l_{{\text{m}}} Z_{{\text{r}}} + l_{{\text{s}}} N} \right)\theta _{{\text{s}}} - \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma_{{\text{t}}}^{{\text{c}}} } + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma_{{\text{t}}}^{{\text{r}}} } } \right)} \right]} \right. \\ & \left. {\,+ \cos \left[ {l_{{\text{m}}} Z_{{\text{r}}} \Omega _{{\text{f}}} t - \left( {l_{{\text{m}}} Z_{{\text{r}}} - l_{{\text{s}}} N} \right)\theta _{{\text{s}}} - \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma _{{\text{t}}}^{{\text{c}}}} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma _{{\text{t}}}^{{\text{r}}}} } \right)} \right]} \right\} \end{aligned}$$
(14)

Eq. (14) implies that the resulting excitation is a function of the time and space, where \(l_{\text{m}} Z_{\text{r}} \pm l_{\text{s}} N\) is the wave order, denoting the elastic vibration with the same order. The results are summarized in Table 3. It can be observed from Eqs. (10) and (11) that there exist two types of fundamental excitation frequencies related to the ring gear tooth count and planet count. In fact, the counts describe their geometrical topologies on the ring gear side and the planet side.

Table 3 Exciting conditions for mesh and planet-pass vibrations
Full size table

Comparison between Tables 1 and 2 implies that \(q_{\text{m}}\) can be the lsth harmonic in the planet-pass excitation, and \(q_{\text{s}}\) can be the lmth harmonic in the mesh excitation. Table 3 unifies the previous results and shows that whatever the tooth and planet counts are, the excited wavenumber is mathematically equal to their linear combination, where the coefficients are the harmonic orders of the excitations on the planet and ring gear teeth, respectively.

3 Mesh Sideband Analysis

The mesh and planet-pass excitations interact with one another leading to sideband. This section addresses it on the basis of symmetries, where the distinction is the treatment using two types of signal collection patterns with the modulation between the mesh and planet-pass signals.

3.1 Signal from Ring-Planet Meshes

For the convenience of signal collection, the accelerometer is normally fixed on the ring gear such that the signals from planets can be easily collected. This section takes the radial direction as an example to address the sideband behaviors. The distinction here is the introducing of mesh phase. The amplitude-modulating signal induced by the ith planet motion is written as

$$x_{i}^{{v_{\text{m}} }} = a_{i}^{{v_{\text{m}} }} \cos v_{\text{m}} \left( {\theta_{\text{m}} + \psi_{i}^{\text{c}} } \right),$$
(15)

where \(a_{i}^{{v_{\text{m}} }}\), \(\theta_{\text{m}}\), and \(v_{\text{m}}\) are amplitude, position angle, and harmonic order, respectively. Similar to the mesh and planet-pass vibration analyses, the amplitude in the following derivation is also unknown but does not affect the desired results.

Assuming that the lmth signal generated by the ith mesh position is

$$y_{i}^{{l_{\text{m}} }} = b_{i}^{{l_{\text{m}} }} \cos l_{\text{m}} \left( {Z_{\text{r}} \varOmega_{\text{f}} t + \varphi_{i}^{\text{c}} } \right),$$
(16)

where \(b_{i}^{{l_{\text{m}} }}\) is also an unknown amplitude.

Wherever the static accelerometer is, the harmonic signal from the ith planet is the product of the amplitude-modulating and meshing vibration signals [39, 41],

$$z_{i} = x_{i}^{{v_{\text{m}} }} \cdot y_{i}^{{l_{\text{m}} }} .$$
(17)

The overall signal is the superposition of those generated from N mesh positions, which is written as

$$Z_{\text{m}} = \sum\limits_{i = 1}^{N} {z_{i} } .$$
(18)

From Eqs. (5) and (15)–(18), the sidebands are summarized in Table 4. They are determined by basic parameters, though only those orders being multiples of planet count can survive. In this table, vm and \(Q^{\prime}_{\text{m}}\) are the modulating order and integer, respectively.

Table 4 Exciting conditions for sidebands excited by mesh excitations on planets
Full size table

3.2 Signal from Ring Gear Tooth

The existing studies are generally focused on the vibration signal from the planets, but there exists an alternative view. The resulting signals can be determined by examining the excitation upon the ring gear teeth. If the accelerometer is still fixed on ring gear and the radial direction is used, the amplitude-modulating signal induced by the excitation on the jth ring gear tooth can be written as

$$x_{j}^{{v_{\text{s}} }} = a_{j}^{{v_{\text{s}}}}\cos v_{\text{s}} \left( {\theta_{\text{s}} + \psi_{j}^{\text{r}} } \right),$$
(19)

where \(a_{j}^{{v_{\text{s}} }}\), \(\theta_{\text{s}}\), and \(v_{\text{s}}\) are the unknown amplitude, position angle, and harmonic order, respectively. The lsth signal generated from the jth ring gear tooth is assumed as

$$y_{j}^{{l_{\text{s}} }} = b_{j}^{{l_{\text{s}} }} \cos l_{\text{s}} \left( {N\omega_{\text{f}} t + \varphi_{j}^{\text{r}} } \right),$$
(20)

where \(b_{j}^{{l_{\text{s}} }}\) is the amplitude.

Similarly, the harmonic signal from the jth ring gear tooth is the product of amplitude-modulating and meshing vibration signals

$$z_{j} = x_{j}^{{v_{\text{s}} }} \cdot y_{j}^{{l_{\text{s}} }} .$$
(21)

The net signal is obtained by the superposition of those from Zr gear teeth as

$$Z_{\text{c}} = \sum\limits_{j = 1}^{{Z_{\text{r}} }} {z_{j} } .$$
(22)

From Eqs. (5) and (19)‒(22) and after some operations similar to the preceding sections, the mesh sidebands are determined, as given in Table 5, where only the orders that are multiples of ring gear tooth count can survive.

Table 5 Exciting conditions for sidebands excited by mesh excitations on ring gear teeth
Full size table

3.3 Comparison between Signal Collections

Similar to the elastic vibration induced by the mesh excitation, the sidebands collected from the ring-planet meshes and ring gear teeth also have inherent connections. While their physical natures are different, the sideband ranges are the same due to the modulation between the two types of excitations, especially the act-react relation between planets and ring gear. A comparison between Tables 4 and 5 shows that the sidebands equals the linear combination of ring gear tooth and planet counts; \(Q^{\prime}_{\text{m}}\) can be the harmonic \(l_{\text{s}}\) in the planet-pass excitation, and \(Q^{\prime}_{\text{c}}\) can be the lmth harmonic in the mesh excitation. Consequently, the results in Tables 4 and 5 are unified in Table 6, where v is the modulating order.

Table 6 Exciting conditions for mesh sideband
Full size table

4 Unique Vibration of Helical Ring Gear

This work uses analytical methods to deal with various excitations and presents simple expressions governing the occurrence or suppression of the mesh and planet-pass vibrations. The results imply that the two types of apparently isolated vibrations have inherent connections and share the same exciting conditions. The excited wavenumber is the linear combination of the ring gear tooth and planet counts, which is equal to the modulating signal order. The mesh and corresponding planet-pass vibrations are excited simultaneously, and the sideband is the external behavior of the excitations’ modulation.

To further refine results, this section introduces the greatest common divisor (GCD) of the ring gear tooth and planet counts, C, where C = 1, 1 < C < N, and C = N, like those in Refs. [1, 52]. Based on Tables 3 and 6, the mesh and sideband vibrations are classified into three groups, and each has a specific wavenumber and modulating signal order, as summarized in Table 7. The results clarify the relationships between basic parameters, dual-frequency excitations, and mesh and planet-pass vibrations.

Table 7 Exciting conditions for elastic mesh and sideband vibrations
Full size table

This classification includes three types of phasing relations: the in-phase, sequential-phase, and counter-phase [3], which corresponds to the cases where phasing factors are zero, one, and others, respectively [25]. The forgoing analyses verify that the sideband can arise even in healthy PGT, in particular when the elasticity is significant for the thin ring gear subjected to heavy load. For this case, the sideband can be even more significant because of the transition effect between the sensor and planets and the traditional planet-pass errors. Whether the specific mesh-frequency, sideband, or its harmonics are excited or not depends on the lead or lag timing-relation between different mesh positions, that is, the combination of the ring gear tooth and planet counts, and to what degree the excitation frequency is close to a natural frequency.

5 Numerical Verification

This section verifies the analytical results based on three sample helical PGT with equally-spaced planets and distinct mesh phases. For comparison purpose, the planet count is set to be fixed while the difference between the central gear tooth counts is small, as shown in Table 8. While most of the basic parameters are presented here, only those related to the ring gear are utilized because the focus is on the ring gear’s vibration.

Table 8 Specifications of three sample PGT with distinct phases
Full size table

More specifically, the ring gear tooth and planet counts are different from one case to another. In the three cases, the GCDs are four, two, and one, respectively. The configurations create different mesh phases and lead to distinctive elastic vibrations. Since the tooth count is slightly changed to ensure comparability, the ring gear’s modal properties can be reasonably considered to be unchanged such that the main difference between the forced responses is mainly caused by the mesh phase.

5.1 Free Vibration

The free vibration is first calculated to better interpret the forced vibration. The Finite Element analysis is performed and the ring gear’s modal information is extracted, as given in Table 9 and Figure 3. Four types of vibration modes, according to deformation period, are categorized as radial inextensional (RIN) modes (Figure 3a), extensional (EXT) modes (Figure 3b), out-of-plane bending (OPB) modes (Figure 3c), and torsional (TOR) modes (Figure 3d). These modes provide necessary information for the verification of the analytical predictions. All modes exhibit periodicity due to the geometrically closed shape of the ring gear.

Table 9 Natural frequencies (Hz)
Full size table
Figure 3
figure 3

Typical helical ring gear's vibration modes

Full size image

5.2 Forced Vibration

Harmonic response is performed. For the sake of convenience, the mesh excitation is simulated in the three orthogonal directions. This work enters both the real and imaginary components of each harmonic excitation to accomplish the phase lags between different mesh positions. According to the PGT' symmetries, the phase lags can be written as 2πl(i − 1) × 64/4, 2πl(i − 1) × 66/4, and 2πl(i − 1) × 65/4, respectively, where i = 1, 2, 3, 4, and l = 1, 2, 3,…. Owing to the similarities between different harmonic responses, only the first harmonic in case I, the first and second harmonics in case II, and the first, second and fourth harmonics in case III are presented here. In order to illustrate the phasing effect, Figure 4 plots the mesh excitations in the three directions, where the three projections are different in amplitude and direction.

Figure 4
figure 4

Mesh excitations on the helical ring gears

Full size image

Figure 5 illustrates the responses for a range of mesh frequencies. For case I, no matter what the harmonic is, the exciting condition is always satisfied when the wavenumber w is zero or the multiple of the value of four. It can be observed from Figure 5(a) that the combinations of the harmonic l and wavenumber w satisfied with resonance are {l, w} = {1, 4(RIN)}, {1, 4(OPB)}, {1, 0(TOR)}, {1, 0(EXT)}, {1, 8(RIN)}, {1, 4(TOR)}, and {1, 8(OPB)}. That is, only the zero, four, and eight wavenumbers are excited, but others are absent. For case II, the combinations become {l, w} = {1, 2(RIN)}, {1, 2(OPB)}, {1, 6(RIN)}, {1, 2(TOR)}, {1, 6(OPB)}, and {1, 2(EXT)}, and {l, w} = {2, 4(RIN)}, {2, 4(OPB)}, {2, 0(TOR)}, {2, 0(EXT)}, {2, 8(RIN)}, {2, 4(TOR)}, and {2, 8(OPB)}, as shown in Figures 5(b) and (c), respectively, which are also satisfied with that condition. For case III, the corresponding combinations are {l, w} = {1, 3(RIN)}, {1, 3(OPB)}, {1, 5(RIN)}, {1, 5(OPB)}, {1, 1(TOR)}, {1, 7(RIN)}, {1, 7(RIN)}, {1, 1(EXT)}, {1, 3(TOR)}, {1, 7(OPB)}, and {1, 9(RIN)}, {l, w} = {2, 2(RIN)}, {2, 2(OPB)}, {2, 6(RIN)}, {2, 2(TOR)}, {2, 6(OPB)}, and {2, 2(EXT)}, and {l, w} = {4, 4(RIN)}, {4, 4(OPB)}, {4, 0(TOR)}, {4, 0(EXT)}, {4, 8(RIN)}, {4, 4(TOR)}, and {4, 8(OPB)}, as shown in Figures 5(d) to (f), respectively, also well consistent with the analytical predictions.

Figure 5
figure 5

Harmonic responses of the helical ring gears, where a case I, b, c case II, and d–f case III

Full size image

The wavenumber in the analytical results governs various deformations. The distinct behaviors of the mesh and sideband vibrations are the excitation or neutralization of the harmonic mesh and planet-pass excitations due to their distinct phases. The fundamental reason behind this is the structure, excitation, and deformation periodicities (symmetries) in the three orthogonal directions. According to the current results, if the transducer is mounted in the axial direction, the same results can be obtained because the symmetries are still held.

6 Comparison and Discussion

The above sections examine the typical vibrations of the helical planetary ring gears. The analytical results regarding mesh vibrations have been verified by numerical method, though the sideband vibration has been not yet. This section makes the following comparisons with the existing results and discusses the mesh and planet-pass vibrations.

6.1 Analysis Method

This work employs the superposition and modulation methods to examine the mesh and sideband vibrations. Different from Refs. [1, 52,53,54,55], this work introduces the dual-frequency excitations to deal with the elastic vibration and signal analysis. The modulation method has been used by the existing literature to address signal modulation between the classical mesh and shaft frequency excitations, though this work uses this idea to examine the excitation interaction between the helical ring gear and planets. Further, the deformations here cover more possibilities, including in-plane bending and extensional, out-of-plane bending and torsional deformations. The superposition and modulation methods have different views toward the mesh and sideband vibrations. The former is focused on the response related to individual component and phase lag needs to be introduced, but the later is concerned with the excitation on concentric components without introducing the phase lag. In spite of the differences, they have been successfully used to deal with the elastic vibration and signal analysis by introducing the dual-frequency excitations and signals.

6.2 Mesh Vibration

Mesh vibrations have been studied by previous researchers with various methods. Wu and Parker [11] and Parker and Wu [12] built up an elastic-discrete model and examined the rigid-elastic vibration of spur PGT, and they proved the rotational, translational, planet, and purely ring modes, each of which has specific ring gear wavenumber. Authors of this work obtained the first three elastic modes by using the superposition method [1, 52]. Since only the ring gear and ring-planet mesh are included there, the purely ring modes in Ref. [11] cannot be found. Similar vibration modes have been found for spur and helical ring gears, though the wavenumber links more deformations. The reason behind this is that the methods focus on the deformation’s period instead of its amplitude such that they have general meaning. This has been verified by the comparison between the results in this work and those in Ref. [1].

6.3 Sideband Vibration

Mcfadden and Smith [38], Mcnames [39], and Zhang et al. [41] examined the sideband vibration and gained much valuable insights. Compared with the previous studies, the distinction here is the dual-signal collection aimed at the two typical excitations. In doing so, the relationships between the sideband vibrations are identified. They are similar in mathematical expressions for different excitations. The sideband order is equal to the modulating signal order. This has practical meaning in fault diagnosis, where special attention needs to be paid to the recognition between the normal elastic vibration and those excited by planet-pass errors in order to identify the actual fault, especially for thin ring gear subjected to heavy load. While this work takes the radial direction as an example, the results are not confined by this. The same results can be obtained by detecting axial deformation without any essential changes to the above analyses.

6.4 Relation between Mesh and Sideband Vibrations

The mesh and planet-pass excitations interact with one another through amplitude modulation leading to mesh sidebands. The present results imply that the elastic vibration and sidebands share the same exciting rules. That is, the excited wavenumber is determined by the mesh and planet-pass excitations, and the same is true for the sideband order. The excited wavenumber and modulating signal order are always mathematically equal to each other. Whether the mesh, sideband, or their harmonics can be excited or not depends on the phase lag, and to what extent the exciting frequency is close to the natural frequency. Although some insights have been gained in this work, only the amplitude modulation is considered. More efforts can be made to identify the source of additional harmonics induced by frequency modulation, and in particular the connections between the mesh and sideband vibrations of the helical ring gears when incorporating the base motions [56], worm gear [57], and even integrated system [58].

7 Conclusions

  1. (1)

    This paper examines the mesh and sideband vibrations of the helical planetary ring gears. Methods and results have been verified by numerical approach and strict comparisons with the existing studies.

  2. (2)

    Dual-frequency superposition and modulation methods are used to address the mesh and sideband vibrations. The relationships between the ring gear tooth count, planet count, and unique vibrations are obtained as simple closed-form expressions.

  3. (3)

    Two types of excitations are combined to examine the mesh and sideband vibrations, which is based on the structure and excitation symmetries and action-reaction relation between the engaged components.

  4. (4)

    The wavenumbers regarding the three distinct mesh phases are QN, QN ± 1, and QN ± (C, 2C, 3C,…, C × INT(N/(2C))), each of which creates distinct sidebands and covers in-plane bending and extensional, out-of-plane bending and torsional deformations.

  5. (5)

    Sidebands can be induced by elastic vibration instead of the planet-pass errors only, where the wavenumber is equal to modulating harmonic order. The mesh and sideband vibrations are determined by the lead or lag timing-relation between the mesh positions and the excitations.

  6. (6)

    Symmetry provides a basis for the superposition and modulation methods, which is also the root cause of the typical vibrations. Since no other restriction is imposed except for symmetry, the methods can find application in the symmetry-related issues in other power-transmission systems.