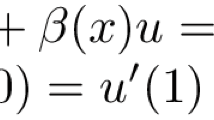Existence and uniqueness of solutions for fourth-order periodic boundary value problems under two-parameter nonresonance conditions

Abstract

This paper deals with the existence and uniqueness of solutions of the fourth-order periodic boundary value problem

$$\{\begin{array}{c}{u}^{(4)}(t)=f(t,u(t),u^{″}(t)),t\in [0,1],\hfill \\ u^{(i)}(0)=u^{(i)}(1),i=0,1,2,3,\hfill \end{array}$$

where $f:[0,1]\times \mathbf{R}\times \mathbf{R}\to \mathbf{R}$ is continuous. Under two-parameter nonresonance conditions described by rectangle and ellipse, some existence and uniqueness results are obtained by using fixed point theorems. These results improve and extend some existing results.

MSC:34B15.

1 Introduction and main results

In mathematics, the equilibrium state of an elastic beam is described by fourth-order boundary value problems. According to the difference of supported condition on both ends, it brings out various fourth-order boundary value problems; see [1]. In this paper, we deal with the periodic boundary value problem (PBVP) of the fourth-order ordinary differential equation

(1)

(2)

where $f:[0,1]\times \mathbf{R}\times \mathbf{R}\to \mathbf{R}$ is continuous. PBVP (1)-(2) models the deformations of an elastic beam in equilibrium state with a periodic boundary condition. Owing to its importance in physics, the existence of solutions to this problem has been studied by many authors; see [2–6].

Throughout this paper, we denote that $I=[0,1]$, $\mathbf{R}=(-\mathrm{\infty },+\mathrm{\infty })$, $\mathbf{Z}=\{\dots ,-2,-1,0,1,2,\dots \}$, $\mathbf{N}=\{1,2,\dots \}$, ${\mathbf{N}}^{\ast }=\mathbf{N}\cup \{0\}$. In [7–10], authors showed the existence of solutions to Eq. (1) under the boundary condition

$$u(0)=u(1)=u^{″}(0)=u^{″}(1)=0.$$

(3)

At first, the existence of a solution to two-point boundary value problem (BVP) (1)-(3) was studied by Aftabizadeh in [7] under the restriction that f is a bounded function. Then, under the following growth condition:

$$|f(t,u,v)|\le a|u|+b|v|+c,a,b,c>0,\frac{a}{{\pi }^4}+\frac{b}{{\pi }^2}<1,$$

Yang in [[8], Theorem 1] extended Aftabizadeh’s result and showed the existence to BVP (1)-(3). Later, Del Pino and Manasevich in [9] further extended the result of Aftabizadeh and Yang in [7, 8] and obtained the following existence theorem.

Theorem A Assume that the pair $(\alpha ,\beta )$ satisfies

$$\frac{\alpha }{{(k\pi )}^4}+\frac{\beta }{{(k\pi )}^2}\ne 1,\mathrm{\forall }k\in \mathbf{N},$$

(4)

and that there are positive constants a, b, and c such that

$$a\underset{k\in \mathbf{N}}{max}\frac{1}{|{(k\pi )}^4-\alpha -\beta {(k\pi )}^2|}+b\underset{k\in \mathbf{N}}{max}\frac{{(k\pi )}^2}{|{(k\pi )}^4-\alpha -\beta {(k\pi )}^2|}<1,$$

(5)

and f satisfies the growth condition

$$|f(t,u,v)-(\alpha u-\beta v)|\le a|u|+b|v|+c,\mathrm{\forall }t\in I,u,v,\in \mathbf{R}.$$

Then BVP (1)-(3) possesses at least one solution.

Condition (4)-(5) trivially implies that

$$\frac{a+b{(k\pi )}^2}{|{(k\pi )}^4-\alpha -\beta {(k\pi )}^2|}<1,\mathrm{\forall }k\in \mathbf{N}.$$

(6)

It is easy to prove that condition (6) is equivalent to the fact that the rectangle

$$R(\alpha ,\beta ;a,b)=[\alpha -a,\alpha +a]\times [\beta -b,\beta +b]$$

does not intersect any of the eigenlines of the two-parameter linear eigenvalue problem corresponding to BVP (1)-(3).

In [2], Ma applied Theorem A to PBVP (1)-(2) successfully and obtained the following existence theorem.

Theorem B Assume that the pair $(\alpha ,\beta )$ satisfies

$$\alpha +\beta {(2k\pi )}^2\ne {(2k\pi )}^4,\mathrm{\forall }k\in {\mathbf{N}}^{\ast },$$

(7)

and that there are positive constants a, b, and c such that

$$a\underset{k\in {\mathbf{N}}^{\ast }}{max}\frac{1}{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}+b\underset{k\in {\mathbf{N}}^{\ast }}{max}\frac{{(2k\pi )}^2}{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}<1,$$

(8)

and f satisfies the growth condition

$$|f(t,u,v)-(\alpha u-\beta v)|\le a|u|+b|v|+c,\mathrm{\forall }t\in I,u,v,\in \mathbf{R}.$$

(9)

Then PBVP (1)-(2) has at least one solution.

Condition (7)-(9) concerns a nonresonance condition involving the two-parameter linear eigenvalue problem (LEVP)

$$\{\begin{array}{c}{u}^{(4)}(t)+\beta u^{″}(t)-\alpha u(t)=0,t\in I,\hfill \\ u^{(i)}(0)=u^{(i)}(1),i=0,1,2,3.\hfill \end{array}$$

(10)

In [2], it has been proved that $(\alpha ,\beta )$ is an eigenvalue pair of LEVP (10) if and only if $\alpha +\beta {(2k\pi )}^2={(2k\pi )}^4$, $k\in {\mathbf{N}}^{\ast }$. Hence, for each $k\in {\mathbf{N}}^{\ast }$, the straight line

$${\ell }_k=\{(\alpha ,\beta )|\alpha +\beta {(2k\pi )}^2={(2k\pi )}^4\}$$

is called an eigenline of LEVP (10). Condition (7)-(8) trivially implies that

$$\frac{a+b{(2k\pi )}^2}{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}<1,\mathrm{\forall }k\in {\mathbf{N}}^{\ast }.$$

(11)

It is easy to prove that condition (11) is equivalent to the fact that the rectangle $R(\alpha ,\beta ;a,b)$ does not intersect any of the eigenline ${\ell }_k$ of LEVP (10). Hence, we call (11) and (9) the two-parameter nonresonance condition described by rectangle, which is a direct extension from a single-parameter nonresonance condition to a two-parameter one.

The purpose of this paper is to improve and extend the above-mentioned results. Different from the two-parameter nonresonance condition described by rectangle, we will present new two-parameter nonresonance conditions described by ellipse and circle. Under these nonresonance conditions, we obtain several existence and uniqueness theorems.

The main results are as follows.

Theorem 1 Assume that the pair $(\alpha ,\beta )$ satisfies (7). If there exist positive constants a, b, and c such that (11) and

$$|f(t,u,v)-(\alpha u-\beta v)|\le \sqrt{a^2{u}^2+b^2{v}^2}+c,\mathrm{\forall }t\in I,u,v\in \mathbf{R}$$

(12)

hold, then PBVP (1)-(2) has at least one solution.

When the partial derivatives $f_u$ and $f_v$ exist, if $\sqrt{u^2+v^2}$ is large enough such that

$$(f_u(t,u,v),-f_v(t,u,v))\in E(\alpha ,\beta ;a,b),\mathrm{\forall }t\in I,\sqrt{u^2+v^2}\ge R_0,$$

(13)

where $E(\alpha ,\beta ;a,b)=\{(x,y)|\frac{{(x-\alpha )}^2}{a^2}+\frac{{(y-\beta )}^2}{b^2}\le 1\}$ is a certain ellipse, and the corresponding close rectangle $R(\alpha ,\beta ;a,b)$ satisfies

$$R(\alpha ,\beta ;a,b)\cap {\ell }_k=\mathrm{\varnothing },\mathrm{\forall }k\in {\mathbf{N}}^{\ast },$$

(14)

by the theorem of differential mean value, we easily see that (7), (11), and (12) hold. Hence, by Theorem 1, we have the following corollary.

Corollary 1 Assume that the partial derivatives $f_u$ and $f_v$ exist in $I\times \mathbf{R}\times \mathbf{R}$. If there exists an ellipse $E(\alpha ,\beta ;a,b)$ such that (13) holds for a positive real number $R_0$ large enough, and the corresponding close rectangle $R(\alpha ,\beta ;a,b)$ satisfies (14), then PBVP (1)-(2) has at least one solution.

Condition (11) is weaker than condition (8), but condition (12) is stronger than condition (9). Hence, Theorem 1 and Corollary 1 partly improve Theorem B.

In the nonresonance condition of Theorem 1, condition (11) can be weakened as

$$\frac{\sqrt{a^2+b^2{(2k\pi )}^4}}{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}<1,\mathrm{\forall }k\in {\mathbf{N}}^{\ast }.$$

(15)

In this case, we have the following results.

Theorem 2 Assume that the pair $(\alpha ,\beta )$ satisfies (7). If there exist positive constants a, b, and c such that (12) and (15) hold, then PBVP (1)-(2) has at least one solution.

Condition (15) is equivalent to the fact that

$$E(\alpha ,\beta ;a,b)\cap {\ell }_k=\mathrm{\varnothing },\mathrm{\forall }k\in {\mathbf{N}}^{\ast }.$$

(16)

Condition (16) indicates that the ellipse $E(\alpha ,\beta ;a,b)$ does not intersect any of the eigenline ${\ell }_k$ of LEVP (10). Hence, we call (15) and (12) the two-parameter nonresonance condition described by ellipse, which is another extension of a single-parameter nonresonance condition. Similar to Corollary 1, we have the following corollary.

Corollary 2 Assume that the partial derivatives $f_u$ and $f_v$ exist in $I\times \mathbf{R}\times \mathbf{R}$. If there exists an ellipse $E(\alpha ,\beta ;a,b)$ such that (13) and (16) hold for a positive real number $R_0$ large enough, then PBVP (1)-(2) has at least one solution.

Theorem 3 Assume that the partial derivatives $f_u$ and $f_v$ exist in $I\times \mathbf{R}\times \mathbf{R}$. If there exists an ellipse $E(\alpha ,\beta ;a,b)$ such that (16) and

$$(f_u(t,u,v),-f_v(t,u,v))\in E(\alpha ,\beta ;a,b),\mathrm{\forall }t\in I,u,v\in \mathbf{R},$$

(17)

hold, then PBVP (1)-(2) has a unique solution.

In Theorem 2, Theorem 3, and Corollary 2, we present a new two-parameter nonresonance condition described by ellipse, which is another extension of a single-parameter nonresonance condition. As a special case, we replace the ellipse $E(\alpha ,\beta ;a,b)$ by a circle

$$\overline{B}(\alpha ,\beta ;r)=\{(x,y)|{(x-\alpha )}^2+{(y-\beta )}^2\le r^2\},r>0,$$

and obtain the following results.

Corollary 3 Assume that there exist a circle $\overline{B}(\alpha ,\beta ;r)$ and a positive constant c such that

$$\overline{B}(\alpha ,\beta ;r)\cap {\ell }_k=\mathrm{\varnothing },\mathrm{\forall }k\in {\mathbf{N}}^{\ast },$$

(18)

and f satisfies the growth condition

$$|f(t,u,v)-(\alpha u-\beta v)|\le r\sqrt{u^2+v^2}+c,\mathrm{\forall }t\in I,u,v\in \mathbf{R}.$$

(19)

Then PBVP (1)-(2) has at least one solution.

Condition (18) indicates that the circle $\overline{B}(\alpha ,\beta ;r)$ does not intersect any of the eigenline ${\ell }_k$ of LEVP (10). Hence, we call condition (18)-(19) the two-parameter nonresonance condition described by circle, which is also an extension of a single-parameter nonresonance condition. Similarly to Corollary 2 and Theorem 3, we have the following corollaries.

Corollary 4 Assume that the partial derivatives $f_u$ and $f_v$ exist in $I\times \mathbf{R}\times \mathbf{R}$. If there exists a circle $\overline{B}(\alpha ,\beta ;r)$ such that (18) and

$$(f_u(t,u,v),-f_v(t,u,v))\in \overline{B}(\alpha ,\beta ;r),\mathrm{\forall }t\in I,\sqrt{u^2+v^2}\ge R_0$$

(20)

hold for a positive real number $R_0$ large enough, then PBVP (1)-(2) has at least one solution.

Corollary 5 Assume that the partial derivatives $f_u$ and $f_v$ exist in $I\times \mathbf{R}\times \mathbf{R}$. If there exists a circle $\overline{B}(\alpha ,\beta ;r)$ such that (18) and

$$(f_u(t,u,v),-f_v(t,u,v))\in \overline{B}(\alpha ,\beta ;r),\mathrm{\forall }t\in I,u,v\in \mathbf{R}$$

(21)

hold, then PBVP (1)-(2) has a unique solution.

2 Preliminaries

Let $(\alpha ,\beta )$ be not eigenvalue pair of LEVP (10), i.e., $(\alpha ,\beta )\notin \mathcal{L}:={\bigcup }_{k=0}^{+\mathrm{\infty }}{\ell }_k$. For any $h\in L^2(I)$, we consider the linear periodic boundary value problem (LPBVP)

$$\{\begin{array}{c}{u}^{(4)}(t)+\beta u^{″}(t)-\alpha u(t)=h(t),t\in I,\hfill \\ u^{(i)}(0)=u^{(i)}(1),i=0,1,2,3.\hfill \end{array}$$

(22)

By the Fredholm alternative, LPBVP (22) has a unique solution $u\in H^4(I)$. If $h\in C(I)$, then the solution $u\in C^4(I)$. We define an operator T by

$$Th=u,\mathrm{\forall }h\in L^2(I).$$

Then $T:L^2(I)\to H^4(I)$ is a bounded linear operator, and we call it the solution operator of LPBVP (22). By compactness of the embedding $H^4(I)\hookrightarrow H^2(I)$, $T:L^2(I)\to H^2(I)$ is a compact linear operator.

Let $a,b>0$. We choose an equivalent norm in the Sobolev space $H^2(I)$ by

$${\parallel u\parallel }_{E_{a,b}}=\sqrt{a^2{\parallel u\parallel }_2^2+b^2{\parallel u^{″}\parallel }_2^2}$$

and denote the Banach space $H^2(I)$ reendowed norm ${\parallel \cdot \parallel }_{E_{a,b}}$ by $E_{a,b}$.

Lemma 1 Let $(\alpha ,\beta )\notin \mathcal{L}$. Then the solution operator of LPBVP (22) $T:L^2(I)\to E_{a,b}$ is a compact linear operator and its norm satisfies

$${\parallel T\parallel }_{B(L^2(I),E_{a,b})}\le \underset{k\in {\mathbf{N}}^{\ast }}{max}\frac{\sqrt{a^2+b^2{(2k\pi )}^4}}{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}.$$

(23)

Proof We only need to prove that (23) holds.

Since $\{e^{2k\pi it}|k\in \mathbf{Z}\}$ is a complete orthogonal system of $L^2(I)$, every $h\in L^2(I)$ can be expressed by the Fourier series expansion

$$h(t)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{h}_k\cdot e^{2k\pi it},$$

where $h_k={\int }_0^{1}h(s)e^{2k\pi is}ds$, $k\in \mathbf{Z}$. By the Parseval equality, we have

$${\parallel h\parallel }_2^2=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{|h_k|}^2,$$

where ${\parallel \cdot \parallel }_2$ is the norm in $L^2(I)$. Now, by uniqueness of the Fourier series expansion, the solution $u=Th$ of LPBVP (22) has the Fourier series expansion

$$u(t)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{h_k}{{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2}\cdot e^{2k\pi it},$$

and $u^{″}$ can be expressed by the Fourier series expansion

$$u^{″}(t)=-\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{{(2k\pi )}^2{h}_k}{{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2}\cdot e^{2k\pi it}.$$

Hence, by the Parseval equality, we have

(24)

(25)

From (24) and (25), we have

$$\begin{array}{rcl}{\parallel Th\parallel }_{E_{a,b}}^2& =& {\parallel u\parallel }_{E_{a,b}}^2=a^2{\parallel u\parallel }_2^2+b^2{\parallel u^{″}\parallel }_2^2=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{(a^2+b^2{(2k\pi )}^4){|h_k|}^2}{{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}^2}\\ \le & {\left(\underset{k\in {\mathbf{N}}^{\ast }}{max}\frac{\sqrt{a^2+b^2{(2k\pi )}^4}}{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}\right)}^2\cdot \sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{|h_k|}^2\\ =& {\left(\underset{k\in {\mathbf{N}}^{\ast }}{max}\frac{\sqrt{a^2+b^2{(2k\pi )}^4}}{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}\right)}^2\cdot {\parallel h\parallel }_2^2.\end{array}$$

This implies that (23) holds. The proof of Lemma 1 is completed. □

Lemma 2 Let $\alpha ,\beta \notin \mathcal{L}$ and $a,b>0$. Then the rectangle $R(\alpha ,\beta ;a,b)$ satisfies condition (14) if and only if condition (11) holds.

Proof Condition (14) holds

⇔ $(\alpha -a,\beta -b)$ and $(\alpha +a,\beta +b)$ on the same side of every eigenline ${\ell }_k$,

⇔ ${(2k\pi )}^4-(\alpha -a)-(\beta -b){(2k\pi )}^2$ and ${(2k\pi )}^4-(\alpha +a)-(\beta +b){(2k\pi )}^2$ have the same sign,

⇔ ${({(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2)}^2-{(a+b{(2k\pi )}^2)}^2>0$,

⇔ $\frac{a+b{(2k\pi )}^2}{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}<1$.

The proof of Lemma 2 is completed. □

Lemma 3 Let $\alpha ,\beta \notin \mathcal{L}$ and $a,b>0$. Then the ellipse $E(\alpha ,\beta ;a,b)$ satisfies condition (16) if and only if condition (15) holds.

Proof Condition (16) holds

⇔ for $\mathrm{\forall }\theta \in [0,2\pi ]$, $(\alpha -acos\theta ,\beta -bsin\theta )$ and $(\alpha +acos\theta ,\beta +bsin\theta )$ on the same side of every eigenline ${\ell }_k$,

⇔ ${(2k\pi )}^4-(\alpha -acos\theta )-(\beta -bsin\theta ){(2k\pi )}^2$ and ${(2k\pi )}^4-(\alpha +acos\theta )-(\beta +bsin\theta ){(2k\pi )}^2$ have the same sign,

⇔ ${({(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2)}^2-{(acos\theta +bsin\theta {(2k\pi )}^2)}^2>0$,

⇔ $\frac{|acos\theta +bsin\theta {(2k\pi )}^2|}{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}<1$,

⇔ ${max}_{\theta \in [0,2\pi ]}\frac{|acos\theta +bsin\theta {(2k\pi )}^2|}{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}<1$,

⇔ $\frac{\sqrt{a^2+b^2{(2k\pi )}^4}}{|{(2k\pi )}^4-\alpha -\beta {(2k\pi )}^2|}<1$.

The proof of Lemma 3 is completed. □

3 Proof of the main results

Proof of Theorem 1 We define a mapping $F:E_{a,b}\to L^2(I)$ by

$$F(u)(t)=f(t,u(t),u^{″}(t))-\alpha u(t)+\beta u^{″}(t).$$

(26)

It follows from (12) that $F:E_{a,b}\to L^2(I)$ is continuous and satisfies

$${\parallel F(u)\parallel }_2\le {\parallel u\parallel }_{E_{a,b}}+c,\mathrm{\forall }u\in E_{a,b}.$$

(27)

Therefore, the mapping defined by

$$Q=T\circ F:E_{a,b}\to E_{a,b}$$

(28)

is a completely continuous mapping. By the definition of the operator T, the solution of PBVP (1)-(2) is equivalent to the fixed point of the operator Q.

From (7), (11), and Lemma 1, it follows that ${\parallel T\parallel }_{B(L^2(I),E_{a,b})}<1$. We choose $R\ge \frac{c\cdot {\parallel T\parallel }_{B(L^2(I),E_{a,b})}}{1-{\parallel T\parallel }_{B(L^2(I),E_{a,b})}}$. Let $\overline{B}(\theta ,R)=\{u\in E_{a,b}|{\parallel u\parallel }_{E_{a,b}}\le R\}$. Then for any $u\in \overline{B}(\theta ,R)$, from (27) and (28), we have

$$\begin{array}{rcl}{\parallel Qu\parallel }_{E_{a,b}}& =& {\parallel T(F(u))\parallel }_{E_{a,b}}\le {\parallel T\parallel }_{B(L^2(I),E_{a,b})}\cdot {\parallel F(u)\parallel }_2\\ \le & {\parallel T\parallel }_{B(L^2(I),E_{a,b})}\cdot ({\parallel u\parallel }_{E_{a,b}}+c)\\ \le & {\parallel T\parallel }_{B(L^2(I),E_{a,b})}\cdot (R+c)\le R.\end{array}$$

Therefore, $Q(\overline{B}(\theta ,R))\subset \overline{B}(\theta ,R)$. By the Schauder’s fixed point theorem, Q has at least one fixed point in $\overline{B}(\theta ,R)$, which is a solution of PBVP (1)-(2). □

By Lemma 2, we can obtain the following existence result:

Corollary 6 Assume that the pair $(\alpha ,\beta )$ satisfies (7). If there exist positive constants a, b, and c such that (12) and (14) hold, then PBVP (1)-(2) has at least one solution.

Proof of Theorem 2 Let $F:E_{a,b}\to L^2(I)$ be a mapping defined by (26). Then it follows from (12) that $F:E_{a,b}\to L^2(I)$ is continuous and satisfies

$${\parallel F(u)\parallel }_2\le {\parallel u\parallel }_{E_{a,b}}+c,\mathrm{\forall }u\in E_{a,b}.$$

Thus, the mapping $Q=T\circ F:E_{a,b}\to E_{a,b}$ is completely continuous. By using (7), (15), and Lemma 1, a similar argument as in the proof of Theorem 1 shows that Q has at least one fixed point in $\overline{B}(\theta ,R)$, which is the solution of PBVP (1)-(2). □

Proof of Theorem 3 Let $F:E_{a,b}\to L^2(I)$ be defined by (26). Then $F:E_{a,b}\to L^2(I)$ is continuous. For any $u_1,u_2\in E_{a,b}$, from (17), we have

$$\begin{array}{rcl}|F(u_2)-F(u_1)|& =& |f(t,u_2,u_2^{″})-\alpha u_2+\beta u_2^{″}-[f(t,u_1,u_1^{″})-\alpha u_1+\beta u_1^{″}]|\\ =& |(f_u-\alpha )(u_2-u_1)+(f_v+\beta )(u_2^{″}-u_1^{″})|\\ =& |\frac{f_u-\alpha }{a}\cdot a(u_2-u_1)+\frac{f_v+\beta }{b}\cdot b(u_2^{″}-u_1^{″})|\\ \le & \sqrt{\frac{{(f_u-\alpha )}^2}{a^2}+\frac{{(f_v+\beta )}^2}{b^2}}\cdot \sqrt{a^2{(u_2-u_1)}^2+b^2{(u_2^{″}-u_1^{″})}^2}\\ \le & \sqrt{a^2{(u_2-u_1)}^2+b^2{(u_2^{″}-u_1^{″})}^2}.\end{array}$$

It follows from the above that ${\parallel F(u_2)-F(u_1)\parallel }_2\le {\parallel u_2-u_1\parallel }_{E_{a,b}}$. Thus, $Q=T\circ F:E_{a,b}\to E_{a,b}$ is a continuous mapping and it satisfies

$$\begin{array}{rcl}{\parallel Q(u_2)-Q(u_1)\parallel }_{a,b}& =& {\parallel T(F(u_2)-F(u_1))\parallel }_{E_{a,b}}\\ \le & {\parallel T\parallel }_{B(L^2(I),E_{a,b})}\cdot {\parallel F(u_2)-F(u_1)\parallel }_2\\ \le & {\parallel T\parallel }_{B(L^2(I),E_{a,b})}{\parallel u_2-u_1\parallel }_{E_{a,b}}.\end{array}$$

It follows from (16) and Lemma 3 that (15) holds. By (15) and Lemma 1, it is easy to see that ${\parallel T\parallel }_{B(L^2(I),E_{a,b})}<1$. Hence, $Q:E_{a,b}\to E_{a,b}$ is a contraction mapping. By the Banach contraction mapping principle, Q has a unique fixed point, which is the unique solution of PBVP (1)-(2). □

As in Corollary 6, in Theorem 2 we can use condition (16) to replace condition (15), and in Theorem 3, we use condition (15) to replace condition (16).