Abstract
In the present work, we study the qualitative behavior of two systems of higher-order rational difference equations. More precisely, we study the local asymptotic stability, instability, global asymptotic stability of equilibrium points and rate of convergence of positive solutions of these systems. Our results considerably extend and improve some recent results in the literature. Some numerical examples are given to verify our theoretical results.
MSC:39A10, 40A05.
Similar content being viewed by others
1 Introduction
Recently, studying the qualitative behavior of difference equations and systems is a topic of great interest. Applications of discrete dynamical systems and difference equations have appeared recently in many areas such as ecology, population dynamics, queuing problems, statistical problems, stochastic time series, combinatorial analysis, number theory, geometry, electrical networks, neural networks, quanta in radiation, genetics in biology, economics, psychology, sociology, physics, engineering, economics, probability theory and resource management. Unfortunately, these are only considered as the discrete analogs of differential equations. It is a well-known fact that difference equations appeared much earlier than differential equations and were instrumental in paving the way for the development of the latter. It is only recently that difference equations have started receiving the attention they deserve. Perhaps this is largely due to the advent of computers where differential equations are solved by using their approximate difference equation formulations. The theory of discrete dynamical systems and difference equations developed greatly during the last twenty-five years of the twentieth century. The theory of difference equations occupies a central position in applicable analysis. There is no doubt that the theory of difference equations will continue to play an important role in mathematics as a whole. Nonlinear difference equations of order greater than one are of paramount importance in applications. It is very interesting to investigate the behavior of solutions of a system of higher-order rational difference equations and to discuss the local asymptotic stability of their equilibrium points. Systems of rational difference equations have been studied by several authors. Especially there has been a great interest in the study of the attractivity of the solutions of such systems. For more results on the qualitative behavior of nonlinear difference equations, we refer the interested reader to [1–19].
Zhang et al. [20] studied the dynamics of a system of rational third-order difference equations
Din et al. [11] investigated the dynamics of a system of fourth-order rational difference equations
To be motivated by the above studies, our aim in this paper is to investigate the qualitative behavior of the following -order systems of rational difference equations:
where the parameters α, β, γ, , , and initial conditions , are positive real numbers, and
where the parameters a, b, c, , , and initial conditions , are positive real numbers. This paper is a natural extension of [11, 20, 21].
Let us consider -dimensional discrete dynamical system of the form
where and are continuously differentiable functions and I, J are some intervals of real numbers. Furthermore, a solution of system (3) is uniquely determined by initial conditions for . Along with system (3), we consider the corresponding vector map . An equilibrium point of (3) is a point that satisfies
The point is also called a fixed point of the vector map F.
Definition 1 Let be an equilibrium point of system (3).
-
(i)
An equilibrium point is said to be stable if for every there exists such that for every initial condition , , implies for all , where is the usual Euclidian norm in .
-
(ii)
An equilibrium point is said to be unstable if it is not stable.
-
(iii)
An equilibrium point is said to be asymptotically stable if there exists such that and as .
-
(iv)
An equilibrium point is called a global attractor if as .
-
(v)
An equilibrium point is called an asymptotic global attractor if it is a global attractor and stable.
Definition 2 Let be an equilibrium point of the map
where f and g are continuously differentiable functions at . The linearized system of (3) about the equilibrium point is
where
and is the Jacobian matrix of system (3) about the equilibrium point .
Lemma 1 [22]
Assume that , , is a system of difference equations and is the fixed point of F. If all eigenvalues of the Jacobian matrix about lie inside an open unit disk , then is locally asymptotically stable. If one of them has norm greater than one, then is unstable.
Lemma 2 [23]
Assume that , , is a system of difference equations and is the equilibrium point of this system. The characteristic polynomial of this system about the equilibrium point is , with real coefficients and . Then all roots of the polynomial lie inside the open unit disk if and only if for , where is the principal minor of order k of the matrix
Let us consider a system of difference equations
where is an m-dimensional vector, is a constant matrix, and is a matrix function satisfying
as , where denotes any matrix norm which is associated with the vector norm
Proposition 1 (Perron’s theorem)[24]
Suppose that condition (6) holds. If is a solution of (5), then either for all large n or
exists and is equal to the modulus of one of the eigenvalues of matrix A.
Proposition 2 [24]
Suppose that condition (6) holds. If is a solution of (5), then either for all large n or
exists and is equal to the modulus of one of the eigenvalues of matrix A.
2 On the system ,
In this section, we shall investigate the qualitative behavior of system (1). Let be an equilibrium point of system (1), then for and , system (1) has two positive equilibrium points , , where and .
To construct the corresponding linearized form of system (1), we consider the following transformation:
where , , , … , and , , , … , . The Jacobian matrix about the fixed point under the transformation (9) is given by
where , , and .
Theorem 1 Let and , then every solution of system (1) is bounded.
Proof It is easy to verify that
and
Take and . Then and for all . □
Theorem 2 The equilibrium point of system (1) is locally asymptotically stable.
Proof The linearized system of (1) about the equilibrium point is given by
where
and
Let denote the eigenvalues of matrix E. Let be a diagonal matrix, where , , , and
Clearly, D is invertible. Computing , we obtain
We obtain the following two inequalities:
which implies that
and
Furthermore,
and
It is a well-known fact that E has the same eigenvalues as . Hence, we obtain
Hence, the equilibrium point of system (1) is locally asymptotically stable. □
Theorem 3 The positive equilibrium point of system (1) is unstable.
Proof The linearized system of (1) about the equilibrium point is given by
where
and
where and . The characteristic polynomial of is given by
From (10), we have
It is clear that not all of . Therefore, by Lemma 1, the unique positive equilibrium point is unstable. □
Theorem 4 Let and , and let be a solution of system (1). Then, for , the following statements are true:
-
(i)
If , then
-
(ii)
If , then
Proof It follows from induction. □
Theorem 5 Let and , then the equilibrium point of system (1) is globally asymptotically stable.
Proof For and , from Theorem 2, is locally asymptotically stable. From Theorem 1, every positive solution is bounded, i.e., and for all , where and . So, it is sufficient to prove that is decreasing. From system (1), one has
This implies that and . Hence, the subsequences
are decreasing, i.e., the sequence is decreasing. Also,
This implies that and . Hence, the subsequences
are decreasing, i.e., the sequence is decreasing. Hence, . □
Theorem 6 Let and . Then, for a solution of system (1), the following statements are true:
-
(i)
If , then .
-
(ii)
If , then .
2.1 Rate of convergence
We investigate the rate of convergence of a solution that converges to the equilibrium point of system (1).
Assume that and . First we will find a system of limiting equations for the map F. The error terms are given as
Set and , one has
where for ,
Taking the limits, we obtain for , , for , for , for and . Hence, the limiting system of error terms at can be written as
where
which is similar to the linearized system of (1) about the equilibrium point . Using proposition (1), one has the following result.
Theorem 7 Assume that is a positive solution of system (1) such that , and , where . Then the error vector of every solution of (1) satisfies both of the following asymptotic relations:
where are the characteristic roots of the Jacobian matrix about .
3 On the system ,
In this section, we shall investigate the qualitative behavior of system (2). Let be an equilibrium point of system (2), then system (2) has a unique equilibrium point . To construct the corresponding linearized form of system (2), we consider the following transformation:
, , , …, and , , , … , . The Jacobian matrix about the fixed point under the transformation (13) is given by
where , , and .
Theorem 8 Let be a positive solution of system (2), then for every , the following results hold.
Lemma 3 Let , then every solution of system (2) is bounded.
Proof Assume that
and
Then from Theorem 8 one can easily see that and for all . □
Theorem 9 The equilibrium point of equation (2) is locally asymptotically stable.
Proof The linearized system of (2) about the equilibrium point is given by
where
and
Let denote the eigenvalues of matrix E. Let be a diagonal matrix, where , , and
Clearly, D is invertible. Computing , we obtain
Next, we have the following two inequalities:
which implies that
and
Furthermore,
and
Now H has the same eigenvalues as , we obtain that
Hence, the equilibrium point of system (2) is locally asymptotically stable. □
Theorem 10 Let and , then the equilibrium point of system (2) is globally asymptotically stable.
Proof Assume that and . Then from Theorem 9 the equilibrium point of system (2) is locally asymptotically stable. Moreover, from Lemma 3 every positive solution is bounded, i.e., and for all , where and . Now, it is sufficient to prove that is decreasing. From system (2) one has
This implies that and .
This implies that
Hence, and . Hence, the subsequences
and
are decreasing. Therefore the sequences and are decreasing. Hence, . □
3.1 Rate of convergence
Assume that and . First we will find a system of limiting equations for system (2). The error terms are given as
Set and , then one has
where
for , , for ,
and . Taking the limits, we obtain for , for , , for , , for , So, the limiting system of error terms can be written as
where
and
which is similar to the linearized system of (2) about the equilibrium point . Using proposition (1), one has the following result.
Theorem 11 Assume that is a positive solution of system (2) such that , and , where . Then the error vector of every solution of (2) satisfies both of the following asymptotic relations:
where are the characteristic roots of the Jacobian matrix about .
4 Examples
In order to verify our theoretical results, we consider some interesting numerical examples in this section. These examples show that the equilibrium point of both systems (1) and (2) is globally asymptotically stable.
Example 1 Consider system (1) with initial conditions , , , , , , , , , , , , , , , , , . Moreover, choose the parameters , , , , , . Then system (1) can be written as
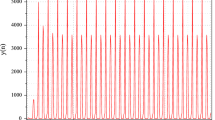
with initial conditions , , , , , , , , , , , , , , , , , . Moreover, in Figure 1, the plot of is shown in Figure 1a, the plot of is shown in Figure 1b, and an attractor of system (14) is shown in Figure 1c.
Example 2 Consider system (1) with initial conditions , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , . Moreover, choose the parameters , , , , , . Then system (1) can be written as
with initial conditions , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , . Moreover, in Figure 2, the plot of is shown in Figure 2a, the plot of is shown in Figure 2b, and an attractor of system (15) is shown in Figure 2c.
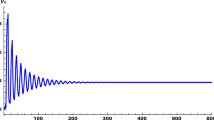
Example 3 Consider system (2) with initial conditions , , , , , , , , , , , , , . Moreover, choose the parameters , , , , , . Then system (2) can be written as
with initial conditions , , , , , , , , , , , , , . Moreover, in Figure 3, the plot of is shown in Figure 3a, the plot of is shown in Figure 3b, and an attractor of system (16) is shown in Figure 3c.
Example 4 Consider system (2) with initial conditions , , , , , , , , , , , , , , , , , , , , , , , , , . Moreover, choose the parameters , , , , , . Then system (2) can be written as
with initial conditions , , , , , , , , , , , , , , , , , , , , , , , , , . Moreover, in Figure 4, the plot of is shown in Figure 4a, the plot of is shown in Figure 4b, and an attractor of system (17) is shown in Figure 4c.
Conclusion
This work is a natural extension of [11, 20, 21]. In the paper, we have investigated the qualitative behavior of -dimensional discrete dynamical systems. Each system has only one equilibrium point which is stable under some restriction to parameters. The linearization method is used to show that equilibrium point is locally asymptotically stable. The main objective of dynamical systems theory is to predict the global behavior of a system based on the knowledge of its present state. An approach to this problem consists of determining the possible global behaviors of the system and determining which initial conditions lead to these long-term behaviors. In case of higher-order dynamical systems, it is crucial to discuss global behavior of the system. Some powerful tools such as semiconjugacy and weak contraction cannot be used to analyze global behavior of systems (1) and (2). In the paper, we prove the global asymptotic stability of equilibrium point by using simple techniques. We have carried out a systematical local and global stability analysis of both systems. The most important finding here is that the unique equilibrium point can be a global asymptotic attractor for systems (1) and (2). Moreover, we have determined the rate of convergence of a solution that converges to the equilibrium point of systems (1) and (2). Some numerical examples are provided to support our theoretical results. These examples are experimental verifications of theoretical discussions.
References
Cinar C:On the positive solutions of the difference equation system ; . Appl. Math. Comput. 2004, 158: 303-305.
Stević S: On some solvable systems of difference equations. Appl. Math. Comput. 2012, 218: 5010-5018.
Kurbanli AS:On the behavior of positive solutions of the system of rational difference equations , , . J. Differ. Equ. 2011., 2011: Article ID 40
Stević S: On a third-order system of difference equations. Appl. Math. Comput. 2012, 218: 7649-7654.
Bajo I, Liz E: Global behaviour of a second-order nonlinear difference equation. J. Differ. Equ. Appl. 2011, 17(10):1471-1486.
Kalabuŝić S, Kulenović MRS, Pilav E: Dynamics of a two-dimensional system of rational difference equations of Leslie-Gower type. Adv. Differ. Equ. 2011. 10.1186/1687-1847-2011-29
Kalabuŝić S, Kulenović MRS, Pilav E: Global dynamics of a competitive system of rational difference equations in the plane. Adv. Differ. Equ. 2009., 2009: Article ID 132802
Kurbanli AS, Çinar C, Yalçinkaya I:On the behavior of positive solutions of the system of rational difference equations . . Math. Comput. Model. 2011, 53: 1261-1267.
Din Q: Dynamics of a discrete Lotka-Volterra model. Adv. Differ. Equ. 2013, 1: 1-13.
Din Q, Donchev T: Global character of a host-parasite model. Chaos Solitons Fractals 2013, 54: 1-7.
Din Q, Qureshi MN, Khan AQ: Dynamics of a fourth-order system of rational difference equations. Adv. Differ. Equ. 2012, 1: 1-15.
Din Q, Khan AQ, Qureshi MN: Qualitative behavior of a host-pathogen model. Adv. Differ. Equ. 2013. 10.1186/1687-1847-2013-263
Din Q: Global behavior of a rational difference equation. Acta Univ. Apulensis 2013, 34: 35-49.
Din Q, Ibrahim TF: Global behavior of a neural networks system. Indian J. Comput. Appl. Math. 2013, 1(1):79-92.
Qureshi MN, Khan AQ, Din Q: Global behavior of third order system of rational difference equations. Int. J. Eng. Res. Technol. 2013, 2(5):2182-2191.
El-Metwally H, Elsayed EM: Form of solutions and periodicity for systems of difference equations. J. Comput. Anal. Appl. 2013, 15(5):852-857.
Touafek N, Elsayed EM: On the solutions of systems of rational difference equations. Math. Comput. Model. 2012, 55: 1987-1997.
Elsayed EM, El-Metwally HA: On the solutions of some nonlinear systems of difference equations. Adv. Differ. Equ. 2013. 10.1186/1687-1847-2013-161
Elsayed EM: Solution and attractivity for a rational recursive sequence. Discrete Dyn. Nat. Soc. 2011., 2011: Article ID 982309
Zhang Q, Yang L, Liu J: Dynamics of a system of rational third order difference equation. J. Differ. Equ. 2012. 10.1186/1687-1847-2012-136
Shojaei M, Saadati R, Adibi H: Stability and periodic character of a rational third order difference equation. Chaos Solitons Fractals 2009, 39: 1203-1209.
Sedaghat H: Nonlinear Difference Equations: Theory with Applications to Social Science Models. Kluwer Academic, Dordrecht; 2003.
Kocic VL, Ladas G: Global Behavior of Nonlinear Difference Equations of Higher Order with Applications. Kluwer Academic, Dordrecht; 1993.
Pituk M: More on Poincare’s and Perron’s theorems for difference equations. J. Differ. Equ. Appl. 2002, 8: 201-216.
Acknowledgements
This work was supported by the Higher Education Commission of Pakistan.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors have no competing interests.
Authors’ contributions
All authors contributed equally in drafting this manuscript and giving the main proofs.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Khan, A.Q., Qureshi, M.N. & Din, Q. Global dynamics of some systems of higher-order rational difference equations. Adv Differ Equ 2013, 354 (2013). https://doi.org/10.1186/1687-1847-2013-354
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-354