Abstract
Since in some application mathematical problems finding the analytical solution is too complicated, in recent years a lot of attention has been devoted by researchers to find the numerical solution of this equations. In this paper, an application of the Bernstein polynomials expansion method is applied to solve linear second kind Fredholm and Volterra integral equations systems. This work reduces the integral equations system to a linear system in generalized case such that the solution of the resulting system yields the unknown Bernstein coefficients of the solutions. Illustrative examples are provided to demonstrate the preciseness and effectiveness of the proposed technique. The results are compared with the exact solution by using computer simulations.
Similar content being viewed by others
1 Introduction
As a matter of fact, it might be said that many phenomena of almost all practical engineering and applied science problems like physical applications, potential theory and electrostatics are reduced to solving integral equations. Since these equations usually cannot be solved explicitly, so it is required to obtain approximate solutions. There are numerous numerical methods which have been focusing on the solution of integral equations. For example, Tricomi in his book [1], introduced the classical method of successive approximations for integral equations. Variational iteration method [2] and Adomian decomposition method [3] were effective and convenient for solving integral equations. Also, the Homotopy analysis method (HAM) was proposed by Liao [4] and then has been applied in [5]. Taylor expansion approach was presented for solving integral equations by Kanwal and Liu in [6] and then has been extended in [7, 8]. In addition, Babolian et al. [9] solved some integral equations systems by using the orthogonal triangular basis functions. Jafari et al. [10] applied Legendre wavelets method to find numerical solution system of linear integral equations. Moreover, some different valid methods for solving this kind of equations have been developed. First time, the Bernstein polynomials have been used for the solution of some linear and nonlinear differential equations in [11–14]. Mandal and Bhattacharya [15] obtained approximate numerical solutions of some classes of integral equations by using Bernstein polynomials. Also, they used these polynomials to approximate solution of linear Volterra integral equations [16]. In addition, Maleknejad et al. [17] has applied the polynomials for solving Volterra integral equations of the second kind. Furthermore, in [18] an architecture of artificial neural networks (ANNs) was suggested to approximate solution of linear integral equations systems. For this aim, first the truncations of the Taylor expansions for unknown functions were substituted in the original system. Then the proposed neural network has been applied for adjusting the real coefficients of the given expansions in the resulting system.
In this paper, we are going to propose a new numerical approach to approximate the solutions of linear Fredholm and Volterra integral equations systems of the second kind. This method converts the given systems with unique solutions, into a system of linear algebraic equations in generalized case. To do this, first the Bernstein polynomials of certain degree n of unknown functions are substituted in the given integral equations system. Suppose that the given closed interval is partitioned into uniform spacing and nodes (for ). If we put (for ), the given system of integral equations, yields a linear algebraic system. The solution of the resulting system yields the unknown Bernstein coefficients of the solution functions.
Here is an outline of the paper. Section 2 describes how to find approximate solutions of the given linear integral equations systems by using the proposed approach. In Section 3, the convergence of the method is established for each class of integral equations systems. Finally in Section 4, two numerical examples are provided and the results are compared with the analytical solutions to demonstrate the validity and applicability of the method. Also, a comparison is made with other numerical approaches that were proposed recently for solving the given systems.
2 The general method
The basic definition of integral equation is given in [15, 17, 19]. In this section, we intend to use the Bernstein polynomials to get a new numerical method for solving the linear Fredholm and Volterra integral equations systems of the second kind. In other words, it will be described how to apply these polynomials for approximating solutions of the unknowns in the systems.
2.1 System of the Fredholm integral equations
In this subdivision, we want to obtain a numerical solution of the linear Fredholm integral equations system of the second kind in the form
or
Let us consider
where
which are the Bernstein expansions of degree n for the unknown functions for . After substituting these polynomials instead of the unknowns in the system (2), we have:
In order to find in Eq. (3), the system (4) is converted to an algebraic system of linear equations by replacing t with (for ). Notice that in this way we can skip the singularity problem. After this work, the system is transformed to the following form:
For brevity, we define below symbols as:
Now we can write the system (5) in the form
Consequently, the expression (6) can be summarized in a matrix form as follows:
where
Parochial matrices , for () are defined with following elements:
where
The resulting generalized linear system can be solved for for ; by a standard method, and hence is obtained.
2.2 System of Volterra integral equations
At first, consider again the system of linear Volterra integral equations (1). For numerical solving of the present system, the unknown function is approximated by its Bernstein approximation (3). Now we have the following system:
Similarly, by replacing the variable t with for , we obtain the generalized linear system
where
Consequently, the expression (6) can be summarized in a matrix form as follows:
where
and
In the above generalized linear system, the symbols are defined as follows:
3 Convergence analysis
In this section, we prove that the present numerical method converges to the exact solutions of the systems (2) and (1).
Theorem 1 Let for be the Bernstein polynomials of degree n such that their coefficients have been produced by solving the generalized linear system (7). Then the given polynomials converge to the exact solution of the Fredholm integral equations system (2), when .
Proof Consider the system (2). Since the series (3) converge to for , respectively, then we conclude that:
and it holds that
We defined the error function by subtracting Eqs. (2) and (11) as follows:
where
We must prove that when , the error function tends to zero. Hence, we proceed as follows:
Since and are bounded, therefore, implies that and the proof is completed. □
Theorem 2 Suppose that for are the Bernstein polynomials of degree n such that their coefficients have been produced by solving the generalized linear system (10). Then the given polynomials converge to the exact solution of the Volterra integral equations system (1), when .
Proof Consider the system (1). Using a similar procedure as an outline in mentioned Theorem 1, we have the following corollary in which we are refrained from going through proof details. Now the error of the approximation method can be written as
where
Due to Theorem 1, the error function must tend to zero, when . Hence, we proceed as follows:
Since and are bounded, therefore, implies that and the proof follows immediately. The stability and the convergence of Bernstein polynomials is studied in [12, 13]. □
4 Numerical examples
In this section, in order to investigate the accuracy of the proposed method, we have chosen three examples of linear integral equations systems of the second kind. Also, to show the efficiency of the present method for our problem, results will be compared with the exact solution. Moreover, the present method is compared with artificial neural network (ANN) method and the trapezoidal quadrature rule (TQR) [18].
Example 1 Consider the system of linear Fredholm integral equations
with
where the exact solution is and . In this example, we illustrate the use of the present technique to approximate solution of this integral equations system. Using Eq. (7), the coefficients matrices W, V and E are calculated for as following:
where
Now by using the above matrices, the vector solution of the generalized linear system (7) is obtained as follows:
Consequently, the approximate functions and can be written as follows:
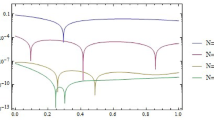
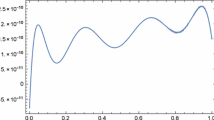
Figures 1 and 2 show the accuracy of the solution functions and , respectively. As shown, the difference between the exact solutionand the computed solution is dispensable. Numerical results can be seen in Table 1 and also Table 2 illustrates the absolute values of the errors obtained here and the absolute errors of [18] for this example.
Trapezoidal rule Moreover, this example is going to show the difference between the present method and the trapezoidal quadrature rule.Consider again Example 1, let the region of integration be subdivided into 4 equal intervals of width , 5 integration nodes for . Table 2 illustrates the absolute values of the errors obtained here and the absolute errors of [18] for this example. It should be noted that the Lagrange basis functions have been used for finding the 4th degree collocation polynomials through the points for ; .
Example 2 Let the system of linear Volterra integral equations
with
The exact solution of the present problem is, and . Similarly, the present method is applied to approximate solution of the integral equations system. We calculate the coefficients matrices W, V and E by using Eq. (10) for as following:
where
Now by using the above matrices, the vector solution of the generalized linear system (10) is obtained as follows:
Consequently, the approximate functions and can be written as follows:
Similarly, Figures 3 and 4 show the accuracy of the solution functions and , respectively. As shown, the difference between the exact solution and the computed solution is dispensable. Similarly, numerical results can be seen in Table 3.
Trapezoidal rule Suppose that the region of integration is subdivided into 5 equal intervals of width , 6 integration nodes for . Table 4 illustrates the absolute values of the errors obtained here and the absolute errors of [18] for this example. Furthermore, the Lagrange interpolation method has been used to design the interpolation polynomials.
Example 3 Consider
where
with the exact solution, , and . Again, we solved this example by this method and the results are given in Table 5. Table 6 illustrates the absolute errors of ANN method and TQR for this example.
As we can see this method will be useful when the exact solution is a polynomial. In other word, the proposed method give the analytical solution for the system, if the exact solution be polynomials of degree n or less than n.
5 Conclusions
In some cases, an analytical solution cannot be found for integral equations system, therefore, numerical methods have been applied. In this study, we have worked out a computational method to approximate solution of the Fredholm and Volterra integral equations systems of the second kind. The present course is a method for approximating unknown functions in terms of truncated sequences including Bernstein polynomials. It is clear that to get the best approximating solutions of the given systems, the truncation degree n must be chosen large enough. An interesting feature of this method is finding the analytical solution for given system, if the exact solution be polynomials of degree n or less than n. Additionally, the proposed method has been compared with ANN method [18] and TQR. The analyzed examples illustrated the ability and reliability of the present method. The obtained solutions, in comparison with exact solutions admit a remarkable accuracy. Extensions to the case of more general systems of integral equations are left for future studies.
References
Tricomi FG: Integral Equations. Dover, New York; 1982.
Lan X: Variational iteration method for solving integral equations. Comput. Math. Appl. 2007, 54: 1071–1078. 10.1016/j.camwa.2006.12.053
Babolian E, Sadeghi Goghary S, Abbasbandy S: Numerical solution of linear Fredholm fuzzy integral equations of the second kind by Adomian method. Appl. Math. Comput. 2005, 161: 733–744. 10.1016/j.amc.2003.12.071
Liao SJ: Beyond Perturbation: Introduction to the Homotopy Analysis Method. Chapman & Hall/CRC Press, Boca Raton; 2003.
Abbasbandy S: Numerical solution of integral equation: homotopy perturbation method and Adomian’s decomposition method. Appl. Math. Comput. 2006, 173: 493–500. 10.1016/j.amc.2005.04.077
Kanwal RP, Liu KC: A Taylor expansion approach for solving integral equations. Int. J. Math. Educ. Sci. Technol. 1989, 2: 411–414.
Maleknejad K, Aghazadeh N: Numerical solution of Volterra integral equations of the second kind with convolution kernel by using Taylor-series expansion method. Appl. Math. Comput. 2005, 161: 915–922. 10.1016/j.amc.2003.12.075
Nas S, Yalcynbas S, Sezer M: A Taylor polynomial approach for solving high-order linear Fredholm integrodifferential equations. Int. J. Math. Educ. Sci. Technol. 2000, 31: 213–225. 10.1080/002073900287273
Babolian E, Masouri Z, Hatamzadeh-Varmazyar S: A direct method for numerically solving integral equations system using orthogonal triangular functions. Int. J. Ind. Math. 2009, 2: 135–145.
Jafari H, Hosseinzadeh H, Mohamadzadeh S: Numerical solution of system of linear integral equations by using Legendre wavelets. Int. J. Open Probl. Comput. Sci. Math. 2010, 5: 63–71.
Bhatti MI, Bracken P: Solutions of differential equations in a Bernstein polynomial basis. J. Comput. Appl. Math. 2007. doi:10.1016/j.cam.2006.05.002
Farouki RT, Goodman TNT: On the optimal stability of the Bernstein basis. Math. Comput. 1996, 65(216):1553–1566. 10.1090/S0025-5718-96-00759-4
Yousefi SA, Behroozifar M: Operational matrices of Bernstein polynomials and their applications. Int. J. Syst. Sci. 2010, 41(6):709–716. 10.1080/00207720903154783
Bhatta DD, Bhatti MI: Numerical solution of KdV equation using modified Bernstein polynomials. Appl. Math. Comput. 2006, 174: 1255–1268. 10.1016/j.amc.2005.05.049
Mandal BN, Bhattachary S: Numerical solution of some classes of integral equations using Bernstein polynomials. Appl. Math. Comput. 2007, 191: 1707–1716.
Bhattacharya S, Mandal BN: Use of Bernstein polynomials in numerical solution of Volterra integral equations. Appl. Math. Sci. 2008, 6: 1773–1787.
Maleknejad K, Hashemizadeh E, Ezzati R: A new approach to the numerical solution of Volterra integral equations by using Bernstein’s approximation. Commun. Nonlinear Sci. Numer. Simul. 2011, 161: 647–655.
Jafarian A, Measoomy NS: Utilizing feed-back neural network approach for solving linear Fredholm integral equations system. Appl. Math. Model. 2012. doi:10.1016/j.apm.2012.09.029
Hochstadt H: Integral Equations. Wiley, New York; 1973.
Acknowledgements
We would like to thank the referees for their comments and remarks.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors have equal contributions and they have approved the final version of the manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jafarian, A., Measoomy Nia, S.A., Golmankhaneh, A.K. et al. Numerical solution of linear integral equations system using the Bernstein collocation method. Adv Differ Equ 2013, 123 (2013). https://doi.org/10.1186/1687-1847-2013-123
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-123