Abstract
Background
Mining novel biomarkers from gene expression profiles for accurate disease classification is challenging due to small sample size and high noise in gene expression measurements. Several studies have proposed integrated analyses of microarray data and protein-protein interaction (PPI) networks to find diagnostic subnetwork markers. However, the neighborhood relationship among network member genes has not been fully considered by those methods, leaving many potential gene markers unidentified. The main idea of this study is to take full advantage of the biological observation that genes associated with the same or similar diseases commonly reside in the same neighborhood of molecular networks.
Results
We present EgoNet, a novel method based on egocentric network-analysis techniques, to exhaustively search and prioritize disease subnetworks and gene markers from a large-scale biological network. When applied to a triple-negative breast cancer (TNBC) microarray dataset, the top selected modules contain both known gene markers in TNBC and novel candidates, such as RAD51 and DOK1, which play a central role in their respective ego-networks by connecting many differentially expressed genes.
Conclusions
Our results suggest that EgoNet, which is based on the ego network concept, allows the identification of novel biomarkers and provides a deeper understanding of their roles in complex diseases.
Similar content being viewed by others
Background
Complex human diseases, e.g. cancer, diabetes, or autism, are caused by dysregulations of biological networks. Genetic analysis approaches focused on individual genetic determinants are unlikely to characterize the network architecture of complex diseases comprehensively. Creating effective therapies for these diseases requires a thorough understanding of how cells integrate enormous amounts of genomic, proteomic, and environmental information to produce specific cellular functions, and furthermore, how such functions are perturbed in the disease state. Transcriptomics, metabolomics, proteomics and other -omics technologies have the potential to provide insights into complex disease pathogenesis and heterogeneity, especially if they are applied within a network biology framework. “Network medicine” is the rapidly developing field which applies systems biology and network science methods to human disease [1–3].
In the past decade, extensive work has been done to identify differentially expressed genes across different phenotypes, which can be used as diagnostic markers for classifying different disease states or predicting clinical outcomes [4–7]. However, gene markers based on expression data alone are still not reliable [8]. To meet this challenge, many have turned to network medicine to gain a comprehensive understanding of the complex disease process. In contrast to studying individual genes in isolation, mapping human disease-associated genes to interactome data has greatly empowered our understanding of human disease mechanisms [9]. Network-based approaches have multiple potential biological and clinical applications, including a better understanding of the effects of interconnection of disease genes and disease pathways, which, in turn, may offer better targets for drug development. These advances may also lead to more reliable biomarkers to monitor the functional integrity of networks that are perturbed by diseases.
To date, many computational methods have been developed to integrate gene expression profiles with protein-protein interaction maps or pathway databases, with the goal of identifying significant subnetwork markers for predicting biological or clinical outcomes [10–18]. More recently, different machine learning and data mining strategies for feature selection have been applied to identifying a subset of genes that can maximize the prediction performance [19]. Dutkowski et al.[20] proposed Network-Guided Forests (NGF) which integrates the key ideas of Random Forests (RF) into the selection of disease modules. However, it involves a random search over subnetworks, leading to possibly different results from different runs with no guarantee of the optimality of the final result. Zhu et al.[21] applied network-based Support Vector Machine (SVM) for classification of microarray samples but the method only worked for small subnetworks. More importantly, the above methods are largely heuristic, and the definition of output subnetworks is ambiguous without a formal topological feature. Hence, selected network modules tend to include only significant genes based on their expression profiles, but exclude the non-differentially expressed genes despite the fact that they are functionally linked to many differentially expressed disease genes.
In this study, we developed a novel method called EgoNet to identify significant subnetworks that are functionally associated with diseases, as well as accurately predict clinical outcomes. The type of subnetwork sought by our method is called ego-network, which is well-defined in the study of social networks [22]. In particular, an ego-network is the part of a network that involves a particular node we are focusing on, which we call ego. In addition to the ego, the network consists of a neighborhood including all nodes to which the ego is connected to at a certain path length. The one-step neighborhood contains the nodes the ego is directly connected to (referred to as the ego’s alters), and the links between the ego’s alters. In studying ego-networks, we are interested in examining how egos make use of or are influenced by their alters in terms of associating with disease outcomes. It has been reported that the ego-network played an important role in the inference of novel disease genes and supported predictions in pathogenesis studies [23].
The underlying assumption of our model is that if the majority of neighbors of a central disease gene are disease genes, then its other neighbors are likely to be involved in the disease pathway (Figure 1A). Alternatively, if most neighbors of the ego node are associated with a disease, the ego gene itself is considered highly likely to play a role in the disease (Figure 1B). We intend to find the hidden genes that show no significance by themselves but are clustered in a subnetwork module whose genes collectively are highly predictive of the disease status. The ego-network model has been used for network module over-representation analysis in ConsensusPathDB [24]. In this study, we use machine-learning techniques to assess the association between an ego-network with the clinical outcome. This approach allows compensatory effects between the genes in an ego-network, as well as nonlinear relations between the genes and the clinical outcome.
We evaluated the performance of EgoNet in human protein-protein interaction network and a triple negative breast cancer (TNBC) microarray data set. The method not only successfully identified known breast cancer susceptibility genes TP53, BRCA1, BRCA2 from significant ego-networks, but also detected several novel targets, like ABL1 and RAD51 as predictive factors for TNBC patients. We expect that EgoNet can be widely used to infer novel biomarkers for phenotypic outcome prediction of many human diseases.
Results and discussion
Overview of EgoNet algorithm
The goal of EgoNet algorithm is to identify significant ego-networks from gene expression and large-scale biological network data. As outlined in Figure 2, the algorithm takes the network and gene expression data as input. The input biological network can be a gene regulatory network, a signaling pathway network, or a protein-protein interaction network. The gene expression data needs to be associated with a certain biological or clinical outcome, which can be a categorical, continuous, or survival outcome.
EgoNet iteratively scans through all genes with two or more neighbors in the network. With each initial gene (the ego node), it first finds the score of the level-one ego-network based on how well the genes as a collection predicts the clinical outcome. Then it spreads outward from the ego node progressively to involve more genes in the predictive model. The spreading stops when the prediction accuracy drops (Figure 2; Methods). The above process of growing ego-network is also known as snowball sampling [25]. After obtaining the score of an ego-network, the significance is evaluated by permutation test.
Simulation studies
To evaluate the capability of an ego network to predict the clinical outcome, a machine-learning method needs to be chosen. In this study, we selected three widely used methods: support vector machines (SVM) [26], K-nearest neighbors (KNN) [27] and random forests (RF) [28], and compared their performance for subnetwork identification through a simulation study.
In each simulation, a scale-free network was generated, and one subnetwork was selected as the ground truth. The subnetwork was linked to the outcome variable through linear or nonlinear relationship. We applied the EgoNet algorithm in conjunction with the three classifiers for subnetwork selection, and inspected if the top identified ego-netowork (s) recovered the true subnetwork. In general, SVM performed the best (Table 1). In both linear and non-linear settings, if we only selected the top ego-netowork in every simulation, SVM successfully recovered the true subnetwork more than 50% of the time. When we increased the number of identified ego-networks to top 5, SVM was able to recover the true subnetwork over 80% of the time. Thus we chose SVM for the subsequent data analysis.
Next we compared the performance of EgoNet with the method proposed by Chuang et al. [11], which scores subnetworks using the mutual information between aggregated gene Z-scores and class labels. We simulated two scenarios: (1) All genes in an ego-network, including the ego gene, are associated with the clinical outcome; and (2) All genes in an ego-network, except the ego gene, are associated with the clinical outcome. The second scenario was motivated by our consideration that sometimes a gene functionally related to a disease may not be differentially expressed, while it is surrounded by differentially expressed genes in the network (Figure 1B). In each of the scenarios, we further simulated both linear and nonlinear associations between gene expression and clinical outcome.
The methods were compared in two ways. The first is the accuracy in predicting the clinical outcome, and the second is the rate of correctly recovering the true ego network. For prediction accuracy, we employed the area under the ROC curve (AUC) as the metric to evaluate performance. Additional file 1: Figure S1A shows EgoNet outperformed Chuang et al.’s method in terms of classification accuracy, albeit the difference is relatively small. For true ego network recovery, we calculated the rate of the top selected subnetwork capturing the true ego node. We found EgoNet showed substantially higher proportions of recovering the true ego node (Additional file 1: Figure S1B). As expected, the difference was most pronounced in the scenarios where the ego node itself was not directly associated with the clinical outcome.
Gene modules differentiate breast cancer subtypes
We applied EgoNet to analyze human PPI network with the expression profiles of the two cohorts of breast cancer patients previously reported by Li et al. [29], which compared the gene expression of 24 sporadic triple negative breast cancer (TNBC) samples against 51 primary breast tumor samples representing all subtypes (NCBI GSE18864). TNBC is characterized by the lack of expression of estrogen receptor (ER), progesterone receptor (PgR), and the human epidermal growth factor receptor 2 (ERBB2, or HER2) [30]. It largely overlaps with the basal-like subtype of breast cancer [31].
The PPI network was obtained from HINT database [32], which collected data from several databases and filtered both systematically and manually to remove low-quality/erroneous interactions. The network contained 8292 human proteins and 27493 high-quality binary physical interactions.
We applied our algorithm to this dataset. We allowed only nodes with more than one connection to serve as egos. From every ego node, we progressively grew the ego-networks by levels, and tested the predictive power. For every ego network, the procedure stopped when the predictive power dropped with the growth. Following this procedure, a total of 5375 ego-networks were examined, and the average of nodes in an ego-network is 30. Since ego-networks spread out in levels, which are the maximum network distance from ego to its alters, we found ~76% of the generated ego-networks were level 1 and ~24% of them were level 2 (Additional file 2: Figure S2). Prediction accuracy for phenotypic outcome of those ego-networks varied between 0.63 and 0.95. We identified the top 50 discriminative ego-networks by setting the accuracy cutoff at 0.9. All were significant with p < 0.001 in permutation tests with 1000 permutations.
BRCA1 and BRCA2 are well-known breast cancer susceptibility genes that belong to tumor suppressor genes [33]. TP53 is a tumor suppressor gene whose mutation is associated with a variety of cancers. Distinct mutation patterns of TP53 was found between the luminal subtypes of breast cancer and TNBC [31]. We explored the three genes in our identified subnetworks. Interestingly, we found they were clustered in one ego-network in which BRCA2 was the ego node (Figure 3A). This observation is consistent with the local property of disease networks – proteins involved in the same disease have an increased tendency to interact with each other [2]. We conducted single-gene level differential expression analysis. At the FDR cutoff of 0.05, none of the three genes showed differential expression between TNBC and non-TNBC breast cancer patients. We further evaluated the importance of each gene on the classification accuracy using a tree-based feature selection algorithm (Method). We found genes with high importance scores were mostly differentially expressed. In the BRCA2 ego-network, breast cancer susceptibility genes ABL1 and RAD51 [34, 35] were under such scenario.
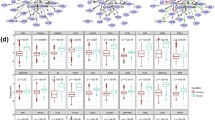
Identified ego-networks in the TNBC breast cancer dataset. Module (A) contains major breast cancer genes BRCA1, BRCA2 and TP53. Modules (B) and (C) contain ERBB2 and ESR1 respectively. Examples of other top-scoring modules are shown in (D-F). The area of each node scales with its importance in the classification of the phenotype. Red color indicates differential expression (FDR <0.05 based on a two-tailed t-test with Benjamini & Hochberg FDR adjustment).
The ABL1 proto-oncogene encodes a cytoplasmic and nuclear protein tyrosine kinase that has been implicated in processes of cell differentiation, cell division, and so on [36]. ABL1 is activated into an oncogene and forms a fusion gene with break point cluster (BCR) gene due to missense mutations within the ABL1 kinase domain. The chimeric oncogene BCR-ABL1 has been implicated to play a critical role in the development of chronic myelogenous leukemia [37]. The over-expressed BCR-ABL gene will increase the transmembrane plasma protein expression and constitutively activate the downstream signaling molecules such as Src family kinases [38], including DOK1 and NCOA2, which we discuss below. Thus it is logical to believe that ABL1 is a critical factor in breast cancer development. A detailed examination of the expression level of ABL1 revealed it was substantially over-expressed in TNBC, as compared to other primary breast cancer subtypes (Additional file 3: Figure S3a). Our study suggests ABL1 may be regarded as a predictive factor for differentiating TNBC from other primary breast cancer.
RAD51 encodes the major eukaryotic homologous recombinase [39], which assists in the repair of DNA double strand breaks. The RAD51 protein has been demonstrated to interact with the ssDNA-binding protein BRCA2, a well-known breast cancer susceptibility gene [40]. BRCA2 controls and regulates both the intracellular localization and DNA–binding ability of RAD51 [41, 42]. There were some reports suggesting that dysfunctional variants of RAD51 is associated with breast cancer risk. One recent study suggested the association of RAD51 polymorphis with DNA repair in BRCA1 mutation carriers and sporadic breast cancer risk [43]. Smolarz et al. reported that there was a significant positive association between RAD51 polymorphisms and TNBC [44]. In our current study, RAD51 is significantly under-expressed in the TNBC samples (Additional file 3: Figure S3b).
TNBC lacks the expression of three receptors, ER, ERBB2 and PgR [30]. We found two of the corresponding genes from our identified subnetworks, of which ERBB2 was in the DOK1 ego-network (Figure 3B) and ESR1 in the NCOA2 ego-network (Figure 3C). DOK1 is known to be a tumor suppressor gene in epithelial ovarian cancer [45] and lung cancer [46]. It is a substrate of several non-receptor tyrosine kinases [47, 48], including breast tumor kinase (BRK) [49]. Since most of DOK1’s alters were differentially expressed, DOK1 may play a role in the molecular pathways of TNBC. DOK1 itself showed a minor under-expression in TNBC (Additional file 3: Figure S3c), though not statistically significant at the FDR level of 0.05. ERBB2 is a member of the DOK1 ego-network. Because the receptor itself is not expressed in TNBC, as expected, the ERBB2 gene was under-expressed in TNBC as compared with other primary breast cancer subtypes (Additional file 3: Figure S3d). ESR1 showed a similar pattern (Additional file 3: Figure S3e).
Our results also suggest NCOA2 could be an important factor in the TNBC gene regulatory pathways. NCOA2, the nuclear receptor coactivator 2, which belongs to the steroid receptor coactivator (SRC) family, has been reported to be broadly involved in many cancers [50]. The SRC family comprises three members, SRC-1 (NCOA1), SRC-2 (NCOA2) and SRC-3 (NCOA3), which are known to be overexpressed in breast cancer and essentially involved in estrogen mediated cancer cell proliferation [51]. Currently, most research on the SRC family has been focused on NCOA1 and NCOA3. Clinical and preclinical studies have demonstrated that overexpressed NCOA1 and NCOA3 are linked to resistance to therapies in breast cancers [52]. For example, overexpression of NCOA3, especially in conjunction with high levels EGF receptor (EGFR) and HER2 (ERBB2), is associated with poor outcome after tamoxifen treatment [53, 54]. In ERBB2–overexpressing breast cancer cells, overexpression of NCOA3 also contributes to resistance against the ERBB2 targeting drug transtuzumab [55]. In the current study, NCOA2 is significantly under-expressed in the TNBC samples as compared with other subtypes of primary breast cancer (Additional file 3: Figure S3f). Our results indicate that NCOA2 could be as important as the other two members and play an important role in the TNBC gene regulation.
We shall note that the current study is to compare TNBC with the pool of other subtypes of breast cancer. Thus the resulting sub-networks have more to do with the differences between TNBC and other subtypes, as opposed to directly explaining the clinical characteristics of TNBC itself. Although EgoNet pointed to DOK1 and NCOA2 ego-networks as among the best to separate TNBC from other primary breast cancers, it is still far from establishing a mechanistic explanation. This limitation has to be addressed by future biological studies.
Given an ego-network, a “structural hole” is the absence of an edge among a pair of nodes in the ego network. A well-established proposition in social network analysis is that egos with lots of structural holes are better performers in certain competitive settings [22]. Among our identified ego-networks, we found examples containing few structural holes (Figure 3C-D), and those containing many (Figure 3E-F). The binding mechanism may imply ego genes such as ERCC8 and GGA1 whose ego-networks include many structural holes are key factors to distinguish the TNBC patients.
Network-based ranking of marker genes
Next, we evaluated the importance of individual genes by considering all the subnetworks together. An important property of disease genes in a molecular network is that the nodes with much higher degrees of linkages, so called hubs, should typically be associated with disease genes [19]. We assume that a putative disease hub is important, and thus should be included in more identified disease subnetworks. For each ego-network, a classification accuracy score is available, and the relative importance values are calculated for genes included in the ego-network. We propose a metric that is the summation of the product of subnetwork score (S i ) and node importance (V ij ) over all the considered subnetworks, namely
where i is the ego-network index, and V ij is the importance score of the jth gene in the ith subnetwork which takes value zero if the gene is not in the subnetwork. Node importance (V ij ) is calculated using tree-based feature selection method (Methods).
Table 2 shows the top 20 ranked genes based on their M values. We found the list included both differentially expressed (DE) genes and non-DE genes. In the DE group, a notable example of biomarker gene in TNBC, EGFR [56] is present, which suggests the ranking derived by our proposed metric is sensible. The non-DE genes could not have been identified based on the gene expression data alone. However, by integrating the network and gene expression profiles, we could identify these putative biomarker genes that were not differentially expressed.
For the non-DE genes in Table 2, there have been literatures reporting TGFBR1 and SMAD1 signaling pathways to be related to breast cancer [57, 58]. Previous studies also showed MAPK signaling pathway to be activated in triple-negative breast cancer [59]. Gene Ontology (GO) and KEGG pathway enrichment analysis for the top 100 genes by their M values was carried out using the DAVID tool [60]. The identified genes were highly enriched in cancer processes or pathways (Additional file 4: Table S1). We further investigated the network degree distribution for the 100 genes. The results showed that these genes tend to be higher degree nodes in the large PPI network (Additional file 5: Figure S4). Our results demonstrated that disease-associated genes have significantly higher connectivity in the PPI network. Similar conclusions have also been reported in the literature [61, 62].
EgoNet can be viewed as a feature selection technique that identifies sets of genes to build a predictive model. Specifically, the gene sets considered are an ‘ego’ and its neighboring genes that can be reached from the ego at a certain path length. We leveraged the EgoNet method to search for subnetworks that can distinguish triple negative breast cancer tumors from other breast cancer subtypes, recovering several known breast cancer-related genes. Importantly, our results revealed a list of novel candidate genes that may provide a deeper understanding in breast cancer studies.
Conclusions
In this study, we proposed EgoNet, an algorithm for selecting subnetworks whose gene expression is predictive of a disease phenotype. The key advantage of EgoNet is its capability to discover potential markers that are not differentially expressed, but are functionally associated with many differentially expressed genes. EgoNet is a general framework for ego-network selection. In this study, we paired EgoNet with SVM to solve a two-class (case/control) decision problem. However, when paired with an appropriate machine learning approach, EgoNet can be readily applied to datasets with continuous, multi-class, and survival outcome variables.
Methods
EgoNet algorithm
The EgoNet algorithm is described in the following quasi-code.

Accessing the significance of the identified ego-network
When an ego-network is identified, a test of significance is performed to obtain the statistical significance. The null distribution of classification accuracy is derived by randomly permuting the phenotypic labels B times and calculating the score from the same ego-network each time. The actual score of this ego network is then indexed on the null distribution to obtain a p-value (Figure 2).
Computation of ego-network node importance
We employ Random Forest to rank the importance of variables, in this case, the importance of nodes of an ego-network for making disease outcome predictions. The relative importance (RI) of a predictor in a Random Forest model is obtained by the out-of-bag (OOB) error estimation, which is the increase of mean squared error (MSE) when the predictor values are permuted.
For each tree t, let OOB t be the associated sample and errOOB t be the error of t on this OOB t sample. Randomly permute the value of predictor Xj in OOB t to get a perturbed sample denoted by and compute . The variable importance score of predictor Xj is derived by
Where T is the number of trees. We used the Python package “sklearn” to implement this procedure.
The design of simulation study
We simulated each scenario 100 times. In each simulation, we generated a scale-free undirected and no-self-loop network with 500 nodes. Together with the network data, a gene expression dataset with 500 genes and 100 samples was generated by random sampling the expression values from the standard normal distribution. An ego-network is selected by first randomly selecting a node as ego with its network degree between 5 and 20, and then taking the level 1 ego-network from the selected ego node. Eighty percent of the nodes in the ego-network were marked as disease genes, and the phenotypic outcomes were generated based on the expression values of those disease genes using linear and nonlinear models. The linear relationship was formulated as Y = ∑ X i , while the nonlinear relationship was formulated as Y = ∑ X i 3. Finally, Y was dichotomized to 0 if Y < 0 or 1 if Y ≥ 0.
Availability
The EgoNet algorithm is implemented by Python scripts and available at https://github.com/cauyrd/EgoNet.
Abbreviations
- TNBC:
-
Triple negative breast cancer
- PPI:
-
Protein-protein interaction
- RF:
-
Random forest
- SVM:
-
Support vector machine
- KNN:
-
K-nearest neighbor
- FDR:
-
False discovery rate
- DE:
-
Differentially expressed
- MSE:
-
Mean square error
- RI:
-
Relative importance
- OOB:
-
Out of bag.
References
Barabási A-L: Network medicine–from obesity to the “diseasome”. N Engl J Med. 2007, 357: 404-407. 10.1056/NEJMe078114.
Barabási A-L, Gulbahce N, Loscalzo J: Network medicine: a network-based approach to human disease. Nat Rev Genet. 2011, 12: 56-68. 10.1038/nrg2918.
Chan SY, Loscalzo J: The emerging paradigm of network medicine in the study of human disease. Circ Res. 2012, 111: 359-374. 10.1161/CIRCRESAHA.111.258541.
Boutros PC, Lau SK, Pintilie M, Liu N, Shepherd FA, Der SD, Tsao M-S, Penn LZ, Jurisica I: Prognostic gene signatures for non-small-cell lung cancer. Proc Natl Acad Sci U S A. 2009, 106: 2824-2828. 10.1073/pnas.0809444106.
Stratford JK, Bentrem DJ, Anderson JM, Fan C, Volmar KA, Marron JS, Routh ED, Caskey LS, Samuel JC, Der CJ, Thorne LB, Calvo BF, Kim HJ, Talamonti MS, Iacobuzio-Donahue CA, Hollingsworth MA, Perou CM, Yeh JJ: A six-gene signature predicts survival of patients with localized pancreatic ductal adenocarcinoma. PLoS Med. 2010, 7: e1000307-10.1371/journal.pmed.1000307.
van 't Veer LJ, Dai H, van de Vijver MJ, He YD, Hart AAM, Mao M, Peterse HL, van der Kooy K, Marton MJ, Witteveen AT, Schreiber GJ, Kerkhoven RM, Roberts C, Linsley PS, Bernards R, Friend SH: Gene expression profiling predicts clinical outcome of breast cancer. Nature. 2002, 415: 530-536. 10.1038/415530a.
Yeoh E-J, Ross ME, Shurtleff SA, Williams WK, Patel D, Mahfouz R, Behm FG, Raimondi SC, Relling MV, Patel A, Cheng C, Campana D, Wilkins D, Zhou X, Li J, Liu H, Pui C-H, Evans WE, Naeve C, Wong L, Downing JR: Classification, subtype discovery, and prediction of outcome in pediatric acute lymphoblastic leukemia by gene expression profiling. Cancer Cell. 2002, 1: 133-143. 10.1016/S1535-6108(02)00032-6.
Venet D, Dumont JE, Detours V: Most random gene expression signatures are significantly associated with breast cancer outcome. PLoS Comput Biol. 2011, 7: e1002240-10.1371/journal.pcbi.1002240.
Goh K-I, Cusick ME, Valle D, Childs B, Vidal M, Barabási A-L: The human disease network. Proc Natl Acad Sci U S A. 2007, 104: 8685-8690. 10.1073/pnas.0701361104.
Chen L, Xuan J, Riggins RB, Wang Y, Clarke R: Identifying protein interaction subnetworks by a bagging Markov random field-based method. Nucleic Acids Res. 2013, 41: e42-10.1093/nar/gks951.
Chuang H-Y, Lee E, Liu Y-T, Lee D, Ideker T: Network-based classification of breast cancer metastasis. Mol Syst Biol. 2007, 3: 140-
Ciriello G, Cerami E, Sander C, Schultz N: Mutual exclusivity analysis identifies oncogenic network modules. Genome Res. 2012, 22: 398-406. 10.1101/gr.125567.111.
Hwang T, Tian Z, Kuangy R, Kocher J-P: Learning on Weighted Hypergraphs to Integrate Protein Interactions and Gene Expressions for Cancer Outcome Prediction. Eighth IEEE International Conference on Data Mining: 2008. 2008, Washington DC: IEEE Computer Society, 293-302.
Nie Y, Yu J: Mining breast cancer genes with a network based noise-tolerant approach. BMC Syst Biol. 2013, 7: 49-10.1186/1752-0509-7-49.
Pujana MA, Han J-DJ, Starita LM, Stevens KN, Tewari M, Ahn JS, Rennert G, Moreno V, Kirchhoff T, Gold B, Assmann V, Elshamy WM, Rual J-F, Levine D, Rozek LS, Gelman RS, Gunsalus KC, Greenberg RA, Sobhian B, Bertin N, Venkatesan K, Ayivi-Guedehoussou N, Solé X, Hernández P, Lázaro C, Nathanson KL, Weber BL, Cusick ME, Hill DE, Offit K, et al: Network modeling links breast cancer susceptibility and centrosome dysfunction. Nat Genet. 2007, 39: 1338-1349. 10.1038/ng.2007.2.
Su J, Yoon B-J, Dougherty ER: Identification of diagnostic subnetwork markers for cancer in human protein-protein interaction network. BMC Bioinforma. 2010, 11 (Suppl 6): S8-10.1186/1471-2105-11-S6-S8.
Taylor IW, Linding R, Warde-Farley D, Liu Y, Pesquita C, Faria D, Bull S, Pawson T, Morris Q, Wrana JL: Dynamic modularity in protein interaction networks predicts breast cancer outcome. Nat Biotechnol. 2009, 27: 199-204. 10.1038/nbt.1522.
Winter C, Kristiansen G, Kersting S, Roy J, Aust D, Knösel T, Rümmele P, Jahnke B, Hentrich V, Rückert F, Niedergethmann M, Weichert W, Bahra M, Schlitt HJ, Settmacher U, Friess H, Büchler M, Saeger H-D, Schroeder M, Pilarsky C, Grützmann R: Google goes cancer: improving outcome prediction for cancer patients by network-based ranking of marker genes. PLoS Comput Biol. 2012, 8: e1002511-10.1371/journal.pcbi.1002511.
Wang X, Gulbahce N, Yu H: Network-based methods for human disease gene prediction. Brief Funct Genomics. 2011, 10: 280-293. 10.1093/bfgp/elr024.
Dutkowski J, Ideker T: Protein networks as logic functions in development and cancer. PLoS Comput Biol. 2011, 7: e1002180-10.1371/journal.pcbi.1002180.
Zhu Y, Shen X, Pan W: Network-based support vector machine for classification of microarray samples. BMC Bioinforma. 2009, 10 (Suppl 1): S21-10.1186/1471-2105-10-S1-S21.
Borgatti SP, Mehra A, Brass DJ, Labianca G: Network analysis in the social sciences. Science. 2009, 323: 892-10.1126/science.1165821.
Jordán F, Nguyen T-P, Liu W-C: Studying protein-protein interaction networks: a systems view on diseases. Brief Funct Genomics. 2012, 11: 497-504. 10.1093/bfgp/els035.
Kamburov A, Pentchev K, Galicka H, Wierling C, Lehrach H, Herwig R: ConsensusPathDB: toward a more complete picture of cell biology. Nucleic Acids Res. 2011, 39: D712-D717. 10.1093/nar/gkq1156.
Goodman LA: Snowball sampling. Ann Math Stat. 1961, 32: 148-170. 10.1214/aoms/1177705148.
Cortes C, Vapnik V: Support-vector networks. Mach Learn. 1995, 20: 273-297.
Cover T, Hart P: Nearest neighbor pattern classification. IEEE Trans Inf Theory. 1967, 13: 21-27.
Breiman LEO: Random forests. Mach Learn. 2001, 45: 5-32. 10.1023/A:1010933404324.
Li Y, Zou L, Li Q, Haibe-Kains B, Tian R, Li Y, Desmedt C, Sotiriou C, Szallasi Z, Iglehart JD, Richardson AL, Wang ZC: Amplification of LAPTM4B and YWHAZ contributes to chemotherapy resistance and recurrence of breast cancer. Nat Med. 2010, 16: 214-218. 10.1038/nm.2090.
Gluz O, Liedtke C, Gottschalk N, Pusztai L, Nitz U, Harbeck N: Triple-negative breast cancer–current status and future directions. Ann Oncol. 2009, 20: 1913-1927. 10.1093/annonc/mdp492.
Cancer Genome Atlas N: Comprehensive molecular portraits of human breast tumours. Nature. 2012, 490 (7418): 61-70. 10.1038/nature11412.
Das J, Yu H: HINT: high-quality protein interactomes and their applications in understanding human disease. BMC Syst Biol. 2012, 6: 92-10.1186/1752-0509-6-92.
Buchholz TA, Weil MM, Story MD, Strom EA, Brock WA, McNeese MD: Tumor suppressor genes and breast cancer. Radiat Oncol Investig. 1999, 7: 55-65. 10.1002/(SICI)1520-6823(1999)7:2<55::AID-ROI1>3.0.CO;2-#.
Kato M, Yano K, Matsuo F, Saito H, Katagiri T, Kurumizaka H, Yoshimoto M, Kasumi F, Akiyama F, Sakamoto G, Nagawa H, Nakamura Y, Miki Y: Identification of Rad51 alteration in patients with bilateral breast cancer. J Hum Genet. 2000, 45: 133-137. 10.1007/s100380050199.
Srinivasan D, Plattner R: Activation of Abl tyrosine kinases promotes invasion of aggressive breast cancer cells. Cancer Res. 2006, 66: 5648-5655. 10.1158/0008-5472.CAN-06-0734.
Szczylik C, Skorski T, Nicolaides NC, Manzella L, Malaguarnera L, Venturelli D, Gewirtz AM, Calabretta B: Selective inhibition of leukemia cell proliferation by BCR-ABL antisense oligodeoxynucleotides. Science. 1991, 253 (5019): 562-565. 10.1126/science.1857987.
Parker BC, Engels M, Annala M, Zhang W: Emergence of FGFR family gene fusions as therapeutic targets in a wide spectrum of solid tumours. J Pathol. 2014, 232 (1): 4-15. 10.1002/path.4297.
An X, Tiwari AK, Sun Y, Ding PR, Ashby CR, Chen ZS: BCR-ABL tyrosine kinase inhibitors in the treatment of Philadelphia chromosome positive chronic myeloid leukemia: a review. Leuk Res. 2010, 34 (10): 1255-1268. 10.1016/j.leukres.2010.04.016.
Conway AB, Lynch TW, Zhang Y, Fortin GS, Fung CW, Symington LS, Rice PA: Crystal structure of a Rad51 filament. Nat Struct Mol Biol. 2004, 11 (8): 791-796. 10.1038/nsmb795.
Buisson R, Dion-Cote AM, Coulombe Y, Launay H, Cai H, Stasiak AZ, Stasiak A, Xia B, Masson JY: Cooperation of breast cancer proteins PALB2 and piccolo BRCA2 in stimulating homologous recombination. Nat Struct Mol Biol. 2010, 17 (10): 1247-1254. 10.1038/nsmb.1915.
Bhattacharyya A, Ear US, Koller BH, Weichselbaum RR, Bishop DK: The breast cancer susceptibility gene BRCA1 is required for subnuclear assembly of Rad51 and survival following treatment with the DNA cross-linking agent cisplatin. J Biol Chem. 2000, 275 (31): 23899-23903. 10.1074/jbc.C000276200.
Le Calvez-Kelm F, Oliver J, Damiola F, Forey N, Robinot N, Durand G, Voegele C, Vallee MP, Byrnes G, Registry BC, Hopper JL, Southey MC, Andrulis IL, John EM, Tavtigian SV, Lesueur F: RAD51 and breast cancer susceptibility: no evidence for rare variant association in the Breast Cancer Family Registry study. PLoS One. 2012, 7 (12): e52374-10.1371/journal.pone.0052374.
Ricks-Santi LJ, Sucheston LE, Yang Y, Freudenheim JL, Isaacs CJ, Schwartz MD, Dumitrescu RG, Marian C, Nie J, Vito D, Edge SB, Shields PG: Association of Rad51 polymorphism with DNA repair in BRCA1 mutation carriers and sporadic breast cancer risk. BMC Cancer. 2011, 11: 278-10.1186/1471-2407-11-278.
Smolarz B, Zadrożny M, Duda-Szymańska J, Makowska M, Samulak D, Michalska MM, Mojs E, Bryś M, Forma E, Romanowicz-Makowska H: RAD51 genotype and triple-negative breast cancer (TNBC) risk in Polish women. Pol J Pathol. 2013, 64: 39-43.
Mercier P-L, Bachvarova M, Plante M, Gregoire J, Renaud M-C, Ghani K, Têtu B, Bairati I, Bachvarov D: Characterization of DOK1, a candidate tumor suppressor gene, in epithelial ovarian cancer. Mol Oncol. 2011, 5: 438-453. 10.1016/j.molonc.2011.07.003.
Berger AH, Niki M, Morotti A, Taylor BS, Socci ND, Viale A, Brennan C, Szoke J, Motoi N, Rothman PB, Teruya-Feldstein J, Gerald WL, Ladanyi M, Pandolfi PP: Identification of DOK genes as lung tumor suppressors. Nat Genet. 2010, 42: 216-223. 10.1038/ng.527.
Goel RK, Miah S, Black K, Kalra N, Dai C, Lukong KE: The unique N-terminal region of SRMS regulates enzymatic activity and phosphorylation of its novel substrate docking protein 1. FEBS J. 2013, 280 (18): 4539-4559. 10.1111/febs.12420.
Nelms K, Snow AJ, Noben-Trauth K: Dok1 encoding p62(dok) maps to mouse chromosome 6 and human chromosome 2 in a region of translocation in chronic lymphocytic leukemia. Genomics. 1998, 53 (2): 243-245. 10.1006/geno.1998.5514.
Miah S, Goel RK, Dai C, Kalra N, Beaton-Brown E, Bagu ET, Bonham K, Lukong KE: BRK Targets Dok1 for ubiquitin-mediated proteasomal degradation to promote cell proliferation and migration. PLoS One. 2014, 9 (2): e87684-10.1371/journal.pone.0087684.
Wang Y, Lonard DM, Yu Y, Chow DC, Palzkill TG, Wang J, Qi R, Matzuk AJ, Song X, Madoux F, Hodder P, Chase P, Griffin PR, Zhou S, Liao L, Xu J, O'Malley BW: Bufalin is a potent small-molecule inhibitor of the steroid receptor coactivators SRC-3 and SRC-1. Cancer Res. 2014, 74 (5): 1506-1517. 10.1158/0008-5472.CAN-13-2939.
Paruthiyil S, Cvoro A, Tagliaferri M, Cohen I, Shtivelman E, Leitman DC: Estrogen receptor beta causes a G2 cell cycle arrest by inhibiting CDK1 activity through the regulation of cyclin B1, GADD45A, and BTG2. Breast Cancer Res Treat. 2011, 129 (3): 777-784. 10.1007/s10549-010-1273-5.
Wagner M, Koslowski M, Paret C, Schmidt M, Tureci O, Sahin U: NCOA3 is a selective co-activator of estrogen receptor alpha-mediated transactivation of PLAC1 in MCF-7 breast cancer cells. BMC Cancer. 2013, 13: 570-10.1186/1471-2407-13-570.
Siouda M, Yue J, Shukla R, Guillermier S, Herceg Z, Creveaux M, Accardi R, Tommasino M, Sylla BS: Transcriptional regulation of the human tumor suppressor DOK1 by E2F1. Mol Cell Biol. 2012, 32 (23): 4877-4890. 10.1128/MCB.01050-12.
Mc Ilroy M, Fleming FJ, Buggy Y, Hill AD, Young LS: Tamoxifen-induced ER-alpha-SRC-3 interaction in HER2 positive human breast cancer; a possible mechanism for ER isoform specific recurrence. Endocr Relat Cancer. 2006, 13 (4): 1135-1145. 10.1677/erc.1.01222.
Nahta R: Pharmacological strategies to overcome HER2 cross-talk and Trastuzumab resistance. Curr Med Chem. 2012, 19 (7): 1065-1075. 10.2174/092986712799320691.
Burness ML, Grushko TA, Olopade OI: Epidermal growth factor receptor in triple-negative and basal-like breast cancer: promising clinical target or only a marker?. Cancer J. 2010, 16 (1): 23-32. 10.1097/PPO.0b013e3181d24fc1.
Liu X, Yue J, Frey RS, Zhu Q, Mulder KM: Transforming growth factor beta signaling through Smad1 in human breast cancer cells. Cancer Res. 1998, 58: 4752-4757.
Scollen S, Luccarini C, Baynes C, Driver K, Humphreys MK, Garcia-Closas M, Figueroa J, Lissowska J, Pharoah PD, Easton DF, Hesketh R, Metcalfe JC, Dunning AM: TGF-β signaling pathway and breast cancer susceptibility. Cancer Epidemiol Biomarkers Prev. 2011, 20: 1112-1119. 10.1158/1055-9965.EPI-11-0062.
Bartholomeusz C, Gonzalez-Angulo AM, Liu P, Hayashi N, Lluch A, Ferrer-Lozano J, Hortobágyi GN: High ERK protein expression levels correlate with shorter survival in triple-negative breast cancer patients. Oncologist. 2012, 17: 766-774. 10.1634/theoncologist.2011-0377.
Huang DW, Sherman BT, Lempicki RA: Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources. Nat Protoc. 2009, 4: 44-57.
Jonsson PF, Bates PA: Global topological features of cancer proteins in the human interactome. Bioinformatics. 2006, 22: 2291-2297. 10.1093/bioinformatics/btl390.
Wachi S, Yoneda K, Wu R: Interactome-transcriptome analysis reveals the high centrality of genes differentially expressed in lung cancer tissues. Bioinformatics. 2005, 21: 4205-4208. 10.1093/bioinformatics/bti688.
Acknowledgements
This work was partially supported by NIH grants P20 HL113451, P01 AI096187 and U19 AI057266.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
RY, ZQ and TY conceived and designed the study. RY implemented the method and conducted the simulation study. RY and TY conducted the data analysis. RY and YB interpreted the biological results. RY, YB and TY wrote the manuscript. All authors read and approved the final manuscript.
Electronic supplementary material
12864_2013_6005_MOESM1_ESM.pdf
Additional file 1: Figure S1: Classification performance (A) and proportion of ego node coverage (B) for the proposed EgoNet method and Chuang et al.’s method in different simulation settings. (PDF 16 KB)
12864_2013_6005_MOESM4_ESM.xlsx
Additional file 4: Table S1: Enriched GO and KEGG categories for the top 100 disease-associated genes ranked by M value. (XLSX 18 KB)
12864_2013_6005_MOESM5_ESM.pdf
Additional file 5: Figure S4: Network degree distribution of the top 100 identified disease-associated genes ranked by M value (red curve) and all genes from the human PPI network (blue curve). (PDF 60 KB)
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Yang, R., Bai, Y., Qin, Z. et al. EgoNet: identification of human disease ego-network modules. BMC Genomics 15, 314 (2014). https://doi.org/10.1186/1471-2164-15-314
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2164-15-314