1 Introduction

The vacuum Einstein equations \(R_{\mu \nu }-1/2g_{\mu \nu }R=0\) are scale invariant in the sense that the Einstein tensor is dimensionally homogeneous: each of the two terms on the left-hand side are homogeneous of degree two in the derivatives of the metric and there is no length with respect to which one can measure the size of any dimensionful constant. The introduction of a cosmological constant into the energy density of the (Lorentz-invariant) vacuum breaks scale invariance by adding an energy-momentum tensor of the form \(T_{\mu \nu }=-\Lambda g_{\mu \nu }\) to the vacuum field equations [1] and permits the usual inflationary cosmological solutions. However, it also creates a scale given by \(\Lambda =(8\pi G)^{-1/2}\), and hence a discrepancy between the observed energy density of empty space, which is measured to be around \(10^{-47}\text {GeV} ^{4}\) using general relativity, and the expected vacuum field energy \( \Lambda ^{4}/16\pi ^{2}\approx 2\times 10^{71}\text {GeV}^{4}\), from quantum field theory. This is sometimes called the ‘cosmological constant problem’ [2,3,4,5]. By introducing \(\Lambda \) into the vacuum Einstein equations we introduce the possibility of inflationary (accelerating) de Sitter solutions at the expense of an anomalously large vacuum energy density.

The main proposal advanced in this paper is that this discrepancy points to a fundamental failure of both general relativity and quantum field theory. For they are unable to deal with the cosmological constant in a meaningful way simply because \(\Lambda \) is something extraneous to both theories. We take it as a basic point of departure that the cosmological constant implies that some new physics operates at a hyper-classical scale, not reducible to either the classical domain of general relativity or that of quantum fields. The ideas of the multiverse and the anthropic principle [2] contain some of the spirit of the present work, but our starting point and implementation are entirely different. It is one of the basic results of this paper that the cosmological constant and the energy of the vacuum are random and accidental attributes of our observable universe, indicative of the existence of a much wider, unexplored structure operating on a truly cosmological scale - that of containing the various presently causally disconnected regions. We show that although the cosmological constant is an arbitrary one appearing in the field equations of the theory, it can be equated to its presently observed value in our local, causally connected region, provided there is a distribution of such values, one for each such independent domain in the multiverse. Here we have in mind not one region (like ours) containing local subregions that were causally disconnected before the occurrence of inflation and became causally related after inflation, but completely separate regions like those that are constantly produced in the self-regenerating inflationary universe [6,7,8,9]. However, our model is not based or dependent on that process.

In our approach, we can retain the presence of inflationary solutions in the theory without automatically admitting the possibility of a vacuum energy density because as we show in this paper both the cosmological constant and the vacuum energy can be generally unrelated arbitrary constants. In Sect. 2, we describe formulation of the traceless version of the Einstein equations, first proposed by Einstein, and we prove using the Weyl tensor that the vacuum traceless Einstein equations include all the vacuum solutions of general relativity plus all solutions having a non-constant Weyl tensor (having a non-zero cosmological constant). As we show in Sect. 2.2 for the first time, the vacuum traceless theory is conformally equivalent to general relativity plus a self-interacting scalar field with an exponential potential. This result uses in an essential way a new effect that we highlight here, namely, the dimensional homogeneity of the traceless equations, a property closely related (in a sense which we make precise) to the traceless equations being ‘scale invariant’. We also discuss the physical relevance of the exponential potential of the theory. In Sect. 3, which is the main Section of this work, after reviewing certain relevant features of the standard f(R) theory, we introduce and study a new variant, the no-scale f(R) gravity. In Sect. 3.2, we show that the no-scale f(R) theory bears a similar relation to standard f(R) gravity as traceless GR does to standard GR with a cosmological constant, we provide the integrability condition, making the cosmological constant an arbitrary constant in this case. In Sect. 3.3, we show that the no-scale f(R) theory in spacetime dimension D is conformally equivalent to general relativity with a scalar field \(\phi \) with a potential given by a scale-invariant form: \(V(\phi )=\frac{D-2}{4D}Re^{-\phi }\), where \(\phi =[2/(D-2)]\ln f^{\prime }(R),\) and \(f^{\prime }\equiv \partial f/\partial R\) . This scalar field potential is quite different from the one we know from the standard conformal relation of f(R) gravity and general relativity found in ref. [10]. Its most interesting property is that, unlike in the conformal equivalent of full general relativity, flat potentials in no-scale theories are found to be possible in all spacetime dimensions for polynomial lagrangians of all orders. In Sect. 3.4, we discuss the example of the no-scale \(R+R^{n}\) theory, and we demonstrate how in this theory the cosmological constant, the vacuum energy and the height of the inflationary plateau are all unrelated arbitrary constants. Hence, no-scale higher-order gravity, like traceless general relativity, avoids a cosmological constant problem associated with an energy density of the vacuum, and we are led to a statistical distribution of values of the possible vacuum energies of individual components. In Sect. 4, we calculate the slow-roll parameters and show that no-scale higher-order gravity provides many possible inflationary models in agreement with microwave background data, and avoids fine tuning problems. In particular, we calculate the the primordial tilt and the tensor-to-scalar ratio for the no-scale \(R+R^{2}\) theory in four and general dimensions. The generic prediction is that any future measurement of the form \(r=12/(b^{2}N^{2}),b \ne 1\), will be in favor of the no-scale \(R+R^{2}\) theory. We also generalize these results to spacetime dimension D and polynomial degree n of the scalar field potential. We present our conclusions in Sect. 5. In the Appendix, we present the details of the conformal techniques leading to the scalar field potentials for the no-scale general relativity (Appendix A1) and no-scale f(R) gravity (Appendix A2) respectively.

2 No-scale general relativity

We seek a situation where the cosmological constant problem is absent but the possibility of inflation remains. We note that there is a way, first suggested by Einstein [11], to cancel the effects of a cosmological constant by using only the traceless parts of the Einstein equations to define the theory of gravitation [3, 11,12,13]. Before extending this approach to higher-order lagrangians, we summarize the structure of traceless general relativity introduced by Einstein and clearly expounded by Ellis in ref. [13].

2.1 General properties

For any tensor \(L_{\mu \nu }\), its traceless part in D spacetime dimensions is defined to be the new tensor,

$$\begin{aligned} {\widehat{L}}_{\mu \nu }=L_{\mu \nu }-\frac{1}{D}g_{\mu \nu }L,\quad L=\text {Tr }L_{\mu \nu }, \end{aligned}$$
(1)

so that \({\widehat{L}}=\text {Tr}{\widehat{L}}_{\mu \nu }=0\). For the Einstein tensor, defined by \(G_{\mu \nu }=R_{\mu \nu }-(1/2)g_{\mu \nu }R\), and setting the Einstein constant \(8\pi G/c^{4}=1\), we find that in D dimensions its traceless part is [11],

$$\begin{aligned} {\widehat{G}}_{\mu \nu }=R_{\mu \nu }-\frac{1}{D}g_{\mu \nu }R, \end{aligned}$$
(2)

(since \(1/D=1/2+(2-D)/2D\)), so it coincides with the traceless Ricci tensor. The traceless Einstein equations are then postulated to be

$$\begin{aligned} {\widehat{G}}_{\mu \nu }={\widehat{T}}_{\mu \nu },\quad {\widehat{T}}_{\mu \nu }=T_{\mu \nu }-\frac{1}{D}g_{\mu \nu }T, \end{aligned}$$
(3)

where \(T_{\mu \nu }\) is the usual energy-momentum tensor of matter, and T its trace. The vacuum traceless Einstein equations are scale invariant, being dimensionally homogeneous, like the standard vacuum Einstein equations. All the vacuum solutions of general relativity remain unchanged and the nine traceless field equations are a subset of the full (ten) Einstein equations. Crucially, however, although the stress tensor \(T_{\mu \nu }\) can have a trace, only the tracefree part gravitatesFootnote 1.

In the following, we shall mostly be interested in the vacuum equations, \( {\widehat{G}}_{\mu \nu }=0\), which are obtained when \(T_{\mu \nu }=0\). In the case of a cosmological constant, \(T_{\mu \nu }=-\Lambda g_{\mu \nu }\), the terms on the right-hand side of the traceless equations (3) cancel each other leading to the vacuum traceless equations as well. This means that in the traceless theory, unlike in general relativity, the cosmological constant has nothing to do with an energy density of the vacuum or a constant term in the gravitational action. In fact, it can easily be shown to be simply related to an arbitrary integration constant, \(\lambda \), that appears in the Einstein equations,

$$\begin{aligned} G_{\mu \nu }-\lambda g_{\mu \nu }=T_{\mu \nu }, \end{aligned}$$
(4)

with [3, 12, 13],

$$\begin{aligned} R+T=-D\lambda . \end{aligned}$$
(5)

In this way, the traceless equations (3) reduce to the equivalent system of equations (4), (5).

To gain a better idea of the structure of the solution space of the vacuum traceless Einstein equations, we can compare the Weyl tensor \( C^{\rho \,}_{\,\,\,\alpha \beta \gamma }\) in this context to that of the vacuum Einstein equations \(R_{\mu \nu }=0\) (for simplicity we consider the case \(D=4 \)). Using the standard formula (equivalent to the Bianchi identities),

$$\begin{aligned} \nabla _\rho \, C^{\rho \,}_{\,\,\,\alpha \beta \gamma }=R_{\alpha [\gamma ;\beta ]}- \frac{1}{6}g_{\alpha [\gamma }R_{;\beta ]}, \end{aligned}$$
(6)

and the vacuum traceless equations \({\widehat{G}}_{\mu \nu }=0\), or equivalently the system (4), (5), we find that

$$\begin{aligned} \nabla _\rho \, C^{\rho \,}_{\,\,\,\alpha \beta \gamma }=0\quad \text {if and only if}\quad \lambda =0. \end{aligned}$$
(7)

This result is important because it shows that unlike the vacuum Einstein equations where the Weyl tensor is covariantly constant, the vacuum traceless equations \({\widehat{G}}_{\mu \nu }=0\) have a more general solution space which includes all vacuum solutions of general relativity (\(\lambda =0\) ), but also many more solutions all of which have a non-constant Weyl conformal curvature (corresponding to \(\lambda \ne 0\).) Since the Weyl tensor is a conformal invariant, we shall see in the next subsection why the vacuum traceless Einstein theory is able to produce inflationary solutions ‘without a trace of lambda’.

2.2 The conformal potential and inflation

Before we examine the inflationary structure of the vacuum traceless theory, we make a comment about the inclusion of scalar fields in the traceless general relativity context. Since for a scalar field \(\phi \) with potential \( V(\phi )\), the traceless part of its energy-momentum tensor, \({\widehat{T}} _{\mu \nu }=\partial _{\mu }\phi \partial _{\nu }\phi -(1/D)g_{\mu \nu }(\partial \phi )^{2}\), does not contain the potential \(V(\phi )\) and we have \({\widehat{T}} =0\), it follows that in the traceless theory given by (3) the scalar field \(\phi \) gravitates but without a potential. Therefore, any property of the solutions of the traceless field equations (3) which depends implicitly on the potential \(V(\phi )\), such as the possibility of slow-roll inflation, should probably be considered as an ‘off-shell’ effect requiring some sort of fine-tuning.

We now move on to examine the conformal structure and possibility of inflation in the vacuum traceless theory \({\widehat{G}}_{\mu \nu }=0\). We can restrict the metric variations \(\delta g_{\mu \nu }\) used in the action principle by moving to a metric conformally related to \(g_{\mu \nu }\) (that enters in the vacuum traceless field equations), by introducing an analytic function f(R) by setting [10]

$$\begin{aligned} {\tilde{g}}_{\mu \nu }=e^{\phi }g_{\mu \nu },\quad \phi =\frac{2}{D-2}\ln f^{\prime }. \end{aligned}$$
(8)

Then, following the steps in the Appendix (Part A), we find that the vacuum traceless Einstein equations

$$\begin{aligned} {\widehat{G}}_{\mu \nu }=0, \end{aligned}$$
(9)

transform into,

$$\begin{aligned} \widetilde{{\widehat{G}}}_{\mu \nu }+\frac{D-2}{2}\nabla _{\mu }\nabla _{\nu }\phi = {\tilde{T}}_{\phi ,\mu \nu } \end{aligned}$$
(10)

where,

$$\begin{aligned} {\tilde{T}}_{\phi ,\mu \nu }= & {} \frac{D-2}{4}\bigg [ \nabla _{\mu }\phi \nabla _{\nu }\phi \nonumber \\&\quad - \frac{1}{2}{\tilde{g}}_{\mu \nu }\left( \frac{2(D-1)}{D}(\nabla \phi )^{2}+2V(\phi )\right) \bigg ] , \end{aligned}$$
(11)

with

$$\begin{aligned} V(\phi )=\frac{-\lambda }{(D-1)}e^{-\phi }, \end{aligned}$$
(12)

where we have also used the constraint (5) with \(T=0\).

The equations (10), (11) are scale invariant in the sense of being dimensionally homogeneous: Each one of the terms in the two sides of these equations has the same degree, namely two, in the derivatives because they contain two derivatives of the metric or of the scalar field (in the potential term we have substituted \(R=-D\lambda \) from the constraint). Therefore, we can freely perform a scale transformation \(\phi \rightarrow a\phi +b\), with a, b arbitrary constants in the potential (and also redefine the location of the minimum of \(V(\phi )\) by performing \(V(\phi )\rightarrow V(\phi )+d\), where d is any constant), without spoiling the property of the equations being dimensionally homogeneous. Hence, we end up with a conformal potential of the general form \(V(\phi )=ge^{-a\phi }\), with \(g=-\lambda e^{b},a\) being arbitrary constants. Note that when \(\lambda =0\), the potential vanishes and we are back to the case of vacuum general relativity.

Unfortunately, this generic prediction of the vacuum traceless general relativity theory for inflation with an exponential potential is ruled out both due to the fact that in this model there is no graceful exit from inflation, but also because of its disagreement with current observations (cf. eg., [14], Section 10.2).

3 No-scale f(R) gravity

3.1 Scale invariance in f(R) gravity

Adding a cosmological constant term is not the only way to break the scale invariance of the vacuum Einstein equations. The addition of higher-order curvature terms to the lagrangian also introduces a scale (see for example, [15], p. 153), and can lead to inflation in a natural way [16,17,18,19,20]. We consider the theory derived from a gravitational lagrangian that is an arbitrary analytic function of the scalar curvature, f(R),  [19]. The field equations in vacuum, with \(f^{\prime }=df/dR\), derived by varying the action formed from the lagrangian f(R),  are

$$\begin{aligned} M_{\mu \nu }=f^{\prime }R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }f-\nabla _{\mu }\nabla _{\nu }f^{\prime }+g_{\mu \nu }\Box f^{\prime }=0. \end{aligned}$$
(13)

These equations are fourth order in the spacetime derivatives of the metric, \(g_{\mu \nu }\). The most interesting property they possess for our present purposes is that they miss being scale invariant, in the sense of being dimensionally homogeneous in the spacetime derivatives, simply because of the presence of the term proportional to \(g_{\mu \nu }f\). If this term were absent, Eq. (13) would be uniform in scale in the same way that the vacuum Einstein equations are for the spacetime metric \(g_{\mu \nu }\) – but now containing second-order terms in the spacetime derivatives of the metric as well as those of the ‘field’ \(f^{\prime }\). We further note that the scale invariance breaking term containing f is also present in the trace \( M=\text {Tr}M_{\mu \nu }\), where for instance when \(D=4\), we have

$$\begin{aligned} M=f^{\prime }R-2f+3\Box f^{\prime }. \end{aligned}$$
(14)

There is also the more suggestive form for these vacuum equations (assuming \( f^{\prime }\ne 0\) for all R), first introduced in Ref. [10], for \(M_{\mu \nu }\) which picks out the Einstein tensor explicitly:

$$\begin{aligned} M_{\mu \nu }= & {} f^{\prime }G_{\mu \nu }+\frac{1}{2}g_{\mu \nu }(Rf^{\prime }-f)\nonumber \\&-\nabla _{\mu }\nabla _{\nu }f^{\prime }+g_{\mu \nu }\Box f^{\prime }=0, \end{aligned}$$
(15)

and also introduces the term proportional to \(Rf^{\prime }-f\) which can provide an inflationary potential. This potential, which was found in Ref. [10] to be proportional precisely to the scale invariance breaking term \((Rf^{\prime }-f)f^{\prime -2}\), is important in the conformal picture of general relativity with a self-interacting scalar field as source [21], as it allows an inflationary phase in cosmological solutions of these theories [10, 22].

3.2 No-scale f(R) gravity

The question then arises as to whether the traceless version of Eq. (13) can solve the scale invariance breaking problem of the standard f(R) gravity while maintaining the inflationary character of solutions of the theory. In such a theory, like in the traceless version of general relativity studied in the previous Section, there will be no particular scale with respect to which one can measure the sizes of dimensionful constants, it will be a no-scale version of f(R)-theory.

Setting \({\widehat{M}}_{\mu \nu }=M_{\mu \nu }-(1/D)g_{\mu \nu }M,\) with \(M=\text {Tr} M_{\mu \nu }\), we find

$$\begin{aligned} {\widehat{M}}_{\mu \nu }=f^{\prime }\left( {\widehat{G}}_{\mu \nu }-(f^{\prime })^{-1} \left( \nabla _{\mu }\nabla _{\nu }f^{\prime }-\frac{1}{D}g_{\mu \nu }\Box f^{\prime }\right) \right) .\nonumber \\ \end{aligned}$$
(16)

In contrast to the original higher-order field equations for f(R) gravity (13), we see that there is now no term proportional to \(g_{\mu \nu }f\) because it is cancelled by a similar term in the trace M. So in terms of the notional scalar ‘field’ \(\Phi =(g_{\mu \nu },f^{\prime })\), the tensor \( {\widehat{M}}_{\mu \nu }\) is scale invariant in the sense, like before, that it is a homogeneous polynomial of degree two in the spacetime derivatives of the field \(\Phi \).

Following the traceless general relativity development, we postulate the full traceless (or ‘no-scale’) f(R) field equations to be

$$\begin{aligned} {\widehat{M}}_{\mu \nu }={\widehat{T}}_{\mu \nu },\quad {\widehat{T}} _{\mu \nu }=T_{\mu \nu }-\frac{1}{D}g_{\mu \nu }T, \end{aligned}$$
(17)

where the left-hand side is given by (16). The stress tensor of matter and radiation \(T_{\mu \nu }\) on the right-hand side of this equation will in general have a nonzero trace but only its traceless part will gravitate. We note that by setting \(T_{\mu \nu }=0,\,\,\text {or}\,\,-\Lambda g_{\mu \nu }\), Eq. (17) becomes the vacuum, scale invariant equation

$$\begin{aligned} {\widehat{M}}_{\mu \nu }=0, \end{aligned}$$
(18)

We will show that Eq. (17) is related to the standard f(R) -matter equations through a new, nontrivial integrability condition and, as in traceless general relativity, Eq. (5), the cosmological constant emerges an arbitrary integration constant. In this respect, the traceless f(R) situation is completely analogous to that of traceless general relativity [3, 13]. From (17), we find by covariant differentiation that

$$\begin{aligned} \nabla ^{\mu }{\widehat{M}}_{\mu \nu }=-\frac{1}{D}\nabla _{\nu }T, \end{aligned}$$
(19)

since we assume the usual conservation law, \(\nabla ^{\mu }T_{\mu \nu }=0\). However, since (13) gives

$$\begin{aligned} \nabla ^{\mu }{M}_{\mu \nu }=0, \end{aligned}$$
(20)

it follows from the definition of the traceless tensor \({\widehat{M}}_{\mu \nu }\) that

$$\begin{aligned} \nabla ^{\mu }{\widehat{M}}_{\mu \nu }=-\frac{1}{D}\nabla _{\nu }M, \end{aligned}$$
(21)

so that,

$$\begin{aligned} -\frac{1}{D}\nabla _{\nu }M=-\frac{1}{D}\nabla _{\mu }T, \end{aligned}$$
(22)

which means that \(M-T\) is a constantFootnote 2:

$$\begin{aligned} M-T=D\lambda . \end{aligned}$$
(23)

Using (23), the traceless f(R) equations (17), become

$$\begin{aligned} {M}_{\mu \nu }-\frac{1}{D}g_{\mu \nu }M+\frac{1}{D}g_{\mu \nu }T=T_{\mu \nu }, \end{aligned}$$
(24)

or finally,

$$\begin{aligned} {M}_{\mu \nu }-\lambda g_{\mu \nu }=T_{\mu \nu }. \end{aligned}$$
(25)

We see that traceless f(R) theory, like its non-traceless version [10], reduces to traceless general relativity when we take \(f(R)=R\). This means that here, like in traceless general relativity [11], the quantity \(\lambda \) is an arbitrary integration constant, and not a fundamental parameter of the whole theory. Similarly, for the vacuum equations (18), the equivalent system (23, 25) becomes

$$\begin{aligned} {M}_{\mu \nu }-\lambda g_{\mu \nu }=0,\quad \text {with}\quad \lambda = M /D. \end{aligned}$$
(26)

3.3 The no-scale conformal potential

We now wish to take the vacuum, no-scale f(R) theory given by the field equation (18) into the conformal frame. Before we do so, we note a rather subtle point. Since the theory is completely equivalent to the system (26), one might be tempted to think that this can be done by simply finding the conformal picture of the first equation in (26). This equation is exactly the original f(R) equation only having the extra \(\lambda \) term on the left-hand side, and so a conformal transformation leads to the same potential as was found in Ref. [10], but now with an extra term proportional to \(\lambda \). For example, when \(D=4\) and f(R) is quadratic, the potential is \(V(\phi )=e^{-\phi }\left[ (e^{2\phi }-e^{\phi })^{2}+\lambda \right] \).Footnote 3 However, this is not really correct because one has to also find the conformal image of the integrability constraint \(M=D \lambda \). This will generate new terms which will amend the original potential, and therefore for the current traceless case will end up with a different function than the old one.

Instead, we have found that the simplest way to proceed is to conformally transform directly the original equation (18), and not work with the equivalent system (26). To do this, we introduce a new scalar field \(\phi \) as in Eq. (8) and following the steps detailed in the Appendix, Part B, we find that the conformally transformed field equation (18) becomes,

$$\begin{aligned} {\tilde{G}}_{\mu \nu }={\tilde{T}}_{\phi ,\mu \nu }, \end{aligned}$$
(29)

where

$$\begin{aligned} {\tilde{T}}_{\phi ,\mu \nu }= & {} \frac{1}{4}(D-1)(D-2)\nabla _{\mu }\phi \nabla _{\nu }\phi \nonumber \\&-\frac{1}{2}{\tilde{g}}_{\mu \nu }\left( \frac{(D-1)(D-2)}{4} (\nabla \phi )^{2}+2V(\phi )\right) , \end{aligned}$$
(30)

with the effective scalar field potential given by

$$\begin{aligned} V(\phi )=\left( \frac{D-2}{4D}\right) e^{-\phi }R. \end{aligned}$$
(31)

This is the self-interacting scalar field potential for the traceless vacuum f(R) field equations (18) in the conformal frame. It has a number of properties. Firstly, it is important to realize that this potential is different from the standard f(R) potential \( (1/2)(Rf^{\prime }-f)f^{\prime D/(2-D)}\) found in [10]. Secondly, its sign is determined by the inversion of f(R) and by using (8), and this in fact provides, when possible, the simplest way to obtain the scalar curvature R in the present context. Thirdly, in general, R satisfies the constraint (23) with M given by Eq. (14), which for a given function f(R) gives a second order differential equation for R (in distinction to the GR case where R is a constant leading to the exponential potential (12)). Lastly, in the variables \( (g,f^{\prime })\) the potential (31) is scale-invariant (something which is not true of the potential in the conformal transformation of the ‘standard’ (non-traceless) higher-order gravity theory derived in [10]), in the sense of dimensional homogeneity, precisely like in Sect. 2. Therefore, like in the traceless GR case, we are allowed here to make arbitrary linear transformations \(\phi \rightarrow a\phi +b\), and shifts in the origin of the potential, without affecting the property of dimensional homogeneity of the field equations (29, 30).

3.4 \(R^n\)-inflation and the cosmological constant

As an direct application of these properties, the no-scale f(R)-theory in the conformal frame shares a number of novel features, different from those of the standard f(R) theory. First, it is important to notice that in all traceless higher-order polynomial gravity theories, flat potentials occur quite generally in the conformal traceless sub-theory. For the generic leading-order lagrangian,

$$\begin{aligned} f(R)=R+AR^{n},\quad n\ge 2, \end{aligned}$$
(32)

solving for R and using (8) we find the potential to be:

$$\begin{aligned} V_n(\phi )=ce^{-\phi }\left( e^{\frac{D-2}{2}\phi }-1\right) ^{\frac{1}{n-1} }, \end{aligned}$$
(33)

where the constant \(c\equiv ((D-2)/4D)(1/nA)^{1/(n-1)}\). This potential is different from that of the standard \(R^n\)-inflation for any n (for the special case \(D=4\), compare, eg., Eq. 10 in Ref. [24]). Taking into account the above mentioned property of scale invariance for the conformal traceless potential, this form leads to a huge variety of flat potentials in all dimensions and any leading degree of the gravitational lagrangian. We recall that in the standard conformal correspondence between f(R) gravity theory and general relativity plus a scalar field first studied in [10] there is a different structure: flat plateaux in \(V(\phi )\) arise in D spacetime dimensions only when the highest polynomial term in R in the f(R) lagrangian is \(\frac{1}{2}D\), and so for \(D=4\) this allows at most a quadratic term.

By contrast, here we see that a flat potential conducive to exponential inflation is easy to achieve for the theory in (32) in all dimensions: because the potential (31), so also (33) is scale invariant, we have the freedom to shift and stretch it (and its graph) anyway we like without altering the theory. For example, we can move the graph to the origin by shifting it suitably, and also replace \(\phi \) by \(a\phi +b\) for any constants a, b. If we shift and stretch in a suitable neighborhood of the origin, then we end up with the characteristic flat plateau for any n.

For example, when \(D=4, n=2\), instead of the standard quadratic potential proportional to the combination \((1-e^{-\phi })^2\), we find

$$\begin{aligned} V_2=\frac{1}{16A}\left( 1- e^{-\phi }\right) , \end{aligned}$$
(34)

which using the scale freedom this can be written as,

$$\begin{aligned} V_2=a(1-g e^{-b\phi })+d , \end{aligned}$$
(35)

where a, b, d, g are arbitrary constants. This potential satisfies, \(V(0)=d \) and \(\lim _{\phi \rightarrow \infty }V=a+d.\) It is reminiscent of the supergravity potentials studied in Refs. [25], Eqns. (70), (72), and [26], Eqn. (2.10). But here there is a crucial difference that the potential is not an approximate form obtained after some truncation of an asymptotic expansion like in the supergravity models, but an exact result.

Therefore, we conclude that slow-roll inflation is possible in traceless nonlinear f(R) theories. Quite a large family of underlying models lead to observationally compatible outcomes for inflation without requiring any fine-tuning.

A second implication is that the cosmological constant, as well as the height of the inflationary plateau and the potential minimum (vacuum energy) are all unrelated, arbitrary constants. In this scenario, the well-known graceful exit problem for inflation is not well-defined because what drives inflation is generally unrelated to the phase after it. For instance, in the traceless \(R^2\)-inflation example with \(D=4\), the cosmological constant is an arbitrary constant because of the traceless constraint (23), the vacuum has energy \(V(0)=d\) - another arbitrary constant, and the inflationary plateau is at another arbitrary value, \(a+d\).

This means that the cosmological constant \(\lambda \) may take random values in any causal domain in the multiverse landscape (and the same is true for the other two parameters of the theory, V(0) and the asymptotic potential value \(V_\infty =a+d\)). It is like an arbitrary constant in the solution set of a differential equation, its possible values form the set of all solutions of the equation, the general solution. Likewise, the fact that the cosmological constant appears in the fundamental law of the theory as an arbitrary constant satisfying an integrability condition, leads to the interpretation that its possible values form the set of all local domains-a multiverse of local regions each satisfying a different law (see below) and all of them coexisting in the ‘parent’ set.

Of course, the fact that the cosmological constant is an arbitrary constant in this model does not imply that it cannot be equated to its presently observable value. This then provides an unconventional explanation of the presently observed value of the cosmological constant: In the context of a no-scale theory that leads to inflation, it is not a fundamental property of the fundamental laws but a random outcome of them.

Using these results, we imagine a large number N of causal domains (‘universes’) such that \(n_{1}\) of them have vacuum energy \(\lambda _{1}\), \( n_{2}\) have vacuum energy \(\lambda _{2}\), \(\dots \), etc, with the total number of universes forming the partition

$$\begin{aligned} N=n_{1}+n_{2}+\cdots , \end{aligned}$$
(36)

and the total vacuum energy of the partition system (‘the multiverse’) is

$$\begin{aligned} \Lambda =n_{1}\lambda _{1}+n_{2}\lambda _{2}+\cdots . \end{aligned}$$
(37)

We may import the required elements from statistical mechanics in this scheme, with the difference that here we speak of vacuum energies of the domains in the partition. We assume that there is a most probable partition in the multiverse, and when this is achieved, we say that the multiverse is in statistical equilibrium. If we assume that this partition is given by the Maxwell-Boltzmann distribution law, then the partition function will be given by the form,

$$\begin{aligned} Z=\sum _{i}g_{i}e^{-\lambda _{i}/kT}. \end{aligned}$$
(38)

Here there is no restriction on the number of universes that can occupy a given vacuum energy state, there are different intrinsic probabilities \(g_{i} \) for a given vacuum state \(\lambda _{i}\). From these definitions we see that there is a temperature T associated with the multiverse that is related to the average vacuum energy of each universe (\(\Lambda /N\)).

Assuming that Z is the Maxwell-Boltzmann distribution, we find that the occupation numbers decrease as their vacuum energy increases. So at very low temperatures, we expect from Eq. (38) that only the lowest vacuum energy states can be occupied, and the very low vacuum energies of individual universes become more probable observationally. At higher temperatures, higher vacuum energies become more probable, and we expect the multiverse to become more disordered at higher temperatures (at zero temperature only the lowest vacuum energy is occupied).

4 Slow-roll inflation predictions for the CMB

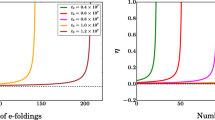
We can calculate the simple first-order predictions that our theory makes for the CMB in the \((n_{s}-r)\)-plane (‘tilt’ and ‘tensor-to-scalar’ ratio). We define the potential slow-roll parameters in the usual way, [27, 28], by

$$\begin{aligned} \epsilon =\frac{1}{2}\left( \frac{V^{\prime }}{V}\right) ^{2},\quad \eta =\frac{ V^{\prime \prime }}{V},\;n_{s}=2\eta -6\epsilon \end{aligned}$$
(39)

and the e-folding function that gauges the length of inflation by,

$$\begin{aligned} N=\int _{\phi _{f}}^{\phi _{i}}\frac{1}{\sqrt{2\epsilon }}d\phi . \end{aligned}$$
(40)

4.1 The no-scale \(R+AR^2\) theory in four dimensions

For the no-scale potential (33) with \(D=4,n=2\), namely, Eq. (34 ),

$$\begin{aligned} V=\frac{1}{16A}\left( 1-e^{-\phi }\right) , \ \end{aligned}$$

when \(\phi _{i}\gg \phi _{f}\), we find that

$$\begin{aligned} \epsilon =\frac{1}{2}e^{-2\phi },\quad \eta =-e^{-\phi },\quad N=e^{\phi }, \end{aligned}$$
(41)

so

$$\begin{aligned} \epsilon =\frac{1}{2N^{2}},\quad \eta =-\frac{1}{N}, \end{aligned}$$
(42)

and the spectral index and tensor to scalar ratio are,

$$\begin{aligned} 1-n_{s}=\frac{2}{N},\quad r=16\epsilon =\frac{8}{N^{2}}. \end{aligned}$$
(43)

For instance, when \(N=50\), \(n_{s}=0.96\) and \(r=3.2\times 10^{-3}\). However, to compare these values with the standard one, we have to normalize the kinetic term of the scalar field. Redefining \(\phi \) in Eq. (30) by,

$$\begin{aligned} {\widehat{\phi }}=\frac{\sqrt{(D-1)(D-2)}}{2}\phi , \end{aligned}$$
(44)

we get the right kinetic term, and then using the second definition in Eq. (8), we find,

$$\begin{aligned} {\widehat{\phi }}=\sqrt{\frac{D-1}{D-2}}\ln f^{\prime }, \end{aligned}$$
(45)

which when \(D=4\) gives the standard factor \({\widehat{\phi }}=\sqrt{2/3}\,\phi .\) In general, using the scale freedom the potential is given by Eq. (35), for which the slow-roll parameters read:

$$\begin{aligned} \epsilon= & {} \frac{1}{2}\left( \frac{Aa\lambda b}{Aa+d}\right) ^2e^{-2b\phi }, \\ \eta= & {} -\frac{Aa\lambda b^2}{Aa+d}\,e^{-b\phi }, \\ N= & {} \frac{Aa+d}{Aa\lambda }\frac{1}{b^2}\,e^{b\phi }. \end{aligned}$$

Therefore we find the forms

$$\begin{aligned} \epsilon =\frac{1}{2b^2N^{2}},\quad \eta =-\frac{1}{b^2N}, \end{aligned}$$
(46)

so that for the unnormalized value of \(\phi \),

$$\begin{aligned} r=16\epsilon =\frac{8}{b^2N^{2}}, \end{aligned}$$
(47)

whereas for the normalized scalar field, we find that the final prediction of the traceless \(R+AR^2\) theory in four dimensions, ie, the conformal potential (35), is:

$$\begin{aligned} r=\frac{12}{b^2N^{2}}. \end{aligned}$$
(48)

Notice that the arbitrary constant b is the one appearing in Eq. (35). When we put \(b=1\) in Eq. (48) (or equivalently, when \(b=\sqrt{2/3} \) in Eq. (47)) we obtain exactly the standard [29] form \( r=12/N^2\).

This means that for this particular value \(b=1\) for the normalized field, the two predictions of the traceless and non-traceless versions of the \( R+AR^2\) theory in four dimensions coincide. Therefore, any future prediction of the form

$$\begin{aligned} r=\frac{12}{b^2N^{2}},\quad b\ne 1, \end{aligned}$$
(49)

will be a sign for the traceless \(R+AR^2\) theory. Same conclusions hold if we decide to use the unnormalized prediction (47), namely, \(r= \frac{8}{b^2N^{2}},\quad b\ne \sqrt{2/3}.\) For example, \(b=1/8\), gives the main value \(r=0.20\) of the BICEP2 result [30], whereas the standard [29] \(R+AR^2\) theory prediction, that is when \(b=\sqrt{2/3})\), would be \(r=0.005\), too small for the BICEP2 measurement.

4.2 The no-scale \(R+AR^n\) theory, general dimensions

More generally, if we analyse Eq. (33) for general n and D at large \(\phi \), we find that the general results which fall into two classes according as (a) \(D=2n,\) or, (b) \(D\ne 2n\):

(a) \(D=2n:\) For \(D>2\) and \(n>1,\) we have

$$\begin{aligned} \frac{V^{\prime }}{V}=\frac{1}{e^{(n-1)\phi }-1}, \end{aligned}$$
(50)

hence, we find,

$$\begin{aligned} \epsilon= & {} \frac{1}{2[e^{(n-1)\phi }-1]^{2}}\rightarrow \frac{1}{2} e^{-2(n-1)\phi }, \end{aligned}$$
(51)
$$\begin{aligned} \eta= & {} \frac{V^{\prime \prime }}{V}=\frac{1-(n-1)e^{(n-1)\phi }}{ {[}e^{(n-1)\phi }-1]^{2}}\nonumber \\&\rightarrow -(n-1)e^{-(n-1)\phi }, \end{aligned}$$
(52)
$$\begin{aligned} N= & {} \int [e^{(n-1)\phi }-1]d\phi \rightarrow \frac{e^{(n-1)\phi }}{n-1}, \end{aligned}$$
(53)

and so, to first order in slow roll,

$$\begin{aligned} \epsilon \rightarrow \frac{1}{2(n-1)^{2}N^{2}},\quad \eta \rightarrow -\frac{ 1}{N}, \end{aligned}$$
(54)

so that

$$\begin{aligned} n_{s}-1=2\eta -6\epsilon =-\frac{2}{N}-\frac{3}{(n-1)^{2}N^{2}}\rightarrow - \frac{2}{N}. \end{aligned}$$
(55)

(b) \(D\ne 2n:\) In this case for large \(\phi ,\) we have an asymptotically exponential potential of the form,

$$\begin{aligned} V\rightarrow c\exp \left[ \frac{(D-2n)\phi }{2(n-1)}\right] . \end{aligned}$$
(56)

Hence, in that limit,

$$\begin{aligned} \epsilon \rightarrow \frac{(D-2n)^{2}}{8(n-1)^{2}},\quad \eta \rightarrow \frac{(D-2n)^{2}}{4(n-1)^{2}}, \end{aligned}$$
(57)

so that

$$\begin{aligned} n_{s}-1\rightarrow -\frac{(D-2n)^{2}}{4(n-1)^{2}}. \end{aligned}$$
(58)

Introducing a new parameter, p, defined by

$$\begin{aligned} p=\frac{4(n-1)^{2}}{(D-2n)^{2}}, \end{aligned}$$
(59)

we have,

$$\begin{aligned} \epsilon =\frac{\eta }{2}=\frac{1}{2p}. \end{aligned}$$
(60)

We conclude that when \(D-2n\rightarrow 0\), we have \(p\rightarrow \infty \), corresponding to de Sitter spacetime asymptotically. On the other hand, when \(D-2n\sim 0\), then \(p\gg 1\), and the slow-roll conditions for \(\epsilon ,\eta \) are satisfied. Finally, there is the case when D and n take values such that the difference \(D-2n\) is far from zero. This means that the difference \(D-2n\) is neither exactly zero, nor near zero, nor asymptotic to zero. In this case, we can always take advantage of the scaling freedom in the potential to rescale \(\phi \) and \(V(\phi )\) to obtain a potential which has a flat plateau in some finite neighborhood of zero.

We therefore conclude that in all cases the present solution to the cosmological constant problem is confirmed because, with our results, is not necessary anymore to tune the absolute scale of V to have any special value to achieve the ‘right’ final state (cf. Ref. [2], p. 438).

5 Conclusions

In this paper we have generalised an idea, originally due to Einstein, to consider the traceless version of the gravitational field equations. Einstein applied this idea to general relativity but we have extended it to f(R) gravity theories.

In the case of traceless general relativity, we have shown that the solution space of the vacuum theory has the property that the Weyl tensor evaluated on solutions of the theory is covariantly constant iff the cosmological constant is zero. This is unlike the vacuum Einstein equations where the Weyl tensor is always covariantly constant.

In this paper we are particularly interested in those solutions of the vacuum traceless equations having a non-constant Weyl tensor. We have shown that under a conformal transformation the theory becomes general relativity with a scalar field source having an exponential potential. The conformally related version of the traceless theory has the further interesting property that the field equations in the conformal frame are dimensionally homogeneous. This means that we have an extra freedom to scale the conformal potential, thus obtaining interesting inflationary solutions. Unfortunately, the exponential potential of the conformal version of the theory has certain undesirable features such as a graceful exit problem from inflation and also sets incompatible constraints with respect to current CMB observations.

We then applied the previous ideas to f(R) gravity and this has led to a new version of the theory, the no-scale f(R) gravity theory. This theory has certain novel features which become apparent if one takes the traceless version of the vacuum f(R) gravity to the conformal frame. After deriving the traceless f(R) field equations for the first time in this paper, we have shown that in vacuum these higher-order equations are conformally equivalent to general relativity plus a self-interacting scalar field, Eqs. (29)–(30), with a scale-invariant potential given by Eq. (31). This potential is quite distinct from the one found in the case of standard f(R) gravity, and in addition, like in the ‘no-scale’ general relativity case it has a scaling freedom that leads to a whole new family of exact forms conducive to new types of cosmological evolution.

Indeed, the consideration of inflation in the framework of the no-scale f(R) gravity has a number of novel features. Perhaps the most distinctive one is the fact that (as it follows from the analysis of the \(R^n\)-inflation) the cosmological constant, the vacuum energy (the zero of the scalar field potential), as well as the height of the inflationary plateau are all unrelated arbitrary constants. This means that they can take on values in a random way, and this fact leads to a new statistical interpretation of the cosmological constant and the multiverse scenario. We believe that similar features like those leading to a statistical interpretation of the multiverse scenario discussed here may also arise in other versions of modified gravity which contain the no-scale aspect considered here.

The conformal potential of the no-scale f(R) gravity also gives rise to flat plateaux which offer the possibility of exponentially rapid, slow-roll inflation with values of \(n_{s}\) and r that agree well with observational bounds from Planck [29, 31]. We have delineated the outcomes of slow-roll inflation in the two distinctive situations defined by the relation between the spacetime dimension and the highest polynomial order of f(R). Specialising to four-dimensional spacetimes, we have derived the slow roll parameters for these types of inflation and shown how the results are compatible with microwave limits on inflationary parameters without requiring any fine-tuning or choosing special values of initial conditions.

This considerably enlarges the range of observationally acceptable inflationary models significantly beyond those mapped in Ref. [31]. In particular, in the case of a quadratic lagrangian theory, we are led to a generic prediction that the tensor-to-scalar ratio given by Eq. (48) contains the free adjustable parameter b with the value \(b=1\) corresponding to the standard, non-traceless quadratic theory. If future observations prove that b takes exactly the value one, then this will mean that no-scale theories are strongly disfavored. Any other value of b will be a strong signal in favor of the novel no-scale aspects of gravity discussed in this paper.

At the end of this inflationary phase, the separation of the cosmological constant term from any quantum vacuum energy density means that it can be arbitrarily small, and remain small for billions of years, consistent with current observations of our local domain.