Probing cosmic opacity with the type Ia supernovae and Hubble parameter

Abstract

In this paper, we probe the cosmic opacity with the newest Pantheon type Ia supernovae (SNIa) and the observational Hubble parameter $\left( H(z)\right)$ data based on the $\Lambda$CDM and wCDM models with or without spatial curvature. In the analysis, we marginalize the likelihood function of SNIa data over the pertinent nuisance parameter ${\mathcal {M}}$, a combination of the absolute magnitude of SNIa $M_{\mathrm{B}}$ and the Hubble constant $H_0$, with a flat prior. Two parameterizations of the optical depth $\tau (z)$ associated to the cosmic absorption, namely $\tau (z)=2\varepsilon z$ and $\tau (z)= (1+z)^{2\varepsilon }-1$, are adopted. We find that the results are not sensitive to the fiducial cosmological models, the spatial curvature and parameterizations of $\tau (z)$. Moreover, the results from the Pantheon data alone are consistent with a transparent universe ($\varepsilon =0$). And once the H(z) data is combined, $\varepsilon =0$ falls within the 68% confidence level (CL) of the best fit when a flat $H_0$ prior or the distance priors are used, while it falls within the 95% CL when a Gaussian distribution prior of $H_0=74.03\pm 1.42$ km $\mathrm {s}^{-1}\, \mathrm {Mpc}^{-1}$ is used.

1 Introduction

The unexpected dimming of the type Ia supernovae (SNIa) provides the evidence of the current cosmic acceleration for the first time [1, 2]. Usually, there are two proper physical explanations of this phenomenon. One possibility is that there exists an exotic energy component in our universe with negative pressure, dubbed dark energy. One can also explain the cosmic acceleration by the theories of modified gravity at cosmological scales. Indeed, in addition to the above two explanations, there are also some other physical mechanisms for the observed SNIa dimming, such as the non-conservation of the total number of photons resulting from the presence of scattering and absorption of some opacity sources [3], or axion-photon mixing due to the dust in our galaxy [4], and possible oscillation of photons propagating in extragalactic magnetic fields [5, 6]. In this paper, we focus on the former case because any change in the photon flux during propagation toward the Earth will affect the luminosity distance ($D_{\mathrm{L}}$) measurement.

Since the deviation of photon number conservation is related to the correction of the Tolman test, equivalent to measurements of the well-known cosmic distance-duality relation (CDDR), the cosmic opacity has been probed by performing the tests of CDDR with various astronomical observations [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. The CDDR connects $D_{\mathrm{L}}$ to the angular diameter distance ($D_{\mathrm{A}}$) by [29]

$$\begin{aligned} \frac{D_{\mathrm{L}}}{D_{\mathrm{A}}}(1+z)^{-2}=1. \end{aligned}$$

(1)

This relation is independent of gravity equation and the universe components, and it is valid for all cosmological models based on the Riemannian geometry, requiring only that light always travels along null geodesics in a Riemannian geometry and the number of photons is conserved in cosmic evolution [30]. Therefore, a violation of CDDR can be considered as the evidence for a nonmetric theory of gravity in which photons do not follow null geodesic and non-conservation of the number of photons. If one considers that the photon travelling along the null geodesic is more fundamental and unassailable, the violation of CDDR most likely implies non-conservation of the photon number, which can be related to the presence of nonstandard exotic physics and some opacity sources, such as gravitational lensing and dust extinction [7, 31]. Thus, it is worthy to probe CDDR to test the validity of photon conservation and related phenomena. In this case, since any effect reducing the photon number would dim the luminosity, the received flux from the source would be decreased by a factor $e^{-\tau (z)}$ with $\tau (z)$ being the optical depth related to the cosmic absorption. Therefore, the observed luminosity distance ($D_{\mathrm{L,obs}}$) is related to the true luminosity distance ($D_{\mathrm{L,true}}$) by

$$\begin{aligned} D_{\mathrm{L,obs}}=D_{\mathrm{L,true}}e^{\tau (z)/2}. \end{aligned}$$

(2)

Testing the above quality with high accuracy can also provide a powerful probe of the transparency of the universe.

In order to rule out the presence of some opaque sources, many tests on the transparency of the universe have been proposed in the past years [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. Typically, within the flat $\Lambda$CDM model analysis, Avgoustidis et al. [32, 33] carried out the constraints on the cosmic opacity by combining Union SNIa data [50] and the measurements of H(z) parameter, and then Holanda et al. [40] updated the constraints by using the Union2.1 SNIa sample [51] and 19 Hubble parameter data. Recently, Hu et al. [44] have used the JLA SNIa sample [52] and 19 H(z) data to probe the opacity of the universe within the flat $\Lambda$CDM and flat wCDM models. All these studies based on a fiducial cosmological model have suggested that a transparent universe is consistent with the data within a $1\sigma$ confidence level (CL). Meanwhile, some model-independent methods have also been proposed to probe the cosmic opacity. Initially, Holanda et al. [39] used the estimation of $D_{\mathrm{L}}$ obtained from a numerical integration of H(z) data and then confronted with the observed one from SNIa data. Then, this method was extended by Liao et al. [36] with three model-independent methods in which the luminosity distances of SNIa data at the redshifts corresponding to H(z) data were obtained through the interpolation method, the smoothing method, and the nearby SNIa method. They have also explored the influence of the correlations between different redshifts when opacity-free distances are derived from H(z) data [38]. Using these model-independent methods, the authors have also found that a transparent universe is very well consistent with the data within a $1\sigma$ CL.

Most recently, Wang et al. [45] constrained the curvature and the cosmic opacity simultaneously with JLA SNIa sample [52] and 30 H(z) data by a model-independent way, in which the distance modulus from SNIa data was confronted with those obtained by integrating the function H(z) reconstructed with the Gaussian process [53]. In the analysis, they also investigated the effect of different priors for Hubble constant $H_0$ on the reconstructed H(z) and the following estimations of the spatial curvature and the cosmic opacity. Since there was a strong degeneracy between $H_0$ and the absolute magnitude of B band of SNIa $(M_{\mathrm{B}})$ and the value of $M_{\mathrm{B}}$ would influence the estimation of distance modulus dramatically, it was suggested that different priors of $H_0$ influenced significantly on the the results. And they found that a flat and transparent universe was consistent with the data within a $1\sigma$ CL when the function H(z) was reconstructed with no prior or the prior of $H_0=67.74\pm 0.46$ km $\mathrm {s}^{-1} \mathrm {Mpc}^{-1}$, while it was only within a $3\sigma$ CL when reconstructing the function H(z) with prior of $H_0=73.24\pm 1.74$ km $\mathrm {s}^{-1} \mathrm {Mpc}^{-1}$.

Given that the pertinent parameter $M_B$ is in general set to be a constant or a free parameter when the SNIa data is used to probe the cosmic opacity in the literature and that it influences the estimation of the cosmic opacity dramatically when different priors of $H_0$ are used [45], in this paper, we plan to use the latest Pantheon SNIa sample [54] and H(z) data to probe the cosmic opacity by marginalizing the likelihood function of SNIa data over the combination of $M_{\mathrm{B}}$ and $H_0$ within the $\Lambda$CDM model, as well as wCDM model for a comparison. Since Wang et al. [45] have found that there is a strong degeneracy between the cosmic curvature and opacity, we will also investigate the influences of the spatial curvature on the results.

2 Cosmic opacity and luminosity distance

In order to probe whether the universe is transparent, we parameterize $\tau (z)$ using the following two forms:

$$\begin{aligned} \tau (z)=2\varepsilon z \quad \mathrm{(P1)} \end{aligned}$$

(3)

and

$$\begin{aligned} \tau (z)= (1+z)^{2\varepsilon }-1 \quad \mathrm{(P2)}\,. \end{aligned}$$

(4)

Here, $\varepsilon$ describes the cosmic opacity. And these two parameterizations are not strongly wavelength dependent on the optical band [32]. The former one is linear while the second is not linear, and both of them can be derived from the CDDR parameterization $D_{\mathrm{L}} = D_{\mathrm{A}}(1+ z)^{2+\varepsilon }$ for small $\varepsilon$ and redshift [32]. Then the observed distance modulus is given by

$$\begin{aligned} \mu _{\mathrm{obs}}(z)=\mu _{\mathrm{true}}(z)+2.5\left( \mathrm{log}\ e\right) \tau (z), \end{aligned}$$

(5)

where $\mu _{\mathrm{true}}(z)$ is related to $D_{\mathrm{L,true}}$ with $\mu _{\mathrm{true}}(z)=5\mathrm{log}\left[ D_{\mathrm{L,true}}(z)\right] +25$. And for a Friedmann–Lemaître–Robertson–Walker (FLRW) cosmology,

$$\begin{aligned} D_{\mathrm{L,true}}(z)=\frac{(1+z)c}{H_0}\int ^z_0 \frac{dz'}{E(z)}, \end{aligned}$$

(6)

where c is the speed of light, and $E(z)\equiv H(z)/H_0$, which can be written in terms of the energy density of matter $\Omega _{\mathrm{m}}$, the spatial curvature parameter $\Omega _{\mathrm{K}}$ and the equation of state of dark energy w through

$$\begin{aligned} E(z)= & {} \left[ \Omega _{\mathrm{m}}(1+z)^3+\Omega _{\mathrm{K}}(1+z)^2\right. \nonumber \\&\left. +(1-\Omega _{\mathrm{m}}-\Omega _{\mathrm{K}})(1+z)^{3(1+w)}\right] ^{1/2}. \end{aligned}$$

(7)

In the above expression, we have the so-called $\Lambda$CDM model if $w=-1$ and the wCDM model if w is a free parameter. Given the existence of a number of recent complementary studies, such as the Refs. [55,56,57], in which the authors have found that the $\Lambda$CDM model still has the best efficiency to explain the data through the Bayesian analysis, we consider the $\Lambda$CDM model, as well as the wCDM model for a comparison, in our analysis in order to obtain tighter limits of the cosmic opacity.

3 Data and inference method

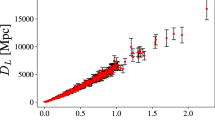
We first introduce the SNIa data and the corresponding inference method used in our analysis. We use the Pantheon compilation released by the Pan-STARRS1 Medium Deep Survey [54], which is the largest SNIa sample released yet and consists of 1048 SNIa data covering the redshift range $0.01< z < 2.3$. And the observed distance modulus of each SNIa in this compilation is given by

$$\begin{aligned} \mu _{\mathrm{obs}} = m^*_{\mathrm{B}}+\alpha X_1 - \beta C - M_{\mathrm{B}}, \end{aligned}$$

(8)

where $m^*_{\mathrm{B}}$ is the observed peak magnitude in rest frame B-band, $X_1$ is the time stretching of the light-curve, C is the SNIa color at maximum brightness. And $\alpha$, $\beta$ are two nuisance parameters, which should be fitted simultaneously with the cosmological parameters. However, this method strongly depends on a specific cosmological model. To avoid this, Kessler et al. [58] have proposed a new method called BEAMS with Bias Corrections (BBC) to calibrate the SNIa, and the corrected apparent magnitude $m^*_{\mathrm{B,corr}} = m^*_{\mathrm{B}}+\alpha X_1 - \beta C +\Delta _{\mathrm{B}}$ for all the SNIa is reported in Ref. [54], where $\Delta _{\mathrm{B}}$ is the correction term. Then the observed distance modulus is rewritten as

$$\begin{aligned} \mu _{\mathrm{obs}} = m^*_{\mathrm{B,corr}} - M_{\mathrm{B}}. \end{aligned}$$

(9)

On the other hand, introducing the Hubble-free luminosity $d_{\mathrm{L}}(z) = H_0 D_{\mathrm{L}}(z)/c$, the true distance modulus $\mu _{\mathrm{true}}$ in Eq. 5 can be rewritten as

$$\begin{aligned} \mu _{\mathrm{true}}(z) = 5\mathrm {log}\left[ d_{\mathrm{L}}(z)\right] +\mu _0, \end{aligned}$$

(10)

where $\mu _0=42.38-5\mathrm {log}h$ ($h=H_0/100$ km $\mathrm {s}^{-1} \mathrm {Mpc}^{-1}$). Therefore, the $\chi ^2$ function for the Pantheon data with the consideration of the cosmic opacity can be written as

$$\begin{aligned} \chi ^2_{\mathrm{SNIa}}\equiv {\Delta \vec {\mu }}^{\mathrm{T}}\cdot \mathrm {Cov}^{-1}\cdot \Delta \vec {\mu }, \end{aligned}$$

(11)

where $\Delta \mu _i\equiv \Delta m_i-{\mathcal {M}}=m^*_{\mathrm {B,corr},i}-5\mathrm {log}\left[ d_{\mathrm{L}}(z)\right] - 2.5\left( \mathrm{log}\ e\right) \tau (z) -{\mathcal {M}}$ with ${\mathcal {M}}$ being $M_{\mathrm{B}}+\mu _0$, and $\mathrm {Cov}$ is the covariance matrix, respectively.

Fig. 1

The one-dimensional and two-dimensional marginalized distributions with $1\sigma$ and $2\sigma$ contours for the cosmological parameters and the cosmic opacity from SNIa data alone

Table 1 The 68% Limits for the cosmological parameters and the cosmic opacity from SNIa data alone

Since Wang et al. [45] have found that the values of $H_0$ and $M_{\mathrm{B}}$ influence the constraints on $\varepsilon$ significantly, we, therefore, marginalize analytically the likelihood function of SNIa over the combination of $H_0$ and $M_{\mathrm{B}}$, i.e. the term of ${\mathcal {M}}$ in the above equation, through the approach proposed in [59] by assuming a flat prior on ${\mathcal {M}}$. Finally, the marginalized $\chi ^2$ function of SNIa can be written as

$$\begin{aligned} \chi ^2_{\mathrm{SNIa,marg}}= a - \frac{b^2}{f}+\mathrm{ln}\frac{f}{2 \pi }, \end{aligned}$$

(12)

where $a\equiv {\Delta \vec {m}}^{\mathrm{T}}\cdot \mathrm {Cov}^{-1}\cdot \Delta \vec {m}$, $b\equiv {\Delta \vec {m}}^{\mathrm{T}}\cdot \mathrm {Cov}^{-1}\cdot \vec {1}$, and $f\equiv {\vec {1}}^{\mathrm{T}}\cdot \mathrm {Cov}^{-1}\cdot \vec {1}$.

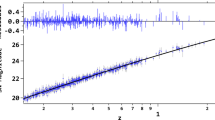
Now we focus on the H(z) data, which are independent of the cosmic opacity and have been used extensively for the exploration of the evolution of the universe and the nature of dark energy. In this paper, we use the latest 31 H(z) data compiled in [60] to conduct our analysis, and its $\chi ^2$ is expressed as

$$\begin{aligned} \chi ^2_{H(z)}=\sum _{i=1}^{31}\frac{\left( H_{\mathrm {obs},i} -H_{\mathrm {th},i}\right) ^2}{\sigma _{H_i}}, \end{aligned}$$

(13)

where $\sigma _{H,i}$ is the standard deviation of the i-th measurement. In addition, since the authors in Ref. [45, 61] have found that different priors of $H_0$ could affect the final constraints on $\Omega _{\mathrm{K}}$ and $\varepsilon$ dramatically when reconstructing the function H(z) with the Gaussian process, it is worthy to test the impact of different $H_0$ priors on the results. And we have three cases when combining the H(z) data:

• (a) with a flat prior on $H_0$ (FP);

• (b) with a Gaussian prior $H_0=74.03\pm 1.42$ km $\mathrm {s}^{-1} \,\mathrm {Mpc}^{-1}$ (R19) from SH0ES given in [62];

• (c) with the distance priors (P18) [63] from the finally released Planck cosmic microwave background (CMB) data given in [64], which can give a strong constraint on $H_0$.

Here, the $\chi ^2_{\mathrm{FP}}=0$ for the case (a) and the $\chi ^2_{\mathrm{R19}}$ has a the same form as Eq. 13 for the case (b). For the distance priors, the $\chi ^2_{\mathrm{P18}}$ is described as

$$\begin{aligned} \chi ^2_{\mathrm{P18}}=\sum \left( x_{i}^{\mathrm{th}}-x_{i}^{\mathrm{obs}}\right) C^{-1}_{ij} \left( x_{j}^{\mathrm{th}}-x_{j}^{\mathrm{obs}}\right) , \end{aligned}$$

(14)

where $x_i\equiv \left( {\mathcal {R}}(z_\star ),l_A(z_\star ),\omega _b\right)$ with ${\mathcal {R}}(z_\star )$, $l_A(z_\star )$ and $\omega _b$ being the shift parameter, the acoustic scale at the redshift of decoupling epoch ($z=z_\star$) and the current value of the baryon density, respectively. And $C_{ij}$ is the correlation matrix. All the details on the distance priors, $\chi ^2_{\mathrm{P18}}$ and code are provided in Ref [63]. Here, it is noted that we have neglected the overlap between the low-z anchor sample for Pantheon and Hubble Flow sample in SH0ES when testing the impacts of $H_0$ priors on the inferred value of transparency with the prior (b).

Finally, we can obtain the constraints on the set of parameters by using the publicly available Cosmological Monte Carlo (CosmoMC) code [65] to minimize the $\chi ^2$ function with

$$\begin{aligned} \chi ^2=\chi ^2_{\mathrm{SNIa,marg}}+\chi ^2_{H(z)}+\chi ^2_{\mathrm {FP/R19/P18}}. \end{aligned}$$

(15)

4 Results

We start by performing the constraints on the transparency with the Pantheon data alone within the flat $\Lambda$CDM model and flat wCDM model. The contour plots of cosmological parameters are shown in Fig. 1 with the corresponding 68% limits given in Table 1. From Fig. 1 and Table 1, one can see that the SNIa data cannot give an effective constraint on the parameter $\Omega _{\mathrm{m}}$ when the P1 parameterization is used, and there is a strong positive correlation between $\varepsilon$ and $\Omega _{\mathrm{m}}$. In addition, the value of $\varepsilon$ is not sensitive to the value of w, and $w=-1$ falls within the 68% CL of the best fit within the wCDM model analysis. Moreover, the SNIa data are compatible with a transparent universe ($\varepsilon$ = 0) within a $1\sigma$ CL, no matter which parameterization of $\tau (z)$ is used.

Fig. 2

The one-dimensional and two-dimensional marginalized distributions with $1\sigma$ and $2\sigma$ contours for the cosmological parameters and the cosmic opacity from SNIa+H(z)

We now conduct the analysis by combining the SNIa data with H(z) measurements and the prior (a) is used at first. The results are shown in Fig. 2 and Table 2. We find that once the H(z) data are combined, there is a significant improvement on the constraints on the cosmological parameters. And similar to the results from SNIa data alone, $\varepsilon$ is positively associated with $\Omega _{\mathrm{m}}$, but it is negatively correlated with $H_0$. Meanwhile, $\varepsilon$ is basically independent of w. And although there is a strong anticorrelation between $\Omega _{\mathrm{m}}$ and $\Omega _{K}$, the value of $\varepsilon$ is very little dependent of $\Omega _{\mathrm{K}}$. Furthermore, from Table 2, one can see that $w=-1$ and $\Omega _{\mathrm{K}}=0$ are allowed at 1$\sigma$ CL, and the result is consistent with negligible optical depth in this case.

Table 2 The 68% Limits for the cosmological parameters and the cosmic opacity from SNIa+H(z)

Fig. 3

The one-dimensional and two-dimensional marginalized distributions with $1\sigma$ and $2\sigma$ contours for the cosmological parameters and the cosmic opacity from SNIa+H(z)+R19

Then, the prior (b) is used to conduct the analysis, and the results are shown in Fig. 3 and Table 3. One can see that once the the prior case (b) is used, the value of $H_0$ tends to be large, while the values of $\Omega _{\mathrm{m}}$ and $\varepsilon$ become small. Meanwhile, $w=-1$ and $\Omega _K=0$ in general are preferred by the observations, and their impacts on the value of $\varepsilon$ are insignificant. Moreover, different from the results from SNIa+H(z), $\varepsilon =0$ only falls within the 95% CL of the best fit once the R19 $H_0$ prior is used.

The results from SNIa+H(z)+P18 are shown in Fig. 4 and Table 4. It is easy to see that the values of $H_0$, $\Omega _{\mathrm{m}}$ and w in the case of prior (c) are well consistent with that from SNIa+H(z). This is because that the local Hubble parameter reconstructed from the H(z) data is quite similar with the one driven form the CMB data [45, 66]. Furthermore, a flat and transparent universe is consistent with the observational data very well in this case.

Table 3 The 68% Limits for the cosmological parameters and the cosmic opacity from SNIa+H(z)+R19

Finally, we compare our results with the most recent analyses performed to probe the cosmic opacity with the SNIa samples and H(z) data. From the above tables, one can find that no matter which parameterization of $\tau (z)$ is used, a transparent universe is consistent well with the current observational data when prior (a) or (c) is used. This agrees well with the results obtained in [44], in which the authors have probed the cosmic opacity with JLA SNIa sample within the $\Lambda$CDM and wCDM models by setting $M_{\mathrm{B}}$ to be free. This also agrees with the results given in [45] when reconstructing the function H(z) with no prior of $H_0$ and with prior of $H_0=67.74\pm 0.46$ km $\mathrm {s}^{-1} \mathrm {Mpc}^{-1}$. When the prior of (b) is used in our analysis, $\varepsilon =0$ falls within the $2\sigma$ CL of the best fit. This, however, is different from the the result given in [45], in which it has been found that the observational data are compatible with a transparent universe only at $3\sigma$ CL when the prior of $H_0=73.24.\pm 1.74$ km $\mathrm {s}^{-1}\, \mathrm {Mpc}^{-1}$ is used.

Fig. 4

The one-dimensional and two-dimensional marginalized distributions with $1\sigma$ and $2\sigma$ contours for the cosmological parameters and the cosmic opacity from SNIa+H(z)+P18

Table 4 The 68% Limits for the cosmological parameters and the cosmic opacity from SNIa+H(z)+P18

5 Conclusions

In the last few years, many works have been performed to probe the cosmic opacity by using the SNIa data and the measurements of Hubble parameter. And it has been found that the value of $H_0$ affects the results significantly since there is a strong degeneracy between $H_0$ and $M_{\mathrm{B}}$ and the value of $M_{\mathrm{B}}$ will influence the estimation of distance modulus dramatically [45]. In this paper, we therefore use the latest Pantheon SNIa sample and 31 H(z) data to probe the cosmic opacity by marginalizing the likelihood function of SNIa data over the pertinent nuisance parameter ${\mathcal {M}}$, a combination of $M_{\mathrm{B}}$ and $H_0$, with a flat prior. And three different priors on $H_0$ are considered when the H(z) data is combined. The analysis is conducted within the $\Lambda$CDM and wCDM models with two parameterizations of the optical depth $\tau (z)$, namely $\tau (z)=2\varepsilon z$ and $\tau (z)= (1+z)^{2\varepsilon }-1$. And the influence of spatial curvature on the constraint results is also investigated.

The results show that the Pantheon SNIa data alone supports a transparent universe. And when H(z) data is combined, the constraints on $\varepsilon$ and $\Omega _{\mathrm{M}}$ are sensitive to the prior of $H_0$, while they are not sensitive to the fiducial cosmological models and parameterizations of $\tau (z)$. In addition, the value of $\varepsilon$ is very little dependent of $\Omega _{\mathrm{K}}$. Moreover, a transparent universe is consistent with the current observational data within the 68% CL of the best fit when a flat $H_0$ prior or the distance priors are used, but it is only within the 95% CL when the prior of $H_0=74.03\pm 1.42$ km $\mathrm {s}^{-1} \mathrm {Mpc}^{-1}$ is used.