Strong decays of the $\varXi (1620)^0$ as a $\varLambda {\bar{K}}$ and $\varSigma {\bar{K}}$ molecule

Abstract

In this work, we study the strong decays of the newly observed $\varXi (1620)^0$ assuming that it is a meson-baryon molecular state of $\varLambda {\bar{K}}$ and $\varSigma {\bar{K}}$. We consider four possible spin-parity assignments $J^P=1/2^{\pm }$ and $3/2^{\pm }$ for the $\varXi (1620)^0$, and evaluate its partial decay width into $\varXi \pi$ and $\varXi \pi \pi$ via hadronic loops with the help of effective Lagrangians. In comparison with the Belle data, the calculated decay width favors the spin-party assignment $1/2^-$ while the other spin-parity assignments do not yield a decay width consistent with data in the molecule picture. We find that about 52–68% of the total width comes from the ${\bar{K}}\varLambda$ channel, while the rest is provided by the ${\bar{K}}\varSigma$ channel. As a result, both channels are important in explaining the strong decay of the $\varXi (1620)^0$. In addition, the transition $\varXi (1620)^0\rightarrow \pi \varXi$ is the main decay channel in the $J^{P}=1/2^{-}$ case, which almost saturates the total width. These information are helpful to further understand the nature of the $\varXi (1620)^0$.

1 Introduction

Understanding baryon spectroscopy and searching for missing baryon resonances are hot topics in hadron physics. From the viewpoint of the quark model, the number of $\varXi$ states should be comparable with that of nucleon resonances. At present, there are eleven $\varXi$ baryons listed in the review of the Particle Data Group (PDG) [1], which is far less than the number of nucleon baryons. Among them, the $\varXi (1620)$, $\varXi (2120)$, and $\varXi (2500)$ are three peculiar states, since they are catalogued in the PDG with only one star and their spin and parity are unknown [1]. In other words, the experimental evidence for these three $\varXi$ bayrons are quit poor, and it is not yet clear whether they really exist. Fortunately, the $\varXi (1620)^0$ was recently observed in the $\varXi ^{-}\pi ^{+}$ final state by the Belle Collaboration [2]. Its mass and width are, respectively,

$$\begin{aligned} M&=1610.4\pm {6.0}(stat)^{+5.9}_{-3.5}(syst)\, \mathrm{MeV},\nonumber \\ \varGamma&=59.9\pm 4.8(stat)^{+2.8}_{-3.0}(syst)\,\mathrm{MeV}, \end{aligned}$$

(1)

which are consistent with the earlier measured values [3, 4]. Its spin-parity, however, remains unknown.

It needs to be stressed that the quark model, originally pioneered by Gell–Mann and Zweig, still remains a useful yardstick for baryon spectroscopy. However, one common characteristic of the quark model is that it is very difficult to accommodate the $\varXi (1620)$ [5, 6]. In particular, the low mass of the $\varXi (1620)$ is puzzling in the quark model if its existence is further confirmed by future experiments. It is very interesting to note that the authors of Ref. [7] tried to assign the $\varXi (1620)$ to a conventional uss or dss state with $J^P=1/2^{-}$. Although their model satisfies the Gell–Mann–Okubo mass relation, it requires the existence of very low mass nucleon and $\varLambda$ resonances, which have not been discovered yet.

These peculiar properties of the $\varXi (1620)$ can be naturally accounted for in the hadronic molecule picture. Indeed, in Ref. [8], Ramos et al. suggested to identify the $\varXi (1620)$ as a dynamically generated S-wave $\varXi$ resonance based on an unitary extension of chiral perturbation theory, which predicts a $\varXi$ resonance with a mass around 1606 MeV. In other similar approaches (that differ in details) [9,10,11], the $\varXi (1620)$ is also dynamically generated, with a relatively larger decay width. This state strongly couples to $\pi \varXi$ and ${\bar{K}}\varLambda$, and it is thought to originate from the strong attraction in the $\pi \varXi$ channel  [9,10,11]. In the Skyrme model [12], Yongseok predicted two $\varXi$ resonances with $J^P=1/2^{-}$, which have masses consistent with those of the $\varXi (1620)$ and $\varXi (1690)$.

Following the discovery of the $\varXi$(1620), several theoretical studies have been performed [13, 14]. In the Bethe–Salpeter equation approach under the ladder and instantaneous approximations, based on the analysis of the mass spectrum and the two-body strong decays, the $\varXi$(1620) is explained as ${\bar{K}}\varLambda$ or $\varSigma {}{\bar{K}}$ bound states with spin-parity $J^P = 1/2^-$ [13]. We note that the decay widths are 36.94 MeV and 9.35 MeV for the ${\bar{K}}\varLambda$ and $\varSigma {}{\bar{K}}$ bound states, respectively. In comparison with the Belle data, it is obvious that the $\varXi$(1620) has a larger contribution from the ${\bar{K}}\varLambda$ component than the $\varSigma {}{\bar{K}}$ component. From this perspective, it is easy to understand the results of Ref. [14], where it was shown that the ${\bar{K}}\varLambda$ interaction is strong enough to form a $\varXi$ bound state with a mass about 1620 MeV and $J^P=1/2^{-}$ in the framework of the one-boson-exchange (OBE) model.

Fig. 1

Self-energy of the $\varXi$(1620) state

Although the studies of Refs. [8,9,10,11,12,13,14] seem to indicate that the $\varXi (1620)^0$ is a hadronic molecular state, more theoretical efforts are needed to fully understand its nature. Considering both the theoretical results [9,10,11, 14] and the latest experimental measurement that the mass of $\varXi (1620)^{0}$ is about 3 MeV below the ${\bar{K}}^{0}\varLambda$ threshold [1], it is reasonable to regard $\varXi (1620)^{0}$ as a bound state of ${\bar{K}}^{0}\varLambda$. Note that in Refs. [8, 13] the $\varXi (1620)$ is treated as a meson-baryon state with large $\varLambda {\bar{K}}$ and $\varSigma {\bar{K}}$ components. In the present work we study the $\varXi \pi$ decay mode of the $\varXi$(1620), using an effective Lagrangian approach and assuming that the $\varXi$(1620) is a hadronic molecular state of $\varLambda {\bar{K}}$ and $\varSigma {\bar{K}}$ with the following four spin-parity assignments: $J^P=1/2^{\pm }$ and $3/2^{\pm }$.

This work is organized as follows. The theoretical formalism is explained in Sect. 2. The predicted partial decay width is presented in Sect. 3, followed by a short summary in the last section.

2 Formalism and ingredients

In order to calculate the strong decay width, $\varXi (1620)^0[\equiv \varXi ^{*}]\rightarrow \varXi \pi$, in the molecular scenario with different spin-parity assignments for the $\varXi ^{*}$, we first need to compute the couplings with its components ${\bar{K}}\varLambda$ and ${\bar{K}}\varSigma$ via the loop diagrams shown in Fig. 1.

The simplest effective Lagrangian describing the $\varXi ^{*}{\bar{K}}Y$ coupling can be expressed as [15, 16]

$$\begin{aligned} \mathcal{{L}}^{1/2^{\pm }}_{\varXi ^{*}}(x)&=g_{\varXi ^{*}{\bar{K}}Y}\int {}d^4y\varPhi (y^2){\bar{K}}(x+\omega _{Y}y)\varGamma \nonumber \\&\quad \times {}Y(x-\omega _{{\bar{K}}}y){\bar{\varXi }}^{*}(x),\end{aligned}$$

(2)

$$\begin{aligned} \mathcal{{L}}^{3/2^{\pm }}_{\varXi ^{*}}(x)&=g_{\varXi ^{*}{\bar{K}}Y}\int {}d^4y\varPhi (y^2){\bar{K}}(x+\omega _{Y}y)\varGamma \nonumber \\&\quad \times \partial _{\mu }Y(x-\omega _{K}y){\bar{\varXi }}^{*\mu }(x), \end{aligned}$$

(3)

where Y denotes either $\varLambda$ or $\varSigma$ (for an isovector baryon Y, Y should be replaced with $\mathbf {Y}\cdot \mathbf {\tau }$, where $\tau$ is the isospin matrix), $\omega _{{\bar{K}}}=m_{{\bar{K}}}/(m_{{\bar{K}}}+m_{Y})$, $\omega _{Y}=m_{Y}/(m_{{\bar{K}}}+m_{Y})$, and $\varGamma$ is the corresponding Dirac matrix reflecting the spin-parity of the $\varXi ^*$. Here $\varGamma =\gamma ^{5}$ for $J^{p}=1/2^{+}$ and $3/2^{-}$, while for $J^{p}=1/2^{-}$ and $3/2^{+}$, $\varGamma =1$. In the above Lagrangian, an effective correlation function $\varPhi (y^2)$ is introduced not only to describe the distribution of the constituents, ${\bar{K}}$ and Y, in the hadronic molecular $\varXi ^{*}$ state but also to make the Feynmann diagrams ultraviolet finite, which is often chosen to be of the following form [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32],

$$\begin{aligned} \varPhi (p_E^2)\doteq \exp (-p_E^2/\beta ^2) \end{aligned}$$

(4)

with $p_E$ being the Euclidean Jacobi momentum and $\beta$ being the size parameter which characterizes the distribution of the components inside the molecule. At present, the value of $\beta$ still could not be accurately determined from first principles, therefore it should better be determined by experimental data. The experimental total widths of some states that can be considered as molecules [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32] can be well explained with $\beta =1.0$ GeV. Therefore we take $\beta =1.0$ GeV in this work to study whether the $\varXi ^{*}$ can be interpreted as a molecule composed of ${\bar{K}}\varLambda$ and ${\bar{K}}\varSigma$.

Fig. 2

Feynman diagrams for the $\varXi ^{*0}\rightarrow {}\pi ^{+}\varXi ^{-}$(top) and $\pi ^{0}\varXi ^{0}$(below) decay processes. We also show the definitions of the kinematics ($p,k_1,k_2,p_1,p_2$, and q) used in the calculation

Fig. 3

Feynman diagrams for the $\varXi ^{*0}\rightarrow {}\pi ^{+}\varXi ^{-}\pi ^0,\pi ^{0}\varXi ^{0}\pi ^{0}$ and $\pi ^{+}\varXi ^{0}\pi ^{-}$ decay processes. We also show the definitions of the kinematics ($p,k_1,k_2,p_1,p_2,p_3$, and q) used in the calculation

With the effective Lagrangians in Eqs. (2) and Eq. (3), we can compute the Feynmann diagrams shown in Fig. 1, and obtain the self-energy of the $\varXi (1620)$,

$$\begin{aligned} \varSigma ^{1/2}_{\varXi ^{*}}(k_0)&=\sum _{Y=\varLambda ,\varSigma ^0,\varSigma ^{+}}\mathcal{{C}}_{Y}g^2_{\varXi ^{*}{\bar{K}}Y}\int \frac{d^4k_1}{(2\pi )^4}\varPhi ^2[(k_1-k_0\omega _{Y})_E^2]\nonumber \\&\quad \times \varGamma \frac{k\!\!\!/_1+m_{Y}}{k_1^2-m^2_{Y}}\varGamma \frac{1}{(k_1-k_0)^2-m^2_{{\bar{K}}}},\end{aligned}$$

(5)

$$\begin{aligned} \varSigma ^{\mu \nu 3/2}_{\varXi ^{*}}(k_0)&=\sum _{Y=\varLambda ,\varSigma ^0,\varSigma ^{+}}\mathcal{{C}}_{Y}g^2_{\varXi ^{*}{\bar{K}}Y}\int \frac{d^4k_1}{(2\pi )^4}\varPhi ^2[(k_1-k_0\omega _{Y})_E^2]\nonumber \\&\quad \times \varGamma \frac{k\!\!\!/_1+m_{Y}}{k_1^2-m^2_{Y}}\varGamma \frac{1}{(k_1-k_0)^2-m^2_{{\bar{K}}}}k_1^{\mu }k_1^{\nu }, \end{aligned}$$

(6)

where $k_0^2=m^2_{\varXi ^{*}}$ with $k_0, m_{\varXi ^{*}}$ denoting the four momenta and the mass of the $\varXi ^*$, respectively, $k_1$, $m_{{\bar{K}}}$, and $m_{Y}$ are the four-momenta, the mass of the ${\bar{K}}$ meson, and the mass of the Y baryon, respectively. Here, we set $m_{\varXi ^{*}}=m_{Y}+m_{{\bar{K}}}-E_b$ with $E_b$ being the binding energy of $\varXi ^*$. Isospin symmetry implies that

$$\begin{aligned} \mathcal{{C}}_Y=\left\{ \begin{aligned} 1&\quad {Y=\varLambda } \\ 1/3&\quad {Y=\varSigma ^0} \\ 2/3&\quad {Y=\varSigma ^+}. \end{aligned} \right. \end{aligned}$$

(7)

The coupling constant $g_{\varXi ^{*}{\bar{K}}Y}$ is determined by the compositeness condition [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. It implies that the renormalization constant of the hadron wave function is set to zero, i.e.,

$$\begin{aligned} Z_{\varXi ^{*}}=X_{{\bar{K}}\varSigma }+X_{{\bar{K}}\varLambda }-\frac{d\varSigma ^{1/2(3/2-T)}_{\varXi ^{*}}}{dk\!\!\!/_0}|_{k\!\!\!/_0=m_{\varXi ^{*}}}=0, \end{aligned}$$

(8)

where $X_{AB}$ is the probability to find the $\varXi (1620)^0$ in the hadronic state AB with normalization $X_{{\bar{K}}\varSigma }+X_{{\bar{K}}\varLambda }=1.0$. The $\varSigma ^{3/2-T}_{\varXi ^{*}}$ is the transverse part of the self-energy operator $\varSigma ^{\mu \nu 3/2}_{\varXi ^{*}}$, related to $\varSigma ^{\mu \nu 3/2}_{\varXi ^{*}}$ via

$$\begin{aligned} \varSigma ^{\mu \nu 3/2}_{\varXi ^{*}}(k_0)=(g_{\mu \nu }-\frac{k_0^{\mu }k_0^{\nu }}{k_0^2})\varSigma ^{3/2-T}_{\varXi ^{*}}+\cdots . \end{aligned}$$

(9)

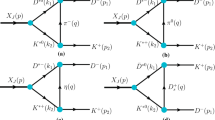
For the $\varXi (1620)$, because of phase space, only the strong decay into $\varXi \pi$, $\varXi \pi \pi$ and radiative decay are allowed. However, radiative decay widths are often in the keV regime and are far less than their strong counterparts. Therefore, in the present work, we focus on the $\pi \varXi$ two body decay and $\varXi \pi \pi$ three body decay of the $\varXi (1620)$ in the ${\bar{K}}\varLambda -{\bar{K}}\varSigma$ molecular picture mediated by the exchange of ${\bar{K}}^{*}$, $\varLambda$, and $\varSigma$. The corresponding Feynman diagrams are shown in Figs. 2 and 3, respectively.

To evaluate the diagrams, in addition to the Lagrangians in Eqs. (2) and (3), the following effective Lagrangians, responsible for the interactions of light pseudoscalar and vector mesons are needed as well [33]

$$\begin{aligned} \mathcal{{L}}_{VPP}&=-ig\langle [P,\partial _{\mu }P]V^{\mu }\rangle , \end{aligned}$$

(10)

where P and $V^{\mu }$ are the SU(3) pseudoscalar and vector meson matrices, respectively, and $\langle ...\rangle$ denotes trace in the flavor space. The meson matrices are [33]

$$\begin{aligned} P= \left( \begin{array}{ccc} \frac{\pi ^{0}}{\sqrt{2}}+\frac{\eta }{\sqrt{6}} &{} \pi ^{+} &{} K^{+}\\ \pi ^{-} &{} -\frac{\pi ^{0}}{\sqrt{2}}+\frac{\eta }{\sqrt{6}} &{} K^{0}\\ K^{-} &{} {\bar{K}}^{0} &{} -\frac{2}{\sqrt{6}}\eta \end{array} \right) . \end{aligned}$$

(11)

and

$$\begin{aligned} V_{\mu }= \left( \begin{array}{cccc} \frac{1}{\sqrt{2}}(\rho ^{0}+\omega ) &{} \rho ^{+} &{} K^{*+} \\ \rho ^{-} &{} \frac{1}{\sqrt{2}}(-\rho ^{0}+\omega ) &{} K^{*0} \\ K^{*-} &{} {\bar{K}}^{*0} &{} \phi \\ \end{array} \right) _{\mu }. \end{aligned}$$

(12)

The coupling g is fixed from the strong decay width of $K^{*}\rightarrow {}K\pi$. With the help of Eq. (10), the two-body decay width $\varGamma (K^{*+}\rightarrow {}K^{0}\pi ^{+})$ is related to g as

$$\begin{aligned} \varGamma (K^{*+}\rightarrow {}K^{0}\pi ^{+})=\frac{g^2}{6\pi {}m^2_{K^{*+}}}\mathcal{{P}}^3_{\pi {}K^{*}}=\frac{2}{3}\varGamma _{K^{*+}}, \end{aligned}$$

(13)

where $\mathcal{{P}}_{\pi {}K^{*}}$ is the three-momentum of the $\pi$ in the rest frame of the $K^{*}$. Using the experimental strong decay width, $\varGamma _{K^{*+}}=50.3\pm 0.8$ MeV, and the masses of the particles listed in Table 1, we obtain $g=4.64$ [1].

Table 1 Masses of the particles needed in the present work (in units of MeV)

Moreover, meson-baryon interactions are also needed and can be obtained from the following chiral Lagrangians [33, 34]

$$\begin{aligned} \mathcal{{L}}_{VBB}&=g(\langle {\bar{B}}\gamma _{\mu }[V^{\mu },B]\rangle +\langle {\bar{B}}\gamma _{\mu }B\rangle \langle {}V^{\mu }\rangle ),\end{aligned}$$

(14)

$$\begin{aligned} \mathcal{{L}}_{PBB}&=\frac{F}{2}\langle {\bar{B}}\gamma _{\mu }\gamma _5[u^{\mu },B]\rangle +\frac{D}{2}\langle {\bar{B}}\gamma _{\mu }\gamma _5\{u^{\mu },B\}\rangle ,\end{aligned}$$

(15)

$$\begin{aligned} \mathcal{{L}}_{PBPB}&=\frac{i}{4f^2}\langle {\bar{B}}\gamma ^{\mu }[(P\partial _{\mu }P-\partial _{\mu }PP)B\nonumber \\&\quad -B(P\partial _{\mu }P-\partial _{\mu }PP)]\rangle \end{aligned}$$

(16)

where $F=0.51$, $D=0.75$ [33, 35] and at the lowest order $u^{\mu }=-\sqrt{2}\partial ^{\mu }P/f$ with $f=93$ MeV, and B is the SU(3) matrix of the baryon octet

$$\begin{aligned} B= \left( \begin{array}{ccc} \frac{1}{\sqrt{2}}\varSigma ^{0}+\frac{1}{\sqrt{6}}\varLambda &{} \varSigma ^{+} &{} p \\ \varSigma ^{-} &{} -\frac{1}{\sqrt{2}}\varSigma ^{0}+\frac{1}{\sqrt{6}}\varLambda &{} n \\ \varXi ^{-} &{} \varXi ^{0} &{} -\frac{2}{\sqrt{6}}\varLambda \\ \end{array} \right) . \end{aligned}$$

(17)

Putting all the pieces together, we obtain the following strong decay amplitudes,

$$\begin{aligned} \mathcal{{M}}_{a}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{+})=-(i)^3\frac{3}{\sqrt{6}}g^2g_{\varXi ^{*}\varLambda {\bar{K}}}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varLambda }-k_2\omega _{{\bar{K}}^{0}})^2]{\bar{u}}(p_1)\gamma _{\mu }\nonumber \\&\times \frac{k\!\!\!/_2+m_{\varLambda }}{k_2^2-m^2_{\varLambda }}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{{\bar{K}}^{0}}}\nonumber \\&\times (k_{1\nu }+p_{2\nu })\frac{-g^{\mu \nu }+q^{\mu }q^{\nu }/m^2_{K^{*-}}}{q^{2}-m^2_{K^{*-}}},\end{aligned}$$

(18)

$$\begin{aligned} \mathcal{{M}}_{b}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{+})=(i)^3\frac{1}{\sqrt{6}}g^2g_{\varXi ^{*}\varSigma ^0{\bar{K}}^0}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varSigma ^0}-k_2\omega _{{\bar{K}}^{0}})^2]{\bar{u}}(p_1)\gamma _{\mu }\nonumber \\&\times \frac{k\!\!\!/_2+m_{\varSigma ^{0}}}{k_2^2-m^2_{\varSigma ^{0}}}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{{\bar{K}}^{0}}}\nonumber \\&\times (k_{1\nu }+p_{2\nu })\frac{-g^{\mu \nu }+q^{\mu }q^{\nu }/m^2_{K^{*-}}}{q^{2}-m^2_{K^{*-}}},\end{aligned}$$

(19)

$$\begin{aligned} \mathcal{{M}}_{c}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{+})=(i)^3\sqrt{\frac{2}{3}}g^2g_{K^{-}\varSigma ^{+}\varXi ^{*}}\nonumber \\&\times \int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varSigma ^{+}}-k_2\omega _{K^{-}})^2]{\bar{u}}(p_1)\gamma _{\mu }\nonumber \\&\times \frac{k\!\!\!/_2+m_{\varSigma ^{+}}}{k_2^2-m^2_{\varSigma ^{+}}}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{K^{-}}}\nonumber \\&\times (k_{1\nu }+p_{2\nu })\frac{-g^{\mu \nu }+q^{\mu }q^{\nu }/m^2_{K^{*0}}}{q^{2}-m^2_{K^{*0}}},\end{aligned}$$

(20)

$$\begin{aligned} \mathcal{{M}}_{d}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{+})=-(i)^3\frac{D(D-3F)}{3\sqrt{6}f^2}g_{\varXi ^{*}\varSigma ^{+}K^-}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varSigma ^{+}}-k_2\omega _{{K}^{-}})^2]{\bar{u}}(p_1)k\!\!\!/_1\gamma _5\nonumber \\&\times {}\frac{q\!\!\!/+m_{\varLambda }}{q^2-m^2_{\varLambda }}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varSigma ^{+}}}{k_2^2-m^2_{\varSigma ^{+}}}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\nonumber \\&\times \frac{1}{k_1^2-m^2_{K^-}},\\ \mathcal{{M}}_{e}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{+})=-(i)^3\frac{F(D+F)}{2f^2}g_{\varXi ^{*}\varSigma ^{+}K^-}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varSigma ^{+}}-k_2\omega _{{K}^{-}})^2]{\bar{u}}(p_1)k\!\!\!/_1\nonumber \\&\times {}\gamma _5\frac{q\!\!\!/+m_{\varSigma ^{0}}}{q^2-m^2_{\varSigma ^{0}}}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varSigma ^{+}}}{k_2^2-m^2_{\varSigma ^{+}}}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\nonumber \end{aligned}$$

(21)

$$\begin{aligned}&\times \frac{1}{k_1^2-m^2_{K^-}},\\ \mathcal{{M}}_{f}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{+})=-(i)^3\frac{(D+F)F}{\sqrt{6}f^2}g_{\varXi ^{*}\varSigma ^0{\bar{K}}^{0}}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varSigma ^0}-k_2\omega _{{\bar{K}}^{0}})^2]{\bar{u}}(p_1)k\!\!\!/_1\nonumber \\&\times \gamma _5\frac{q\!\!\!/+m_{\varSigma ^{-}}}{q^2-m^2_{\varSigma ^{-}}}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varSigma ^{0}}}{k_2^2-m^2_{\varSigma ^{0}}}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\nonumber \\&\times \frac{1}{k_1^2-m^2_{{\bar{K}}^0}},\end{aligned}$$

(22)

$$\begin{aligned} \mathcal{{M}}_{g}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{+})=(i)^3\frac{D(D+F)}{\sqrt{6}f^2}g_{\varXi ^{*}\varLambda {\bar{K}}}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varLambda }-k_2\omega _{{\bar{K}}^{0}})^2]{\bar{u}}(p_1)k\!\!\!/_1\nonumber \\&\times {}\gamma _5\frac{q\!\!\!/+m_{\varSigma ^{+}}}{q^2-m^2_{\varSigma ^{+}}}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varLambda }}{k_2^2-m^2_{\varLambda }}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\nonumber \\&\times \frac{1}{k_1^2-m^2_{{\bar{K}}^0}},\end{aligned}$$

(23)

$$\begin{aligned} \mathcal{{M}}_{h}&(\varXi ^{*0}\rightarrow \varXi ^{0}\pi ^{0})=-(i)^3\frac{D(D+F)}{\sqrt{6}f^2}g_{\varXi ^{*}\varLambda {\bar{K}}}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varLambda }-k_2\omega _{{\bar{K}}^{0}})^2]{\bar{u}}(p_1)k\!\!\!/_1\nonumber \\&\times {}\gamma _5\frac{q\!\!\!/+m_{\varSigma ^{0}}}{q^2-m^2_{\varSigma ^{0}}}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varLambda }}{k_2^2-m^2_{\varLambda }}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\nonumber \\&\times \frac{1}{k_1^2-m^2_{{\bar{K}}^0}},\end{aligned}$$

(24)

$$\begin{aligned} \mathcal{{M}}_{i}&(\varXi ^{*0}\rightarrow \varXi ^{0}\pi ^{0})=-(i)^3\frac{F(D+F)}{\sqrt{3}f^2}g_{\varXi ^{*}\varSigma ^{+}K^-}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varSigma ^{+}}-k_2\omega _{{K}^{-}})^2]{\bar{u}}(p_1)k\!\!\!/_1\nonumber \\&\times {}\gamma _5\frac{q\!\!\!/+m_{\varSigma ^{+}}}{q^2-m^2_{\varSigma ^{+}}}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varSigma ^{+}}}{k_2^2-m^2_{\varSigma ^{+}}}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\nonumber \\&\times \frac{1}{k_1^2-m^2_{K^-}},\end{aligned}$$

(25)

$$\begin{aligned} \mathcal{{M}}_{j}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{+})=(i)^3\frac{(D-3F)D}{6\sqrt{3}f^2}g_{\varXi ^{*}\varSigma ^0{\bar{K}}^{0}}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varSigma ^0}-k_2\omega _{{\bar{K}}^{0}})^2]{\bar{u}}(p_1)k\!\!\!/_1\nonumber \\&\times {}\gamma _5\frac{q\!\!\!/+m_{\varLambda }}{q^2-m^2_{\varLambda }}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varSigma ^{0}}}{k_2^2-m^2_{\varSigma ^{0}}}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\nonumber \\&\times \frac{1}{k_1^2-m^2_{{\bar{K}}^0}},\end{aligned}$$

(26)

$$\begin{aligned} \mathcal{{M}}_{m}&(\varXi ^{*0}\rightarrow \varXi ^{0}\pi ^{0})=(i)^3\frac{1}{\sqrt{3}}g^2g_{\varXi ^{*}\varSigma ^+{K}^{-}}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varSigma ^+}-k_2\omega _{K^{-}})^2]{\bar{u}}(p_1)\gamma _{\mu }\nonumber \\&\times \frac{k\!\!\!/_2+m_{\varSigma ^+}}{k_2^2-m^2_{\varSigma ^+}}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{{K}^{-}}}\nonumber \end{aligned}$$

(27)

$$\begin{aligned}&\times (k_{1\nu }+p_{2\nu })\frac{-g^{\mu \nu }+q^{\mu }q^{\nu }/m^2_{K^{*-}}}{q^{2}-m^2_{K^{*-}}},\\ \mathcal{{M}}_{n}&(\varXi ^{*0}\rightarrow \varXi ^{0}\pi ^{0})=(i)^3\frac{\sqrt{3}}{2}g^2g_{\varXi ^{*}\varLambda {\bar{K}}}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varLambda }-k_2\omega _{{\bar{K}}^{0}})^2]{\bar{u}}(p_1)\gamma _{\mu }\nonumber \\&\times \frac{k\!\!\!/_2+m_{\varLambda }}{k_2^2-m^2_{\varLambda }}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{{\bar{K}}^{0}}}\nonumber \\&\times (k_{1\nu }+p_{2\nu })\frac{-g^{\mu \nu }+q^{\mu }q^{\nu }/m^2_{K^{*0}}}{q^{2}-m^2_{K^{*0}}},\end{aligned}$$

(28)

$$\begin{aligned} \mathcal{{M}}_{r}&(\varXi ^{*0}\rightarrow \varXi ^{0}\pi ^{0})=(i)^3\frac{1}{2\sqrt{3}}g^2g_{\varXi ^{*}\varSigma ^0{\bar{K}}^0}\nonumber \\&\times {}\int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varSigma ^0}-k_2\omega _{{\bar{K}}^{0}})^2]{\bar{u}}(p_1)\gamma _{\mu }\nonumber \\&\times \frac{k\!\!\!/_2+m_{\varSigma ^{0}}}{k_2^2-m^2_{\varSigma ^{0}}}\varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{{\bar{K}}^{0}}}\nonumber \\&\times (k_{1\nu }+p_{2\nu })\frac{-g^{\mu \nu }+q^{\mu }q^{\nu }/m^2_{K^{*0}}}{q^{2}-m^2_{K^{*0}}}, \end{aligned}$$

(29)

where $\{u(p)$, and $ik_2^{\rho }u_{\rho }(p)\}$ are $J^P=1/2$ and $J^P=3/2$ $\varXi (1620)$ fields,respectively.

The amplitudes of the $\varXi ^{0}(1620)\rightarrow \pi \pi \varXi$ that are shown in Fig. 3 can be also easily obtained from the Lagrangians

$$\begin{aligned} \mathcal{{M}}_{a}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{0}\pi ^{+},\varXi ^{0}\pi ^{-}\pi ^{+})=i(i)^3\frac{D}{f^3}g_{\varXi ^{*}\varSigma {\bar{K}}}\nonumber \\&\times {}\left\{ \frac{\sqrt{6}}{24},\frac{-\sqrt{3}}{12}\right\} \int \frac{d^4q}{(2\pi )^4}\varPhi \left[ (k_1\omega _{\varSigma ^{+}}-k_2\omega _{K^{-}})^2\right] \nonumber \\&\times {\bar{u}}(p_1)k\!\!\!/_1\frac{q\!\!\!/+m_{\varLambda }}{q^2-m^2_{\varLambda }}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varSigma ^{+}}}{k^2_2-m^2_{\varSigma ^{+}}}\nonumber \\&\times \varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{K^{-}}},\end{aligned}$$

(30)

$$\begin{aligned} \mathcal{{M}}_{b}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{0}\pi ^{+},\varXi ^{0}\pi ^{-}\pi ^{+})=i(i)^3\frac{F}{f^3}g_{\varXi ^{*}\varSigma {\bar{K}}}\nonumber \\&\times {}\left\{ -\frac{1}{12},\frac{1}{4\sqrt{6}}\right\} \int \frac{d^4q}{(2\pi )^4}\varPhi \left[ (k_1\omega _{\varSigma ^{+}}-k_2\omega _{K^{-}})^2\right] \nonumber \\&\times {\bar{u}}(p_1)k\!\!\!/_1\frac{q\!\!\!/+m_{\varSigma ^0}}{q^2-m^2_{\varSigma ^0}}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varSigma ^{+}}}{k^2_2-m^2_{\varSigma ^{+}}}\nonumber \\&\times \varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{K^{-}}},\end{aligned}$$

(31)

$$\begin{aligned} \mathcal{{M}}_{c}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{0}\pi ^{+},\varXi ^{0}\pi ^{-}\pi ^{+})=i(i)^3\frac{F}{f^3}g_{\varXi ^{*}\varSigma {\bar{K}}}\nonumber \\&\times {}\left\{ \frac{1}{4\sqrt{6}},-\frac{1}{4\sqrt{3}}\right\} \int \frac{d^4q}{(2\pi )^4}\varPhi \left[ (k_1\omega _{\varSigma ^{0}}-k_2\omega _{{\bar{K}}^{0}})^2\right] \nonumber \\&\times {\bar{u}}(p_1)k\!\!\!/_1\frac{q\!\!\!/+m_{\varSigma ^+}}{q^2-m^2_{\varSigma ^+}}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varSigma ^{0}}}{k^2_2-m^2_{\varSigma ^{0}}}\nonumber \\&\times \varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{{\bar{K}}^{0}}},\end{aligned}$$

(32)

$$\begin{aligned} \mathcal{{M}}_{d}&(\varXi ^{*0}\rightarrow \varXi ^{-}\pi ^{0}\pi ^{+},\varXi ^{0}\pi ^{-}\pi ^{+})=i(i)^3\frac{D}{f^3}g_{\varXi ^{*}\varSigma {\bar{K}}}\nonumber \end{aligned}$$

(33)

$$\begin{aligned}&\times {}\left\{ -\frac{1}{4\sqrt{6}},\frac{1}{4\sqrt{3}}\right\} \int \frac{d^4q}{(2\pi )^4}\varPhi \left[ (k_1\omega _{\varLambda }-k_2\omega _{{\bar{K}}^{0}})^2\right] \nonumber \\&\times {\bar{u}}(p_1)k\!\!\!/_1\frac{q\!\!\!/+m_{\varSigma ^{+}}}{q^2-m^2_{\varSigma ^{+}}}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varLambda }}{k^2_2-m^2_{\varLambda }}\nonumber \\&\times \varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{{\bar{K}}^{0}}},\end{aligned}$$

(34)

$$\begin{aligned} \mathcal{{M}}_{E}&(\varXi ^{*0}\rightarrow \varXi ^{0}\pi ^{0}\pi ^{0},\varXi ^{-}\pi ^{+}\pi ^{0})=i(i)^3\frac{D}{f^3}g_{\varXi ^{*}\varSigma {\bar{K}}}\nonumber \\&\times {}\left\{ \frac{1}{8\sqrt{3}},\frac{1}{4\sqrt{6}}\right\} \int \frac{d^4q}{(2\pi )^4}\varPhi \left[ (k_1\omega _{\varLambda }-k_2\omega _{{\bar{K}}^{0}})^2\right] \nonumber \\&\times {\bar{u}}(p_1)k\!\!\!/_1\frac{q\!\!\!/+m_{\varSigma ^0}}{q^2-m^2_{\varSigma ^0}}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varLambda }}{k^2_2-m^2_{\varLambda }}\nonumber \\&\times \varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{{\bar{K}}^{0}}},\end{aligned}$$

(35)

$$\begin{aligned} \mathcal{{M}}_{f}&(\varXi ^{*0}\rightarrow \varXi ^{0}\pi ^{0}\pi ^{0},\varXi ^{-}\pi ^{+}\pi ^{0})=i(i)^3\frac{F}{f^3}g_{\varXi ^{*}\varSigma {\bar{K}}}\nonumber \\&\times {}\left\{ -\frac{1}{4\sqrt{3}},-\frac{\sqrt{6}}{12}\right\} \int \frac{d^4q}{(2\pi )^4}\varPhi [(k_1\omega _{\varSigma ^{+}}-k_2\omega _{K^{-}})^2]\nonumber \\&\times {\bar{u}}(p_1)k\!\!\!/_1\frac{q\!\!\!/+m_{\varSigma ^+}}{q^2-m^2_{\varSigma ^+}}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varSigma ^{+}}}{k^2_2-m^2_{\varSigma ^{+}}}\nonumber \\&\times \varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{K^{-}}},\end{aligned}$$

(36)

$$\begin{aligned} \mathcal{{M}}_{g}&(\varXi ^{*0}\rightarrow \varXi ^{0}\pi ^{0}\pi ^{0},\varXi ^{-}\pi ^{+}\pi ^{0})=i(i)^3\frac{D}{f^3}g_{\varXi ^{*}\varSigma {\bar{K}}}\nonumber \\&\times {}\left\{ -\frac{1}{8},\frac{\sqrt{2}}{8}\right\} \int \frac{d^4q}{(2\pi )^4}\varPhi \left[ (k_1\omega _{\varSigma ^{0}}-k_2\omega _{{\bar{K}}^{0}})^2\right] \nonumber \\&\times {\bar{u}}(p_1)k\!\!\!/_1\frac{q\!\!\!/+m_{\varLambda }}{q^2-m^2_{\varLambda }}p\!\!\!/_2\gamma _5\frac{k\!\!\!/_2+m_{\varSigma ^{0}}}{k^2_2-m^2_{\varSigma ^{0}}}\nonumber \\&\times \varGamma {}\{u(p),ik_2^{\rho }u_{\rho }(p)\}\frac{1}{k_1^2-m^2_{{\bar{K}}^{0}}}. \end{aligned}$$

(37)

Once the amplitudes are determined, the corresponding partial decay width can be easily obtained, which reads as,

$$\begin{aligned} \varGamma (\varXi (1620)^{0}\rightarrow \pi \varXi )&=\int \frac{1}{2J+1}\frac{1}{32\pi ^2}\frac{|\mathbf {p}_1|}{m^2_{\varXi ^{*0}}}\bar{|\mathcal{{M}}|^2}d\Omega ,\end{aligned}$$

(38)

$$\begin{aligned} \varGamma (\varXi (1620)^{0}\rightarrow \pi \varXi \pi )&=\int \frac{1}{2J+1}\frac{1}{(2\pi )^5}\frac{1}{16M^2}\bar{|\mathcal{{M}}|^2}|\mathbf {p}^{*}_3|\nonumber \\&\quad \times {}|\mathbf {p}_2|dm_{\pi \varXi }d\Omega ^{*}_{p_3}d\Omega _{p_2}, \end{aligned}$$

(39)

where J is the total angular momentum of the $\varXi (1620)$, $|\mathbf {p}_1|$ is the three-momenta of the decay products in the center of mass frame, the overline indicates the sum over the polarization vectors of the final hadrons. The ($\mathbf {p}^{*}_3,\Omega ^{*}_{p_3}$) is the momentum and angle of the particle $\varXi$ in the rest frame of $\varXi$ and $\pi$, and $\Omega _{p_2}$ is the angle of the $\pi$ in the rest frame of the decaying particle. The $m_{\pi \varXi }$ is the invariant mass for $\pi$ and $\varXi$ and $m_{\pi }+m_{\varXi }\le {}m_{\pi \varXi }\le {}M-m_{\pi }$. The total decay width of the $\varXi (1620)^0$ is the sum of $\varGamma (\varXi (1620)^{0}\rightarrow \pi \varXi )$ and $\varGamma (\varXi (1620)^{0}\rightarrow \pi \pi \varXi )$.

3 Results and discussions

Before calculating the two body decay width, we need to determine the coupling constants relevant to the effective Lagrangians listed in Eqs. (2) and (3). Considering $\varXi (1620)^{0}$ as a ${\bar{K}}\varLambda -{\bar{K}}\varSigma$ hadronic molecule, the coupling constants $g_{{\bar{K}}\varXi ^{*}\varLambda }$ and $g_{{\bar{K}}\varXi ^{*}\varSigma }$ can be estimated from the compositeness condition that we introduced in the previous section. The $x_{{\bar{K}}\varLambda }$ dependence of the coupling constants $g_{{\bar{K}}\varXi ^{*}\varLambda }$ and $g_{{\bar{K}}\varXi ^{*}\varSigma }$ are presented in Fig. 4. The coupling $g_{{\bar{K}}\varXi ^{*}\varLambda }$ monotonously increases with increasing $X_{\varLambda {\bar{K}}}$, and the dependence on $X_{\varLambda {\bar{K}}}$ is the weakest for the $J^P =1/2^{-}$ case, where the $\varXi ^{*}(1620)$ is an S-wave ${\bar{K}}\varLambda -{\bar{K}}\varSigma$ molecular state, while it is the strongest for the $J^p=3/2^-$ case. Comparing $g_{{\bar{K}}\varXi ^{*}\varSigma }$ with $g_{{\bar{K}}\varXi ^{*}\varLambda }$, we find that their line shapes are very different, i.e., the coupling constant $g_{{\bar{K}}\varXi ^{*}\varSigma }$ decreases with increasing $X_{\varLambda {\bar{K}}}$. We find that $g_{{\bar{K}}\varXi ^{*}\varSigma }$ is the largest for the $J^P=3/2^{-}$ case, is intermediate for the $J^P=1/2^+$ and $J^P=3/2^+$ cases, and is the smallest for the $J^P=1/2^{-}$ case. The opposite trend can be easily understood, as the coupling constants $g_{{\bar{K}}\varXi ^{*}\varLambda }$ and $g_{{\bar{K}}\varXi ^{*}\varSigma }$ are directly proportional to the corresponding molecular compositions [23]. Moreover, the relations between the coupling constants $g_{{\bar{K}}\varXi ^{*}\varSigma }$ and $g_{{\bar{K}}\varXi ^{*}\varLambda }$ can be deduced from Eq. (8) and are given in Table 2.

Fig. 4

Coupling constants of the $\varXi (1620)$ with different $J^P$ assignments as a function of the parameter $X_{\varSigma {\bar{K}}}$ and $X_{\varLambda {\bar{K}}}$ which is the probability to find the $\varXi (1620)^0$ in the hadronic components ${\bar{K}}\varSigma$ and ${\bar{K}}\varLambda$, respectively

Table 2 Relations between the coupling constants $g_{{\bar{K}}\varXi ^{*}\varSigma }$ and $g_{{\bar{K}}\varXi ^{*}\varLambda }$

With the obtained couplings $g_{{\bar{K}}\varXi ^{*}\varLambda }$ and $g_{{\bar{K}}\varXi ^{*}\varSigma }$, the partial decay width of the $\varXi (1620)^0$ can be calculated straightforwardly. The dependence of the partial decay width on $X_{{\bar{K}}\varLambda }$ of the $\varXi (1620)$ for various quantum numbers is given in Fig. 5. In the present study, we vary $X_{{\bar{K}}\varLambda }$ from 0.0 to 1.0. For small $X_{{\bar{K}}\varLambda }$, the total decay width decreases with increasing $X_{{\bar{K}}\varLambda }$. However, it increases when $X_{{\bar{K}}\varLambda }$ varies from 0.91 to 1.00 and 0.54 to 1.00 for the $J^P = 1/2^{\pm }$ and $J^P = 3/2^{\pm }$ assignments, respectively.

Fig. 5

Partial decay widths of the $\varXi (1620)^0\rightarrow \pi \varXi$ (black solid line), $\varXi (1620)^0\rightarrow \pi \pi \varXi$ (blue dash dot line), and the total decay width (red dash line) with different $J^P$ assignments depending on the parameter $X_{{\bar{K}}\varLambda }$ and $X_{{\bar{K}}\varSigma }$. The LT Cyan bands correspond to the total experimental decay width

As shown in Fig. 5, the LT Cyan bands in these plots denote the experimental data. For the $J^P=1/2^{+}$ case, the predicted total decay width increases from 0.011 to 6.787 MeV and is much smaller than the experimental total width, which disfavors such a spin-parity assignment for the $\varXi (1620)^0$ in the ${\bar{K}}\varLambda -{\bar{K}}\varSigma$ molecular picture. For the $J^{P}=3/2^{-}$ assignment, the total decay width is also much smaller than the experimental total width. This disfavors the assignment of this state as a ${\bar{K}}\varLambda -{\bar{K}}\varSigma$ molecular state as well. The same is also true for the $J^P=3/2^{+}$ case. Hence, only the assignment as an $S-$wave ${\bar{K}}\varLambda -{\bar{K}}\varSigma$ molecular state for the $\varXi (1620)^{0}$ is consistent with the Belle data [2] when $X_{{\bar{K}}\varLambda }$ is in the range of 0.52–0.68. In this region, the total decay width for this state is predicted to be about 50.39–68.79 MeV. From Fig. 5 we conclude that the total experimental decay width can be well reproduced, which provides direct evidence that the observed $\varXi (1620)^{0}$ is an $S-$ wave ${\bar{K}}\varLambda -{\bar{K}}\varSigma$ molecular state.

Fig. 5 also tell us that the transition $\varXi (1620)^0\rightarrow \pi \varXi$ is the main decay channel, which almost saturates the total width of $\varXi (1620)^0$. However, the transition $\varXi (1620)^0\rightarrow \pi \pi \varXi$ that is not considered in Ref. [13] gives minor contributions and the $\pi \pi \varXi$ three-body transition strength is of the order of about 1.0 KeV.

From Fig. 5, we also note that the decay width of the observed $\varXi (1620)^{0}$ can not be well reproduced in a pure ${\bar{K}}\varLambda$ or pure ${\bar{K}}\varSigma$ molecular state picture. Namely, the interference among the two channels is sizable, leading to a total decay width consistent with the experimental data in the case of the $J^P=1/2^{-}$. In other words, the ${\bar{K}}\varLambda$ channel strongly couples to the ${\bar{K}}\varSigma$ channel. Comparing our results with those in Ref. [14], it seems that a study of the spectroscopy alone does not give a complete picture of its nature. Furthermore, the ${\bar{K}}\varLambda$ component provides the dominant contribution to the partial decay width of the $\pi \varXi$ two-body channel. This is consistent with the result of Ref. [13] that the $\varXi$(1620) has a larger contribution from the ${\bar{K}}\varLambda$ channel than the $\varSigma {}{\bar{K}}$ channel.

The coupling constants and the partial decay width of the $\varXi (1620)$ with different $J^P$ assignments as a function of the parameter $X_{\varSigma {\bar{K}}}$ which is the probability to find the $\varXi (1620)^0$ in the hadronic component ${\bar{K}}\varSigma$ are also shown in Figs. 4 and 5, respectively. Both the coupling constants and the decay width exhibit opposite trend to the $X_{{\bar{K}}\varLambda }$ dependence. Moreover, the individual contributions are presented in Fig. 6. One can see that the contribution from the $\varSigma$ and $\varLambda$ exchanges is smaller than those from ${\bar{K}}^{*}$ meson exchanges for the $X_{{\bar{K}}\varLambda }$ and $X_{{\bar{K}}\varSigma }$ range studied.

Fig. 6

Decomposed contributions to the decay width of the $\varXi (1620)^0$ into $\pi \varXi$ and $\pi \pi \varXi$ as a function of the parameter $X_{{\bar{K}}\varLambda }$ and $X_{{\bar{K}}\varSigma }$

It should be noted that Ref. [8] showed that the $\varXi (1620)$ couples strongly to the $\pi \varXi$ and the ${\bar{K}}\varLambda$ channels but very weakly to $\eta \varXi$ and $\varSigma {}{\bar{K}}$. If we treat the $\varXi (1620)$ as a pure $\eta \varXi$ molecular state, we find that the $\eta \varXi$ channel provides a negligible contribution to the partial decay width into $\pi \varXi$. Furthermore, based on the Weinberg–Salam compositeness condition, we find the $\pi \varXi$ component is significantly suppressed and it contributes negligibly to the partial decay width into $\pi \varXi$. A possible explanation for this may be that the threshold for $\pi \varXi$ is too low to allow for a bound state at 1620 MeV [28]. Because of these reasons, the $\eta \varXi$ and $\pi \varXi$ channels are not considered in this work.

The $\varXi ^{*}(1620)$ is one of the peculiar resonances discovered during past few years and its properties cannot be simply explained in the context of conventional constituent quark models. As indicated in Refs. [8,9,10,11,12,13,14] and our work, the $\varXi ^{*}(1620)$ can be understood as a pure molecular state in comparison with the Belle data [2]. However, at present we cannot fully exclude other possible explanations such as a mixture of three quark and five quark components (as long as quantum numbers allow, it might well be the case). We note that such studies in the quark pair creation model still suffer from relatively large uncertainties [36].

4 Summary

We have studied the strong decay of the newly observed $\varXi (1620)^{0}$ into $\pi \varXi$ and $\pi \pi \varXi$ with different spin-parity assignments and assuming that it is a ${\bar{K}}\varLambda -{\bar{K}}\varSigma$ molecular state. With the coupling constants between the $\varXi (1620)^{0}$ and its components determined by the compositeness condition, we calculated its partial decay width into $\pi \varXi$ and $\pi \pi \varXi$ via triangle diagrams in an effective Lagrangian approach. In such a picture, the decay into $\pi \varXi$ and $\pi \pi \varXi$ occurs by exchanging $K^{*}$, $\varLambda$, and $\varSigma$. We found that the total decay width can be reproduced with the assumption that the $\varXi (1620)^{0}$ is an $S-$wave ${\bar{K}}\varLambda -{\bar{K}}\varSigma$ bound state with $J^P=1/2^{-}$, while the P- and D-wave assignments are excluded. The ${\bar{K}}\varLambda$ component provides the dominant contribution to the partial decay width into $\pi \varXi$ and $\pi \pi \varXi$. More specifically, about 52–68% of the total decay width is from the ${\bar{K}}\varLambda$ channel, while the ${\bar{K}}\varSigma$ channel provides the rest. We find that if the $\varXi (1620)^{0}$ is a ${\bar{K}}\varLambda -{\bar{K}}\varSigma$ molecular state, the $\pi \pi \varXi$ three-body transition strength is quite small and the decay width is of the order of about 1.0 keV. Future experimental measurements of such a process can be quite useful to test the molecule interpretation of the $\varXi (1620)^{0}$.