1 Introduction

The theoretical evolution of the gravitational collapse [1, 2] guided by the general theory of relativity leads to either a black hole or a naked singularity, which can communicate with far-away observers in the universe. The radiating Schwarzschild spacetime, also known as the Vaidya spacetime [3], describes the geometry outside a radiating spherically symmetric star. In particular, Papapetrou [4] first showed that the solution of null dust fluid with spherical symmetry in gravitational collapse can give rise to the formation of naked singularities. It provides one of the counter examples to the cosmic censorship conjecture (CCC) [5, 6]. In [7, 8], they have described the causal trajectories joining the singularities in the ingoing Vaidya situation. Also a relatively complete description of constraints is provided classifying the non-spacelike geodesics that connect the naked singularity in the past. It is then shown to be a strong curvature singularity in a more substantial sense. The generalization of the Vaidya solution [9,10,11,12,13,14], includes all the known solutions of Einstein’s field equations with a combination of Type-I and Type-II matter fields. It was given by Husain [15] and Wang and Wu [16]. The generalization of the Vaidya solution is also known as the generalized Vaidya spacetime. In the context of the cosmic censorship hypothesis, the gravitational collapse for the generalised Vaidya spacetime has been studied in [17]. They showed that the classes of generalized Vaidya mass functions have come in the scenario indicating the termination of collapse with a locally naked central singularity. They calculated the strength of these singularities. A general mathematical framework was developed to study the conditions on the mass function so that non-spacelike geodesics directed towards future can terminate at the singularity in the past. They also exhibited that, for a given generalized Vaidya mass function, how the final fate of collapse is determined in terms of either a black hole or a naked singularity. In [18], the gravitational collapse of higher-dimensional is discussed in the charged-Vaidya spacetime. They have shown that singularities arising in a charged null fluid in higher dimension. These singularities are always naked, violating strong cosmic censorship hypothesis (CCH). This hypothesis is not necessarily on weak cosmic censorship. In [19, 20], the holographic complexity and the holographic entropy cone in AdS-Vaidya spacetime have been explored. The attempt to revisit Vaidya-Tikekar stellar model in the linear regime has been explored in [21].

To be more specific on the k-essence model, we note that it is a scalar field model. In this model, the kinetic energy of the field dominates over the potential energy of the field. The theoretical form of the k-essence field Lagrangian is non-canonical. The Lagrangian cannot be separated in the terms corresponding to kinetic energy and potential energy. Also, it does not depend explicitly on the field itself. A theory with a non-canonical kinetic term was first proposed by Born and Infeld [22,23,24]. It was proposed to get rid of the problem related to the infinite self-energy of the electron. The general form of the lagrangian for k-essence model is: \(L=-V(\phi )F(X)\) where \(\phi \) is k-essence scalar field, \(X=\frac{1}{2}g^{\mu \nu }\nabla _{\mu }\phi \nabla _{\nu }\phi \) and does not depend explicitly on \(\phi \) to start with [25,26,27,28,29, 50,51,52,53,54]. The Lagrangian for k-essence scalar fields contain non-canonical kinetic terms. The differences between the k-essence theory with non-canonical kinetic terms and the relativistic field theories with canonical kinetic terms lie in the non-trivial dynamical solutions of the k-essence equation of motion (EOM). The solutions of the EOM not only spontaneously breaks the Lorentz invariance but also changes the metric for the perturbations around these solutions. Thus the perturbations propagate in the so-called emergent or analogue curved spacetime [25,26,27,28,29] with the metric which is different from the gravitational one. The emergent gravity metric \({\tilde{G}}_{\mu \nu }\) is not conformally equivalent to the gravitational metric \(g_{\mu \nu }\).

In [30], the gravitational collapse is analyzed in the context of gravity’s rainbow [31]. The rainbow gravity is basically a possible step towards repairing the rifts between the theories of general relativity and quantum mechanics. In [32, 33], they have studied the energy dependent deformation and time dependent geometry of massive gravity using the formalism of massive gravity’s rainbow. Both the Vainshtein and the dRGT mechanisms are used for the energy dependent massive gravity (Vaidya spacetime). Relevant theories of rainbow gravity and their subsequent explorations in Charged dilatonic black holes, Gauss-Bonnet gravity, Lovelock gravity, combination of Rastall and rainbow theories, \(AdS_{4}\) dyonic black holes, Deformed Starobinsky model, Thermodynamics of black holes, Galileon gravity, Horizon effect, Violation of weak cosmic censorship and Branes are addressed in [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. Also, we clearly mention that in this work we cannot study the Rainbow gravity in the framework of the k-essence emergent Vaidya spacetime.

In this paper, we explore the gravitational collapse for the k-essence emergent Vaidya spacetime in the context of cosmic censorship hypothesis. Here, we consider the background gravitational metric as the generalised Vaidya metric [15,16,17].

The paper is organized as follows: The brief review of the k-essence theory based on the Dirac-Born-Infeld action is presented in Sect. 2. It makes us familiar with the so-called emergent gravity spacetime where the gravitational metric is not conformally equivalent to the emergent gravity metric. In the next section, we construct the k-essence emergent Vaidya spacetime for the generalized Vaidya spacetime background. It is accompanied by a scalar field with a restriction of being an arbitrary function of the advanced or retarded Eddington-Finkelstein time. This scalar field is independent of the other variables of the four-dimensional spacetime. We also construct the Ricci and Einstein tensors corresponding to our k-essence emergent Vaidya metric. We also compute the components of the emergent energy-momentum tensor by direct substitution into an emergent Einstein equation. This emergent tensor must obey the energy conditions of the emergent geometry. In Sect. 4, we develope the collapsing scenario for the k-essence emergent Vaidya spacetime. In this section, we analyze the structure of the central singularity to find out the conditions on the k-essence emergent Vaidya mass function, existence of outgoing nonspacelike geodesic and the strength of the singularities for the above emergent geometry. Some examples of the subclasses of generalized Vaidya backgrounds have also been discussed in Sect. 5. In the last section, we conclude over the whole work.

2 Brief review of K-essence theory and emergent gravity

In this section, we narrate a brief description of the development of construction of the effective metric for the emergent spacetime corresponding to a general background geometry and a very general k-essence scalar field sector. The k-essence scalar field \(\phi \) minimally coupled to the background spacetime metric \(g_{\mu \nu }\) has action [25,26,27,28,29]

$$\begin{aligned} S_{k}[\phi ,g_{\mu \nu }]= \int d^{4}x {\sqrt{-}g} L(X,\phi ) \end{aligned}$$
(1)

where \(X={1\over 2}g^{\mu \nu }\nabla _{\mu }\phi \nabla _{\nu }\phi \). The energy-momentum tensor is

$$\begin{aligned} T_{\mu \nu }\equiv {2\over \sqrt{-g}}{\delta S_{k}\over \delta g^{\mu \nu }}= L_{X}\nabla _{\mu }\phi \nabla _{\nu }\phi - g_{\mu \nu }L \end{aligned}$$
(2)

\(L_{\mathrm X}= {dL\over dX},~~ L_{\mathrm XX}= {d^{2}L\over dX^{2}}, ~~L_{\mathrm \phi }={dL\over d\phi }\) and \(\nabla _{\mu }\) is the covariant derivative defined with respect to the gravitational metric \(g_{\mu \nu }\). The scalar field equation of motion is

$$\begin{aligned} -{1\over \sqrt{-g}}{\delta S_{k}\over \delta \phi }= {\tilde{G}}^{\mu \nu }\nabla _{\mu }\nabla _{\nu }\phi +2XL_{X\phi }-L_{\phi }=0 \end{aligned}$$
(3)

where

$$\begin{aligned} {\tilde{G}}^{\mu \nu }\equiv L_{X} g^{\mu \nu } + L_{XX} \nabla ^{\mu }\phi \nabla ^{\nu }\phi \end{aligned}$$
(4)

and \(1+ {2X L_{XX}\over L_{X}} > 0\).

We adopt the conformal transformation \(G^{\mu \nu }\equiv {c_{s}\over L_{x}^{2}}{\tilde{G}}^{\mu \nu }\), with \(c_s^{2}(X,\phi )\equiv {(1+2X{L_{XX}\over L_{X}})^{-1}}\). Then the inverse metric of \(G^{\mu \nu }\) takes shape as

$$\begin{aligned} G_{\mu \nu }={L_{X}\over c_{s}} \left[ g_{\mu \nu }-{c_{s}^{2}}{L_{XX}\over L_{X}}\nabla _{\mu }\phi \nabla _{\nu }\phi \right] . \end{aligned}$$
(5)

A further conformal transformation [50, 51] \({\bar{G}}_{\mu \nu }\equiv {c_{s}\over L_{X}}G_{\mu \nu }\) gives

$$\begin{aligned} {\bar{G}}_{\mu \nu } ={g_{\mu \nu }-{{L_{XX}}\over {L_{X}+2XL_{XX}}}\nabla _{\mu }\phi \nabla _{\nu }\phi } \end{aligned}$$
(6)

Here one must always have \(L_{X}\ne 0\) for \(c_{s}^{2}\) to be positive definite and only then Eqs. (1)–(4) will be physically meaningful.

It is clear that, for non-trivial spacetime configurations of \(\phi \), the emergent metric \(G_{\mu \nu }\) is, in general, not conformally equivalent to \(g_{\mu \nu }\). So \(\phi \) has the properties different from canonical scalar fields with the local causal structure distinct from those defined with \(g_{\mu \nu }\). Further, if L is not an explicit function of \(\phi \), the equation of motion (3) reduces to;

$$\begin{aligned} -{1\over \sqrt{-g}}{\delta S_{k}\over \delta \phi } = {\bar{G}}^{\mu \nu }\nabla _{\mu }\nabla _{\nu }\phi =0 \end{aligned}$$
(7)

We shall take the Lagrangian as \(L=L(X)=1-V\sqrt{1-2X}\) with V is a constant. This is a particular case of the Dirac-Born-Infeld (DBI) lagrangian [22,23,24, 50,51,52]

$$\begin{aligned} L(X,\phi )= 1-V(\phi )\sqrt{1-2X} \end{aligned}$$
(8)

for \(V(\phi )=V=constant\)  and  \(kinetic ~ energy ~ of~\phi>>V\) i.e.\(({\dot{\phi }})^{2}>>V\). This is typical for the k-essence fields where the kinetic energy dominates over the potential energy. Then \(c_{s}^{2}(X,\phi )=1-2X\). For scalar fields \(\nabla _{\mu }\phi =\partial _{\mu }\phi \). Thus effective emergent metric (6) becomes

$$\begin{aligned} {\bar{G}}_{\mu \nu }= g_{\mu \nu } - \partial _{\mu }\phi \partial _{\nu }\phi \end{aligned}$$
(9)

Consider the second conformal transformation \({\bar{G}}_{\mu \nu }\equiv {c_{s}\over L_{X}}G_{\mu \nu }\). Following [50, 55] the new Christoffel symbols can be related to the old ones by

$$\begin{aligned} {\bar{\varGamma }} ^{\alpha }_{\mu \nu }= & {} \varGamma ^{\alpha }_{\mu \nu } + (1-2X)^{-1/2}G^{\alpha \gamma }[G_{\mu \gamma }\partial _{\nu }(1-2X)^{1/2}\nonumber \\&+G_{\nu \gamma }\partial _{\mu }(1-2X)^{1/2}-G_{\mu \nu }\partial _{\gamma }(1-2X)^{1/2}]\nonumber \\&=\varGamma ^{\alpha }_{\mu \nu } -\frac{1}{2(1-2X)}[\delta ^{\alpha }_{\mu }\partial _{\nu }X + \delta ^{\alpha }_{\mu }\partial _{\nu }X \end{aligned}$$
(10)

Note that the second term on the right hand side is symmetric under exchange of \(\mu \) and \(\nu \) so that the symmetry of \({\bar{\varGamma }}\) is maintained. The second term has its origin solely to the k-essence lagrangian and this additional term signifies additional interactions (forces). The geodesic equation for the k-essence theory in terms of the new Christoffel connections \({\bar{\varGamma }}\) now becomes

$$\begin{aligned} \frac{d^{2}x^{\alpha }}{d\lambda ^{2}} + {\bar{\varGamma }} ^{\alpha }_{\mu \nu }\frac{dx^{\mu }}{d\lambda }\frac{dx^{\nu }}{d\lambda }=0 \end{aligned}$$
(11)

where \(\lambda \) is an affine parameter.

3 Emergent spacetime for the generalized Vaidya background

We consider the background gravitational metric as the generalized Vaidya metric. The line element for the generalized Vaidya spacetime is [15,16,17]:

$$\begin{aligned} ds^{2}=-\left( 1-\frac{2m(v,r)}{r}\right) dv^{2}+2dvdr+r^{2}d\varOmega ^{2} \end{aligned}$$
(12)

where \(d\varOmega ^{2}=d\theta ^{2}+d\Phi ^{2}\). Here m(v, r) is the mass function related to the gravitational energy within a given radius r and v is the null coordinate corresponding to the Eddington advanced time with r decreasing toward the future along a ray related to \(v=constant\).

From (9), the k-essence emergent line element can be written as

$$\begin{aligned} dS^{2}=ds^{2}-\partial _{\mu }\phi \partial _{\nu }\phi dx^{\mu }dx^{\nu }. \end{aligned}$$
(13)

We consider the k-essence scalar field \(\phi (x)=\phi (v)\) only, so that the emergent line element (13) is

$$\begin{aligned} dS^{2}=-\Big [1-\frac{2m(v,r)}{r}-\phi _{v}^{2}\Big ]dv^{2}+2 dvdr+r^{2}d\varOmega ^{2}~~~\nonumber \\ \end{aligned}$$
(14)

where \(\phi _{v}=\frac{\partial \phi }{\partial v}\) and \(\phi _{v}^{2}\) is the kinetic energy of the k-essence scalar field which cannot be zero. Notice that this assumption on \(\phi \) actually violates local Lorentz invariance, since in general, spherical symmetry would only require that \(\phi (x)=\phi (v,r)\). The additional assumption of the independence of \(\phi \) i.e., \(\phi (v,r)=\phi (v)\) implies that outside of this particular choice of frame, a spherically symmetric \(\phi \) is actually a function of both v and r. Mention that the k-essence theory allows us this type of Lorentz violation, since the dynamical solutions of the k-essence equation of motion spontaneously break Lorentz invariance and also change the metric for the perturbations around these solutions.

The k-essence emergent Vaidya line element (14) also written as

$$\begin{aligned} dS^{2}=-\Bigg [1-\frac{2{\mathcal {M}}(v,r)}{r}\Bigg ]dv^{2}+2 dvdr+r^{2}d\varOmega ^{2}~~~ \end{aligned}$$
(15)

where we define the k-essence emergent Vaidya mass function

$$\begin{aligned} {\mathcal {M}}(v,r)=m(v,r)+\frac{r}{2}\phi _{v}^{2} \end{aligned}$$
(16)

which is related to the gravitational energy of the k-essence emergent gravity within a given radius r.

Now we compute the non-vanishing components of the emergent Ricci tensor and the emergent Einstein’s tensor following [16, 17], with the notations having subscripts on r and v denote derivatives with respect to those variables.

Using the following definitions:

$$\begin{aligned} {\mathcal {M}}_{v}&=\dot{{\mathcal {M}}}(v,r)\equiv \frac{\partial {\mathcal {M}}(v,r)}{\partial v}~;~\nonumber \\ {\mathcal {M}}_{r}&={\mathcal {M}}^{'}(v,r)\equiv \frac{\partial {\mathcal {M}}(v,r)}{\partial r} \end{aligned}$$
(17)

the nonvanishing components of the emergent Ricci tensor are

$$\begin{aligned} \bar{R}^{v}_{v}= & {} \bar{R}^{r}_{r}=\frac{{\mathcal {M}}_{rr}}{r}=\frac{m_{rr}}{r}~;~\nonumber \\ \bar{R}^{\theta }_{\theta }= & {} \bar{R}^{\Phi }_{\Phi }=\frac{2{\mathcal {M}}_{r}}{r^{2}}=\frac{2m_{r}}{r^{2}}+\frac{\phi _{v}^{2}}{r^{2}} \end{aligned}$$
(18)

and the Ricci scalar is given by

$$\begin{aligned} \bar{R}=\frac{2{\mathcal {M}}_{rr}}{r} +\frac{4{\mathcal {M}}_{r}}{r^{2}} =\frac{2m_{rr}}{r} +\frac{4m_{r}}{r^{2}}+\frac{2\phi _{v}^{2}}{r^{2}}. \end{aligned}$$
(19)

The nonvanishing components of the Einstein’s tensor are

$$\begin{aligned} {\mathcal {G}}^{v}_{v}= & {} {\mathcal {G}}^{r}_{r}=-\frac{2{\mathcal {M}}_{r}}{r^{2}}=-\frac{2m_{r}}{r^{2}}-\frac{\phi _{v}^{2}}{r^{2}}~;~\nonumber \\ {\mathcal {G}}^{r}_{v}= & {} \frac{2{\mathcal {M}}_{v}}{r^{2}}=\frac{2m_{v}}{r^{2}}+\frac{2\phi _{v}\phi _{vv}}{r}~;~\nonumber \\ {\mathcal {G}}^{\theta }_{\theta }= & {} {\mathcal {G}}^{\Phi }_{\Phi }=-\frac{{\mathcal {M}}_{rr}}{r}=-\frac{m_{rr}}{r} \end{aligned}$$
(20)

The ‘emergent’ Einstein equation is

$$\begin{aligned} {\mathcal {G}}^{\mu }_{\nu } = \kappa {{{\mathcal {T}}}}^{\mu }_{\nu } \end{aligned}$$
(21)

where, \(\kappa \equiv 8\pi G\) leads to the components \({{{\mathcal {T}}}}^{\mu }_{ \nu }\), which can be parametrized exactly as in Ref. [15,16,17] in terms of the components \(\gamma , \rho \) and \(\varSigma \) given by

$$\begin{aligned} {{{\mathcal {T}}}}_{\mu \nu }={{{\mathcal {T}}}}_{\mu \nu }^{(n)} + {{{\mathcal {T}}}}_{\mu \nu }^{(m)}= \left[ \begin{array}{cccc} (\gamma /2+\rho ) &{} \gamma /2 &{} 0 &{} 0 \\ \gamma /2 &{} (\gamma /2-\rho ) &{} 0 &{} 0 \\ 0 &{} 0 &{} \varSigma &{} 0 \\ 0 &{} 0 &{} 0 &{} \varSigma \end{array}\right] \nonumber \\ \end{aligned}$$
(22)

where \({{{\mathcal {T}}}}_{\mu \nu }^{(n)}=\gamma l_{\mu }l_{\nu }\);  \({{{\mathcal {T}}}}_{\mu \nu }^{(m)}=(\rho +\varSigma )(l_{\mu }n_{\nu }+l_{\nu }n_{\mu })+\varSigma \bar{G}_{\mu \nu }\) with \(l_{\mu }\) and \(n_{\mu }\) are two null vectors. Contractions of all indices are performed through the emergent metric \(\bar{G}_{\mu \nu }\). The expressions for the three independent components are given by,

$$\begin{aligned} \gamma= & {} \frac{2{\mathcal {M}}_{v}}{\kappa r^{2}}= \frac{2m_{v}}{\kappa r^{2}}+\frac{2\phi _v \phi _{vv}}{\kappa r} \end{aligned}$$
(23)
$$\begin{aligned} \rho= & {} \frac{2{\mathcal {M}}_{r}}{\kappa r^{2}}= \frac{2m_{r}}{\kappa r^{2}}+\frac{\phi _{v}^{2}}{\kappa r^{2}} \end{aligned}$$
(24)
$$\begin{aligned} \varSigma= & {} -\frac{{\mathcal {M}}_{rr}}{\kappa r}=-\frac{m_{rr}}{\kappa r}. \end{aligned}$$
(25)

The energy conditions for the combination of Type-I and Type-II fluids energy momentum tensor \({{{\mathcal {T}}}}_{\mu \nu }\) as defined in [56] are as follow:

  1. (a)

    The weak and strong energy conditions

    $$\begin{aligned} \gamma \ge 0~,~\rho \ge 0~,~\varSigma \ge 0~~~(\gamma \ne 0). \end{aligned}$$
    (26)
  2. (b)

    The dominant energy conditions

    $$\begin{aligned} \gamma \ge 0~,~\rho \ge \varSigma \ge 0 ~~~~~(\gamma \ne 0). \end{aligned}$$
    (27)

It is obvious that the above energy conditions (26) and (27) imposed on \({{{\mathcal {T}}}}_{\mu \nu }\) will, in turn, constrain m(v, r) and \(\phi (v)\) and their derivatives. Thus,

$$\begin{aligned} \gamma> 0\Rightarrow & {} m_{v}+r\phi _v \phi _{vv} > 0 , \end{aligned}$$
(28)
$$\begin{aligned} \rho> 0\Rightarrow & {} 2m_{r}+\phi _{v}^{2}>0, \end{aligned}$$
(29)
$$\begin{aligned} \varSigma >0\Rightarrow & {} m_{rr} < 0 . \end{aligned}$$
(30)

4 Collapsing scenario for the k-essence emergent Vaidya spacetime

We note \(K^{\mu }\) as the tangent to the nonspacelike geodesics with \(K^{\mu }=\frac{dx^{\mu }}{d\lambda }\) where \(\lambda \) is the affine parameter. The geodesic equation can be written as

$$\begin{aligned} K^{\nu }\nabla _{\nu }K^{\mu }=0~~and~~\bar{G}_{\mu \nu }K^{\mu }K^{\nu }=\beta \end{aligned}$$
(31)

where \(\beta \) is a constant. \(\beta =0\) describes the null geodesics and \(\beta <0\) describes the timelike geodesics. The emergent geodesic Eq. (11) can be re-written in terms of \(K^{\mu }\) as

$$\begin{aligned} \frac{dK^{\alpha }}{d\lambda }+{\bar{\varGamma }} ^{\alpha }_{\mu \nu }K^{\mu }K^{\nu }=0. \end{aligned}$$
(32)

Using the Eqs. (32) and (15) the geodesic Eqs. [7, 17] have the forms:

$$\begin{aligned}&\frac{dK^{v}}{d\lambda }+\Big [\frac{{\mathcal {M}}}{r^{2}}-\frac{{\mathcal {M}}_{r}}{r}\Big ](K^{v})^{2}-r\Big [(K^{\theta })^{2}+sin^{2}\theta (K^{\Phi })^{2}\Big ]=0\nonumber \\&\quad \quad \Rightarrow \frac{dK^{v}}{d\lambda }+\Big [\frac{{\mathcal {M}}}{r^{2}}-\frac{{\mathcal {M}}_{r}}{r}\Big ](K^{v})^{2}-\frac{l^{2}}{r^{3}}=0\nonumber \\&\quad \quad \Rightarrow \frac{dK^{v}}{d\lambda }+\Big [\frac{m}{r^{2}}-\frac{m_{r}}{r}\Big ](K^{v})^{2}-\frac{l^{2}}{r^{3}}=0, \end{aligned}$$
(33)
$$\begin{aligned}&\frac{dK^{r}}{d\lambda }+\frac{{\mathcal {M}}_{v}}{r}(K^{v})^{2}\nonumber \\&\quad +\Big [\frac{{\mathcal {M}}}{r^{2}}-\frac{{\mathcal {M}}_{r}}{r}\Big ]\Big [\Big (1-\frac{2{\mathcal {M}}}{r}\Big )(K^{v})^{2}-2K^{r}K^{v}\Big ]\nonumber \\&\quad -\Big (1-\frac{2{\mathcal {M}}}{r}\Big )r\Big [(K^{\theta })^{2}+sin^{2}\theta (K^{\Phi })^{2}\Big ]=0\nonumber \\&\Rightarrow \frac{dK^{r}}{d\lambda }+\frac{{\mathcal {M}}_{v}}{r}(K^{v})^{2}-\frac{l^{2}}{r^{3}}\Big (1-\frac{2{\mathcal {M}}}{r}\Big )\nonumber \\&\quad -\beta \Big [\frac{{\mathcal {M}}}{r^{2}}-\frac{{\mathcal {M}}_{r}}{r}\Big ]=0\nonumber \\&\Rightarrow \frac{dK^{r}}{d\lambda }+\Big (\frac{m_{v}}{r}+\phi _{v}\phi _{vv}\Big )(K^{v})^{2}-\frac{l^{2}}{r^{3}}\Big (1-\frac{2m}{r}-\phi _{v}^{2}\Big )\nonumber \\&\quad -\beta \Big [\frac{m}{r^{2}}-\frac{m_{r}}{r}\Big ]=0,~~~~~~~ \end{aligned}$$
(34)
$$\begin{aligned} \frac{dK^{\theta }}{d\lambda }+\frac{2}{r}K^{\theta }K^{r}-sin\theta ~cos\theta (K^{\Phi })^{2}= & {} 0, \end{aligned}$$
(35)
$$\begin{aligned} \frac{d}{d\lambda }(r^{2}sin^{2}\theta K^{\Phi })= & {} 0. \end{aligned}$$
(36)

Following [7], we use the relation

$$\begin{aligned} K^{\Phi }=\frac{lcos\delta }{r^{2}sin^{2}\theta }~~,~~K^{\theta }=\frac{l}{r^{2}}sin\delta cos\Phi \end{aligned}$$
(37)

where l and \(\delta \) are constant of integration. Here l is the impact parameter and \(\delta \) is the isotropy parameter such that \(sin\Phi ~tan\delta =cot\theta \).

We define \(K^{v}\) [7, 17] as

$$\begin{aligned} K^{v}=\frac{P(v,r)}{r} \end{aligned}$$
(38)

where P(v, r) is an arbitrary function, then from the relation \(\bar{G}_{\mu \nu }K^{\mu }K^{\nu }=\beta \) gives

$$\begin{aligned} K^{r}=\frac{P}{2r}\Big (1-\frac{2m}{r}-\phi _{v}^{2}\Big )-\frac{l^{2}}{2Pr}+\frac{\beta r}{2P} \end{aligned}$$
(39)

By differentiating the Eq. (38) with respect to \(\lambda \) we get

$$\begin{aligned} \frac{dP}{d\lambda }= & {} \frac{1}{r}\Big (r^{2}\frac{dK^{v}}{d\lambda }+P\frac{dr}{d\lambda }\Big )\nonumber \\= & {} \frac{P^{2}}{2r^{2}}\Big (1-\frac{4{\mathcal {M}}}{r}+2{\mathcal {M}}_{r}\Big )+\frac{l^{2}}{2r^{2}}+\frac{\beta }{2}\nonumber \\= & {} \frac{P^{2}}{2r^{2}}\Big (1-\frac{4m}{r}+2m_{r}\Big )+\frac{l^{2}}{2r^{2}}+\frac{\beta }{2}-\frac{P^{2}}{2r^{2}}\phi _{v}^{2}~~~~ \end{aligned}$$
(40)

We check for the given k-essence emergent generalised Vaidya mass function (16), how the final fate of collapse is determined in terms of either a black hole or a naked singularity. If there are families of future directed nonspacelike trajectories reaching faraway observers in spacetime and terminating in the past at the singularity, we have a naked singularity forming as the collapse final state. Otherwise an event horizon forms sufficiently early to cover the singularity in the absence of such families, we have a black hole.

Using Eqs. (38) and (39), we have the equation for the radial null geodesics \((l=0,~\beta =0)\) for the line element (15) is

$$\begin{aligned} \frac{dv}{dr}=\frac{2r}{r-2m(v,r)-r\phi _{v}^{2}} \end{aligned}$$
(41)

which has a singularity at \(r=0,~v=0\) provided \(\phi _{v}^{2}\ne 0\).

(a) Struture of the central singularity for the emergent spacetime (15)

In general, the above Eq. (41) can be written as [17]

$$\begin{aligned} \frac{dv}{dr}=\frac{M(v,r)}{N(v,r)} \end{aligned}$$
(42)

with the singular point \(r=0, v=0\), where both the above functions M(v, r) and N(v, r) vanish. In [17], they have proved, in general, the existence and uniqueness of the above form of differential Eq. (42) in the vicinity of this singularity. In this proof, they also have established the characteristic equation as

$$\begin{aligned} \chi ^{2}-(A+D)\chi +AD-BC=0 \end{aligned}$$
(43)

where \(A=M_{v}(0,0)~,~B=M_{r}(0,0)~,~C=N_{v}(0,0)~,~D=N_{r}(0,0)\) and \(AD-BC\ne 0\). The roots of the above Eq. (43) are

$$\begin{aligned} \chi =\frac{1}{2}\Big [(A+D)\pm \sqrt{(A-D)^{2}+4BC}\Big ]. \end{aligned}$$
(44)

The singularity is classified as a node if \((A-D)^{2}+4BC\ge 0\) and \(BC>0\). Otherwise, it may be a center or focus.

Compairing Eqs. (41) and (42), we have

$$\begin{aligned} M(v,r)= & {} 2r,\nonumber \\N(v,r)= & {} r-2{\mathcal {M}}(v,r) \nonumber \\ {}= & {} r-2m(v,r)-r\phi _{v}^{2}. \end{aligned}$$
(45)

At the central singularity (\(v=0, r=0\)), we define

$$\begin{aligned} {\mathcal {M}}_{0}= & {} \lim \limits _{v\rightarrow 0, r \rightarrow 0}{\mathcal {M}}(v,r)~;~ {\mathcal {M}}_{v0} = \lim \limits _{v\rightarrow 0, r \rightarrow 0}\frac{\partial }{\partial v}{\mathcal {M}}(v,r)~;~\nonumber \\ {\mathcal {M}}_{r0}= & {} \lim \limits _{v\rightarrow 0, r \rightarrow 0}\frac{\partial }{\partial r}{\mathcal {M}}(v,r)~;~ \phi _{v0} = \lim \limits _{v\rightarrow 0, r \rightarrow 0}\frac{\partial }{\partial v}\phi (v)~;~\nonumber \\ m_{v0}= & {} \lim \limits _{v\rightarrow 0, r \rightarrow 0}\frac{\partial }{\partial v}m(v,r)~;~ m_{r0} = \lim \limits _{v\rightarrow 0, r \rightarrow 0}\frac{\partial }{\partial r}m(v,r).\nonumber \\ \end{aligned}$$
(46)

Using Eqs. (45) and (46), we get \(A=0,~B=2,~C=-2m_{v0}~ and ~ D=1-2m_{r0}-\phi _{v0}^{2}\). So, using Eq. (44), we have the roots of the characteristic Eq. (43) becomes

$$\begin{aligned} \chi =\frac{1}{2}\Big [(1-2m_{r0}-\phi _{v0}^{2})\pm \sqrt{(1-2m_{r0}-\phi _{v0}^{2})^{2}-16m_{v0}}\Big ].\nonumber \\ \end{aligned}$$
(47)

For the singular point \((r=0, v=0)\) to be a node, then the condition is

$$\begin{aligned} \Big (1-2m_{r0}-\phi _{v0}^{2}\Big )^{2}\ge 16m_{v0},~ m_{v0}>0~and~\phi _{v0}^{2}>0.\nonumber \\ \end{aligned}$$
(48)

Therefore, if the k-essence emergent Vaidya mass function \({\mathcal {M}}(v,r)\) is chosen in such a manner that the condition (48) is satisfied, the singularity at the origin \((v=0, r=0)\) will be a node and outgoing nonspacelike geodesics can come out of the singlarity with a definite value of the tangent.

Using Eqs. (46) and (41), the linearized null geodesic equation near the central singularity can be written as

$$\begin{aligned} \frac{dv}{dr}=\frac{2r}{(1-2m_{r0}-\phi _{v0}^{2})r-2m_{v0}v} \end{aligned}$$
(49)

which is also singular at \(v=0, r=0\).

(b) Existence of outgoing nonspacelike geodesics for the emergent spacetime (15)

We consider that the emergent mass function \({\mathcal {M}}(v,r)\) obeys the all physical energy conditions (26) and (27) with the constraints (28), (29) and (30) and exists the partial derivatives of the mass function which are continuous in the entire k-essence emergent Vaidya spacetime and also obeys the conditions (48) at the central singularity. We find the condition for the existence of outgoing radial nonspacelike geodesics of this spacetime from the nodal singularity. To this aim, we consider X as the tangent of these curves at the singularity. Following [17, 18], we determine the nature (a black hole or a naked singularity) of the collapsing solutions, for this, we also define

$$\begin{aligned} X_{0}=\lim \limits _{v\rightarrow 0, r \rightarrow 0}X=\lim \limits _{v\rightarrow 0, r \rightarrow 0}\frac{v}{r} \end{aligned}$$
(50)

Using Eqs. (49), (50) and L’Hospital’s rule, we get

$$\begin{aligned} X_{0}=\lim \limits _{v\rightarrow 0, r \rightarrow 0}\frac{v}{r}=\frac{dv}{dr}=\frac{2}{(1-2m_{r0}-\phi _{v0}^{2})-2m_{v0}(\frac{v}{r})}\nonumber \\ \end{aligned}$$
(51)

which can be written as

$$\begin{aligned} X_{0}=\frac{2}{(1-2m_{r0}-\phi _{v0}^{2})-2m_{v0}X_{0}}. \end{aligned}$$
(52)

From (52) we get the values of \(X_{0}\) as

$$\begin{aligned} X_{0}= & {} \frac{(1-2m_{r0}-\phi _{v0}^{2})\pm \sqrt{(1-2m_{r0}-\phi _{v0}^{2})^{2}-16m_{v0}}}{4m_{v0}}\nonumber \\= & {} b_{\pm } \end{aligned}$$
(53)

where \(b_{+}\) is the positive root and \(b_{-}\) is the negative root of \(X_{0}\). For one or more real positive roots of \(X_{0}\), the singularity may be locally naked if the null geodesic lie outside the trapped region. When there is no positive real root of Eq. (53), the singularity is not naked because in that case there is no outgoing future directed null geodesics from the singularity. Hence, in the absence of positive real roots, the collapse ultimately leads to a black hole.

(c) Apparent horizon for the emergent spacetime (15)

During the evolution of collapse, the occurrence of a naked singularity or a black hole is usually decided by causal behaviour of the trapped surfaces. The boundary of the trapped surface region of the emergent spacetime is known as the apparent horizon. The apparent horizon for the k-essence emergent Vaidya spacetime (15) is

$$\begin{aligned}&\frac{2{\mathcal {M}}(v,r)}{r}=1 \nonumber \\&\Rightarrow \frac{2m(v,r)}{r}+\phi _{v}^{2}=1. \end{aligned}$$
(54)

On following [17], we calculate the slope of the emergent apparent horizon in the following manner:

$$\begin{aligned} 2\Big (\frac{\partial {\mathcal {M}}}{\partial v}\Big )\Big (\frac{dv}{dr}\Big )_{AH}+\frac{2\partial {\mathcal {M}}}{\partial r}=1. \end{aligned}$$
(55)

From the above Eq. (55), we obtain the slope of the emergent apparent horizon at the central singularity \((v\rightarrow 0,~r\rightarrow 0)\) as

$$\begin{aligned} \Big (\frac{dv}{dr}\Big )_{AH}=\frac{1-2m_{r0}-\phi _{v0}^{2}}{2m_{v0}} \end{aligned}$$
(56)

Thus the sufficient conditions for the existence of a locally naked singularity for the collapsing k-essence emergent Vaidya spacetime is attained. The emergent mass function \({\mathcal {M}}(v,r)\) obeys all the energy conditions and constraints (28,29,30) and is differentiable in the entire emergent spacetime (15), if the following conditions are satisfied:

  1. (a)

    The limits of the partial derivatives of the mass function \({\mathcal {M}}(v,r)\) at the central singularity obey the conditions (48).

  2. (b)

    One or more positive real roots \(X_{0}\) of Eq. (53) must occur.

  3. (c)

    At least one of the positive real roots is less than \((\frac{dv}{dr})_{AH}\) at the central singularity.

In [17], they have shown that the values of \(X_{0}=b_{\pm }\) must lie below the value of \((\frac{dv}{dr})_{AH}\) and there exist an open set of parameter values for which the singularity is locally naked for the case of generalized Vaidya spacetime.

For the case of k-essence emergent Vaidya spacetime, we can also show that the values of \(X_{0}\) are always below the value of \((\frac{dv}{dr})_{AH}\) provided \(m_{v0}>0\). This statement can be proved as:

$$\begin{aligned} X_{0}< \left( \frac{dv}{dr}\right) _{AH}~;~ \Rightarrow \frac{y\pm \sqrt{y^{2}-16m_{v0}}}{4m_{v0}}< & {} \frac{y}{2m_{v0}}\nonumber \\ \Rightarrow y^{2}-16m_{v0}<y^{2}~;~ \Rightarrow m_{v0}>0 \end{aligned}$$
(57)

where \(y=1-2m_{r0}-\phi _{v0}^{2}\). Therefore, we can also infer that an open set of parameter values must exist for which the singularity is locally naked for the case of k-essence emergent Vaidya spacetime.

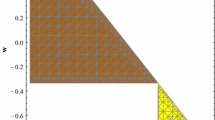
As an example, we consider the value of the kinetic energy of the k-essence scalar field at the central singularity is \(\phi _{v0}^{2}=0.7\) and \(m_{v0}=0.0015\). Figure 1 (\(-2.68\le m_{r0}\le -2.64\)) and Fig. 2 (\(-3\le m_{r0}\le 0.01\)) show that the values of \(X_{0}=b_{\pm }\) become smaller than those appears of \((\frac{dv}{dr})_{AH}\) and thus for our case, the above statement is true as [17].

Fig. 1
figure 1

Variation of \(X_0=b_{+}\) (red) and \(\left( \frac{dv}{dr}\right) _{AH}\) (blue) with \(m_{r0}\) at fixed value \(m_{v0}= 0.0015\)

Full size image
Fig. 2
figure 2

Variation of \(X_0=b_{-}\) (red) and \(\left( \frac{dv}{dr}\right) _{AH}\) (blue) with \(m_{r0}\) at fixed value \(m_{v0}= 0.0015\)

Full size image

(d) Strength of singularity for the emergent spacetime (15):

By following [17, 18, 57,58,59], we can highlight that a singularity \((r=v=\lambda =0)\) would be strong if the condition

$$\begin{aligned} \lim \limits _{\lambda \rightarrow 0}\lambda ^{2}\psi =\lim \limits _{\lambda \rightarrow 0}\lambda ^{2}\bar{R}_{\mu \nu }K^{\mu }K^{\nu }>0 \end{aligned}$$
(58)

is satisfied, where \(\bar{R}_{\mu \nu }\) is Ricci tensor and we define \(\psi =\bar{R}_{\mu \nu }K^{\mu }K^{\nu }\) as a scalar of the k-essence emergent Vaidya spacetime. Mention that this scalar \(\psi \) is not k-essence scalar field also not coupled with the background gravitational metric \(g_{\mu \nu }\). Using Eqs. (18), (38) and (39), we get

$$\begin{aligned} \lambda ^{2}\psi =\Big (2{\mathcal {M}}_{v0}\Big )\Big (\frac{P\lambda }{r^{2}}\Big )^{2}. \end{aligned}$$
(59)

If we assume that \(P(v,r)\ne 0,\infty \) and using L’Hospital rule, we get

$$\begin{aligned} \lim \limits _{\lambda \rightarrow 0}\lambda ^{2}\psi&= \Big (2{\mathcal {M}}_{v0}\Big )\lim \limits _{\lambda \rightarrow 0}\Big (\frac{P\lambda }{r^{2}}\Big )^{2}\nonumber \\&=\Big (2{\mathcal {M}}_{v0}\Big )\lim \limits _{\lambda \rightarrow 0}\Big (\frac{Pd\lambda }{2rdr}\Big )^{2}. \end{aligned}$$
(60)

Using Eq. (38), \(\frac{P}{r}=\frac{dv}{d\lambda }\), we get

$$\begin{aligned} \lim \limits _{\lambda \rightarrow 0}\lambda ^{2}\psi =\Big (2{\mathcal {M}}_{v0}\Big )\Big (\frac{1}{2}\frac{dv}{dr}\Big )^{2}=\Big (2{\mathcal {M}}_{v0}\Big )\frac{1}{4}X_{0}^{2}\nonumber \\ =\Big (2m_{v0}\Big )\frac{1}{4}X_{0}^{2} \end{aligned}$$
(61)

where at the limit \((v\rightarrow 0,r\rightarrow 0)\), \({\mathcal {M}}_{v0}=m_{v0}\) irrespective of the k-essence scalar field. But from Eq. (53) \(X_{0}\) is found to be dependent on limiting value of the k-essence scalar field. Therefore, with the conditions (48) and suitable choice of the emergent mass function (16), it can be shown that

$$\begin{aligned} \lim \limits _{\lambda \rightarrow 0}\lambda ^{2}\psi =\Big (2{\mathcal {M}}_{v0}\Big )\frac{1}{4}X_{0}^{2}>0. \end{aligned}$$
(62)

If this condition is satisfied for some real and positive roots of \(X_{0}\), the naked singularity of the k-essence emergent Vaidya spacetime is strong. Otherwise i.e., if there is no positive real root of \(X_{o}\), we can conclude that there is no outgoing future directed null geodesics from the singularity comes into the picture i.e., the collapse ends into a black hole.

5 Background gravitational metric to be some special subclasses of generalized Vaidya metric

In this section, we evaluate the values of the three independent components (\(\gamma , \rho , \varSigma \)) of energy-momentum tensor \({{\mathcal {T}}}_{\mu \nu }\) using Eqs. (23, 24, 25) and the equations of tangents (52) to the null geodesics at the central singularity \((v\rightarrow 0,r\rightarrow 0)\) for some special subclasses of the generalized Vaidya backgroud spacetime with the specific mass function \({\mathcal {M}}(v,r)\).

A physical situation where a radial influx of null fluid in an initially empty region of the Minkowski spacetime [17, 60] is taken into consideration. The first shell arrives at \(r = 0\) at time \(v = 0\) and the final at \(v = T\). A central singularity of growing mass is developed at \(r = 0\). For \(v < 0\) we have \(m(v) = q(v) = 0\), i.e., an empty Minkowski metric appears, and for \(v > T\), \(m_{v}(v) = q_{v}(v) = 0\), m(v) and \(q^{2}(v)\) are positive definite. The metric for \(v = 0\) to \(v = T\) is the k-essence emergent Vaidya spacetime, and for \(v > T\) we have \(m(v)=M_{0},~q^{2}(v)=q_{0}^{2}\) where \(M_{0}\) and \(q_{0}^{2}\) are some positive constants. In the limit \(v>T\) the emergent gravity metric is analogues to the Barriola–Vilenkin type spacetime for the Schwarzschild background [50] and Robinson–Trautman type spacetime for the Reissner–Nordstrom background [51] where \(\phi _{v}^{2}=constant\) and is also analogues to k-essence generalization of Vaidya spacetime [61] where \(\phi _{v}^{2}\) is function of v only.

(a) The usual Vaidya background In this case, we consider the mass function [4, 17]

$$\begin{aligned} m(v,r)=m(v). \end{aligned}$$
(63)

The k-essence mass function (16) becomes \({\mathcal {M}}(v,r)=m(v)+\frac{r}{2}\phi _{v}^{2}\) and defines the mass function m(v) as

$$\begin{aligned} m(v)={\left\{ \begin{array}{ll} 0 &{}if~v < 0, \\ \frac{1}{2}\epsilon v &{} if~0\le v \le T,\\ M_0 &{} if~v > T. \end{array}\right. } \end{aligned}$$
(64)

where \(\epsilon \) is an arbitrary constant. For this case, the values of \(\gamma ,~\rho ~and~\varSigma \) are

$$\begin{aligned} \gamma =\frac{2m_{v}}{\kappa r^{2}}+\frac{2\phi _{v}\phi _{vv}}{\kappa r};~ \rho =\frac{\phi _{v}^{2}}{\kappa r^{2}};~ \varSigma =0. \end{aligned}$$
(65)

For the above values of \(\gamma ,~\rho ~and~\varSigma \), the energy-momentum tensor \({{\mathcal {T}}}_{\mu \nu }\) belo ngs to type-II class [56] which has a double null vector. The tangent Eq. (53) to the null geodesics at the central singularity \((v\rightarrow 0,r\rightarrow 0)\) for the range \(0\le v \le T\) are

$$\begin{aligned} X_{0}=\frac{(1-\phi _{v0}^{2})\pm \sqrt{(1-\phi _{v0}^{2})-8\epsilon }}{2\epsilon }. \end{aligned}$$
(66)

If we consider \(\phi _{v0}^{2}=0.7\), the above equation gives the positive values of \(X_{0}\) for all values of \(\epsilon \) in the range \(0<\epsilon \le \frac{3}{80}\). Also, from (62) we can show that \(\lim \limits _{\lambda \rightarrow 0}\lambda ^{2}\psi =\frac{1}{4}\epsilon X_{0}^{2}>0\) for all values of \(X_{0}\) in the above range of \(\epsilon \). Therefore, we can say that the singularity is strong.

(b) The charged Vaidya background On the basia of [16, 17, 60], we conider the mass function

$$\begin{aligned} m(v,r)=f(v)-\frac{q^{2}(v)}{2r} \end{aligned}$$
(67)

where f(v) and q(v) are arbitrary functions of mass and electric charge respectively. Thus the k-essence mass function is \({\mathcal {M}}(v,r)=f(v)-\frac{q^{2}(v)}{2r}+\frac{r}{2}\phi _{v}^{2}\). So the values of \(\gamma ,~\rho ~and~\varSigma \) are

$$\begin{aligned} \gamma =\frac{2f_{v}}{\kappa r^{2}}-\frac{2qq_{v}}{\kappa r^{3}}+\frac{2\phi _{v}\phi {vv}}{\kappa r}~;\nonumber \\ \rho =\frac{q^{2}}{\kappa r^{4}}+\frac{\phi _{v}^{2}}{\kappa r^{2}}~;~ \varSigma =\frac{q^{2}}{\kappa r^{4}}. \end{aligned}$$
(68)

which have satisfied the weak and strong energy conditions (26). Now we define f(v) and q(v) as [17, 60]

$$\begin{aligned} f(v)={\left\{ \begin{array}{ll} 0 &{}if~v < 0, \\ \epsilon v(\epsilon>0) &{} if~0\le v \le T,\\ f_{0}(>0) &{} if~v > T. \end{array}\right. } \end{aligned}$$
(69)

and

$$\begin{aligned} q^{2}(v)={\left\{ \begin{array}{ll} 0 &{}if~v < 0, \\ \mu ^{2} v^{2}(\mu ^{2}>0) &{} if~0\le v \le T,\\ q_{0}^{2}(>0) &{} if~v > T. \end{array}\right. } \end{aligned}$$
(70)

then the tangent Eq. (52) in the range \(0\le v \le T\) becomes

$$\begin{aligned} \mu ^{2}X_{0}^{3}-2\epsilon X_{0}^{2}+(1-\phi _{v0}^{2})X_{0}-2=0. \end{aligned}$$
(71)

If the singularity is naked, Eq. (71) must have one or more positive roots of \(X_{0}\) considering \(\phi _{v0}^{2}=0.7\), i.e. at least one outgoing geodesic that will terminate in the past at the singularity. Hence in the absence of positive roots, the collapse will always lead to a black hole. Thus, the occurrence of positive roots implies that the strong CCC is violated, though not necessarily being the weak one. It has been shown that the central shell focusing singularity is at least locally naked if this algebraic Eq. (71) admits one or more positive roots [2]. When there is no positive root to (71), the central singularity is not naked because in that case there is no outgoing future directed null geodesics emerging from the singularity. Hence in the absence of positive roots, the collapse will always lead to a black hole. As an example, we consider \(\mu ^{2}=0.001, \epsilon =0.01~and~ \phi _{v0}^{2}=0.7\) then one of the roots of the Eq. (71) is 10 which is positive. Thus the condition for a strong singularity is satisfied.

(c) The charged Vaidya deSitter background Here we chose the mass function as [62]

$$\begin{aligned} m(v,r)=f(v)-\frac{q^{2}(v)}{2r}+\frac{\varLambda r^{3}}{6} \end{aligned}$$
(72)

where \(\varLambda \ne 0\) is the cosmological constant and the k-essence emergent Vaidya mass function is \({\mathcal {M}}(v,r)=f(v)-\frac{q^{2}(v)}{2r}+\frac{\varLambda r^{3}}{6}+\frac{r}{2}\phi _{v}^{2}\). Thus the values of \(\gamma ,~\rho ~and~\varSigma \) are

$$\begin{aligned} \gamma= & {} \frac{2f_{v}}{\kappa r^{2}}-\frac{2qq_{v}}{\kappa r^{3}}+\frac{2\phi _{v}\phi {vv}}{\kappa r}~;\nonumber \\ \rho= & {} \frac{q^{2}}{\kappa r^{4}}+\frac{\phi _{v}^{2}}{\kappa r^{2}}+\frac{\varLambda }{\kappa }~;~ \varSigma =\frac{q^{2}}{\kappa r^{4}}-\frac{\varLambda }{\kappa } \end{aligned}$$
(73)

which have follow the energy condition (26). We observe that the tangent Eq. (52) for this case is similar to that of charged Vaidya backgroud case (71). So we can say that the singularity is also strong.

6 Conclusion

Based on the Dirac–Born–Infeld Lagrangian, the gravitational collapse of null fluids is analyzed in the the k-essence emergent Vaidya spacetime. The analysis is presented in the context of cosmic censorship hypothesis with the k-essence emergent Vaidya mass function. We develop the Einstein tensor and the energy conditions for the combination of Type-I and Type-II fluids energy momentum tensor for the k-essence emergent Vaidya spacetime. We have studied the classification of non-spacelike geodesic for the k-essence emergent Vaidya spacetime that connect the naked singularity in the past, which is a strong curvature singularity in a stronger sense. The central singularity being a node allows outgoing non-spacelike geodesics to come out of the singlarity with a definite value of the tangent. The positive value of the tangent implies that the strong CCC is violated i.e., the singularity is locally naked, though not necessarily being the weak one. If the value of tangent is not positive, the central singularity is not naked because, in that case, there is no outgoing future directed null geodesics emerging from the singularity i.e., the collapse will always lead to a black hole. We also have the same type of results as Mkenyeleye et. al. [17] in the presence of k-essence scalar field for the k-essence emergent Vaidya spacetime for the collapsing scenario.