1 Introduction

A new era of strong gravitational physics has come with the direct detections of gravitational waves from binary black holes [1,2,3,4,5,6] and with the direct imaging the shadow of the supermassive black hole M87* in the center of galaxy M87 [7,8,9,10,11,12]. Black holes are ideal laboratories for probing nature of gravity in the extreme environments and regimes for searching new phenomena beyond the standard models. Gravitational lensing is a straightforward and magnificent manifestation of the interaction between the gravitational and electromagnetic fields. It not only provides numerous insight into black holes but also plays a critical role in shaping their apparent looks [13].

The gravitational lensing with a weak deflection of light ray has become an indispensable instrument in astronomy [14,15,16,17] and gravitational physics [18,19,20,21,22]. The gravitational lensing with a strong deflection of light ray is the essential to raise the shadow [23] and relativistic images [24] of black holes, since the photons might surround a black hole for several loops [25, 26]. It benefits understanding black holes [27,28,29,30,31] and telling difference of them [32,33,34,35,36,37,38,39,40,41].

Most studies on weak and strong deflection gravitational lensing assumed that the standard Einstein-Maxwell theory is valid [42, 43], whereas new interactions beyond that could also exist. One-loop vacuum polarization on the quantum electrodynamics might make photons travel superluminally [44] due to the tidal gravitational forces caused by the quantum corrections, but this effect is extremely small because it depends on the square of the Compton wavelength of the electron. More general couplings between the gravitational and electromagnetic fields were also proposed [45, 46] and were widely investigated in the context of astrophysics [47,48,49,50] and black hole physics [51,52,53]. The gravitational and electromagnetic fields might interact via the Weyl tensor, which was examined for holographic conductivity and superconductors [54,55,56,57,58,59,60,61] and for the electrodynamics in the vicinity of black holes [62,63,64,65]. Recently, such a coupling has also been considered as a non-minimal coupling in extended theoretical models, for instance, non-minimally coupled Weyl connection gravity [66,67,68], which might be constrained by ocean experiments [69], Solar System tests [70] and gravitational waves [71]. When the gravitational and electromagnetic fields are non-minimally coupled, a photon will never travel along the geodesics of the background spacetime while the geometrical-optics approximation might still be valid under some circumstances [44]. The gravitational lensing of the photons coupled to the Weyl tensor in the Schwarzschild black hole was investigated in both weak [72,73,74] and strong [75, 76] deflection cases. The strong deflection gravitational lensing of the photons coupled to the Weyl tensor in the Kerr black hole was also studied [77].

Inspired by the accelerating expansion of the Universe [78, 79], the phantom scalar fields were introduced as a possible explanation of dark energy since observations suggest its equation of state parameter is \(w<-1\) [80,81,82]. The phantom fields could also affect the characteristics of black holes [83, 84] and change the behaviors of gravitational lensing. The weak and strong deflection gravitational lensing of the phantom black holes were investigated under the standard Einstein-Maxwell theory [85,86,87]. Considering the photons coupled to the Weyl tensor in the regular phantom black hole, its strong deflection gravitational lensing was studied and the positions and brightness difference of the resulting relativistic images were analyzed [88].

In the present work, in order to obtain a more comprehensive picture of the photons coupled to the Weyl tensor in the regular phantom black hole, we investigate its time delay in both weak and strong deflection gravitational lensing, which is absent in the previous work [88]. These time-domain signals are important for determining the properties of black holes [89,90,91,92,93,94] and probing new physics [95,96,97,98,99,100,101,102].

In Sect. 2, we briefly review the effective metric of the photons coupled to the Weyl tensor in the regular phantom black hole and carefully find its parameter space which was missing in the previous work [88]. Meanwhile, the set-up for gravitational lensing is also given. In Sects. 3 and 4, we respectively investigate its time delay in the weak and strong deflection gravitational lensing and discuss its observability by taking the supermassive black hole in the Galactic Center, Sgr A*, and M87* as lenses. Finally, in Sect. 5, we summarize and discuss our results.

2 Effective metric and set-up of gravitational lensing

2.1 Effective metric and parameter space

The metric of the regular phantom black hole reads (\(G=c=1\)) [83]

$$\begin{aligned} \mathrm {d}s^2 = -{\mathcal {A}}(r) \mathrm {d}t^2 + {\mathcal {B}}(r) \mathrm {d}r^2 + {\mathcal {C}}(r)\left( \mathrm {d}\theta ^2 + \sin ^2\theta \mathrm {d}\phi ^2\right) ,\nonumber \\ \end{aligned}$$
(1)

where

$$\begin{aligned} {\mathcal {A}}(r)= & {} [{\mathcal {B}}(r)]^{-1} \nonumber \\= & {} 1-\frac{3m_{\bullet }}{b}\left[ \left( \frac{\pi }{2} - \arctan \frac{r}{b} \right) \left( 1+\frac{r^2}{b^2} \right) -\frac{r}{b} \right] , \end{aligned}$$
(2)

and

$$\begin{aligned} {\mathcal {C}}(r) = r^2 + b^2. \end{aligned}$$
(3)

Here \(m_{\bullet }\) is the mass of the phantom black hole and b is the scalar hair related to the phantom field. When \(b=0\), such a black hole reduces to a Schwarzschild one. The existence of an event horizon for the spacetime (1) requires

$$\begin{aligned} 0<b<\frac{3}{2}\pi m_{\bullet }, \end{aligned}$$
(4)

and the radius of the event horizon \(r_\mathrm {H}\) has the range of

$$\begin{aligned} 0<r_\mathrm {H}<2m_{\bullet }. \end{aligned}$$
(5)

For a nonzero b, the spacetime (1) is regular at \(r=0\) and it is asymptotically flat as \(r\rightarrow +\infty \). The axial perturbations and the monopole type of polar perturbations on this regular black hole were investigated [84]. It was found that the black hole is stable for \(b=3\pi m_{\bullet }/2\) in the linear approximation [84]; however, the full nonlinear analysis of perturbations and the back-reaction of electromagnetic fields with and without the Weyl coupling are still open questions.

If we consider a photon coupled the background spacetime (1) via the Weyl tensor, its Lagrangian density of the electromagnetic field becomes [54]

$$\begin{aligned} {\mathcal {L}}=-\frac{1}{4}F_{\mu \nu }F^{\mu \nu }+{\hat{\alpha }}_{\bullet }C^{\mu \nu \rho \sigma }F_{\mu \nu }F_{\rho \sigma }, \end{aligned}$$
(6)

where \(F_{\mu \nu }=A_{\nu ;\mu }-A_{\mu ;\nu }\) is the electromagnetic field tensor, \({\hat{\alpha }}_{\bullet }\) is the coupling constant with a dimension of the length squared, and \(C^{\mu \nu \rho \sigma }\) is the Weyl tensor. By differentiating \({\mathcal {L}}\) with respect to the electromagnetic 4-vector \(A_{\mu }\), we can obtain the Maxwell equation with an correction from the coupling of the Weyl tensor as

$$\begin{aligned} {\left( F^{\mu \nu }-4{\hat{\alpha }}_{\bullet }C^{\mu \nu \rho \sigma }F_{\rho \sigma }\right) }_{;\mu }=0. \end{aligned}$$
(7)

It is clear that the photon will no longer follow the geodesics of the background spacetime (1) due to its coupling to the Weyl tensor. We assume that the electron Compton wavelength is smaller than the wavelength of the photon which is further less than the typical curvature scale of the spacetime, making the geometric optics approximation valid. Therefore, the electromagnetic field tensor can be written as [44]

$$\begin{aligned} F_{\mu \nu }=f_{\mu \nu }{\exp }(i\theta ), \end{aligned}$$
(8)

where \(f_{\mu \nu }\) is slowly varying with respect to \(\theta \). Making use of the Bianchi identities can lead to [44]

$$\begin{aligned} f_{\mu \nu }=k_{\mu }a_{\nu }-k_{\nu }a_{\mu }, \end{aligned}$$
(9)

where \(k_{\mu }=\theta _{;\mu }\) and \(a_{\mu }\) is a polarization vector satisfying \(k_{\mu }a^{\mu }=0\). With the help of Eqs. (8) and (9), the modified Maxwell equation (7) can be transformed into

$$\begin{aligned} k_{\mu }k^{\mu }a^{\nu }+8{\hat{\alpha }}_{\bullet }C^{\mu \nu \rho \sigma }k_{\sigma }k_{\mu }a_{\rho }=0. \end{aligned}$$
(10)

In the background of the regular phantom black hole (1), the orthonormal tetrad and bivectors can be respectively introduced as [44]

$$\begin{aligned} e_{\mu }^{a}=\left( \sqrt{{\mathcal {A}}(r)}, \sqrt{{\mathcal {B}}(r)}, \sqrt{r^2+b^2}, \sqrt{r^2+b^2}\sin {\theta }\right) , \end{aligned}$$
(11)

and

$$\begin{aligned} U_{\mu \nu }^{ab}=e_{\mu }^{a}e_{\nu }^{b}-e_{\nu }^{b}e_{\mu }^{a}. \end{aligned}$$
(12)

It was shown [44] that its solutions to the equations of motion for the coupled photons depend on the vectors \(l_{\nu }=k^{\mu }U_{\mu \nu }^{01}\) or \(m_{\nu }=k^{\mu }U_{\mu \nu }^{23}\), both of which are orthogonal to \(k_\nu \).

Therefore, the effective metric of the photons coupled to the Weyl tensor in the regular phantom black hole can be obtained as [88]

$$\begin{aligned} \mathrm {d}s^2 = -A(r) \mathrm {d}t^2 + B(r) \mathrm {d}r^2 + C(r)\left( \mathrm {d}\theta ^2 + \sin ^2\theta \mathrm {d}\phi ^2\right) ,\nonumber \\ \end{aligned}$$
(13)

where

$$\begin{aligned} A(r)= & {} [B(r)]^{-1} = {\mathcal {A}}(r),\end{aligned}$$
(14)
$$\begin{aligned} C(r)= & {} \frac{{\mathcal {C}}(r)}{{W(r)}^{s}}, \end{aligned}$$
(15)

with

$$\begin{aligned} W(r)= & {} W_{\mathrm {PPL}}(r) = [W_{\mathrm {PPM}}(r)]^{-1} \nonumber \\= & {} \frac{3{(r^2+b^2)}^2+8{\hat{\alpha }}_{\bullet }(b^2+3m_{\bullet }r)}{3{(r^2+b^2)}^2-16{\hat{\alpha }}_{\bullet }(b^2+3m_{\bullet }r)}. \end{aligned}$$
(16)

If the polarization is along \(l_{\nu }\) (PPL), then \(s=1\); if the polarization is along \(m_{\nu }\) (PPM), \(s=-1\). The non-geodesic worldline of a photon in the spacetime (1) can be mapped into the geodesic one in the spacetime (13) which will be adopted in the following work. When \(b= 0\), the effective metric (13) returns to the case of the photons coupled to the Weyl tensor in the Schwarzschild black hole and the behaviors of these photons have been widely studied [72,73,74,75]. It is worth mentioning that our convention on C(r), see Eq. (15), is slightly different from the one of the work [73] about the photons coupled to the Weyl tensor in the Schwarzschild black hole.

Before we proceed, it is necessary to determine the domain of \(\{b,\hat{\alpha }_{\bullet }\}\) which has not been intensively investigated in the previous work [88]. In order to ensure the validity of the effective metric (13), its coefficients have to keep their properties of either time-like or space-like unchanged during the propagation of the photon, i.e.,

$$\begin{aligned} -A(r)<0, \quad B(r)>0, \quad C(r)>0, \end{aligned}$$
(17)

and the photon must stay outside the event horizon \(r_\mathrm {H}\) of the regular phantom black hole (1) in the gravitational lensing, i.e.,

$$\begin{aligned} r>r_\mathrm {H}. \end{aligned}$$
(18)

For later convenience, we rescale r and \(r_\mathrm {H}\) as

$$\begin{aligned} x= & {} \frac{r}{m_{\bullet }},\end{aligned}$$
(19)
$$\begin{aligned} x_\mathrm {H}= & {} \frac{r_\mathrm {H}}{m_{\bullet }}. \end{aligned}$$
(20)

After a lengthy but straightforward analysis (see Appendix A for details), we find that the complicated domain of \(\{b,\hat{\alpha }_{\bullet }\}\) can be mapped into a neat one of \(\{k,\rho \}\) commonly valid for the polarizations of both PPL and PPM as

$$\begin{aligned} \{b,\hat{\alpha }_{\bullet }\} \mapsto {\mathcal {D}} = \{ (k,\rho ) | 0<k<1, -2<\rho <1 \} \end{aligned}$$
(21)

where we have

$$\begin{aligned} k=\frac{2}{3\pi m_{\bullet }}b, \end{aligned}$$
(22)

and

$$\begin{aligned} \left\{ \begin{aligned} \rho&=\frac{{\hat{\alpha }}_\bullet }{m_{\bullet }^2} \frac{64(3\pi ^2k^2+4x_\mathrm {H})}{{(9\pi ^2k^2+4x_\mathrm {H}^2)}^2} ,\quad \text {for}\quad 0<k\le k_c,\\ \rho&=\frac{{\hat{\alpha }}_\bullet }{m_{\bullet }^2} \frac{64(3\pi ^2k^2+4x_{+})}{{(9\pi ^2k^2+4{x_{+}}^2)}^2},\quad \text {for}\quad k_c<k<1, \end{aligned} \right. \end{aligned}$$
(23)

with a numerical constant

$$\begin{aligned} k_c \approx 0.8012952 \end{aligned}$$
(24)

and a quantity

$$\begin{aligned} x_{+} = \frac{{\pi }k}{2}\left( \sqrt{\pi ^2k^2+3}-{\pi }k\right) . \end{aligned}$$
(25)

We define \(x_{+}\) as the solution to

$$\begin{aligned} \frac{\mathrm {d}W(x)^{-s}}{\mathrm {d}x} = 0, \end{aligned}$$
(26)

and it can be directly found that \(x_+\) is irrelevant to the polarizations of PPL and PPM so that

$$\begin{aligned} x^{\mathrm {PPL}}_{+} = x^{\mathrm {PPM}}_{+} = x_{+}. \end{aligned}$$
(27)

When \(\rho =0\), the coupling between the photons and the Weyl tensor vanishes. It is worth mentioning that, instead of k and \(\rho \), b and \(\hat{\alpha }_{\bullet }\) parametrize the theory of the photons coupled to the Weyl tensor in the regular phantom black hole so that the same constraints on k and \(\rho \) can lead to very different bounds on b and \(\hat{\alpha }_{\bullet }\) because Sgr A* and M87* have completely different masses.

The effective metric (13) permits the existence of the photon sphere (unstable light ring) and its radius \(r_{m}\) is the largest positive root of the equation [28, 103]

$$\begin{aligned} C'(r)A(r)=C(r)A'(r) \end{aligned}$$
(28)

where \('\) means differentiation against the coordinate r. We also rescale \(r_m\) as

$$\begin{aligned} x_{m} = \frac{r_{m}}{m_{\bullet }}. \end{aligned}$$
(29)

Although Eq. (28) has no analytic solution generally, an exact solution for \(\rho =0\) can be found as

$$\begin{aligned} x_m = 3, \end{aligned}$$
(30)

which is the same as the one of the Schwarzschild black hole [23].

The event horizon radius \(x_\mathrm {H}\) for the regular phantom black hole is determined from \({\mathcal {A}}(x)=0\) and it nonlinearly depends on the scalar hair k, i.e., \(x_\mathrm {H}=x_\mathrm {H}(k)\). Determined by Eq. (28), the photon sphere radius \(x_m\) depends on k and \(\rho \), i.e., \(x_m=x_m(k,\rho )\). Figure 1 shows the variation of \(x_m\) and \(x_\mathrm {H}\) against k and \(\rho \) on the domain \({\mathcal {D}}\) for the polarizations of PPL and PPM. For a given k, a bigger coupling constant \(\rho \) can make the photon sphere \(x_m\) shrink. \(x_m\) monotonically increases with k for a negative \(\rho \) and it decreases for a positive \(\rho \). When either \(\rho =1\) for the polarization of PPL or \(\rho =-2\) for PPM, the photon sphere coincides with the event horizon, \(x_m=x_\mathrm {H}\), on the domain of \(0<k<k_c\) and it becomes equivalent to \(x_{+}\) on \(k_c<k<1\). It indicates that \(\rho =1\) is the upper-bound on the coupling constant to ensure the existence of the photon sphere for PPL and \(\rho =-2\) is the lower-bound for the photon sphere of PPM.

Fig. 1
figure 1

The radii of the photon sphere \(x_m\) and the event horizon \(x_\mathrm {H}\) with respect to k and \(\rho \) for the polarizations of PPL (\(s=1\)) in the a and of PPM (\(s=-1\)) in the b. Various colors of the solid curves represent different values of \(\rho \). The dotted line and dashed line respectively denote the variation of \(x_{+}(=x^{\mathrm {PPL}}_{+} = x^{\mathrm {PPM}}_{+})\) and \(x_\mathrm {H}\) against k. The vertical dashed line marks the position of \(k=k_c\)

Full size image

2.2 Lens equation and gravitational time delay

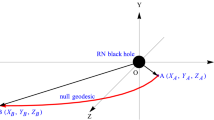
In order to find the time delay between the gravitational lensed images of the photons coupled to the regular phantom black hole via the Weyl tensor, we need the lens equation that tells the geometric relation among the observer, the source and the lens. It is also essential in calculating the lensing observables such as the positions and the brightness of the images. In the following parts of this work, we assume the source and the observer are in the asymptotically flat regions so that the lens equation adopted in this work is [28]

$$\begin{aligned} \tan {\mathcal {B}}=\tan \vartheta -\frac{{D}_{\mathrm {LS}}}{{D}_{\mathrm {OS}}}\left[ \tan \vartheta +\tan \left( \alpha -\vartheta \right) \right] \end{aligned}$$
(31)

where \({\mathcal {B}}\) and \(\vartheta \) respectively denote the angular separations between the source and the optical axis and between the lensed image and the optical axis, \({D}_{\mathrm {LS}}\) and \({D}_{\mathrm {OS}}\) are respectively the projected source-lens distance and source-observer distance, and \(\alpha \) is the deflection angle of the photon. This lens equation demands that the spacetime is asymptotically flat and both the source and the observer are far from the lens.

The exact deflection angle for a static and spherically symmetric metric (13) can be found as [27, 104]:

$$\begin{aligned} \alpha (r_0)=2\int _{r_0}^{\infty }\frac{\sqrt{B(r)}}{\sqrt{C(r)}\sqrt{\frac{A(r_0)C(r)}{A(r)C(r_0)}-1}}\mathrm {d}{r}-\pi , \end{aligned}$$
(32)

where \(r_0\) is the closest distance of the photon to the black hole. In the weak deflection lensing, \(r_0\) is much bigger than the gravitational radius of the black hole \(\sim m_{\bullet }\) so that the deflection angle will be much smaller than unity. In contrast, \(r_0\) is close to \(\sim m_{\bullet }\) in the strong deflection lensing, causing the deflection angle to explode.

While the positions and brightness of the lensed images are important observables in the gravitational lensing, the differential time delays among the images are also valuable observables if the source is emitting a time-variant signal [89]. The time span taken by a photon from the source to the observer is [89, 90, 104]

$$\begin{aligned} T_{\mathrm {tot}}=\int _{R_{\mathrm {src}}}^{R_{\mathrm {obs}}}\left| \frac{{\mathrm {d}}t}{{\mathrm {d}}r}\right| {\mathrm {d}}r =T(R_{\mathrm {obs}})+T(R_{\mathrm {src}}), \end{aligned}$$
(33)

where the function T(R) indicates the flight time for the photon traveling from \(r_0\) to R as

$$\begin{aligned} T(R)=\int _{r_0}^{R}\left| \frac{{\mathrm {d}}t}{{\mathrm {d}}r}\right| {\mathrm {d}}r, \end{aligned}$$
(34)

with

$$\begin{aligned} \left| \frac{{\mathrm {d}}t}{{\mathrm {d}}r}\right| =\frac{\sqrt{A(r_0)B(r)C(r)}}{\sqrt{A(r)}\sqrt{A(r_0)C(r)-A(r)C(r_0)}}. \end{aligned}$$
(35)

Here, \(R_{\mathrm {obs}}\) and \(R_{\mathrm {src}}\) are respectively the radial coordinates of the observer and the source as

$$\begin{aligned} R_{\mathrm {obs}}={D}_{\mathrm {OL}},\quad R_{\mathrm {src}}={({D}_{\mathrm {OL}}^2+{D}_{\mathrm {LS}}^2\tan ^2{\mathcal {B}})}^{1/2}, \end{aligned}$$
(36)

in which \({D}_{\mathrm {OL}}\) is the distance from the observer to the lens. The detailed investigation of the time delay in the weak and strong deflection gravitational lensing will be represented in the next two sections.

3 Time delay in weak deflection gravitational lensing

In the weak deflection gravitational lensing, both the closest distance of the photon to the regular phantom black hole \(r_0\) and its impact parameter

$$\begin{aligned} u^2=\frac{C(r_0)}{A(r_0){W(r_0)}^s} \end{aligned}$$
(37)

are much larger than the gravitational radius of the black hole \(\sim m_{\bullet }\), i.e., \(r_0\gg m_{\bullet }\) and \(u\gg m_{\bullet }\). The deflection angle, Eq. (32), can be expanded as a series in terms of either \(m_{\bullet }\, r_0^{-1}\) or \(m_{\bullet }\, u^{-1}\). Therefore, we can straightforwardly have

$$\begin{aligned} \alpha (r_0)= & {} 4(1-8{\bar{\alpha }}_0s)\frac{m_{\bullet }}{r_0}+\left[ \frac{\pi }{4} \left( k^2+15\right) \right. \nonumber \\&\left. -4-\frac{9}{2} \left( 15 \pi -32\right) {\bar{\alpha }}_0s\right] \frac{m_{\bullet }^2}{r_0^2} \nonumber \\&+ {\mathcal {O}}\left( \frac{m_{\bullet }^3}{r_0^3},{\bar{\alpha }}_0^2, k^4\right) , \end{aligned}$$
(38)

where

$$\begin{aligned} {\bar{\alpha }}_0 = \frac{{\hat{\alpha }}_{\bullet }}{r_0^2}. \end{aligned}$$
(39)

Hereafter, only the leading terms of \(\hat{\alpha }_{\bullet }\) and \(k^2\) are kept. It is clear [18, 105] that \(r_0\) depends on the choice of the coordinates while u is gauge-invariant. Based on the definition of the impact parameter, Eq. (37), we can find the Taylor expanded relation between them as

$$\begin{aligned} \frac{r_0}{u}= & {} 1-(1-12{\bar{\alpha }}s)\frac{m_{\bullet }}{u}-\left( \frac{3+k^2}{2}-36{\bar{\alpha }}s\right) \frac{m_{\bullet }^2}{u^2}\nonumber \\&+ {\mathcal {O}}\left( \frac{m_{\bullet }^3}{u^3},{\bar{\alpha }}^2, k^4\right) , \end{aligned}$$
(40)

in which

$$\begin{aligned} {\bar{\alpha }} = \frac{{\hat{\alpha }}_{\bullet }}{u^2}. \end{aligned}$$
(41)

After replacing \(r_0\) with u using Eq. (40), we obtain the deflection angle as

$$\begin{aligned} \begin{aligned} \alpha (u)&=4(1-8 {\bar{\alpha }} s)\frac{m_{\bullet }}{u}\\&\quad +\frac{1}{4} \pi (k^2+15-270 {\bar{\alpha }} s)\frac{m_{\bullet }^2}{u^2} \\&\quad + {\mathcal {O}}\left( \frac{m_{\bullet }^3}{u^3},{\bar{\alpha }}^2, k^4\right) . \end{aligned} \end{aligned}$$
(42)

When \({{\bar{\alpha }}}=0\) and \(k=0\), the deflection angle returns its value for the Schwarzschild black hole [18]. When \(k=0\), such a deflection angle reduces to the one for the photons coupled to the Weyl tensor in the Schwarzschild black hole [73]. Both the strength \({\bar{\alpha }}\) and the polarization s of the Weyl coupling affect the deflection angle starting from the first order, while the scalar hair k shows its influence from the second order, making the scalar hair more difficult to detect by the deflection angle in the weak deflection gravitational lensing. For current light bending experiments in the Solar System, it is still not possible to detect any effect beyond the leading term of the deflection angle \(\alpha (u)\). Based on available Solar System tests on the photons coupled to the Weyl tensor in the Schwarzschild spacetime which are not sensitive to \(k^2\), it was found [72] that \(|{\bar{\alpha }}_0s|\approx |{\bar{\alpha }}s|\lesssim 3.7\times 10^{-7}\), which is also valid for the Solar System tests on the photons coupled to the Weyl tensor in the spacetime (13) up to its leading term.

For later convenience, we use the angular Einstein ring radius

$$\begin{aligned} \vartheta _\mathrm {E}=\sqrt{\frac{4m_{\bullet }{D}_{\mathrm {LS}}}{{D}_{\mathrm {OS}}{D}_{\mathrm {OL}}}} \end{aligned}$$
(43)

to rescale the following quantities [18]

$$\begin{aligned} \beta =\frac{{\mathcal {B}}}{\vartheta _\mathrm {E}}\qquad \theta =\frac{\vartheta }{\vartheta _\mathrm {E}}\qquad \varepsilon =\frac{\vartheta _{\bullet }}{\vartheta _\mathrm {E}}, \end{aligned}$$
(44)

where \(\vartheta _{\bullet }=\arctan (m_{\bullet }/{D}_{\mathrm {OL}})\) and \(\varepsilon \) will serve as an small parameter.

Assuming that the position of the lensed image can be written into a series in terms of \(\varepsilon \) as

$$\begin{aligned} \theta =\theta _0 + \varepsilon \, \theta _1+{\mathcal {O}}({\varepsilon }^{2}), \end{aligned}$$
(45)

and making use of the lens equation (31) and the deflection angle (42), we can solve \(\theta \) order by order [18] and find that

$$\begin{aligned} \theta _0= & {} \frac{1}{2}\left( \sqrt{\beta ^2+4}+\beta \right) -\frac{8{\bar{\alpha }}s}{\sqrt{\beta ^2+4}} + {\mathcal {O}}({\bar{\alpha }}^2), \end{aligned}$$
(46)
$$\begin{aligned} \theta _1= & {} \frac{(k^2+15)\pi }{16(\theta _0^2+1)}-\frac{15\pi (5+9\theta _0^2)}{8(\theta _0^2+1)}{\bar{\alpha }}s + {\mathcal {O}}({\bar{\alpha }}^2,k^4). \end{aligned}$$
(47)

When \({{\bar{\alpha }}}_\bullet =0\) and \(k=0\), \(\theta _0\) and \(\theta _1\) go back to their values for the Schwarzschild black hole [18]. When \(k=0\), they recover those for the photons coupled to the Weyl tensor in the Schwarzschild black hole [73]. In this work, a positive \(\beta \) corresponds to the case that the lensed image is located on the same side of the lens as the source with the position \(\theta ^+=\theta (|\beta |)\), and a negative \(\beta \) corresponds to the image on the opposite side with the position \(\theta ^-=\theta (-|\beta |)\). As a result, the positions of the images \(\theta ^{\pm }\) remain positive for any given \(\beta \) based on the facts that

$$\begin{aligned} \theta _0^{\pm }= & {} \frac{1}{2}\left( \sqrt{|\beta |^2+4} \pm |\beta | \right) -\frac{8{\bar{\alpha }}s}{\sqrt{|\beta |^2+4}} + {\mathcal {O}}({\bar{\alpha }}^2), \end{aligned}$$
(48)
$$\begin{aligned} \theta _1^{\pm }= & {} \frac{(k^2+15)\pi }{32\sqrt{|\beta |^2+4}} \left( \sqrt{|\beta |^2+4} \mp |\beta |\right) \nonumber \\&-\frac{15\pi {\bar{\alpha }}s}{8(|\beta |^2+4)^2}(7 |\beta |^4 \pm 2 |\beta |^3 \sqrt{|\beta |^2+4} +52|\beta |^2 \nonumber \\&\pm 12 |\beta | \sqrt{|\beta |^2+4} +96 ) + {\mathcal {O}}({\bar{\alpha }}^2,k^4). \end{aligned}$$
(49)

Defining \(h=m_{\bullet } r_{0}^{-1}\), we can Taylor expand the flight time of the photons coupled to the Weyl tensor in the regular phantom black hole T(R), see Eq. (34), and obtain that [18]

$$\begin{aligned} T(R)=T_0(R)+h T_1(R)+ h^2 T_2(r)+{\mathcal {O}}(h^3,{\bar{\alpha }}^2, k^4), \end{aligned}$$
(50)

where

$$\begin{aligned} T_0(R)= & {} \sqrt{R^2-r_0^2}, \end{aligned}$$
(51)
$$\begin{aligned} \frac{T_1(R)}{r_0}= & {} \sqrt{\frac{1-\xi }{1+\xi }} [1-12 {\bar{\alpha }}_0 s (\xi +2)]\nonumber \\&-2 \log \left( \frac{1-\sqrt{1-\xi ^2}}{\xi }\right) ,\end{aligned}$$
(52)
$$\begin{aligned} \frac{T_2(R)}{r_0}= & {} 15\arcsin \sqrt{\frac{1-\xi }{2}} -\frac{5\xi +4}{2}\sqrt{\frac{1-\xi }{{(1+\xi )}^3}}\nonumber \\&+k^2\arcsin \sqrt{\frac{1-\xi }{2}}\nonumber \\&-6{\bar{\alpha }}_0 s\left[ {30}\arcsin \sqrt{\frac{1-\xi }{2}}\right. \nonumber \\&\left. +\sqrt{\frac{1-\xi }{{(1+\xi )}^3}}\left( 3\xi ^3+4\xi ^2-13\xi -12\right) \right] , \end{aligned}$$
(53)

with

$$\begin{aligned} \xi =r_{0}/R. \end{aligned}$$
(54)

When \({{\bar{\alpha }}}=0\) and \(k=0\), \(T_{1,2}(R)\) return to their values for the Schwarzschild black hole [18]. When \(k=0\), they recover those for the photons coupled to the Schwarzschild black hole via the Weyl tensor [73]. The first- and second-order terms are affected by the Weyl coupling while the scalar hair only changes \(T_2(R)\) . The time delay \(\tau \) in the weak deflection gravitational lensing is the difference between the travelling time of the photon with and without the influence of the regular phantom black hole as

$$\begin{aligned} \tau =T(R_{\mathrm {obs}})+T(R_{\mathrm {src}})-\frac{{D}_{\mathrm {OS}}}{\cos {{\mathcal {B}}}}. \end{aligned}$$
(55)

After scaling the time delay as

$$\begin{aligned} \hat{\tau }=\frac{\tau }{\tau _{E}} \end{aligned}$$
(56)

with

$$\begin{aligned} \tau _{E}=4m_{\bullet } \end{aligned}$$
(57)

we can expand it into a Taylor series according to \(\varepsilon \) as

$$\begin{aligned} \hat{\tau }=\hat{\tau }_0+\varepsilon \hat{\tau }_1+{\mathcal {O}}(\varepsilon ^2). \end{aligned}$$
(58)

Substituting the distances \(R_{\mathrm {obs}}\) and \(R_{\mathrm {src}}\) of Eq. (36) into Eq. (50) and replacing \(r_0\) with u by Eq. (40), we obtain that

$$\begin{aligned} \hat{\tau }_0= & {} \frac{1}{2}\left[ 1+\beta ^2-\theta _0^2-\log \left( \frac{{D}_{\mathrm {OL}}\vartheta _\mathrm {E}^2\theta _0^2}{4{D}_{\mathrm {LS}}}\right) \right] \nonumber \\&-12{\bar{\alpha }}s + {\mathcal {O}}({\bar{\alpha }}^2), \end{aligned}$$
(59)
$$\begin{aligned} \hat{\tau }_1= & {} \frac{(15+k^2)\pi }{16\theta _0}-\frac{15(7+3\theta _0^2){\bar{\alpha }}s\pi }{8\theta _0(\theta _0^2+1)} + {\mathcal {O}}({\bar{\alpha }}^2,k^4), \end{aligned}$$
(60)

where we used the following relation

$$\begin{aligned} u={D}_{\mathrm {OL}}\sin \vartheta . \end{aligned}$$
(61)

When \({{\bar{\alpha }}}=0\) and \(k=0\), \(\hat{\tau }_0\) and \(\hat{\tau }_1\) recover their values for the Schwarzschild black hole [18]. When \(k=0\), they return to those for the photons coupled to the Schwarzschild black hole via the Weyl tensor [73]. Like the cases of the deflection angle and the positions of the images, \({{\bar{\alpha }}}\) and s appear in the leading- and next-to-leading-order terms of the time delay, while k only shows its effects starting from the next-to-leading-order term.

In the weak deflection gravitational lensing, two images with positive- and negative-parity are produced on each side of the optical axis. The scaled differential time delay between these two images is defined as

$$\begin{aligned} {\varDelta }\hat{\tau }=\hat{\tau }_{-}-\hat{\tau }_{+} \end{aligned}$$
(62)

in which \(\hat{\tau }_{-} = \hat{\tau }(-|\beta |)\) and \(\hat{\tau }_{+}=\hat{\tau }(|\beta |)\), and the time delay with the unit of time can be restored by

$$\begin{aligned} {\varDelta }{\tau }= \tau _{E}\, {\varDelta }\hat{\tau }. \end{aligned}$$
(63)

It can be expanded into a series in terms of \(\varepsilon \) as

$$\begin{aligned} {\varDelta }\hat{\tau }={\varDelta }\hat{\tau }_0+\varepsilon {\varDelta }\hat{\tau }_1+{\mathcal {O}}(\varepsilon ^2), \end{aligned}$$
(64)

where, with the help of Eqs. (48) and (49), we can have

$$\begin{aligned} {\varDelta }\hat{\tau }_0= & {} \frac{1}{2} |\beta | \sqrt{|\beta |^2+4}+\log \left( \frac{\sqrt{|\beta | ^2+4}+|\beta | }{\sqrt{|\beta | ^2+4}-|\beta |}\right) , \end{aligned}$$
(65)
$$\begin{aligned} {\varDelta }\hat{\tau }_1= & {} \frac{1}{16} \pi |\beta | \left( k^2+15-90 {\bar{\alpha }} s\right) + {\mathcal {O}}({\bar{\alpha }}^2). \end{aligned}$$
(66)

We find that the leading term of the differential time delay between the images \({\varDelta }\hat{\tau }_0\) is immune to both the Weyl coupling and the scalar hair, making the first-order term \({\varDelta }\hat{\tau }_1\) critical for searching the new behavior in the time delay. When \({{\bar{\alpha }}}=0\) and \(k=0\), \({\varDelta }\hat{\tau }_1\) has its value for the Schwarzschild black hole [18]. When \(k=0\), it returns to the one for the photons coupled to the Schwarzschild black hole via the Weyl tensor [73]. Although \(k^2\) and \({\bar{\alpha }}s\) are linearly combined in \( {\varDelta }\hat{\tau }_1\), \(k^2\) dominates due to \(|{\bar{\alpha }}s|\ll 1\) [72].

In order to demonstrate the influence of the background spacetime, we compare the time delays of the photons having the polarizations of PPL and PPM in the regular phantom black hole with those in the Schwarzschild black hole by the indicators as

$$\begin{aligned} \delta {\varDelta }\tau ^{\mathrm {PPL}}= & {} {\varDelta }\tau ^{\mathrm {PPL}}-{\varDelta }\tau ^{\mathrm {Sch}}, \end{aligned}$$
(67)
$$\begin{aligned} \delta {\varDelta }\tau ^{\mathrm {PPM}}= & {} {\varDelta }\tau ^{\mathrm {PPM}}-{\varDelta }\tau ^{\mathrm {Sch}}, \end{aligned}$$
(68)

where

$$\begin{aligned} {\varDelta }\tau ^{\mathrm {PPL}}= & {} {\varDelta }\tau |_{s=1}, \end{aligned}$$
(69)
$$\begin{aligned} {\varDelta }\tau ^{\mathrm {PPM}}= & {} {\varDelta }\tau |_{s=-1}, \end{aligned}$$
(70)
$$\begin{aligned} {\varDelta }\tau ^{\mathrm {Sch}}= & {} {\varDelta }\tau |_{k=\rho =0}. \end{aligned}$$
(71)

Meanwhile, for manifesting the effect of the polarizations on the time delay, we define

$$\begin{aligned} \delta {\varDelta }\tau ={\varDelta }\tau ^{\mathrm {PPL}}-{\varDelta }\tau ^{\mathrm {PPM}} = \delta {\varDelta }\tau ^{\mathrm {PPL}} - \delta {\varDelta }\tau ^{\mathrm {PPM}}. \end{aligned}$$
(72)

Since the supermassive black hole in the Galactic Center, Sgr A*, with the mass of \(m_{\bullet }=4.28\times 10^{6}\) \(M_{\odot }\) and distance \({D}_{\mathrm {OL}}=8.32\) kpc [106], is the only black hole that we can directly observe stars around it for now, we take it as the lens and investigate the time delay between the images of a stellar source with the distance \({D}_{\mathrm {LS}}=10^{-3}\) pc and the angular position \(\beta =0.5\) in the weak deflection gravitational lensing. From top to bottom, Fig. 2 shows \(\delta {\varDelta }\tau ^{\mathrm {PPL}}\), \(\delta {\varDelta }\tau ^{\mathrm {PPM}}\) and \(\delta {\varDelta }\tau \) on the domain \({\mathcal {D}}\) of the coupling strength \(\rho \) and the scalar hair k, see Eq. (21). As a comparison, the differential time delay for the Schwarzschild black hole is \({\varDelta }\tau ^{\mathrm {Sch}}=21.52\) s. Based on Fig. 2a, b, we find that \(\delta {\varDelta }\tau ^{\mathrm {PPL}}\) and \(\delta {\varDelta }\tau ^{\mathrm {PPM}}\) have almost the same pattern, hardly to tell their difference, which is due to the facts that both of them strongly depend on the scalar hair k and are barely affected by the coupling strength \({\bar{\alpha }}s\) as \(k^2\sim 1 \gg |{\bar{\alpha }}s|\). When \(k=1\), \(\delta {\varDelta }\tau ^{\mathrm {PPL}}\) and \(\delta {\varDelta }\tau ^{\mathrm {PPL}}\) reach their biggest values of about 15 ms, whereas these most significant deviations are still much smaller than the differential time delay for the Schwarzschild black hole itself and are much shorter than the time span of an astronomical observation session, making them inaccessible. Figure 2c shows the variation of \(\delta {\varDelta }\tau \) on the domain \({\mathcal {D}}\). Although the difference between the time delays with the polarizations of PPL and PPM becomes distinct with the increment of \(|\rho |\) and k, it never exceeds the level of 1 ms, rendering it even harder to detect. When \(k=0\), \(\delta {\varDelta }\tau \) returns to the one for the photons coupled to the Weyl tensor in the Schwarzschild black hole, ranging from -0.04 to 0.08 ms, which is consistent with the results of Ref. [73]. It suggests that the existence of the scalar hair can enhance the difference between the time delays of PPL and PPM by at least a factor of 10. In a summary, the scalar hair k affects the time delays of the photons coupled to the Weyl tensor in the regular phantom black hole with the polarizations of PPL and PPM more significantly than the coupling strength \(\rho \) does, while neither the effects of the scalar hair nor those of the polarizations in the weak deflection gravitational lensing can be detected with current technology.

Fig. 2
figure 2

From top to bottom, \(\delta {\varDelta }\tau ^{\mathrm {PPL}}\), \(\delta {\varDelta }\tau ^{\mathrm {PPM}}\) and \(\delta {\varDelta }\tau \) in the weak deflection gravitational lensing are respectively shown on the domain \({\mathcal {D}}\) for the time delay of the photons coupled to Weyl tensor in the regular phantom black hole. The supermassive black hole in the Galactic Center, Sgr A*, is taken as the lens. We assume a stellar source with the distance \({D}_{\mathrm {LS}}=10^{-3}\) pc to the lens and the angular position \(\beta =0.5\)

Full size image

4 Time delay in strong deflection gravitational lensing

In the strong deflection gravitational lensing, a photon passes by the vicinity of a black hole, making its deflection angle become much larger than 1. This means the photon might wind several loops around the black hole, generating a set of relativistic images. It is a unique feature that never appears in the weak deflection gravitational lensing. We consider that the source, the lens and the observer are nearly aligned collinearly so that the lens equation (31) can be reduced as [107]

$$\begin{aligned} {\mathcal {B}}=\vartheta -\frac{{D}_{\mathrm {LS}}}{{D}_{\mathrm {OS}}}{\varDelta }\alpha \end{aligned}$$
(73)

where \({\varDelta }\alpha =\alpha -2n\pi \) is the offset of the deflection angle \(\alpha \) from \(2n\pi \) and n is the number of loops that the photon winds the black hole.

In order to find the flight time taken by the photon from the source to the observer, we can split \(|\mathrm {d}{t}/\mathrm {d}{r}|\) into the two parts [89]

$$\begin{aligned} \left| \frac{{\mathrm {d}}t}{{\mathrm {d}}r}\right| =P(r,r_{0})F(r,r_{0}), \end{aligned}$$
(74)

where

$$\begin{aligned} P(r,r_{0})= & {} \frac{\sqrt{A_{0}}}{A(r)}, \end{aligned}$$
(75)
$$\begin{aligned} F(r,r_{0})= & {} \frac{\sqrt{C(r)}}{\sqrt{A_{0}C(r)-A(r)C_{0}}}. \end{aligned}$$
(76)

Hereafter, a subscript 0 stands for valuation of a quantity at \(r=r_{0}\). If the closest approaches of two photons are denoted respectively by \(r_{0,1}\) and \(r_{0,2}\), the time delay between these two photons can be written as [89]

$$\begin{aligned} T_{1}-T_{2}={\tilde{T}}(r_{0,1})-{\tilde{T}}(r_{0,2})+2\int _{r_{0,1}}^{r_{0,2}} \frac{P(r,r_{0,1})}{\sqrt{A_{0,1}}}\mathrm {d}{r}, \end{aligned}$$
(77)

where

$$\begin{aligned} {\tilde{T}}(r_0)= & {} \int _{0}^{1}{\tilde{R}}(z,r_{0})F(z,r_{0})\mathrm {d}{z}, \end{aligned}$$
(78)
$$\begin{aligned} {\tilde{R}}(z,r_{0})= & {} 2\frac{1-A_{0}}{A^{\prime }(z)}\frac{\sqrt{A_{0}}}{A(z)} \left[ 1-\frac{1}{\sqrt{A_{0}}F(z,r_{0})}\right] , \end{aligned}$$
(79)

with the variable

$$\begin{aligned} z=\frac{A(r)-A_{0}}{1-A_{0}}. \end{aligned}$$
(80)

The photons can reach the extreme vicinity of the black hole in the strong deflection gravitational lensing, resulting in \(r_{0,1}\sim r_{0,2} \sim r_m\). Thus the integrand in the last term of Eq. (77) can be approximated as \([A(r_m)]^{-1}\). The function \({\tilde{T}}(r_0)\) can be worked out by the method of the strong deflection limit as [89]

$$\begin{aligned} {\tilde{T}}(u)= & {} -{\tilde{a}}\log \left( \frac{u}{u_{m}}-1\right) +{\tilde{b}}\nonumber \\&+{\mathcal {O}}\left[ (u-u_{m})\log (u-u_m)\right] , \end{aligned}$$
(81)

where u is the impact parameter, see Eq. (37), and the coefficients \({\tilde{a}}\) and \({\tilde{b}}\) are

$$\begin{aligned} {\tilde{a}}= & {} u_m \sqrt{\frac{2}{A_{m}C_{m}^{\prime \prime }-A_{m}^{\prime \prime }C_{m}}}, \end{aligned}$$
(82)
$$\begin{aligned} {\tilde{b}}= & {} -\pi +{\tilde{a}}\log \bigg [\frac{C_{m}{(1-A_{m})}^{2}\left( A_{m}C_{m}^{\prime \prime }-C_{m}A_{m}^{\prime \prime }\right) }{A_{m}^{3}C_{m}^{\prime {2}}} \bigg ] \nonumber \\&+\int _{0}^{1}\left[ {\tilde{R}}(z,r_{m})F(z,r_{m})-\frac{2{\tilde{a}}}{z} \right] \mathrm {d}{z}. \end{aligned}$$
(83)

Here, a subscript m denotes the value of a quantity at \(r=r_{m}\). Figure 3 shows the impact parameter at the photon sphere \(u_m\) against \(\rho \) and k for the polarizations of PPL and PPM. It varies distinctly along both \(\rho \) and k directions unless either \(\rho \sim 1\) for PPL or \(\rho \sim -2\) for PPM. We find that \(u_m\) can reach \(\sim 6\, m_{\bullet }\), about 2 times bigger than the one for the Schwarzschild black hole that is \(u_m=(3\sqrt{3}/2)\, m_{\bullet }\) when \(\rho =0\) and \(k=0\).

Fig. 3
figure 3

The impact parameter at the photon sphere \(u_m\) on the domain \({\mathcal {D}}\) for the photons coupled to the Weyl tensor in the regular phantom black hole with the polarizations of PPL and PPM are respectively shown in the a and b

Full size image

We can find the time delay between the two relativistic images respectively winding n and m loops \((n>m)\) of the photons coupled to the Weyl tensor in the regular phantom black hole as [89]

$$\begin{aligned} {\varDelta }{T}_{n,m}={\varDelta }{T}_{n,m}^{0}+{\varDelta }{T}_{n,m}^{1}, \end{aligned}$$
(84)

where

$$\begin{aligned} {\varDelta }{T}_{n,m}^{0}= & {} 2\pi (n-m)u_{m}, \end{aligned}$$
(85)
$$\begin{aligned} {\varDelta }{T}_{n,m}^{1}= & {} 2\sqrt{2}{\bar{a}}\exp \left( \frac{{\bar{b}}}{2{\bar{a}}}\right) u_{m}\nonumber \\&\times \left[ \exp \left( -\frac{m\pi }{{\bar{a}}}\right) -\exp \left( -\frac{n\pi }{{\bar{a}}}\right) \right] , \end{aligned}$$
(86)

with

$$\begin{aligned} {\bar{a}}= & {} \frac{{\tilde{a}}}{u_m}, \end{aligned}$$
(87)
$$\begin{aligned} {\bar{b}}= & {} -\pi + {\bar{a}}\log \left[ \frac{{(1-A_{m})}^{2}}{A_{m}^{\prime 2}}\left( \frac{C_{m}^{\prime \prime }}{C_{m}}-\frac{A_{m}^{\prime \prime }}{A_{m}}\right) \right] \nonumber \\&+ 2\int _{0}^{1}\left[ \frac{u_m(1-A_{m})}{A^{\prime }(z)\sqrt{C(z)}\sqrt{C(z)-A(z) u_m^2}}-\frac{{\bar{a}}}{z}\right] \mathrm {d}{z}. \end{aligned}$$
(88)

We call \({\varDelta }{T}_{n,m}^{0}\) the perimeter term because it is proportional to the circumference of a circle with the radius of \(u_m\) and call \({\varDelta }{T}_{n,m}^{1}\) the exponential term due to its mathematical form. For the time delay in the strong deflection gravitational lensing of the Schwarzschild black hole, the exponential term is much less the perimeter term [89]. In order to study the contribution of the exponential term \({\varDelta }{T}_{n,m}^{1}\) in the overall time delay \({\varDelta }{T}_{n,m}\), we introduce the indicator \(\eta _{n,m}\) to denote the logarithmic ratio of them as

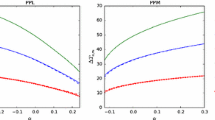
$$\begin{aligned} \eta _{n,m} = \log _{10}\left( \frac{{\varDelta }{T}_{n,m}^{1}}{{\varDelta }{T}_{n,m}}\right) . \end{aligned}$$
(89)

Taking the supermassive black holes respectively at the Galactic center, Sgr A*, and in the center of the galaxy M87, M87*, as the lenses, we investigate the time delays between their relativistic images of the photons coupled to the Weyl tensor in the regular phantom black hole. We assume that Sgr A* has a mass of \(m_{\bullet ,\mathrm {SgrA*}} = 4.28 \times 10^{6}\,M_{\odot }\) [106] and M87* has a mass of \(m_{\bullet , \mathrm {87*}}=6.5\times 10^{9}\,M_{\odot }\) [7]. In order to indicate the deviations of the time delay between the first and second relativistic images with the polarizations of PPL and PPM from the one of the Schwarzschild black hole, we define

$$\begin{aligned} \delta {\varDelta }{T}_{2,1}^{\mathrm {PPL}}={\varDelta }{T}_{2,1}|_{s=1}-{\varDelta }{T}_{2,1}^{\mathrm {Sch}}, \end{aligned}$$
(90)

and

$$\begin{aligned} \delta {\varDelta }{T}_{2,1}^{\mathrm {PPM}}={\varDelta }{T}_{2,1}|_{s=-1}-{\varDelta }{T}_{2,1}^{\mathrm {Sch}}. \end{aligned}$$
(91)

For comparing the effect of the polarizations on the time delay, we also define

$$\begin{aligned} \delta {\varDelta }{T}_{2,1}={\varDelta }{T}_{2,1}|_{s=1}-{\varDelta }{T}_{2,1}|_{s=-1}, \end{aligned}$$
(92)

and \(\eta _{2,1}\) for each polarizations as

$$\begin{aligned} \eta _{2,1}^{\mathrm {PPL}}= & {} \eta _{2,1}|_{s=1}, \end{aligned}$$
(93)
$$\begin{aligned} \eta _{2,1}^{\mathrm {PPM}}= & {} \eta _{2,1}|_{s=-1}. \end{aligned}$$
(94)
Fig. 4
figure 4

From top to bottom, \(\delta {\varDelta }{T}_{2,1}^{\mathrm {PPL}}\), \(\delta {\varDelta }{T}_{2,1}^{\mathrm {PPM}}\) and \(\delta {\varDelta }{T}_{2,1}\) on the domain \({\mathcal {D}}\) are shown for Sgr A* and M87*. Since the time delays have the same pattern but with different ranges, we use one color bar with two specific scales and units for these black holes: minutes for Sgr A* and days for M87*

Full size image

Figure 4 shows \(\delta {\varDelta }{T}_{2,1}^{\mathrm {PPL}}\), \(\delta {\varDelta }{T}_{2,1}^{\mathrm {PPM}}\) and \(\delta {\varDelta }{T}_{2,1}\). Since the time delays caused by Sgr A* and M87* have the same pattern but with different ranges, we use one color bar with two specific scales and units for these two black holes: minutes for Sgr A* and days for M87* due to their masses. We find that \(\delta {\varDelta }{T}_{2,1}^{\mathrm {PPL}}\) and \(\delta {\varDelta }{T}_{2,1}^{\mathrm {PPM}}\) range from \(\sim -10\) to \(\sim 15\) min for Sgr A* and change from \(\sim -10\) to \(\sim 15\) day for M87*, strongly depending on the strength of coupling \(\rho \) and the scalar hair k, see Fig. 4a, b. For a comparison, the time delay between the first and second relativistic images of the Schwarzschild black hole is \({\varDelta }{T}_{2,1}^{\mathrm {Sch}}= 11.6\) min for Sgr A* and \({\varDelta }{T}_{2,1}^{\mathrm {Sch}}= 12.3\) day for M87*. As \(k\approx 1\), the deviations \(\delta {\varDelta }{T}_{2,1}^{\mathrm {PPL}}\) and \(\delta {\varDelta }{T}_{2,1}^{\mathrm {PPM}}\) have their most significant difference from the one of the Schwarzschild black hole, which is helpful for detection. Figure 4c shows that the differential time delay between PPL and PPM \(\delta {\varDelta }{T}_{2,1}\) increases with k and \(|\rho |\). When the coupling of the photons to the Weyl tensor vanishes, i.e, \(\rho =0\), \(\delta {\varDelta }{T}_{2,1}=0\). For a positive \(\rho \), the time delay with the polarization of PPL is smaller than the one with PPM; for a negative \(\rho \), it becomes larger. When \(k=1\), \(\delta {\varDelta }{T}_{2,1}\) becomes most evidently, ranging from \(-24\) to 28 min for Sgr A* and changing from \(-26\) to 29 day for M87*. When \(k=0\), \({\varDelta }{T}_{2,1}\) reduces to the photons coupled to the Weyl tensor in the Schwarzschild black hole. It ranges from \(-6\) to 9 min for Sgr A* and changes from about -6 to 10 day for M87*, which are consistent with those of Ref.  [76]. Figure 5 displays the ratio of the exponential term to the total time delay with the polarizations of PPL and PPM \(\eta _{2,1}^{\mathrm {PPL}}\) and \(\eta _{2,1}^{\mathrm {PPM}}\). We find that \(\eta _{2,1}^{\mathrm {PPL}}\) grows with the increment of \(\rho \) while \(\eta _{2,1}^{\mathrm {PPM}}\) decreases with that, and both of them are insensitive to k. \(\eta _{2,1}^{\mathrm {PPL}}\) can reach about \(-0.21\) as \(\rho \approx 1\) and \(\eta _{2,1}^{\mathrm {PPM}}\) can arrive about \(-0.17\) as \(\rho \approx -2\). For a reference, \(\eta _{2,1}\) is about \(-1.82\) for the Schwarzschild black hole. It suggests that the exponential term of the time delay for the Schwarzschild black hole is less than the first term by about two orders of magnitude, hardly to detect, whereas the exponential one of the time delay for the photons coupled to the Weyl tensor in the regular phantom black hole might be bigger than the perimeter term and augment to \(\sim 60\%\) of the total delay, easier to measure and distinguish. This also means that these time delay signals could be dramatically different from those of the Schwarzschild black hole. The time delays caused by Sgr A* are shorter than the time span of a typical observational session, while those caused by M87* is theoretically accessible. However, the angular resolution for separating the relativistic images of the photons coupled to the Weyl tensor in the regular phantom black hole is demanded to be at least \(\sim 0.1\) \(\mu \) as [88], making these signals undetectable with current technology.

Fig. 5
figure 5

The logarithmic ratio of the correction term to the whole time delay for the polarizations of PPL and PPM \(\eta _{2,1}^{\mathrm {PPL}}\) (top) and \(\eta _{2,1}^{\mathrm {PPM}}\) (bottom) on the domain \({\mathcal {D}}\) are shown

Full size image

In summary, the time delay in the strong deflection gravitational lensing significantly depends on the strength of coupling \(\rho \), the scalar hair k and the polarizations of PPL and PPM, while such a delay barely can be measured in the near future. In contrast, the time delay in the weak deflection gravitational lensingsensitively relies on k and is insensitive to \(\rho \). Therefore, in order to fully understand and distinguish the coupling between the photons and the regular phantom black hole via the Weyl tensor, it is necessary to measure the time delays in the weak and strong deflection gravitational lensing.

5 Conclusions and discussion

We investigate the time delay in the weak and strong deflection gravitational lensing of the photons coupled to the Weyl tensor in the regular phantom black hole. We obtain a neat and transformed domain of the scalar hair and the strength of the coupling, which is absent in the previous work. For the weak deflection gravitational lensing, we find the positions of the primary and secondary images and the differential time delay between them, up to the next-to-leading order. For the strong deflection gravitational lensing, we work out the time delay between the first and second relativistic images, made up of a perimeter and an exponential term.

By assuming the supermassive black hole Sgr A* as the lens, we find that the time delay in the weak deflection gravitational lensing of its surrounding star strongly depends on the scalar hair but is insensitive to the strength of the coupling. The deviation of the time delay from the one for the Schwarzschild black hole is no more than 0.015 s and the difference between the photons with the polarizations of PPL and PPM can never exceed one millisecond. By taking Sgr A* and M87* as lenses, we find that the time delay between the first and second relativistic images in the strong deflection gravitational lensing is significantly affected by both the scalar hair and the strength of the coupling. It can reach about 28 minutes for Sgr A* and about 25 days for M87*. In the total time delay, the exponential term might grow to be bigger than the perimeter term, which never happens in the case of the Schwarzschild black hole. Once the time delay in the weak deflection gravitational lensing had been observed, it may determine the scalar hair which controls the scale of the potential of the phantom field as dark energy since it is immune to the Weyl coupling. Meanwhile, once the time delay in the strong deflection gravitational lensing had been observed only, it would be difficult to obtain a clean bound on the scalar hair, since both the scalar hair and the strength of the Weyl coupling contribute to the time delay. Therefore, we suggest that it is necessary to measure the time delay in both weak and strong deflection gravitational lensing of photons coupled to the Weyl tensor in the regular phantom black hole for fully understanding and distinguishing such an interaction between the gravitational and electromagnetic fields.

Nevertheless, the time delay in the weak deflection gravitational lensing is shorter than the time span of a typical observational session, making it undetectable for now. The angular resolution to separate the first and second relativistic images in the strong deflection gravitational lensing is also beyond the current technology, render measuring the time delay between them impossible in the near future.