Abstract
When the different wavelengths of the scalar and tensor modes of the geometry are all assigned on the same space-like hypersurface the maximally amplified frequencies of the spectrum remain smaller than the Planck mass only if the duration of a stage of accelerated expansion and the corresponding tensor to scalar ratio are severely constrained. All the different wavelengths can be initialized on the same space-like hypersurface at the onset of inflation but this strategy and the related conclusions are plausible only for classical inhomogeneities. We argue that a whole class of potential constraints is easily evaded provided the different wavelengths of the quantum fields are assigned as soon as they cross the corresponding Planckian hypersurfaces. In this case the Cauchy data for the mode functions depend on the wavenumber so that larger wavelengths start evolving earlier while shorter wavelengths are assigned later. Within this strategy the duration of a conventional inflationary phase and the corresponding tensor to scalar ratio are not constrained but the large-scale power spectra inherit specific large-scale corrections that remain however unobservable. We also address the problem of the bouncing dynamics and show that similar constraints do no not appear at the beginning of the bouncing phase but rather towards its end.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Already after the discovery of black hole evaporation [1, 2] it was noted that the frequencies of massless species along the paths emerging from the past null infinity and heading towards \({{\mathscr {I}}}^{+}\) can experience arbitrarily large redshifts as the particles pass through the collapsing dust cloud prior to the formation of the event horizon. The range of frequencies that can be seen by distant observers at late times would have had to originate at \({{\mathscr {I}}}^{-}\) with ultrahigh frequencies including frequencies above the Planck scale. Local Lorentz invariance would be violated if such frequencies were arbitrarily cut-off. Many questions have been raised through the years concerning the survival of Hawking radiation in the case of a breaking of local Lorentz-invariance (see e.g. [3,4,5,6,7]). With the purpose of investigating the stability of the process of black hole evaporation the dispersion relations have been purposely modified above a (nearly Planckian) energy scale. Different physical approaches led independently to the conclusion that the thermal emission is likely not to be destroyed by quantum gravitational effect even if the tools employed to deduce the black hole evaporation may not be valid for arbitrarily small wavelengths [4, 5, 7].
The very same objection raised in the case of Hawking radiation has been subsequently brought up in the discussion of the inflationary power spectra since arbitrarily small wavelengths may appear when a phase of accelerated expansion is about to start [8,9,10,11,12,13,14,15,16,17]. All along the past two decades these effects have been analyzed [18,19,20,21,22,23] and there is consensus that physical frequencies larger than a certain reference energy (be it for instance the Planck or string mass) could mildly modify the scalar and tensor power spectra at large scales. However these modifications have not been observed in spite of the repeated observational scrutiny [22,23,24] so that it is fair to say (as in the case of black hole evaporation) that the discussion of the scalar and tensor power spectra is not crucially affected by the wavelengths shorter than the Planck length even if the tools used for the actual derivation could well be invalid for arbitrarily short wavelengths. In spite of the latter conclusion it has been recently suggested [25, 26] (see also [27, 28]) that frequencies above the Planck energy scale forbid, in practice, any sufficiently long conventional stage of inflationary expansion and imply anyway severe bounds on the tensor to scalar ratio (e.g. \(r_{T} < {{\mathcal {O}}}(10^{-30})\)). According to this further reprise of the original theme, if relic gravitons will ever be observed through a suitable B-mode polarization [29] they will not come from conventional inflationary scenarios since the techniques used to derive the scalar and tensor power spectra are not consistent.
To spell out more clearly the terms of the problem it is useful to remind that in a conformally flat background of Friedmann–Robertson–Walker type the physical (i.e. \(\lambda _{\mathrm {ph}}\)) and the comoving (i.e. \(\lambda \)) wavelengths of the scalar and tensor modes of the geometry are notoriously related as \(\lambda _{\mathrm {ph}}(\lambda , \tau ) = \lambda \, a(\tau )\), where \(a(\tau )\) is the scale factor and \(\tau \) is the conformal time coordinate. As \(\tau \rightarrow - \infty \) there are two extreme physical possibilities:
where the overdot denotes a derivation with respect to the cosmic time coordinate t which is related to \(\tau \) as \(a(\tau ) \, d\tau = d\,t\). In the context of conventional inflationary scenarios the limit (1) applies since the background is characterized by a phase of accelerated expansion (i.e. \({\dot{a}} > 0\) and \(\ddot{a} > 0\)) with mildly decreasing curvature. As an example, for a power-law inflationary expansion [i.e. \(a(t) \sim (t/t_{1})^{\alpha }\) with \(\alpha > 1\) and \(t > t_{1}\)] we have \(a(\tau ) \sim (- \tau /\tau _{1})^{-\beta }\) with \(\beta = \alpha /(\alpha -1)\) so that the condition (1) is verified. Similarly in the instance of a power-law contraction \(a(t) \sim (- t/t_{1})^{\gamma }\) (with \(0<\gamma <1\) and \(t < - t_{1}\)) the limit of Eq. (2) easily follows. The evolution equations for the scalar and tensor modes of the geometry cannot be valid for arbitrarily short wavelengths as it seems instead implied by Eq. (1): this is the same kind of aporia appearing in the context of Hawking radiation [3,4,5,6,7].
In the context of the conventional inflationary models the limit \(\tau \rightarrow -\infty \) should be handled with some care since an ever expanding inflationary evolution is not past geodesically complete [30]. With this caveat, in terms of the physical frequencies the two limits of Eqs. (1) and (2) are interchanged:
where we used the notation \(\omega (k, \tau ) = k/a(\tau )\) together with \(k = 2\pi /\lambda \). Thus the physical frequencies may become easily super-Planckian (or trans-Planckian as some like to say) in the case of conventional inflationary models and sub-Planckian for bouncing scenarios based on a stage of accelerated contraction. All in all the same class of problems originally pointed out in the context of black hole evaporation arise in conventional inflationary scenarios but, apparently, not in the case of bouncing scenarios, at least in the limit \(\tau \rightarrow - \infty \) [25, 26]. To be fair bouncing models are not totally immune from these potential issues as sometimes affirmed. In fact Eqs. (1) and (2) should probably be complemented by two supplementary limits:
Equation (5) suggests that the physical wavelengths are naturally larger than the Planck (or string) length-scale close to the end of the accelerated expansion (i.e. for \(\tau \rightarrow 0^{-}\)). Equation (6) implies instead that the physical wavelengths may well get shorter than the Planck (or string) length-scale close to the end of a phase of accelerated contraction: since \(a(\tau )\) shrinks for \(\tau \rightarrow 0^{-}\) the wavelengths can easily become sub-Planckian as the bouncing stage develops. While in the case of inflationary dynamics the trans-Planckian problem arise at the onset of the inflationary evolution (as discussed in Eqs. (1) and (2)), the same kind of ambiguity may also arise at the end of a bouncing stage. This observation is relevant since there are some claiming that the bouncing models do not suffer of trans-Planckian problems. In practice the trans-Planckian problems possibly arising in bouncing scenarios are also related to the so-called gradient instability stipulating that either the scalar or the tensor modes of the geometry may inherit an imaginary sound speed (see for instance [31, 32]). This phenomenon normally occurs when the contracting evolution turns into the expanding stage: since the transition involves either higher derivatives in the matter fields or higher-order curvature corrections an effective sound speeds for the scalar and tensor modes develops. Whenever the sound speed becomes imaginary an instability of the scalar or tensor modes suddenly develops close to the end of the bouncing phase.
The implications of Eqs. (1)–(2) and Eqs. (3)–(4) depend on the initial Cauchy hypersurface that can be assigned in two complementary ways. According to the first strategy the various modes are initialized on a given space-like hypersurface at the same initial conformal time \(\tau _{i}\). This approach is physically meaningful for classical fluctuations that are assigned, once forever, at the onset of inflation (and subsequently ironed provided the inflationary stage is sufficiently long [33,34,35]). According to the second strategy the different modes of the field are assigned on different space-like hypersurfaces: in this context we will have that \(\tau _{i} = \tau _{i}(k)\) so that the initial normalization depends on the comoving wavenumber. This second perspective cannot be applied to classical fluctuations but it is physically meaningful for the quantum inhomogeneities that keep on reappearing all along an initial inflationary (or bouncing) stage.Footnote 1 These two possibilities will now be separately scrutinized and swiftly compared in the light of the conditions of Eqs. (1)–(2) and (3)–(4).
Let us therefore consider a stage of accelerated expansion and assume that all the k-modes are assigned at the same time \(\tau _{i}\). The only way to prevent the presence of super-Planckian frequencies is to demand that \(\omega (k, \tau _{i}) \le M\) for all the different k-modes at the same time \(\tau _{i}\); more precisely
where M is a given physical scale that does not exceed, by construction, the Planck (or string) energy scale; \(\epsilon \) is the standard slow-roll parameter. The condition (7) is valid for all the modes of the spectrum provided it is verified for the maximally amplified wavenumber \(k_{max}\). For the sake of concreteness we can consider the case of the curvature inhomogeneities and the tensor modes induced by a single scalar field \(\varphi \) where \(z = a \varphi ^{\prime }/{{\mathcal {H}}}\) and \({{\mathcal {H}}} = a^{\prime }/a \equiv a\, H\); in this situation the maximal wavenumbers for the scalar and tensor modes (i.e. \(k_{s\,\,max}\) and \( k_{t\,\,max}\)) are determined from the following pair of conditions:
where the two expressions at the right-hand side of both equations are evaluated at the time \(\tau _{f}\) that conventionally defines the final stage of the inflationary expansion; around \(\tau _{f}\) the slow-roll parameters (i.e. \(\epsilon \) and \(\eta \)) are all \({{\mathcal {O}}}(1)\). Neglecting the minor differences induced in Eq. (8) by the slow-roll parameters we will have thatFootnote 2
so that the common values of \(k_{s\, max}\) and \(k_{t\, max}\) can be approximately estimated by \(k_{max} \simeq a_{f}\, H_{f} \simeq a_{f} \, H\) where H denotes the Hubble rate during inflation. Equations (8) and (9) imply that the condition of Eq. (7), if applied to \(k_{max}\), leads to the following chain of inequalities:
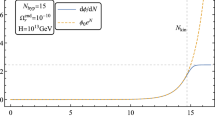
where \(N = \ln {(a_{f}/a_{i})}\) denotes throughout the total number of inflationary e-folds. The last inequality of Eq. (10) demands an upper limit on the total number of inflationary e-folds. For actual estimates we shall always choose \(M= {{\mathcal {O}}}(M_{P})\) (even if we shall insist later on that \(M< M_{P}\) ); in this case Eq. (10) suggests that \( N < - \ln {(H/M_{P})}\). Assuming the temperature correlations from the Cosmic Microwave Background are due to the curvature inhomogeneities amplified during inflation we have that the inflationary curvature scale is given by \(H/M_{P} = \sqrt{ \pi \, r_{T}\, {{\mathcal {A}}}_{{{\mathcal {R}}}}}\) where \({{\mathcal {A}}}_{{{\mathcal {R}}}} = {{\mathcal {O}}}(2.4)\times 10^{-9}\) is the amplitude of the scalar modes and \(r_{T}\) is the tensor to scalar ratioFootnote 3. Equation (10) implies that N can be at most \({{\mathcal {O}}}(14)\) supposing \(r_{T} = {{\mathcal {O}}}(0.01)\). This result has been interpreted in Refs. [25, 26] as a prohibitive condition forbidding, in practice, the existence of sufficiently long inflationary phases. The results of Eqs. (7), (8)–(9) and (10) demonstrate that these severe constraints follow from the assumption that all the different wavelengths of the scalar and tensor mode of the geometry are assigned on the same Cauchy hypersurface. It might be useful to remark that in Refs. [25, 26] the condition (10) has been simply assumed as a conjecture with the purpose of deriving a certain number of restrictions on the properties of inflationary potentials. In the present approach the condition (10) is not a conjecture but rather a result that only follows by assigning all the modes of the quantum fields at the same initial time \(\tau _{i}\). Even if the two viewpoints are formally different they are in practice complementary and this is the reason why it seems useful to investigate how the condition (10) can be evaded or superseded.
For a successful inflationary evolution we must fit the event horizon at the onset of inflation within the present size of the Hubble radius. Since the typical size of the event horizon at \(\tau _{i}\) is \({{\mathcal {O}}}(H^{-1})\) we should require that \((a_{0}/a_{i}) = (H/H_{0})\) where \(a_{0}\) and \(H_{0}\) denote the scale factor and the Hubble rate at the present epoch while \(a_{i}\) is the scale factor at the onset of inflationFootnote 4. This requirement can be made more explicit:
where \(\Omega _{R0}\) is the critical fraction of the energy density attributed to massless species in the concordance paradigm (i.e. \(h_{0}^2 \, \Omega _{R0} = 4.15 \times 10^{-5}\)). The second relation in Eq. (11) gives the maximum number of e-folds compatible with Eq. (10); if the two expressions in Eq. (11) are combined and solved with respect to N we get a critical number of e-folds, i.e. \(N_{c} = {{\mathcal {O}}}(45.3)\). Thus we must have \(r_{T} < 16/( \pi \, {{\mathcal {A}}}_{{{\mathcal {R}}}}) e^{ - 2 N_{c}}\), i.e. \(r_{T} < 9.5 \times 10^{-31}\). According to this estimate any tensor mode potentially detected through the B-mode autocorrelations should not be attributed to a conventional inflationary stage (see e.g. [29]).
The prohibitive limits explored in the two previous paragraphs ultimately follow from Eqs. (7) and (9) suggesting that all the different k-modes should be assigned on the same space-like hypersurface. If this strategy is adopted the maximal amplified frequency exceeds the Planck scale at \(\tau _{i}\) for any sound duration of inflation given the current observational bounds on the tensor to scalar ratio. According to the viewpoint conveyed here, the approach leading to Eqs. (10) and (11) is reasonable in the case of classical fluctuations. Conversely there is no compelling reason why all the wavelengths of the scalar and tensor modes of the geometry should be assigned on the same space-like hypersurface when the inhomogeneities are generated quantum mechanically. This observation is not new and has be been discussed, with different techniques and motivations, in Refs. [10, 11, 13,14,15] and it responds to the logic of effective theories [37]. The different k-modes are then assigned as soon as the corresponding physical frequencies “cross” the scale M:
The condition (12) defines, in practice, what we could call Planckian hypersurface even if different nomenclatures exist in the literature and they reflect slightly different physical interpretations. It is important to appreciate that while in Eq. (7) \(\tau _{i}\) is the same for different k-modes, in Eq. (12) \(\tau _{i} = \tau _{i}(k)\) and the specific k-dependence is ultimately dictated by the dynamics of the background. For a phase of accelerated expansion we have:Footnote 5
Equation (13) requires that long wavelengths (i.e. small k-modes) are normalized ealrier while short wavelengths (i.e. large k-modes) are normalized later. If \(\tau _{*}\) conventionally marks the onset of inflation, the smallest wavenumber of the spectrum (i.e. \(k_{*} \simeq \tau _{*}^{-1}\)) will be assigned at \(|\tau _{i}(k_{*})| \gg |\tau _{i}(k_{max})|\) where \(\tau _{i}(k_{max})\) denotes instead the time at which the largest mode of the spectrum is initialized (see Eqs. (8)–(9) for the definition of \(k_{max}\)). Note that in the limit \(\epsilon \rightarrow 0\) (which is mathematically convenient for order of magnitude estimates) we have that \(|\tau _{i}(k_{*})| \simeq e^{N} |\tau _{i}(k_{max})|\) where N is the total number of e-folds. Let us finally consider a phase of accelerated contraction where the scale factor can be parametrized, in cosmic time, as \(a(t) = (-t/t_{1})^{\gamma }\) with \(0<\gamma < 1\) and \(t < - t_{1}\). The condition (12) implies, in this case,
where \(H_{1} < M_{P}\) represents the maximal curvature scale for \( t = {{\mathcal {O}}}(t_{1})\) and \(|k \tau _{1} |< 1\). The condition (14) does not guarantee that the physical frequencies will remain smaller than the Planck mass towards the end of the bouncing phase, as already stressed by Eqs. (5) and (6) in the case of the corresponding wavelengths.
If the different k-modes are assigned as in Eq. (13) the constraint of Eq. (10) does not arise. More specifically, the total duration of the inflationary phase is not constrained since the maximal frequency coincides with M and it is always smaller than \(M_{P}\) by construction:
The approach based on Eq. (15) leads to the correct form of the scalar and tensor power spectra together with a series of oscillating corrections controlled, for each k-mode, by the dimensionless parameter \(x_{i}(k)\) introduced in Eqs. (13)–(14). The oscillating contributions however, do not solely depend on Eqs. (12) and (13) but also on the way the initial vacuum state is defined, i.e. on which Hamiltonian is minimized [14, 15] at \(\tau _{i}(k)\). Since the problem depends upon time, there is always the possibility of performing a time-dependent canonical transformation that changes the explicit form of the Hamiltonian without affecting the classical evolution. The different Hamiltonians will be minimized by different vacua at \(\tau _{i}(k)\) and this will ultimately lead to the different corrections of the corresponding power spectra.
To illustrate the different forms of the power spectra following from the minimization of the various Hamiltonians on the Planckian hypersurfaces it is practical to consider the scalar modes of the geometry:
where \({{\mathcal {R}}}\) denotes the curvature perturbation on comoving orthogonal hypersurfaces and \(\Pi \) is the conjugate momentum.Footnote 6 If the classical fields are promoted to the status of quantum operators and subsequently represented in Fourier space, the Hamiltonian operator corresponding to Eq. (16) is
where the Fourier amplitudes of the quantum fields and of the canonical momenta are defined by:
The Hermiticity of the fields and of the momenta in real space obviously implies that \(\hat{{{\mathcal {R}}}}_{\vec {k}}^{\,\, \dagger } = \hat{{{\mathcal {R}}}}_{-\vec {k}}\) and \({\hat{\Pi }}_{\vec {k}}^{\,\, \dagger } = {\hat{\Pi }}_{-\vec {k}}\). The Hamiltonian (17) can be diagonalized at the initial time \(\tau _{i}(k)\) in terms of the operator \({\hat{Q}}_{\vec {k}}\) and \({\hat{Q}}_{-\vec {k}}\) defined as:
where \(z_{i}(k) = z[\tau _{i}(k)]\); the canonical commutation relations between conjugate field operators demand from Eq. (19) that \([{\hat{Q}}_{\vec {k}}, {\hat{Q}}_{\vec {p}}^{\dagger } ] = \delta ^{(3)}(\vec {k} - \vec {p})\). The diagonal form of the Hamiltonian (17) is finally given by:
The state minimizing the Hamiltonian (20) at \(\tau _{i}(k)\) is defined by \({\hat{Q}}_{\vec {k}} |0^{(1)}\rangle =0\) and \({\hat{Q}}_{-\vec {k}} |0^{(1)}\rangle =0\); these two conditions provide the Cauchy data for the evolution equations in the Heisenberg description so that the scalar power spectrum is
The explicit form of the power spectrum \({{\mathcal {P}}}^{(1)}_{{{\mathcal {R}}}}(k,\tau _{i})\) contains a leading term (which is the standard scalar power spectrum typical of single-field inflationary models) and a series of corrections in the inverse of \(k \tau _{i}(k)\). More specifically we will have that
where, as before, W denotes the inflaton potential. Since \(\epsilon \) and \({\overline{\eta }}\) are both much smaller than one when the largest wavelengths exit the Hubble radius during inflation the first oscillating correction goes as \(x_{i}^{-1} \simeq (H/M)\).
If we now perform a canonical transformation with the appropriate generating functional, the Hamiltonian (16) changes its form even if the evolution remains the same. Let us consider for instance the transformation [14]:
In this case the Hamiltonian (16) changes its form and the final result will be
The Hamiltonian (24) can be minimized by following a procedure similar to the one examined above. The power spectrum will be given this time
where \(| \tau _{i}(k), 0^{(2)} \rangle \) now denotes the state minimizing the Hamiltonian (24) and \({{\mathcal {P}}}^{(2)}_{{{\mathcal {R}}}}(k,\tau _{i})\) will now be given by [14]:
where, this time, \(c^{(s)}_{2}(\epsilon , {\overline{\eta }}) = - c^{(s)}_{0}(\epsilon , {\overline{\eta }})/2\). A further Hamiltonian canonically related to the one of Eq. (24) is
The transformations \(H^{(1)}(\tau ) \rightarrow H^{(2)}(\tau )\) and \(H^{(2)}(\tau ) \rightarrow H^{(3)}(\tau )\) are both canonical; for instance \(H^{(2)}(\tau ) \rightarrow H^{(3)}(\tau )\) corresponds to a generating functional that depends on the old fields q, on the new momenta \({\tilde{\pi }}\) and on the background evolution
By differentiating the generating functional, we obtain the relation between the old momenta (i.e. \(\pi \)) and the new ones, as well as a change in the Hamiltonian
Bearing in mind Eq. (28) the right-hand side of Eq. (29) leads exactly to Eq. (27). With similar considerations, all the Hamiltonians (16)–(29) can be related to one another by suitable canonical transformations. Denoting by \(| \tau _{i}(k), 0^{(3)} \rangle \) the state minimizing the quantum version of the Hamiltonian \(H^{(3)}(\tau )\), the corresponding power spectrum will now be given by:
The comparison of Eqs. (22), (26) and (30) demonstrates that the leading term of the spectrum is the same in the three cases even if the corrections are sharply different. The correction to the power spectrum goes as \(1/x_i^2\) in the case of (26); this figure is much smaller than the one appearing in (22). For instance assuming \(M \sim M_{\mathrm{P}}\) the correction will be \({{\mathcal {O}}}(10^{-12})\), i.e. six orders of magnitude smaller than in the case of (22). In Eq. (30) the correction arising from the initial state goes instead as \(1/x_i^3\) and, again, if \(M \sim M_{\mathrm{P}}\) it is \(\mathcal{O}(10^{-18})\), i.e. 12 orders of magnitude smaller than in the case discussed in Eq. (22). Similar figures arise in the case of the tensor modes but will not be specifically discussed here (see [14, 15] for further details on this point). The corrections of the scalar power spectra are correlated with the rate at which the pump fields of each Hamiltonian go to zero in the limit \(\tau \rightarrow - \infty \): the faster the free Hamiltonian is recovered in the limit \(\tau \rightarrow - \infty \) the smaller is the correction to the power spectrum. This degree of adiabaticity is also correlated with the backreaction effects of the initial vacuum state which are negligible in the case of Eqs. (26) and (30) but not in the case of Eq. (22) [14].
So far all the discussion has been conducted in the Einstein frame. The same conclusions can be however reached in any conformally related frame and, in particular, in the string frame. In the string frame the string mass is constant while the Planck mass depends on the value of the dilaton coupling \( e^{\varphi /2}\) according to a relation that can be parametrized at low energies as \(M_{s} = e^{\varphi /2} M_{P}\). Recalling that the relation between the metric tensors in the Einstein and in the string frames can be written, in four dimensions, as \(g_{\mu \nu }^{(e)}= e^{-\varphi } g_{\mu \nu }^{(s)}\) (with \(\varphi _{s} = \varphi _{e} = \varphi \)), the connection between the scale factors in the two frames will be given by \(a_{s} = e^{\varphi /2} a_{e}\). Assuming for simplicity \(M = M_{P}\) we have, for instance, that the condition (12) is the same in both frames:
where the first equation is the same as Eq. (12) while the second relation is its analog in the string frame. The metric fluctuations of the geometry in the two frames are in principle different however the curvature perturbations on comoving orthogonal hypersurfaces are the same in the two frames, \({{\mathcal {R}}}_{s} = {{\mathcal {R}}}_{e}= {{\mathcal {R}}}\); a similar property holds for the tensor modes of the geometry [32].
The approach pursued in the present Letter can be corroborated by a conceptually different viewpoint that has been already mentioned earlier on. It was actually noticed in Ref. [11] that as long as the WKB condition is not violated at super-high frequencies, the predictions for the scalar and tensor power spectra remain unchanged. To briefly account for this perspective we define a rescaled wavenumber \({\widetilde{k}} = k/a\). Within these notations the validity of the WKB approximation for the evolution of the mode functions stipulates that
where, as usual, the overdot denotes a derivation with respect to the cosmic time coordinate. Equation (32) has been purposely written in terms of a putative scale M and it shows the WKB condition is verified also in the limit \(\omega > M\) provided \(H< M\) and as long as the dispersion relations \(\omega = \omega ({\widetilde{k}})\) do not vanish; different explicit proposals can be considered starting from the ones already used in the context of black-hole physics [4]. All in all Eq. (32) is stronger than the conditions of Eqs. (7) and (12) insofar as it suggests that the approximation scheme used to derive the scalar and tensor power spectra remains valid for arbitrarily large frequencies under the plausible condition (32). The results of Eq. (32) also answer some of the potential questions related to the validity of the effective approach in the context of conventional (and unconventional) inflationary models (see e.g. [37]). There might actually be some who object that when nonlinear interactions are taken into account the different modes may mix so that if the Planckian (i.e. \(\omega > M\)) fluctuations are not defined these interactions cannot be included. This objection implicitly rejects the logic of the effective theory which seems instead pretty reasonable in the present as well as in other contexts. Even if the validity of an effective description is rejected, the result of Eq. (32) demonstrates that the WKB approximation is still valid for the trans-Planckian modes.
It is also useful to remind that the concept of Planckian hypersurface used here has also been adopted in Ref. [38] in connection with the possibility of the trans-Planckian creation of massive particle and it has been dubbed new-physics hypersurface following the earlier terminology employed in Refs. [14, 15]. The main idea, in this context, is that the number of created particles above a certain cut-off (i.e. M in our notations) is not exponentially suppressed but just power suppressed. The authors of [38] assume a phenomenological parametrization that could be written, within the present notations, as \({\overline{n}}_{k} = b (H_{k}/M)^{\gamma }\) where b and \(\gamma \) are two constants. The modification of the dispersion relations above the putative scale M may also have relevant effects at the present time both for massive and for massless particles [39, 40]. The implications of this interesting observation in the case of ultra high-energy cosmic rays has been studied in Refs. [39, 40]. These problems are potentially relevant also in the present context but they are beyond the scopes of this investigation.
Before concluding the discussion we wish to stress two final themes that might clarify the perspective of the present investigation. Since the Hamiltonians of the scalar and tensor modes of the geometry have been minimized at \(\tau _{i}(k)\) (see Eqs. (13) and (14)), there might be some wandering how the evolution between \(\tau _{*}\) and \(\tau _{i}(k)\) should be interpreted. The answer to this question strongly depends on the dynamics and it is different if we either consider an inflationary or a bouncing evolution (i.e. Eqs. (1)–(2) and (5)–(6)). In the case of accelerated expansion the physical wavelengths can become smaller than the Planck length close to the onset of inflation but the same issue occurs at the end of a phase of accelerated contraction so that the answer to the above question is trivial in the bouncing case. In the case of the inflationary dynamics the answer to the above question has been already presented after Eq. (13) but it is useful to phrase it in an even more elementary form. Let us start with the mode \(\tau _{*} \simeq k_{*}^{-1}\). When does it start the evolution of this mode? At \(\tau _{i} (k_{*})\) where \(\tau _{i}(k)\) is given by Eq. (13). Let us then consider a second mode \(|\tau _{2}| \simeq k_{2}^{-1}\) with \(a(\tau _{2})> a(\tau _{*})\). When does it start the evolution of this mode? At \(\tau _{i}(k_{2})\); the time elapsed from \(\tau _{*}\) to \(\tau _{2}\) can be computed from the number of e-folds between \(a_{*}\) and \(a_{2}\). A further question could be, at this point: what is the evolution of the mode function corresponding to \(k_{2}\) between \(\tau _{*}\) and \(\tau _{i}(k_{2})\)? The answer is that there is no evolution since the mode \(k_{2}\) is normalized (and starts evolving) as soon as it crosses the Planckian hypersurface \(k_{2}/a(\tau ) = M < M_{P}\): this is exactly the condition defining \(\tau _{i}(k_{2})\). The implications of this approach are potentially observable and have been discussed in Eqs. (22), (26) and (30). However the corrections to the scalar and tensor power spectra depend on which Hamiltonian in minimized on the Planckian hypersurface and in the case of adiabatic Hamiltonians the resulting corrections are, in practice, unobservable. In a complementary perspective, since the WKB condition of Eq. (32) is not violated, it is also possible to follow the modes between \(\tau _{*}\) and \(\tau _{2}\) and this aspect has already been discussed above in connection with Refs. [11, 38,39,40].
The second possible question could be: which is the quantum gravity underlying the present discussion? The ideas conveyed here do not require a specific theory of quantum gravity as it has been instead argued, in a related context, by Refs. [25, 26] where the authors suggested that quantum gravity in general (and string theory in particular) demands a set of very restrictive conditions on the inflationary dynamics. In practice a sufficiently long stage of accelerated expansion should be obliterated (or strongly constrained) by quantum gravitational effects exactly because the tools employed in the analysis are not valid for arbitrarily small wavelengths. The present considerations show indeed the opposite, i.e. that a detailed theory of quantum gravity is not mandatory to give a sensible discussion of the scalar and tensor modes of the geometry either during a phase of accelerated expansion or during a stage of accelerated contraction. Indeed, the aporia discussed in the present Letter originates from the observation that the evolution equations for the scalar and tensor modes of the geometry cannot be valid for arbitrarily short wavelengths: this is the same kind of problem appearing in the context of Hawking radiation [3,4,5,6,7] and the answer obtained here is, in a sense, similar. If the largest amplified wavenumber is always smaller than a certain reference scale M none of the wavelengths gets shorter than the Planck length throughout the inflationary evolution but this requirement is sufficient, not necessary. In this Letter we gave an explicit example where none of the restrictive conditions of Eqs. (10) and (11) arise while none of the wavelengths of scalar and tensor modes of the geometry becomes shorter than the Planck or string lengths. The conditions of Eqs. (10) and (11) coincide indeed with some recent conjectures proposed in Refs. [25, 26] on the basis of string theoretical considerations. The conclusions of the present investigation show instead that these string theoretical conjectures may be viewed as a consequence of a much more mundane assumption stipulating that the maximal amplified wavenumber of the inflationary power spectra should never exceed the Planck or string mass. Since this condition is however only sufficient (and may be evaded) it is fair to conclude that the conjectures proposed in Refs. [25, 26] are sufficient but not necessary. In other words it can well happen that the maximal amplified wavenumber does not exceed the Planck or string scale without implying either a very short phase of accelerated expansion or even a vanishing tensor to scalar ratio.
Since the quantum mechanical fluctuations are continuously generated during a primeval inflationary (or bouncing) stage, all the different wavelengths of the scalar and tensor modes of the geometry do not have to be assigned on the same space-like hypersurface. We showed that some prohibitive constraints either on the total number of inflationary e-folds or on the tensor to scalar ratio can be evaded if the various wavelengths are assigned as soon as their associated physical frequency is still smaller than the Planck (or string) scale. According to this strategy the initial Cauchy data for the mode functions effectively depend on the wavenumber so that larger wavelengths start their evolution earlier than those that are comparatively shorter. The same problems in conventional inflationary scenarios also occurs in the context of backgrounds with different kinematical properties (e.g. contracting stages): while in the case of an accelerated expansion the physical wavelengths get potentially shorter than the Planck length at the onset of inflation, for a phase of accelerated contraction the physical wavelengths suffer the same problem but at the end of the bouncing regime (when the scale factor shrinks and the absolute value of the curvature increases). The oscillating contributions arising in the large-scale power spectra as a result of the normalization on the Planckian hypersurfaces turn out to be arbitrarily small. The present results suggest that the duration of a conventional inflationary phase and the tensor to scalar ratio remain unconstrained if the quantum inhomogeneities are appropriately assigned on the Planckian hypersurfaces.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This manuscript has no associated data since this is a theoretical study. The observational data recalled in this paper have been already published elsewhere and are quoted in the paper.]
Notes
The Hamiltonian is minimized at the initial space-like hypersurface \(\tau _{i}(k)\) so that the Cauchy data for the evolution of the field operators in the Heisenberg description are defined at \(\tau _{i}(k)\). Using the same terminology, in the standard approach, the initial conditions for the field operators are all given at \(\tau _{*}\) for the different wavenumbers so that, for the standard case, it is somehow true (and potentially confusing) that all the modes suddenly appear at \(\tau _{*}\).
The slow-roll parameters are defined, in what follows, as \(\epsilon = - {\dot{H}}/H^2\) (already introduced in Eq. (7)), \(\eta = \ddot{\varphi }/(H \, {\dot{\varphi }})\) and \({\overline{\eta }} = (\epsilon - \eta ) \equiv {\overline{M}}_{P}^2 (W_{\,\varphi \varphi }/W)\), where \({\overline{M}}_{P} = M_{P}/\sqrt{8 \pi }\) and W denotes the inflaton potential.
We shall be assuming throughout the validity of the consistency relations stipulating that \(16 \epsilon = r_{T} = - 8 n_{T}\) where \(n_{T}\) is the tensor spectral index [29]. If the consistency relations are not assumed some of the constraints discussed below could be probably relaxed.
We are assuming here that inflation starts on a time scale \({{\mathcal {O}}}(\tau _{i})\).
An analog form of the Hamiltonian can be discussed in the case of the tensor modes but, for the sake of conciseness, we shall limit the attention to the scalar case which is also the one more relevant for the observations of the temperature and polarization anisotropies.
References
S.W. Hawking, Nature 248, 30 (1974)
S.W. Hawking, Commun. Math. Phys. 43, 199 (1975)
T. Jacobson, Phys. Rev. D 44, 1731 (1991)
W.G. Unruh, Phys. Rev. D 51, 2827 (1995)
S. Deser, O. Levin, Class Quant. Gravit. 14, L163 (1997)
S. Deser, O. Levin, Phys. Rev. D 59, 064004 (1999)
I. Agullo, J. Navarro-Salas, G.J. Olmo, L. Parker, Phys. Rev. D 77, 104034 (2008)
A. Kempf, J.C. Niemeyer, Phys. Rev. D 64, 103501 (2001)
R. Easther, B. Greene, W. Kinney, G. Shiu, Phys. Rev. D 64, 103502 (2001)
L. Mersini-Houghton, M. Bastero-Gil, P. Kanti, Phys. Rev. D 64, 043508 (2001)
A.A. Starobinsky, Pisma. Zh. Eksp. Teor. Fiz. 73, 415 (2001)
R. Brandenberger, J. Martin, Phys. Rev. D 65, 103514 (2002)
U. Danielsson, Phys. Rev. D 66, 023511 (2002)
M. Giovannini, Class. Quant. Gravit. 20, 5455 (2003)
V. Bozza, M. Giovannini, G. Veneziano, JCAP 0305, 001 (2003)
U.H. Danielsson, Phys. Rev. D 71, 023516 (2005)
B. Greene, M. Parikh, J.P. van der Schaar, JHEP 0604, 057 (2006)
M.G. Jackson, K. Schalm, Phys. Rev. Lett. 108, 111301 (2012)
P.A.R. Ade et al., Planck Collaboration. Astron. Astrophys. A 571, 22 (2014)
Y.F. Cai et al., Phys. Rev. D 92, 121303 (2015)
S. Bahrami, E.E. Flanagan, JCAP 1601, 027 (2016)
P.A.R. Ade et al., Planck Collaboration. Astron. Astrophys. A 594, 20 (2016)
C. Zeng et al., Phys. Rev. D 99, 043517 (2019)
Y. Akrami et al. [Planck Collaboration], arXiv:1807.06211 [astro-ph.CO]
A. Bedroya, C. Vafa, arXiv:1909.11063 [hep-th]
A. Bedroya, R. Brandenberger, M. Loverde, C. Vafa, arXiv:1909.11106 [hep-th]
K. Schmitz, arXiv:1910.08837 [hep-ph]
R. Saito, S. Shirai, M. Yamazaki, arXiv:1911.10445 [hep-th]
M. Giovannini, arXiv:1912.07065 [hep-th]
A. Borde, A. Vilenkin, Phys. Rev. D 56, 717 (1997)
A. Ijjas, P.J. Steinhardt, Phys. Lett. B 764, 289 (2017)
M. Giovannini, Phys. Rev. D 95, 083506 (2017)
A. A. Starobinsky, JETP Lett. 37, 66 (1983)
A. A. Starobinsky, Pis’ma Zh. Eksp. Teor. Fiz. 37, 55 (1983)
R.M. Wald, Phys. Rev. D 28, 2118 (1983)
A.R. Liddle, S.M. Leach, Phys. Rev. D 68, 103503 (2003)
S. Weinberg, Phys. Rev. D 77, 123541 (2008)
E.W. Kolb, A.A. Starobinsky, I.I. Tkachev, JCAP 0707, 005 (2007)
A. A. Starobinsky, I. I. Tkachev, JETP Lett. 76, 235 (2002)
A. A. Starobinsky, I. I. Tkachev, Pisma Zh. Eksp. Teor. Fiz. 76, 291 (2002)
Acknowledgements
The author wishes to thank T. Basaglia, A. Gentil-Beccot, S. Rohr and J. Vigen of the CERN Scientific Information Service for their kind assistance.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Giovannini, M. Planckian hypersurfaces, inflation and bounces. Eur. Phys. J. C 80, 555 (2020). https://doi.org/10.1140/epjc/s10052-020-8121-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-8121-5