The effect of an anomalous Higgs trilinear self-coupling on the $h \rightarrow \gamma \, Z$ decay

Abstract

We compute the two-loop effects induced by an anomalous Higgs trilinear self-coupling in the partial decay width $\Gamma (h \rightarrow \gamma Z)$. The computation is performed using the anomalous coupling approach, working in the unitary gauge, and in a theory in which the anomalous coupling is generated via the addition to the scalar potential part of the Standard Model Lagrangian of an (in)finite tower of $(\Phi ^\dagger \Phi )^n$ terms. The former computation is automatically finite while the latter requires the renormalization of the lowest order contribution. We discuss the renormalization conditions that should be employed in order to obtain the same result in the two approaches. We find that the $h \rightarrow \gamma Z$ process is one of the most sensitive mode to an anomalous trilinear Higgs self-coupling. As a by-product of this work we confirm one of two different results present in the literature concerning the contribution of an anomalous Higgs trilinear coupling in the $h \rightarrow \gamma \gamma$ decay.

1 Introduction

The properties of the scalar particle with mass around 125 GeV discovered at the Large Hadron Collider (LHC) in 2012 [1, 2] have been extensively studied since its observation. These studies show strong evidence that the couplings of this particle to fermions and vector bosons are compatible within 10–20% with those of the Higgs boson as predicted in the Standard Model (SM) of elementary particles.

The complete identification of the scalar particle discovered in 2012 with the Higgs boson of the SM requires also the study of the Higgs self-interactions that come from the scalar potential part in the SM Lagrangian. In the SM, the Higgs potential in the unitary gauge reads

$$\begin{aligned} V(h) = \frac{m_{ \scriptscriptstyle H}^2}{2} h^2 + \lambda _{3}v h^3 + \frac{\lambda _4}{4} h^4 \end{aligned}$$

(1)

where the Higgs mass ($m_{ \scriptscriptstyle H}$) and the trilinear $(\lambda _{3})$ and quartic $(\lambda _{4})$ interactions are linked by the relations $\lambda _{4}^{\mathrm{SM}}=\lambda _{3}^{\mathrm{SM}}= \lambda =m_{ \scriptscriptstyle H}^2/(2\,v^2)$, where $v=(\sqrt{2} \,G_\mu )^{-1/2}$ is the vacuum expectation value, and $\lambda$ is the coefficient of the $(\Phi ^\dagger \Phi )^2$ interaction, $\Phi$ being the Higgs doublet field.

The experimental verification of these relations relies on the measurements of double Higgs and triple Higgs productions. However, since the cross sections for these processes are quite small, constraining $\lambda _{3}$ and $\lambda _4$ couplings within few times their predicted SM value is already extremely challenging. In the case of double Higgs production, at present only exclusion limits are available. The most stringent result, coming from the ATLAS combination of the $b{\bar{b}}b{\bar{b}},\, b{\bar{b}}\tau \tau$ and $b{\bar{b}} \gamma \gamma$ channels, allows to set a bound $-5\, \lambda _{3}^{\mathrm{SM}}< \lambda _{3}< 12\, \lambda _{3}^{\mathrm{SM}}$ at 95% CL [3]. It is not yet clear whether double Higgs production will be observed at the end of the high luminosity (HL) period of LHC with a collected luminosity of 3000 $\hbox {fb}^{-1}$ or just ${{\mathcal {O}}}$ (1) bounds on $\lambda _{3}$ are going to be set. Concerning $\lambda _{4}$, given the smallness of the triple Higgs production cross section (around 0.1 fb at $\sqrt{s}= 14$ TeV), this self-coupling will be only very loosely constrained at the HL-LHC.

In order to constrain the trilinear Higgs self-coupling, a complementary strategy based on precise measurements was proposed. In this approach the effects induced at the loop level on various processes by a modified $\lambda _{3}$ coupling are studied. This approach builds on the assumption that New Physics (NP) couples to the SM via the Higgs potential in such a way that the lowest-order Higgs couplings to the other fields of the SM (and in particular to the top quark and vector bosons) are still given by the SM prescriptions or, equivalently, modifications to these couplings are so small that do not swamp the loop effects one is considering. This strategy was first applied to ZH production at an $e^+ e^-$ collider in Ref. [4], later to Higgs production and decay modes at the LHC [5,6,7,8,9,10,11] and also to the study of electroweak precision observables [12, 13]. Using this strategy a recent analysis of the ATLAS Collaboration set a more stringent bound, $-2.3\, \lambda _{3}^{\mathrm{SM}}< \lambda _{3}< 10.3\, \lambda _{3}^{\mathrm{SM}}$ at 95% C.L., by combining the single Higgs boson analyses targeting the $\gamma \gamma ,\, Z Z^\star ,\, W W^\star ,\, \tau ^{+} \tau ^-$ and $b {\overline{b}}$ decay channels and the double Higgs boson analyses in the $b{\bar{b}}b{\bar{b}},\, b{\bar{b}}\tau \tau$ and $b{\bar{b}} \gamma \gamma$ decay channels using data collected at $\sqrt{s} = 13$ TeV [14].

The aim of this work is twofold. On one side we continue the program of identifying in single Higgs processes the $\lambda _{3}$-dependent loop contributions by examining the $h\rightarrow \gamma Z$ decay. On the other side we use this decay to show in detail, for contributions that arise at two-loop level, the equivalence, at the loop order we are working, of two approaches. In the first one, following Ref. [5], the $\lambda _{3}$-dependent loop contributions are studied via the introduction of a rescaling factor multiplying the trilinear SM coupling, $\lambda _{3}= \kappa _{\lambda }\lambda _{3}^{\mathrm{SM}}$, with $\lambda _{3}^{\mathrm{SM}}\equiv G_\mu \,m_{ \scriptscriptstyle H}^2/\sqrt{2}$, working in the unitary gauge (UG): this is the so called $\kappa$-framework or anomalous coupling approach. The second one is based on the modification of the SM scalar potential via the addition of higher-dimensional operators that affect only the Higgs self-coupling, i.e an (in)finite tower of $(\Phi ^\dagger \Phi )^n$ terms $(n >2)$. The latter, when only the term $n=3$ is assumed, corresponds to the SM effective field theory (SMEFT) approach with one single dimension-six operator, the $O_6 = (\Phi ^\dagger \Phi )^3$ one.¹

The calculation of $\lambda _{3}$-dependent loop contributions in the $h\rightarrow \gamma Z$ decay shares many similarities with the analogous calculation for $h\rightarrow \gamma \gamma$. For this process the results in the literature obtained using the anomalous coupling approach [5] and the SMEFT approach [6] are not in agreement. In Ref. [6] the Wilson coefficient, $c_6$, of the operator $O_6$ of the SMEFT approach was found to be dependent upon the energy scale at which it is evaluated. On the contrary, in Ref. [5] the parameter $\kappa _{\lambda }$ of the anomalous coupling approach was found to be energy-scale independent.² As a by-product of our $h\rightarrow \gamma Z$ analysis we resolve this discrepancy.

The paper is organized as follows. In Sect. 2 we present the general structure of the $\lambda _{3}$-dependent contribution in $\Gamma (h\rightarrow \gamma Z)$ outlining the (approximate) way this contribution is evaluated. In Sect. 3 we discuss the renormalization conditions that should be imposed on the scalar potential of a $(\Phi ^\dagger \Phi )^n$ theory in order to obtain a result for the anomalous trilinear contribution that is identical to the one obtained in the $\kappa$-framework working in the UG, where the renormalization of the one-loop contribution is not needed. Section 4 presents our results for the $\lambda _{3}$-dependent contribution in the partial width $\Gamma (h\rightarrow \gamma Z)$ and its corresponding branching ratio (BR). Finally, in the Conclusions we shortly discuss the contribution due to an anomalous trilinear Higgs coupling in $\Gamma (h\rightarrow \gamma \gamma )$ confirming the equivalence between the $\kappa$-framework and the SMEFT with the $O_6$ operator.

2 $\lambda _{3}$-dependent contribution in $\Gamma (h \rightarrow \gamma Z)$

We begin by recalling the structure of the $\lambda _{3}$-dependent contribution in single Higgs processes as discussed in Ref. [5]. This contribution arises from next-to-leading order (NLO) electroweak (EW) corrections and can be organized in two categories: a universal part proportional to $(\kappa _{\lambda })^2$ due to the wave-function renormalization of the external Higgs boson, and a process-dependent part linear in $\kappa _{\lambda }$ that in general depends on the kinematics of the process under consideration.

Specializing to the $h \rightarrow \gamma Z$ decay we write for the $\lambda _{3}$-dependent contribution in the width

$$\begin{aligned} \Gamma _{\lambda _{3}} = Z_H\,\Gamma _{{\mathrm{{LO}}}} \left( 1 + \kappa _{\lambda }C_1 \right) , \end{aligned}$$

(2)

with

$$\begin{aligned} Z_H= & {} \frac{1}{1- \kappa _{\lambda }^2\, \delta Z_H}, \end{aligned}$$

(3)

$$\begin{aligned} \delta Z_{H}= & {} -\frac{9}{16} \, \frac{G_\mu \,m_{ \scriptscriptstyle H}^2 }{\sqrt{2}\, \pi ^2} \left( \frac{2\pi }{3\sqrt{3}}-1\right) = -1.536 \cdot 10^{-3} \,. \end{aligned}$$

(4)

In Eq. (2) $C_1$ is the process-dependent contribution that will be presented in this paper while $\Gamma _{{\mathrm{{LO}}}}$ stands for the LO prediction. Neglecting ${\mathcal {O}}(\kappa _{\lambda }^3\,\alpha ^2)$ terms the relative corrections induced by an anomalous trilinear Higgs self-coupling can be expressed as

$$\begin{aligned} d \Gamma _{\lambda _{3}} \equiv \frac{\Gamma _{{\mathrm{{NLO}}}} - \Gamma ^{\mathrm{SM}}_{{\mathrm{{NLO}}}}}{\Gamma _{{\mathrm{{LO}}}}} = (\kappa _{\lambda }-1) C_1+(\kappa _{\lambda }^2-1) C_2 \,, \end{aligned}$$

(5)

where $\Gamma ^{{\mathrm{SM}}}_{{\mathrm{{NLO}}}}$ is the NLO SM result³ and

$$\begin{aligned} C_2 = \frac{\delta Z_H}{(1- \kappa _{\lambda }^2 \delta Z_H)}~. \end{aligned}$$

(6)

The range of validity of Eq. (5) can be identified according to Ref. [5] with $|\kappa _{\lambda }| \lesssim 20$, where this bound was derived via an estimate of the missing terms in the perturbative calculation of single Higgs processes.

Because the photon does not couple directly to neutral particles, the decay process $h \rightarrow \gamma Z$ receives contribution at LO from one-loop diagrams. Then, the evaluation of the $C_1$ coefficient requires a two-loop calculation. An exact evaluation of the $\lambda _{3}$-dependent two-loop diagrams is currently not possible. Then, we employ the same strategy used in the analogous calculation of $\Gamma ( h \rightarrow \gamma \gamma )$ [5], namely the relevant diagrams are computed via a Taylor expansion in the external momenta. Calling $q_1$ and $q_2$ the momenta of the photon and of the Z, respectively, we make an expansion in the parameters $q^2_1/(4 m^2)$, $q^2_2/(4 m^2)$ and $(q_1 \cdot q_2)/(4 m^2)$ where m is the mass of any particle running into the loops, i.e. $m=m_{t}, \,m_{ \scriptscriptstyle H},\, m_{ \scriptscriptstyle W},\,m_{ \scriptscriptstyle Z}$, and at the end of the computation we set $q_1^2 =0 , \,q^2_2= m_{ \scriptscriptstyle Z}^2$ and $(q_1 \cdot q_2)= (m_{ \scriptscriptstyle H}^2 - m_{ \scriptscriptstyle Z}^2)/2$. We point out that our expansion parameters are all smaller than 1 although not always very small.

In order to test the consistency of our small-momentum expansion approach we first compare the LO contribution computed exactly, with its evaluation via a small momentum expansion in the UG.

The $h \rightarrow \gamma Z$ decay width can be written as

$$\begin{aligned} \Gamma (h \rightarrow \gamma Z) = \frac{G_\mu ^2 m_{ \scriptscriptstyle Z}^2 \alpha ~ m_{ \scriptscriptstyle H}^3}{64 \pi ^4} \Biggl (1-\frac{m_{ \scriptscriptstyle Z}^2}{m_{ \scriptscriptstyle H}^2} \Biggr )^3 |{\mathcal {F}} |^2 \end{aligned}$$

(7)

with

$$\begin{aligned} {\mathcal {F}} = N_c Q_t ~ (I_{3 t}-2Q_t \sin ^2 \theta _W) {\mathcal {F}}_t + \cos ^2 \theta _W {\mathcal {F}}_W \end{aligned}$$

(8)

where $\theta _W$ is the weak angle, while ${\mathcal {F}}_t$ and ${\mathcal {F}}_W$ are the fermionic and bosonic contributions to the amplitude, respectively. In the former we are considering only the dominant top quark contribution that sets the color factor, the electric charge and the weak isospin to be $N_c=3, \,Q_t =2/3,\, I_{3t} =1/2$.

At LO the ${\mathcal {F}}_t$ and ${\mathcal {F}}_W$ terms can be written [17, 18]

$$\begin{aligned} {\mathcal {F}}_t^{{\mathrm{{LO}}}}= & {} 2 \Bigl [I_1(1/h_{4t}, 1/z_{4t}) - I_2 (1/h_{4t}, 1/z_{4t}) \Bigr ] \end{aligned}$$

(9)

$$\begin{aligned} {\mathcal {F}}_W^{{\mathrm{{LO}}}}= & {} 4(3 - \tan ^2 \theta _W) I_2(1/h_{4w}, 1/z_{4w})\nonumber \\&+ \Bigl [ (1+ 2 h_{4w} ) \tan ^2 \theta _W - (5+2 h_{4w} ) \Bigr ]\nonumber \\&I_1 (1/h_{4w}, 1/z_{4w}) \end{aligned}$$

(10)

where $h_{4 i} = m_{ \scriptscriptstyle H}^2/(4 m_i^2)$ and $z_{4 i} = m_{ \scriptscriptstyle Z}^2/(4 m_i^2)$. The functions $I_1$ and $I_2$ are defined as

$$\begin{aligned} I_1 (\tau , \lambda )= & {} \frac{\tau \lambda }{2(\tau -\lambda )} + \frac{\tau ^2 \lambda ^2}{2(\tau -\lambda )^2} \Bigl [f(\tau ) -f(\lambda ) \Bigr ] \nonumber \\&+ \frac{\tau ^2 \lambda }{(\tau - \lambda )^2} \Bigl [ g(\tau ) - g(\lambda ) \Bigr ], \nonumber \\&\ \end{aligned}$$

(11)

$$\begin{aligned} I_2 (\tau , \lambda )= & {} - \frac{\tau \lambda }{2(\tau -\lambda )} \Bigl [f(\tau )- f(\lambda ) \Bigr ], \end{aligned}$$

(12)

where (for $x \ge 1$)

$$\begin{aligned} f(x)= & {} \arcsin ^2 \Biggl (\frac{1}{\sqrt{x}} \Biggr )\, , \nonumber \\ g(x)= & {} \sqrt{x -1} \arcsin \Biggl (\frac{1}{\sqrt{x}} \Biggr ) . \end{aligned}$$

(13)

Using the small-momentum expansion we obtain the following expressions for the fermionic and bosonic contributions

$$\begin{aligned} {\mathcal {F}}_t^{{\mathrm{{LO}}}}&= \frac{2}{3}+\frac{1}{45}\, h_{4t} (7+11 z_h) + \frac{4}{315} \,h_{4t}^2 \left( 5+8 z_h+11 z_h^2\right) \nonumber \\&\quad + \frac{4}{1575}\, h_{4t}^3 \left( 13+21 z_h+29 z_h^2+37 z_h^3 \right) \nonumber \\&\quad + \frac{128}{51975}\, h_{4t}^4 \left( 8+13 z_h+18 z_h^2+23 z_h^3+28 z_h^4 \right) \nonumber \\&\quad + {\mathcal {O}}(h_{4t}^5) \end{aligned}$$

(14)

$$\begin{aligned} {\mathcal {F}}_W^{{\mathrm{{LO}}}}&= - 7-\frac{2}{15}\, h_{4w} (11-37 z_h)\nonumber \\&\quad + \frac{4}{105}\, h_{4w}^2 \left( -19-z_h+31 z_h^2\right) \nonumber \\&\quad - \frac{8}{1575}\, h_{4w}^3 \left( 87+19 z_h-39 z_h^2-97 z_h^3\right) \nonumber \\&\quad - \frac{16}{17325}\, h_{4w}^4 \left( 328+93 z_h-32 z_h^2-157 z_h^3-282 z_h^4\right) \nonumber \\&\quad + {\mathcal {O}}(h_{4w}^5) \end{aligned}$$

(15)

where $z_h= m_{ \scriptscriptstyle Z}^2/m_{ \scriptscriptstyle H}^2$.

We checked that Eqs. (14) and (15) match exactly the expansion of the expressions in Eqs. (9) and (10) in the limit of small $h_{4 i}$ and $z_{4 i}$.

Neglecting the last known contribution in Eqs. (14, 15), i.e. ${\mathcal {O}}(h_{4t}^4)$ and ${\mathcal {O}}(h_{4w}^4)$, the numerical result for the decay width obtained with the small-momentum expansion differs from the evaluation of the exact expression by 2.6%. Including also this last term the difference reduces to 1.3%. Then, we can estimate that the evaluation of the two-loop contribution via a small momentum expansion including ${\mathcal {O}}(h_{4t}^3)$ and ${\mathcal {O}}(h_{4w}^3)$ is expected to differ from the exact result by ${\mathcal {O}}(5\%)$.

Fig. 1

Examples of two-loop diagrams contributing to the $h\rightarrow \gamma Z$ amplitude: a diagram contributing to ${\mathcal {F}}_t$; b diagram contributing to ${\mathcal {F}}_W$

The $C_1$ coefficient in Eq. (5) can be defined as [5]

$$\begin{aligned} C_1= \frac{\int d\Phi ~ 2 \text {Re}\Bigl ({\mathcal {M}}^{0 *} {\mathcal {M}}^1_{\lambda _3^{\text {SM}}}\Bigr )}{\int d\Phi ~|{\mathcal {M}}^0|^2} \end{aligned}$$

(16)

where the integration in $d \Phi$ is over the phase space of the final-state particles, ${\mathcal {M}}^{0}$ is the Born amplitude and ${\mathcal {M}}^1_{\lambda _3^{\text {SM}}}$ is the $\lambda _{3}^{\mathrm{SM}}$-linearly-dependent contribution in the the loop-corrected amplitude evaluated in the SM. However, since in the $h \rightarrow \gamma Z$ case the phase-space integral is just a multiplicative factor and both amplitudes are purely real, $C_1$ can be more easily written as

$$\begin{aligned} C_1 = \frac{2 ~ {\mathcal {F}}^{\mathrm{{NLO}}}_{\text {1PI}}}{{\mathcal {F}}^{{\mathrm{{LO}}}}}, \end{aligned}$$

(17)

where ${\mathcal {F}}^{{\mathrm{{NLO}}}}_{\text {1PI}}$ represents the one-particle irreducible (1PI) two-loop diagrams containing an $h^3$ interaction.

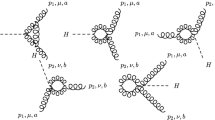
In order to evaluate the $C_1$ coefficient we generated, in the UG, the two-loop diagrams contributing to the $h \rightarrow \gamma Z$ amplitude using the Mathematica package FeynArts [19]. As in the one-loop case the diagrams can be assigned to the two categories ${\mathcal {F}}_t, \, {\mathcal {F}}_W$, see Fig. 1. The diagrams were manipulated using the package FeynCalc [20, 21], expanded in the external momenta and reduced to scalar integrals using a private code. After the reduction to scalar integrals we were left with the evaluation of two-loop vacuum integrals that were computed analytically using the results of Ref. [22].

The result for $C_1$ is automatically finite in the unitary gauge, i.e. no renormalization is needed, since the LO result does not depend on the trilinear coupling. As expected the fermionic and bosonic contributions are separately finite.

3 $\lambda _{3}$-dependent contribution in a $(\Phi ^\dagger \Phi )^n$ theory

This section is devoted to discuss how the result obtained in the $\kappa$-framework working in the UG can be recovered using a SM Lagrangian with a modified scalar potential of the form

$$\begin{aligned} V^{NP}= & {} \sum _{n=1}^N c_{2n} ( \Phi ^\dagger \Phi )^n\,, \nonumber \\ \Phi= & {} \left( {\begin{array}{c}\phi ^+\\ \frac{1}{\sqrt{2}}( v+ h+ i \phi _2)\end{array}}\right) \,, \end{aligned}$$

(18)

working in a renormalizable gauge that we choose for simplicity to be the Feynman gauge (FG). In Eq. (18) N can be a finite integer or infinite, and in the latter case we assume the series to be convergent, while the SM potential is recovered setting $N=2$ with $c_2 = - m^2$ and $c_4 = \lambda$, where $-m^2$ is the Higgs mass term in the SM Lagrangian in the unbroken phase.

A simplified discussion of the equivalence of the $\kappa$-framework with a $(\Phi ^\dagger \Phi )^n$ theory, when the modification of the trilinear Higgs self-coupling appears at the two-loop level, was presented in Ref. [12]. In that reference the renormalization of the scalar potential in Eq. (18) was not discussed in detail because it was not needed. While the calculation of $\Gamma (h \rightarrow \gamma Z)$ in the $\kappa$-framework is automatically finite, the one in a $(\Phi ^\dagger \Phi )^n$ theory requires to address the renormalization of the scalar potential. It is then natural to try to devise a renormalization procedure such that one obtains automatically the same result in the two approaches.

The potential $V^{NP}$ in Eq. (18) up to quintic interactions can be written as

$$\begin{aligned} V_{5\phi }^{NP}= & {} v\, \tau \, h+ \tau \left[ \phi ^+\phi ^-+ \frac{1}{2} \phi _2^2 \right] + \frac{1}{2} m_{ \scriptscriptstyle H}^2 \,h^2 + \left( \frac{M_{ \scriptscriptstyle H}^2}{2 v} + v\,d \lambda _{3}\right) h^3 \nonumber \\&+ \frac{M_{ \scriptscriptstyle H}^2}{ v} \,h\left[ \phi ^+\phi ^-+ \frac{1}{2} \phi _2^2 \right] + \frac{M_{ \scriptscriptstyle H}^2}{2\,v^2} \left[ \phi ^+\phi ^-+ \frac{1}{2} \phi _2^2 \right] ^2 \nonumber \\&+ \left( \frac{M_{ \scriptscriptstyle H}^2}{2\, v^2} + d \lambda _4\right) \frac{1}{4} h^4 + \left( \frac{M_{ \scriptscriptstyle H}^2}{2 v^2} + 3 \,d \lambda _{3}\right) h^2 \left[ \phi ^+\phi ^-+ \frac{1}{2} \phi _2^2 \right] \nonumber \\&+ \frac{1}{v} \left\{ d\lambda _5 h^5 + \left( -3 \,d \lambda _{3}+ d \lambda _4 \right) h^3 \,\left[ \phi ^+\phi ^-+ \frac{1}{2} \phi _2^2 \right] \right. \nonumber \\&\left. + 3 \,d \lambda _{3}\, h\,\left[ \phi ^+\phi ^-+ \frac{1}{2} \phi _2^2 \right] ^2 \right\} ~, \end{aligned}$$

(19)

where the various parameters that appear in Eq. (19), i.e. $\tau ,\, m_{ \scriptscriptstyle H}^2,\, M_{ \scriptscriptstyle H}^2$ etc., can be expressed, as explained in Ref. [12], as a combination of $c_{2n}$ coefficients and powers of v that comes from the identification inside any $(\Phi ^\dagger \Phi )^n$ term of the various $h^i\, [\phi ^+\phi ^-+ \phi _2^2/2]^j$ ($i=0,\ldots ,5; \, j=0,1,2$) interactions.

Fig. 2

Examples of one-loop diagrams contributing in the FG to the $h \rightarrow \gamma Z$ process whose renormalization gives rise to a contribution proportional to an anomalous Higgs self-coupling

In particular the condition of the minimum of the potential specifies $\tau$, or

$$\begin{aligned} \left. \frac{d \, V^{NP}}{d \, h} \right| _{h=0} = v\,\tau = v\,\sum _{n=1}^N c_{2n}\, n \left( \frac{v^2}{2}\right) ^{n-1} =0, \end{aligned}$$

(20)

while the Higgs mass term reads

$$\begin{aligned} m_{ \scriptscriptstyle H}^2= & {} v^2\,\sum _{n=1}^N c_{2 n}\, n(n-1) \left( \frac{v^2}{2}\right) ^{n-2} \nonumber \\&+ \sum _{n=1}^N c_{2 n}\, n \left( \frac{v^2}{2}\right) ^{n-1} \equiv M_{ \scriptscriptstyle H}^2 + \tau \end{aligned}$$

(21)

that enforcing the minimum condition implies $m_{ \scriptscriptstyle H}^2 = M_{ \scriptscriptstyle H}^2$. The anomalous contributions in Eq. (19) are:

$$\begin{aligned} d \lambda _{3}= & {} \frac{1}{3} \sum _{n=3}^N c_{2n} \, n(n-1)(n-2) \left( \frac{v^2}{2}\right) ^{n-2} \,, \end{aligned}$$

(22)

$$\begin{aligned} d \lambda _4= & {} \frac{2}{3} \sum _{n=3}^N c_{2n} \, n^2(n-1)(n-2) \left( \frac{v^2}{2}\right) ^{n-2} \,, \end{aligned}$$

(23)

$$\begin{aligned} d \lambda _5= & {} \frac{1}{30} \sum _{n=3}^N c_{2n} \, n(n-1)(n-2)\nonumber \\&\times \left( \frac{3}{2}-4 \,n+ 2 n^2\right) \left( \frac{v^2}{2}\right) ^{n-2} ~. \end{aligned}$$

(24)

Equations (22–24) give rise to anomalous trilinear and quadrilinear Higgs self-interactions as well as a quintic one. The $h^5$ interaction proportional to $d \lambda _5$ is not relevant for our discussion while from the $h^3$ interaction we are going to identify $\kappa _{\lambda }= 1 + 2 v^2/m_{ \scriptscriptstyle H}^2 \, d\lambda _{3}$, as already done in Ref. [12].

All the diagrams contributing to $h \rightarrow \gamma Z$ in the UG at the one-loop level contain only quantities (i.e. the gauge couplings, the top and W mass) whose one-loop renormalization is not affected by Higgs self-interactions.⁴ Instead, the situation is different in the FG where, at one loop, there are diagrams, see Fig. 2, that contain a coupling proportional to $M_{ \scriptscriptstyle H}^2/v$ whose renormalization is affected by anomalous Higgs self-couplings. Then, the calculation in the FG requires to set a renormalization procedure for $M_{ \scriptscriptstyle H}^2/v$ as well as for the masses of the unphysical scalars.

Before discussing the renormalization of $V^{NP}$ we would like to notice few things concerning the one-particle-irreducible (1PI) two-loop diagrams in the FG. The 1PI diagrams contain terms proportional to $(d \lambda _{3})^2$, i.e. $(\kappa _{\lambda })^2$, see Fig. 3a, besides those from the wave-function renormalization of the external Higgs fields. Furthermore, there are 1PI diagrams proportional to $d \lambda _4$ from the quintic $h^3 \phi ^+\phi ^-$ coupling, see Fig. 3b. Neither of these two kind of contributions are present in the $\kappa$-framework result and we expect our renormalization procedure to cancel exactly these contributions.

Fig. 3

Examples of 1PI diagrams that contain contributions not present in the $\kappa$-framework result. The dot (square) represents a coupling containing $d \lambda _{3}$ ($d \lambda _4$): a Contributions proportional to $(d \lambda _{3})^2$. b Contributions proportional to $d \lambda _4$

We are actually interested in defining the one-loop counterterms associated to $M_{ \scriptscriptstyle H}^2,\, \tau$ and v. Following closely Ref. [23] we assumed $V^{NP}$ to be written in terms of bare quantities that are shifted according to: $c_{2n} \rightarrow c_{2n}^r - \delta c_{2n},\, v \rightarrow v^r - \delta v$. As a consequence

$$\begin{aligned} V^{NP} = V^{NP}_r - \delta V^{NP}~, \end{aligned}$$

(25)

where the renormalized potential up to quintic couplings has exactly the same form given in Eq. (19) but written in terms of renormalized quantities, while the relevant terms in $\delta V^{NP}$ that require to be defined at one-loop are: $\tau ,\, m_{ \scriptscriptstyle H}^2,\, M_{ \scriptscriptstyle H}^2,\, v$.

To identify the vacuum as the minimum of the radiatively corrected potential we set:

$$\begin{aligned} \delta ( v\, \tau )= & {} v\, \delta \tau = v\,\sum _{n=1}^N \left( \frac{v^2}{2}\right) ^{n-1} \nonumber \\&\times \left[ \delta c_{2n}\, n + c_{2n}\, n (n-1)\, 2 \frac{\delta v}{v} \right] = - T \end{aligned}$$

(26)

where iT is the sum of the tadpole diagrams with external leg extracted. We identify $m_{ \scriptscriptstyle H}^2$ in Eq. (19) as the on-shell Higgs mass leading to the condition (see Eq. (21))

$$\begin{aligned} \delta m_{ \scriptscriptstyle H}^2 = \delta M_{ \scriptscriptstyle H}^2 + \delta \tau = {\mathrm{Re}}\, \Pi _{hh}(m_{ \scriptscriptstyle H}^2) \end{aligned}$$

(27)

where $-i\, \Pi _{hh}(q^2)$ is the sum of all 1PI self-energy diagrams and in Eq. (27) no tadpole contribution is present because Eq. (26) is enforced. Eqs. (26, 27) imply

$$\begin{aligned} \delta M_{ \scriptscriptstyle H}^2 = {\mathrm{Re}}\, \Pi _{hh}(m_{ \scriptscriptstyle H}^2) + \frac{T}{v}~. \end{aligned}$$

(28)

The quantities ${\mathrm{Re}}\, \Pi _{hh}(m_{ \scriptscriptstyle H}^2)$ and T do contain terms proportional to $d \lambda _{3}$ and $d \lambda _4$ that will be relevant for our discussion. The other quantity we are interested in is v, whose renormalization can be set, for example, either from the muon-decay process or the W mass. In both cases the corresponding counterterm $\delta v$ does not contain (at one-loop) terms proportional to an Higgs anomalous self-coupling and therefore will not enter in our discussion.

Equations (26) and (28) are the two definitions needed to address the two-loop calculation in the FG of the effect induced by an anomalous Higgs trilinear coupling on processes that are not sensitive at the tree or one-loop level to an $h^3$ interaction.

We find for the contribution proportional to $d \lambda _{3}$ and $d \lambda _4$ in T/v and ${\mathrm{Re}}\, \Pi _{hh}(m_{ \scriptscriptstyle H}^2)$ in units $\alpha /(4 \pi \sin ^2 \theta _{W})\, m_{ \scriptscriptstyle H}^2/( 8 \,m_{ \scriptscriptstyle W}^2)$:

$$\begin{aligned} \frac{T^{d\lambda }}{v}= & {} \left( 1+ 2 \frac{v^2}{m_{ \scriptscriptstyle H}^2} d \lambda _{3}\right) \,3 \, m_{ \scriptscriptstyle H}^2 \left( \frac{1}{\epsilon } +1- \ln \frac{m_{ \scriptscriptstyle H}^2}{\mu ^2} \right) \end{aligned}$$

(29)

$$\begin{aligned} {\mathrm{Re}}\, \Pi ^{d \lambda }_{hh}(m_{ \scriptscriptstyle H}^2)= & {} - \left( 1+ 2 \frac{v^2}{m_{ \scriptscriptstyle H}^2} d \lambda _{3}\right) ^2\, 9\, m_{ \scriptscriptstyle H}^2 \left( \frac{1}{\epsilon } +2 - \frac{\pi }{\sqrt{3}} - \ln \frac{m_{ \scriptscriptstyle H}^2}{\mu ^2} \right) \nonumber \\&- \left( 1+ 2 \frac{v^2}{m_{ \scriptscriptstyle H}^2} d \lambda _4 \right) \,3 \, m_{ \scriptscriptstyle H}^2 \left( \frac{1}{\epsilon } +1- \ln \frac{m_{ \scriptscriptstyle H}^2}{\mu ^2} \right) \nonumber \\&- \left( 1+ 6 \frac{v^2}{m_{ \scriptscriptstyle H}^2} d \lambda _{3}\right) \left[ 2\, m_{ \scriptscriptstyle W}^2 \left( \frac{1}{\epsilon } +1-\ln \frac{m_{ \scriptscriptstyle W}^2}{\mu ^2} \right) \right. + \nonumber \\&\left. m_{ \scriptscriptstyle Z}^2 \left( \frac{1}{\epsilon } +1-\ln \frac{m_{ \scriptscriptstyle Z}^2}{\mu ^2} \right) \right] \end{aligned}$$

(30)

where $\epsilon =(4 - nd)/2$, nd being the dimension of the space-time, and $\mu$ is t Hooft mass.

From the inspection of Eq. (30) one sees that the counterterm associated to $M_{ \scriptscriptstyle H}^2$ (Eq. (28)) contains terms proportional to $(d\lambda _{3})^2$ and $d \lambda _4$. It is easy to show that the renormalization of the one-loop diagrams proportional to $M_{ \scriptscriptstyle H}^2$ (see Fig. 2) cancels exactly the 1PI two-loop contribution proportional to $(d \lambda _{3})^2$, see Fig. 3a, as well as the one proportional to $d \lambda _4$, see Fig. 3b, restoring in the FG the same dependence on the anomalous coupling found in the $\kappa$-framework, i.e linear in $\kappa _{\lambda }$, apart the quadratic contribution related to the wave function renormalization, and no dependence on $\lambda _4$.

The renormalization condition Eq. (26) specifies also the part of the mass counterterms for the unphysical scalars that is affected by anomalous Higgs self-couplings, i.e. $\delta \tau$. A detailed discussion of the role of this counterterm in the cancellations in the FG between 1PI and counterterm diagrams can be found in Ref. [12].

Fig. 4

Two-loop reducible diagrams that give rise to a contribution proportional to $d \lambda _{3}$ in the FG. The meaning of the dot is as in Fig. 3

To complete the calculation of the contribution of an anomalous trilinear Higgs self-coupling in the FG one has to take into account also the effect of the reducible diagrams shown in Fig. 4. In a renormalizable gauge diagrams that contain a $\gamma Z$ self-energy evaluated at vanishing external momentum also contribute to ${\mathcal {F}}_W$. These diagrams do not contribute in the UG because in this gauge the $\gamma Z$ self-energy evaluated at vanishing external momentum is zero.

We have computed the functions ${{{\mathcal {F}}}}_t$ and ${{{\mathcal {F}}}}_W$ in the FG and found agreement with the result in the UG within the order of our approximation, as discussed in the next section. We remark that with our choice of renormalization conditions the agreement is found in a straightforward way because both results are expressed in terms of physical quantities.

As a final remark we notice that the potential in Eq. (18) has N $c_{2n}$ coefficients, that are assumed to be bare quantities, while we needed to impose only two renormalization conditions, Eq. (26) and (27). Furthermore, the modifications of the Higgs self-couplings with respect to the SM values, $d \lambda _i, i=3 \ldots$, involve only coefficients with $n \ge 3$ (see Eqs. (22–24)). Then, on one side we have constructed a framework such that the limit to the SM case is straightforward. On the other, because we did not need to specify any renormalization condition on the modifications $d \lambda _i$, the renormalization of the latter is still free and can be specified via other processes.

4 Results

In this section we present the results for the $C_1$ coefficient. In Table 1 we give the numerical results for the first four orders of the expansion of ${\mathcal {F}}_t^{{\mathrm{{NLO}}}}$ and ${\mathcal {F}}_W^{{\mathrm{{NLO}}}}$ up to and including terms of ${\mathcal {O}}(h_{4t}^3)$ and ${\mathcal {O}}(h_{4w}^3)$, respectively. The input parameters used are the same of Ref. [5], or

$$\begin{aligned} m_{ \scriptscriptstyle W}= & {} 80.385,\, m_{ \scriptscriptstyle Z}= 91.1876,\,\nonumber \\ m_{ \scriptscriptstyle H}= & {} 125, \, m_{t}= 172.5 \end{aligned}$$

(31)

where all the masses are in GeV.

Table 1 Small-momentum expansion results for the two-loop $\lambda _3$-dependent contributions to the $h \rightarrow \gamma Z$ amplitude. The importance of each term in the expansion with respect to the first one is also shown

Fig. 5

Modification of the $h \rightarrow \gamma Z$ decay width (a) and branching ratio (b) due to an anomalous $\lambda _3$

Table 2 Relative importance of the difference between the UG and FG results for the bosonic contributions, for different orders of the expansion

The table shows that the expansions of both the fermionic and bosonic contribution have a good convergence. In particular the last term in the fermionic expansion, ${\mathcal {O}} (h_{4t}^3)$, contributes to the total fermionic contribution at the level of 1%, while in the bosonic case the last term, ${\mathcal {O}} (h_{4w}^3)$, contributes to the total at the level of 2%. Given ${\mathcal {F}}^{{\mathrm{{LO}}}}=-5.29$ we find $C_1 = 0.72 \cdot 10^{-2}$, a value larger than the $C_1$ coefficient for the $h \rightarrow \gamma \gamma$ decay ($C_1^{\gamma \gamma }=0.49 \cdot 10^{-2}$) and close to the one of the $h \rightarrow ZZ$ decay ($C_1^{ZZ}=0.83 \cdot 10^{-2}$) that is the decay mode most sensitive to an anomalous trilinear coupling.

The effect of an anomalous $\lambda _3$ in the partial decay width $\Gamma (h \rightarrow \gamma Z)$ and in the corresponding BR is presented in Fig. 5 as a function of $\kappa _{\lambda }$. Similarly to the other decay modes of the Higgs boson [5], the correction to the partial decay width can be substantial even for $-10 \lesssim \kappa _{\lambda }\lesssim 10$, while for the same range of $\kappa _{\lambda }$ values the correction to the BR is much smaller because in the BR the universal quadratic dependence on $\kappa _{\lambda }$ in Eq. (5) cancels out.

Finally we want to comment on the numerical agreement between the calculation using the $\kappa$-framework working in the UG and the one in a $(\Phi ^\dagger \Phi )^n$ theory working in the FG. While the results of the expansion for the fermionic contribution in the UG and in FG are equal at the analytic level term by term, the same is not true for the bosonic contribution. The reason is related to the fact that the expansion in the external momenta is, in general, not the same in the two gauges. Indeed, at any order of the expansion, part of the kinematic dependence in the UG is transfer in a FG to couplings as can be easily understood looking at the one-loop diagrams. The diagrams in Fig. 2, that appear in the FG, are proportional to $m_{ \scriptscriptstyle H}$ from the coupling $h\phi ^+\phi ^-$, while in the UG the only dependence on $m_{ \scriptscriptstyle H}$ at one-loop is of kinematical origin when the external momenta are evaluated on-shell. In this situation we expect that the evaluation of two-loop integrals via an expansion in kinematical variables will not give, at a fixed order, the same number in the UG and FG. However, we expect the numerical difference between the two results to be of higher order with respect to the last known term.

Defining the quantity

$$\begin{aligned} \Delta {\mathcal {F}}_W = \Biggl |\frac{2 ({\mathcal {F}}_W^\text {UG}-{\mathcal {F}}_W^\text {FG})}{ ({\mathcal {F}}_W^\text {UG}+{\mathcal {F}}_W^\text {FG})}\Biggr | \end{aligned}$$

(32)

as the relative difference between the results in the UG and the FG, we find $\Delta {\mathcal {F}}_W =2.3\%$ for the total result, that is well within the expected accuracy of an expanded result up to and including $h_{4w}^3$ terms. In Table 2 we present $\Delta {\mathcal {F}}_W$ order by order in the expansion, to show the nice convergence pattern between the numerical values in the UG and in the FG.

5 Conclusions

In this work we have discussed the modifications in the partial decay width $\Gamma (h \rightarrow \gamma Z)$ and in its BR induced by an anomalous trilinear Higgs self-coupling. The two-loop computation has been performed in the $\kappa$-framework and in a $(\Phi ^\dagger \Phi )^n$ theory. In the latter case we had to address the renormalization of the scalar potential. We showed that the conditions on the minimum of the potential (Eq. (26)) and on the Higgs mass (Eq. (28)) are sufficient in order to obtain a finite result in the $(\Phi ^\dagger \Phi )^n$ theory in agreement with the one obtained in the $\kappa$-framework within the order of our approximate calculation. It should be remarked that the parameter $\kappa _{\lambda }$ found is not, at this order of the computation, energy-scale dependent. Furthermore, the two above renormalization conditions do not actually specify the Wilson coefficients of operators with dimension larger than 4.

We have found that the sensitivity of the $h \rightarrow \gamma Z$ process to an anomalous trilinear Higgs self-coupling is very similar to that of the $h \rightarrow WW$ mode that is the second most sensitive mode after the $h \rightarrow ZZ$ one [5].

The same renormalization framework employed in this work can be used to discuss the $h \rightarrow \gamma \gamma$ decay in a $(\Phi ^\dagger \Phi )^n$ theory or, if only the terms $n\le 3$ are considered, in the SMEFT with only the $O_6$ operator. For this decay there are in the literature two results, not in agreement, one obtained in the $\kappa$-framework via an expansion in the external momenta up to and including $h^3_{4t}$, $h^3_{4w}$ terms [5] and one in the SMEFT where the diagrams were evaluated in the limit $m_{ \scriptscriptstyle W}\rightarrow \infty$ or equivalently $m_{ \scriptscriptstyle H}\rightarrow 0$ [6]. As said in the Introduction these two results show a different dependence on the energy scale at which the contribution to the $h \rightarrow \gamma \gamma$ width induced by an anomalous Higgs trilinear coupling is evaluated. Instead, the result of Ref. [6] is expected to correspond to the leading term in the expansion of Ref. [5] showing the same energy-scale dependence.

We proved by an explicit calculation that, in the case of the $h \rightarrow \gamma \gamma$ decay width, the result obtained using a $(\Phi ^\dagger \Phi )^n$ theory with the renormalization conditions discussed in section 3 is identical, at the analytic level term by term, with that obtained in the $\kappa$-framework confirming the result of Ref. [5].

It is not easy to pin down the source of discrepancy with the result in Ref. [6]. We suspect that it could be due to a different way of taking into account the renormalization of $M_{ \scriptscriptstyle H}^2$ that gives a contribution also in the limit $m_{ \scriptscriptstyle H}\rightarrow 0$ taken in that work.