1 Introduction

The Event Horizon Telescope (EHT) collaboration has recently released an image of a supermassive black hole in M87 [1,2,3,4,5,6]. The image shows that there is a dark interior surrounded by a bright ring, which are called the black hole shadow and photon ring, respectively. The shadow and photon ring result from the deflections of light, or gravitational lensing by the black holes, a prediction from Einstein’s general relativity (GR) [7]. Therefore, the shadow image of black hole in M87 from EHT is strong evidence for GR.

The deflection of light by an intense star or black holes was initiated in [8, 9]. Later, it was extended to a black hole surrounded by a thin accretion disk [10]. According to these papers, there exists a critical curve in the observed image of the black hole. When traced backwards from the distant observer, the light ray from this critical curve will asymptotically approach a bound photon orbit. This bound orbits for Schwarzschild black hole is \(r=3M\) (M is the mass of the black hole), and the critical curve has the radius of \(b=\sqrt{27}M\) (b is called the impact parameter). Thus, the shadow of the black hole represents the dark interior of the critical curve. In [11], the authors stated that the size and the profile of the shadow would depend on the location and form of the accretion surrounding the black hole. However, this is not always true. The models in [11] were not so realistic as to describe the real world, as commented by [12]. In fact, for some kind of accretion, such as advection dominated accretion flow, which is more realistic in the Universe, the size of the shadow will only weakly be affected by the profile of the accretion [12].

So far, the study of shadows of black holes has become a subject of great interest [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. In particular, the shadows of a high-redshift supermassive black hole may serve as the standard rulers [22], which would constrain the cosmological parameters. Moreover, the EHT data may impose constraints in particle physics via the mechanism of superradiance [16, 24, 25].

Recent astronomical observations show that the Universe is undergoing accelerating expansion [40,41,42], implying a state of negative pressure. Quintessence dark energy is one of the candidates to interpret the negative pressure. The state equation of quintessence dark energy is governed by the pressure p and the energy density \(\rho \) with \(p=w\rho \), where w is the state parameter. It is assumed that the range \(-\,1<w<-\,1/3\) causes the acceleration of the Universe. Black holes in quintessence dark energy models were extensively studied [43]. Investigating the shadows of black hole in the quintessence dark energy model will bring new insights and impose restrictions to the quintessence model. Previous related work on null geodesics or shadows in the dark energy model can be found in [44, 45].

In this paper, we will investigate the shadow images of quintessence black holes with different accretions. In particular, we study the geometrically thin and optically thin-disk accretion and spherically symmetric accretion. Apparently different accretions will lead to different shadow images. Specifically, for the thin-disk accretion, the images of the black hole comprise the shadows, the lensing rings and the photon rings. The last result from the intersections of the light rays and the thin accretion for many times. Although the existence of different emission profiles of the accretion is important to the observed specific intensities, the direct image from accretion makes major contributions to the brightness of the image. Besides, the lensing ring makes small contributions and the photon ring makes negligible contributions to the observed specific intensities. For the spherically symmetric accretions, the shadows and photon rings are also spherically symmetric. The static accretion and an infalling accretion will have different impacts to the observed specific intensities, although the radii of the shadows are not changed. Specifically, the infalling accretion will have an extra Doppler effect, which will lead to darker shadows than the static case. A key point in the cosmological black hole is that there exists a domain of outer communication between the event horizon and the cosmological horizon [46, 47]. Therefore, various quintessence state parameters w will lead to different distances between the event horizon and the cosmological horizon. This will certainly have an impact on the distance between the observer (near cosmological horizon) and the accretion (near the event horizon). Therefore, different quintessence state parameters will lead to different forms of the observed specific intensities.

This paper is arranged as follows: in Sect. 2 the black hole solutions surrounded by quintessence matter and the light deflections by the quintessence black hole are introduced; in Sect. 3 the shadow images of the black hole with thin-disk accretion are given; in Sect. 4, we show the images of the black hole with spherically symmetric accretions; finally, we draw the conclusions and present discussions in Sect. 5.

2 Light deflection by a black hole in quintessence dark energy

The geometry of a black hole in a quintessence dark energy model can be expressed as [43]

$$\begin{aligned} \mathrm{d}s^2 = -f(r) \mathrm{d}t^2 + f(r)^{-1} \mathrm{d}r^2 + r^2 ( \mathrm{d} \theta ^2 + \sin ^2\theta \mathrm{d} \psi ^2), \end{aligned}$$
(2.1)

where

$$\begin{aligned} f(r)= 1 - \frac{2 M}{r}- \frac{a}{ r^{ 3 w + 1} }, \end{aligned}$$
(2.2)

in which M is the mass of the black hole, a and w are the normalization factor and state parameter, respectively. One should note that the line element in Eqs. (2.1) and (2.2) is a special single-component form from [43]. However, this solution is neither a perfect fluid spacetime, nor is the cosmologist’s notion of quintessence as discussed in [48]. Only after averaging all the directions, its stress–energy tensor can be related to the dark energy. For the case of \(w= -\,1\), the metric in Eq. (2.2) reduces to the Schwarzschild–de Sitter black hole with

$$\begin{aligned} f(r)= 1 - \frac{ 2 M}{ r}- a r^2, \end{aligned}$$
(2.3)

which has both an event horizon \(r_{h}\) and a cosmological horizon \(r_{c}\). For \(w = -\frac{2}{3}\), we can obtain the event horizon and cosmological horizon as

$$\begin{aligned} r_{h} = \frac{ 1 - \sqrt{ 1 - 8 M a} }{ 2 a}, \quad r_{c} = \frac{ 1 + \sqrt{ 1 - 8 M a} }{ 2 a}, \end{aligned}$$
(2.4)

where the restriction \( 8 M a <1\) has been imposed. For \(w= -\,1/3\), the metric in Eq. (2.2) reduces to the Schwarzschild black hole, which has only an event horizon. In this paper, we are interested in the quintessence dark energy model, in which the state parameter w is restricted to the region \(-\,1< w < -\frac{1}{3}\), and there always exist an event horizon and a cosmological horizon.Footnote 1 The region between the two horizons is called the domain of outer communication [46, 47], since any two observers in this region may communicate with each other without being hindered by a horizon.

The equation of state for the quintessence dark energy is

$$\begin{aligned} p = w \rho , \quad \rho = - \frac{a}{2}\frac{3 w}{r^{3(1+w)}} \end{aligned}$$
(2.5)

in which p is the pressure, while \(\rho \) is the energy density. In order to cause cosmic acceleration, the pressure of the quintessence dark energy p should be negative, thus the energy density \(\rho \) is positive if the normalization factor a is positive. In this paper, we will only focus on the effect of the state parameter on the shadows of a quintessence black hole, and we will set the normalization factor \(a=0.05\) and black hole \(M=1\) thereafter.Footnote 2

In order to investigate the light deflection in the quintessence black hole, we need to find how the light ray moves in this spacetime. We will resort to the following Euler–Lagrange equation:

$$\begin{aligned} \frac{d}{ds}\left( \frac{\partial {\mathcal {L}}}{\partial \dot{x}^{\mu }}\right) =\frac{\partial {\mathcal {L}}}{\partial x^{\mu }}, \end{aligned}$$
(2.6)

in which s is the affine parameter of the light trajectory, the symbol  \(\dot{}\)  is the derivative with respect to s, thus \(\dot{x}^{\mu }\) the four-velocity of the light ray and \({\mathcal {L}}\) is the Lagrangian, taking the form

$$\begin{aligned} {\mathcal {L}}&=\frac{1}{2}g_{\mu \nu }\dot{x}^{\mu }\dot{x}^{\nu }\nonumber \\&=\frac{1}{2}\left( - f(r)\dot{t}^2+\frac{\dot{r}^2}{f(r)}+r^2\left( \dot{\theta }^2+\sin ^2{\theta }~ \dot{\psi }^2 \right) \right) . \end{aligned}$$
(2.7)

We will also impose the initial conditions \(\theta = \pi /2\), \(\dot{\theta } = 0\). That is, the light rays always move in the equatorial plane. In addition, since the metric coefficients do not depend explicitly on time t and azimuthal angle \(\psi \), there are two conserved quantities correspondingly. Combining Eqs. (2.2), (2.6) and (2.7), the time, azimuthal and radial components of the four-velocity satisfy the following equations of motions:

$$\begin{aligned}&\dot{t}=\frac{1}{b \left( 1 - \frac{2 M}{r}- \frac{a}{ r^{ 3 w + 1} }\right) }, \end{aligned}$$
(2.8)
$$\begin{aligned}&\dot{\psi }=\pm \frac{1}{r^2}, \end{aligned}$$
(2.9)
$$\begin{aligned}&\dot{r}^2+\frac{1}{r^2} \left( 1 - \frac{2 M}{r}- \frac{a}{ r^{ 3 w + 1} }\right) = \frac{1}{b^2}, \end{aligned}$$
(2.10)

where \(+\) and − in Eq. (2.9) correspond to the counterclockwise and clockwise direction, respectively, for the motion of light rays. The parameter \(b={|L|}/{E} \) is the impact parameter, in which E and L are the conserved quantities with respect to the time and azimuthal direction. Moreover, Eq. (2.10) can be rewritten as

$$\begin{aligned} \dot{r}^2+V(r)=\frac{1}{b^2}, \end{aligned}$$
(2.11)

where

$$\begin{aligned} V(r)=\frac{1}{r^2} \left( 1 - \frac{2 M}{r}- \frac{a}{ r^{ 3 w + 1} }\right) \end{aligned}$$
(2.12)

is an effective potential. At the photon sphere, the motions of the light ray satisfy \(\dot{r}=0\), and \(\ddot{r}=0\), which also means

$$\begin{aligned} V(r)=\frac{1}{b^2}, \quad V^{'}(r) = 0, \end{aligned}$$
(2.13)

where the prime denotes the derivative with respect to the radial coordinate r. Based on Eq. (2.13), we can obtain the radius and impact parameter of the photon sphere for different w. Generically, it is difficult to obtain the analytic results of the radius and impact parameter. But for \(w=-\,2/3\) the metric function can be simplified; thus the radius and impact parameter of the photon sphere can be expressed as

$$\begin{aligned}&r_{ph}= \frac{1-\sqrt{1-6 a M}}{a}, \end{aligned}$$
(2.14)
$$\begin{aligned}&b_{ph}= \frac{\sqrt{2} \sqrt{6 M \sqrt{1-6 a M}-\frac{\sqrt{1-6 a M}}{a}+\frac{1}{a}-9 M}}{\sqrt{8 a^2 M-a}}.\nonumber \\ \end{aligned}$$
(2.15)

For the other w, the numerical results of radii and impact parameters of the photon sphere, and of the event horizons and cosmological horizons are listed in Table 1. From this table, we see that, as one increases the absolute value of w, the event horizon \(r_h\) and impact parameter \(b_{ph}\) increase as well, while the cosmological horizon \(r_c\) decreases. The radius of the photon sphere, however, is non-monotonic, it increases at first and then decreases around \(w=-\,0.7\). In addition, from Table 1 we see that the locations of the event horizon and the cosmological horizon become closer as |w| increases, which leads to a narrower domain of the outer communication.

Table 1 The values of radius \(r_{ph}\) and impact parameter \(b_{ph}\) of the photon sphere, and of the event horizon \(r_h\) and cosmological horizon \(r_c\) for various w with \(M=1\), \(a=0.05\)
Full size table
Fig. 1
figure 1

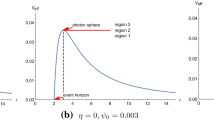
The profile of the effective potential (blue lines) for \(w=-\,0.5\) (left panel) and \(w=-\,0.7\) (right panel) with \(M=1\) and \(a=0.05\). The dashed lines indicate the radii of the photon sphere \(r_{ph}\). Region 2 (green lines) correspond to \(V(r)=1/b_{ph}^2\), while Region 1 and Region 3 correspond to \(V(r)<1/b_{ph}^2\) and \(V(r)>1/b_{ph}^2\), respectively

Full size image

From Eq. (2.11), we see that the motion of the particle depends on the impact parameter and the effective potential. In Fig. 1, the effective potential is plotted for different state parameters \(w=-\,0.5\) and \(w=-\,0.7\). We can see that, at the event horizon, the effective potential vanishes. Then it increases and reaches a maximum at the photon sphere \(r_{ph}\), and subsequently decreases and vanishes at the cosmological horizon. Let us consider a light ray that moves in the radially inward direction. In Region 1, if the light ray starts its motion at \(r>r_{ph}\), the light ray will encounter the potential barrier and be reflected back to the outward direction. If the photon starts the motion at \(r<r_{ph}\), the photons will fall into the singularity. In Region 2, namely \(b=b_{ph}\), as the light ray approaches the photon sphere, it will revolve around the black hole infinitely many times since the angular velocity is non-zero. Actually, this orbit is circular and unstable [11]. In Region 3, the light ray will continue moving in the inward direction since it does not encounter the potential barrier. Finally, it will enter the inside of the black hole and fall into the singularity.

Since we have already obtained the effective potential, it is also convenient to obtain the effective force on the photon, which isFootnote 3

$$\begin{aligned} F = -\frac{1}{2} \frac{ \mathrm{d} V(r)}{\mathrm{d}r} =-\frac{3 M}{r^4}+\frac{1}{r^3}-\frac{1}{2} 3 a (w+1) r^{-3 w-4}.\nonumber \\ \end{aligned}$$
(2.16)

The first term, \(-\,{3 M}/{r^4}\), called the Newtonian term, is attractive as it is negative, while the second term, \(1/r^3\), is repulsive. The contribution of the quintessence dark energy comes from the third term \(-\,\frac{1}{2} 3 a (w+1) r^{-3 w-4}\), which plays the role of an attractive force.

Fig. 2
figure 2

The trajectories of the light ray for \(w=-\,0.5\) (left) and \(w=-\,0.7\) (right) with \(M=1\), \(a=0.05\). They are shown in the polar coordinates \((r, \psi )\). The red lines, green lines and blue lines correspond to \(b=b_{ph}\), \(b<b_{ph}\) and \(b>b_{ph}\) respectively. The spacing of the impact parameter is \(\Delta b=1/5\) for each light ray. The black hole is shown as the solid black disk and the photon orbit as a dashed line

Full size image

The trajectory of the light ray can be depicted on the basis of the equation of motion. Combining Eqs. (2.9) and (2.10), we have

$$\begin{aligned} \frac{\mathrm{d}r}{\mathrm{d}\psi }=\pm r^2 \sqrt{\frac{1}{b^2}-\frac{1}{r^2}\left( 1 - \frac{2 M}{r}- \frac{a}{ r^{ 3 w + 1} }\right) }. \end{aligned}$$
(2.17)

In order to integrate it out conveniently, we set \(u=1/r\). Thus, Eq. (2.17) becomes

$$\begin{aligned} \frac{\mathrm{d}u}{\mathrm{d}\psi }=\sqrt{\frac{1}{b^2}-u^2 (-a u^{3 w+1}-2 M u+1 )}\equiv \Phi (u). \end{aligned}$$
(2.18)

The geometry of the geodesics depends on the roots of the equation \( \Phi (u) =0\). In particular, for \( b>b_{ph}\), light will be deflected at the radial position \( u_i\), which satisfies \( \Phi (u_i) =0\). Therefore, it is important to find the radial position \(u_i\) in order to obtain the trajectory of the light ray. In addition, the location of the observer is important. Usually, the observer is located at an infinite boundary for the asymptotically flat spacetime. However, for the model of the quintessence black hole in our paper, the cosmological horizon is present. Physically, the observer should be located in the domain of outer communication, which is between the event horizon and cosmological horizon, just as in the de Sitter spacetime. For convenience, the observer in our paper is set near the cosmological horizon.Footnote 4

By virtue of Eq. (2.18), we can solve the trajectories of the light rays, shown in Fig. 2. All the light rays approach the black hole from the right side. The green, red and blue lines correspond to \(b<b_{ph}\), \(b=b_{ph}\) and \(b>b_{ph}\) respectively. Specifically, for the case of \(b<b_{ph}\), the light rays (green lines) drop all the way into the black hole. For \(b>b_{ph}\), the light rays (blue lines) are deflected but never enter the black hole. In particular, the light rays close to the black hole can even be reflected back to the right side, i.e., the side on which they approach the black hole. For \(b=b_{ph}\), the light rays (red lines) revolve around the black hole. This conclusion is consistent with those from the analysis of effective potential in Fig. 1. Indeed, Regions 1, 2, 3 in Fig. 1 correspond to the blue, red and green lines in Fig. 2, respectively.

We need to emphasize that, due to the existence of the cosmological horizon, different w will result in different geometries of the light rays. We have assumed that the observer is in the domain of the outer communications and sitting close to the cosmological horizon. Therefore, for the case of \(w=-\,0.5\) (left panel in Fig. 2), the cosmological horizon is very far from the event horizon (see Table 1 ). Therefore, the observed entering light rays are approximately parallel, which can be seen from the left panel of Fig. 2. However, for the case of \(w=-\,0.7\), the cosmological horizon is close to the event horizon (see Table 1). Therefore, the observed entering light rays behave significantly different from those of \(w=-\,0.5\) (see the right panel of Fig. 2), i.e., the entering light rays for \(w=-\,0.7\) are not parallel.

As the light is deflected, a shadow of the black hole will be formed. The light is emitted by the accretion matters; the profiles of the accretion matters thus are important for the shadows of the black holes. Next, we will investigate the effect of the profiles of the accretions on the shadows of the black holes. We will take the thin-disc accretion and spherical accretion as two examples.

3 Shadows, photon rings and lensing rings with thin-disk accretion

In this section, we consider an optically and geometrically thin-disk accretion around the black hole, viewed face-on. From [11], we know that an important feature of thin-disk accretion is that there are photon rings and lensing rings surrounding the black hole shadow. The lensing ring consists of light rays that intersect the plane of the disk twice outside the horizon, while the photon ringFootnote 5 comprises light rays that intersect the plane of the disk three or more times. Thus, the trajectory of the photon is important to distinguish the photon ring and lensing ring.

3.1 Number of orbits of the deflected light trajectories

Fig. 3
figure 3

Behavior of photons in the quintessence black hole as a function of impact parameter b with \(M=1\), \(a=0.05\), \(w=-\,0.5\) (top row) and \(w=-\,0.7\) (bottom row). (Left column) We show the fractional number of orbits, \(n =\psi /2 \pi \), where \(\psi \) is the total change in azimuthal angle outside the horizon. The direct, lensing and photon ring correspond to \( n<3/4\) (red), \( 3/4<n<5/4\) (blue), and \( n>5/4\) (green), respectively. (Right column) We show a selection of associated photon trajectories in the polar coordinates \((b, \psi )\). The spacings in impact parameter are 1/5, 1/100, 1/1000, for the direct (red), lensing (blue), and photon ring (green) bands, respectively. The black holes are shown solid black disks

Full size image

The trajectories of the light rays are shown on the right column of Fig. 3 for \(w=-\,0.5\) (top row) and \(w=-\,0.7\) (bottom row), respectively. In these figures, the red lines, blue lines and green lines are direct emission, lensing rings and photon rings, respectively.Footnote 6 This can be understood from the definition in [11]: these light rays intersect the disk plane once, twice and more than twice. It should be noted that due to the domain of outer communications, the light rays going towards the observer will behave differently for different state parameters w. For the case of \(w=-\,0.5\), the observer located near the cosmological horizon which is far away from the event horizon (see Table 1). Thus, the light rays near the observer are almost parallel, which is similar to the Schwarzschild black hole [11]. However, for \(w=-\,0.7\) the cosmological horizon is near the event horizon (refer to Table 1). Therefore, the light rays going towards the observer are not parallel, which is shown in the bottom row of the right panel of Fig. 3.

One can also use the total number of orbits, defined by \(n=\psi /2 \pi \), to distinguish the trajectories of the light rays [11]. The total numbers of orbits are shown in the left column of Fig. 3 for \(w=-\,0.5\) (top row) and \(w=-\,0.7\) (bottom row), respectively. We still use the red lines, blue lines and green lines to represent the direct emission, lensing rings and photon rings, respectively. Therefore, from the definitions of these light rings we can explicitly see that the direct emissions correspond to \(n<3/4\), while the lensing rings correspond to \(3/4<n<5/4\) and photon rings correspond to \(n>5/4\). For the case of \(w=-\,0.5\) and \(w=-\,0.7\), the parameter intervals of b for the direct emission, photon rings and lensing rings are listed in Eqs. (3.1) and (3.2). We have

$$\begin{aligned} w&=-\,0.5 {\left\{ \begin{array}{ll} \text {Direct emission}: n<3/4,~~~ b< 5.71774 \\ \quad \text {and} ~~ b> 7.76682 ,\\ \text {Lensing ring}: 3/4<n<5/4,~~~ 5.71774<b\\ \quad< 5.97314 \text {and} ~~ 6.04784<b< 7.76682 , \\ \text {Photon ring}: n>5/4,\\ \quad 5.97314< b < 6.04784, \end{array}\right. } \end{aligned}$$
(3.1)
$$\begin{aligned} w&=-\,0.7 {\left\{ \begin{array}{ll} \text {Direct emission}: n<3/4,~~~ b< 6.92848\\ \quad \text {and} ~~ b> 8.36103, \\ \text {Lensing ring}: 3/4<n<5/4,~~~ 6.92848\\ \quad<b< 7.2156 \text {and} ~~ 7.28972<b< 8.36103 , \\ \text {Photon ring}: n>5/4,\\ \quad 7.2156< b < 7.28972. \end{array}\right. } \end{aligned}$$
(3.2)

3.2 Observed specific intensities and transfer functions

Next, we will investigate the observed specific intensity of the thin-disk accretion. We assume that the thin disk emits isotropically in the rest frame of static worldlines. As in [11], we take the disk to lie in the equatorial plane of the black hole, with a static observer at the North pole. We denote the emitted specific intensity and frequency as \(I_{e}(r)\) and \(\nu _{e}\), the observed specific intensity and frequency as \(I_{obs}(r)\) and \(\nu \). Since \(I_{e}/\nu _e^3\) is conserved along a light ray from Liouville’s theorem, the observed specific intensity thus can be written as

$$\begin{aligned} I_{obs}(r)=f(r)^{3/2}I_{e}(r). \end{aligned}$$
(3.3)

The total specific intensity is obtained by integrating specific intensity with different frequencies:

$$\begin{aligned} I=\int I_{obs}(r) \mathrm{d}\nu =\int f(r)^{2}I_{e}(r)\mathrm{d}\nu _e=f(r)^{2}I_{em}(r), \end{aligned}$$
(3.4)

where \(I_{em}(r)=\int I_{e}(r)d\nu _e\) is the total emitted specific intensity near the accretion.

If a light ray traced backwards from the observer intersects the disk, it will pick up brightness from the disk emission. For \(3/4<n<5/4\), the light ray will bend around the black hole and hit the opposite side of the disk from the back (see the blue lines in Fig. 3). Thus, it will pick up additional brightness from this second passage through the disk. For \(n>5/4\), the light ray will bend around the black hole more, and then hit the front side of the disk once again (see the green lines in Fig. 3). This leads to additional brightness from the third passage through the disk. Therefore, the observed intensity is a sum of the intensities from each intersection, that is,

$$\begin{aligned} I(r)= \sum \limits _{m} f(r)^{2}I_{em}\mid _{r=r_m(b)}, \end{aligned}$$
(3.5)

where \(r_{m(b)}\), called the transfer function, is the radial position of the mth intersection with the disk plane outside the horizon. For simplicity, we have neglected absorption of the light for the thin accretion, which may decrease the observed intensity from the additional passages.

The transfer function describes the relation between the radial coordinate r and the impact parameter b. The slope of the transfer function, dr/db, is the demagnification factor. For different state parameters w, the transfer functions with respect to impact parameter b are shown in Fig. 4. The black line, orange line and red line represent the first (\(m=1\)), second (\(m=2\)) and third (\(m=3\)) transfer functions. The first transfer function corresponds to the direct image of the disk, and its slope is about 0.85 (0.67) for \(w=-\,0.5\) (\(w=-\,0.7\)). Therefore, the direct image profile is actually the redshifted source profile. The second transfer function corresponds to the lensing ring (including the photon ring). In this case, the observer will see a highly demagnified image of the back side of the disk. Finally, the third transfer function corresponds to the photon ring. In this case, one will see an extremely demagnified image of the front side of the disk since the slope is about infinite. It thus contributes negligibly to the total brightness of the image.

Fig. 4
figure 4

The first three transfer functions \(r_m(b)\) for the thin disk in the quintessence black hole with \(w=-\,0.5\) (left panel) and \(w=-\,0.7\) (right panel). The black lines, orange lines and red lines stand for the radial coordinate of the first, second, and third intersections with a face-on thin disk outside the horizon

Full size image

3.3 Shadows, lensing rings and photon rings

Having obtained the transfer functions, we can further obtain the specific intensity on the basis of Eq. (3.5) as the emitted specific intensity is given. In this paper, we assume the following toy-model functions which may emit by some thin matters. Firstly, we assume that \(I_{em}(r)\) is a decay function of the power of second order,

$$\begin{aligned} I_{em}(r) ={\left\{ \begin{array}{ll}\left( \frac{1}{r-5}\right) ^2, &{} r> 6 \\ 0, &{}r \le 6. \end{array}\right. } \end{aligned}$$
(3.6)

This profile is plotted in the top left panels in Fig. 5 for \(w=-\,0.5\) and Fig. 6 for \(w=-\,0.7\). This emission is sharply peaked at \(r = 6M\), and then drops to zero abruptly as \(r<6M\). In this example, the region of emission is well outside the photon sphere (see Table 1). Secondly, we assume that the emission is a decay function of the power of third order,

$$\begin{aligned} I_{em}(r) ={\left\{ \begin{array}{ll}\left( \frac{1}{r-(r_{ph}-1)}\right) ^3, &{} r> r_{ph} \\ 0, &{}r \le r_{ph} . \end{array}\right. } \end{aligned}$$
(3.7)

But this time the peak of the mission is at the photon sphere \(r_{ph}\). The profiles of this emission can be seen from the middle left panels in Fig. 5 for \(w=-\,0.5\) and Fig. 6 for \(w=-\,0.7\). Finally, we assume a moderate decay of emission,

$$\begin{aligned} I_{em}(r) ={\left\{ \begin{array}{ll} \frac{\frac{\pi }{2}-\tan ^{-1}(r-5)}{\frac{\pi }{2}-\tan ^{-1}(-3)} , &{} r>r_h , \\ 0, &{}r \le r_h . \end{array}\right. } \end{aligned}$$
(3.8)

This emission is outside of the horizon \(r_{h}\), which is shown in the bottom left panels in Fig. 5 for \(w=-\,0.5\) and Fig. 6 for \(w=-\,0.7\).

Fig. 5
figure 5

Observational appearances of a geometrically and optically thin disk with different profiles near black hole with \(M=1\), \(a=0.05\), \(w=-\,0.5\), viewed from a face-on orientation. The left column shows the profiles of various emissions \(I_{em}(r)\). The middle column exhibits the observed emission I(r) as a function of the impact parameter b. The right column shows the two-dimensional density plots of the observed emission I(r). The details can be found in the text

Full size image

For the case of \(w=-\,0.5\), the observed specific intensities are shown in the middle and right columns in Fig. 5. The middle column is for the one-dimensional functions of I(r) with respect to b, while the right column is for the two-dimensional density plots of I(r), viewed faced-on. In the first row the emission from the accretion is well outside the photon sphere (left panel). The corresponding observed direct image decays similarly as \(b>7.5M\) due to the gravitational lensing (middle panel). However, the observed lensing ring emission is confined to a thin region, \(6.4M<b<7.4M\), since the back side image is highly demagnified for \(r>6M\). The photon ring emission is the spike at \(b\sim 6M\), which is hard to see in the right panel of the density plots. One needs to zoom in in the plot to see the photon ring. Therefore, from the observer, the lensing ring makes a small contribution to the total brightness, while the photon ring makes negligible contributions.

In the second row of Fig. 5, the emission starts from the photon sphere \(r_{ph}=3.216\). The most important difference from the first row is that the observed lensing ring and photon ring emission are now superimposed on the direct image emission, which decays from \(b>4.25M\). The lensing ring has a spike in the brightness in the range of \(6M<b<6.5M\), while the photon ring has an even narrower spike at \(b\sim 6M\), which can hardly be distinguished from the lensing ring. In this case, the lensing ring still makes a very small contribution to the total brightness and the photon ring makes a negligible contribution.

Finally, in the third row of Fig. 5, the emission extends to the event horizon \(r_h=2.158\) and the decay of the emission is very moderate compared to the first and second row. The inner edge of the observed intensity at \(b\sim 3.2M\) is the lensed position of the event horizon. The increase of the intensity outside of the central dark area is due to the gravitational redshift. The very narrow spike at \(b\sim 6M\) is the photon ring, while the broader bump at \(b\sim 6.2M\) is the lensing ring. In this case, the lensing ring makes a prominent brightness contribution to the observed intensity, but the photon ring is still entirely negligible.

From Fig. 5, we see that the dark central regions are different for different profiles of the emissions. But the locations of the photon ring always stay at \(b\sim 6M\). In addition, for all the cases, we find that the observed brightness mainly stems from the direct emission, while the lensing ring provides only a small contribution, and the photon sphere provides a negligible contribution.

Fig. 6
figure 6

Observational appearances of a geometrically and optically thin disk with different profiles near black hole with \(M=1\), \(a=0.05\), \(w=-\,0.7\), viewed from a face-on orientation. The left column shows the profiles of various emissions \(I_{em}(r)\). The middle column exhibits the observed emission I(r) as a function of the impact parameter b. The right column shows the two-dimensional density plots of the observed emission I(r). The profiles are similar to those of \(w=-\,0.5\) in Fig. 5

Full size image

For the case of \(w=-\,0.7\), we plot the profiles of the emission and observed intensities in Fig. 6. They behave similarly to those of \(w=-\,0.5\). The differences are the quantities of the intensities and the locations of photon ring and lensing ring.

4 Shadows and photon spheres with spherical accretions

In this section, we are going to investigate the shadows and photon spheres with the spherical accretions for various state parameters w.

4.1 Shadows and photon spheres with a static spherical accretion

In this section, we intend to investigate the shadow and photon sphere of a quintessence black hole with a static spherical accretion. We mainly focus on the specific intensity observed by the observer \((\mathrm{erg} \, \mathrm{s}^{-1} \, \mathrm{cm}^{-2} \, \mathrm{str}^{-1} \, \mathrm{Hz}^{-1})\), which can be expressed as [13, 15]

$$\begin{aligned} I = \int _\gamma g^3 j (\nu _{\mathrm{e}}) \mathrm{d}l_{\mathrm{p}} , \end{aligned}$$
(4.1)

in which \(g = \nu _{\mathrm{o}}/\nu _{\mathrm{e}}\) is the redshift factor, while \(\nu _{\mathrm{e}}\) is the radiated photon frequency and \(\nu _{\mathrm{o}}\) is the observed photon frequency, \(j (\nu _{ \mathrm e})\) is the emissivity per unit volume measured in the static frame of the emitter, \(\mathrm{d}l_{\mathrm{p}}\) is the infinitesimal proper length, and \(\gamma \) stands for the trajectory of the light ray.

In the quintessence black hole (2.1), the redshift factor \(g =f(r)^{1/2}\). In addition, we assume that the radiation of light is monochromatic with fixed a frequency \(\nu _s\); thus the specific emissivity takes the form

$$\begin{aligned} j (\nu _{\mathrm{e}})\propto \frac{\delta (\nu _e-\nu _s)}{r^2}, \end{aligned}$$
(4.2)

where we have adopted the \(1/r^2\) profile as in [15]. According to Eq. (2.1), the proper length measured in the rest frame of the emitter is

$$\begin{aligned} \mathrm{d}l_{\mathrm{p}}= & {} \sqrt{f(r)^{-1}\mathrm{d}r^2+r^2 \mathrm{d} \psi ^2} \nonumber \\= & {} \sqrt{f(r)^{-1}+r^2 \left( \frac{\mathrm{d} \psi }{\mathrm{d}r}\right) ^2}~ \mathrm{d}r, \end{aligned}$$
(4.3)

in which \( \mathrm{d} \psi /\mathrm{d}r\) is given by the inverse of Eq. (2.17). In this case, the specific intensity observed by the static observer is

$$\begin{aligned} I = \int _\gamma \frac{f(r)^{3/2}}{ r^2} \sqrt{f(r)^{-1}+r^2 \left( \frac{\mathrm{d} \psi }{\mathrm{d}r}\right) ^2}~ \mathrm{d}r. \end{aligned}$$
(4.4)
Fig. 7
figure 7

Profiles of the specific intensity I(b) cast by a static spherical accretion, viewed face-on by an observer near the cosmological horizon. We set \(M=1\), \(a=0.05\), \(w=-\,0.5\) (top row) and \(w=-\,0.7\) (bottom row) as two examples. The details can be seen in the main texts

Full size image

Next we will employ Eq. (4.4) to investigate the shadow of the quintessence black hole with the static spherical accretion. Since the intensity depends on the trajectory of the light ray, which is determined by the impact parameter b, we will investigate how the intensity varies with respect to the impact parameter b. The observed specific intensities are shown in Fig. 7 with \(w=-\,0.5\) (top row) and \(w=-\,0.7\) (bottom row). From Fig. 7, we see that, as b increases, the intensity ramps up first, then reaches a peak at \(b_{ph}\) (\(b_{ph}=5.98M\) for \(w=-\,0.5\) and \(b_{ph}=7.23M\) for \(w=-\,0.7\)), and finally drops rapidly to smaller values. This result is consistent with Figs. 1 and 2. Because for \(b<b_{ph}\) the intensity originating from the accretion matter is absorbed mostly by the black hole, the observed intensity is small. For \(b=b_{ph}\), the light ray revolves around the black hole several times, thus the observed intensity is maximal. For \(b>b_{ph}\), only the refracted light contributes to the observed intensity. In particular, as b becomes larger, the refracted light becomes smaller. The observed intensity thus vanishes for large enough b.

From Fig. 7, we can also see how the state parameter of dark energy will affect the observed intensity. For a fixed a and M, we find that the larger the state parameter is, the stronger the intensity will be, i.e., the intensity of \(w=-\,0.5\) is stronger than that of \(w=-\,0.7\). The two-dimensional plots of the shadows are shown in the right column of Fig. 7, with the impact parameter b of the radius. We can see clearly that the shadow is circularly symmetric for the quintessence black hole, and outside the black hole, there is a bright ring, which is the photon sphere. The radius of the photon sphere for different w are listed in Table 1. Obviously, the result in Fig. 7 is consistent with that in Table 1. That is, the larger the state parameter is, the smaller the radius of the photon sphere will be.

In addition, inside the photon sphere, we see that the specific intensity does not vanish but has a small finite value. The reason is that part of the radiation has escaped from the black hole. For \(r<r_{ph}\), the solid angle of the escaping radiation is \(2 \pi (1-\cos \theta )\), while for \(r>r_{ph}\), the solid angle is \(2 \pi (1+\cos \theta )\), in which \(\theta \) is given by

$$\begin{aligned} \sin \theta =\frac{r_{ph}^{3/2}}{r} \left( 1 - \frac{2 M}{r}- \frac{a}{ r^{ 3 w + 1} }\right) ^{1/2}. \end{aligned}$$
(4.5)

In principle, one can calculate the escaped net luminosity by the following relation:

$$\begin{aligned}&L_{o}=\int _{r_h}^{r_{ph}} 4 \pi r^2 j (\nu _{\mathrm{e}}) 2 \pi (1-\cos \theta ) \mathrm{d}r\nonumber \\&\quad +\int _{r_{ph}}^{\text {observer}} 4 \pi r^2 j (\nu _{\mathrm{e}}) 2 \pi (1+\cos \theta ) \mathrm{d}r. \end{aligned}$$
(4.6)

Obviously, for different state parameters, the net luminosity observed by a static observer in the quintessence black hole is different, since the solid angle is dependent on the state parameter. This result is consistent with the result in Fig. 7.

4.2 Shadows and photon spheres with an infalling spherical accretion

In this section, the optically thin accretion is supposed to be due to infalling matters. This infalling model is thought to be more realistic than the static accretion model, since most of the accretion matters are dynamical in the Universe. We still employ Eq. (4.4) to investigate the shadow cast by the infalling accretion. Different from the static accretion, the redshift factor for the infalling accretion is related to the velocity of the accretion, that is,

$$\begin{aligned} g = \frac{k_\beta u^\beta _{\mathrm{o}}}{k_\gamma u^\gamma _{\mathrm{e}}} , \end{aligned}$$
(4.7)

in which \(k^\mu =\dot{x_\mu }\) is the four-velocity of the photon, \(u^\mu _{\mathrm{o}} = (1,0,0,0)\) is the four-velocity of the static observer, and \(u^\mu _{\mathrm{e}}\) is the four-velocity of the accretion under consideration, given by

$$\begin{aligned} u^t_{\mathrm{e}} = \frac{1}{f(r)}, \quad u^r_{\mathrm{e}} = - \sqrt{ 1 - f(r) }, \quad u^\theta _{\mathrm{e}} = u^\psi _{\mathrm{e}} = 0. \end{aligned}$$
(4.8)

The four-velocity of the photon has been obtained previously from Eqs. (2.8) to (2.10). From these equations, we know that \(k_t=1/b\) is a constant, and \(k_r\) can be inferred from the equation \(k_\alpha k^\alpha = 0\), that is,

$$\begin{aligned} \frac{k_r}{k_t} = \pm \frac{1}{f(r)}\sqrt{ 1 - \frac{b^2 f(r)}{r^2} } , \end{aligned}$$
(4.9)

in which the \(+\)/− corresponds to the case that the photon gets close to/away from the black hole. With Eq. (4.9), the redshift factor in Eq. (4.7) can be simplified as

$$\begin{aligned} g = \frac{1}{u^{t}_e+k_r/k_e u^r_e}, \end{aligned}$$
(4.10)

which is different from the static accretion case.

Fig. 8
figure 8

Profiles of the specific intensity I(b) cast by an infalling spherical accretion, viewed face-on by an observer near the cosmological horizon. We set \(M=1\), \(a=0.05\), \(w=-\,0.5\) (top row) and \(w=-\,0.7\) (bottom row) as two examples. The details can be seen in the main texts

Full size image

In addition, the proper distance is defined by

$$\begin{aligned} \mathrm{d}l_{\mathrm{p}} = k_\gamma u^\gamma _{\mathrm{e}} \mathrm{d}s=\frac{k_t}{g | k_r |} \mathrm{d}r, \end{aligned}$$
(4.11)

where s is the affine parameter along the photon path \(\gamma \). With regard to the specific emissivity, we also assume that it is monochromatic, so that Eq. (4.2) is still valid. Integrating Eq. (4.1) over the observed frequencies, we obtain

$$\begin{aligned} I \propto \int _\gamma \frac{g^3 k_t \mathrm{d}r}{r^2 | k_r |} . \end{aligned}$$
(4.12)

Now we will use Eq. (4.12) to investigate the shadow of the quintessence black hole numerically with infalling accretion. Note that there is an absolute sign for \( k_r\) in the denominator. Therefore, when the photon changes the direction of its motion, the sign before \( k_r\) should also change. For different state parameters w, the observed intensity with respect to b are shown in Fig. 8, in which the top row is for \(w=-\,0.5\) while the bottom row is for \(w=-\,0.7\). From Fig. 8, we find that, as b increases, the intensity will increase as well to a peak \(b=b_{ph}\); after the peak it drops to smaller values. This behavior is similar to that in the static accretion in Fig. 7. We can also observe the effect of w on the intensity and find that the intensity increases as the value of w increases, i.e., the intensity for \(w=-\,0.5\) is stronger than \(w=-\,0.7\). The two-dimensional image of the intensity is shown on the right column in Fig. 8. We see that the radii of the shadows and the locations of the photon spheres are the same as in the static case. That means the motion of the accretion does not affect the radii of the shadows and the locations of the photon spheres. However, different from the static accretion, the central region of the intensity for the infalling accretion is darker, which can be accounted for by the Doppler effect. In particular, near the event horizon of the black hole, this effect is more obvious.

5 Conclusions and discussions

We investigated the images of a black hole in the quintessence dark energy model. In particular, we studied the quintessence black hole surrounded by a geometrically and optically thin-disk accretion, as well as a spherically symmetric accretion. We found that, for the observed specific intensities, there exists a dark interior (shadow), a lensing ring and a photon ring for the thin-disk accretion. But their positions depend on the profiles of the emission from the accretion near the black hole. Despite these distinctions, the direct image of the accretion makes a major contribution to the brightness of the black hole, while the lensing ring makes a minor contribution and the photon ring makes a negligible contribution. The effects of the quintessence state parameter are also important to the shadow images of the black hole, since this parameter would have impact on the distances between the observer and the event horizon.

We also studied the cases of static and infalling spherically symmetric accretion; the images of the black hole would have a dark interior and a photon sphere. The infalling accretion would have a darker interior than the static case, which is due to the Doppler effect of the infalling matter. Different quintessence state parameters would change the positions of the photon spheres of the image. We expect that this study would bring about insights and have implications for the quintessence dark energy model.

In this paper we only dealt with geometrically thin and optically thin accretions. However, in reality geometrically thick and optically thin accretion may occur. As argued by the authors of Ref. [11] (although their model is not so physically realistic), for geometrically thick and optically thin-disk accretion, the observed appearance of the shadow will have significant difference from that of geometrically thin and optically thin accretion. Because in this case the brightness at each impact parameter is an integrated volume emissivity along the line of sight. Therefore, the observed appearance of the shadow is a complex function of the emission profile and the shape of the emitting region. These authors found that, for geometrically thick emission, the lensing ring would provide a more significant feature in the observed appearance than in the thin-disk case. Besides, in the Universe black holes exist as rotating objects. Therefore, extending the static quintessence black hole solution to a Kerr-like solution is a natural extension. We will leave this for future work.