1 Introduction

CPT invariance [1], which is a simultaneous reversal of charge, parity and time, is well known as one of the fundamental laws of physics. Since it was proposed, it has been tested with high precision by a variety of observations in laboratories and astronomy [2, 3]. The measurements of the net polarization of gamma-ray bursts have displayed the strictest testes of CPT invariance in the pure photon sector [4,5,6]. There were also strict tests in the pure neutrino sector [6, 7]. However, few constraints have been placed on possible deviations from CPT invariance in the pure gravitational sector. Theoretically, the quantum gravity at Planck scale \(\sim 10^{19}\,\mathrm{GeV}\) is expected to leave low-energy relic effects [8,9,10,11], wherein CPT violation is one famous example. Since CPT invariance is a fundamental law in nature, it is well justified to be unstinting in one’s efforts to explore CPT violation under various circumstances.

The discovery of binary black hole(BBH) coalescences by the Laser Interferometer Gravitational-Wave Observatory (LIGO) [12] opens a clean observational window to provide strict tests of fundamental physics [13,14,15,16,17,18,19,20,21,22]. Here, we perform such a test of CPT invariance in gravitational waves (GWs). When CPT invariance was deviated, if any, GWs with left-handed and right-handed circular polarizations could gain a slight difference in propagating speeds [23, 24]. As a consequence, the birefringence is induced and there is a rotation of plus (\(+\)) and cross (\(\times \)) modes [25, 26]. The birefringent effect depends on the GW frequency and can be accumulated along the trajectory of GWs, which are emitted from compact binary coalescences at cosmological distances. Therefore, we can perform measurements of the polarizations to test CPT invariance in GWs or detect possible deviations from it.

This study aims at testing the CPT invariance in GWs and placing strict limits on the leading-order CPT violation in GWs. Higher-order CPT violations are ignored since they are expected to lead smaller effects in the spirits of effective field theory (EFT) [27]. In this work the CPT-violating dispersion relation is manifested as

$$\begin{aligned} \omega ^{2}=k^{2}\pm 2\zeta k^{3}\ , \end{aligned}$$
(1)

where a sign ± takes \(+/-\) for the left-/right-handed circular polarization and \(\zeta \) is a length-dimensional parameter characterizing the size of CPT violating effect. We assume a convention \(\hbar =1\). Hence, \(\omega \) and k denote the energy and momentum of gravitons, respectively. Equation (1) could be related to a dimension-5 CPT-violating operator \(\mathrm {\mathring{k}}_{(V)}^{(5)}\) [24], which is of leading order that causes the birefringence of GWs. We note \(\zeta \simeq \mathrm {\mathring{k}}_{(V)}^{(5)}\) here.

Laboratory experiments in the non-relativistic limit are insensitive to such a dimension-5 CPT-violating operator, since Newton’s law remains unchanged by it [28]. However, GWs from cosmologically distant BBHs provide a potential approach to measure it [24,25,26]. In the pure gravity sector, the only existing upper limit on the dimension-5 CPT-violating operator (absolute value) was reported to be less than \(2\times 10^{-14}\mathrm{m}\) [24], which was obtained by measuring the width of the peak at the maximal amplitude of GW150914 [12]. It stands for a \({\mathcal {O}}(0.01)\,\text {GeV}\) test of CPT invariance in GWs.

We would adopt Bayesian parameter inferences [29] and obtain stricter limits on CPT violation in this paper. Due to CPT violation, the plus and cross modes of GWs rotate along the propagating direction. Instead of the net polarization, the knowledge of gravitational waveform is essential to our data analysis, since a method named as matched filtering [30] is used for extracting the signals. Fortunately, in general relativity (GR), one can predict exactly the coalescing process of a compact binary system as well as the waveform generated during the process [31]. We assume that the CPT-violating effect is minimal and it can be ignored at the source [14]. The source effect is believed to be far smaller than the leading/GR term and appear at a time scale of radiation reaction that is much shorter than the propagating time of GWs. It is thus probably negligible compared with the propagation effect accumulated along a cosmologically distant trajectory. In fact, to proceed a self-consistent study, one need use the technique of numerical relativity, which is tricky for the current work. However, our study stands for the first step towards a complete understanding of CPT violation in GWs. It can put valuable physical insights on this field and provide helpful guides to future numerical-relativity investigations. Given the above assumption, to detect possible deviations from CPT invariance, we still need knowledges of the CPT-violating propagation effect on gravitational waveform. It has been done in Refs. [25, 26].

The remainder of this work is arranged as follows. In Sect. 2, we introduce the gravitational waveform which is corrected by CPT violation. In Sect. 3, we demonstrate the method of data analysis. In Sect. 4, we obtain new constraints on the CPT-violating parameter. Our conclusions are given in Sect. 5.

2 Theory

We could evaluate the CPT-violating contribution to the gravitational waveform [25, 26]. The eigenstates are consist of two circular polarizations. Based on Eq. (1), the phase speed of the left-handed circular polarization is given as \(v_{\mathrm {L}}\simeq 1-\zeta \omega \). To first order, we obtain the gravitational strain as \(h_{\mathrm {L}}(t)\sim \mathrm {e}^{-i\omega (t-l/v_{\mathrm {L}})}\simeq \mathrm {e}^{i\zeta \omega ^{2} l}\mathrm {e}^{-i\omega (t-l)}\), where t and l denote the time and distance to the source, respectively. Hence, the phase is shifted by \(\zeta \omega ^{2} l\). Due to the expansion of the universe, we should take the redshift of the energy into account by considering an infinitesimal change in the phase, namely, \(d\varPsi _{\mathrm {tot}}=d\varPsi ^{\mathrm {GR}}+\zeta \omega ^{2}dl\). Upon an integration from the source to the detector, the former part gives the phase predicted by GR, while the later one gives the correction term due to modified dispersion, i.e., \(\delta \varPsi =\int \zeta \omega ^{2}dl\). We can replace dl with \(dt=-dz/[(1+z)H(z)]\) at zeroth order and multiply \(\omega \) by a factor \((1+z)\). Here, H(z) denotes the Hubble parameter at the redshift z. Therefore, we obtain a finite change in the phase, i.e.,

$$\begin{aligned} \delta \varPsi = 4\pi ^2 \zeta f^{2} \int _{0}^{z_{\text {BBH}}}{(1+z)}/{H(z)}dz\ , \end{aligned}$$
(2)

where \(f=\omega /2\pi \) denotes the GW frequency in the observer frame, and \(z_{\text {BBH}}\) denotes the redshift of a BBH in this paper. The integration over the redshift reveals that the CPT-violating effect accumulates with an increase of cosmological distance. For the right-handed circular polarization, the phase speed is given as \(v_{\mathrm {R}}\simeq 1+\zeta \omega \) and the finite change in the phase becomes \(-\delta \varPsi \).

Due to CPT violation, the gravitational waveform for circular polarization states is given as \(h_{\mathrm {L,R}}=h_{\mathrm {L,R}}^{\mathrm {GR}}~\mathrm {e}^{\pm i\delta \varPsi }\), where \(h^{\mathrm {GR}}\) denotes the waveform predicted by GR and \(\delta \varPsi \) is explicitly given by Eq. (2). The circular polarizations are usually decomposed into the plus and cross modes, namely, \(h_{\mathrm {L,R}}=h_{+}\pm ih_{\times }\) and \(h_{\mathrm {L,R}}^{\mathrm {GR}}=h_{+}^{\mathrm {GR}}\pm ih_{\times }^{\mathrm {GR}}\). Through a few algebraic operation, therefore, we can represent the CPT-violating waveform \(h_{+,\times }\) as a rotation of the CPT-invariant waveform, namely,

$$\begin{aligned} \left( \begin{array}{c} h_{+} \\ h_{\times } \end{array}\right) =\left( \begin{array}{cc} \cos (\delta \varPsi ) &{}\quad -\sin (\delta \varPsi ) \\ \sin (\delta \varPsi ) &{}\quad \cos (\delta \varPsi ) \end{array}\right) \left( \begin{array}{c} h_{+}^{\mathrm {GR}} \\ h_{\times }^{\mathrm {GR}} \end{array}\right) \ . \end{aligned}$$
(3)

For \(h^{\mathrm {GR}}\), we adopt the IMRPhenomPv2 waveform [32, 33]. Based on Eq. (3), we should note that \(\delta \varPsi \) is twice the rotation angle due to CPT violation. The GR waveform would be recovered when we take \(\zeta =0\). Furthermore, the gravitational strain on a given detector is [30]

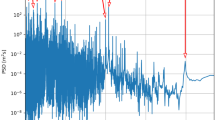
$$\begin{aligned} h=F_{+}h_{+}+F_{\times }h_{\times } \ , \end{aligned}$$
(4)

where \(F_{+,\times }\) denote a set of response pattern functions for the detector such as LIGO-Hanford, LIGO-Livingston and Virgo [34]. In Fig. 1, we plot the birefringent gravitational waveform \(h_+\) in frequency domain. The CPT-violating parameter is set to be \(\zeta =10^{-14}\,\text {m}\). For comparison, we also depict the GR and non-birefringent waveforms, the latter of which is got by simply replacing “±” with “\(+\)” in Eq. (1). In fact, the non-birefringent case has been extensively studied in Ref. [14]. Based on Fig. 1, we show that CPT violation can be quantitatively distinguished from other effects.

Fig. 1
figure 1

Birefringent gravitational waveform \(h_+\) in frequency domain. We let the CPT-violating parameter be \(\zeta =10^{-14}\,\text {m}\). The GR and non-birefringent waveforms are depicted for comparison

Full size image

3 Method

For the first time, we perform a parallel Bayesian analysis software. i.e. pBilby [35], to estimate the posterior probability distribution functions (PDFs) of the CPT-violating parameter \(\zeta \) and fifteen binary parameters. We consider a compilation of ten signals of BBH coalescences which were reported in the LIGO-Virgo catalog GWTC-1 [36]. Since the CPT violating effect is expected to be small, a uniform prior PDF of \(\zeta \) is set as \([-4,4]\times 10^{-14}\,\mathrm {m}\), which is proved to be wide enough for our purpose in the following. Other independent parameters have prior PDFs matched with Ref. [14].

The log-likelihood for a signal with Gaussian noise is defined as [29]

$$\begin{aligned} \log {\mathcal {L}}=\langle s,h(\theta ) \rangle -\frac{1}{2}\langle h(\theta ),h(\theta ) \rangle \ , \end{aligned}$$
(5)

where s denotes a GW signal and \(h(\theta )\) denotes a waveform template with parameter space \(\theta \). An inner product is defined as

$$\begin{aligned} \langle a,b \rangle =4\mathfrak {R}\int _{0}^{\infty }\frac{a(f)b^*(f)}{S_{n}(f)}df \ , \end{aligned}$$
(6)

where \(S_{n}(f)\) denotes a single-sided power spectral density (PSD) of detector noise and \(\mathfrak {R}\) means the real part. The waveform template modified by CPT violation is given by Eqs. (2) and (3). For each signal in the GWTC-1, we analyze the data collected by detectors which responded to the signal. In addition, we employ the noise PSDs of corresponding detectors [34]. For multiple detectors, the uncorrelated noises are assumed and the likelihoods should be multiplied together. To check the correctness of our method, we reproduce the results of Table III in Ref. [36], without considering the effects of CPT violation.

4 Results and discussion

The results of this study are showed as follows. Figure 2 and Table 1 show the strict observational constraints on the CPT-violating parameter \(\zeta \) at 90% confidence level from the ten signals of BBHs in GWTC-1. Since the constraints are well compatible with \(\zeta =0\), we find no substantial deviations from CPT invariance, indicating stringent upper limits on \(|\zeta |\). Typically, we obtain \(|\zeta |\lesssim \mathrm {few}\times 10^{-15}\,\mathrm {m}\). The most stringent constraint is revealed as \(\zeta =-0.00^{+0.16}_{-0.17}\times 10^{-14}\,\mathrm {m}\), which is given by GW151226 [37]. By transforming the posterior PDF of \(\zeta \) to that of \(|\zeta |\), we find that the upper limit on \(|\zeta |\) for GW151226 is at least one order of magnitude better than the only existing limit \(\lesssim 2\times 10^{-14}\mathrm{m}\) [24], which was given by GW150914 [12]. Even for GW150914 itself, our constraint is still one order of magnitude better. For other events, we also obtain the stricter constraints than the existing one.

We can combine the posterior PDFs of the ten events and obtain a more stringent limit on \(\zeta \) than that from an individual event. By using Monte Python [38], we perform a detailed analysis and obtain

$$\begin{aligned} \zeta =0.14^{+0.22}_{-0.31}\times 10^{-15}\,\text {m}\ , \end{aligned}$$
(7)

at \(1\sigma \) confidence level. This limit becomes \(0.14^{+0.70}_{-0.56}\times 10^{-15}\,\text {m}\) and \(0.14^{+0.94}_{-0.69}\times 10^{-15}\,\text {m}\) at \(2\sigma \) and \(3\sigma \) confidence levels, respectively. Indeed, it is tighter than any individual event. Therefore, we obtain the up-to-date strictest constraints on CPT violation in GWs. In addition, our results stand for the first self-consistent test of CPT invariance in GWs. Moreover, it is interesting to compare our method and results with those in a similar work [39], which constrained the anisotropic birefringence with the GWTC-1. Different from our method, the author utilized the posterior parameter samples released by LIGO-Virgo Collaborations. He also obtained a combined limit on the CPT-violating parameter, i.e., \(|k_{(V)00}^{(5)}|<3.3\times 10^{-16}\,\mathrm {m}\) at \(1\sigma \) confidence level. This limit is compatible with ours, since the abnormal propagation of GWs due to CPT violation, if any, should reside in the residual uncertainty. However, it is about three times stronger than ours, since the author followed the different method mentioned above and used all of the GWTC-1 events including GW170817.

Fig. 2
figure 2

Constraints on the CPT-violating parameter \(\zeta \) from the ten signals of BBHs in the LIGO-Virgo catalog GWTC-1 [36]. A capital H/L/V denotes a LIGO-Hanford/LIGO-Livingston/Virgo detector. A dot/square denotes HL/HLV. Blue/orange color denotes O1/O2. The error bars denote 90% confidence interval

Full size image
Table 1 Same caption as Fig. 2. Typically, we report the stringent constraints as \(|\zeta |\lesssim \mathrm {few}\times 10^{-15}\,\mathrm {m}\). The strictest limit is given by GW151226 [37]. The uncertainties denote 90% confidence interval
Full size table

It is interesting to qualitatively explore the sources of the observational uncertainties of \(\zeta \). Naively speaking, we expect a better limit or smaller uncertainty from a more distant BBH, since the CPT-violating effect accumulates with the increase of cosmological distance according to Eq. (2). Indeed, it is roughly true for BBHs with the same chirp mass. However, a full story should consider the chirp mass, which determines a cutoff frequency of the signal. A BBH system with smaller chirp mass could generate on the detectors a temporally longer signal, which is important for an efficient extraction of the CPT-violating effect. The side effect is a smaller signal-to-noise (SNR) [30], leading larger uncertainties of other parameters. Therefore, the total uncertainty of \(\zeta \) mainly depends on the chirp mass and cosmological distance, as well as the uncertainties of them. A longer distance or lighter chirp mass is good for the accumulation of the CPT-violating propagation effect, while can reduce SNR.

The above discussion is also applicable to GW170817, which is the first detected binary neutron stars. Though it is lightest, GW170817 is the loudest signal in GWTC-1, since it is nearest. In fact, we could obtain a stricter constraint on \(\zeta \) from GW170817, following our method. However, we would not consider this event in this work. Since neutron stars are composed of matter, such as neutrons, it is not pure-gravitational and may involve unknown matter effects. To be conservative, therefore, we only focus on tests of CPT invariance with BBHs.

5 Conclusions

In this work, we have shown a systematic test of CPT invariance in GWs. We demonstrated that CPT violation induces the rotation of plus and cross modes of GWs. We showed that the measurements of GWs from BBHs provide a clean observational window to test CPT invariance, since only the different circular polarizations are involved. We performed Bayesian parameter inferences over the ten signals of BBHs in GWTC-1, but reported no substantial deviations from CPT invariance in GWs. The strictest limit on the CPT-violating parameter was given by GW151226, i.e. \(\zeta =0.00^{+0.16}_{-0.17}\times 10^{-14}\,\mathrm {m}\), which is one order of magnitude better than the only existing limit. Combining the results of all the ten events, the joint constraint on \(\zeta \) was shown to be further improved, i.e., \(\zeta =0.14^{+0.22}_{-0.31}\times 10^{-15}\,\text {m}\), which stands for the up-to-date strictest test of CPT invariance in GWs.

Our study represents the first self-consistent Bayesian constraints on CPT violation in GWs, though similar methods have been employed to study other modifications to GR [14]. In principle, we could also study higher-order CPT-violating effects on GWs in the same way. However, we expect significantly weaker constraints on them [25], which are left to future works. Furthermore, we should note that a multi-band observation may improve our results significantly, since the CPT-violating effect is proportional to the square of GW frequency. In addition, we expect CPT invariance to be further tested in the near future [25], since more and more BBHs will be detected by upcoming observing runs of LIGO and Virgo and other observatories under construction [40, 41].