Decay properties of $P_c$ states through the Fierz rearrangement

Abstract

We systematically study hidden-charm pentaquark currents with the quark configurations $[\bar{c} u][u d c]$, $[\bar{c} d][u u c]$, and $[\bar{c} c][u u d]$. Some of their relations are derived using the Fierz rearrangement of the Dirac and color indices, and the obtained results are used to study strong decay properties of $P_c$ states as $\bar{D}^{(*)} \varSigma _c$ hadronic molecules. We calculate their relative branching ratios for the $J/\psi p$, $\eta _c p$, $\chi _{c0} p$, $\chi _{c1} p$, $\bar{D}^{(*)0} \varLambda _c^+$, $\bar{D}^{0} \varSigma _c^{+}$, and $\bar{D}^{-} \varSigma _c^{++}$ decay channels. We propose to search for the $P_c(4312)$ in the $\eta _c p$ channel and the $P_c(4440)/P_c(4457)$ in the $\bar{D}^{0} \varLambda _c^+$ channel.

1 Introduction

Since the discovery of the X(3872) in 2003 by Belle [1], many charmonium-like XYZ states were discovered in the past twenty years [2]. Besides, the LHCb Collaboration observed three enhancements in the $J/\psi p$ invariant mass spectrum of the $\varLambda _b\rightarrow J/\psi p K$ decays [3, 4]:

$$\begin{aligned} P_c(4312)^+: M= & {} 4311.9 \pm 0.7 ^{+6.8}_{-0.6} \, \text{ MeV } , \nonumber \\ \varGamma= & {} 9.8 \pm 2.7 ^{+3.7}_{-4.5} \, \text{ MeV },\nonumber \\ P_c(4440)^+: M= & {} 4440.3 \pm 1.3 ^{+4.1}_{-4.7} \, \text{ MeV } , \nonumber \\ \varGamma= & {} 20.6 \pm 4.9 ^{+8.7}_{-10.1} \, \text{ MeV } ,\nonumber \\ P_c(4457)^+: M= & {} 4457.3 \pm 0.6 ^{+4.1}_{-1.7} \, \text{ MeV },\nonumber \\ \varGamma= & {} 6.4 \pm 2.0 ^{+5.7}_{-1.9} \, \text{ MeV }. \end{aligned}$$

(1)

These structures contain at least five quarks, $\bar{c} c u u d$, so they are perfect candidates of hidden-charm pentaquark states. Together with the charmonium-like XYZ states, their studies are significantly improving our understanding of the non-perturbative behaviors of the strong interaction at the low energy region [5,6,7,8,9,10,11,12,13,14].

The $P_c(4312)$, $P_c(4440)$, and $P_c(4457)$ are just below the $\bar{D} \varSigma _c$ and $\bar{D}^{*} \varSigma _c$ thresholds, so it is quite natural to interpret them as $\bar{D}^{(*)} \varSigma _c$ hadronic molecular states, whose existence had been predicted in Refs. [15,16,17,18,19] before the LHCb experiment performed in 2015 [3]. This experiment observed two structures $P_c(4380)$ and $P_c(4450)$. Later in 2019 another LHCb experiment [4] observed a new structure $P_c(4312)$ and further separated the $P_c(4450)$ into two substructures $P_c(4440)$ and $P_c(4457)$.

To explain these $P_c$ states, various theoretical interpretations were proposed, such as loosely-bound meson-baryon molecular states [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38] and tightly-bound pentaquark states [39,40,41,42,43,44,45,46,47,48], etc. Since they have only been observed in the $J/\psi p$ invariant mass spectrum by LHCb [3, 4], it is crucial to search for some other decay channels in order to better understand their nature. There have been some theoretical studies on this subject, using the heavy quark symmetry [49, 50], effective approaches [51,52,53,54], QCD sum rules [55], and the quark interchange model [56], etc. We refer to reviews [5,6,7,8,9,10,11,12,13,14] and references therein for detailed discussions.

In this paper we shall apply the Fierz rearrangement of the Dirac and color indices to study strong decay properties of $P_c$ states as $\bar{D}^{(*)} \varSigma _c$ hadronic molecules, which method has been used in Ref. [57] to study strong decay properties of the $Z_c(3900)$ and X(3872). A similar arrangement of the spin and color indices in the nonrelativistic case was used to study decay properties of XYZ and $P_c$ states in Refs. [49, 56, 58,59,60,61,62].

In this paper we shall use the $\bar{c}$, c, u, u, and d ($q=u/d$) quarks to construct hidden-charm pentaquark currents with the three configurations: $[\bar{c} u][u d c]$, $[\bar{c} d][u u c]$, and $[\bar{c} c][u u d]$. In Refs. [63,64,65] we have found that these three configurations can be related as a whole, while in the present study we shall further find that two of them are already enough to be related to each other, just with the color-octet-color-octet meson-baryon terms included. Using these relations, we shall study strong decay properties of $P_c$ states as $\bar{D}^{(*)} \varSigma _c$ molecular states.

Our strategy is quite straightforward. First we need a hidden-charm pentaquark current, such as

$$\begin{aligned} \eta _1(x,y)= & {} [\delta ^{ab} \bar{c}_a(x) \gamma _5 u_b(x)] \nonumber \\&\times [\epsilon ^{cde} u_c^T(y) {\mathbb {C}} \gamma _\mu d_d(y) \gamma ^\mu \gamma _5 c_e(y)], \end{aligned}$$

(2)

where $a \cdots e$ are color indices. It is the current best coupling to the $\bar{D}^0 \varSigma _c^{+}$ molecular state of $J^P =1/2^-$, through

$$\begin{aligned} \langle 0 | \eta _1(x,y) | \bar{D}^0 \varSigma _c^{+}; 1/2^-(q) \rangle = f_{P_c} u(q), \end{aligned}$$

(3)

where u(q) is the Dirac spinor of the $P_c$ state.

After the Fierz rearrangement of the Dirac and color indices, we can transform it to be

$$\begin{aligned} \eta _1(x,y)\rightarrow & {} - {1\over 12} ~ [\bar{c}_a(x^\prime ) \gamma _5 c_a(x^\prime )]~N(y^\prime )\nonumber \\&+ {1\over 24} ~ [\bar{c}_a(x^\prime ) \gamma _\mu c_a(x^\prime )] ~\gamma ^\mu \gamma _5 N(y^\prime ) + \cdots , \end{aligned}$$

(4)

where

$$\begin{aligned} N = \epsilon ^{abc} (u_a^T {\mathbb {C}} d_b) \gamma _5 u_c -\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma _5 d_b) u_c , \end{aligned}$$

(5)

is the Ioffe’s light baryon field well coupling to the proton [66,67,68]. Hence, $\eta _1(x^\prime ,y^\prime )$ couples to the $\eta _c p$ and $J/\psi p$ channels simultaneously:

$$\begin{aligned} \langle 0 | \eta _1(x^\prime ,y^\prime ) | \eta _c p \rangle\approx & {} - {1\over 12} \langle 0 | \bar{c}_{a} \gamma _5 c_a | \eta _c \rangle ~\langle 0 | N | p \rangle + \cdots ,\nonumber \\ \langle 0 | \eta _1(x^\prime ,y^\prime ) | \psi p \rangle\approx & {} {1\over 24} \langle 0 | \bar{c}_{a} \gamma _\mu c_a | \psi \rangle ~\gamma ^\mu \gamma _5 \langle 0 | N | p \rangle + \cdots . \end{aligned}$$

(6)

The above two equations can be easily used to calculate the relative branching ratio of the $P_c$ decay into $\eta _c p$ to its decay into $J/\psi p$ [69]. Detailed discussions on this will be given below.

This paper is organized as follows. In Sect. 2 we systematically study hidden-charm pentaquark currents with the quark content $\bar{c} c u u d$. We consider three different configurations, $[\bar{c} u][u d c]$, $[\bar{c} d][u u c]$, and $[\bar{c} c][u u d]$, whose relations are derived in Sect. 3 using the Fierz rearrangement of the Dirac and color indices. In Sect. 4 we extract some strong decay properties of $\bar{D}^{(*)0} \varSigma _c^+$ and $\bar{D}^{(*)-} \varSigma _c^{++}$ molecular states, which are combined in Sect. 5 to further study strong decay properties of $\bar{D}^{(*)} \varSigma _c$ molecular states with $I = 1/2$. The results are summarized in Sect. 6.

2 Hidden-charm pentaquark currents

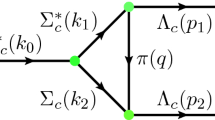
We can use $\bar{c}$, c, u, u, and d ($q=u/d$) quarks to construct many types of hidden-charm pentaquark currents. In the present study we need the following three, as illustrated in Fig. 1:

$$\begin{aligned} \eta (x,y)= & {} [\bar{c}_a(x) \varGamma ^\eta _1 u_b(x)] ~\left[ [u^T_c(y) {\mathbb {C}} \varGamma ^\eta _2 d_d(y)] ~ \varGamma ^\eta _3 c_e(y) \right] ,\nonumber \\ \xi (x,y)= & {} [\bar{c}_a(x) \varGamma ^\xi _1 d_b(x)] ~\left[ [u^T_c(y) {\mathbb {C}} \varGamma ^\xi _2 u_d(y)] ~ \varGamma ^\xi _3 c_e(y) \right] ,\nonumber \\ \theta (x,y)= & {} [\bar{c}_a(x) \varGamma ^\theta _1 c_b(x)] ~\left[ [q^T_c(y) {\mathbb {C}} \varGamma ^\theta _2 q_d(y)] ~\varGamma ^\theta _3 q_e(y)\right] ,\nonumber \\ \end{aligned}$$

(7)

where $\varGamma _{1/2/3}^{\eta /\xi /\theta }$ are Dirac matrices, the subscripts $a \cdots e$ are color indices, and the sum over repeated indices (both superscripts and subscripts) is taken.

Fig. 1

Three types of hidden-charm pentaquark currents. Quarks are shown in red/green/blue color, and antiquarks are shown in cyan/magenta/yellow color

All the independent hidden-charm tetraquark currents of $J^{PC} =1^{+\pm }$ have been constructed in Refs. [57, 70,71,72]. However, in this case there are hundreds of hidden-charm pentaquark currents, and it is difficult to find out all the independent ones (see Refs. [63, 64] for relevant discussions). Hence, in this paper we shall not construct all the currents, but just investigate those that are needed to study decay properties of the $P_c(4312)$, $P_c(4440)$, and $P_c(4457)$. We shall separately investigate their color and Lorentz structures in the following subsections.

2.1 Color structure

Taking $\eta (x,y)$ as an example, there are two possibilities to compose a color-singlet field: $[\bar{c} u]_{\mathbf {1}_c} [u d c]_{\mathbf {1}_c}$ and $[\bar{c} u]_{\mathbf {8}_c} [u d c]_{\mathbf {8}_c}$. We can use the color-singlet-color-singlet meson-baryon term

$$\begin{aligned} {[}\delta ^{ab}\bar{c}_a u_b] [\epsilon ^{cde} u_c d_d c_e], \end{aligned}$$

(8)

to describe the former, while there are three color-octet-color-octet meson-baryon terms for the latter:

$$\begin{aligned}&{[}\lambda ^{ab}_n\bar{c}_a u_b] [\epsilon ^{cdf} \lambda ^{fe}_n u_c d_d c_e] ,\nonumber \\&{[}\lambda ^{ab}_n\bar{c}_a u_b] [\epsilon ^{def} \lambda ^{fc}_n u_c d_d c_e],\nonumber \\&{[}\lambda ^{ab}_n\bar{c}_a u_b] [\epsilon ^{ecf} \lambda ^{fd}_n u_c d_d c_e] . \end{aligned}$$

(9)

Only two of them are independent due to

$$\begin{aligned} \epsilon ^{cdf} \lambda ^{fe}_n + \epsilon ^{def} \lambda ^{fc}_n +\epsilon ^{ecf} \lambda ^{fd}_n = 0, \end{aligned}$$

(10)

which is consistent with the group theory that there are two and only two octets in $\mathbf {3}_c \otimes \mathbf {3}_c \otimes \mathbf {3}_c = \mathbf {1}_c \oplus \mathbf {8}_c \oplus \mathbf {8}_c \oplus \mathbf {10}_c$. Similar argument applies to $\xi (x,y)$ and $\theta (x,y)$.

In Refs. [63, 64] we use the color rearrangement

$$\begin{aligned} \delta ^{ab} \epsilon ^{cde} = \delta ^{ac} \epsilon ^{bde} +\delta ^{ad} \epsilon ^{cbe} + \delta ^{ae} \epsilon ^{cdb}, \end{aligned}$$

(11)

together with the Fierz rearrangement to derive the relations among all the three types of currents, e.g., we can transform an $\eta$ current into the combination of many $\xi$ and $\theta$ currents:

$$\begin{aligned} \eta \rightarrow \xi + \theta . \end{aligned}$$

(12)

In the present study we further derive another color rearrangement:

$$\begin{aligned} \delta ^{ab} \epsilon ^{cde} = {1\over 3}~\delta ^{ae} \epsilon ^{bcd} -{1\over 2}~\lambda ^{ae}_n \epsilon ^{bcf} \lambda ^{fd}_n + {1\over 2} ~\lambda ^{ae}_n \epsilon ^{bdf} \lambda ^{fc}_n. \end{aligned}$$

(13)

Note that the other color-octet-color-octet meson-baryon term $\lambda ^{ae}_n \epsilon ^{cdf} \lambda ^{fb}_n$ can also be included, but the first coefficient 1/3 always remains the same. This is reasonable because the probability of the relevant fall-apart decay is just 33% if only considering the color degree of freedom, as shown in Figs. 2a and 3a.

Using the above color rearrangement in the color space, together with the Fierz rearrangement in the Lorentz space to interchange the $u_b$ and $c_e$ quark fields, we can transform an $\eta$ current into the combination of many $\theta$ currents (both color-singlet-color-singlet and color-octet-color-octet ones). Similar arguments can be applied to relate

$$\begin{aligned} \eta \leftrightarrow \xi ,\quad \xi \leftrightarrow \theta , \quad \theta \leftrightarrow \eta , \end{aligned}$$

(14)

whose explicit formulae will be given in Sect. 3.

2.2 $\eta /\xi (x,y)$ and heavy baryon fields

In this subsection we construct the $\eta (x,y)$ and $\xi (x,y)$ currents. To do this, we need charmed meson operators as well as their couplings to charmed meson states, which can be found in Table 1 (see Ref. [57] and references therein for detailed discussions). We also need “ground-state” charmed baryon fields, which have been systematically constructed and studied in Refs. [78,79,80] using the method of QCD sum rules [81, 82] within the heavy quark effective theory [83,84,85]. We briefly summarize the results here.

Table 1 Couplings of meson operators to meson states, where color indices are omitted for simplicity. Taken from Ref. [57]

The interpolating fields coupling to the $J^P = 1/2^+$ ground-state charmed baryons $\varLambda _c$ and $\varSigma _c$ are

$$\begin{aligned} J_{\varLambda _c^+}= & {} \epsilon ^{abc} [u_a^T {\mathbb {C}} \gamma _{5} d_b] c_c,\nonumber \\ \sqrt{2} J_{\varSigma _c^{++}}= & {} \epsilon ^{abc} [u_a^T {\mathbb {C}} \gamma _{\mu } u_b] \gamma ^{\mu }\gamma _{5} c_c,\nonumber \\ J_{\varSigma _c^{+}}= & {} \epsilon ^{abc} [u_a^T {\mathbb {C}} \gamma _{\mu } d_b] \gamma ^{\mu }\gamma _{5} c_c , \nonumber \\ \sqrt{2} J_{\varSigma _c^{0}}= & {} \epsilon ^{abc} [d_a^T {\mathbb {C}} \gamma _{\mu } d_b] \gamma ^{\mu }\gamma _{5} c_c . \end{aligned}$$

(15)

Their couplings are defined as

$$\begin{aligned} \langle 0 | J_{{\mathcal {B}}} | {\mathcal {B}} \rangle =f_{{\mathcal {B}}} u_{{\mathcal {B}}}, \end{aligned}$$

(16)

where $u_{{\mathcal {B}}}$ is the Dirac spinor of the charmed baryon ${{\mathcal {B}}}$, and the decay constants $f_{{\mathcal {B}}}$ have been calculated in Refs. [78,79,80] to be

$$\begin{aligned} f_{\varLambda _c}= & {} 0.015 \mathrm{~GeV}^3, \nonumber \\ f_{\varSigma _c}= & {} 0.036 \mathrm{~GeV}^3 . \end{aligned}$$

(17)

The above results are evaluated within the heavy quark effective theory, but for light baryon fields we shall use full QCD decay constants (see Sect. 2.3). This causes some, but not large, theoretical uncertainties.

Actually, there are several other charmed baryon fields, such as:

• the “ground-state” field of pure $J^P = 3/2^+$

  $$\begin{aligned} J^{\mu }_{\varSigma _c^{*+}} = P_{3/2}^{\mu \alpha } ~ \epsilon ^{abc} [u_a^T {\mathbb {C}} \gamma _\alpha d_b] c_c, \end{aligned}$$

  (18)

  which couples to the $J^P = 3/2^+$ ground-state charmed baryons $\varSigma _c^{*+}$, with $P_{3/2}^{\mu \alpha }$ the $J=3/2$ projection operator

  $$\begin{aligned} P_{3/2}^{\mu \alpha } = g^{\mu \alpha } - {\gamma ^\mu \gamma ^\alpha \over 4}. \end{aligned}$$

  (19)

• the “excited” charmed baryon field

  $$\begin{aligned} J^*_{{\mathcal {B}}} = \epsilon ^{abc} [u_a^T {\mathbb {C}} d_b] \gamma _{5} c_c, \end{aligned}$$

  (20)

  which contains the excited diquark field $\epsilon ^{abc} u_a^T {\mathbb {C}} d_b$ of $J^P = 0^-$.

For completeness, we list all of them in Appendix B, and refer to Ref. [86] for detailed discussions. The major advantage of using the heavy quark effective theory is that within this framework all these charmed baryon fields do not couple to the $J^P = 1/2^+$ ground-state charmed baryons $\varLambda _c$ and $\varSigma _c$ [87]. However, some of them, both “ground-state” and “excited” fields, can couple to the $J^P = 3/2^+$ ground-state charmed baryon $\varSigma _c^{*}$. Hence, we do/can not study decays of $P_c$ states into the $\bar{D} \varSigma _c^*$ final state in the present study.

Combing charmed meson operators and ground-state charmed baryon fields, we can construct the $\eta (x,y)$ and $\xi (x,y)$ currents. In the molecular picture the $P_c(4312)$, $P_c(4440)$, and $P_c(4457)$ can be interpreted as the $\bar{D} \varSigma _c$ hadronic molecular state of $J^P = {1/2}^-$, the $\bar{D}^* \varSigma _c$ one of $J^P ={1/2}^-$, and the $\bar{D}^* \varSigma _c$ one of $J^P ={3/2}^-$ [19,20,21]:

$$\begin{aligned}&| \bar{D} \varSigma _c; {1/2}^- ; \theta _1 \rangle \nonumber \\&\quad = \cos \theta _1~| \bar{D}^0 \varSigma _c^+ \rangle _{J=1/2} + \sin \theta _1~| \bar{D}^- \varSigma _c^{++} \rangle _{J=1/2},\nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned}&| \bar{D}^* \varSigma _c; {1/2}^- ; \theta _2 \rangle \nonumber \\&\quad = \cos \theta _2~| \bar{D}^{*0} \varSigma _c^+ \rangle _{J=1/2} + \sin \theta _2~| \bar{D}^{*-} \varSigma _c^{++} \rangle _{J=1/2},\nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned}&| \bar{D}^* \varSigma _c; {3/2}^- ; \theta _3 \rangle \nonumber \\&\quad = \cos \theta _3~| \bar{D}^{*0} \varSigma _c^+ \rangle _{J=3/2} + \sin \theta _3~| \bar{D}^{*-} \varSigma _c^{++} \rangle _{J=3/2},\nonumber \\ \end{aligned}$$

(23)

where $\theta _i$ ($i=1,2,3$) are isospin parameters ($\theta _i = -55^\mathrm{o}$ for $I=1/2$ and $\theta _i = 35^\mathrm{o}$ for $I=3/2$). Their relevant interpolating currents are:

$$\begin{aligned} J_i^{(\alpha )}= & {} \cos \theta _i~\eta _i^{(\alpha )} +\sin \theta _i~\xi _i^{(\alpha )}, \end{aligned}$$

(24)

where

$$\begin{aligned} \eta _1= & {} [\bar{c}_a \gamma _5 u_a] ~ \varSigma _c^+\nonumber \\= & {} [\delta ^{ab} \bar{c}_a \gamma _5 u_b] ~ [\epsilon ^{cde} u_c^T {\mathbb {C}} \gamma _\mu d_d \gamma ^\mu \gamma _5 c_e],\end{aligned}$$

(25)

$$\begin{aligned} \eta _2= & {} [\bar{c}_a \gamma _\nu u_a] ~ \gamma ^\nu \gamma _5 \varSigma _c^+\nonumber \\= & {} [\delta ^{ab} \bar{c}_a \gamma _\nu u_b] ~ \gamma ^\nu \gamma _5 ~ [\epsilon ^{cde} u_c^T {\mathbb {C}} \gamma _\mu d_d \gamma ^\mu \gamma _5 c_e],\end{aligned}$$

(26)

$$\begin{aligned} \eta _3^\alpha= & {} P_{3/2}^{\alpha \nu } ~ [\bar{c}_a \gamma _\nu u_a] ~ \varSigma _c^+\nonumber \\= & {} [\delta ^{ab} \bar{c}_a \gamma _\nu u_b] ~ P_{3/2}^{\alpha \nu }[\epsilon ^{cde} u_c^T {\mathbb {C}} \gamma _\mu d_d \gamma ^\mu \gamma _5 c_e] , \end{aligned}$$

(27)

and

$$\begin{aligned} \xi _1= & {} [\bar{c}_a \gamma _5 d_a] ~ \varSigma _c^{++}\nonumber \\= & {} {1\over \sqrt{2}} ~ [\delta ^{ab} \bar{c}_a \gamma _5 d_b] ~[\epsilon ^{cde} u_c^T {\mathbb {C}} \gamma _\mu u_d \gamma ^\mu \gamma _5 c_e],\end{aligned}$$

(28)

$$\begin{aligned} \xi _2= & {} [\bar{c}_a \gamma _\nu d_a] ~ \gamma ^\nu \gamma _5 \varSigma _c^{++}\nonumber \\= & {} {1\over \sqrt{2}} ~ [\delta ^{ab} \bar{c}_a \gamma _\nu d_b] ~ \gamma ^\nu \gamma _5 ~[\epsilon ^{cde} u_c^T {\mathbb {C}} \gamma _\mu u_d \gamma ^\mu \gamma _5 c_e],\end{aligned}$$

(29)

$$\begin{aligned} \xi _3^\alpha= & {} P_{3/2}^{\alpha \nu } ~ [\bar{c}_a \gamma _\nu d_a] ~ \varSigma _c^{++}\nonumber \\= & {} {1\over \sqrt{2}} ~ [\delta ^{ab} \bar{c}_a \gamma _\nu d_b] ~P_{3/2}^{\alpha \nu }[\epsilon ^{cde} u_c^T {\mathbb {C}} \gamma _\mu u_d \gamma ^\mu \gamma _5 c_e]. \end{aligned}$$

(30)

In the above expressions we have written $J_{{\mathcal {B}}}$ as ${\mathcal {B}}$ for simplicity.

2.3 $\theta (x,y)$ and light baryon fields

In this subsection we construct the $\theta (x,y)$ currents, which can be constructed by combing charmonium operators and light baryon fields. Hence, we need charmonium operators as well as their couplings to charmonium states, which can be found in Table 1 (see Ref. [57] and references therein for detailed discussions). We also need light baryon fields, which have been systematically studied in Refs. [66,67,68, 88,89,90,91,92]. We briefly summarize the results here.

According to the results of Ref. [88], we can use u, u, and d ($q=u/d$) quarks to construct five independent baryon fields:

$$\begin{aligned} N_1= & {} \epsilon ^{abc} (u_a^T {\mathbb {C}} d_b) \gamma _5 u_c ,\nonumber \\ N_2= & {} \epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma _5 d_b) u_c,\nonumber \\ N_3^\mu= & {} P_{3/2}^{\mu \alpha } ~ \epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma _\alpha \gamma _5 d_b) \gamma _5 u_c,\\ N_4^\mu= & {} P_{3/2}^{\mu \alpha } ~ \epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma _\alpha d_b) u_c,\nonumber \\ N_5^{\mu \nu }= & {} P_{3/2}^{\mu \nu \alpha \beta } ~ \epsilon ^{abc} (u_a^T {\mathbb {C}} \sigma _{\alpha \beta } d_b) \gamma _5 u_c,\nonumber \end{aligned}$$

(31)

where the projection operator $P_{3/2}^{\mu \nu \alpha \beta }$ is

$$\begin{aligned} P_{3/2}^{\mu \nu \alpha \beta }= & {} {g^{\mu \alpha }g^{\nu \beta }\over 2} -{g^{\mu \beta }g^{\nu \alpha }\over 2} - {g^{\mu \alpha }\over 4}\gamma ^\nu \gamma ^\beta + {g^{\mu \beta }\over 4}\gamma ^\nu \gamma ^\alpha \nonumber \\&+ {g^{\nu \alpha }\over 4}\gamma ^\mu \gamma ^\beta - {g^{\nu \beta }\over 4} \gamma ^\mu \gamma ^\alpha + {1\over 6} \sigma ^{\mu \nu }\sigma ^{\alpha \beta }. \end{aligned}$$

(32)

All the other light baryon fields (including other $\epsilon ^{abc }[u^T_a {\mathbb {C}} \varGamma _1 d_b]\varGamma _2 u_c$ fields as well as all the $\epsilon ^{abc }[u^T_a {\mathbb {C}} \varGamma _3 u_b]\varGamma _4 d_c$ fields) can be transformed to $N^{(\mu \nu )}_{1,2,3,4,5}$, as shown in Appendix B.

Among the five fields defined in Eqs. (31), the former two $N_{1,2}$ have pure spin $J=1/2$, and the latter three $N^{\mu (\nu )}_{3,4,5}$ have pure spin $J=3/2$. In the present study we shall study decays of $P_c$ states into charmonia and protons, but not study their decays into charmonia and $\varDelta /N^*$, since the couplings of $N^{\mu (\nu )}_{3,4,5}$ to $\varDelta /N^*$ have not been (well) investigated in the literature. Therefore, we only keep $N_{1,2}$ but omit $N^{\mu (\nu )}_{3,4,5}$. Moreover, we shall find that all the terms in our calculations do not depend on $N_1 + N_2$, so we only need to consider the Ioffe’s light baryon field

$$\begin{aligned} N \equiv N_1 - N_2 . \end{aligned}$$

(33)

This field has been well studied in Refs. [66,67,68] and suggested to couple to the proton through

$$\begin{aligned} \langle 0 | N | p \rangle = f_p u_p, \end{aligned}$$

(34)

with the decay constant evaluated in Ref. [93] to be

$$\begin{aligned} f_p = 0.011 \mathrm{~GeV}^3. \end{aligned}$$

(35)

3 Fierz rearrangement

In this section we study the Fierz rearrangement of the $\eta (x,y)$ and $\xi (x,y)$ currents, which will be used to investigate fall-apart decays of $P_c$ states in Sect. 4. Taking $\eta (x,y)$ as an example, when the $\bar{c}_a(x)$ and $c_e(y)$ quarks meet each other and the $u_b(x)$, $u_c(y)$, and $d_d(y)$ quarks meet together at the same time, a $\bar{D}^{(*)0} \varSigma _c^{+}$ molecular state can decay into one charmonium meson and one light baryon. This is the decay process depicted in Fig. 2a:

$$\begin{aligned}&\left[ \delta ^{ab} \bar{c}_a(x) u_b(x)\right] ~ \left[ \epsilon ^{cde} u_c(y) d_d(y) c_e(y)\right] \nonumber \\&\quad \rightarrow \delta ^{ab} \bar{c}_a(x \rightarrow x^\prime ) u_b(x \rightarrow y^\prime )\nonumber \\&\quad \otimes \, \epsilon ^{cde} u_c(y \rightarrow y^\prime ) d_d(y \rightarrow y^\prime ) c_e(y \rightarrow x^\prime )\nonumber \\&\quad = {1\over 3}\delta ^{ae} \epsilon ^{bcd} \otimes \bar{c}_a(x^\prime ) u_b(y^\prime ) \otimes u_c(y^\prime ) d_d(y^\prime ) c_e(x^\prime ) + \cdots \nonumber \\&\quad = {1\over 3} \left[ \delta ^{ae}\bar{c}_a(x^\prime ) c_e(x^\prime )\right] \oplus \left[ \epsilon ^{bcd}u_b(y^\prime ) u_c(y^\prime ) d_d(y^\prime )\right] + \cdots .\nonumber \\ \end{aligned}$$

(36)

The first step is a dynamical process, during which we assume that all the color, flavor, spin and orbital structures remain unchanged, so the relevant current also remains the same. The second and third steps can be described by applying the Fierz rearrangement to interchange both the color and Dirac indices of the $u_b(y^\prime )$ and $c_e(x^\prime )$ quark fields.

Fig. 2

Fall-apart decays of $P_c$ states as $\bar{D}^{(*)0} \varSigma _c^{+}$ molecular states, investigated through the $\eta (x,y)$ currents. There are three possibilities: a $\eta \rightarrow \theta$, b $\eta \rightarrow \eta$, and c $\eta \rightarrow \xi$. Their probabilities are the same (33%), if only considering the color degree of freedom

Fig. 3

Fall-apart decays of $P_c$ states as $\bar{D}^{(*)-} \varSigma _c^{++}$ molecular states, investigated through the $\xi (x,y)$ currents. There are three possibilities: a $\xi \rightarrow \theta$, b $\xi \rightarrow \eta$, and c again $\xi \rightarrow \eta$. Their probabilities are the same (33%), if only considering the color degree of freedom

Still taking $\eta (x,y)$ as an example: when the $\bar{c}_a(x)$ and $u_c(y)$ quarks meet each other and the $u_b(x)$, $d_d(y)$, and $c_e(y)$ quarks meet together at the same time, a $\bar{D}^{(*)0} \varSigma _c^{+}$ molecular state can decay into one charmed meson and one charmed baryon, as depicted in Fig. 2b; when the $\bar{c}_a(x)$ and $d_d(y)$ quarks meet each other and the $u_b(x)$, $u_c(y)$, and $c_e(y)$ quarks meet together at the same time, a $\bar{D}^{(*)0} \varSigma _c^{+}$ molecular state can also decay into one charmed meson and one charmed baryon, as depicted in Fig. 2c. Similarly, decays of $\bar{D}^{(*)-} \varSigma _c^{++}$ molecular states can be investigated through the $\xi (x,y)$ currents, as depicted in Fig. 3a–c.

In the following subsections we shall study the above fall-apart decay processes, by applying the Fierz rearrangement [94] of the Dirac and color indices to relate the $\eta$, $\xi$, and $\theta$ currents. This method has been used to systematically study light baryon and tetraquark operators/currents in Refs. [70, 71, 88,89,90,91,92, 95,96,97,98,99]. We note that the Fierz rearrangement in the Lorentz space is actually a matrix identity, which is valid if each quark field in the initial and final operators is at the same location, e.g., we can apply the Fierz rearrangement to transform a non-local $\eta$ current with the quark fields $\eta = [\bar{c}(x^\prime ) u(y^\prime )] ~ [u(y^\prime ) d(y^\prime ) c(x^\prime )]$ into the combination of many non-local $\theta$ currents with the quark fields at same locations $\theta = [\bar{c}(x^\prime ) c(x^\prime )] ~[u(y^\prime ) u(y^\prime ) d(y^\prime )]$. Hence, this rearrangement exactly describes the third step of Eq. (36).

3.1 $\eta \rightarrow \theta$ and $\xi \rightarrow \theta$

Using Eq. (13), together with the Fierz rearrangement to interchange the $u_b$ and $c_e$ quark fields, we can transform an $\eta (x,y)$ current into the combination of many $\theta$ currents:

$$\begin{aligned} \eta _1&\rightarrow {1\over 12} ~ [\bar{c}_a c_a]~\gamma _5 N -{1\over 12} ~ [\bar{c}_a \gamma _5 c_a]~N\nonumber \\&\quad + {1\over 24} ~ [\bar{c}_a \gamma _\mu \gamma _5 c_a] ~\gamma ^\mu N + {1\over 24} ~ [\bar{c}_a \gamma _\mu c_a] ~\gamma ^\mu \gamma _5 N\nonumber \\&\quad +~\cdots , \end{aligned}$$

(37)

$$\begin{aligned} \eta _2&\rightarrow {1\over 6} ~ [\bar{c}_a c_a]~\gamma _5 N + {1\over 6} ~ [\bar{c}_a \gamma _5 c_a]~N\nonumber \\&\quad + {1\over 12} ~ [\bar{c}_a \gamma _\mu \gamma _5 c_a] ~\gamma ^\mu N - {1\over 12} ~ [\bar{c}_a \gamma _\mu c_a] ~\gamma ^\mu \gamma _5 N\nonumber \\&\quad - {1\over 12} ~ [\bar{c}_a \sigma _{\mu \nu } c_a] ~\sigma ^{\mu \nu } \gamma _5 N+\cdots , \end{aligned}$$

(38)

$$\begin{aligned} \eta _3^\alpha&\rightarrow [\bar{c}_a \gamma _\mu \gamma _5 c_a] ~\left( {1\over 16} g^{\alpha \mu } \gamma _5 + {i\over 48} \sigma ^{\alpha \mu } \gamma _5 \right) N\nonumber \\&\quad + [\bar{c}_a \gamma _\mu c_a] ~ \left( -{1\over 16} g^{\alpha \mu } - {i\over 48} \sigma ^{\alpha \mu } \right) N+\cdots . \end{aligned}$$

(39)

In the above transformations we have changed the coordinates according to the first step of Eq. (36), which are not shown explicitly here for simplicity. Besides, we have omitted in $\cdots$ that: (a) the color-octet-color-octet meson-baryon terms, and (b) terms depending on the $J=3/2$ light baryon fields $N^{\mu (\nu )}_{3,4,5}$. Hence, we have only kept, but kept all, the color-singlet-color-singlet meson-baryon terms depending on the $J=1/2$ fields $N_1$ and $N_2$. This is not an easy task because we need to use many identities given in Eqs. (B.27) and (B.28) of Appendix B in order to safely omit $N^{\mu (\nu )}_{3,4,5}$. Moreover, we can find in the above expressions that all terms contain the Ioffe’s light baryon field $N \equiv N_1 - N_2$, and there are no terms depending on $N_1 + N_2$.

The above transformations can be used to describe the fall-apart decay process depicted in Fig. 2a for $\bar{D}^{(*)0} \varSigma _c^{+}$ molecular states. Similarly, we can investigate the fall-apart decay process depicted in Fig. 3a for $\bar{D}^{(*)-} \varSigma _c^{++}$ molecular states. To do this, we need to use Eq. (13), together with the Fierz rearrangement to interchange the $d_b$ and $c_e$ quark fields, to transform a $\xi (x,y)$ current into the combination of many $\theta$ currents:

$$\begin{aligned} \sqrt{2}\xi _1&\rightarrow - {1\over 6} ~ [\bar{c}_a c_a] ~\gamma _5 N + {1\over 6} ~ [\bar{c}_a \gamma _5 c_a]~N\nonumber \\&\quad - {1\over 12} ~ [\bar{c}_a \gamma _\mu \gamma _5 c_a]~\gamma ^\mu N -{1\over 12} ~ [\bar{c}_a \gamma _\mu c_a]~\gamma ^\mu \gamma _5 N\nonumber \\&\quad + \cdots , \end{aligned}$$

(40)

$$\begin{aligned} \sqrt{2}\xi _2&\rightarrow - {1\over 3} ~ [\bar{c}_a c_a]~\gamma _5 N -{1\over 3} ~ [\bar{c}_a \gamma _5 c_a]~N\nonumber \\&\quad - {1\over 6} ~ [\bar{c}_a \gamma _\mu \gamma _5 c_a] ~\gamma ^\mu N + {1\over 6} ~ [\bar{c}_a \gamma _\mu c_a]~\gamma ^\mu \gamma _5 N\nonumber \\ {}&\quad + {1\over 6} ~ [\bar{c}_a \sigma _{\mu \nu } c_a] ~\sigma ^{\mu \nu } \gamma _5 N + \cdots , \end{aligned}$$

(41)

$$\begin{aligned} \sqrt{2}\xi _3^\alpha&\rightarrow [\bar{c}_a \gamma _\mu \gamma _5 c_a] ~\left( -{1\over 8} g^{\alpha \mu } \gamma _5 - {i\over 24} \sigma ^{\alpha \mu } \gamma _5 \right) N \nonumber \\&\quad + [\bar{c}_a \gamma _\mu c_a] ~ \left( {1\over 8} g^{\alpha \mu } + {i\over 24} \sigma ^{\alpha \mu } \right) N +\cdots . \end{aligned}$$

(42)

3.2 $\eta \rightarrow \eta$ and $\eta \rightarrow \xi$

First we derive a color rearrangement similar to Eq. (13):

$$\begin{aligned} \delta ^{ab} \epsilon ^{cde} = {1\over 3}~\delta ^{ac} \epsilon ^{bde} -{1\over 2}~\lambda ^{ac}_n \epsilon ^{bdf} \lambda ^{fe}_n +{1\over 2}~\lambda ^{ac}_n \epsilon ^{bef} \lambda ^{fd}_n.\nonumber \\ \end{aligned}$$

(43)

Using this identity, together with the Fierz rearrangement to interchange the $u_b$ and $u_c$ quark fields, we can transform an $\eta (x,y)$ current into the combination of many $\eta$ currents.

Besides, we can derive another similar color rearrangement:

$$\begin{aligned} \delta ^{ab} \epsilon ^{cde} = {1\over 3}~\delta ^{ad} \epsilon ^{cbe} + {1\over 2}~\lambda ^{ad}_n \epsilon ^{bcf} \lambda ^{fe}_n -{1\over 2}~\lambda ^{ad}_n \epsilon ^{bef} \lambda ^{fc}_n.\nonumber \\ \end{aligned}$$

(44)

Using this identity, together with the Fierz rearrangement to interchange the $u_b$ and $d_d$ quark fields, we can transform an $\eta (x,y)$ current into the combination of many $\xi$ currents.

The above two transformations describe the fall-apart decay processes depicted in Fig. 2b, c for $\bar{D}^{(*)0} \varSigma _c^{+}$ molecular states. Altogether, we obtain:

$$\begin{aligned} \eta _1&\rightarrow {1\over 12}~[\bar{c}_a \gamma _\mu u_a] ~\gamma ^\mu \gamma _5 \varLambda _c^+\nonumber \\&\quad - {1\over 12}~[\bar{c}_a \gamma _5 u_a] ~ \varSigma _c^{+} -{\sqrt{2}\over 12}~[\bar{c}_a \gamma _5 d_a] ~ \varSigma _c^{++}\nonumber \\&\quad - {1\over 24}~[\bar{c}_a \sigma _{\mu \nu } u_a] ~ \epsilon ^{\mu \nu \rho \sigma } \gamma _\sigma \gamma _5 \left( - {1\over 4} \gamma _\rho \gamma _5 \varSigma _c^{+} \right) \nonumber \\&\quad - {\sqrt{2}\over 24}~[\bar{c}_a \sigma _{\mu \nu } d_a] \epsilon ^{\mu \nu \rho \sigma } \gamma _\sigma \gamma _5 \left( - {1\over 4} \gamma _\rho \gamma _5 \varSigma _c^{++} \right) + \cdots , \end{aligned}$$

(45)

$$\begin{aligned} \eta _2&\rightarrow {1\over 3}~[\bar{c}_a \gamma _5 u_a] ~ \varLambda _c^+ -{1\over 12}~[\bar{c}_a \sigma _{\mu \nu } u_a] ~ \sigma ^{\mu \nu } \gamma _5 \varLambda _c^+\nonumber \\&\quad - {1\over 6} [\bar{c}_a \gamma _\mu u_a] ~ \left( - {1\over 4} \gamma ^\mu \gamma _5 \varSigma _c^{+} \right) \nonumber \\&\quad - {i\over 6} [\bar{c}_a \gamma _\mu \gamma _5 u_a] ~ \sigma ^{\mu \nu } \gamma _5 \left( - {1\over 4} \gamma _\nu \gamma _5 \varSigma _c^{+} \right) \nonumber \\&\quad - {\sqrt{2}\over 6} [\bar{c}_a \gamma _\mu d_a] ~ \left( - {1\over 4} \gamma ^\mu \gamma _5 \varSigma _c^{++} \right) \nonumber \\&\quad - {i\sqrt{2}\over 6} [\bar{c}_a \gamma _\mu \gamma _5 d_a] ~\sigma ^{\mu \nu } \gamma _5 \left( - {1\over 4} \gamma _\nu \gamma _5 \varSigma _c^{++} \right) + \cdots , \end{aligned}$$

(46)

$$\begin{aligned} \eta _3^\alpha&\rightarrow \left( - {i\over 48} g^{\alpha \mu } \gamma ^\nu + {i\over 48} g^{\alpha \nu } \gamma ^\mu - {1\over 48} \epsilon ^{\alpha \beta \mu \nu } \gamma _\beta \gamma _5 \right) \nonumber \\&\quad \times ~[\bar{c}_a \sigma _{\mu \nu } u_a] ~ \varLambda _c^+\nonumber \\&\quad + \left( - {1\over 12} g^{\alpha \mu } \gamma ^\nu \gamma _5 - {1\over 12} g^{\alpha \nu } \gamma ^\mu \gamma _5 + {1\over 24} g^{\mu \nu } \gamma ^\alpha \gamma _5 \right) \nonumber \\&\quad \times ~[\bar{c}_a \gamma _\mu u_a] ~ \left( - {1\over 4} \gamma _\nu \gamma _5 \varSigma _c^{+} \right) \nonumber \\&\quad + \left( {1\over 24} g^{\alpha \mu } \gamma ^\nu - {1\over 24} g^{\alpha \nu } \gamma ^\mu - {i\over 24} \epsilon ^{\alpha \beta \mu \nu } \gamma _\beta \gamma _5 \right) \nonumber \\&\quad \times ~[\bar{c}_a \gamma _\mu \gamma _5 u_a] ~ \left( - {1\over 4} \gamma _\nu \gamma _5 \varSigma _c^{+} \right) \nonumber \\&\quad \times \left( - {1\over 12} g^{\alpha \mu } \gamma ^\nu \gamma _5 - {1\over 12} g^{\alpha \nu } \gamma ^\mu \gamma _5 + {1\over 24} g^{\mu \nu } \gamma ^\alpha \gamma _5 \right) \nonumber \\&\quad \times ~\sqrt{2}~[\bar{c}_a \gamma _\mu d_a] ~\left( - {1\over 4} \gamma _\nu \gamma _5 \varSigma _c^{++} \right) \nonumber \\&\quad + \left( {1\over 24} g^{\alpha \mu } \gamma ^\nu - {1\over 24} g^{\alpha \nu } \gamma ^\mu - {i\over 24} \epsilon ^{\alpha \beta \mu \nu } \gamma _\beta \gamma _5 \right) \nonumber \\&\quad \times \sqrt{2}[\bar{c}_a \gamma _\mu \gamma _5 d_a] \left( - {1\over 4} \gamma _\nu \gamma _5 \varSigma _c^{++} \right) +\cdots . \end{aligned}$$

(47)

In the above transformations we have only kept, but kept all, the color-singlet-color-singlet meson-baryon terms depending on the $J^P=1/2^+$ “ground-state” charmed baryon fields given in Eqs. (15). Again, this is not an easy task because we need to carefully omit the terms depending on the other charmed baryon fields, $B^G_{\bar{\mathbf {3}},1}$, $B^G_{\bar{\mathbf {3}},3}$, $B^G_{\bar{\mathbf {3}},\mu }$, $B^U_{\mathbf {6},5}$, $B^{U}_{\mathbf {6},\mu }$, $B^{\prime U}_{\mathbf {6},\mu }$, and $B^U_{\mathbf {6},\mu \nu }$, whose definitions can be found in Appendix B.

3.3 $\xi \rightarrow \eta$

Following the procedures used in the previous subsection, we can transform a $\xi (x,y)$ current into the combination of many $\eta$ currents (without $\xi$ currents):

$$\begin{aligned} \sqrt{2}\xi _1&\rightarrow - {1\over 6}~[\bar{c}_a \gamma _\mu u_a]~\gamma ^\mu \gamma _5 \varLambda _c^+ - {1\over 6}~[\bar{c}_a \gamma _5 u_a]~\varSigma _c^{+}\nonumber \\&\quad - {1\over 12}~[\bar{c}_a \sigma _{\mu \nu } u_a] ~ \epsilon ^{\mu \nu \rho \sigma } \gamma _\sigma \gamma _5 \left( - {1\over 4} \gamma _\rho \gamma _5 \varSigma _c^{+} \right) \nonumber \\&\quad + \cdots , \end{aligned}$$

(48)

$$\begin{aligned} \sqrt{2}\xi _2&\rightarrow - {2\over 3} ~ [\bar{c}_a \gamma _5 u_a] ~ \varLambda _c^+ + {1\over 6}~[\bar{c}_a \sigma _{\mu \nu } u_a] ~ \sigma ^{\mu \nu } \gamma _5 \varLambda _c^+\nonumber \\&\quad - {1\over 3}~[\bar{c}_a \gamma _\mu u_a] ~ \left( - {1\over 4} \gamma ^\mu \gamma _5 \varSigma _c^{+} \right) \nonumber \\&\quad - {i\over 3}~[\bar{c}_a \gamma _\mu \gamma _5 u_a] ~ \sigma ^{\mu \nu } \gamma _5 \left( - {1\over 4} \gamma _\nu \gamma _5 \varSigma _c^{+} \right) + \cdots , \end{aligned}$$

(49)

$$\begin{aligned} \sqrt{2}\xi _3^\alpha&\rightarrow \left( {i\over 24} g^{\alpha \mu } \gamma ^\nu -{i\over 24} g^{\alpha \nu } \gamma ^\mu + {1\over 24} \epsilon ^{\alpha \beta \mu \nu } \gamma _\beta \gamma _5 \right) \nonumber \\&\quad \times ~[\bar{c}_a \sigma _{\mu \nu } u_a] ~ \varLambda _c^+\nonumber \\&\quad + \left( - {1\over 6} g^{\alpha \mu } \gamma ^\nu \gamma _5 - {1\over 6} g^{\alpha \nu } \gamma ^\mu \gamma _5 + {1\over 12} g^{\mu \nu } \gamma ^\alpha \gamma _5 \right) \nonumber \\&\quad \times ~[\bar{c}_a \gamma _\mu u_a] ~ \left( - {1\over 4} \gamma _\nu \gamma _5 \varSigma _c^{+} \right) \nonumber \\&\quad + \left( {1\over 12} g^{\alpha \mu } \gamma ^\nu - {1\over 12} g^{\alpha \nu } \gamma ^\mu - {i\over 12} \epsilon ^{\alpha \beta \mu \nu } \gamma _\beta \gamma _5 \right) \nonumber \\&\quad \times ~[\bar{c}_a \gamma _\mu \gamma _5 u_a] ~ \left( - {1\over 4} \gamma _\nu \gamma _5 \varSigma _c^{+} \right) +\cdots . \end{aligned}$$

(50)

The above transformations describe the fall-apart decay processes depicted in Fig. 3b, c for $\bar{D}^{(*)-} \varSigma _c^{++}$ molecular states.

4 Decay properties of $\bar{D}^{(*)0} \varSigma _c^+$ and $\bar{D}^{(*)-} \varSigma _c^{++}$ molecular states

In this section we use the Fierz rearrangements derived in the previous section to extract some strong decay properties of $\bar{D}^{(*)0} \varSigma _c^+$ and $\bar{D}^{(*)-} \varSigma _c^{++}$ molecular states. We shall separately investigate:

• $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$, the $\bar{D}^0 \varSigma _c^{+}$ molecular state of $J^P = 1/2^-$, through the $\eta _1(x,y)$ current and the Fierz rearrangements given in Eqs. (37) and (45);

• $|\bar{D}^- \varSigma _c^{++}; 1/2^- \rangle$, the $\bar{D}^- \varSigma _c^{++}$ molecular state of $J^P = 1/2^-$, through the $\xi _1(x,y)$ current and the Fierz rearrangements given in Eqs. (40) and (48);

• $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$, the $\bar{D}^{*0} \varSigma _c^{+}$ molecular state of $J^P = 1/2^-$, through the $\eta _2(x,y)$ current and the Fierz rearrangements given in Eqs. (38) and (46);

• $|\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle$, the $\bar{D}^{*-} \varSigma _c^{++}$ molecular state of $J^P = 1/2^-$, through the $\xi _2(x,y)$ current and the Fierz rearrangements given in Eqs. (41) and (49);

• $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$, the $\bar{D}^{*0} \varSigma _c^{+}$ molecular state of $J^P = 3/2^-$, through the $\eta _3^\alpha (x,y)$ current and the Fierz rearrangements given in Eqs. (39) and (47);

• $|\bar{D}^{*-} \varSigma _c^{++}; 3/2^- \rangle$, the $\bar{D}^{*-} \varSigma _c^{++}$ molecular state of $J^P = 3/2^-$, through the $\xi _3^\alpha (x,y)$ current and the Fierz rearrangements given in Eqs. (42) and (50).

The obtained results will be combined in Sect. 5 to further study decay properties of $\bar{D}^{(*)} \varSigma _c$ molecular states with definite isospins.

4.1 $\eta _1 \rightarrow \theta / \eta / \xi$

In this subsection we study strong decay properties of $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$ through the $\eta _1(x,y)$ current. First we use the Fierz rearrangement given in Eq. (37) to study the decay process depicted in Fig. 2a, i.e., decays of $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$ into one charmonium meson and one light baryon. Together with Table 1, we extract the following decay channels that are kinematically allowed:

• 1. The decay of $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$ into $\eta _c p$ is contributed by both $[\bar{c}_a \gamma _5 c_a]~N$ and $[\bar{c}_a \gamma _\mu \gamma _5 c_a]~\gamma ^\mu N$:

  $$\begin{aligned}&\langle \bar{D}^0 \varSigma _c^{+}; 1/2^-(q) ~|~\eta _c(q_1)~p(q_2) \rangle \nonumber \\&\quad \approx {ia_1\over 12}~\lambda _{\eta _c} f_p ~ \bar{u} u_p + {ia_1\over 24} ~f_{\eta _c} f_p ~ q_1^\mu \bar{u} \gamma _\mu u_p\nonumber \\&\quad \equiv A_{\eta _c p}~\bar{u} u_p + A^\prime _{\eta _c p} ~q_1^\mu \bar{u} \gamma _\mu u_p, \end{aligned}$$

  (51)

  where u and $u_p$ are the Dirac spinors of the $P_c$ state with $J^P = 1/2^-$ and the proton, respectively; $a_1$ is an overall factor, related to the coupling of $\eta _1(x,y)$ to $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$ as well as the dynamical process of Fig. 2a; the two coupling constants $A_{\eta _c p}$ and $A^\prime _{\eta _c p}$ are defined for the two different effective Lagrangians

  $$\begin{aligned} {\mathcal {L}}_{\eta _c p}= & {} A_{\eta _c p}~\bar{P}_c N~\eta _c, \end{aligned}$$

  (52)
  $$\begin{aligned} {\mathcal {L}}^\prime _{\eta _c p}= & {} A^\prime _{\eta _c p}~\bar{P}_c \gamma _\mu N ~\partial ^\mu \eta _c. \end{aligned}$$

  (53)

• 2. The decay of $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$ into $J/\psi p$ is contributed by $[\bar{c}_a \gamma _\mu c_a]~\gamma ^\mu \gamma _5 N$:

  $$\begin{aligned}&\langle \bar{D}^0 \varSigma _c^{+}; 1/2^-(q) | J/\psi (q_1,\epsilon _1)~p(q_2) \rangle \nonumber \\&\quad \approx {a_1\over 24}~ m_{J/\psi } f_{J/\psi } f_p ~ \epsilon _1^\mu \bar{u} \gamma _\mu \gamma _5 u_p \nonumber \\&\quad \equiv A_{\psi p}~\epsilon _1^\mu \bar{u} \gamma _\mu \gamma _5 u_p, \end{aligned}$$

  (54)

  where $A_{\psi p}$ is defined for

  $$\begin{aligned} {\mathcal {L}}_{\psi p} = A_{\psi p}~\bar{P}_c \gamma _\mu \gamma _5 N~\psi ^\mu . \end{aligned}$$

  (55)

Then we use the Fierz rearrangement given in Eq. (45) to study the decay processes depicted in Fig. 2b, c, i.e., decays of $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$ into one charmed meson and one charmed baryon. Together with Table 1, we extract only one decay channel that is kinematically allowed:

• 3. The decay of $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$ into $\bar{D}^{*0} \varLambda _c^+$ is contributed by $[\bar{c}_a \gamma _\mu u_a]~\gamma ^\mu \gamma _5 \varLambda _c^+$:

  $$\begin{aligned}&\langle \bar{D}^0 \varSigma _c^{+}; 1/2^-(q) ~|~\bar{D}^{*0}(q_1,\epsilon _1) ~\varLambda _c^+(q_2) \rangle \nonumber \\&\quad \approx {a_2\over 12}~ m_{D^*} f_{D^*} f_{\varLambda _c} ~ \epsilon _1^\mu \bar{u} \gamma _\mu \gamma _5 u_{\varLambda _c}\nonumber \\&\quad \equiv A_{\bar{D}^{*} \varLambda _c}~\epsilon _1^\mu \bar{u} \gamma _\mu \gamma _5 u_{\varLambda _c^+}, \end{aligned}$$

  (56)

  where $u_{\varLambda _c}$ is the Dirac spinor of the $\varLambda _c^+$; $a_2$ is an overall factor, related to the coupling of $\eta _1(x,y)$ to $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$ as well as the dynamical processes of Fig. 2b, c; the coupling constant $A_{\bar{D}^{*} \varLambda _c}$ is defined for

  $$\begin{aligned} {\mathcal {L}}_{\bar{D}^{*} \varLambda _c}= & {} A_{\bar{D}^{*} \varLambda _c}~\bar{P}_c \gamma _\mu \gamma _5 \varLambda _c^+~\bar{D}^{*,\mu }. \end{aligned}$$

  (57)

In the molecular picture the $P_c(4312)$ is usually interpreted as the $\bar{D} \varSigma _c$ hadronic molecular state of $J^P = {1/2}^-$. Accordingly, we assume the mass of $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$ to be 4311.9 MeV (more parameters can be found in Appendix A), and summarize the above decay amplitudes to obtain the following (relative) decay widths:

$$\begin{aligned} \varGamma (|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle \rightarrow \eta _c p )= & {} a_1^2 ~ 1.1 \times 10^{5}~\mathrm{GeV}^7,\nonumber \\ \varGamma (|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle \rightarrow J/\psi p )= & {} a_1^2 ~ 2.8 \times 10^{4}~\mathrm{GeV}^7,\nonumber \\ \varGamma (|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+ )= & {} a_2^2 ~ 2.0 \times 10^{4}~\mathrm{GeV}^7.\nonumber \\ \end{aligned}$$

(58)

There are two different effective Lagrangians for the $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$ decays into the $\eta _c p$ final state, as given in Eqs. (52) and (53). It is interesting to see their individual contributions:

$$\begin{aligned} \varGamma (|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle \rightarrow \eta _c p ) \big |_{{\mathcal {L}}_{\eta _c p}}= & {} a_1^2 ~ 4.9 \times 10^{4}~\mathrm{GeV}^7,\nonumber \\ \varGamma (|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle \rightarrow \eta _c p ) \big |_{{\mathcal {L}}^\prime _{\eta _c p}}= & {} a_1^2 ~ 1.1 \times 10^{4}~\mathrm{GeV}^7.\nonumber \\ \end{aligned}$$

(59)

Hence, the former is about four times larger than the latter. We note that their interference can be important, but the phase angle between them, i.e., the phase angle between the two coupling constants $A_{\eta _c p}$ and $A^\prime _{\eta _c p}$, can not be well determined in the present study. We shall investigate its relevant uncertainty in Appendix C.

4.2 $\xi _1 \rightarrow \theta / \eta$

In this subsection we follow the procedures used in the previous subsection to study decay properties of $|\bar{D}^{-} \varSigma _c^{++}; 1/2^- \rangle$, through the $\xi _1(x,y)$ current and the Fierz rearrangements given in Eqs. (40) and (48). Again, we assume its mass to be 4311.9 MeV, and obtain the following (relative) decay widths:

$$\begin{aligned} \varGamma (|\bar{D}^- \varSigma _c^{++}; 1/2^- \rangle \rightarrow \eta _c p)= & {} b_1^2 ~ 2.1 \times 10^{5}~\mathrm{GeV}^7,\nonumber \\ \varGamma (|\bar{D}^- \varSigma _c^{++}; 1/2^- \rangle \rightarrow J/\psi p )= & {} b_1^2 ~ 5.7 \times 10^{4}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^- \varSigma _c^{++}; 1/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+ )= & {} b_2^2 ~ 3.9 \times 10^{4}~\mathrm{GeV}^7 .\nonumber \\ \end{aligned}$$

(60)

Here $b_1$ and $b_2$ are two overall factors, which we simply assume to be $b_1 = a_1$ and $b_2 = a_2$ in the following analyses.

The above widths of the $|\bar{D}^{-} \varSigma _c^{++}; 1/2^- \rangle$ decays into the $\eta _c p$, $J/\psi p$, and $\bar{D}^{*0} \varLambda _c^+$ final states are all two times larger than those given in Eq. (58) for the $|\bar{D}^{0} \varSigma _c^{+}; 1/2^- \rangle$ decays.

4.3 $\eta _2 \rightarrow \theta / \eta / \xi$

In this subsection we follow the procedures used in Sect. 4.1 to study decay properties of $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ through the $\eta _2(x,y)$ current. First we use the Fierz rearrangement given in Eq. (38) to study the decay process depicted in Fig. 2a:

• 1. The decay of $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ into $\eta _c p$ is

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 1/2^-(q) ~|~\eta _c(q_1)~p(q_2) \rangle \nonumber \\&\quad \approx - {ic_1\over 6}~\lambda _{\eta _c} f_p ~ \bar{u} u_p + {ic_1\over 12} ~f_{\eta _c} f_p ~ q_1^\mu \bar{u} \gamma _\mu u_p\nonumber \\&\quad \equiv C_{\eta _c p}~\bar{u} u_p + C^\prime _{\eta _c p} ~q_1^\mu \bar{u} \gamma _\mu u_p , \end{aligned}$$

  (61)

  where $c_1$ is an overall factor.

• 2. The decay of $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ into $J/\psi p$ is contributed by both $[\bar{c}_a \gamma _\mu c_a]~\gamma ^\mu \gamma _5 N$ and $[\bar{c}_a \sigma _{\mu \nu } c_a]~\sigma ^{\mu \nu } \gamma _5 N$:

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 1/2^-(q) | J/ \psi (q_1,\epsilon _1)~p(q_2) \rangle \nonumber \\&\quad \approx - {c_1\over 12}~ m_{J/\psi } f_{J/\psi } f_p ~ \epsilon _1^\mu \bar{u} \gamma _\mu \gamma _5 u_p\nonumber \\&\qquad - {i c_1\over 6}~ f^T_{J/\psi } f_p ~ q_1^\mu \epsilon _1^\nu \bar{u} \sigma _{\mu \nu } \gamma _5 u_p\nonumber \\&\quad \equiv C_{\psi p}~\epsilon _1^\mu \bar{u} \gamma _\mu \gamma _5 u_p + C^\prime _{\psi p}~q_1^\mu \epsilon _1^\nu \bar{u} \sigma _{\mu \nu } \gamma _5 u_p, \end{aligned}$$

  (62)

  where the two coupling constants $C_{\psi p}$ and $C^\prime _{\psi p}$ are defined for

  $$\begin{aligned} {\mathcal {L}}_{\psi p}= & {} C_{\psi p}~\bar{P}_c \gamma _\mu \gamma _5 N~\psi ^\mu , \end{aligned}$$

  (63)
  $$\begin{aligned} {\mathcal {L}}^\prime _{\psi p}= & {} C^\prime _{\psi p}~\bar{P}_c \sigma _{\mu \nu } \gamma _5 N~\partial ^\mu \psi ^\nu . \end{aligned}$$

  (64)

• 3. The decay of $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ into $\chi _{c0}(1P) p$ is contributed by $[\bar{c}_a c_a]~ \gamma _5 N$:

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 1/2^-(q) | \chi _{c0}(q_1)~p(q_2) \rangle \nonumber \\&\quad \approx {c_1\over 6}~ m_{\chi _{c0}} f_{\chi _{c0}} f_p ~ \bar{u} \gamma _5 u_p\nonumber \\&\quad \equiv C_{\chi _{c0} p}~\bar{u} \gamma _5 u_p , \end{aligned}$$

  (65)

  where $C_{\chi _{c0} p}$ is defined for

  $$\begin{aligned} {\mathcal {L}}_{\chi _{c0} p}= & {} C_{\chi _{c0} p} ~\bar{P}_c \gamma _5 N~\chi _{c0}. \end{aligned}$$

  (66)

• 4. The decay of $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ into $\chi _{c1}(1P) p$ is contributed by $[\bar{c}_a \gamma _\mu \gamma _5 c_a]~\gamma ^\mu N$:

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 1/2^-(q) | \chi _{c1} (q_1,\epsilon _1)~p(q_2) \rangle \nonumber \\&\quad \approx {c_1\over 12}~ m_{\chi _{c1}} f_{\chi _{c1}} f_p ~ \epsilon _1^\mu \bar{u} \gamma _\mu u_p\nonumber \\&\quad \equiv C_{\chi _{c1} p}~\epsilon _1^\mu \bar{u} \gamma _\mu u_p, \end{aligned}$$

  (67)

  where $C_{\chi _{c1} p}$ is defined for

  $$\begin{aligned} {\mathcal {L}}_{\chi _{c1} p}= & {} C_{\chi _{c1} p}~\bar{P}_c \gamma _\mu N~\chi _{c1}^\mu . \end{aligned}$$

  (68)

  This decay channel may be kinematically allowed, depending on whether the $P_c(4457)$ is interpreted as $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ or not.

Then we use the Fierz rearrangement given in Eq. (46) to study the decay processes depicted in Fig. 2b, c:

• 5. The decay of $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ into $\bar{D}^{0} \varLambda _c^+$ is contributed by $[\bar{c}_a \gamma _5 u_a]~ \varLambda _c^+$:

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 1/2^-(q) ~|~\bar{D}^{0}(q_1) ~\varLambda _c^+(q_2) \rangle \nonumber \\&\quad \approx -{ic_2\over 3}~ \lambda _{D} f_{\varLambda _c} ~ \bar{u} u_{\varLambda _c}\nonumber \\&\quad \equiv C_{\bar{D} \varLambda _c}~\bar{u} u_{\varLambda _c}, \end{aligned}$$

  (69)

  where $c_2$ is an overall factor, and the coupling constant $C_{\bar{D} \varLambda _c}$ is defined for

  $$\begin{aligned} {\mathcal {L}}_{\bar{D} \varLambda _c}= & {} C_{\bar{D} \varLambda _c} ~\bar{P}_c \varLambda _c^+~\bar{D}^{0}. \end{aligned}$$

  (70)

• 6. The decay of $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ into $\bar{D}^{*0} \varLambda _c^+$ is contributed by $[\bar{c}_a \sigma _{\mu \nu } u_a] ~ \sigma ^{\mu \nu } \gamma _5 \varLambda _c^+$:

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 1/2^-(q) ~| ~\bar{D}^{*0}(q_1,\epsilon _1)~\varLambda _c^+(q_2) \rangle \nonumber \\&\quad \approx - {i c_2\over 6}~ f^T_{D^*} f_{\varLambda _c} ~ q_1^\mu \epsilon _1^\nu \bar{u} \sigma _{\mu \nu } \gamma _5 u_{\varLambda _c}\nonumber \\&\quad \equiv C^\prime _{\bar{D}^{*} \varLambda _c}~q_1^\mu \epsilon _1^\nu \bar{u} \sigma _{\mu \nu } \gamma _5 u_{\varLambda _c}, \end{aligned}$$

  (71)

  where $C^\prime _{\bar{D}^{*} \varLambda _c}$ is defined for

  $$\begin{aligned} {\mathcal {L}}^\prime _{\bar{D}^{*} \varLambda _c} = C^\prime _{\bar{D}^{*} \varLambda _c}~\bar{P}_c \sigma _{\mu \nu } \gamma _5 \varLambda _c^+ ~\partial ^\mu \bar{D}^{*0,\nu }. \end{aligned}$$

  (72)

• 7. Decays of $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ into the $\bar{D}^{0} \varSigma _c^+$ and $\bar{D}^{-} \varSigma _c^{++}$ final states are:

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 1/2^-(q) ~|~\bar{D}^{0}(q_1) ~\varSigma _c^+(q_2) \rangle \nonumber \\&\quad \approx {ic_2\over 8}~ f_{D} f_{\varSigma _c} ~ q_1^\mu \bar{u} \gamma _\mu u_{\varSigma _c}\nonumber \\&\quad \equiv C_{\bar{D} \varSigma _c}~ q_1^\mu \bar{u} \gamma _\mu u_{\varSigma _c},\end{aligned}$$

  (73)
  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 1/2^-(q) ~|~\bar{D}^{-} (q_1)~\varSigma _c^{++}(q_2) \rangle \nonumber \\&\quad \approx {i\sqrt{2}c_2\over 8}~ f_{D} f_{\varSigma _c} ~ q_1^\mu \bar{u} \gamma _\mu u_{\varSigma _c}\nonumber \\&\quad \equiv \sqrt{2}C_{\bar{D} \varSigma _c}~q_1^\mu \bar{u} \gamma _\mu u_{\varSigma _c}, \end{aligned}$$

  (74)

  where $C_{\bar{D} \varSigma _c}$ is defined for

  $$\begin{aligned} {\mathcal {L}}_{\bar{D} \varSigma _c}= & {} C_{\bar{D} \varSigma _c} ~\bar{P}_c \gamma _\mu \varSigma _c^+~\partial ^\mu \bar{D}^{0}\nonumber \\&+ \sqrt{2}C_{\bar{D} \varSigma _c}~\bar{P}_c \gamma _\mu \varSigma _c^{++} ~\partial ^\mu \bar{D}^{-}. \end{aligned}$$

  (75)

In the molecular picture the $P_c(4440)$ is sometimes interpreted as the $\bar{D}^* \varSigma _c$ hadronic molecular state of $J^P = {1/2}^-$. Accordingly, we assume the mass of $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ to be 4440.3 MeV, and summarize the above decay amplitudes to obtain the following (relative) decay widths:

$$\begin{aligned} \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle \rightarrow \eta _c p )= & {} c_1^2 ~ 5.8 \times 10^{4}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle \rightarrow J/\psi p )= & {} c_1^2 ~ 4.6 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle \rightarrow \chi _{c0} p )= & {} c_1^2 ~ 2.0 \times 10^{3}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle \rightarrow \bar{D}^{0} \varLambda _c^+ )= & {} c_2^2 ~ 5.5 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+ )= & {} c_2^2 ~ 1.9 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ )= & {} c_2^2 ~ 1.6 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle \rightarrow \bar{D}^{-} \varSigma _c^{++} )= & {} c_2^2 ~ 3.2 \times 10^{5}~\mathrm{GeV}^7 .\nonumber \\ \end{aligned}$$

(76)

Besides, $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ can also couple to $\chi _{c1} p$, but this channel is kinematically forbidden under the assumption $M_{|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle } =4440.3$ MeV.

There are two different effective Lagrangians for the $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ decays into the $J/\psi p$ final state, as given in Eqs. (63) and (64). It is interesting to see their individual contributions:

$$\begin{aligned} \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle \rightarrow J/\psi p) \big |_{{\mathcal {L}}_{\psi p}}= & {} c_1^2 ~ 1.5 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle \rightarrow J/\psi p) \big |_{{\mathcal {L}}^\prime _{\psi p}}= & {} c_1^2 ~ 6.1 \times 10^{5}~\mathrm{GeV}^7 .\nonumber \\ \end{aligned}$$

(77)

Hence, the former is about four times smaller than the latter. Again, the phase angle between them can be important, whose relevant uncertainty will be investigated in Appendix C.

4.4 $\xi _2 \rightarrow \theta / \eta$

In this subsection we follow the procedures used in the previous subsection to study decay properties of $|\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle$, through the $\xi _2(x,y)$ current and the Fierz rearrangements given in Eqs. (41) and (49). Again, we assume its mass to be 4440.3 MeV, and obtain the following (relative) decay widths:

$$\begin{aligned} \varGamma (|\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle \rightarrow \eta _c p )= & {} d_1^2 ~ 1.2 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle \rightarrow J/\psi p )= & {} d_1^2 ~ 9.3 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle \rightarrow \chi _{c0} p )= & {} d_1^2 ~ 4.1 \times 10^{3}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle \rightarrow \bar{D}^{0} \varLambda _c^+ )= & {} d_2^2 ~ 1.1 \times 10^{6}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+ )= & {} d_2^2 ~ 3.8 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ )= & {} d_2^2 ~ 3.2 \times 10^{5}~\mathrm{GeV}^7 .\nonumber \\ \end{aligned}$$

(78)

Here $d_1$ and $d_2$ are two overall factors, which we simply assume to be $d_1 = c_1$ and $d_2 = c_2$ in the following analyses.

The above results suggest that $|\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle$ can not fall-apart decay into the $\bar{D}^{-} \varSigma _c^{++}$ final state, as depicted in Fig. 3b, c, while $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ can. The widths of the $|\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle$ decays into other final states, including $\eta _c p$, $J/\psi p$, $\chi _{c0} p$, $\bar{D}^{0} \varLambda _c^+$, $\bar{D}^{*0} \varLambda _c^+$, and $\bar{D}^{0} \varSigma _c^+$, are all two times larger than those given in Eq. (76) for the $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ decays.

4.5 $\eta _3^\alpha \rightarrow \theta / \eta / \xi$

In this subsection we follow the procedures used in Sects. 4.1 and 4.3 to study decay properties of $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$ through the $\eta _3^\alpha (x,y)$ current. First we use the Fierz rearrangement given in Eq. (39) to study the decay process depicted in Fig. 2a:

• 1. The decay of $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$ into $\eta _c p$ is

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 3/2^-(q) ~|~\eta _c(q_1)~p(q_2) \rangle \nonumber \\&\quad \approx ie_1 ~ f_{\eta _c} f_p ~ q_1^\mu \bar{u}^\alpha \left( {1\over 16} g^{\alpha \mu } \gamma _5 + {i\over 48} \sigma ^{\alpha \mu } \gamma _5 \right) u_p ,\nonumber \\ \end{aligned}$$

  (79)

  where $u^\alpha$ is the spinor of the $P_c$ state with $J^P =3/2^-$, and $e_1$ is an overall factor.

• 2. The decay of $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$ into $J/\psi p$ is

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 3/2^-(q) | J/\psi (q_1,\epsilon _1)~p(q_2) \rangle \nonumber \\&\quad \approx e_1 ~ m_{J/\psi } f_{J/\psi } f_p ~ \epsilon _1^\mu \bar{u}^\alpha \left( -{1\over 16} g^{\alpha \mu } - {i\over 48} \sigma ^{\alpha \mu } \right) u_p .\nonumber \\ \end{aligned}$$

  (80)

• 3. The decay of $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$ into $\chi _{c1}(1P) p$ is

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 3/2^-(q) | \chi _{c1}(q_1,\epsilon _1)~p(q_2) \rangle \nonumber \\&\quad \approx e_1 ~ m_{\chi _{c1}} f_{\chi _{c1}} f_p ~\epsilon _1^\mu \bar{u}^\alpha \left( {1\over 16} g^{\alpha \mu } \gamma _5 + {i\over 48} \sigma ^{\alpha \mu } \gamma _5 \right) u_p.\nonumber \\ \end{aligned}$$

  (81)

  This decay channel may be kinematically allowed, depending on whether the $P_c(4457)$ is interpreted as $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$ or not.

Then we use the Fierz rearrangement given in Eq. (47) to study the decay processes depicted in Fig. 2b, c:

• 4. The decay of $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$ into $\bar{D}^{*0} \varLambda _c^+$ is

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 3/2^-(q) ~|~\bar{D}^{*0}(q_1,\epsilon _1)~\varLambda _c^+(q_2) \rangle \nonumber \\&\quad \approx 2i e_2 ~ f^T_{D^*} f_{\varLambda _c} ~ q_1^\mu \epsilon _1^\nu \nonumber \\&\qquad \times \bar{u}^\alpha \left( - {i\over 48} g^{\alpha \mu } \gamma ^\nu {+}{i\over 48} g^{\alpha \nu } \gamma ^\mu - {1\over 48} \epsilon ^{\alpha \beta \mu \nu } \gamma _\beta \gamma _5 \right) u_{\varLambda _c},\nonumber \\ \end{aligned}$$

  (82)

  where $e_2$ is an overall factor.

• 5. Decays of $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$ into the $\bar{D}^{0} \varSigma _c^+$ and $\bar{D}^{-} \varSigma _c^{++}$ final states are:

  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 3/2^-(q) ~|~\bar{D}^{0}(q_1) ~\varSigma _c^+(q_2) \rangle \nonumber \\&\quad \approx i e_2 ~ f_{D} f_{\varSigma _c} ~ q_1^\mu \nonumber \\&\qquad \times ~ \bar{u}^\alpha \left( {1\over 24} g^{\alpha \mu } \gamma ^\nu - {1\over 24} g^{\alpha \nu } \gamma ^\mu - {i\over 24} \epsilon ^{\alpha \beta \mu \nu } \gamma _\beta \gamma _5 \right) \nonumber \\&\qquad \times \left( - {1\over 4} \gamma _\nu \gamma _5 \right) u_{\varSigma _c},\end{aligned}$$

  (83)
  $$\begin{aligned}&\langle \bar{D}^{*0} \varSigma _c^{+}; 3/2^-(q) ~|~\bar{D}^{-}(q_1) ~\varSigma _c^{++}(q_2) \rangle \nonumber \\&\quad \approx \sqrt{2} i e_2 ~ f_{D} f_{\varSigma _c} ~ q_1^\mu \nonumber \\&\qquad \times ~ \bar{u}^\alpha \left( {1\over 24} g^{\alpha \mu } \gamma ^\nu - {1\over 24} g^{\alpha \nu } \gamma ^\mu - {i\over 24} \epsilon ^{\alpha \beta \mu \nu } \gamma _\beta \gamma _5 \right) \nonumber \\&\qquad \times \left( - {1\over 4} \gamma _\nu \gamma _5 \right) ~ u_{\varSigma _c}. \end{aligned}$$

  (84)

In the molecular picture the $P_c(4457)$ is sometimes interpreted as the $\bar{D}^* \varSigma _c$ hadronic molecular state of $J^P ={3/2}^-$. Accordingly, we assume the mass of $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$ to be 4457.3 MeV, and summarize the above decay amplitudes to obtain the following (relative) decay widths:

$$\begin{aligned} \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle \rightarrow \eta _c p)= & {} e_1^2 ~ 240~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle \rightarrow J/\psi p)= & {} e_1^2 ~ 4.7 \times 10^{4}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle \rightarrow \chi _{c1} p)= & {} e_1^2 ~ 15~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+ )= & {} e_2^2 ~ 1.6 \times 10^{4}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ )= & {} e_2^2 ~ 5.7 ~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle \rightarrow \bar{D}^{-} \varSigma _c^{++} )= & {} e_2^2 ~ 11~\mathrm{GeV}^7 . \end{aligned}$$

(85)

Hence, $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$ does not couple to the $\chi _{c0} p$ channel, different from $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$.

4.6 $\xi _3^\alpha \rightarrow \theta / \eta$

In this subsection we follow the procedures used in the previous subsection to study decay properties of $|\bar{D}^{*-} \varSigma _c^{++}; 3/2^- \rangle$, through the $\xi _3^\alpha (x,y)$ current and the Fierz rearrangements given in Eqs. (42) and (50). Again, we assume its mass to be 4457.3 MeV, and obtain the following (relative) decay widths:

$$\begin{aligned} \varGamma (|\bar{D}^{*-} \varSigma _c^{++}; 3/2^- \rangle \rightarrow \eta _c p )= & {} f_1^2 ~ 490~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*-} \varSigma _c^{++}; 3/2^- \rangle \rightarrow J/\psi p )= & {} f_1^2 ~ 9.3 \times 10^{4}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*-} \varSigma _c^{++}; 3/2^- \rangle \rightarrow \chi _{c1} p )= & {} f_1^2 ~ 30~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*-} \varSigma _c^{++}; 3/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+ )= & {} f_2^2 ~ 3.3 \times 10^{4}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*-} \varSigma _c^{++}; 3/2^- \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ )= & {} f_2^2 ~ 11 ~\mathrm{GeV}^7 . \end{aligned}$$

(86)

Here $f_1$ and $f_2$ are two overall factors, which we simply assume to be $f_1 = e_1$ and $f_2 = e_2$ in the following analyses.

The above results suggest that $|\bar{D}^{*-} \varSigma _c^{++}; 3/2^- \rangle$ can not fall-apart decay into the $\bar{D}^{-} \varSigma _c^{++}$ final state, as depicted in Fig. 3b, c, while $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$ can. The widths of the $|\bar{D}^{*-} \varSigma _c^{++}; 3/2^- \rangle$ decays into other final states, including $\eta _c p$, $J/\psi p$, $\chi _{c1} p$, $\bar{D}^{*0} \varLambda _c^+$, and $\bar{D}^{0} \varSigma _c^+$, are all two times larger than those given in Eq. (85) for the $|\bar{D}^{*0} \varSigma _c^{+}; 3/2^- \rangle$ decays.

5 Isospin of $\bar{D}^{(*)} \varSigma _c$ molecular states

In this section we collect the results calculated in the previous section to further study decay properties of $\bar{D}^{(*)} \varSigma _c$ molecular states with definite isospins.

The $\bar{D}^{(*)} \varSigma _c$ molecular states with $I = 1/2$ can be obtained by using Eqs. (21), (22), and (23) with $\theta _i = -55^\mathrm{o}$:

$$\begin{aligned}&\left| \bar{D}^{(*)} \varSigma _c; {1\over 2}^-/{3\over 2}^- \right\rangle \nonumber \\&\quad = \sqrt{1\over 3}~| \bar{D}^{(*)0} \varSigma _c^+ \rangle _{J={1\over 2}/{3\over 2}} - \sqrt{2\over 3}~| \bar{D}^{(*)-} \varSigma _c^{++} \rangle _{J={1\over 2}/{3\over 2}}.\nonumber \\ \end{aligned}$$

(87)

Combining the results of Sects. 4.1 and 4.2, we obtain:

$$\begin{aligned} \varGamma (|\bar{D} \varSigma _c; 1/2^- \rangle \rightarrow \eta _c p )= & {} a_1^2 ~3.2 \times 10^{5}~\mathrm{GeV}^7 \, ,\nonumber \\ \varGamma (|\bar{D} \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p )= & {} a_1^2 ~8.5 \times 10^{4}~\mathrm{GeV}^7 \, ,\nonumber \\ \varGamma (|\bar{D} \varSigma _c; 1/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+)= & {} a_2^2 ~ 5.9 \times 10^{4}~\mathrm{GeV}^7 \, . \end{aligned}$$

(88)

Combining the results of Sects. 4.3 and 4.4, we obtain:

$$\begin{aligned} \varGamma (|\bar{D}^{*} \varSigma _c; 1/2^- \rangle \rightarrow \eta _c p )= & {} c_1^2 ~ 1.7 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p )= & {} c_1^2 ~ 1.4 \times 10^{6}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 1/2^- \rangle \rightarrow \chi _{c0} p )= & {} c_1^2 ~ 6.1 \times 10^{3}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 1/2^- \rangle \rightarrow \bar{D}^{0} \varLambda _c^+ )= & {} c_2^2 ~ 1.7 \times 10^{6}~\mathrm{GeV}^7,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 1/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+ )= & {} c_2^2 ~ 5.6 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 1/2^- \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ )= & {} c_2^2 ~ 5.4 \times 10^{4}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 1/2^- \rangle \rightarrow \bar{D}^{-} \varSigma _c^{++} )= & {} c_2^2 ~ 1.1 \times 10^{5}~\mathrm{GeV}^7 .\nonumber \\ \end{aligned}$$

(89)

Combining the results of Sects. 4.5 and 4.6, we obtain:

$$\begin{aligned} \varGamma (|\bar{D}^{*} \varSigma _c; 3/2^- \rangle \rightarrow \eta _c p )= & {} e_1^2 ~ 730~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 3/2^- \rangle \rightarrow J/\psi p )= & {} e_1^2 ~ 1.4 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 3/2^- \rangle \rightarrow \chi _{c1} p )= & {} e_1^2 ~ 46~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 3/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+ )= & {} e_2^2 ~ 4.9 \times 10^{4}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 3/2^- \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ )= & {} e_2^2 ~ 1.9 ~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 3/2^- \rangle \rightarrow \bar{D}^{-} \varSigma _c^{++} )= & {} e_2^2 ~ 3.8 ~\mathrm{GeV}^7 . \end{aligned}$$

(90)

Comparing the above values with those given in Eqs. (58), (76), and (85), we find that the decay widths of the three $\bar{D}^{(*)} \varSigma _c$ molecular states with $I = 1/2$ into the $\eta _c p$, $J/\psi p$, $\chi _{c0} p$, $\chi _{c1} p$, $\bar{D}^{0} \varLambda _c^+$, and $\bar{D}^{*0} \varLambda _c^+$ final states also with $I = 1/2$ are increased by three times, and their decay widths into the $\bar{D}^{0} \varSigma _c^+$ and $\bar{D}^{-} \varSigma _c^{++}$ final states are decreased by three times. We shall further discuss these results in Sect. 6.

For completeness, we also list here the results for the three $\bar{D}^{(*)} \varSigma _c$ molecular states with $I = 3/2$ (as if they existed), which can be obtained by using Eqs. (21), (22), and (23) with $\theta _i =35^\mathrm{o}$:

$$\begin{aligned}&\left| \bar{D}^{(*)} \varSigma _c; {1\over 2}^{-\prime }/{3\over 2}^{-\prime } \right\rangle \nonumber \\&\quad = \sqrt{2\over 3}~| \bar{D}^{(*)0} \varSigma _c^+ \rangle _{J={1\over 2}/{3\over 2}} + \sqrt{1\over 3}~| \bar{D}^{(*)-} \varSigma _c^{++} \rangle _{J={1\over 2}/{3\over 2}}.\nonumber \\ \end{aligned}$$

(91)

Naively assuming their masses to be 4311.9 MeV, 4440.3 MeV, and 4457.3 MeV, respectively, we obtain the following non-zero (relative) decay widths:

$$\begin{aligned} \varGamma (|\bar{D}^{*} \varSigma _c; 1/2^{-\prime } \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ )= & {} c_2^2 ~ 4.3 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 1/2^{-\prime } \rangle \rightarrow \bar{D}^{-} \varSigma _c^{++} )= & {} c_2^2 ~ 2.2 \times 10^{5}~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 3/2^{-\prime } \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ )= & {} e_2^2 ~ 15~\mathrm{GeV}^7 ,\nonumber \\ \varGamma (|\bar{D}^{*} \varSigma _c; 3/2^{-\prime } \rangle \rightarrow \bar{D}^{-} \varSigma _c^{++} )= & {} e_2^2 ~ 7.6 ~\mathrm{GeV}^7 . \end{aligned}$$

(92)

Comparing them with Eqs. (58), (76), and (85), we find that the three $\bar{D}^{(*)} \varSigma _c$ molecular states with $I = 3/2$ can not fall-apart decay into the $\eta _c p$, $J/\psi p$, $\chi _{c0} p$, $\chi _{c1} p$, $\bar{D}^{0} \varLambda _c^+$, and $\bar{D}^{*0} \varLambda _c^+$ final states with $I = 1/2$, their widths into the $\bar{D}^{0} \varSigma _c^+$ final state are increased by a factor of 8/3, and their widths into the $\bar{D}^{-} \varSigma _c^{++}$ final state are reduced to two third. We summarize these results in Appendix C, which we shall not discuss any more.

6 Summary and conclusions

In this paper we systematically study hidden-charm pentaquark currents with the quark content $\bar{c} c u u d$. We investigate three different configurations, $\eta = [\bar{c} u][u d c]$, $\xi =[\bar{c} d][u u c]$, and $\theta = [\bar{c} c][u u d]$. Some of their relations are derived using the Fierz rearrangement of the Dirac and color indices, and the obtained results are used to study strong decay properties of $\bar{D}^{(*)} \varSigma _c$ molecular states with $I = 1/2$ and $J^P = 1/2^-$ and $3/2^-$.

Before drawing conclusions, we would like to generally discuss about the uncertainty. In the present study we work under the naive factorization scheme, so our uncertainty is larger than the well-developed QCD factorization scheme [100,101,102], that is at the 5% level when being applied to conventional (heavy) hadrons [103]. On the other hand, the pentaquark decay constants, such as $f_{P_c}$, are removed when calculating relative branching ratios. This significantly reduces our uncertainty. Accordingly, we roughly estimate our uncertainty to be at the $X^{+100\%}_{-~50\%}$ level.

In the molecular picture the $P_c(4312)$ is usually interpreted as the $\bar{D} \varSigma _c$ hadronic molecular state of $J^P = {1/2}^-$, and the $P_c(4440)$ and $P_c(4457)$ are sometimes interpreted as the $\bar{D}^* \varSigma _c$ hadronic molecular states of $J^P = {1/2}^-$ and ${3/2}^-$ respectively (sometimes interpreted as states of $J^P = {3/2}^-$ and ${1/2}^-$ respectively) [19,20,21]. Using their masses measured in the LHCb experiment [4] as inputs, we calculate some of their relative decay widths. The obtained results have been summarized in Eqs. (88), (89), and (90), from which we further obtain:

• We obtain the following relative branching ratios for the $|\bar{D} \varSigma _c; 1/2^- \rangle$ decays:

  $$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D} \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\quad : \eta _c p: \bar{D}^{*0} \varLambda _c^+\right) \over {\mathcal {B}}\left( |\bar{D} \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\right) }\nonumber \\&\quad \approx 1: 3.8 : 0.69t . \end{aligned}$$

  (93)

• We obtain the following relative branching ratios for the $|\bar{D}^* \varSigma _c; 1/2^- \rangle$ decays:

$$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p: \eta _c p :\chi _{c0} p: \bar{D}^{0} \varLambda _c^+ : \bar{D}^{*0} \varLambda _c^+ : \bar{D}^{0} \varSigma _c^+ : \bar{D}^{-} \varSigma _c^{++}\right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\right) } \nonumber \\&\quad \approx 1 : 0.13: 0.004 : 1.2t : 0.41t : 0.04t :0.08t. \end{aligned}$$

(94)

• We obtain the following relative branching ratios for the $|\bar{D}^* \varSigma _c; 3/2^- \rangle$ decays:

  $$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow J/\psi p : \eta _c p : \chi _{c1} p: \bar{D}^{*0} \varLambda _c^+ : \bar{D}^{0} \varSigma _c^+ : \bar{D}^{-} \varSigma _c^{++}\right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow J/\psi p\right) } \nonumber \\&\quad \approx 1 : 0.005 : 10^{-4} : 0.35t : 10^{-5}t : 10^{-5}t. \end{aligned}$$

  (95)

In these expressions, $t \equiv {a_2^2 \over a_1^2} \approx {c_2^2 \over c_1^2} \approx {e_2^2 \over e_1^2}$ is the parameter measuring which processes happen more easily, the processes depicted in Figs. 2 and 3a or the processes depicted in Figs. 2 and 3b, c. Generally speaking, the exchange of one light quark with another light quark seems to be easier than the exchange of one light quark with another heavy quark [104], so it can be the case that $t \ge 1$. There are two phase angles, which have not been taken into account in the above expressions yet. We investigate their relevant uncertainties in Appendix C, where we also give the relative branching ratios for the $\bar{D}^{(*)} \varSigma _c$ hadronic molecular states of $I = 3/2$, and separately for the $\bar{D}^{(*)0} \varSigma _c^+$ and $\bar{D}^{(*)-} \varSigma _c^{++}$ hadronic molecular states.

To extract these results:

• We have only considered the leading-order fall-apart decays described by color-singlet-color-singlet meson-baryon currents, but neglected the ${\mathcal {O}}(\alpha _s)$ corrections described by color-octet-color-octet meson-baryon currents, so there can be other possible decay channels.

• We have omitted all the charmed baryon fields of $J=3/2$, so we can not study decays of $P_c$ states into the $\bar{D} \varSigma _c^*$ final state. However, we have kept all the charmed baryon fields that can couple to the $J^P=1/2^+$ ground-state charmed baryons $\varLambda _c$ and $\varSigma _c$, i.e., fields given in Eqs. (15), so decays of $P_c$ states into the $\bar{D}^{(*)} \varLambda _c$ and $\bar{D} \varSigma _c$ final states have been well investigated in the present study.

• We have omitted all the light baryon fields of $J=3/2$, so we can not study decays of $P_c$ states into charmonia and $\varDelta /N^*$. However, we have kept all the light baryon fields of $J^P=1/2^+$, i.e., terms depending on $N_1$ and $N_2$, so decays of $P_c$ states into charmonia and protons have been well investigated in the present study.

Our conclusions are:

• Firstly, we compare the $\eta _c p$ and $J/\psi p$ channels:

  $$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D} \varSigma _c; 1/2^- \rangle \rightarrow \eta _c p \right) \over {\mathcal {B}}\left( |\bar{D} \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\right) } \approx 3.8,\nonumber \\&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow \eta _c p \right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\right) } \approx 0.13,\nonumber \\&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow \eta _c p \right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow J/\psi p\right) } \approx 0.005. \end{aligned}$$

  (96)

  These ratios are quite similar to those obtained using the heavy quark spin symmetry [49]. This is quite reasonable because no spin symmetry breaking is introduced during the calculation before using the decay constants for the mesons, so that the heavy quark spin symmetry is automatically built in our formalism. Since the width of the $|\bar{D} \varSigma _c; 1/2^- \rangle$ decay into the $\eta _c p$ final state is comparable to its decay width into $J/\psi p$, we propose to confirm the existence of the $P_c(4312)$ in the $\eta _c p$ channel.

• Secondly, we compare the $\bar{D}^{(*)} \varLambda _c$ and $J/\psi p$ channels:

  $$\begin{aligned} {{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow \bar{D}^{0} \varLambda _c^+ \right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\right) } \approx 1.2t, \end{aligned}$$

  (97)

  and

  $$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D} \varSigma _c; 1/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+ \right) \over {\mathcal {B}}\left( |\bar{D} \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\right) } \approx 0.69t ,\nonumber \\&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+ \right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\right) } \approx 0.41t,\nonumber \\&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow \bar{D}^{*0} \varLambda _c^+ \right) \over {\mathcal {B}} \left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow J/\psi p\right) }\approx 0.35t. \end{aligned}$$

  (98)

  Accordingly, we propose to observe the $P_c(4312)$, $P_c(4440)$, and $P_c(4457)$ in the $\bar{D}^{*0} \varLambda _c^+$ channel. Moreover, the $\bar{D}^{0} \varLambda _c^+$ channel can be an ideal channel to extract the spin-parity quantum numbers of the $P_c(4440)$ and $P_c(4457)$.

• Thirdly, we compare the $\bar{D} \varSigma _c$ and $J/\psi p$ channels:

  $$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ \right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\right) } \approx 0.04t,\nonumber \\&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow \bar{D}^{-} \varSigma _c^{++} \right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\right) } \approx 0.08t, \end{aligned}$$

  (99)

  and

  $$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ \right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow J/\psi p\right) } \approx 10^{-5}t ,\nonumber \\&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow \bar{D}^{-} \varSigma _c^{++} \right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow J/\psi p\right) } \approx 10^{-5}t . \end{aligned}$$

  (100)

  Accordingly, we propose to observe the $P_c(4440)$ and $P_c(4457)$ in the $\bar{D}^{-} \varSigma _c^{++}$ channel, which is another possible channel to extract their spin-parity quantum numbers.

Appendices

Appendix A: Parameters and decay formulae

We list masses of $P_c$ states used in the present study, taken from the LHCb experiment [4]:

$$\begin{aligned} P_c(4312)^+ ~:~ m= & {} 4311.9 \text{ MeV },\nonumber \\ P_c(4440)^+ ~:~ m= & {} 4440.3 \text{ MeV },\nonumber \\ P_c(4457)^+ ~:~ m= & {} 4457.3 \text{ MeV } . \end{aligned}$$

(A.1)

We list masses of charmonium mesons and charmed mesons used in the present study, taken from PDG [2] and partly averaged over isospin:

$$\begin{aligned} \eta _c(1S) ~:~ m= & {} 2983.9 \text{ MeV } ,\nonumber \\ J/\psi (1S) ~:~ m= & {} 3096.900 \text{ MeV },\nonumber \\ \chi _{c0}(1P) ~:~ m= & {} 3414.71 \text{ MeV } ,\nonumber \\ \chi _{c1}(1P) ~:~ m= & {} 3510.67 \text{ MeV } ,\nonumber \\ D/\bar{D} ~:~ m= & {} 1867.24 \text{ MeV } ,\nonumber \\ D^*/\bar{D}^* ~:~ m= & {} 2008.55 \text{ MeV } . \end{aligned}$$

(A.2)

We list masses of the proton and charmed baryons used in the present study, taken from PDG [2] and partly averaged over isospin:

$$\begin{aligned} \mathrm{proton} ~:~ m= & {} 938.272 \text{ MeV } ,\nonumber \\ \varLambda _c^+ ~:~ m= & {} 2286.46 \text{ MeV } ,\nonumber \\ \varSigma _c ~:~ m= & {} 2453.44 \text{ MeV } . \end{aligned}$$

(A.3)

In this paper we only investigate two-body decays, and their widths can be easily calculated. In the calculations we use the following formula for baryon fields of spin 1/2 and 3/2:

$$\begin{aligned} \sum _{spin} u(p) \bar{u}(p)= & {} \left( p\!\!\!/+ m \right) , \end{aligned}$$

(A.4)

$$\begin{aligned} \sum _{spin} u_{\mu }(p) \bar{u}_{\mu ^\prime }(p)= & {} \left( g_{\mu \mu ^\prime } - {1\over 3} \gamma _\mu \gamma _{\mu ^\prime }- {p_\mu \gamma _{\mu ^\prime } - p_{\mu ^\prime }\gamma _{\mu } \over 3m}\right. \nonumber \\&\left. - {2p_{\mu }p_{\mu ^\prime } \over 3m^2} \right) \left( p\!\!\!/+ m \right) \, . \end{aligned}$$

(A.5)

Appendix B: Heavy and light baryon fields

First we construct charmed baryon interpolating fields. We refer to Ref. [86] for detailed discussions. There are altogether nine independent charmed baryon fields:

$$\begin{aligned} B^G_{\bar{\mathbf {3}},1}= & {} \epsilon _{abc} \epsilon ^{ABG} (q_A^{aT} {\mathbb {C}} q_B^b) \gamma _5 c^c, \end{aligned}$$

(B.6)

$$\begin{aligned} B^G_{\bar{\mathbf {3}},2}= & {} \epsilon _{abc} \epsilon ^{ABG} (q_A^{aT} {\mathbb {C}} \gamma _5 q_B^b) c^c, \end{aligned}$$

(B.7)

$$\begin{aligned} B^G_{\bar{\mathbf {3}},3}= & {} \epsilon _{abc} \epsilon ^{ABG} (q_A^{aT} {\mathbb {C}} \gamma _\mu \gamma _5 q_B^b) \gamma ^\mu c^c, \end{aligned}$$

(B.8)

$$\begin{aligned} B^G_{\bar{\mathbf {3}},\mu }= & {} P^{3/2}_{\mu \nu } \epsilon _{abc} \epsilon ^{ABG} (q_A^{aT} {\mathbb {C}} \gamma ^\nu \gamma _5 q_B^b) \gamma _5 c^c, \end{aligned}$$

(B.9)

$$\begin{aligned} B^U_{\mathbf {6},4}= & {} \epsilon _{abc} S^U_{AB} (q_A^{aT} {\mathbb {C}} \gamma _\mu q_B^b) \gamma ^\mu \gamma _5 c^c , \end{aligned}$$

(B.10)

$$\begin{aligned} B^U_{\mathbf {6},5}= & {} \epsilon _{abc} S^U_{AB} (q_A^{aT} {\mathbb {C}} \sigma _{\mu \nu } q_B^b) \sigma ^{\mu \nu } \gamma _5 c^c , \end{aligned}$$

(B.11)

$$\begin{aligned} B^U_{\mathbf {6},\mu }= & {} P^{3/2}_{\mu \nu } \epsilon _{abc} S^U_{AB} (q_A^{aT} {\mathbb {C}} \gamma ^\nu q_B^b) c^c, \end{aligned}$$

(B.12)

$$\begin{aligned} B^{\prime U}_{\mathbf {6},\mu }= & {} P^{3/2}_{\mu \nu } ( B^{U,\nu }_{\mathbf {6},7} + B^{U,\nu }_{\mathbf {6},8\nu }), \end{aligned}$$

(B.13)

$$\begin{aligned} B^U_{\mathbf {6},\mu \nu }= & {} P^{3/2}_{\mu \nu \alpha \beta } ( B^{U,\alpha \beta }_{\mathbf {6},7} + B^{U,\alpha \beta }_{\mathbf {6},8}) , \end{aligned}$$

(B.14)

where

$$\begin{aligned} B^U_{\mathbf {6},7\mu }= & {} \epsilon _{abc} S^U_{AB} (q_A^{aT} {\mathbb {C}} \sigma _{\mu \nu } q_B^b) \gamma ^\nu c^c, \end{aligned}$$

(B.15)

$$\begin{aligned} B^U_{\mathbf {6},8\mu }= & {} \epsilon _{abc} S^U_{AB} (q_A^{aT} {\mathbb {C}} \sigma _{\mu \nu } \gamma _5 q_B^b) \gamma ^\nu \gamma _5 c^c, \end{aligned}$$

(B.16)

$$\begin{aligned} B^U_{\mathbf {6},7\mu \nu }= & {} \epsilon _{abc} S^U_{AB} (q_A^{aT} {\mathbb {C}} \sigma _{\mu \nu } q_B^b) \gamma _5 c^c, \end{aligned}$$

(B.17)

$$\begin{aligned} B^U_{\mathbf {6},8\mu \nu }= & {} \epsilon _{abc} S^U_{AB} (q_A^{aT} {\mathbb {C}} \sigma _{\mu \nu } \gamma _5 q_B^b) c^c . \end{aligned}$$

(B.18)

In the above expressions, a, b, c are color indices and the sum over repeated indices is taken; A, B, G, U are SU(3) flavor indices, so that $q_A = \{u,d,s\}$; $\epsilon ^{ABG}$ is the totally antisymmetric matrix with $G=1,2,3$, so that $B^G_{\bar{\mathbf {3}},i}$ belong to the SU(3) flavor $\bar{\mathbf {3}}_F$ representation; $S^U_{AB}$ are the totally symmetric matrices with $U=1\cdots 6$, so that $B^U_{\mathbf {6},i}$ belong to the SU(3) flavor $\mathbf {6}_F$ representation; $c^c$ is the charm quark field with the color index c; ${\mathbb {C}}$ is the charge-conjugation matrix; $P^{3/2}_{\mu \nu }$ and $P^{3/2}_{\mu \nu \alpha \beta }$ are two $J=3/2$ projection operators.

Among the nine fields given in Eqs. (B.6–B.14), $B^G_{\bar{\mathbf {3}},1}$, $B^G_{\bar{\mathbf {3}},2}$, $B^G_{\bar{\mathbf {3}},3}$, $B^U_{\mathbf {6},4}$, and $B^U_{\mathbf {6},5}$ have pure spin $J=1/2$, and $B^G_{\bar{\mathbf {3}},\mu }$, $B^U_{\mathbf {6},\mu }$, $B^{\prime U}_{\mathbf {6},\mu }$, and $B^U_{\mathbf {6},\mu \nu }$ have pure spin $J=3/2$. In the present study we only take into account the $J^P =1/2^+$ “ground-state” charmed baryon fields, $B^G_{\bar{\mathbf {3}},2}$ and $B^U_{\mathbf {6},4}$; while we omit other charmed baryon fields, $B^G_{\bar{\mathbf {3}},1}$, $B^G_{\bar{\mathbf {3}},3}$, $B^G_{\bar{\mathbf {3}},\mu }$, $B^U_{\mathbf {6},5}$, $B^{U}_{\mathbf {6},\mu }$, $B^{\prime U}_{\mathbf {6},\mu }$, and $B^U_{\mathbf {6},\mu \nu }$, all of which do not couple to the $J^P = 1/2^+$ ground-state charmed baryons $\varLambda _c$ and $\varSigma _c$ within the framework of heavy quark effective theory [87].

Then we give the relations among light baryon fields. We refer to Refs. [66,67,68, 88,89,90,91,92] for detailed discussions. According to the results of Ref. [88], we can use u, u, and d ($q=u/d$) quarks to construct five independent baryon fields:

$$\begin{aligned} N_1= & {} \epsilon ^{abc} (u_a^T {\mathbb {C}} d_b) \gamma _5 u_c , \end{aligned}$$

(B.19)

$$\begin{aligned} N_2= & {} \epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma _5 d_b) u_c , \end{aligned}$$

(B.20)

$$\begin{aligned} N_{3}^{\prime \mu }= & {} \epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma ^\mu \gamma _5 d_b) \gamma _5 u_c, \end{aligned}$$

(B.21)

$$\begin{aligned} N_{4}^{\prime \mu }= & {} \epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma ^\mu d_b) u_c , \end{aligned}$$

(B.22)

$$\begin{aligned} N_{5}^{\prime \mu \nu }= & {} \epsilon ^{abc} (u_a^T {\mathbb {C}} \sigma ^{\mu \nu } d_b) \gamma _5 u_c. \end{aligned}$$

(B.23)

Among these fields, the former two $N_{1,2}$ have pure spin $J=1/2$, but the latter three $N^{\prime \mu (\nu )}_{3,4,5}$ do not have pure spin $J=3/2$. We need to further use the projection operators $P_{3/2}^{\mu \alpha }$ and $P_{3/2}^{\mu \nu \alpha \beta }$ to obtain $N^{\mu (\nu )}_{3,4,5}$, already given in Eq. (31), which have pure spin $J=3/2$. The relations between $N^{\mu (\nu )}_{3,4,5}$ and $N^{\prime \mu (\nu )}_{3,4,5}$ are

$$\begin{aligned} N_3^\mu= & {} P_{3/2}^{\mu \alpha } \times N_{3\alpha }^{\prime } \nonumber \\= & {} N_{3}^{\prime \mu } + {1\over 4} \gamma ^\mu \gamma _5 (N_1 - N_2) , \end{aligned}$$

(B.24)

$$\begin{aligned} N_4^\mu= & {} P_{3/2}^{\mu \alpha } \times N_{4\alpha }^{\prime }\nonumber \\= & {} N_{4}^{\prime \mu } + {1\over 4} \gamma ^\mu \gamma _5 (N_1 - N_2) , \end{aligned}$$

(B.25)

$$\begin{aligned} N_5^{\mu \nu }= & {} P_{3/2}^{\mu \nu \alpha \beta } \times N_{5\alpha \beta }^{\prime }\nonumber \\= & {} N_{5}^{\prime \mu \nu } + {i\over 2} \gamma ^\nu \gamma _5 (N_{3}^{\prime \mu } + N_{4}^{\prime \mu })\nonumber \\&- {i\over 2} \gamma ^\mu \gamma _5 (N_{3}^{\prime \nu } +N_{4}^{\prime \nu }) + {1\over 3} \sigma ^{\mu \nu } (2 N_1 - N_2) . \end{aligned}$$

(B.26)

All the other baryon fields can be transformed to $N^{(\prime \mu \nu )}_{1,2,3,4,5}$ (and so to $N^{(\mu \nu )}_{1,2,3,4,5}$) through:

$$\begin{aligned}&\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma ^\mu d_b) \gamma _\mu \gamma _5 u_c = N_1 - N_2 \, ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma ^\mu \gamma _5 d_b) \gamma _\mu u_c = N_1 - N_2 \, ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \sigma ^{\mu \nu } d_b) \sigma _{\mu \nu } \gamma _5 u_c = - 2 N_1 - 2 N_2 \, ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma _\nu d_b) \sigma ^{\mu \nu } u_c\nonumber \\&\quad = - i N_{4}^{\prime \mu } - i \gamma ^\mu \gamma _5 (N_1 - N_2) \, ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma _\nu \gamma _5 d_b) \sigma ^{\mu \nu } \gamma _5 u_c\nonumber \\&\quad = - i N_{3}^{\prime \mu } - i \gamma ^\mu \gamma _5 (N_1 - N_2) \, ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \sigma ^{\mu \nu } d_b) \gamma _\nu u_c\nonumber \\&\quad = i N_{3}^{\prime \mu } + i N_{4}^{\prime \mu } + i \gamma ^\mu \gamma _5 N_1 \, ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \sigma ^{\mu \nu } \gamma _5 d_b) \gamma _\nu \gamma _5 u_c\nonumber \\&\quad = - i N_{3}^{\prime \mu } - i N_{4}^{\prime \mu } + i \gamma ^\mu \gamma _5 N_2 \, ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \sigma ^{\mu \nu } \gamma _5 d_b) u_c\nonumber \\&\quad = N_{5}^{\prime \mu \nu } + i \gamma ^\nu \gamma _5 (N_{3}^{\prime \mu } + N_{4}^{\prime \mu })\nonumber \\&\qquad -i \gamma ^\mu \gamma _5 (N_{3}^{\prime \nu } +N_{4}^{\prime \nu }) + \sigma ^{\mu \nu } (N_1 - N_2),\nonumber \\&\epsilon ^{abc} \epsilon ^{\mu \nu \rho \sigma } (u_a^T {\mathbb {C}} \sigma _{\rho \alpha } d_b) \sigma _{\sigma \alpha } u_c\nonumber \\&\quad = - 2 N_{5}^{\prime \mu \nu } - i \gamma ^\nu \gamma _5 (N_{3}^{\prime \mu } + N_{4}^{\prime \mu })\nonumber \\&\qquad + i \gamma ^\mu \gamma _5 (N_{3}^{\prime \nu } +N_{4}^{\prime \nu }) - 2 \sigma ^{\mu \nu } N_1,\nonumber \\&\epsilon ^{abc} \epsilon ^{\mu \nu \rho \sigma } (u_a^T {\mathbb {C}} \gamma _\rho d_b) \gamma _\sigma u_c\nonumber \\&\quad = - i \gamma ^\nu \gamma _5 N_{4}^{\prime \mu } + i \gamma ^\mu \gamma _5 N_{4}^{\prime \nu } - \sigma ^{\mu \nu } (N_1 - N_2) ,\nonumber \\&\epsilon ^{abc} \epsilon ^{\mu \nu \rho \sigma } (u_a^T {\mathbb {C}} \gamma _\rho \gamma _5 d_b) \gamma _\sigma \gamma _5 u_c\nonumber \\&\quad = - i \gamma ^\nu \gamma _5 N_{3}^{\prime \mu } + i \gamma ^\mu \gamma _5 N_{3}^{\prime \nu } - \sigma ^{\mu \nu } (N_1 - N_2) , \end{aligned}$$

(B.27)

and

$$\begin{aligned}&\epsilon ^{abc} (u_a^T {\mathbb {C}} u_b) \gamma _5 d_c = 0,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma _5 u_b) d_c = 0,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma ^\mu u_b) \gamma _\mu \gamma _5 d_c = - 2 N_1 + 2 N_2 ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma ^\mu \gamma _5 u_b) \gamma _\mu d_c = 0 \, ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \sigma ^{\mu \nu } u_b) \sigma _{\mu \nu } \gamma _5 d_c = 4 N_1 + 4 N_2 ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma ^\mu u_b) d_c\nonumber \\&\quad = N_{3}^{\prime \mu } + N_{4}^{\prime \mu } + \gamma ^\mu \gamma _5 (N_1 - N_2),\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma ^\mu \gamma _5 u_b) \gamma _5 d_c = 0 ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma _\nu u_b) \sigma ^{\mu \nu } d_c\nonumber \\&\quad = - i N_{3}^{\prime \mu } - i N_{4}^{\prime \mu } + i \gamma ^\mu \gamma _5 (N_1 - N_2),\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \gamma _\nu \gamma _5 u_b) \sigma ^{\mu \nu } \gamma _5 d_c = 0 ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \sigma ^{\mu \nu } u_b) \gamma _\nu d_c\nonumber \\&\quad = - i N_{3}^{\prime \mu } + i N_{4}^{\prime \mu } - i \gamma ^\mu \gamma _5 (N_1 + N_2) ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \sigma ^{\mu \nu } \gamma _5 u_b) \gamma _\nu \gamma _5 d_c\nonumber \\&\quad = i N_{3}^{\prime \mu } - i N_{4}^{\prime \mu } - i \gamma ^\mu \gamma _5 (N_1 + N_2) ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \sigma ^{\mu \nu } u_b) \gamma _5 d_c\nonumber \\&\quad = N_{5}^{\prime \mu \nu } + i \gamma ^\nu \gamma _5 N_{3}^{\prime \mu } - i \gamma ^\mu \gamma _5 N_{3}^{\prime \nu } + \sigma ^{\mu \nu } N_1 ,\nonumber \\&\epsilon ^{abc} (u_a^T {\mathbb {C}} \sigma ^{\mu \nu } \gamma _5 u_b) d_c\nonumber \\&\quad = N_{5}^{\prime \mu \nu } + i \gamma ^\nu \gamma _5 N_{4}^{\prime \mu } - i \gamma ^\mu \gamma _5 N_{4}^{\prime \nu } + \sigma ^{\mu \nu } N_1 ,\nonumber \\&\epsilon ^{abc} \epsilon ^{\mu \nu \rho \sigma } (u_a^T {\mathbb {C}} \sigma _{\rho \alpha } u_b) \sigma _{\sigma \alpha } d_c\nonumber \\&\quad = - 2 N_{5}^{\prime \mu \nu } - i \gamma ^\nu \gamma _5 (N_{3}^{\prime \mu } + N_{4}^{\prime \mu })\nonumber \\&\qquad + i \gamma ^\mu \gamma _5 (N_{3}^{\prime \nu } +N_{4}^{\prime \nu }) + 2 \sigma ^{\mu \nu } N_2 ,\nonumber \\&\epsilon ^{abc} \epsilon ^{\mu \nu \rho \sigma } (u_a^T {\mathbb {C}} \gamma _\rho u_b) \gamma _\sigma d_c\nonumber \\&\quad = - i \gamma ^\nu \gamma _5 (N_{3}^{\prime \mu } +N_{4}^{\prime \mu }) + i \gamma ^\mu \gamma _5 (N_{3}^{\prime \nu } +N_{4}^{\prime \nu }),\nonumber \\&\epsilon ^{abc} \epsilon ^{\mu \nu \rho \sigma } (u_a^T {\mathbb {C}} \gamma _\rho \gamma _5 u_b) \gamma _\sigma \gamma _5 d_c = 0 . \end{aligned}$$

(B.28)

Appendix C: Uncertainties due to phase angles

There are two different effective Lagrangians for the $|\bar{D}^0 \varSigma _c^{+}; 1/2^- \rangle$ (and $|\bar{D}^- \varSigma _c^{++}; 1/2^- \rangle$) decay into the $\eta _c p$ final state, as given in Eqs. (52) and (53):

$$\begin{aligned} {\mathcal {L}}_{\eta _c p}= & {} g_{\eta _c p}~\bar{P}_c N~\eta _c , \end{aligned}$$

(C.29)

$$\begin{aligned} {\mathcal {L}}^\prime _{\eta _c p}= & {} g^\prime _{\eta _c p}~\bar{P}_c \gamma _\mu N~\partial ^\mu \eta _c . \end{aligned}$$

(C.30)

There are also two different effective Lagrangians for the $|\bar{D}^{*0} \varSigma _c^{+}; 1/2^- \rangle$ (and $|\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle$) decay into the $J/\psi p$ final state, as given in Eqs. (63) and (64):

$$\begin{aligned} {\mathcal {L}}_{\psi p}= & {} g_{\psi p}~\bar{P}_c \gamma _\mu \gamma _5 N~\psi ^\mu , \end{aligned}$$

(C.31)

$$\begin{aligned} {\mathcal {L}}^\prime _{\psi p}= & {} g^\prime _{\psi p} ~\bar{P}_c \sigma _{\mu \nu } \gamma _5 N~\partial ^\mu \psi ^\nu . \end{aligned}$$

(C.32)

There can be a phase angle $\theta$ between $g_{\eta _c p}$ and $g^\prime _{\eta _c p}$ and another phase angle $\theta ^\prime$ between $g_{\psi p}$ and $g^\prime _{\psi p}$, both of which can not be determined in the present study. In this appendix we rotate $\theta /\theta ^\prime$ and redo all the calculations.

• We obtain the following relative branching ratios for the $\bar{D}^{(*)} \varSigma _c$ hadronic molecular states of $I = 1/2$:

$$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D} \varSigma _c; 1/2^- \rangle \rightarrow ~J/\psi p~ : \quad \eta _c p\quad : ~\bar{D}^{*0} \varLambda _c^+\right) \over {\mathcal {B}}\left( |\bar{D} \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\right) }\nonumber \\&\quad \approx \quad 1 ~~ : ~~~0.5\sim 3.8~~ : ~~0.69t, \end{aligned}$$

(C.33)

$$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow ~~J/\psi p~~ : \,~~~~\eta _c p~\, : \,~\chi _{c0} p~\, : ~\bar{D}^{0} \varLambda _c^+~ : ~\bar{D}^{*0} \varLambda _c^+~ : ~\bar{D}^{0} \varSigma _c^+~ : ~\bar{D}^{-} \varSigma _c^{++}~ \right) \over {\mathcal {B}} \left( |\bar{D}^* \varSigma _c; 1/2^- \rangle \rightarrow J/\psi p\right) \big |_{\theta ^\prime = 0}}\nonumber \\&\quad \approx \quad 1\sim 1.8 ~\, : ~0.1\sim 1.1~ : ~0.004~ : \,~~1.2t ~~\, : \,~~0.41t~~\, : ~~0.04t~~ : \,~~~0.08t~ \, , \end{aligned}$$

(C.34)

$$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow ~~J/\psi p~~ : ~~\eta _c p~~ : \,~\chi _{c1} p~\, : ~\bar{D}^{*0} \varLambda _c^+~ : ~\bar{D}^{0} \varSigma _c^+~ : ~\bar{D}^{-} \varSigma _c^{++}~ \right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^- \rangle \rightarrow J/\psi p\right) }\nonumber \\&\quad \approx \quad 1 ~~ : ~0.005~ : ~10^{-4}~ : \,~~0.35t ~~\, : \,~10^{-5}t~\, : ~~~10^{-5}t~ . \end{aligned}$$

(C.35)

• We obtain the following relative branching ratios for the $\bar{D}^{(*)} \varSigma _c$ hadronic molecular states of $I = 3/2$:

  $$\begin{aligned} {{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^{-\prime } \rangle \rightarrow \bar{D}^{-} \varSigma _c^{++} \right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 1/2^{-\prime } \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ \right) }\approx & {} 0.5 \, , \end{aligned}$$

  (C.36)
  $$\begin{aligned} {{\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^{-\prime } \rangle \rightarrow \bar{D}^{-} \varSigma _c^{++} \right) \over {\mathcal {B}}\left( |\bar{D}^* \varSigma _c; 3/2^{-\prime } \rangle \rightarrow \bar{D}^{0} \varSigma _c^+ \right) }\approx & {} 0.5. \end{aligned}$$

  (C.37)

• We obtain the following relative branching ratios for the $\bar{D}^{(*)0} \varSigma _c^+$ hadronic molecular states:

$$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^0 \varSigma _c^+; 1/2^- \rangle \rightarrow ~J/\psi p~ : \quad \eta _c p\quad : ~\bar{D}^{*0} \varLambda _c^+~ \right) \over {\mathcal {B}}\left( |\bar{D}^0 \varSigma _c^+; 1/2^- \rangle \rightarrow J/\psi p\right) }\nonumber \\&\quad \approx \quad 1 \quad : \quad 0.5\sim 3.8~~ : ~~0.69t, \end{aligned}$$

(C.38)

$$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^{*0} \varSigma _c^+; 1/2^- \rangle \rightarrow ~~J/\psi p~~ : \,~~~~\eta _c p~~ : \,~\chi _{c0} p~\, : ~\bar{D}^{0} \varLambda _c^+~ : ~\bar{D}^{*0} \varLambda _c^+~ : ~\bar{D}^{0} \varSigma _c^+~ : ~\bar{D}^{-} \varSigma _c^{++}~ \right) \over {\mathcal {B}}\left( |\bar{D}^{*0} \varSigma _c^+; 1/2^- \rangle \rightarrow J/\psi p\right) \big |_{\theta ^\prime = 0}}\nonumber \\&\quad \approx \quad 1\sim 1.8 ~\, : ~0.1\sim 1.1~ : ~0.004~ : \,~~1.2t ~~\, : \,~~0.41t~~\, : ~~0.35t~~ : \,~~~0.70t, \end{aligned}$$

(C.39)

$$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^{*0} \varSigma _c^+; 3/2^- \rangle \rightarrow ~~J/\psi p~~ : ~~\eta _c p~~ : \,~\chi _{c1} p~\, : ~\bar{D}^{*0} \varLambda _c^+~ : ~\bar{D}^{0} \varSigma _c^+~ : ~\bar{D}^{-} \varSigma _c^{++}~ \right) \over {\mathcal {B}}\left( |\bar{D}^{*0} \varSigma _c^+; 3/2^- \rangle \rightarrow J/\psi p\right) }\nonumber \\&\quad \approx \quad 1 ~~ : ~0.005~ : ~10^{-4}~ : \,~~0.35t ~~\, : \,~10^{-4}t~\, : ~~~10^{-4}t . \end{aligned}$$

(C.40)

• We obtain the following relative branching ratios for the $\bar{D}^{(*)-} \varSigma _c^{++}$ hadronic molecular states:

$$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^- \varSigma _c^{++}; 1/2^- \rangle \rightarrow ~~J/\psi p~~ : \quad \eta _c p\quad : ~~~\bar{D}^{*0} \varLambda _c^+~ \right) \over {\mathcal {B}}\left( |\bar{D}^- \varSigma _c^{++}; 1/2^- \rangle \rightarrow J/\psi p\right) }\nonumber \\&\quad \approx \quad 1 \quad : \quad 0.5\sim 3.8~~ : ~~0.69t, \end{aligned}$$

(C.41)

$$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle \rightarrow ~~J/\psi p~~ : ~~\eta _c p~~ : \,~\chi _{c0} p~\, : ~\bar{D}^{0} \varLambda _c^+~ : ~\bar{D}^{*0} \varLambda _c^+~ : ~\bar{D}^{0} \varSigma _c^+~ : ~\bar{D}^{-} \varSigma _c^{++}~ \right) \over {\mathcal {B}}\left( |\bar{D}^{*-} \varSigma _c^{++}; 1/2^- \rangle \rightarrow J/\psi p\right) \big |_{\theta ^\prime = 0}}\nonumber \\&\quad \approx \quad 1\sim 1.8 ~\, : ~0.1\sim 1.1~ : ~0.004~ : \,~~1.2t ~~\, : \,~~0.41t~~\, : ~~0.35t~~ : ~~0, \end{aligned}$$

(C.42)

$$\begin{aligned}&{{\mathcal {B}}\left( |\bar{D}^{*-} \varSigma _c^{++}; 3/2^- \rangle \rightarrow ~~J/\psi p~~ : ~~\eta _c p~~ : \,~\chi _{c1} p~\, : ~\bar{D}^{*0} \varLambda _c^+~ : ~\bar{D}^{0} \varSigma _c^+~ : ~\bar{D}^{-} \varSigma _c^{++}~ \right) \over {\mathcal {B}} \left( |\bar{D}^{*-} \varSigma _c^{++}; 3/2^- \rangle \rightarrow J/\psi p\right) }\nonumber \\&\quad \approx \quad 1 ~~ : ~0.005~ : ~10^{-4}~ : \,~~0.35t ~~\, : \,~10^{-4}t~\, : ~~0. \end{aligned}$$

(C.43)